Abstract
The re-kindled fascination in machine learning (ML), observed over the last few decades, has also percolated into natural sciences and engineering. ML algorithms are now used in scientific computing, as well as in data-mining and processing. In this paper, we provide a review of the state-of-the-art in ML for computational science and engineering. We discuss ways of using ML to speed up or improve the quality of simulation techniques such as computational fluid dynamics, molecular dynamics, and structural analysis. We explore the ability of ML to produce computationally efficient surrogate models of physical applications that circumvent the need for the more expensive simulation techniques entirely. We also discuss how ML can be used to process large amounts of data, using as examples many different scientific fields, such as engineering, medicine, astronomy and computing. Finally, we review how ML has been used to create more realistic and responsive virtual reality applications.
1. Introduction
Over the last half-century, we have experienced unprecedented progress in scientific research and discoveries. With breakthroughs ranging from fundamental physics, such as particle physics [1,2], to engineering applications, such as in biomedicine [3,4], electronics [5,6], and materials science [7,8], this exponential technological evolution is undeniable.
Of paramount importance to these advances is the massive increase in computational power and capabilities. While theoretical physics lay down the foundations that govern our universe, these fundamental laws come in the form of partial differential equations that for all but the most trivial problems, cannot be solved analytically. The above necessitates the use of computer simulations that numerically solve these equations, thus resolving complex physical systems and help optimize engineering solutions. However, even computational modelling is currently falling short. The computational resources required by many modern physical problems–usually those involving phenomena at multiple length and time scales–are quickly becoming prohibitive.
Quantum Mechanics (QM) is the most fundamental theory to date. Quantum mechanical simulations such as Density Functional Theory (DFT) [9], are practically limited to a small number of atoms and is therefore not useful for most engineering problems. Instead, Molecular Dynamics (MD) simulations model atomic trajectories, updating the system in time using Newton’s second law of motion. MD is often used to study systems that usually have nano- to micrometer characteristic dimensions, such as micro- and nano-fluidics [10], or suspensions [11,12], as well as many chemical applications. Interactions between particles are dictated by semi-empirical models that are usually derived from QM data. These, however, tend to be accurate for specific, targeted properties and thermodynamic states (e.g., room temperature and atmospheric conditions), and do not necessarily generalize well to other properties and conditions. Furthermore, covalent bonds are often explicitly pre-defined and fixed. Thus, chemical reactions are not inherently captured by MD and specific models, such as Reactive Force-Fields [13], must be used for such tasks, which are often inaccurate and resource intensive. Finally, atomistic methods are still very computationally expensive, usually limited to a few hundred thousand particles. Larger systems that still require particle-based methods will require some hybrid, mesoscale or reduced model, at the expense of accuracy [14,15].
Many engineering problems are much more extensive than what can be described by QM or particle-based methods. Continuous-based physics, such as fluid dynamics, ignore the molecular structure of a system and consider averaged properties (e.g., density, pressure, velocity), as a function of time and space. This significantly reduces the computational cost. Simulation methods, such as computational fluid dynamics (CFD), segregate space using a grid. As the grid density increases, so does the accuracy, but at the expense of computational cost. Such techniques have been beneficial for industries ranging from aerospace and automotive, to biomedical. The challenges are both numerical and physical, and there are several reviews keyed towards specific industrial applications or areas of physics [16,17,18,19].
And despite great advances in the field, there are still unresolved problems. Perhaps the most critical example is turbulence, a flow regime characterized by velocity and pressure fluctuations, instabilities, and rotating fluid structures, called eddies, that appear at different scales, from vast, macroscopic distances, down to molecular lengths. An accurate description of the transient flow physics using CFD, would require an enormous number of grid points. Such an approach where the Navier–Stokes equations are directly applied is referred to as Direct Navier–Stokes (DNS) and is accompanied by an extraordinary computational overhead. As such, it is practically limited to specific problems and requires large High-Performance Computing (HPC) facilities and very long run-times. Reduced turbulent models are often used at the expense of accuracy. Moreover, while there are many such techniques, there is no universal model that works consistently across all turbulent flows.
So, while there are many computational methods for different problems, the computational barrier is often unavoidable. Recent efforts in numerical modelling frequently focus on how to speed up computations, a task that would benefit many major industries. A growing school of thought is to couple these numerical methods with data-driven algorithms to improve accuracy and performance. This is where machine learning (ML) becomes relevant.
At the onset of this discussion, we should provide some clarity about the perceived definition of ML. Specifically we use the definition by Mitchell et al. [20] by which “A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E”. Put simply, ML is a technology that allows computer systems to solve problems by learning from experience and examples, provided in the form of data. This contrasts with traditional programming methods that rely on coded, step-by-step instructions, which are set for solving a problem systematically.
ML-based algorithms can alleviate some of the computational burdens of simulations by partly replacing numerical methods with empiricism. Fortunately, the terabytes of computational and experimental data collected over the last few decades complement one of the main bottlenecks of ML algorithms: the requirement for extensive training datasets. With enough data, complex ML systems, such as Artificial Neural Networks (ANN), are capable of highly non-linear predictions.
ML can also assist in processing the terabytes of data produced by experiments and computations. Extracting meaningful properties of scientific value from such data is not always straightforward, and can sometimes be just as time-consuming as the computations or experiments producing them. Statistics, signal processing algorithms and sophisticated visualization techniques are often necessary for the task. Again, ML can be a useful tool, with a long-standing track record in pattern recognition, classification and regression problems.
Traditionally, ML is often associated with signal and image processing, with topics like self-driving vehicles, natural language processing, and optical character recognition coming to mind. Most industrial sectors are currently investing a significant amount of time and money into incorporating ML techniques into their practices for the betterment of their products and services. This increasing demand is also reflected in the massive rise of ML-related publications over the last few decades (Figure 1)
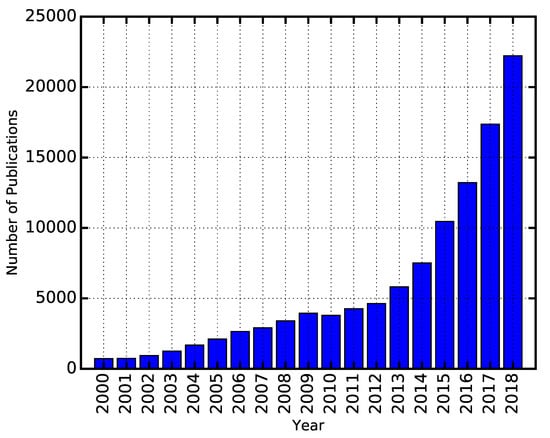
Figure 1.
Number of ML-related publications as since 2000. Data obtained from Web of Science (https://apps.webofknowledge.com/)
Still, we believe that the recent success of ML is a glimpse of a technology that is yet to be fully used. We envision that ML will help shed light upon complex, multi-scale, multi-physics, engineering problems and play a leading role in the continuation of today’s technological advancements. In this paper, we review some of the work that has applied ML algorithms for the advancement of applied sciences and engineering.
The paper is structured as follows (also, see Figure 2):
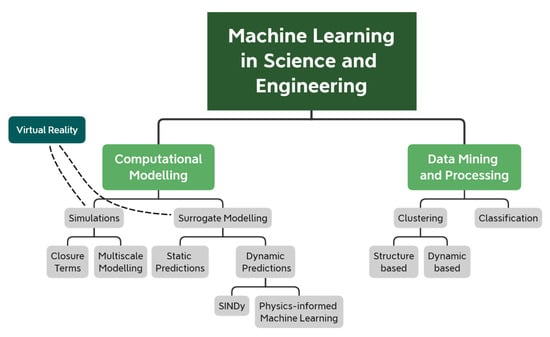
Figure 2.
Overview of ML in science and engineering.
- Section 2 reviews recent ML-based methods that speed up or improve the accuracy of computational models. We further break down computational modelling into computer simulations and surrogate models. Here, simulations refer to the computational models that explicitly solve a set of differential equations that govern some physical processes. Instead, surrogate models refer to (semi-) empirical models that replace and substantially simplify the governing equations, thus providing predictive capabilities at a fraction of the time.
- Section 3 reviews ML-based methods that have been used in science and engineering to process large and complex datasets and extract meaningful quantities.
- Section 5 summarizes the current efforts for ML in engineering and discusses future perspective endeavors.
Please note that ML is a broad and complex topic. The purpose of this study is not to detail the mathematical framework and specifics of every ML algorithm–a task better suited for a textbook–but to highlight some important and relevant areas and direct an interested reader for further investigation.
Furthermore, the number of relevant disciplines to ML is too large to address in a single article adequately. Our choice of scientific applications was not necessarily based on importance but was naturally driven by our research which is primarily in micro and nano flows, turbulence, multiphase flows, as well as in virtual environments.
2. Machine Learning for Computational Modelling
In this section, we review research that uses ML algorithms in scientific computing to achieve a better balance between computational cost an accuracy. We divide the section into two subcategories: simulations and surrogate modelling. The first regards the application of ML to improve or speed up simulation techniques (e.g., DFT, MD, and CFD), while the second refers to the use of ML to create reduced-order models that completely circumvent the need for the computationally expensive yet more physically accurate simulations.
2.1. Simulations
An important goal in computational modelling and simulations is to find a good balance between computational resources and accuracy. For example, in the absence of computational limits, QM-based simulations could be used to resolve complex, turbulent flows accurately; yet practically this is an inconceivable task. In this section, we present research that uses ML, aiming to improve the balance between accuracy and speed.
A good starting point is MD, a simulation technique that resolves the system down to the atomic scale. MD is based on Newtonian physics. Each atom is represented as a single point. Its electronic structure, the dynamics of which are described by QM, is ignored. The forces acting on the particles are calculated as the gradient (i.e., spatial derivative) of the potentials: semi-empirical functions of the atomic coordinates that are usually derived through regressions from QM-based data. Once the forces are calculated, the system can evolve in time by integrating Newton’s second law of motion. The computational complexity of MD scales with the number of atoms and is usually limited to systems comprising a few hundred thousand particles.
The semi-empirical potentials used in MD, however, are not always accurate. Depending on the data used for the extraction of these potentials, they might be tailored to specific situations, such as a specific range of thermodynamic states (e.g., specific temperature and pressure). For example, there are many potential functions available for the interaction of water molecules, each with its own strengths and weaknesses [21].
On the other hand, QM-based models resolve the system down to individual electrons, and as such can accurately calculate the inter- and intra-molecular forces and interactions. Such techniques, however, are even more computationally demanding than MD, as atoms consist of many electrons that are correlated with each other (i.e., quantum entanglement). Simulation methods such as DFT attempt to simplify such many-body systems while still providing a quantum mechanical resolution. Regardless of the relative efficiency of DFT, however, it is still exceptionally computationally expensive compared to larger-scale approaches.
To approximate the accuracy of QM-based methods, while retaining the computational advantage of MD, ML-based methods, trained on QM data, can be used to derive accurate force-fields that can then be used by MD simulations. ML algorithms, such as ANNs [22,23,24,25], or Gaussian processes (GP) [26,27], have been trained, using DFT simulations, to reconstruct more general and accurate Potential Energy Surfaces (PES). The gradient of these PES provides the interatomic forces used by MD simulations. Chmiela et al. [27] have used Kernel Ridge Regression (KRR) to calculate interatomic forces by taking as input the atomic coordinates. More recently, an ANN was trained to produce potentials that match the accuracy of the computationally demanding but accurate Coupled-Cluster approach, a numerical scheme that can provide exact solutions to the time-independent Schröedinger equation, exceeding the accuracy of DFT [28].
Yet these potentials usually have a constant functional form. As such, they do not always generalize well, and cannot accurately capture complex transitions such as chemical reactions and phase change. Hybrid models referred to as First Principle Molecular Dynamics (FPMD), use Newton’s laws to integrate the system in time (i.e., as in normal, classical MD), but use quantum mechanical simulations such as DFT to calculate the force-fields at each timestep. Variations of this approach attempt to limit the quantum mechanical calculations only to when and where necessary [29]. ML algorithms, such as GP [30] or KRR [31], can reduce the computational cost of such approaches. The general idea is that when a new state is encountered, the QM simulation will calculate the force-fields. The data, however, will also be used to train some ML algorithm, such that, if any similar states are encountered, the fast ML component will replace the computationally expensive QM simulation. Only when a new process is encountered are the computationally expensive QM simulations considered.
Such ML-based MD methods have successfully been used to simulate complex physical systems. ANNs have been used to simulate phase-change materials [32,33,34,35], make accurate predictions on the many phases of silicon [36] and describe the structural properties of amorphous silicon [37], as well as efficiently and accurately calculate infrared spectra of materials [38].
Clustering methods have also been used to evaluate the accuracy of classical MD force-fields for various tasks. Pérez et al. [39] used a combination of Principal Component Analysis (PCA) and K-means classification to evaluate and categorize different force-fields used for modelling carbohydrates in MD. The PCA reduced the dimensionality of the system from individual positions and energetics into a two-dimensional orthonormal basis. The above reduction resulted in a high-level map indicating similarities or differences between different force-fields. A hierarchical k-means clustering algorithm was used on the PCA data to formally categorize the force-fields. Raval et al. [40] used k-means clustering on data produced by MD simulations in order to assess the effectiveness of various classical force-fields in simulating the formation of specific proteins, i.e., for homology modelling, and propose alternatives that can mitigate the identified weaknesses.
For macroscopic fluid dynamics, on the other hand, the most common simulation technique is CFD. This method solves the fluid dynamics equations: the continuity equation, derived from the conservation of mass; the momentum equations, derived from the conservation of momentum; and the energy equation, derived from the conservation of energy. These equations ignore the molecular nature of fluids, and instead consider material properties as continuum functions of space and time. For a computer to solve these equations, they must first be discretized. This is achieved by mapping the physical domain into a grid, and the equations are solved, using numerical methods, on discrete points (e.g., grid points, cell centers). As you increase the density of grid points the accuracy of the solution will also increase, at the expense of computational resources.
In between the nanoscale (commonly treated with QM-based methods and MD) and macroscopic systems (usually treated with CFD or a similar continuous method), there are physical problems that lie in an intermediate scale. For example, microfluidic systems, systems with micrometer characteristic dimensions, are usually composed of a massive number of molecules (i.e., in liquid water there are ∼ molecules in a cubic micrometer). Classical MD is, practically speaking, not an option. On the other hand, such scales are often too small for continuum methods. Models such as CFD are often incapable of capturing the complex physics that emerge at solid-liquid interfaces, such as variations in the thermodynamic properties [41,42], or accounting for surface roughness [43,44,45].
Instead, hybrid models have been proposed, in which the computationally favorable continuum solver is predominantly used, while using a molecular solver for the under-resolved flow features. However, the MD simulations must run relatively frequently, sometimes at each macroscopic timestep, which significantly increases the computational requirements. Instead ANNs have been used to provide molecular-level information to a CFD solver, thus enabling a computationally efficient resolution of such scales [46,47]. As with the QM-based simulations described above, the MD solver is only used when it encounters relatively new states, i.e., states that are outside a pre-defined confidence interval from previously encountered states. As the simulation progresses and more states are encountered, the ANN is primarily used. The ANN-based hybrid model captures the flow physics very well. Furthermore, while the thermal noise, inherent in MD simulations, prevented the continuum solver from converging satisfactory, the NN-based hybrid model suppressed the thermal fluctuations resulting in lower residuals and better convergence of the solution (Figure 3).
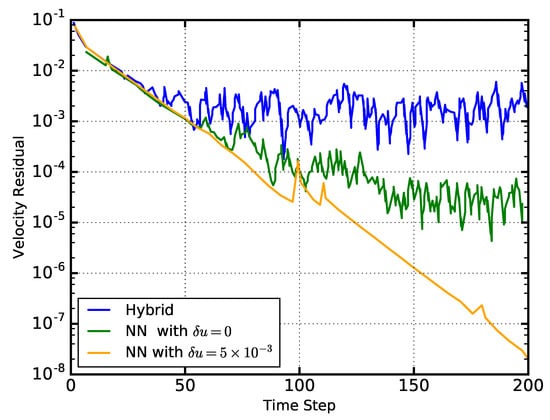
Figure 3.
Comparison of the velocity residuals of a Couette flow through a microchannel as a function of the simulation timesteps. The blue curve corresponds to a hybrid, molecular-continuum solver, where the molecular solver is used at each timestep (blue). The green curve corresponds to a hybrid solver, where a NN replaces the molecular solver, but learns and adjusts its weights from the MD solver at each timestep (i.e., a vanishing confidence interval ). The orange curve corresponds to the same NN-based hybrid solver, but with the weights of the NN being adjusted only when the input data, in this case the velocity u, is outside of a confidence interval with respect to previously encountered velocities. Increasing the confidence interval for re-training the NN decreases the residual which results in better convergence of the continuum solution. The figure is reconstructed from [47]
A long-standing, unresolved problem of fluid dynamics, is turbulence, a flow regime characterized by unpredictable, time-dependent velocity and pressure fluctuations [48,49,50,51]. As mentioned in the introduction, accurate resolution of all the turbulent scales requires an extremely fine grid, resulting in often prohibitive run-times. Instead, reduced turbulent models are often used at the expense of accuracy. A simplified approach is the Reynolds Averaged Navier–Stokes (RANS) equations that describe the time-averaged flow physics, and consider turbulent fluctuations as an additional stress term, the Reynolds stress, which encapsulates the velocity perturbations. This new term requires additional models to close the system of equations. While several such models are available, e.g., k-epsilon, k-, Spallart–Allmaras (SA), none of them is universal, meaning that different models are appropriate under different circumstances. Choosing the correct model, as well as appropriate parameters for the models (e.g., turbulence kinetic energy, and dissipation rate), is crucial for an accurate representation of the average behavior of the flow. Furthermore, this choice (particularly the choice of parameters) is often empirical, requiring a trial-and-error process to validate the model against experimental data.
ML has been used for turbulent modelling for the last two decades. Examples include the use of ANNs to predict the instantaneous velocity vector field in turbulent wake flows [52], or for turbulent channel flows [53,54]. The use of data-driven methods for fluid dynamics has increased significantly over the last few years, providing new modelling tools for complex turbulent flows [55].
A significant amount of effort is currently put into using ML algorithms to improve the accuracy of RANS models. GPs have been used to quantify and reduce uncertainties in RANS models [56]. Tracey et al. [57] used an ANN that takes flow properties as its input and reconstructs the SA closure equations. The authors study how different components of ML algorithms, such as the choice of the cost function and feature scaling affect its performance. Overall, these ML-based models performed well for a range of different cases such as a 2D flat plate and transonic flow around 3D wings. The conclusion was that ML can be a useful tool in turbulence modelling, particularly if the ANN is trained on high-fidelity data such as data from DNS or Large Eddy Simulation (LES) simulations. Similarly, Zhu et al. [58] trained an ANN with one hidden layer on flow data using the SA turbulence model to predict the flow around an airfoil.
Deep Neural Networks (DNNs) incorporating up to 12 hidden layers have also been used to make accurate predictions of the Reynolds stress anisotropy tensor [59,60]. The ML model preserved Galilean invariance, meaning that the choice of inertial frame of reference does not affect the predictions of the DNN. The authors of the paper further discuss the effect of more layers and nodes, indicating that more is not necessarily better. They also stressed the importance of cross-validation in providing credence to the ML model. Bayesian inference has been used to optimize the coefficients of RANS models [61,62], as well as to derive functions that quantify and reduce the gap between the model predictions and high-fidelity data, such as DNS data [63,64,65]. Similarly, a Bayesian Neural Network (BNN) has been used to improve the predictions of RANS models and to specify the uncertainty associated with the prediction [66]. Random forests have also been trained on high-fidelity data to quantify the error of RANS models based on mean flow features [67,68].
Another popular approach to turbulence is called Large Eddy Simulation (LES). LES resolves eddies of a particular length scale. Unresolved scales, i.e., those that are comparable or smaller than the cell size, are predicted through subgrid models. Several papers have successfully used ANN to replace these subgrid models [69,70]. Convolutional Neural Networks (CNNs) have also been used for the calculation of subgrid closure terms [71]. The model requires no a priori information, generalizes well to various types of flow, and produces results that compare well with current LES closure models. Similarly, Maulik et al. [72] used a DNN, taking as input vorticity and stream function stencils that predicts a dynamic, time and space-dependent closure term for the subgrid models.
A recent study successfully used ML algorithms that take very coarse CFD results of two-dimensional turbulent data, and reconstruct a very high-resolution flow field [73]. The coarse input data was obtained by using average or max pooling on the DNS data. The authors downsampled the data to different resolutions: medium, low, and very low. They reconstructed the data back to the DNS resolution, either using basic bicubic interpolation, CNNs, or a ML hybrid algorithm, called Downsampled Skip-Connection/Multi-Scale (DSC/MS), which, in a way, is a specific CNN architecture. For various two-dimensional cases, the reconstructed output accurately matched the original DNS data. The kinetic energy spectra calculated by the DSC/MS matched the results of the DNS (Figure 4) very well, at least within the resolution of the corresponding downsampled input, i.e., the data resulting from reconstructing the medium resolution input matched the DNS data for a larger range of wave numbers than that obtained from the low resolution input (c.f. grey and orange curved in Figure 4).
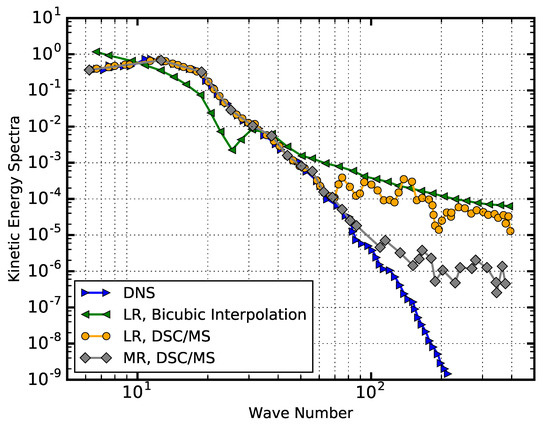
Figure 4.
Kinetic energy spectra as a function of the wave number. The data reconstructed from both the low resolution (LR) and medium resolution (ML) inputs, using the DSC/MS models, are in excellent agreement with the DNS results, within the spatial limits imposed by the downsampled input grid. This contrasts with the more conventional bicubic interpolation which does not come close to capturing the DNS data. Figure reconstructed from [73].
ML can also be used to predict closure terms in systems of equations in other multi-scale, multi-physics problems [74,75]. Ma et al. [76] have used ANNs to predict the behavior of multiphase, bubbly flows. The ANN consists of a single hidden layer with 10 neurons and uses data from DNS-based multiphase flows, to provide closure terms for a two-fluid model.
Another complex problem when studying the flow behavior of immiscible fluids is to describe the shape of the interface between them [75]. Qi et al. [77] used an ANN that takes the volume fractions of cells at the interface and predicts the curvature and shape. The ANN was subsequently incorporated in a multiphase, CFD solver that uses the volume of fluid technique for interface modelling.
A recent study provided a general overview of how ANNs can be used to provide closure models for partial differential equations [78]. The paper presents five different general ML frameworks, mostly consisting of various architectures and combinations of DNNs and CNNs, for the solution of thermo-fluid problems, including turbulent flows. The paper provides a useful roadmap of how to use ANNs to solve engineering problems, and outlines considerations that need to be made according to the nature of the physical problem. A frequent issue with ML algorithms is that they often perform poorly when used in physics that are significantly different from those provided for training. Studies have attempted to provide metrics that indicate a priori how well an ML model will generalize [79,80]. Wu et al. [80], for example, compare the Mahalanobis distance and a Kernel Density Estimation-based distance between points in feature space, to assess how the training data will generalize to other cases.
ANNs have also been used to speed up numerical methods. Feed-forward ANNs [81] and CNNs [82] have been used to accelerate the projection method, a time-consuming numerical scheme used for the solution of the incompressible, Euler equations.
Another application of NNs is for multi-scale modelling of materials. DNNs with two hidden layers have been used to predict the stresses applied on concrete, given the strain calculated by mesoscale simulations as input [83,84]. This information was then used in larger-scale, structure-level simulations. Subsequent studies used similar data-based multi-scale procedures to numerically investigate bone adaptation processes such as the accumulation of apparent fatigue damage of 3D trabecular bone architecture at a given bone site [85,86]. The predictions used ANNs with one hidden layer, trained using mesoscale simulations. The ANN takes stresses as inputs and output homogenized bone properties that the macroscale model takes as input. Sha and Edwards [87] give a brief overview of considerations that need to be taken to create accurate NN-based multiphase models for materials science.
Another severe bottleneck of computational physics and engineering is storage. High-fidelity simulations often require a considerable number of grid cells (or several particles in particle-based methods). Compressing this data before storage has been studied for many years now [88,89,90]. Furthermore, there is an increased interest in high-order methods (spectral methods, MUSCL and WENO schemes) in which even individual cells are characterized by a large number of degrees of freedom. Finally, when simulating transient physics, data on these grid points must be stored at finely spaced increments of time. Reconstructing the time-dependence of the physics requires storing a sequence of datasets, containing the high-order data of meshes with many cells. As such, common industrial problems such as high-speed flows around complex geometries, often require storing petabytes of data.
Carlberg et al. [91] tackle this problem very well by proposing a compression of the spatial data, followed by a compression of the time-sequence. The above study examines high-order methods, specifically the Discontinuous Galerkin (DG) method that represents the solution at each cell as a linear combination of a potentially large number of basis functions. The spatial data is compressed in two stages: the first stage uses an autoencoder to reduce the degrees of freedom within each cell from 320 to 24. The second stage uses PCA to reduce the dimensionality of the encoded vectors across all the cells in the mesh, a reduction from degrees of freedom to only 500. The compressed data is then stored for sparsely separated timesteps. Finally, regression is used on the compressed data that allows the reconstruction of data at any timestep. The authors used several regression algorithms, with the Support Vector Machines (SVM) (with a radial basis kernel function) and the vectoral kernel orthogonal greedy algorithm performing the best.
2.2. Surrogate Modelling
Many engineering applications need to make real-time predictions, whether for safety-critical reasons, such as in nuclear powerplants and aircraft, or simply practical reasons, such as testing many variants of some engineering design. While Section 2.1 discussed ways in which ML can speed up conventional simulation techniques, the associated timescales are still many orders of magnitude greater than the requirements of such applications. Here we discuss ways in which ML can be used to make direct physical predictions, rather than assist numerical simulations of a physical experiment.
In its most basic form, ML algorithms can be trained to make static predictions. Given a set of data, the ML component can calculate instantaneous information that is either inaccessible through experiment or is too time-consuming to calculate through conventional simulation methods. In this sense, the ML algorithm can be viewed as a generic, black-box, purely data-driven component.
ML is often used to directly solve QM-based problems [92], such as the calculation of the ground state of a molecular system, a task that otherwise requires the computationally expensive solution of the Schrodinger’s equation. Rupp et al. [93] predicted the ground state using non-linear ridge regression that takes as its input nuclear charges and atomic positions. The authors investigated the effect of the size of the training set on the accuracy of the predictions and found that as it ranged from 500 to 7000 molecules, a significant drop in the mean absolute error was observed. The trained model can make predictions on new organic molecules at practically no computational cost, with an error of less than 10 kcal/mol, an accuracy that surpasses most semi-empirical quantum chemistry-based methods. Subsequently, Hansen et al. [94] assessed the performance and usage of different ML algorithms for the same task, i.e., the calculation of the ground energy. They considered linear ridge regression, non-linear ridge regression using a Laplacian or Gaussian kernel, Support Vector Machines (SVM), k-nearest neighbor, and fully connected, feed-forward, multilayered neural networks. They found that linear regression and k-nearest neighbor algorithms were inadequate for the task. Instead, kernel-based methods and the ANN yielded errors of less than 3 kcal/mol, a significant improvement to the results presented by Rupp et al. [93]. More recently, a paper proposed a novel method for calculating the ground state and evolution of highly entangled, many-body, QM problems using ANNs [95]. The ANN uses a Restricted Boltzmann Machine (RBM) architecture. In general, RBMs includes two layers: the first acts as the input to the network and is usually referred to as the visible layer, while the second is called the hidden layer. The network outputs the probability of occurrence of the input configuration in the visible layer, which in the present paper represented the configuration of N spins. The RBM therefore acts as the wavefunction of the system.
Handley and Popelier [96] used a feed-forward ANN with one hidden layer, trained on QM-based data, to calculate the multipole moments of a water molecule, based on the relative coordinates of its neighbors. Hautier et al. [97] used Bayesian inference with a Dirichlet prior to identify new compounds and structures. The method generates a shortlist of possible compounds, the stability of which was then verified through DFT simulations. The model was trained on a database with experimental data on various crystal structures and, as a proof-of-concept, it was subsequently used to discover 209 new ternary oxides.
Another area that demonstrates the predictive capability of ML is in applications involving multiphase flows, such as the Oil and Gas industry, where information on the composition and behavior of multiphase fluids is necessary. Yet, measurement might be impossible, and numerical simulations are costly. An example is acquiring information regarding the multiphase-flow regime inside a pipeline. The multiphase-flow regime refers to how different immiscible fluids co-exist within a mixture. Gas can form small bubbles within a liquid or larger structures–sometimes referred to as slugs–, or can even form two parallel streams, with a flat (flat-stratified) or wavy (wavy-stratified) interface. Different types of the multiphase regime can result in significantly different flow fields and pressure losses.
Several studies used ANNs to predict the phase configuration and volume fractions of multiphase flows using different types of data such as from dual-energy gamma densitometers [98], differential pressure measurements [99,100], flow impedance [101], and bubble chord lengths taken at various points in a pipe [102,103]. ANNs have also been used to calculate the regime, phase velocity, and pressure drop in various geometries [104].
ML has been used for flow control. Just over two decades ago, Lee et al. [105] used NNs to create a drag-reduction protocol for aircraft. A blowing and suction mechanism at the wing was employed, actuated by the ML component that takes as its input shear stresses in the spanwise direction on the wall. A more recent study used an ANN to reduce the drag around a cylindrical body, by adjusting the mass flow rates of two jets, depending on velocity readings in the vicinity of the cylinder [106].
ML has also been used in material characterization. NNs have been used in solid mechanics for almost three decades now, in an attempt to understand the stress-strain relationship of materials [107,108]. A good example where ML and NNs have been used is for the investigation of concrete, a material whose properties depend significantly on the proportions of its various constituents. Yeh [109] used experimental data to train a NN with one hidden layer to accurately predict the compressive strength of high-performance concrete, taking as its input the amounts of the various ingredients used for its production. Other studies use NNs that accept a strain tensor as their input, and predict the stress applied on the material [83,84,107,108,109,110]. Waszczyszyn and Ziemiański [110], for example, used several different NN architectures and evaluated their efficacy in several physical problems, such as calculating vibrational properties of buildings, and damage detection in beams. ANNs have also been used in structural dynamics [111,112]
Another good example of material characterization is nanofluids: fluids that contain solid particles of nanometer-sized characteristic dimensions. Properties of nanofluids, such as thermal conductivity and viscosity, are complex functions of many different parameters, including temperature, particle size, and particle aggregation. Expensive experiments [113,114,115] and time-costly simulations [116,117,118,119,120] have attempted to delineate this complex behavior with little success.
Instead, over the last decade, NNs have been used for the prediction of nanofluid properties. These NNs take a subset of system parameters (e.g., particle volume fraction and the thermal conductivity of the base fluid and particles) as inputs and output one or more nanofluid properties. Papari et al. [121] have used a NN with one hidden layer to predict the thermal conductivity enhancement of the nanofluid, i.e., the ratio of the thermal conductivities of the nanofluid and base fluid. The 2-dimensional input vector consists of the thermal conductivity of the base fluid and the particle volume fraction. The authors trained and tested the model on various nanofluids consisting of carbon nanotubes suspended in different liquids. Other studies used similar models, extending, however, the feature vector to include the temperature [122,123,124], and average particle cluster size (to account for aggregation) [123]. Ariana et al. [125] used an ANN with one hidden layer that takes the temperature, volume fraction and particle diameter as input and predicts the thermal conductivity. The authors studied the effect of the number of neurons in the calculation of the thermal conductivity of nanofluids. They concluded that 14 neurons provided optimal results. DNNs with two hidden layers have also been considered for the calculation of the thermal conductivity [126,127,128,129,130,131] and viscosity [131]. An ANN with a single hidden layer and 12 neurons has also been used to calculate the thermal conductivity of hybrid nanofluids, with different types of particles [132].
Fault detection and system health management is another area where ML has been used [133]. ANNs can be employed to identify damage on the aerodynamic surfaces [134] and sensors [135,136,137] on the aircraft flight control system. More advanced RNNs with Long Short-Term Memory (LSTM) have been used for real-time anomaly detection on the aircraft [138].
ANNs have also been used to optimize the design of structures, such as that of a yacht [139], a task which usually requires several time-consuming CFD simulations. Esau [140] used NNs to calculate fluid-structure interactions, even when the surface morphology is not well resolved.
While the static predictions described thus far are often very useful, other applications require predicting how a system will evolve at later time. Designing ML algorithms for such dynamical behavior is tantamount to unsteady simulations and is a highly active topic of research.
ANNs have been used to study transient physics. The most basic form involves providing the ANN with the values of a variable at consecutive times. In turn, it attempts to output the value of the variable for some future point. Equivalently the ANN can output the time-derivatives of the data, which can be integrated in time to yield the future state. The data in the time-series is quite often compressed using some-dimensionality reduction algorithm. This approach has been used successfully to predict the behavior of various physical systems such as the dampened harmonic oscillators [141], and the 2D Navier–Stokes [142,143].
The above approach can also model chaotic, unstable systems. Nakajima et al. [144] used simple ANNs to study fluidized beds, a complex mixture of fluid and solid particles, and have even managed to identify bifurcating patterns [145], indicative of instabilities. The predictive capability of these methods, however, is usually limited to only a short time interval past that of the training set.
For predictions over a longer period of time, ANNs can re-direct their output and append it to the time-series corresponding to its input, and use it for the calculation of data at successively longer periods. However, chaotic systems are susceptible to initial and boundary conditions. Therefore, an accurate long-term prediction requires careful selection and pre-processing of the features [146]; otherwise, the error for highly chaotic systems increases with continuously longer times [147,148]. More recently, regression forests [149], as well LSTM [150] have been used for transient flow physics.
A recent breakthrough in dynamic prediction is called Sparse Identification of Non-linear Dynamics (SINDy) [151]. SINDy reconstructs governing equations, based on data measured across different times. In general, the user empirically selects several possible non-linear functions for the input features. Using sparse regression, SINDy then selects the functions that are relevant to the input data, thus recreating an attractor corresponding to the physical problem. The reconstructed equations can then be used without the need for ML, and can theoretically make predictions outside the scope represented by the training data.
Lui and Wolf [152] used a methodology similar to SINDy, the main difference being that DNNs were used to identify the non-linear functions describing the problem, rather than manually and empirically selecting them. The authors tested their method successfully on non-linear oscillators, as well as compressible flows around a cylinder.
SINDy sounds like the optimal solution to dynamic prediction, as it extracts a relatively global function that is not necessarily restricted to the confines of the training data. Pan and Duraisamy [153], however, identified that while SINDy is near perfect for systems described by polynomial functions, its performance drops significantly when considering nonpolynomial systems. The authors showcased this for the case of a nonrational, nonpolynomial oscillator. They attributed the behavior to the complexity of the dynamic behavior of the system that cannot be decomposed into a sparse number of functions. The paper concluded that for such general cases, the fundamental ANN-based way of dynamic modelling is more appropriate.
Efforts are also directed into incorporating our theoretical knowledge of physics into the ML algorithms, rather than using them as trained, black-box tools. Bayesian inference has long been linked to numerical analysis (i.e., Bayesian numerical analysis), and has recently been used for numerical homogenization [154], i.e., finding solutions to partial differential equations. Subsequent studies have used GP regression that, given the solution of a physical problem, it can discover the underlying linear [155,156] and non-linear [157] differential equations, such as the Navier–Stokes and Schröedinger equations. Alternatively, similar GP-based methods can infer solutions, given the governing differential equations as well as (potentially noisy) initial conditions [158]. A particularly attractive feature of GPs is that they enable accurate predictions with a small amount of data.
While GPs generally allow the injection of knowledge through the covariance operators, creating physics-informed ANNs feels like a more challenging task considering the inherent black-box-nature of traditional ANNs. ANNs can be used for automatic differentiation [159], enabling the calculation of derivatives of a broad range of functions.
Automatic differentiation has been used over the last few years to solve supervised learning problems using ANNs that respect the laws of physics, given as partial differential equations [160,161,162]. An excellent example of the potential use of such an approach is given by Raissi et al. [163]. The paper solves the inverse problem of calculating the lift of a bluff body, given sparse data of the flow field, a difficult task using conventional numerical schemes. The algorithm is based on two coupled DNNs (Figure 5): the first is a traditional black-box ANN that takes flow input parameters, such as time, and coordinates, and outputs details of the flow, such as the velocity components, pressure, and the displacement of the solid body. Sigmoid activation functions were used for the neurons of this ANN. The output of the first network is then linked onto the physics-informed network that generates the equations, where derivatives are used as activation functions. The cost function of the entire NN is the sum of the two cost functions of each NN.
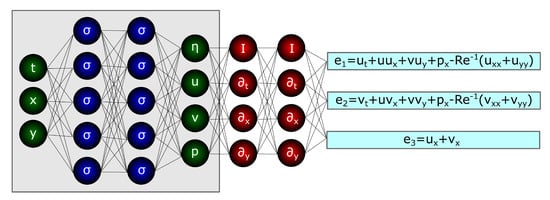
Figure 5.
Schematic representation of a Physics-informed NN. Reproduced from [163].
A recent approach to solving differential equations is the Deep Galerkin Method (DGM) [164]. The conventional Galerkin method reconstructs solutions to partial differential equations as a linear superposition of various basis functions. DGM instead forms more complicated combinations of these basis functions using a DNN.
CNNs have also been used for data-driven approaches that are constrained by the laws of physics [165]. This method carefully embeds the differential equations into the cost function. Thus, it can inherently calculate the error, without requiring provision of the pre-calculated solution for training. The accuracy of the model was comparable to fully connected DNNs, while significantly reducing the required time.
3. Machine Learning in Data-Mining and Processing
In this section, we review research and efforts dedicated in using ML for processing and understanding large datasets produced by computer simulations or experiments, thus providing insight into the respective field.
Biology has long used ML algorithms to process and analyze the large datasets associated with the field, with several relevant textbooks available [166]. Data-driven approaches are used mainly to identify the formation of molecular structures characterized by specific chemical properties. An essential example of the formation of molecular structures is protein folding, i.e., the process that gives rise to proteins.
Clustering methods are particularly useful in identifying such conformational states. The ability of the K-means and average-linkage clustering algorithms to identify and better understand conformational states during MD simulations of biomolecular processes was investigated [167]. The classification was performed on the raw MD data, as well as on PCA-produced subspaces of various dimensions. The paper concluded that k-means clustering performed well, while the average-linkage algorithm produced inconsistent clusters when used on the raw data and PCA-based subspaces. A similar investigation used a combination of hierarchical clustering, PCA and k-means clustering on a transcriptome dataset, obtained through RNA sequencing, to identify molecular signatures of quiescent stem cells found in mammalian brains, and identify transitions between states [168]. Decherchi et al. [169] used k-medoids, a clustering method similar to k-means, to identify ligand binding events in several long MD simulations. The number of medoids was chosen automatically, based on the elbow method. The authors further used Regularized Least Squares with a Gaussian kernel to estimate the free energy.
Most clustering methods discussed above are referred to as structure-based methods, where the time-dependent data produced from MD simulations (or experiments) is treated as one large data set, or as a sequence of independent data through which the clustering is refined. Other studies have used clustering methods more conducive to dynamic data [170]. Such methods are referred to as dynamic-based clustering methods, and consider the simulation data in a more natural, time-dependent manner (e.g., by considering the timesteps as steps along a Markov chain). Dynamic-based clustering attempts to partition the dynamic data into meta-stable states: states that persist for long periods. While the results from structure- and dynamics-based methods are often similar, they also frequently result in major differences [171]. Noé et al. [172] used the Perron Cluster Cluster Analysis (PCCA) method to study the effect of metastability on the folding dynamics of proteins. More robust variants of PCCA have also been derived [173] which were subsequently used for clustering gene expression data with application in breast cancer research [174].
While ANNs have been used in biology for many years [175], such techniques have become more prominent over the last decade [176,177]. The above is particularly true for protein-DNA binding, a process which biophysical models seem to fall short [178] currently. Fully connected ANNs with many inputs, corresponding to genetic features, have been used to predict RNA splicing, thus evaluating the effect of different genetic variants [179]. CNNs have also been used to predict protein-binding, outperforming previous equivalent models [180]. Zeng et al. [181] investigated the effect of various CNN architectures on their predictive capability on DNA–protein binding. While the paper goes into detail regarding various possible CNN considerations, the overall conclusion is that a larger number of filters will result in learning more productive sequence features. Other CNN-based architectures have been used in genetics, such as in classifying DNA sequences [182] and identify the function of noncoding genomic variations [183].
ML has also been used for Computer-Aided Detection (CAD), i.e., computer solutions that assist diagnostic medicine. An important example of the application of ML for CAD is in lung cancer detection, one of the leading causes of death worldwide. While lung cancer can effectively be treated and even cured if detected early, it can often be left undiagnosed, even by experienced medical professionals, until it reaches more advanced stages. Given appropriate data, e.g., provided in the form of scanned images, ML algorithms can help with cancer detection in two respects: (i) first, they can identify the diseased region, a process called segmentation; (ii) they can classify cancers (benign, aggressive etc.). Krishnaiah et al. [184] discuss the potential use of different classifiers for the early detection of lung cancer. The paper considered Naive Bayesian classifiers, association rules (if-then rules), decision trees, and NNs. Subsequent studies used feed-forward NNs to detect lung cancer from Computerized Tomography (CT) scans [185]. The authors initially applied segmentation in the form of thresholding and morphological operations to identify the lungs. Statistical parameters were then calculated based on the pixel intensities of the segmented images. The parameters used were the mean, standard deviation, skewness, kurtosis, and fifth and sixth central moments. These compiled the feature vector used as input to the ANN, which in turn classified the case as cancerous or not. D’Cruz et al. [186] have used a combination of NNs and genetic algorithms to organize data, provided in the form of X-Rays, CT scans, MRIs etc. Following feature extraction on the raw data, a fully connected, feed-forward NN was used to classify the image into normal or abnormal. If an instance were classified as abnormal, the genetic algorithm would further classify it into cancerous and non-cancerous.
More complicated NNs, such as DNNs, CNNs and Autoencoders have also been used for CAD. Autoencoders have been used to extract features from lung nodules found on CT scans that can then be used to classify the nodules as malignant or benign [187]. Song et al. [188] compared the effectiveness of DNNs, CNNs and Autoencoders in classifying lung nodules from CT scans into benign and malignant. The paper concluded that CNNs outperform the other two methods. A similar CNN architecture, e.g., three convolutional and two pooling layers, has also been used to classify lung tumors into adenocarcinoma, squamous cell carcinoma, and small cell carcinoma [189]. Another study [190] defined a protocol that takes as its input a CT scan, segments it using thresholding to identify the lung region, and classifies the detected nodules. The authors claim that directly using a CNN on the thresholded data is insufficient and results in many false positives. Instead, they first used a U-net architecture, a specific CNN architecture that can increase the resolution of the input data through upsampling layers rather than reducing it through pooling layers. The U-net identified potential nodules in the lungs that were then classified into cancerous or non-cancerous by a conventional 3D CNN architecture. Subsequent studies considered several CAD pipelines that include CNN architectures, achieving quite a high level of accuracy [191,192,193]. A recent deep learning algorithm for lung cancer detection combined CNNs into an autoencoder [194]. A 3D CNN, acting as the encoder, reduces a CT scan into a representation, which is then decoded by another CNN. At the same time, the generated representation was also fed to a fully connected NN to be classified as cancerous or benign. Please note that a single cost function, including both the loss from the autoencoder as well as the classification loss, was used for training.
ML has similarly been used for other types of cancer, such as breast cancer [195,196,197,198,199] and prostate cancer [200,201,202,203]. It has also been used for other diseases such as Alzheimer’s [204,205,206,207] and Parkinson’s [208,209,210,211] disease.
The increasing use of microfluidics in biomedical applications is also now being complemented with data-driven approaches to analyze the produced data [212,213]. Berg et al. [214] designed a hand-held device attached to a smartphone that incorporates a 96-well plate for enzyme-linked immunosorbent assay, the gold standard for modern medical diagnostic tests. The camera of the phone reads the test results, subsequently transmitting them to servers that generate diagnostic results through ML algorithms, specifically adaptive boosting (i.e., AdaBoost).
The anti-malware industry is now using ML to better shield computer systems from software threats (viruses, adware, spyware, etc.). One way of identifying and categorizing malicious software is to run it in some controlled environment (aka a sandbox) and analyze its behavior during runtime. In turn, clustering can be used to identify new classes of malware [215,216], while classification can be used to identify a piece of software as belonging to a specific malware class [217]. A combination of both clustering and classification seems to provide even better results [218].
An alternative to dynamic analysis for malware detection is to take the object code (binary) of the malware executable, reshape it into a 2D array and present it as a greyscale image. The idea is that malware with similar features should also produce images with similar patterns, and can thus be classified using image processing methods such as K-Nearest Neighbors (KNN) [219]. Studies used PCA on the greyscale images, and classified the reduced data using ANNs, KNNs and SVMs, with KNNs outperforming the other methods [220]
Another field in which ML has been used significantly is astronomy [221,222,223], where advanced telescopes provide an abundance of imaging data that needs to be processed [224,225]. While ML methods such as ANN have been used for almost 30 years [226], more recent works focus on CNNs, due to their ability to process and analyze images in a relatively computationally efficient way. CNNs have been used to understand the morphology of galaxies [227,228,229], predict photometric redshifts [230,231], detect galaxy clusters [232], identify gravitational lenses [233,234,235,236] and reconstruction of images [237]
Video classification is yet another field that keeps improving along with advances in ML. Karpathy et al. [238] have used CNNs to classify sports-related videos found on YouTube into their corresponding sports. They considered various architectures to effectively embed the time frames of the video into the CNN, as well as improving the computational cost required for training the network. Subsequent studies suggested several different CNN- and RNN-based architectures for video classification [239,240,241,242,243,244]
Knowledge distillation refers to an approach wherein a complex ML algorithm, commonly called the teacher, is trained on a large set of data and is subsequently used to train simpler ML models, referred to as the students, at a lower computational cost. Bhardwaj et al. [245] used knowledge distillation to classify videos efficiently. The teacher was trained using every time frame of each video. The student instead considered only a small subset of time frames. The student’s cost function attempted to minimize the mismatch between the results of the teacher and student. Different CNN and RNN architectures were considered for the teacher and student.
Another active research topic involving ML is predicting a human’s future behavior. ML algorithms (mostly involving CNNs or RNNs) might consider human interactions [246,247,248,249,250], the context of a person (i.e., location and surroundings) [251,252,253], and characteristics of the person (e.g., facial expressions) [254], to predict the future path in which the person will follow. More recently, a study used LSTM and managed to predict not only the future path of the person but also her future activity [255].
4. Machine Learning and Virtual Environments
Data-driven features, automation and machine learning form a new framework for improving the decision-making process in several disciplines (i.e., manufacturing, medicine, e-commerce and defense among others) [256,257,258,259]. To this end, ML is enabling data visualization and simulation of complex systems in an immersive manner with the use of emerging technologies such as virtual reality (VR) and Augmented Reality (AR), as well as virtual and digital prototypes, environments, and models [260]. The immersive and interactive visualization of data through VR and AR can increase productivity, reduce development costs and provide a means of testing various systems in a computer-generated environment [258,259,261].
In the automotive engineering research sector, VR applications, such as VR driving simulators, require the realistic interaction between the user and agent vehicles (i.e., computer-controlled), also known as Non-Player Characters (NPCs) that recreate seamless traffic flow conditions and accident scenarios [262]. A large number of VR driving simulators use ML algorithms to train the NPC vehicles and VR infrastructure (i.e., road network and wireless communications) in order to interact and respond to vehicular or driver simulations and evaluations in a realistic manner [262,263,264].
Charissis and Papanastasiou [265] have developed a series of VR driving simulators which use ML to train the agent vehicles for optimal operation of traffic flow, and for recreation of accident scenarios based on real-life information provided by the relevant traffic monitoring and police authorities. The simulation scenarios recreated with the use of ML-trained agent vehicles were varying from a rear collision due to low visibility weather conditions scenario [261,262] to the rear and side collisions due to driver distraction by in-vehicle infotainment systems [266,267]. The ML component further enriches the simulations to use Vehicular Ad-Hoc Networks systems (VANETs). These were simulated using an NS-3 network simulator and were embedded in the VR driving environment to more realistically portray existing network communication patterns and issues [265,266]. The driving simulator is further trained, improved and enhanced with additional scenarios and systems to produce realistic VR simulations, suitable for evaluating complex Human-Machine Interfaces (HMI) that include gesture recognition and AR [261,267]. The use of ML for biomechanical gesture recognition in VR applications is explored also by Feng and Fei [268], who combined information fusion theory and ML to effectively train a gesture recognition system which entailed ten different gestures. The proposed system aimed to resolve recognition and positioning issues, caused by traditional gesture segmentations.
The requirement for realistic responses from agents further sparked the development of an Intelligent Tutoring System (ITS), which employed ML to train a VR driving simulator [263]. The ML training of the NPC agents is of major importance as it enables a more natural behavior, something that is essential for realistic interaction with the neighboring agent vehicles in various driving simulation scenarios [269]. Lim et al. [270] discuss the rationale for the development of adaptive, affective and autonomous NPCs, where the agents strive towards the achievement of short term goals and adapting relative to user’s choices and responses [270]. Notably, the affective and autonomous agents operating within a VR simulated environment could significantly enhance the simulation immersion [262,263,271].
Yet the relation between VR and ML can also be inverted: the VR can produce realistic data used for training an ML component. Vazquez et al. [272] describe the development and use of virtual environments that could automatically provide precise and rich annotations, in order to train pedestrian detection systems for vehicular applications. The rationale for using virtual environments for ML is the fact that a typical annotation process relies on learnt classifiers that require human attention which is both an intensive and a subjective task. For this reason, collecting training annotations could be replaced from the typical avenues of camera and sensor-based to realistic virtual environments that replicate faithfully the required visual information for the annotations.
Extending the synergy between VR and ML in multidisciplinary applications, Vazquez et al. [273] present a VR-based deep learning (DL) development environment which enables the users to deploy a DL model for image classification [274,275]. This system offers a VR immersive environment in which the user can manually select and train the system. Although the particular system is aiming to support biomedical professionals, the system could be adopted by other disciplines with the introduction of other image sequences required for different classification models [273].
Digital Twins is the use of VR to create digital replicas of engineering systems, equipment, or complete facilities, such as oil-rig installations, enabling the efficient monitoring, evaluation of such systems, as well as identifying potential sources of malfunction [276,277]. Recently, ML has been used with twin technologies. The virtual representation of identical real-life systems (i.e., oil-rig installations) and the incorporation of ML in such models for simulation and monitoring purposes is presented by Madni et al. [278]. In this study, the digital twin systems are categorized into 4 distinctive levels namely the Pre-Digital Twin, Digital Twin, Adaptive Digital Twin and Intelligent Digital Twin, with the latter presenting the most advanced form. The last two levels incorporate ML, yet only the Intelligent Digital Twin incorporates both supervised ML (i.e., operator’s preferences) and unsupervised ML to distinguish various patterns and structures/items appearing in different operational situations. The digital twin modelling and simulation approach is also explored by Jaensch et al. [279], where they present a digital twin platform that incorporates both model-based and data-driven methods. Their approach resolves typical manufacturing and operational issues in a timely and cost-efficiently manner, in contrast to standard methods.
A different way in which ML can improve VR is in networking. It is becoming increasingly important that VR applications are operated over wireless networks. This presents fresh opportunities for collaborative VR environments and immersive experiences access by remotely located users. Such activities could enable the monitoring and maintenance of systems remotely (i.e., digital twin systems), through immersive wireless VR environments. The transmission of VR data through wireless networks, however, could be hindered by poor network performance resulting in poor Quality-of-Service (QoS) [280]. Notably, this occurs in different types of networks due to the volume of data required for VR applications. In this case, Chen et al. [280], propose a novel solution based on ML framework of Echo State Networks (ESNs) in order to mitigate and reduce this issue specifically for Small Cell Networks (SCNs). Further research aiming to minimize such issues by Chen et al. [281] present a data correlation-aware resource management for wireless VR applications. The latter enables multiple users to operate in VR environments simultaneously. As is expected, the spatial data requested or transmitted by the users can exhibit correlations, as VR environment users probably operate in the same VR spaces, differentiating only in orientation or activities within the VR environments. As such, the proposed system uses a machine-learning algorithm that employs ESN with transfer learning. The latter ESN algorithm can rapidly manage the wireless network changes and limitations, offering a better distribution of VR data to the users. In a similar manner, the acquisition, cashing and transmission of 360 degrees VR content from Unmanned Aerial Vehicles (UAVs) to the different users are explored [282]. The paper proposes a solution based on a distributed DL algorithm which entails a novel approach that uses ESNs and Liquid State Machine (LSM). The wireless VR communication and provision of acceptable QoS is also investigated by Alkhateeb et al. [283], who aim to reduce typical transmission issues occurred by Millimeter Wave (mmWave) communication systems and Base Stations (BS). The paper presents a method that defines the user’s signature entailing user’s location and type of interaction. The proposed solution uses a DL model that is trained to predict the user’s requirements and consequently predict the beamforming vectors that provide improved QoS.
As the aforementioned combinations of emerging technologies and ML are becoming the overarching systems between engineering and other disciplines it is evident that in the near future they will be adopted by other sciences and industries requiring timely, adaptable and accessible information for complex systems.
5. Discussion and Conclusions
The previous sections reviewed efforts that use ML in scientific computing and data-mining. This section briefly summarizes the cited literature and attempts to identify fruitful directions for the future of ML in engineering.
In scientific computing, ML can be used to aid pre-existing computational models by having a data-driven component augment some of the model’s features. For example, an ML algorithm can replace closure terms within the computational model or replace a computationally expensive, higher-resolution method during multi-scale modelling.
Currently, most ML algorithms used to enhance computer simulations seem to be using supervised learning. The ML component is usually trained on high-fidelity, pre-existing data so that it can make accurate predictions in the future. As always, general ML procedures and considerations are still necessary. In the case of supervised learning, this includes: (a) split the available data into training and test sets to measure the generalization error, and potentially a cross-validation set for testing ML algorithms and hyperparameters, are required; (b) use learning curves or other methods to identify under- or over-fitting; (c) test different ML algorithms and architectures on a cross-validation set; and (d) select the most optimal set-up; try different features; etc. The choice of algorithm (e.g., ANN, GP, SVM) depends on the availability of training data and size of the feature vector. Such applications of ML have so far produced some impressive results, and we expect to see a significant increase in such works in the upcoming years.
In terms of scientific computing, ML can also be used for surrogate modelling, i.e., rather than aiding a currently existing technique, it can completely replace it with a simplified, computationally favorable model. Surrogate models can go beyond static predictions and can be used to predict the evolution of a system in time, an ongoing effort which is currently receiving much attention. Intuitively, RNNs seem particularly suited for dynamic models. Although currently underused—presumably due to the complexity associated with their training—we expect they will play a more significant role in the upcoming years.
Physics-informed ML models will be vital in advancing the application of ML in scientific computing. Approaches such as SINDy, and automatic differentiation and physics-informed NNs provide us with a robust framework to make predictions bounded by the physical laws. The use of non-parametric algorithms, such as GPs, can potentially be an even more useful tool. The inherent ability to inject information through the covariance matrix renders them ideal for physics-informed ML. Furthermore, the mathematical elegance of these methods, as well as their ability to provide statistical information (rather than just the maximum likelihood estimate), makes them particularly attractive. Finally, as demonstrated by Raissi and Karniadakis [157], it can model general partial differential equations using “small-data”, a more tractable task for many applications.
ML is also very useful in data-mining and processing. Branches such as biomedicine have capitalized on these technologies, using more intelligent algorithms to shed light on the vast and complex data that such disciplines require. We do, however, believe that other branches can also benefit significantly from employing such strategies. Examples include transitional and turbulent flows, where massive, DNS simulations uncover temporary structures that can be too complex to appreciate through visual inspection or traditional techniques. ML algorithms can be used to classify such structures and identify correlations. The same applies to microscopic simulations (e.g., DFT, MD), where the result is often extremely noisy and require statistical treatment to extract meaningful, experimentally verifiable quantities. The above often requires averaging over very long simulations. Again, ML should be able to identify patterns through this unwanted noisy data.
Finally, ML is becoming a key component in applications of VR. Through appropriate training, ML can better emulate realistic conditions, and integrate intelligent agents within the virtual environment. ML algorithms can also improve digital twins, virtual manifestations of some physical system, by personalizing the virtual environment to the user’s or operator’s preferences, or by using unsupervised learning to identify objects and patterns found in the operational environment. NNs, specifically ESNs, can also be used to improve network performance, an important bottleneck to the successful application of collaborative VR environments. Finally, VR can also be used to provide an abundance of realistic, synthetic training data to ML algorithms.
As a concluding remark, we note that “conventional”, theory-based computational methods (e.g., DFT, MD, CFD) are easily obtainable, and are often available as open-source software. Using such models to obtain insight into new systems is potentially exceptionally computationally expensive. On the contrary, training an ML model is often very computationally demanding. However, a trained model can quickly make predictions on new data, a significant advantage over the commonly used numerical methods. Considering the effort, cost, and time required to train ML algorithms such as DNNs, and, additionally, the potential environmental impact [284], we believe that a collective effort should aim at creating a centralized database of trained algorithms that can readily be used for similar problems. Only then will AI and ML truly help scientific fields progress in a brilliant way.
In conclusion, ML algorithms are quickly becoming ubiquitous practically in all scientific fields. This article briefly reviews some of the recent developments and efforts that use ML in science and engineering. We believe that despite its enormous success over recent years, ML is still at its infancy, and will play a significant role in scientific research and engineering over the upcoming years.
Author Contributions
All authors contributed equally in the research, preparation, and review of the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
No additional support was given outside of the contribution by the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AD | Alzheimer’s Disease |
| ANN | Artificial Neural Networks |
| AR | Augmented Reality |
| BNN | Bayesian Neural Networks |
| BS | Base Stations |
| CFD | Computational Fluid Dynamics |
| CNN | Convolutional Neural Networks |
| CT | Computerized Tomography |
| DBM | Deep Boltzmann Machine |
| DFT | Density Functional Theory |
| DL | Deep Learning |
| DNN | Deep Neural Networks |
| DNS | Direct Numerical Simulation |
| DSC/MS | Downsampled Skip-Connection/Multi-Scale |
| ESN | Echo State Networks |
| FPMD | First Principal Molecular Dynamics |
| GP | Gaussian Process |
| HMI | Human-Machine Interfaces |
| HPC | High-Performance Computing |
| ITS | Intelligent Tutoring System |
| KNN | K-Nearest Neighbors |
| KRR | Kernel Ridge Regression |
| LES | Large Eddy Simulation |
| LSM | Liquid State Machine |
| LSTM | Long Short-Term Memory |
| MD | Molecular Dynamics |
| MCI | Mild Cognitive Impairment |
| ML | Machine Learning |
| MRI | Magnetic Resonance Imaging |
| NPCs | Non-Player Characters |
| PCA | Principal Component Analysis |
| PCCA | Perron Cluster Cluster Analysis |
| PES | Potential Energy Surface |
| PET | Positron Emission Tomography |
| QM | Quantum Mechanics |
| QoS | Quality-of-Service |
| RANS | Reynolds Averaged Navier–Stokes |
| RBM | Restricted Boltzmann Machine |
| RNN | Recurrent Neural Networks |
| SA | Spallart–Allmaras |
| SINDy | Sparse Identification of Non-linear Dynamics |
| SCN | Small Cell Networks (SCN) |
| SVM | Support Vector Machine |
| VANETs | Vehicular Ad-Hoc Networks systems |
| UAV | Unmanned Aerial Vehicles |
| VR | Virtual Reality |
References
- Patrignani, C.; Weinberg, D.; Woody, C.; Chivukula, R.; Buchmueller, O.; Kuyanov, Y.V.; Blucher, E.; Willocq, S.; Höcker, A.; Lippmann, C.; et al. Review of particle physics. Chin. Phys. 2016, 40, 100001. [Google Scholar]
- Tanabashi, M.; Hagiwara, K.; Hikasa, K.; Nakamura, K.; Sumino, Y.; Takahashi, F.; Tanaka, J.; Agashe, K.; Aielli, G.; Amsler, C.; et al. Review of particle physics. Phys. Rev. D 2018, 98, 030001. [Google Scholar] [CrossRef]
- Calixto, G.; Bernegossi, J.; de Freitas, L.; Fontana, C.; Chorilli, M. Nanotechnology-based drug delivery systems for photodynamic therapy of cancer: A review. Molecules 2016, 21, 342. [Google Scholar] [CrossRef] [PubMed]
- Jahangirian, H.; Lemraski, E.G.; Webster, T.J.; Rafiee-Moghaddam, R.; Abdollahi, Y. A review of drug delivery systems based on nanotechnology and green chemistry: Green nanomedicine. Int. J. Nanomed. 2017, 12, 2957. [Google Scholar] [CrossRef] [PubMed]
- Contreras, J.; Rodriguez, E.; Taha-Tijerina, J. Nanotechnology applications for electrical transformers—A review. Electr. Power Syst. Res. 2017, 143, 573–584. [Google Scholar] [CrossRef]
- Scheunert, G.; Heinonen, O.; Hardeman, R.; Lapicki, A.; Gubbins, M.; Bowman, R. A review of high magnetic moment thin films for microscale and nanotechnology applications. Appl. Phys. Rev. 2016, 3, 011301. [Google Scholar] [CrossRef]
- Lu, J.; Chen, Z.; Ma, Z.; Pan, F.; Curtiss, L.A.; Amine, K. The role of nanotechnology in the development of battery materials for electric vehicles. Nat. Nanotechnol. 2016, 11, 1031. [Google Scholar] [CrossRef]
- Olafusi, O.S.; Sadiku, E.R.; Snyman, J.; Ndambuki, J.M.; Kupolati, W.K. Application of nanotechnology in concrete and supplementary cementitious materials: A review for sustainable construction. SN Appl. Sci. 2019, 1, 580. [Google Scholar] [CrossRef]
- Giustino, F. Materials Modelling Using Density Functional Theory: Properties and Predictions; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Conlisk, A.T. Essentials oF Micro-and Nanofluidics: With Applications to the Biological and Chemical Sciences; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Hubbe, M.A.; Tayeb, P.; Joyce, M.; Tyagi, P.; Kehoe, M.; Dimic-Misic, K.; Pal, L. Rheology of nanocellulose-rich aqueous suspensions: A review. BioResources 2017, 12, 9556–9661. [Google Scholar]
- Shah, D.A.; Murdande, S.B.; Dave, R.H. A review: Pharmaceutical and pharmacokinetic aspect of nanocrystalline suspensions. J. Pharm. Sci. 2016, 105, 10–24. [Google Scholar] [CrossRef]
- Van Duin, A.C.; Dasgupta, S.; Lorant, F.; Goddard, W.A. ReaxFF: A reactive force field for hydrocarbons. J. Phys. Chem. A 2001, 105, 9396–9409. [Google Scholar] [CrossRef]
- Drikakis, D.; Frank, M. Advances and challenges in computational research of micro-and nanoflows. Microfluidics Nanofluidics 2015, 19, 1019–1033. [Google Scholar] [CrossRef][Green Version]
- Drikakis, D.; Frank, M.; Tabor, G. Multiscale computational fluid dynamics. Energies 2019, 12, 3272. [Google Scholar] [CrossRef]
- Rider, W.; Kamm, J.; Weirs, V. Verification, validation, and uncertainty quantification for coarse grained simulation. Coarse Grained Simul. Turbul. Mix. 2016, 168–189. [Google Scholar]
- Drikakis, D.; Kwak, D.; Kiris, C. Computational Aerodynamics: Advances and Challenges. Aeronaut. J. 2016, 120, 13–36. [Google Scholar] [CrossRef]
- Norton, T.; Sun, D.W. Computational fluid dynamics (CFD) ‚Äì an effective and efficient design and analysis tool for the food industry: A review. Trends Food Sci. Technol. 2006, 17, 600–620. [Google Scholar] [CrossRef]
- Kobayashi, T.; Tsubokura, M. CFD Application in Automotive Industry. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design; Hirschel, E.H., Krause, E., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 100. [Google Scholar]
- Mitchell, T.M. Machine Learning; McGraw Hill: Burr Ridge, IL, USA, 1997; Volume 45, pp. 870–877. [Google Scholar]
- Vega, C.; Abascal, J.L. Simulating water with rigid non-polarizable models: A general perspective. Phys. Chem. Chem. Phys. 2011, 13, 19663–19688. [Google Scholar] [CrossRef]
- Blank, T.B.; Brown, S.D.; Calhoun, A.W.; Doren, D.J. Neural network models of potential energy surfaces. J. Chem. Phys. 1995, 103, 4129–4137. [Google Scholar] [CrossRef]
- Brown, D.F.; Gibbs, M.N.; Clary, D.C. Combining ab initio computations, neural networks, and diffusion Monte Carlo: An efficient method to treat weakly bound molecules. J. Chem. Phys. 1996, 105, 7597–7604. [Google Scholar] [CrossRef]
- Lorenz, S.; Groß, A.; Scheffler, M. Representing high-dimensional potential-energy surfaces for reactions at surfaces by neural networks. Chem. Phys. Lett. 2004, 395, 210–215. [Google Scholar] [CrossRef]
- Behler, J.; Parrinello, M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 2007, 98, 146401. [Google Scholar] [CrossRef] [PubMed]
- Bartók, A.P.; Payne, M.C.; Kondor, R.; Csányi, G. Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 2010, 104, 136403. [Google Scholar] [CrossRef] [PubMed]
- Chmiela, S.; Tkatchenko, A.; Sauceda, H.E.; Poltavsky, I.; Schütt, K.T.; Müller, K.R. Machine learning of accurate energy-conserving molecular force fields. Sci. Adv. 2017, 3, e1603015. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.S.; Nebgen, B.T.; Zubatyuk, R.; Lubbers, N.; Devereux, C.; Barros, K.; Tretiak, S.; Isayev, O.; Roitberg, A.E. Approaching coupled cluster accuracy with a general-purpose neural network potential through transfer learning. Nat. Commun. 2019, 10, 2903. [Google Scholar] [CrossRef] [PubMed]
- Csányi, G.; Albaret, T.; Payne, M.C.; De Vita, A. “Learn on the Fly”: A Hybrid Classical and Quantum-Mechanical Molecular Dynamics Simulation. Phys. Rev. Lett. 2004, 93, 175503. [Google Scholar] [CrossRef]
- Li, Z.; Kermode, J.R.; De Vita, A. Molecular dynamics with on-the-fly machine learning of quantum-mechanical forces. Phys. Rev. Lett. 2015, 114, 096405. [Google Scholar] [CrossRef]
- Botu, V.; Ramprasad, R. Adaptive machine learning framework to accelerate ab initio molecular dynamics. Int. J. Quantum Chem. 2015, 115, 1074–1083. [Google Scholar] [CrossRef]
- Sosso, G.C.; Miceli, G.; Caravati, S.; Behler, J.; Bernasconi, M. Neural network interatomic potential for the phase change material GeTe. Phys. Rev. B 2012, 85, 174103. [Google Scholar] [CrossRef]
- Sosso, G.C.; Miceli, G.; Caravati, S.; Giberti, F.; Behler, J.; Bernasconi, M. Fast crystallization of the phase change compound GeTe by large-scale molecular dynamics simulations. J. Phys. Chem. Lett. 2013, 4, 4241–4246. [Google Scholar] [CrossRef]
- Gabardi, S.; Baldi, E.; Bosoni, E.; Campi, D.; Caravati, S.; Sosso, G.; Behler, J.; Bernasconi, M. Atomistic simulations of the crystallization and aging of GeTe nanowires. J. Phys. Chem. C 2017, 121, 23827–23838. [Google Scholar] [CrossRef]
- Bartók, A.P.; De, S.; Poelking, C.; Bernstein, N.; Kermode, J.R.; Csányi, G.; Ceriotti, M. Machine learning unifies the modeling of materials and molecules. Sci. Adv. 2017, 3, e1701816. [Google Scholar] [CrossRef] [PubMed]
- Behler, J.; Martoňák, R.; Donadio, D.; Parrinello, M. Metadynamics simulations of the high-pressure phases of silicon employing a high-dimensional neural network potential. Phys. Rev. Lett. 2008, 100, 185501. [Google Scholar] [CrossRef] [PubMed]
- Deringer, V.L.; Bernstein, N.; Bartók, A.P.; Cliffe, M.J.; Kerber, R.N.; Marbella, L.E.; Grey, C.P.; Elliott, S.R.; Csányi, G. Realistic atomistic structure of amorphous silicon from machine-learning-driven molecular dynamics. J. Phys. Chem. Lett. 2018, 9, 2879–2885. [Google Scholar] [CrossRef] [PubMed]
- Gastegger, M.; Behler, J.; Marquetand, P. Machine learning molecular dynamics for the simulation of infrared spectra. Chem. Sci. 2017, 8, 6924–6935. [Google Scholar] [CrossRef]
- Pérez, S.; Imberty, A.; Engelsen, S.B.; Gruza, J.; Mazeau, K.; Jimenez-Barbero, J.; Poveda, A.; Espinosa, J.F.; van Eyck, B.P.; Johnson, G.; et al. A comparison and chemometric analysis of several molecular mechanics force fields and parameter sets applied to carbohydrates. Carbohydr. Res. 1998, 314, 141–155. [Google Scholar] [CrossRef]
- Raval, A.; Piana, S.; Eastwood, M.P.; Dror, R.O.; Shaw, D.E. Refinement of protein structure homology models via long, all-atom molecular dynamics simulations. Proteins Struct. Funct. Bioinform. 2012, 80, 2071–2079. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D. Solid-like heat transfer in confined liquids. Microfluidics Nanofluidics 2017, 21, 148. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D. Thermodynamics at Solid–Liquid Interfaces. Entropy 2018, 20, 362. [Google Scholar] [CrossRef]
- Papanikolaou, M.; Frank, M.; Drikakis, D. Nanoflow over a fractal surface. Phys. Fluids 2016, 28, 082001. [Google Scholar] [CrossRef]
- Papanikolaou, M.; Frank, M.; Drikakis, D. Effects of surface roughness on shear viscosity. Phys. Rev. E 2017, 95, 033108. [Google Scholar] [CrossRef]
- Frank, M.; Papanikolaou, M.; Drikakis, D.; Salonitis, K. Heat transfer across a fractal surface. J. Chem. Phys. 2019, 151, 134705. [Google Scholar] [CrossRef] [PubMed]
- Asproulis, N.; Drikakis, D. Nanoscale materials modelling using neural networks. J. Comput. Theor. Nanosci. 2009, 6, 514–518. [Google Scholar] [CrossRef]
- Asproulis, N.; Drikakis, D. An artificial neural network-based multiscale method for hybrid atomistic-continuum simulations. Microfluidics Nanofluidics 2013, 15, 559–574. [Google Scholar] [CrossRef]
- Thornber, B.; Mosedale, A.; Drikakis, D. On the implicit large eddy simulations of homogeneous decaying turbulence. J. Comput. Phys. 2007, 226, 1902–1929. [Google Scholar] [CrossRef]
- Jiménez, J. Near-wall turbulence. Phys. Fluids 2013, 25, 1–28. [Google Scholar] [CrossRef]
- Drikakis, D. Advances in turbulent flow computations using high-resolution methods. Prog. Aerosp. Sci. 2003, 39, 405–424. [Google Scholar] [CrossRef]
- Kobayashi, H.; Matsumoto, E.; Fukushima, N.; Tanahashi, M.; Miyauchi, T. Statistical properties of the local structure of homogeneous isotropic turbulence and turbulent channel flows. J. Turbul. 2011, 12. [Google Scholar] [CrossRef]
- Giralt, F.; Arenas, A.; Ferre-Gine, J.; Rallo, R.; Kopp, G. The simulation and interpretation of free turbulence with a cognitive neural system. Phys. Fluids 2000, 12, 1826–1835. [Google Scholar] [CrossRef]
- Milano, M.; Koumoutsakos, P. Neural network modeling for near wall turbulent flow. J. Comput. Phys. 2002, 182, 1–26. [Google Scholar] [CrossRef]
- Chang, F.J.; Yang, H.C.; Lu, J.Y.; Hong, J.H. Neural network modelling for mean velocity and turbulence intensities of steep channel flows. Hydrol. Process. Int. J. 2008, 22, 265–274. [Google Scholar] [CrossRef]
- Duraisamy, K.; Iaccarino, G.; Xiao, H. Turbulence modeling in the age of data. Annu. Rev. Fluid Mech. 2019, 51, 357–377. [Google Scholar] [CrossRef]
- Xiao, H.; Wu, J.L.; Wang, J.X.; Sun, R.; Roy, C. Quantifying and reducing model-form uncertainties in Reynolds-averaged Navier–Stokes simulations: A data-driven, physics-informed Bayesian approach. J. Comput. Phys. 2016, 324, 115–136. [Google Scholar] [CrossRef]
- Tracey, B.D.; Duraisamy, K.; Alonso, J.J. A machine learning strategy to assist turbulence model development. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1287. [Google Scholar]
- Zhu, L.; Zhang, W.; Kou, J.; Liu, Y. Machine learning methods for turbulence modeling in subsonic flows around airfoils. Phys. Fluids 2019, 31, 15105. [Google Scholar] [CrossRef]
- Ling, J.; Kurzawski, A.; Templeton, J. Reynolds averaged turbulence modelling using deep neural networks with embedded invariance. J. Fluid Mech. 2016, 807, 155–166. [Google Scholar] [CrossRef]
- Kutz, J.N. Deep learning in fluid dynamics. J. Fluid Mech. 2017, 814, 1–4. [Google Scholar] [CrossRef]
- Cheung, S.H.; Oliver, T.A.; Prudencio, E.E.; Prudhomme, S.; Moser, R.D. Bayesian uncertainty analysis with applications to turbulence modeling. Reliab. Eng. Syst. Saf. 2011, 96, 1137–1149. [Google Scholar] [CrossRef]
- Edeling, W.; Cinnella, P.; Dwight, R.P.; Bijl, H. Bayesian estimates of parameter variability in the k–ε turbulence model. J. Comput. Phys. 2014, 258, 73–94. [Google Scholar] [CrossRef]
- Zhang, Z.J.; Duraisamy, K. Machine learning methods for data-driven turbulence modeling. In Proceedings of the 22nd AIAA Computational Fluid Dynamics Conference, Dallas, TX, USA, 22–26 June 2015; p. 2460. [Google Scholar]
- Duraisamy, K.; Zhang, Z.J.; Singh, A.P. New approaches in turbulence and transition modeling using data-driven techniques. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015; p. 1284. [Google Scholar]
- Parish, E.J.; Duraisamy, K. A paradigm for data-driven predictive modeling using field inversion and machine learning. J. Comput. Phys. 2016, 305, 758–774. [Google Scholar] [CrossRef]
- Geneva, N.; Zabaras, N. Quantifying model form uncertainty in Reynolds-averaged turbulence models with Bayesian deep neural networks. J. Comput. Phys. 2019, 383, 125–147. [Google Scholar] [CrossRef]
- Wang, J.X.; Wu, J.L.; Xiao, H. Physics-informed machine learning approach for reconstructing Reynolds stress modeling discrepancies based on DNS data. Phys. Rev. Fluids 2017, 2, 034603. [Google Scholar] [CrossRef]
- Wu, J.L.; Xiao, H.; Paterson, E. Physics-informed machine learning approach for augmenting turbulence models: A comprehensive framework. Phys. Rev. Fluids 2018, 3, 074602. [Google Scholar] [CrossRef]
- Sarghini, F.; De Felice, G.; Santini, S. Neural networks based subgrid scale modeling in large eddy simulations. Comput. Fluids 2003, 32, 97–108. [Google Scholar] [CrossRef]
- Moreau, A.; Teytaud, O.; Bertoglio, J.P. Optimal estimation for large-eddy simulation of turbulence and application to the analysis of subgrid models. Phys. Fluids 2006, 18, 105101. [Google Scholar] [CrossRef]
- Beck, A.D.; Flad, D.G.; Munz, C.D. Deep neural networks for data-driven turbulence models. arXiv 2018, arXiv:1806.04482. [Google Scholar]
- Maulik, R.; San, O.; Rasheed, A.; Vedula, P. Subgrid modelling for two-dimensional turbulence using neural networks. J. Fluid Mech. 2019, 858, 122–144. [Google Scholar] [CrossRef]
- Fukami, K.; Fukagata, K.; Taira, K. Super-resolution reconstruction of turbulent flows with machine learning. J. Fluid Mech. 2019, 870, 106–120. [Google Scholar] [CrossRef]
- Lu, C. Artificial Neural Network for Behavior Learning From Meso-Scale Simulations, Application to Multi-Scale Multimaterial Flows; University of Lowa: Lowa City, IA, USA, 2010. [Google Scholar]
- Gibou, F.; Hyde, D.; Fedkiw, R. Sharp interface approaches and deep learning techniques for multiphase flows. J. Comput. Phys. 2019, 380, 442–463. [Google Scholar] [CrossRef]
- Ma, M.; Lu, J.; Tryggvason, G. Using statistical learning to close two-fluid multiphase flow equations for a simple bubbly system. Phys. Fluids 2015, 27, 092101. [Google Scholar] [CrossRef]
- Qi, Y.; Lu, J.; Scardovelli, R.; Zaleski, S.; Tryggvason, G. Computing curvature for volume of fluid methods using machine learning. J. Comput. Phys. 2019, 377, 155–161. [Google Scholar] [CrossRef]
- Chang, C.W.; Dinh, N.T. Classification of machine learning frameworks for data-driven thermal fluid models. Int. J. Therm. Sci. 2019, 135, 559–579. [Google Scholar] [CrossRef]
- Ling, J.; Templeton, J. Evaluation of machine learning algorithms for prediction of regions of high Reynolds averaged Navier Stokes uncertainty. Phys. Fluids 2015, 27, 085103. [Google Scholar] [CrossRef]
- Wu, J.L.; Wang, J.X.; Xiao, H.; Ling, J. A priori assessment of prediction confidence for data-driven turbulence modeling. Flow Turbul. Combust. 2017, 99, 25–46. [Google Scholar] [CrossRef]
- Yang, C.; Yang, X.; Xiao, X. Data-driven projection method in fluid simulation. Comput. Animat. Virtual Worlds 2016, 27, 415–424. [Google Scholar] [CrossRef]
- Tompson, J.; Schlachter, K.; Sprechmann, P.; Perlin, K. Accelerating eulerian fluid simulation with convolutional networks. In Proceedings of the 34th International Conference on Machine Learning-Volume 70. JMLR. org, Sydney, Australia, 6–11 August 2017; pp. 3424–3433. [Google Scholar]
- Unger, J.F.; Könke, C. Coupling of scales in a multiscale simulation using neural networks. Comput. Struct. 2008, 86, 1994–2003. [Google Scholar] [CrossRef]
- Unger, J.F.; Könke, C. Neural networks as material models within a multiscale approach. Comput. Struct. 2009, 87, 1177–1186. [Google Scholar] [CrossRef]
- Hambli, R. Numerical procedure for multiscale bone adaptation prediction based on neural networks and finite element simulation. Finite Elem. Anal. Des. 2011, 47, 835–842. [Google Scholar] [CrossRef]
- Hambli, R. Apparent damage accumulation in cancellous bone using neural networks. J. Mech. Behav. Biomed. Mater. 2011, 4, 868–878. [Google Scholar] [CrossRef]
- Sha, W.; Edwards, K. The use of artificial neural networks in materials science based research. Mater. Des. 2007, 28, 1747–1752. [Google Scholar] [CrossRef]
- Trott, A.; Moorhead, R.; McGinley, J. Wavelets applied to lossless compression and progressive transmission of floating point data in 3-D curvilinear grids. Proceedings of Seventh Annual IEEE Visualization’96, San Francisco, CA, USA, 27 October–1 November 1996; pp. 385–388. [Google Scholar]
- Kang, H.; Lee, D.; Lee, D. A study on CFD data compression using hybrid supercompact wavelets. KSME Int. J. 2003, 17, 1784–1792. [Google Scholar] [CrossRef]
- Sakai, R.; Sasaki, D.; Nakahashi, K. Parallel implementation of large-scale CFD data compression toward aeroacoustic analysis. Comput. Fluids 2013, 80, 116–127. [Google Scholar] [CrossRef]
- Carlberg, K.T.; Jameson, A.; Kochenderfer, M.J.; Morton, J.; Peng, L.; Witherden, F.D. Recovering missing CFD data for high-order discretizations using deep neural networks and dynamics learning. J. Comput. Phys. 2019, 395, 105–124. [Google Scholar] [CrossRef]
- Rupp, M. Machine learning for quantum mechanics in a nutshell. Int. J. Quantum Chem. 2015, 115, 1058–1073. [Google Scholar] [CrossRef]
- Rupp, M.; Tkatchenko, A.; Müller, K.R.; Von Lilienfeld, O.A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 2012, 108, 058301. [Google Scholar] [CrossRef] [PubMed]
- Hansen, K.; Montavon, G.; Biegler, F.; Fazli, S.; Rupp, M.; Scheffler, M.; Von Lilienfeld, O.A.; Tkatchenko, A.; Müller, K.R. Assessment and validation of machine learning methods for predicting molecular atomization energies. J. Chem. Theory Comput. 2013, 9, 3404–3419. [Google Scholar] [CrossRef] [PubMed]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602–606. [Google Scholar] [CrossRef] [PubMed]
- Handley, C.M.; Popelier, P.L. Dynamically polarizable water potential based on multipole moments trained by machine learning. J. Chem. Theory Comput. 2009, 5, 1474–1489. [Google Scholar] [CrossRef]
- Hautier, G.; Fischer, C.C.; Jain, A.; Mueller, T.; Ceder, G. Finding nature’s missing ternary oxide compounds using machine learning and density functional theory. Chem. Mater. 2010, 22, 3762–3767. [Google Scholar] [CrossRef]
- Bishop, C.M.; James, G.D. Analysis of multiphase flows using dual-energy gamma densitometry and neural networks. Nucl. Instrum. Methods Phys. Res. Sect. A 1993, 327, 580–593. [Google Scholar] [CrossRef]
- Xie, T.; Ghiaasiaan, S.; Karrila, S. Artificial neural network approach for flow regime classification in gas–liquid–fiber flows based on frequency domain analysis of pressure signals. Chem. Eng. Sci. 2004, 59, 2241–2251. [Google Scholar] [CrossRef]
- Al-Rawahi, N.; Meribout, M.; Al-Naamany, A.; Al-Bimani, A.; Meribout, A. A neural network algorithm for density measurement of multiphase flow. Multiph. Sci. Technol. 2012, 24, 89–103. [Google Scholar] [CrossRef]
- Mi, Y.; Ishii, M.; Tsoukalas, L. Flow regime identification methodology with neural networks and two-phase flow models. Nucl. Eng. Des. 2001, 204, 87–100. [Google Scholar] [CrossRef]
- Hernandez, L.; Juliá, J.; Chiva, S.; Paranjape, S.; Ishii, M. Fast classification of two-phase flow regimes based on conductivity signals and artificial neural networks. Measur. Sci. Technol. 2006, 17, 1511. [Google Scholar] [CrossRef]
- Juliá, J.E.; Liu, Y.; Paranjape, S.; Ishii, M. Upward vertical two-phase flow local flow regime identification using neural network techniques. Nuclear Eng. Des. 2008, 238, 156–169. [Google Scholar] [CrossRef]
- Rey-Fabret, I.; Sankar, R.; Duret, E.; Heintze, E.; Henriot, V. Neural networks tools for improving tacite hydrodynamic simulation of multiphase flow behavior in pipelines. Oil Gas Sci. Technol. 2001, 56, 471–478. [Google Scholar] [CrossRef]
- Lee, C.; Kim, J.; Babcock, D.; Goodman, R. Application of neural networks to turbulence control for drag reduction. Phys. Fluids 1997, 9, 1740–1747. [Google Scholar] [CrossRef]
- Rabault, J.; Kuchta, M.; Jensen, A.; Réglade, U.; Cerardi, N. Artificial neural networks trained through deep reinforcement learning discover control strategies for active flow control. J. Fluid Mech. 2019, 865, 281–302. [Google Scholar] [CrossRef]
- Ghaboussi, J.; Garrett, J.; Wu, X. Material modeling with neural networks. In Proceedings of the International Conference on Numerical Methods In Engineering: Theory and Applications, Swansea, UK, 7–11 January 1990; pp. 701–717. [Google Scholar]
- Ghaboussi, J.; Garrett, J., Jr.; Wu, X. Knowledge-based modeling of material behavior with neural networks. J. Eng. Mech. 1991, 117, 132–153. [Google Scholar] [CrossRef]
- Yeh, I.C. Modeling of strength of high-performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Waszczyszyn, Z.; Ziemiański, L. Neural networks in mechanics of structures and materials–new results and prospects of applications. Comput. Struct. 2001, 79, 2261–2276. [Google Scholar] [CrossRef]
- Zimmerman, D.C.; Hasselman, T.; Anderson, M. Approximation and calibration of nonlinear structural dynamics. Nonlinear Dyn. 2005, 39, 113–128. [Google Scholar] [CrossRef]
- Kerschen, G.; Worden, K.; Vakakis, A.F.; Golinval, J.C. Past, present and future of nonlinear system identification in structural dynamics. Mech. Syst. Signal Process. 2006, 20, 505–592. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q. Heat transfer enhancement of nanofluids. Int. J. Heat Fluid Flow 2000, 21, 58–64. [Google Scholar] [CrossRef]
- Eastman, J.A.; Choi, S.; Li, S.; Yu, W.; Thompson, L. Anomalously increased effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Appl. Phys. Lett. 2001, 78, 718–720. [Google Scholar] [CrossRef]
- Choi, S.; Zhang, Z.; Yu, W.; Lockwood, F.; Grulke, E. Anomalous thermal conductivity enhancement in nanotube suspensions. Appl. Phys. Lett. 2001, 79, 2252–2254. [Google Scholar] [CrossRef]
- Keblinski, P.; Phillpot, S.; Choi, S.; Eastman, J. Mechanisms of heat flow in suspensions of nano-sized particles (nanofluids). Int. J. Heat Mass Transf. 2002, 45, 855–863. [Google Scholar] [CrossRef]
- Evans, W.; Fish, J.; Keblinski, P. Role of Brownian motion hydrodynamics on nanofluid thermal conductivity. Appl. Phys. Lett. 2006, 88, 093116. [Google Scholar] [CrossRef]
- Sankar, N.; Mathew, N.; Sobhan, C. Molecular dynamics modeling of thermal conductivity enhancement in metal nanoparticle suspensions. Int. Commun. Heat Mass Transf. 2008, 35, 867–872. [Google Scholar] [CrossRef]
- Frank, M.; Drikakis, D.; Asproulis, N. Thermal conductivity of nanofluid in nanochannels. Microfluidics Nanofluidics 2015, 19, 1011–1017. [Google Scholar] [CrossRef]
- Deepak, K.; Frank, M.; Drikakis, D.; Asproulis, N. Thermal properties of a water-copper nanofluid in a graphene channel. J. Comput. Theor. Nanosci. 2016, 13, 79–83. [Google Scholar] [CrossRef]
- Papari, M.M.; Yousefi, F.; Moghadasi, J.; Karimi, H.; Campo, A. Modeling thermal conductivity augmentation of nanofluids using diffusion neural networks. Int. J. Therm. Sci. 2011, 50, 44–52. [Google Scholar] [CrossRef]
- Hojjat, M.; Etemad, S.G.; Bagheri, R.; Thibault, J. Thermal conductivity of non-Newtonian nanofluids: Experimental data and modeling using neural network. Int. J. Heat Mass Transf. 2011, 54, 1017–1023. [Google Scholar] [CrossRef]
- Longo, G.A.; Zilio, C.; Ceseracciu, E.; Reggiani, M. Application of artificial neural network (ANN) for the prediction of thermal conductivity of oxide–water nanofluids. Nano Energy 2012, 1, 290–296. [Google Scholar] [CrossRef]
- Esfe, M.H.; Afrand, M.; Yan, W.M.; Akbari, M. Applicability of artificial neural network and nonlinear regression to predict thermal conductivity modeling of Al2O3–water nanofluids using experimental data. Int. Commun. Heat Mass Transf. 2015, 66, 246–249. [Google Scholar] [CrossRef]
- Ariana, M.; Vaferi, B.; Karimi, G. Prediction of thermal conductivity of alumina water-based nanofluids by artificial neural networks. Powder Technol. 2015, 278, 1–10. [Google Scholar] [CrossRef]
- Esfe, M.H.; Afrand, M.; Wongwises, S.; Naderi, A.; Asadi, A.; Rostami, S.; Akbari, M. Applications of feedforward multilayer perceptron artificial neural networks and empirical correlation for prediction of thermal conductivity of Mg (OH) 2–EG using experimental data. Int. Commun. Heat Mass Transf. 2015, 67, 46–50. [Google Scholar] [CrossRef]
- Esfe, M.H.; Rostamian, H.; Afrand, M.; Karimipour, A.; Hassani, M. Modeling and estimation of thermal conductivity of MgO–water/EG (60: 40) by artificial neural network and correlation. Int. Commun. Heat Mass Transf. 2015, 68, 98–103. [Google Scholar] [CrossRef]
- Esfe, M.H.; Naderi, A.; Akbari, M.; Afrand, M.; Karimipour, A. Evaluation of thermal conductivity of COOH-functionalized MWCNTs/water via temperature and solid volume fraction by using experimental data and ANN methods. J. Therm. Anal. Calorim. 2015, 121, 1273–1278. [Google Scholar] [CrossRef]
- Esfe, M.H.; Yan, W.M.; Afrand, M.; Sarraf, M.; Toghraie, D.; Dahari, M. Estimation of thermal conductivity of Al2O3/water (40%)–ethylene glycol (60%) by artificial neural network and correlation using experimental data. Int. Commun. Heat Mass Transf. 2016, 74, 125–128. [Google Scholar] [CrossRef]
- Esfe, M.H.; Motahari, K.; Sanatizadeh, E.; Afrand, M.; Rostamian, H.; Ahangar, M.R.H. Estimation of thermal conductivity of CNTs-water in low temperature by artificial neural network and correlation. Int. Commun. Heat Mass Transf. 2016, 76, 376–381. [Google Scholar] [CrossRef]
- Esfe, M.H.; Saedodin, S.; Sina, N.; Afrand, M.; Rostami, S. Designing an artificial neural network to predict thermal conductivity and dynamic viscosity of ferromagnetic nanofluid. Int. Commun. Heat Mass Transf. 2015, 68, 50–57. [Google Scholar] [CrossRef]
- Vafaei, M.; Afrand, M.; Sina, N.; Kalbasi, R.; Sourani, F.; Teimouri, H. Evaluation of thermal conductivity of MgO-MWCNTs/EG hybrid nanofluids based on experimental data by selecting optimal artificial neural networks. Phys. E 2017, 85, 90–96. [Google Scholar] [CrossRef]
- Srivastava, A.N.; Han, J. Machine Learning and Knowledge Discovery for Engineering Systems Health Management; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Napolitano, M.R.; Chen, C.I.; Naylor, S. Aircraft failure detection and identification using neural networks. J. Guid. Control Dyn. 1993, 16, 999–1009. [Google Scholar] [CrossRef]
- Napolitano, M.R.; Neppach, C.; Casdorph, V.; Naylor, S.; Innocenti, M.; Silvestri, G. Neural-network-based scheme for sensor failure detection, identification, and accommodation. J. Guid. Control Dyn. 1995, 18, 1280–1286. [Google Scholar] [CrossRef]
- Napolitano, M.R.; An, Y.; Seanor, B.A. A fault tolerant flight control system for sensor and actuator failures using neural networks. Aircr. Des. 2000, 3, 103–128. [Google Scholar] [CrossRef]
- Chen, Y.; Lee, M. Neural networks-based scheme for system failure detection and diagnosis. Math. Comput. Simul. 2002, 58, 101–109. [Google Scholar] [CrossRef]
- Nanduri, A.; Sherry, L. Anomaly detection in aircraft data using Recurrent Neural Networks (RNN). In Proceedings of the 2016 IEEE Integrated Communications Navigation and Surveillance (ICNS) 2016, Herndon, VA, USA, 19–21 April 2016. [Google Scholar]
- Poloni, C.; Giurgevich, A.; Onesti, L.; Pediroda, V. Hybridization of a multi-objective genetic algorithm, a neural network and a classical optimizer for a complex design problem in fluid dynamics. Comput. Methods Appl. Mech. Eng. 2000, 186, 403–420. [Google Scholar] [CrossRef]
- Esau, I. On application of artificial neural network methods in large-eddy simulations with unresolved urban surfaces. Mod. Appl. Sci. 2010, 4, 3. [Google Scholar] [CrossRef][Green Version]
- Paez, T.L.; Hunter, N. Dynamical System Modeling via Signal Reduction and Neural Network Simulation; Technical report; Sandia National Labs.: Albuquerque, NM, USA, 1997. [Google Scholar]
- Smaoui, N. A Model for the Unstable Manifold of the Bursting Behavior in the 2D Navier–Stokes Flow. SIAM J. Sci. Comput. 2001, 23, 824–839. [Google Scholar] [CrossRef]
- Smaoui, N.; Al-Enezi, S. Modelling the dynamics of nonlinear partial differential equations using neural networks. J. Comput. Appl. Math. 2004, 170, 27–58. [Google Scholar] [CrossRef]
- Nakajima, Y.; Kikuchi, R.; Kuramoto, K.; Tsutsumi, A.; Otawara, K. Nonlinear modeling of chaotic dynamics in a circulating fluidized bed by an artificial neural network. J. Chem. Eng. Jpn. 2001, 34, 107–113. [Google Scholar] [CrossRef]
- Otawara, K.; Fan, L.; Tsutsumi, A.; Yano, T.; Kuramoto, K.; Yoshida, K. An artificial neural network as a model for chaotic behavior of a three-phase fluidized bed. Chaos Solitons Fractals 2002, 13, 353–362. [Google Scholar] [CrossRef]
- Lin, H.; Chen, W.; Tsutsumi, A. Long-term prediction of nonlinear hydrodynamics in bubble columns by using artificial neural networks. Chem. Eng. Process. Process Intensif. 2003, 42, 611–620. [Google Scholar] [CrossRef]
- Bakker, R.; De Korte, R.; Schouten, J.; Van Den Bleek, C.; Takens, F. Neural networks for prediction and control of chaotic fluidized bed hydrodynamics: A first step. Fractals 1997, 5, 523–530. [Google Scholar] [CrossRef]
- Bakker, R.; Schouten, J.C.; Giles, C.L.; Takens, F.; Bleek, C.M.v.d. Learning chaotic attractors by neural networks. Neural Comput. 2000, 12, 2355–2383. [Google Scholar] [CrossRef] [PubMed]
- Jeong, S.; Solenthaler, B.; Pollefeys, M.; Gross, M. Data-driven fluid simulations using regression forests. ACM Trans. Graphics (TOG) 2015, 34, 199. [Google Scholar]
- Wang, Z.; Xiao, D.; Fang, F.; Govindan, R.; Pain, C.C.; Guo, Y. Model identification of reduced order fluid dynamics systems using deep learning. Int. J. Numer. Methods Fluids 2018, 86, 255–268. [Google Scholar] [CrossRef]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef]
- Lui, H.F.; Wolf, W.R. Construction of reduced-order models for fluid flows using deep feedforward neural networks. J. Fluid Mech. 2019, 872, 963–994. [Google Scholar] [CrossRef]
- Pan, S.; Duraisamy, K. Long-time predictive modeling of nonlinear dynamical systems using neural networks. Complexity 2018, 2018. [Google Scholar] [CrossRef]
- Owhadi, H. Bayesian numerical homogenization. Multiscale Model. Simul. 2015, 13, 812–828. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Inferring solutions of differential equations using noisy multi-fidelity data. J. Comput. Phys. 2017, 335, 736–746. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Machine learning of linear differential equations using Gaussian processes. J. Comput. Phys. 2017, 348, 683–693. [Google Scholar] [CrossRef]
- Raissi, M.; Karniadakis, G.E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Numerical Gaussian processes for time-dependent and nonlinear partial differential equations. SIAM J. Sci. Comput. 2018, 40, A172–A198. [Google Scholar] [CrossRef]
- Baydin, A.G.; Pearlmutter, B.A.; Radul, A.A.; Siskind, J.M. Automatic differentiation in machine learning: A survey. J. Mach. Learn. Res. 2018, 18, 5595–5637. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics informed deep learning (part i): Data-driven solutions of nonlinear partial differential equations. arXiv 2017, arXiv:1711.10561. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics informed deep learning (part ii): Data-driven discovery of nonlinear partial differential equations. arXiv 2017, arXiv:1711.10566. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Raissi, M.; Wang, Z.; Triantafyllou, M.S.; Karniadakis, G.E. Deep learning of vortex-induced vibrations. J. Fluid Mech. 2019, 861, 119–137. [Google Scholar] [CrossRef]
- Sirignano, J.; Spiliopoulos, K. DGM: A deep learning algorithm for solving partial differential equations. J. Comput. Phys. 2018, 375, 1339–1364. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.S.; Perdikaris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Ramsundar, B.; Eastman, P.; Walters, P.; Pande, V. Deep Learning for the Life Sciences: Applying Deep Learning to Genomics, Microscopy, Drug Discovery, and More; O’Reilly Media, Inc.: Sebastopol, CA, USA, 2019. [Google Scholar]
- Wolf, A.; Kirschner, K.N. Principal component and clustering analysis on molecular dynamics data of the ribosomal L11· 23S subdomain. J. Mol. Model. 2013, 19, 539–549. [Google Scholar] [CrossRef] [PubMed]
- Shin, J.; Berg, D.A.; Zhu, Y.; Shin, J.Y.; Song, J.; Bonaguidi, M.A.; Enikolopov, G.; Nauen, D.W.; Christian, K.M.; Ming, G.l.; et al. Single-cell RNA-seq with waterfall reveals molecular cascades underlying adult neurogenesis. Cell Stem Cell 2015, 17, 360–372. [Google Scholar] [CrossRef] [PubMed]
- Decherchi, S.; Berteotti, A.; Bottegoni, G.; Rocchia, W.; Cavalli, A. The ligand binding mechanism to purine nucleoside phosphorylase elucidated via molecular dynamics and machine learning. Nat. Commun. 2015, 6, 6155. [Google Scholar] [CrossRef]
- Schütte, C.; Fischer, A.; Huisinga, W.; Deuflhard, P. A direct approach to conformational dynamics based on hybrid Monte Carlo. J. Comput. Phys. 1999, 151, 146–168. [Google Scholar] [CrossRef]
- Huisinga, W.; Best, C.; Roitzsch, R.; Schütte, C.; Cordes, F. From simulation data to conformational ensembles: Structure and dynamics-based methods. J. Comput. Chem. 1999, 20, 1760–1774. [Google Scholar] [CrossRef]
- Noé, F.; Horenko, I.; Schütte, C.; Smith, J.C. Hierarchical analysis of conformational dynamics in biomolecules: Transition networks of metastable states. J. Chem. Phys. 2007, 126, 04B617. [Google Scholar] [CrossRef]
- Deuflhard, P.; Weber, M. Robust Perron cluster analysis in conformation dynamics. Linear Algebra Appl. 2005, 398, 161–184. [Google Scholar] [CrossRef]
- Weber, M.; Kube, S. Robust perron cluster analysis for various applications in computational life science. In Proceedings of the International Symposium on Computational Life Science, Konstanz, Germany, 25–27 September 2005; Springer: Berlin, Germany, 2005; pp. 57–66. [Google Scholar]
- Karpen, M.E.; Tobias, D.J.; Brooks, C.L., III. Statistical clustering techniques for the analysis of long molecular dynamics trajectories: Analysis of 2.2-ns trajectories of YPGDV. Biochemistry 1993, 32, 412–420. [Google Scholar] [CrossRef]
- Angermueller, C.; Pärnamaa, T.; Parts, L.; Stegle, O. Deep learning for computational biology. Mol. Syst. Biol. 2016, 12, 878. [Google Scholar] [CrossRef]
- Pérez, A.; Martínez-Rosell, G.; De Fabritiis, G. Simulations meet machine learning in structural biology. Curr. Opin. Struct. Biol. 2018, 49, 139–144. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.; Kellis, M. Deep learning for regulatory genomics. Nat. Biotechnol. 2015, 33, 825. [Google Scholar] [CrossRef] [PubMed]
- Xiong, H.Y.; Alipanahi, B.; Lee, L.J.; Bretschneider, H.; Merico, D.; Yuen, R.K.; Hua, Y.; Gueroussov, S.; Najafabadi, H.S.; Hughes, T.R.; et al. The human splicing code reveals new insights into the genetic determinants of disease. Science 2015, 347, 1254806. [Google Scholar] [CrossRef] [PubMed]
- Alipanahi, B.; Delong, A.; Weirauch, M.T.; Frey, B.J. Predicting the sequence specificities of DNA-and RNA-binding proteins by deep learning. Nat. Biotechnol. 2015, 33, 831. [Google Scholar] [CrossRef]
- Zeng, H.; Edwards, M.D.; Liu, G.; Gifford, D.K. Convolutional neural network architectures for predicting DNA–protein binding. Bioinformatics 2016, 32, i121–i127. [Google Scholar] [CrossRef]
- Nguyen, N.G.; Tran, V.A.; Ngo, D.L.; Phan, D.; Lumbanraja, F.R.; Faisal, M.R.; Abapihi, B.; Kubo, M.; Satou, K. DNA sequence classification by convolutional neural network. J. Biomed. Sci. Eng. 2016, 9, 280. [Google Scholar] [CrossRef]
- Zhou, J.; Troyanskaya, O.G. Predicting effects of noncoding variants with deep learning–based sequence model. Nat. Methods 2015, 12, 931. [Google Scholar] [CrossRef]
- Krishnaiah, V.; Narsimha, D.G.; Chandra, D.N.S. Diagnosis of lung cancer prediction system using data mining classification techniques. Int. J. Comput. Sci. Inf. Technol. 2013, 4, 39–45. [Google Scholar]
- Kuruvilla, J.; Gunavathi, K. Lung cancer classification using neural networks for CT images. Comput. Methods Programs Biomed. 2014, 113, 202–209. [Google Scholar] [CrossRef]
- D’Cruz, J.; Jadhav, A.; Dighe, A.; Chavan, V.; Chaudhari, J. Detection of lung cancer using backpropagation neural networks and genetic algorithm. Comput. Technol. Appl. 2016, 6, 823–827. [Google Scholar]
- Kumar, D.; Wong, A.; Clausi, D.A. Lung nodule classification using deep features in CT images. In Proceedings of the 2015 IEEE 12th Conference on Computer and Robot Vision, Halifax, NS, Canada, 3–5 June 2015; pp. 133–138. [Google Scholar]
- Song, Q.; Zhao, L.; Luo, X.; Dou, X. Using deep learning for classification of lung nodules on computed tomography images. J. Healthc. Eng. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Teramoto, A.; Tsukamoto, T.; Kiriyama, Y.; Fujita, H. Automated classification of lung cancer types from cytological images using deep convolutional neural networks. BioMed Res. Int. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Chon, A.; Balachandar, N. Deep Convolutional Neural Networks for Lung Cancer Detection; Standford University: Stanford, CA, USA, 2017. [Google Scholar]
- Serj, M.F.; Lavi, B.; Hoff, G.; Valls, D.P. A deep convolutional neural network for lung cancer diagnostic. arXiv 2018, arXiv:1804.08170. [Google Scholar]
- Mendoza, J.; Pedrini, H. Detection and classification of lung nodules in chest X-ray images using deep convolutional neural networks. Comput. Intell. 2019. [Google Scholar] [CrossRef]
- Rehman, M.Z.; Nawi, N.M.; Tanveer, A.; Zafar, H.; Munir, H.; Hassan, S. Lungs Cancer Nodules Detection from CT Scan Images with Convolutional Neural Networks. In Proceedings of the International Conference on Soft Computing and Data Mining, Melaka, Malaysia, 22–23 January 2020; Springer: Berlin, Germany, 2020; pp. 382–391. [Google Scholar]
- Ren, Y.; Tsai, M.Y.; Chen, L.; Wang, J.; Li, S.; Liu, Y.; Jia, X.; Shen, C. A manifold learning regularization approach to enhance 3D CT image-based lung nodule classification. Int. J. Comput. Assisted Radiol. Surg. 2019, 15, 287–295. [Google Scholar] [CrossRef]
- Kharya, S.; Dubey, D.; Soni, S. Predictive machine learning techniques for breast cancer detection. Int. J. Comput. Sci. Inf. Technol. 2013, 4, 1023–1028. [Google Scholar]
- Osareh, A.; Shadgar, B. Machine learning techniques to diagnose breast cancer. In Proceedings of the 2010 5th International Symposium on Health Informatics and Bioinformatics, Antalya, Turkey, 20–22 April 2010; pp. 114–120. [Google Scholar]
- Asri, H.; Mousannif, H.; Al Moatassime, H.; Noel, T. Using machine learning algorithms for breast cancer risk prediction and diagnosis. Procedia Comput. Sci. 2016, 83, 1064–1069. [Google Scholar] [CrossRef]
- Joshi, N.; Billings, S.; Schwartz, E.; Harvey, S.; Burlina, P. Machine Learning Methods for 1D Ultrasound Breast Cancer Screening. In Proceedings of the 2017 16th IEEE International Conference on Machine Learning and Applications (ICMLA), Cancun, Mexico, 18–21 December 2017; pp. 711–715. [Google Scholar]
- Lötsch, J.; Sipilä, R.; Tasmuth, T.; Kringel, D.; Estlander, A.M.; Meretoja, T.; Kalso, E.; Ultsch, A. Machine-learning-derived classifier predicts absence of persistent pain after breast cancer surgery with high accuracy. Breast Cancer Res. Treat. 2018, 171, 399–411. [Google Scholar] [CrossRef]
- Zupan, B.; DemšAr, J.; Kattan, M.W.; Beck, J.R.; Bratko, I. Machine learning for survival analysis: A case study on recurrence of prostate cancer. Artif. Intell. Med. 2000, 20, 59–75. [Google Scholar] [CrossRef]
- Wang, J.; Wu, C.J.; Bao, M.L.; Zhang, J.; Wang, X.N.; Zhang, Y.D. Machine learning-based analysis of MR radiomics can help to improve the diagnostic performance of PI-RADS v2 in clinically relevant prostate cancer. Eur. Radiol. 2017, 27, 4082–4090. [Google Scholar] [CrossRef]
- Nguyen, T.H.; Sridharan, S.; Macias, V.; Kajdacsy-Balla, A.; Melamed, J.; Do, M.N.; Popescu, G. Automatic Gleason grading of prostate cancer using quantitative phase imaging and machine learning. J. Biomed. Opt. 2017, 22, 036015. [Google Scholar] [CrossRef] [PubMed]
- Barlow, H.; Mao, S.; Khushi, M. Predicting high-risk prostate cancer using machine learning methods. Data 2019, 4, 129. [Google Scholar] [CrossRef]
- Li, S.; Shi, F.; Pu, F.; Li, X.; Jiang, T.; Xie, S.; Wang, Y. Hippocampal shape analysis of Alzheimer disease based on machine learning methods. Am. J. Neuroradiol. 2007, 28, 1339–1345. [Google Scholar] [CrossRef] [PubMed]
- Suk, H.I.; Lee, S.W.; Shen, D.; Alzheimer’s Disease Neuroimaging Initiative. Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis. NeuroImage 2014, 101, 569–582. [Google Scholar] [CrossRef]
- Mirzaei, G.; Adeli, A.; Adeli, H. Imaging and machine learning techniques for diagnosis of Alzheimer’s disease. Rev. Neurosci. 2016, 27, 857–870. [Google Scholar] [CrossRef]
- Khagi, B.; Kwon, G.R.; Lama, R. Comparative analysis of Alzheimer’s disease classification by CDR level using CNN, feature selection, and machine-learning techniques. Int. J. Imaging Syst. Technol. 2019, 29, 297–310. [Google Scholar] [CrossRef]
- Tahir, N.M.; Manap, H.H. Parkinson Disease Gait Classification based on Machine Learning Approach. J. Appl. Sci. Faisalabad (Faisalabad) 2012, 12, 180–185. [Google Scholar]
- Salvatore, C.; Cerasa, A.; Castiglioni, I.; Gallivanone, F.; Augimeri, A.; Lopez, M.; Arabia, G.; Morelli, M.; Gilardi, M.; Quattrone, A. Machine learning on brain MRI data for differential diagnosis of Parkinson’s disease and Progressive Supranuclear Palsy. J. Neurosci. Methods 2014, 222, 230–237. [Google Scholar] [CrossRef]
- Abós, A.; Baggio, H.C.; Segura, B.; García-Díaz, A.I.; Compta, Y.; Martí, M.J.; Valldeoriola, F.; Junqué, C. Discriminating cognitive status in Parkinson’s disease through functional connectomics and machine learning. Sci. Rep. 2017, 7, 45347. [Google Scholar] [CrossRef]
- Rastegari, E.; Azizian, S.; Ali, H. Machine Learning and Similarity Network Approaches to Support Automatic Classification of Parkinson’s Diseases Using Accelerometer-based Gait Analysis. In Proceedings of the 52nd Hawaii International Conference on System Sciences, Grand Wailea, Maui, HI, USA, 8–11 January 2019. [Google Scholar]
- Riordon, J.; Sovilj, D.; Sanner, S.; Sinton, D.; Young, E.W. Deep learning with microfluidics for biotechnology. Trends Biotechnol. 2018, 37, 310–324. [Google Scholar] [CrossRef]
- Schneider, G. Automating drug discovery. Nat. Rev. Drug Discov. 2018, 17, 97. [Google Scholar] [CrossRef] [PubMed]
- Berg, B.; Cortazar, B.; Tseng, D.; Ozkan, H.; Feng, S.; Wei, Q.; Chan, R.Y.L.; Burbano, J.; Farooqui, Q.; Lewinski, M.; et al. Cellphone-based hand-held microplate reader for point-of-care testing of enzyme-linked immunosorbent assays. ACS Nano 2015, 9, 7857–7866. [Google Scholar] [CrossRef] [PubMed]
- Bailey, M.; Oberheide, J.; Andersen, J.; Mao, Z.M.; Jahanian, F.; Nazario, J. Automated classification and analysis of internet malware. In Proceedings of the International Workshop on Recent Advances in Intrusion Detection, Gold Coast, Australia, 5–7 September 2007; Springer: Berlin, Germany, 2007; pp. 178–197. [Google Scholar]
- Bayer, U.; Comparetti, P.M.; Hlauschek, C.; Kruegel, C.; Kirda, E. Scalable, behavior-based malware clustering. NDSS Citeseer 2009, 9, 8–11. [Google Scholar]
- Rieck, K.; Laskov, P. Linear-time computation of similarity measures for sequential data. J. Mach. Learn. Res. 2008, 9, 23–48. [Google Scholar]
- Rieck, K.; Trinius, P.; Willems, C.; Holz, T. Automatic analysis of malware behavior using machine learning. J. Comput. Secur. 2011, 19, 639–668. [Google Scholar] [CrossRef]
- Nataraj, L.; Karthikeyan, S.; Jacob, G.; Manjunath, B. Malware images: Visualization and automatic classification. In Proceedings of the 8th International Symposium on Visualization for Cyber Security, Pittsburgh, PA, USA, 20 July 2011; ACM: New York, NY, USA, 2011; p. 4. [Google Scholar]
- Narayanan, B.N.; Djaneye-Boundjou, O.; Kebede, T.M. Performance analysis of machine learning and pattern recognition algorithms for malware classification. In Proceedings of the 2016 IEEE National Aerospace and Electronics Conference (NAECON) and Ohio Innovation Summit (OIS), Dayton, OH, USA, 25–29 July 2016; pp. 338–342. [Google Scholar]
- Ball, N.M.; Brunner, R.J. Data mining and machine learning in astronomy. Int. J. Mod. Phys. D 2010, 19, 1049–1106. [Google Scholar] [CrossRef]
- Way, M.J.; Scargle, J.D.; Ali, K.M.; Srivastava, A.N. Advances in Machine Learning and Data Mining for Astronomy; Chapman and Hall/CRC: Boca Raton, FL, USA, 2012. [Google Scholar]
- Ivezić, Ž.; Connolly, A.J.; VanderPlas, J.T.; Gray, A. Statistics, Data Mining, and Machine Learning in Astronomy: A Practical Python Guide for the Analysis of Survey Data; Princeton University Press: Princeton, NJ, USA, 2014; Volume 1. [Google Scholar]
- VanderPlas, J.; Connolly, A.J.; Ivezić, Ž.; Gray, A. Introduction to astroML: Machine learning for astrophysics. In Proceedings of the 2012 IEEE Conference on Intelligent Data Understanding, Boulder, CO, USA, 24–26 October 2012; pp. 47–54. [Google Scholar]
- Kremer, J.; Stensbo-Smidt, K.; Gieseke, F.; Pedersen, K.S.; Igel, C. Big universe, big data: Machine learning and image analysis for astronomy. IEEE Intell. Syst. 2017, 32, 16–22. [Google Scholar] [CrossRef]
- Andreon, S.; Gargiulo, G.; Longo, G.; Tagliaferri, R.; Capuano, N. Wide field imaging—I. Applications of neural networks to object detection and star/galaxy classification. Mon. Not. R. Astron. Soc. 2000, 319, 700–716. [Google Scholar] [CrossRef]
- Kim, E.J.; Brunner, R.J. Star-galaxy classification using deep convolutional neural networks. Mon. Not. R. Astron. Soc. 2016, 464, 4463–4475. [Google Scholar] [CrossRef]
- Walmsley, M.; Smith, L.; Lintott, C.; Gal, Y.; Bamford, S.; Dickinson, H.; Fortson, L.; Kruk, S.; Masters, K.; Scarlata, C.; et al. Galaxy Zoo: Probabilistic Morphology through Bayesian CNNs and Active Learning. arXiv 2019, arXiv:1905.07424. [Google Scholar] [CrossRef]
- Zhu, X.P.; Dai, J.M.; Bian, C.J.; Chen, Y.; Chen, S.; Hu, C. Galaxy morphology classification with deep convolutional neural networks. Astrophys. Space Sci. 2019, 364, 55. [Google Scholar] [CrossRef]
- Hoyle, B. Measuring photometric redshifts using galaxy images and Deep Neural Networks. Astron. Comput. 2016, 16, 34–40. [Google Scholar] [CrossRef]
- Pasquet, J.; Bertin, E.; Treyer, M.; Arnouts, S.; Fouchez, D. Photometric redshifts from SDSS images using a convolutional neural network. Astron. Astrophys. 2019, 621, A26. [Google Scholar] [CrossRef]
- Chan, M.C.; Stott, J.P. Deep-CEE I: Fishing for Galaxy Clusters with Deep Neural Nets. arXiv 2019, arXiv:1906.08784. [Google Scholar] [CrossRef]
- Hezaveh, Y.D.; Levasseur, L.P.; Marshall, P.J. Fast automated analysis of strong gravitational lenses with convolutional neural networks. Nature 2017, 548, 555. [Google Scholar] [CrossRef] [PubMed]
- Schaefer, C.; Geiger, M.; Kuntzer, T.; Kneib, J.P. Deep convolutional neural networks as strong gravitational lens detectors. Astron. Astrophys. 2018, 611, A2. [Google Scholar] [CrossRef]
- Pearson, J.; Pennock, C.; Robinson, T. Auto-detection of strong gravitational lenses using convolutional neural networks. Emergent Sci. 2018, 2, 1. [Google Scholar] [CrossRef]
- Ribli, D.; Pataki, B.Á.; Matilla, J.M.Z.; Hsu, D.; Haiman, Z.; Csabai, I. Weak lensing cosmology with convolutional neural networks on noisy data. arXiv 2019, arXiv:1902.03663. [Google Scholar] [CrossRef]
- Flamary, R. Astronomical image reconstruction with convolutional neural networks. In Proceedings of the 2017 25th European Signal Processing Conference (EUSIPCO), Kos Island, Greece, 28 August–2 September 2017; pp. 2468–2472. [Google Scholar]
- Karpathy, A.; Toderici, G.; Shetty, S.; Leung, T.; Sukthankar, R.; Fei-Fei, L. Large-scale video classification with convolutional neural networks. In Proceedings of the IEEE conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1725–1732. [Google Scholar]
- Abu-El-Haija, S.; Kothari, N.; Lee, J.; Natsev, P.; Toderici, G.; Varadarajan, B.; Vijayanarasimhan, S. Youtube-8m: A large-scale video classification benchmark. arXiv 2016, arXiv:1609.08675. [Google Scholar]
- Miech, A.; Laptev, I.; Sivic, J. Learnable pooling with context gating for video classification. arXiv 2017, arXiv:1706.06905. [Google Scholar]
- Wang, H.D.; Zhang, T.; Wu, J. The monkeytyping solution to the youtube-8m video understanding challenge. arXiv 2017, arXiv:1706.05150. [Google Scholar]
- Li, F.; Gan, C.; Liu, X.; Bian, Y.; Long, X.; Li, Y.; Li, Z.; Zhou, J.; Wen, S. Temporal modeling approaches for large-scale youtube-8m video understanding. arXiv 2017, arXiv:1707.04555. [Google Scholar]
- Chen, S.; Wang, X.; Tang, Y.; Chen, X.; Wu, Z.; Jiang, Y.G. Aggregating frame-level features for large-scale video classification. arXiv 2017, arXiv:1707.00803. [Google Scholar]
- Skalic, M.; Pekalski, M.; Pan, X.E. Deep learning methods for efficient large scale video labeling. arXiv 2017, arXiv:1706.04572. [Google Scholar]
- Bhardwaj, S.; Srinivasan, M.; Khapra, M.M. Efficient Video Classification Using Fewer Frames. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 354–363. [Google Scholar]
- Alahi, A.; Goel, K.; Ramanathan, V.; Robicquet, A.; Fei-Fei, L.; Savarese, S. Social lstm: Human trajectory prediction in crowded spaces. In Proceedings of the IEEE conference on computer vision and pattern recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 961–971. [Google Scholar]
- Yi, S.; Li, H.; Wang, X. Pedestrian behavior understanding and prediction with deep neural networks. In European Conference on Computer Vision; Springer: Berlin, Germany, 2016; pp. 263–279. [Google Scholar]
- Gupta, A.; Johnson, J.; Fei-Fei, L.; Savarese, S.; Alahi, A. Social gan: Socially acceptable trajectories with generative adversarial networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 2255–2264. [Google Scholar]
- Xu, Y.; Piao, Z.; Gao, S. Encoding crowd interaction with deep neural network for pedestrian trajectory prediction. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5275–5284. [Google Scholar]
- Zou, H.; Su, H.; Song, S.; Zhu, J. Understanding human behaviors in crowds by imitating the decision-making process. In Proceedings of the Thirty-Second AAAI Conference on Artificial Intelligence, New Orleans, LO, USA, 2–7 February 2018. [Google Scholar]
- Kitani, K.M.; Ziebart, B.D.; Bagnell, J.A.; Hebert, M. Activity forecasting. In European Conference on Computer Vision; Springer: Berlin, Germany, 2012; pp. 201–214. [Google Scholar]
- Jaipuria, N.; Habibi, G.; How, J.P. A transferable pedestrian motion prediction model for intersections with different geometries. arXiv 2018, arXiv:1806.09444. [Google Scholar]
- Sadeghian, A.; Kosaraju, V.; Sadeghian, A.; Hirose, N.; Rezatofighi, H.; Savarese, S. Sophie: An attentive gan for predicting paths compliant to social and physical constraints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 1349–1358. [Google Scholar]
- Yagi, T.; Mangalam, K.; Yonetani, R.; Sato, Y. Future person localization in first-person videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7593–7602. [Google Scholar]
- Liang, J.; Jiang, L.; Niebles, J.C.; Hauptmann, A.G.; Fei-Fei, L. Peeking into the future: Predicting future person activities and locations in videos. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 5725–5734. [Google Scholar]
- Laukkanen, S.; Karanta, I.; Kotovirta, V.; Markkanen, J.; Rönkkö, J. Adding intelligence to virtual reality. In Proceedings of the 16th European Conference in Artificial Intelligence, Valencia, Spain, 22–27 August 2004; pp. 1136–1144. [Google Scholar]
- Yang, H.W.; Pan, Z.G.; Xu, B.; Zhang, L.M. Machine learning-based intelligent recommendation in virtual mall. In Proceedings of the IEEE Third International Conference on Machine Learning and Cybernetics, Guangzhou, China, 18–21 August 2004; pp. 2634–2639. [Google Scholar]
- Altarteer, S.; Charissis, V. Technology acceptance model for 3D virtual reality system in luxury brands online stores. IEEE Access 2019, 54, 64053–64062. [Google Scholar] [CrossRef]
- Martínez, H.; Skournetou, D.; Hyppölä, J.; Laukkanen, S.; Heikkilä, A. Drivers and bottlenecks in the adoption of augmented reality applications. J. Multimed. Theory Appl. 2014, 1, 27–44. [Google Scholar] [CrossRef]
- Olshannikova, E.; Ometov, A.; Koucheryavy, Y.; Olsson, T. Visualizing Big Data with augmented and virtual reality: Challenges and research agenda. J. Big Data 2018, 2, 1–27. [Google Scholar] [CrossRef]
- Lagoo, R.; Charissis, V.; Harrison, D. Mitigating Driver’s Distraction with the use of Augmented Reality Head-Up Display and Gesture Recognition system. IEEE Consum. Electron. Mag. 2019, 8, 79–85. [Google Scholar] [CrossRef]
- Charissis, V.; Papanastasiou, S. Artificial Intelligence Rationale for Autonomous Vehicle Agents Behaviour in Driving Simulation Environment. Adv. Robot. Autom. Control 2008, 314–332. [Google Scholar]
- Ropelato, S.; Zünd, F.; Magnenat, S.; Menozzi, M.; Sumner, R.W. Adaptive Tutoring on a Virtual Reality Driving Simulator. In Proceedings of the International SERIES on Information Systems and Management in Creative eMedia (CreMedia), Bangkok, Thailand, 27–30 November 2017; pp. 12–17. [Google Scholar]
- Lin, C.T.; Chung, I.F.; Ko, L.W.; Chen, Y.C.; Liang, S.F.; Duann, J.R. EEG-Based assessment of driver cognitive responses in a dynamic virtual-reality driving environment. IEEE Trans. Biomed. Eng. 2007, 54, 1349–1352. [Google Scholar] [PubMed]
- Charissis, V.; Papanastasiou, S. Human-Machine Collaboration Through Vehicle Head-Up Display Interface. Int. J. Cogn. Technol. Work 2010, 12, 41–50. [Google Scholar] [CrossRef]
- Charissis, V.; Papanastasiou, S.; Chan, W.; Peytchev, E. Evolution of a full-windshield HUD designed for current VANET communication standards. In Proceedings of the 2013 IEEE Intelligent Transportation Systems International Conference, The Hague, Netherlands, 6–9 October 2013; pp. 1637–1643. [Google Scholar]
- Wang, S.; Charissis, V.; Lagoo, R.; Campbell, J.; Harrison, D. Reducing Driver Distraction by Utilising Augmented Reality Head-Up Display System for Rear Passengers. In Proceedings of the 2019 IEEE International Conference on Consumer Electronics (ICCE), Las Vegas, NV, USA, 11–13 January 2019; pp. 1–6. [Google Scholar]
- Feng, L.F.; Fei, J. Gesture recognition algorithm based on image information fusion in virtual reality. Pers. Ubiquitous Comput. 2019, 23, 487–497. [Google Scholar]
- Petrovic, V. Artificial Intelligence and Virtual Worlds—Toward Human-Level AI Agents. IEEE Access 2019, 1–6. [Google Scholar] [CrossRef]
- Lim, M.Y.; Dias, J.; Aylett, R.; Paiva, A. Creating adaptive affective autonomous NPCs. Auton. Agents Multi-Agent Syst. 2012, 24, 287–311. [Google Scholar] [CrossRef]
- Zhou, C.N.; Yu, X.L.; Sun, J.Y.; Yan, X.L. Affective computation based NPC behaviors modeling. In Proceedings of the International Conference on Web Intelligence and Intelligent Agent Technology, Madrid, Spain, 21–23 September 2006; pp. 1–4. [Google Scholar]
- Vazquez, D.; Meyer, L.A.; Marın, J.; Ponsa, D.; Geronimo, D. Virtual and Real World Adaptation for Pedestrian Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 797–809. [Google Scholar] [CrossRef]
- Vazquez, D.; Meyer, L.A.; Marın, J.; Ponsa, D.; Geronimo, D. Deep Learning Development Environment in Virtual Reality. CoRR 2019, 1–10. [Google Scholar]
- Harley, A.W. An interactive node-link visualization of convolutional neural networks. Adv. Visual Comput. 2015, 9474, 867–877. [Google Scholar]
- Harley, A.W.; Ufkes, A.; Derpanis, K.G. Evaluation of deep convolutional nets for document image classification and retrieval. In Proceedings of the 13th International Conference on Document Analysis and Recognition (ICDAR), Nancy, France, 23–26 August 2015; pp. 991–995. [Google Scholar]
- Qi, Q.; Tao, F. Digital Twin and Big Data towards smart manufacturing and industry 4.0: 360 degree comparison. IEEE Access 2018, 6, 3585–3593. [Google Scholar] [CrossRef]
- Qiao, Q.; Wang, J.; Ye, L.; Gao, R.X. Digital Twin for machining tool condition prediction. CIRP Conf. Manuf. Syst. 2019, 81, 1388–1393. [Google Scholar] [CrossRef]
- Madni, A.M.; Madni, C.C.; Lucero, S.D. Leveraging Digital Twin Technology in Model-Based Systems Engineering. Systems 2019, 7, 7. [Google Scholar] [CrossRef]
- Jaensch, F.; Csiszar, A.; Scheifele, C.; Verl, A. Digital Twins of Manufacturing Systems as a Base for Machine Learning. In Proceedings of the IEEE 25th International Conference on Mechatronics and Machine Vision in Practice (IEEE M2VIP), Stuttgart, Germany, 20–22 November 2018; pp. 1–13. [Google Scholar]
- Chen, M.; Saad, W.; Yin, C. Virtual Reality Over Wireless Networks: Quality-of-Service Model and Learning-Based Resource Management. IEEE Trans. Commun. 2018, 66, 5621–5635. [Google Scholar] [CrossRef]
- Chen, M.; Saad, W.; Yin, C.; Dbbah, M. Data Correlation-Aware Resource Management in Wireless Virtual Reality (VR): An Echo State Transfer Learning Approach. IEEE Trans. Commun. 2019, 67, 4267–4280. [Google Scholar] [CrossRef]
- Chen, M.; Saad, W.; Yin, C. Echo-Liquid State Deep Learning for 360° Content Transmission and Caching in Wireless VR Networks With Cellular Connected UAVs. IEEE Trans. Commun. 2019, 67, 6386–6400. [Google Scholar] [CrossRef]
- Alkhateeb, A.; Alex, S.; Varkey, P.; Li, Y.; Qu, Q.; Tujkovic, D. Deep Learning Coordinated Beamforming for Highly-Mobile Millimeter Wave Systems. IEEE Access 2019, 6, 37328–37348. [Google Scholar] [CrossRef]
- Strubell, E.; Ganesh, A.; McCallum, A. Energy and Policy Considerations for Deep Learning in NLP. arXiv 2019, arXiv:1906.02243. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).