First-Principles Calculations of Structural, Mechanical, and Electronic Properties of the B2-Phase NiTi Shape-Memory Alloy Under High Pressure
Abstract
1. Introduction
2. Methodology
3. Results and Discussions
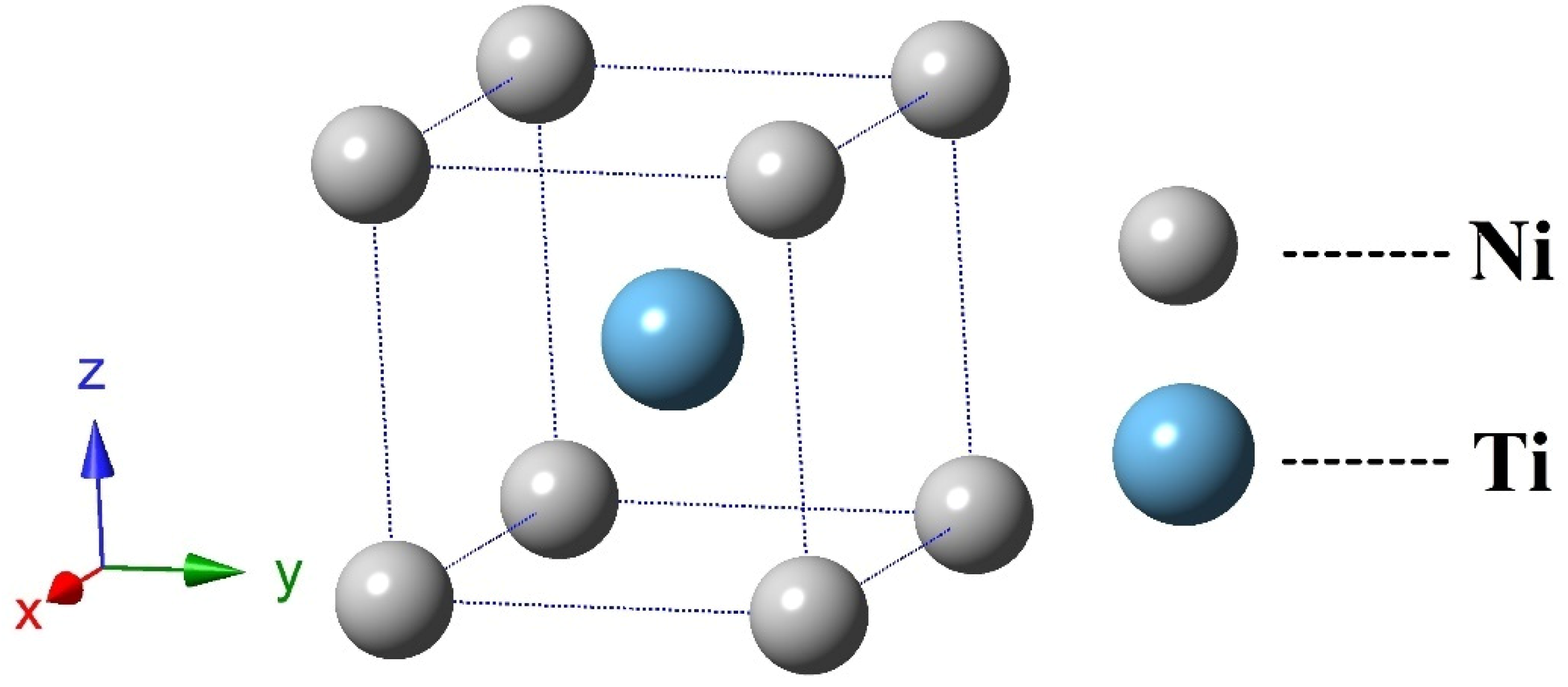
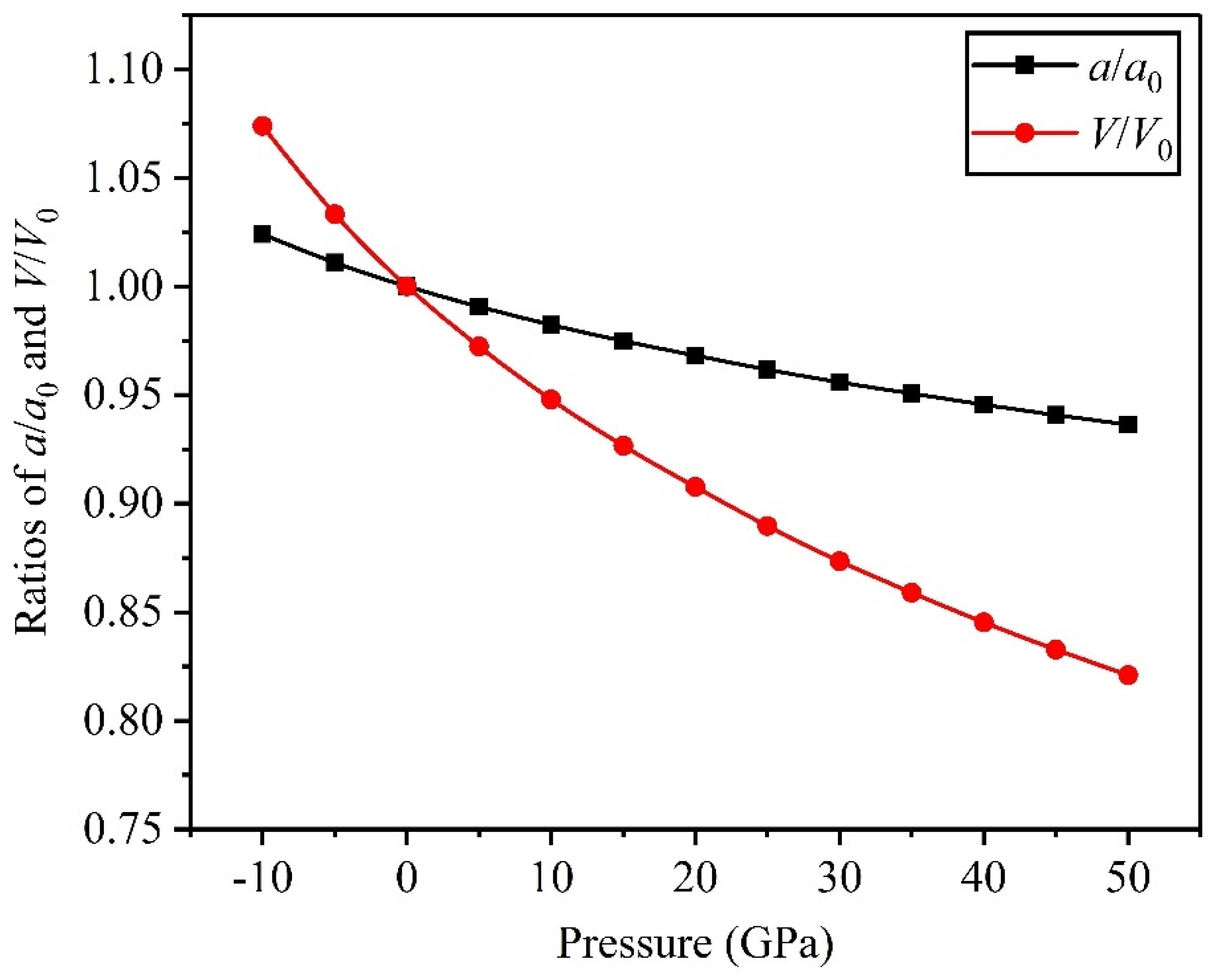
3.1. Structure Properties and Stability
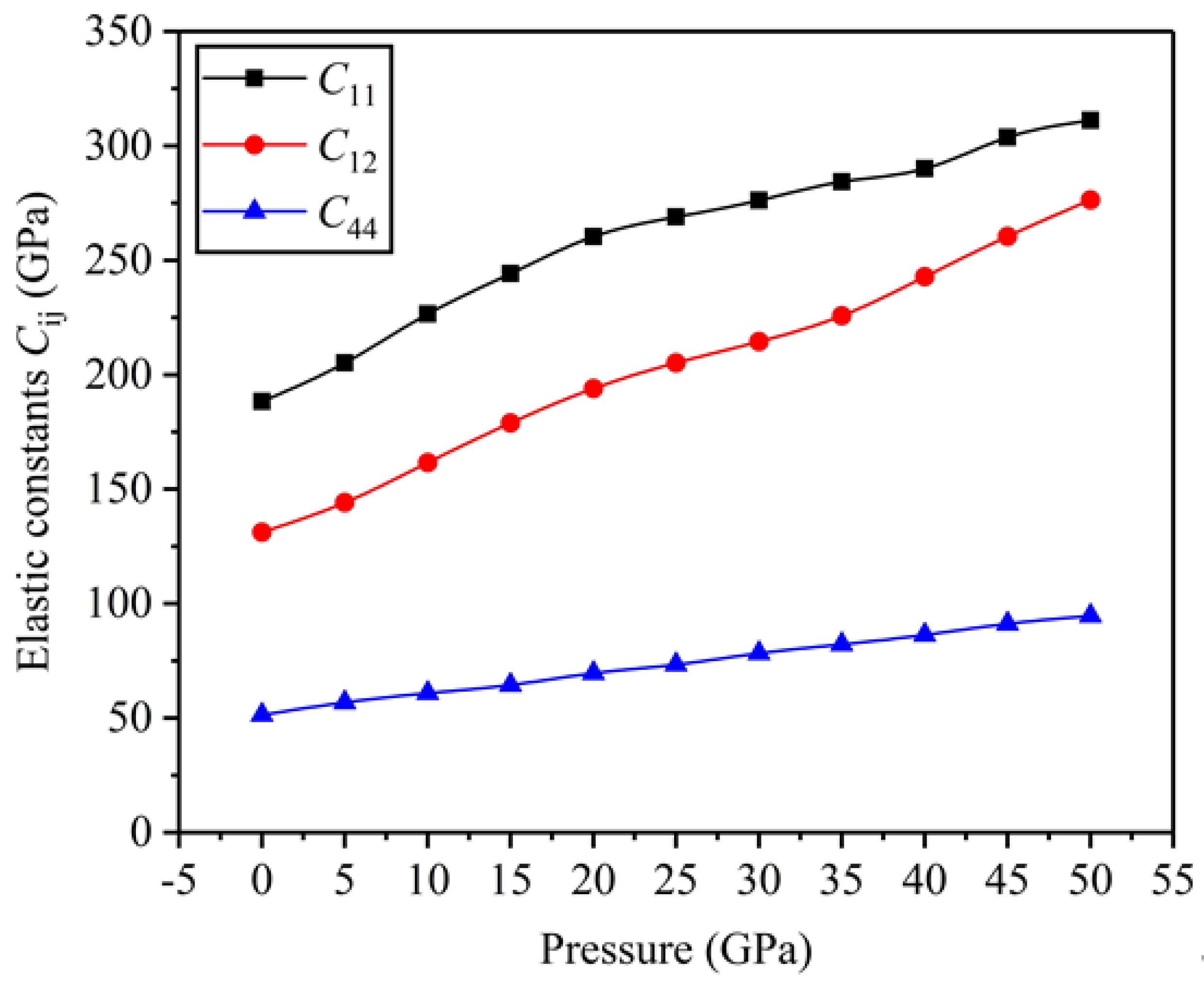
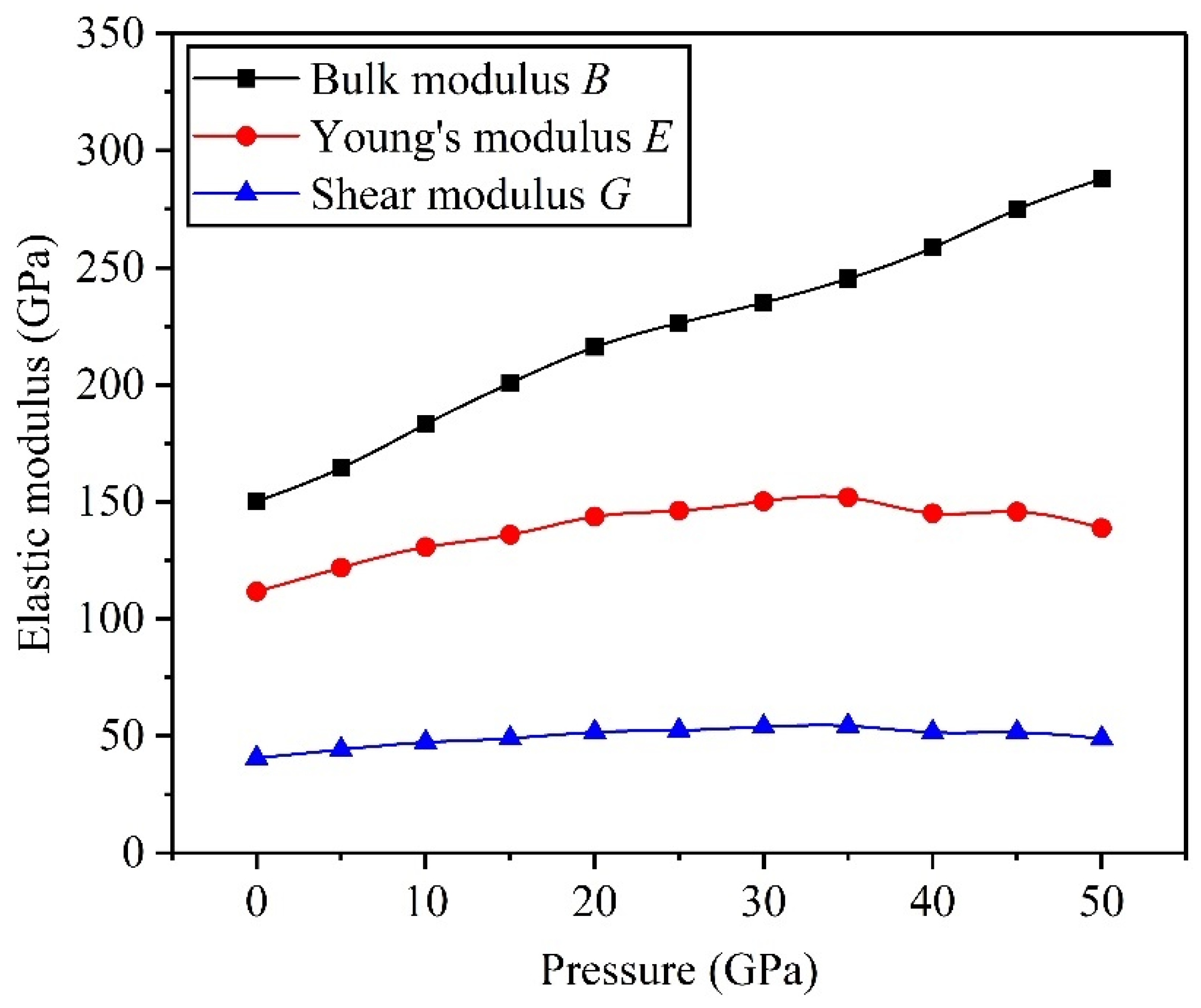
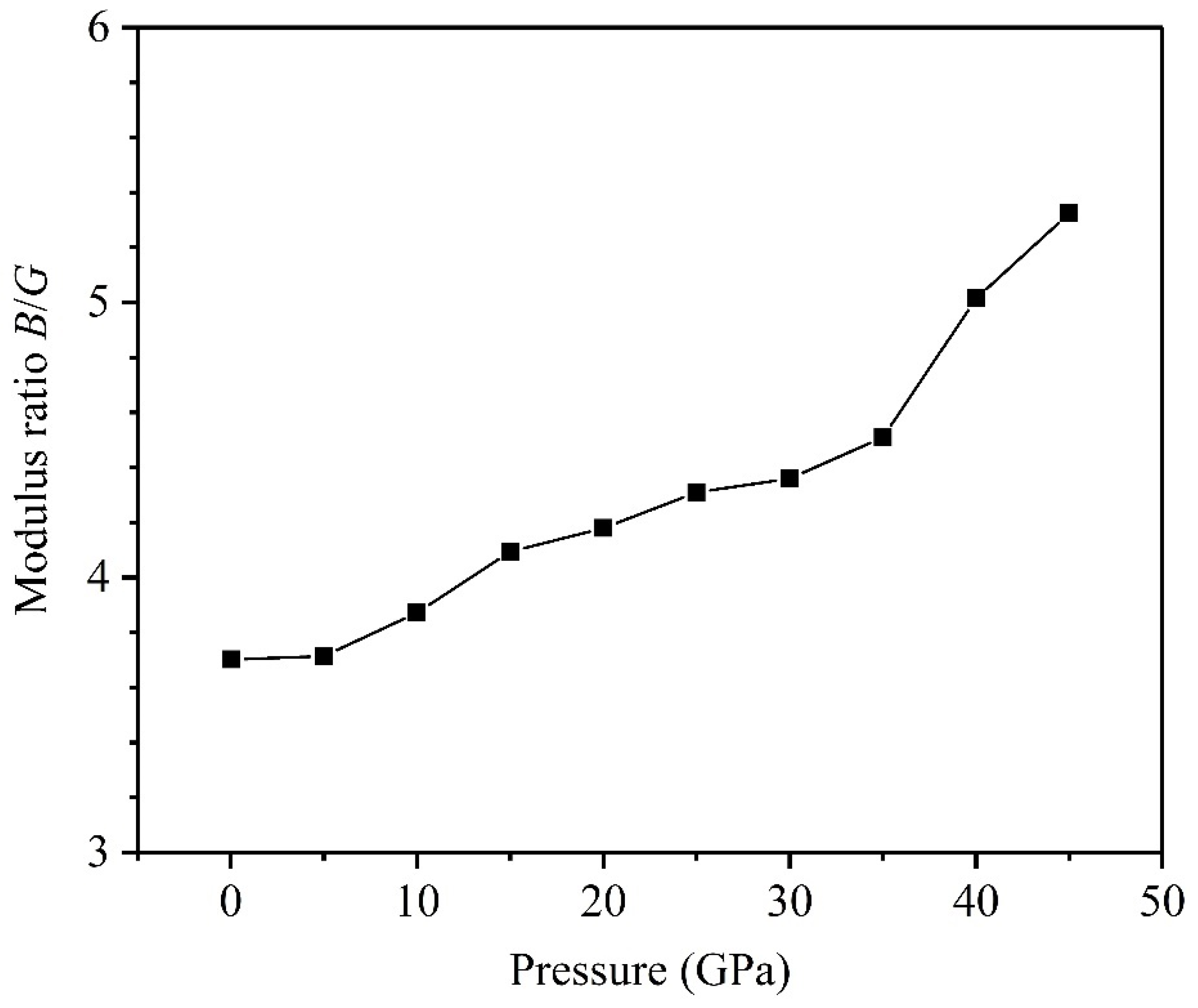
3.2. Mechanical Properties
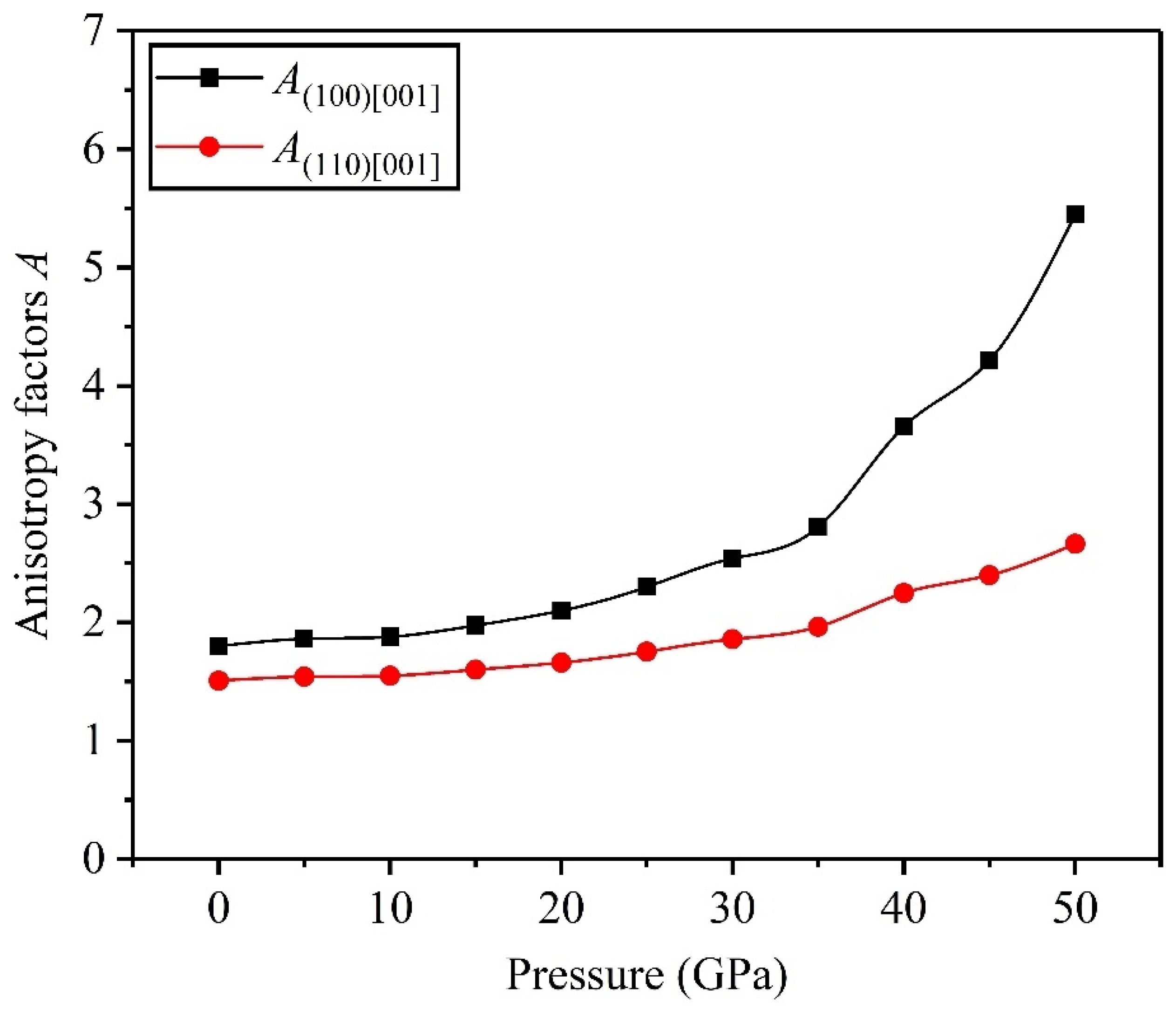
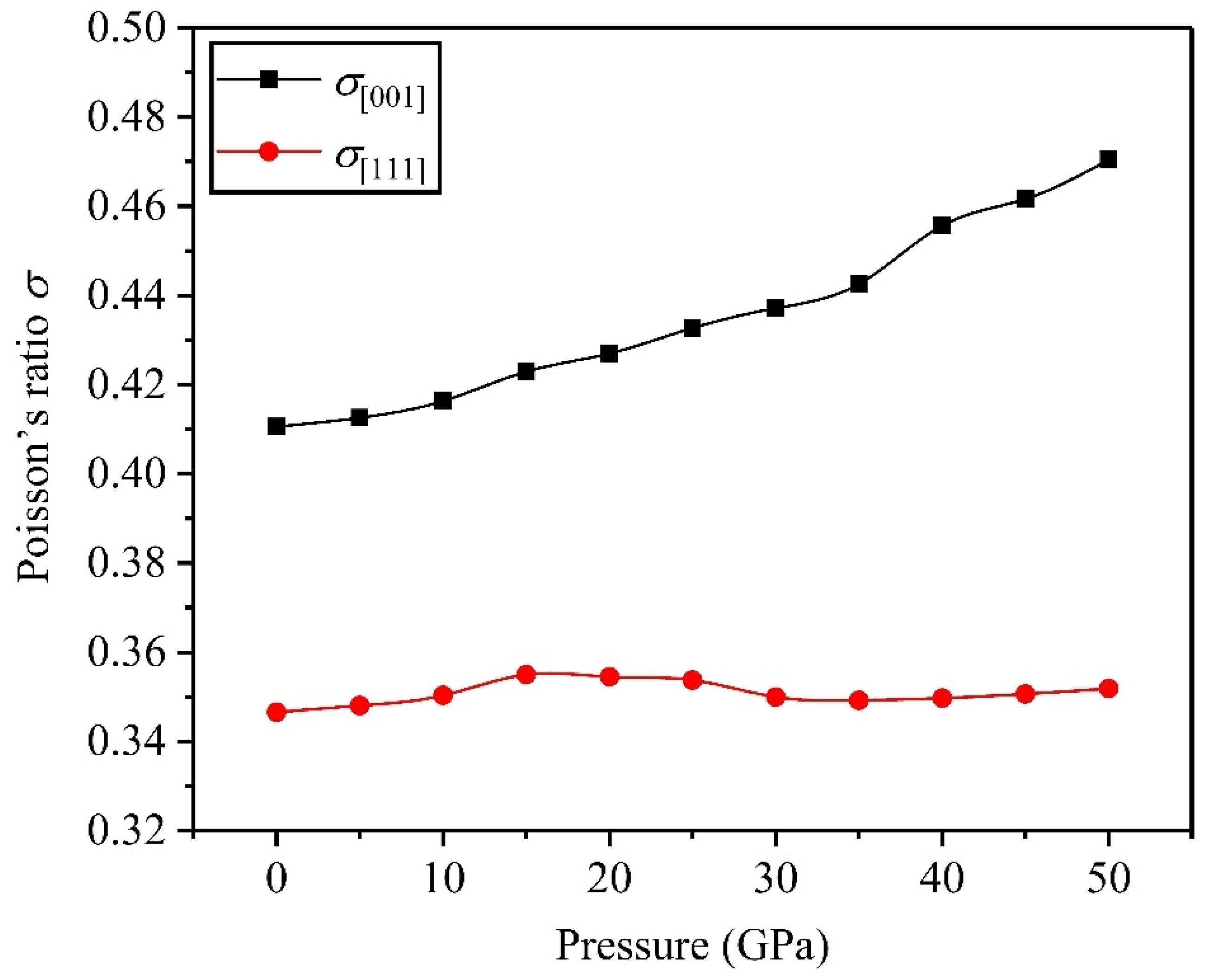
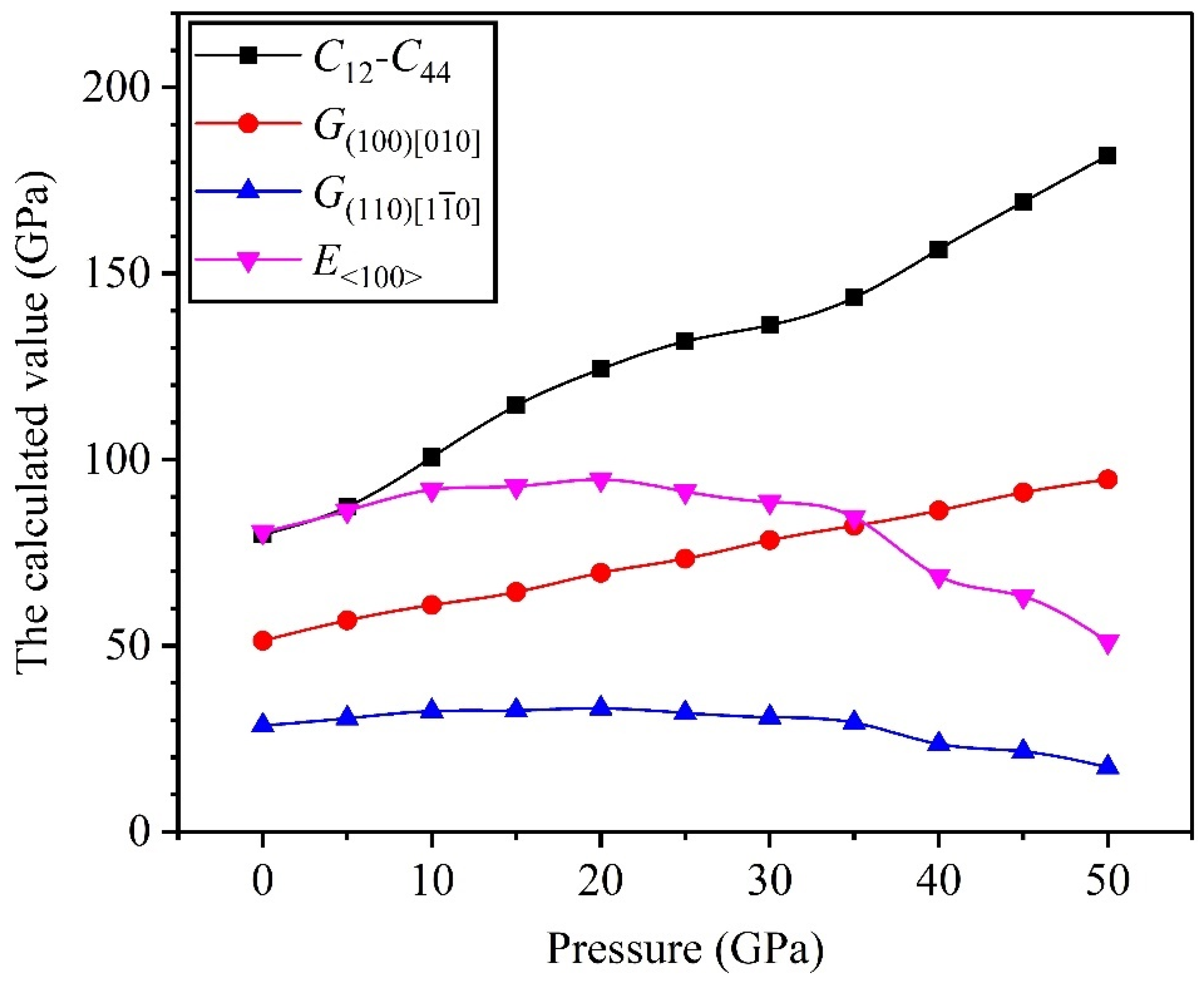
3.3. Elastic Anisotropy
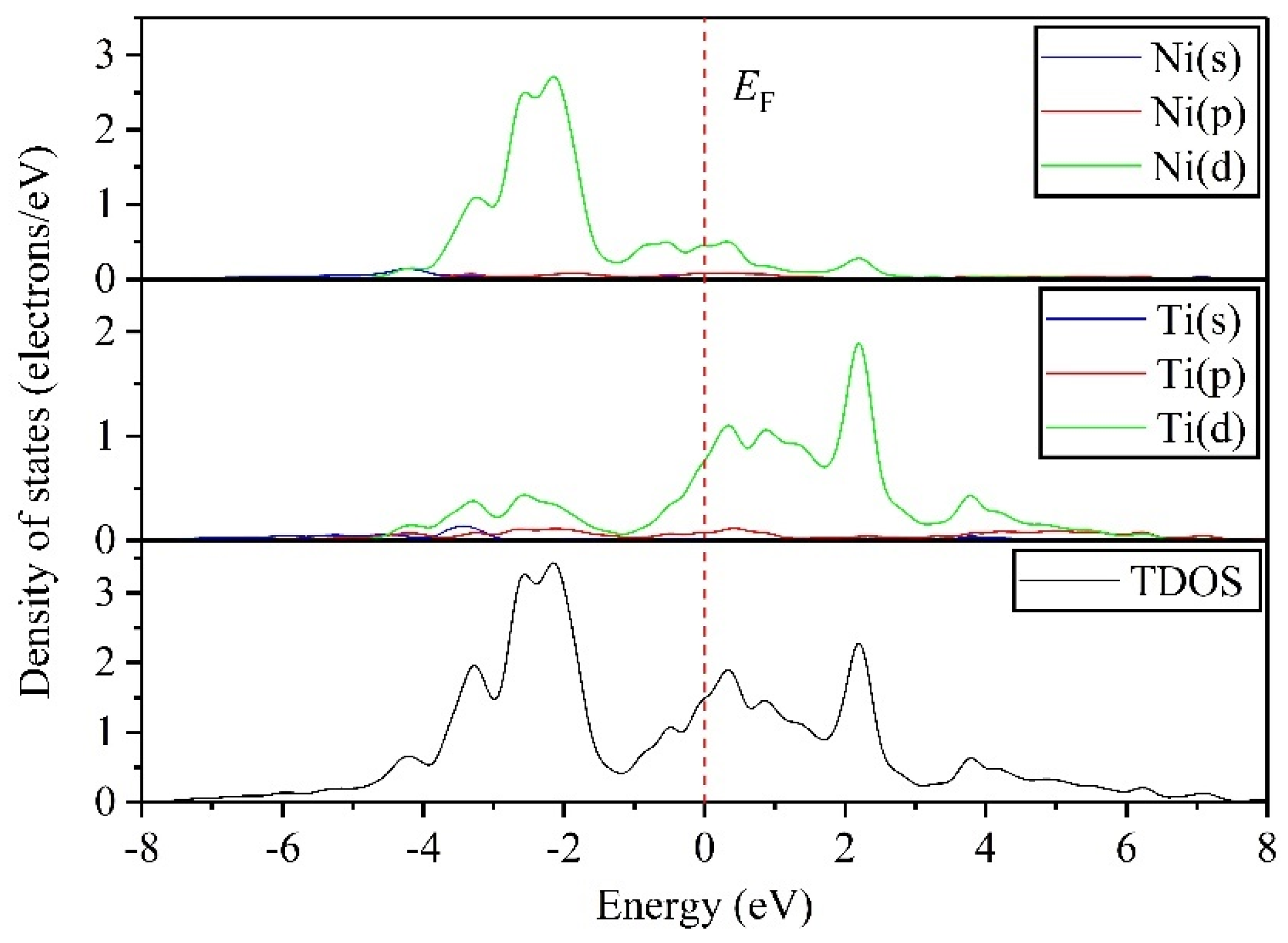
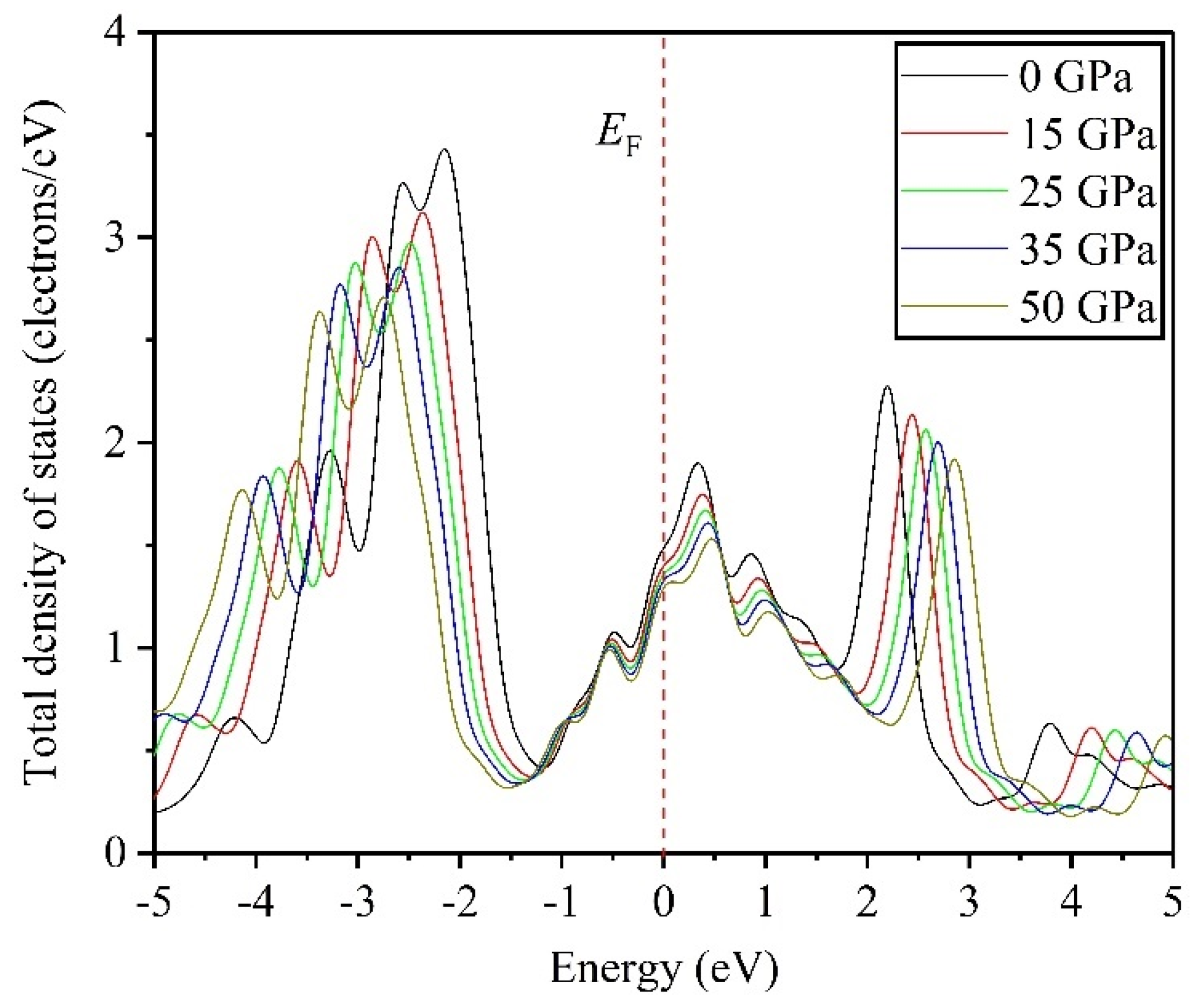
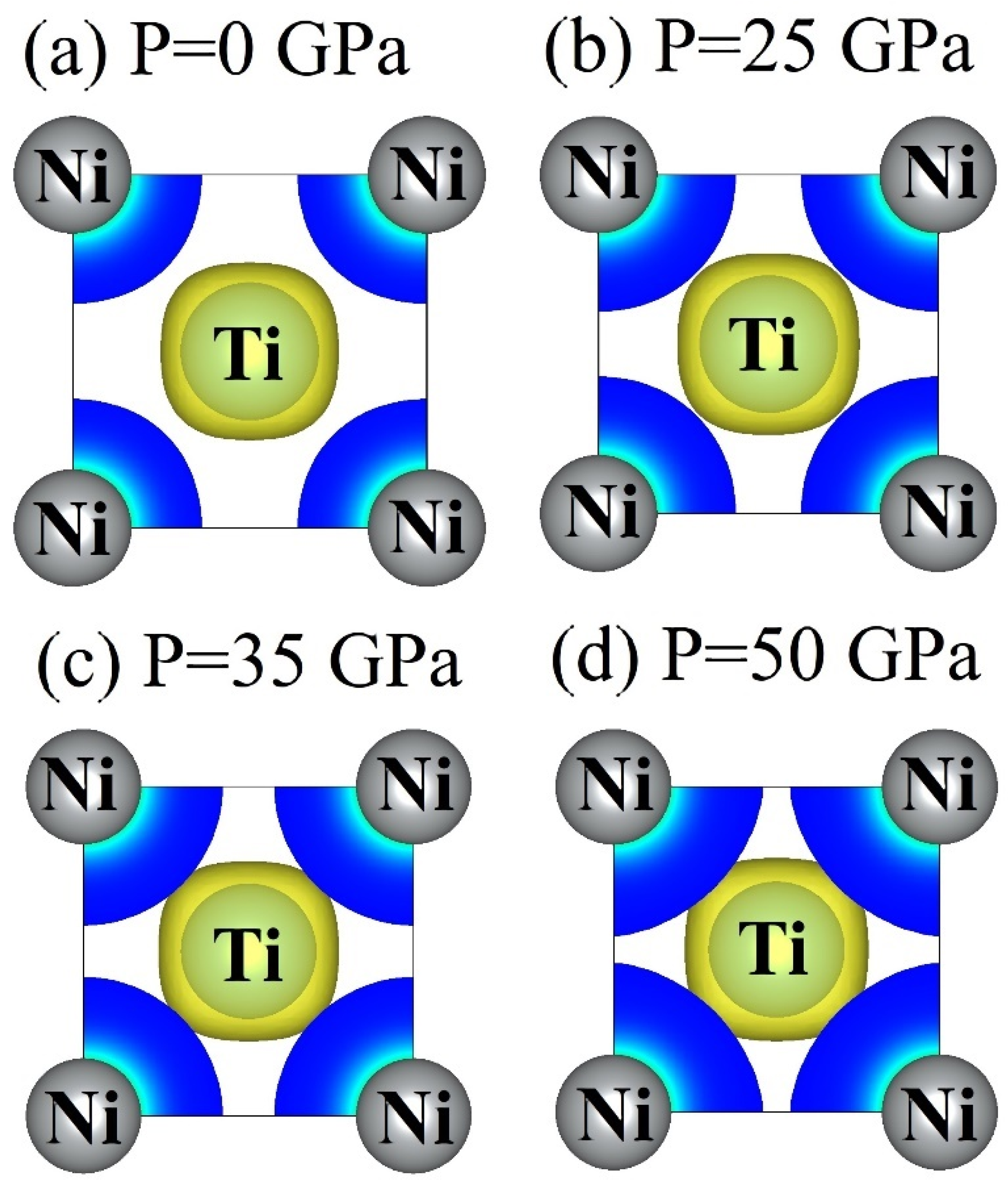
3.4. Electronic Properties
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Duerig, T.; Pelton, A.; Stöckel, D. An overview of nitinol medical applications. Mater. Sci. Eng. A 1999, 273–275, 149–160. [Google Scholar] [CrossRef]
- Michiardi, A.; Aparicio, C.; Planell, J.A.; Gil, F.J. Electrochemical behaviour of oxidized NiTi shape memory alloys for biomedical applications. Surf. Coat. Technol. 2007, 201, 6484–6488. [Google Scholar] [CrossRef]
- Morgan, N.B. Medical shape memory alloy applications—The market and its products. Mater. Sci. Eng. A 2004, 378, 16–23. [Google Scholar] [CrossRef]
- Chau, E.T.F.; Friend, C.M.; Allen, D.M.; Hora, J.; Webster, J.R. A technical and economic appraisal of shape memory alloys for aerospace applications. Mater. Sci. Eng. A 2006, 438–440, 589–592. [Google Scholar] [CrossRef]
- Jani, J.M.; Leary, M.; Subic, A.; Gibson, M.A. A review of shape memory alloy research, applications and opportunities. Mater. Des. 2014, 56, 1078–1113. [Google Scholar] [CrossRef]
- Pozzi, M.; Airoldi, G. The electrical transport properties of shape memory alloys. Mater. Sci. Eng. A 1999, 273–275, 300–304. [Google Scholar] [CrossRef]
- Schetky, L.M. Shape memory alloy applications in space systems. Mater. Des. 1991, 12, 29–32. [Google Scholar] [CrossRef]
- Elahinia, M.H.; Hashemi, M.; Tabesh, M.; Bhaduri, S.B. Manufacturing and processing of NiTi implants: A review. Prog. Mater. Sci. 2012, 57, 911–946. [Google Scholar] [CrossRef]
- Otsuka, K.; Ren, X. Physical metallurgy of Ti–Ni-based shape memory alloys. Prog. Mater. Sci. 2005, 50, 511–678. [Google Scholar] [CrossRef]
- Plietsch, R.; Ehrlich, K. Strength differential effect in pseudoelastic NiTi shape memory alloys. Acta Mater. 1997, 45, 2417–2424. [Google Scholar] [CrossRef]
- Li, D.S.; Zhang, Y.P.; Eggeler, G.; Zhang, X.P. High porosity and high-strength porous NiTi shape memory alloys with controllable pore characteristics. J. Alloys Compd. 2009, 470, L1–L5. [Google Scholar] [CrossRef]
- Starosvetsky, D.; Gotman, I. Corrosion behavior of titanium nitride coated Ni–Ti shape memory surgical alloy. Biomaterials 2001, 22, 1853–1859. [Google Scholar] [CrossRef]
- Es-Souni, M.; Es-Souni, M.; Fischer-Brandies, H. On the properties of two binary NiTi shape memory alloys. Effects of surface finish on the corrosion behaviour and in vitro biocompatibility. Biomaterials 2002, 23, 2887–2894. [Google Scholar] [CrossRef]
- Li, Y.C.; Wang, F.H.; Shang, J.X. Ab initio study of oxygen adsorption on the NiTi (110) surface and the surface phase diagram. Corros. Sci. 2016, 106, 137–146. [Google Scholar] [CrossRef]
- Chowdhury, P.; Patriarca, L.; Ren, G.W.; Sehitoglu, H. Molecular Dynamics Modeling of NiTi Superelasticity in Presence of Nanoprecipitates. Int. J. Plast. 2016, 81, 152–167. [Google Scholar] [CrossRef]
- Šesták, P.; Černý, M.; He, J.Y.; Zhang, Z.L.; Pokluda, J. Multiaxial stress–strain response and displacive transformations in NiTi alloy from first principles. Acta Mater. 2016, 109, 223–229. [Google Scholar] [CrossRef]
- Laplanche, G.; Birk, T.; Schneider, S.; Frenzel, J.; Eggeler, G. Effect of temperature and texture on the reorientation of martensite variants in NiTi shape memory alloys. Acta Mater. 2017, 127, 143–152. [Google Scholar] [CrossRef]
- Xiao, Y.; Zeng, P.; Lei, L.P.; Zhang, Y.Z. In situ observation on temperature dependence of martensitic transformation and plastic deformation in superelastic NiTi shape memory alloy. Mater. Des. 2017, 134, 111–120. [Google Scholar] [CrossRef]
- Haskins, J.B.; Lawson, J.W. Finite temperature properties of NiTi from first principles simulations: Structure, mechanics, and thermodynamics. J. Appl. Phys. 2017, 121, 205103. [Google Scholar] [CrossRef]
- Lee, J.; Ikeda, Y.; Tanaka, I. Solution effect on improved structural compatibility of NiTi-based alloys by systematic first-principles calculations. J. Appl. Phys. 2019, 125, 055106. [Google Scholar] [CrossRef]
- Liu, G.T.; Liu, H.Y.; Feng, X.L.; Redfern, S.A.T. High-pressure phase transitions of nitinol NiTi to a semiconductor with an unusual topological structure. Phys. Rev. B 2018, 97, 140104. [Google Scholar] [CrossRef]
- Ataei, M.; Zarei-Hanzaki, A.; Shamsolhodaei, A. Shape memory response and mechanical properties of warm deformed NiTi intermetallic alloy. Mater. Sci. Eng. A 2017, 680, 291–296. [Google Scholar] [CrossRef]
- Wang, L.; Ma, L.; Liu, C.; Zhong, Z.Y.; Luo, S.N. Texture-induced anisotropic phase transformation in a NiTi shape memory alloy. Mater. Sci. Eng. A 2018, 718, 96–103. [Google Scholar] [CrossRef]
- Zeng, Z.Y.; Hu, C.E.; Cai, L.C.; Chen, X.R.; Jing, F.Q. First-principles determination of the structure, elastic constant, phase diagram and thermodynamics of NiTi alloy. Phys. B 2010, 405, 3665–3672. [Google Scholar] [CrossRef]
- Sandoval, L.; Haskins, J.B.; Lawson, J.W. Stability, structure, and suppression of the martensitic transition temperature by B19’ compound twins in NiTi: Ab initio and classical simulations. Acta Mater. 2018, 154, 182–189. [Google Scholar] [CrossRef]
- Milman, V.; Winkler, B.; White, J.A.; Pickard, C.J.; Payne, M.C.; Akhmatskaya, E.V.; Nobes, R.H. Electronic Structure, Properties, and Phase Stability of Inorganic Crystals: A Pseudopotential Plane-Wave Study. Int. J. Quantum Chem. 2000, 77, 895–910. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J.; Pickard, C.J.; Hasnip, P.J.; Clark, S.J.; Payne, M.C. First-Principles Simulation: Ideas, Illustrations and the CASTEP Code. J. Phys. Condens. Matter 2002, 14, 2717–2744. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.J.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Z. Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Vanderbilt, D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism. Phys. Rev. B 1990, 41, 7892–7895. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special points for Brillouin-zone integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Fischer, T.H.; Almlof, J. General methods for geometry and wave function optimization. J. Phys. Chem. 1992, 96, 9768–9774. [Google Scholar] [CrossRef]
- Birch, F. Finite Elastic Strain of Cubic Crystals. Phys. Rev. 1947, 71, 809–824. [Google Scholar] [CrossRef]
- Cheng, D.Y.; Zhao, S.J.; Wang, S.Q.; Ye, H.Q. First-principles study of the elastic properties and electronic structure of NiTi, CoTi and FeTi. Philos. Mag. A 2001, 81, 1625–1632. [Google Scholar] [CrossRef]
- Hatcher, N.; Kontsevoi, O.Y.; Freeman, A.J. Role of elastic and shear stabilities in the martensitic transformation path of NiTi. Phys. Rev. B 2009, 80, 144203. [Google Scholar] [CrossRef]
- Kadkhodaei, S.; Walle, A.V.D. First-principles calculations of thermal properties of the mechanically unstable phases of the PtTi and NiTi shape memory alloys. Acta Mater. 2018, 147, 296–303. [Google Scholar] [CrossRef]
- Mizuno, M.; Araki, H.; Shirai, Y. Compositional dependence of structures of NiTi martensite from first principles. Acta Mater. 2015, 95, 184–191. [Google Scholar] [CrossRef]
- Chen, L.; Li, Y.F.; Xiao, B.; Zheng, Q.L.; Gao, Y.M.; Zhao, S.Y.; Wang, Z.C. First-principles calculation on the adhesion strength, fracture mechanism, interfacial bonding of the NiTi (111)//α-Al2O3 (0001) interfaces. Mater. Des. 2019, 183, 108119. [Google Scholar] [CrossRef]
- Sittner, P.; Lukás, P.; Neov, D.; Novák, V.; Toebbens, D.M. In situ neutron diffraction studies of martensitic transformations in NiTi. J. Phys. IV 2003, 112, 709–712. [Google Scholar] [CrossRef]
- Wang, J.H.; Yip, S.; Phillpot, S.R.; Wolf, D. Crystal instabilities at finite strain. Phys. Rev. Lett. 1993, 71, 4182–4185. [Google Scholar] [CrossRef]
- Patil, S.K.R.; Khare, S.V.; Tuttle, B.R.; Bording, J.K.; Kodambaka, S. Mechanical stability of possible structures of PtN investigated using first-principles calculations. Phys. Rev. B 2006, 73, 104118. [Google Scholar] [CrossRef]
- Hu, Q.M.; Yang, R.; Lu, J.M.; Wang, L.; Johansson, B.; Vitos, L. Effect of Zr on the properties of (TiZr)Ni alloys from first-principles calculations. Phys. Rev. B 2007, 76, 224201. [Google Scholar] [CrossRef]
- Wagner, M.F.X.; Windl, W. Lattice stability, elastic constants and macroscopic moduli of NiTi martensites from first principles. Acta Mater. 2008, 56, 6232–6245. [Google Scholar] [CrossRef]
- Mercier, O.; Melton, K.N.; Gremaud, G.; Hägi, J. Single-crystal elastic constants of the equiatomic NiTi alloy near the martensitic transformation. J. Appl. Phys. 1980, 51, 1833–1834. [Google Scholar] [CrossRef]
- Bakhtiari, S.R.; Liu, J.Z.; Shariat, B.S.; Yang, H.; Liu, Y.N. Role of hydrostatic pressure on the phase stability, the ground state, and the transformation pathways of NiTi alloy. Scr. Mater. 2018, 151, 57–60. [Google Scholar] [CrossRef]
- Pugh, S.F. XCII. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals. Philos. Mag. 1954, 45, 823–843. [Google Scholar] [CrossRef]
- Cao, Y.; Zhu, J.C.; Nong, Z.S.; Yang, X.W.; Liu, Y.; Lai, Z.H. First-principles studies of the structural, elastic, electronic and thermal properties of Ni3Nb. Comput. Mater. Sci. 2013, 77, 208–213. [Google Scholar] [CrossRef]
- Iotova, D.; Kioussis, N.; Lim, S.P. Electronic structure and elastic properties of the Ni3X (X = Mn, Al, Ga, Si, Ge) intermetallics. Phys. Rev. B 1996, 54, 14413–14422. [Google Scholar] [CrossRef] [PubMed]
- Hill, R. The elastic behaviour of a crystalline aggregate. Proc. Phys. Soc. A 1952, 65, 349–354. [Google Scholar] [CrossRef]
- Mattesini, M.; Ahuja, R.; Johansson, B. Cubic Hf3N4 and Zr3N4: A class of hard materials. Phys. Rev. B 2003, 68, 184108. [Google Scholar] [CrossRef]
- Fu, H.Z.; Li, D.H.; Peng, F.; Gao, T.; Cheng, X.L. Ab initio calculations of elastic constants and thermodynamic properties of NiAl under high pressures. Comput. Mater. Sci. 2008, 44, 774–778. [Google Scholar] [CrossRef]
- Yoo, M.H. On the theory of anomalous yield behavior of Ni3Al—Effect of elastic anisotropy. Scr. Metall. 1986, 20, 915–920. [Google Scholar] [CrossRef]
- Lau, K.; Mccurdy, A.K. Elastic anisotropy factors for orthorhombic, tetragonal, and hexagonal crystals. Phys. Rev. B 1998, 58, 8980–8984. [Google Scholar] [CrossRef]
- Fu, H.Z.; Li, X.F.; Liu, W.F.; Ma, Y.M.; Gao, T.; Hong, X.H. Electronic and dynamical properties of NiAl studied from first principles. Intermetallics 2011, 19, 1959–1967. [Google Scholar] [CrossRef]
- Reed, R.P.; Clark, A.F. American Society of Metals; Metals Park: Geauga County, OH, USA, 1983. [Google Scholar]
- Friák, M.; Šob, M.; Vitek, V. Ab initio calculation of tensile strength in iron. Philos. Mag. 2003, 83, 3529–3537. [Google Scholar] [CrossRef]
- Fu, H.Z.; Peng, W.M.; Gao, T. Structural and elastic properties of ZrC under high pressure. Mater. Chem. Phys. 2009, 115, 789–794. [Google Scholar] [CrossRef]
- Pettifor, D.G. Theoretical predictions of structure and related properties of intermetallics. Mater. Sci. Technol. 1992, 8, 345–349. [Google Scholar] [CrossRef]
- Johnson, R.A. Analytic nearest-neighbor model for FCC metals. Phys. Rev. B 1988, 37, 3924–3931. [Google Scholar] [CrossRef] [PubMed]
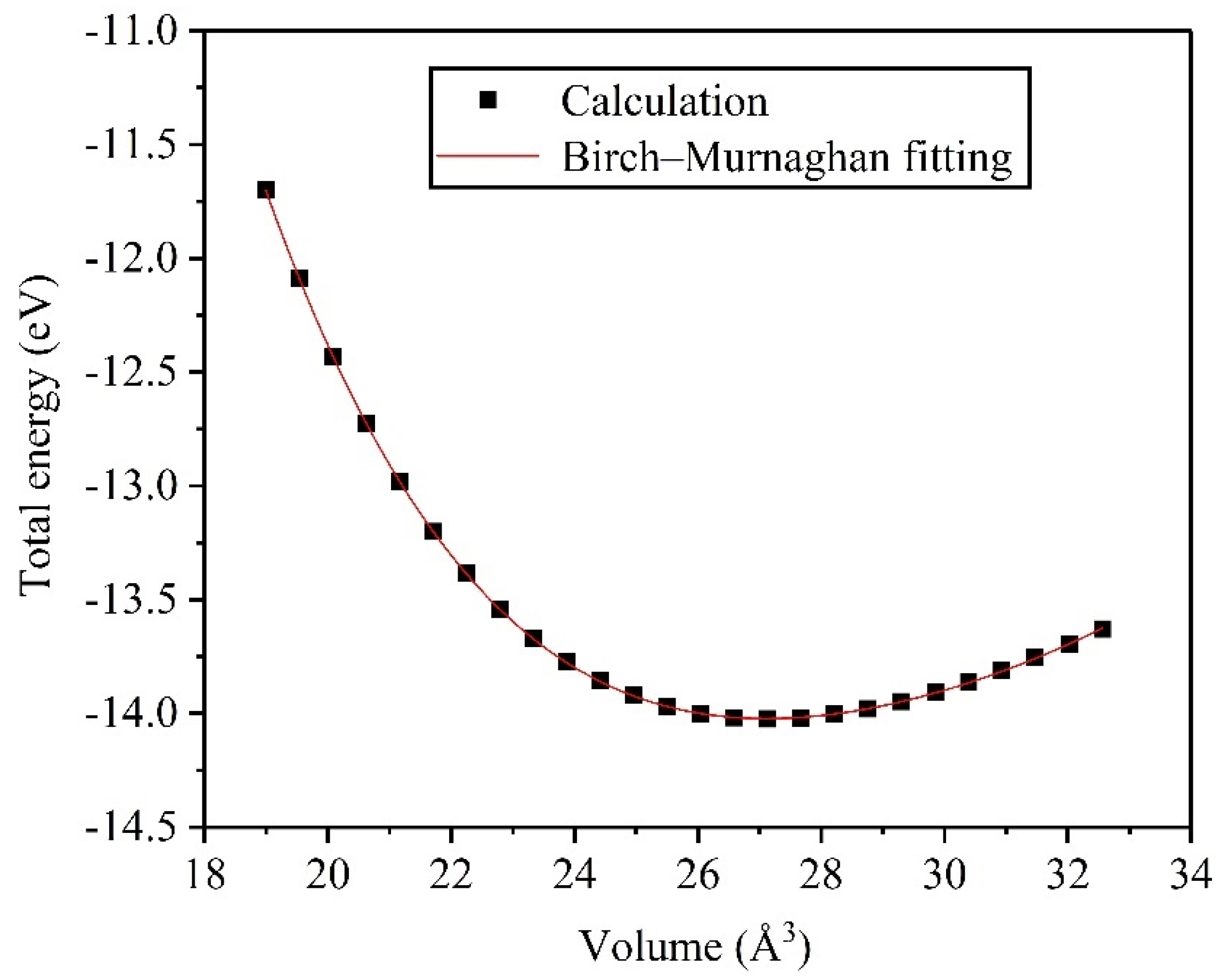
| V (Å3) | 18.990 | 19.540 | 20.080 | 20.620 | 21.160 | 21.710 | 22.250 | 22.790 | 23.330 | 23.880 |
| E (eV) | −11.696 | −12.090 | −12.433 | −12.729 | −12.983 | −13.201 | −13.386 | −13.541 | −13.669 | −13.774 |
| V (Å3) | 24.420 | 24.960 | 25.500 | 26.050 | 26.590 | 27.130 | 27.670 | 28.220 | 28.760 | 29.300 |
| E (eV) | −13.857 | −13.922 | −13.969 | −14.001 | −14.019 | −14.025 | −14.019 | −14.004 | −13.980 | −13.948 |
| B2-phase NiTi | This Work | Theoretical Results | Experimental Results |
|---|---|---|---|
| Lattice constant (Å) | 3.005 | 2.997 [14], 3.021 [15], 3.010 [16], 3.005 [19], 2.940 [34], 3.019 [35], 3.000 [36], 3.007 [37], 3.015 [38] | 3.010 [34], 3.013 [39] |
| B2-Phase NiTi | This Work | Theoretical Results | Experiments |
|---|---|---|---|
| (GPa) | 188 | 184 [19], 218 [34], 183 [35], 204 [42] | 162 [44] |
| (GPa) | 131 | 156 [19], 178 [34], 146 [35], 134 [42] | 132 [44] |
| (GPa) | 51 | 48 [19], 71 [34], 46 [35], 53 [42] | 36 [44] |
| (GPa) | 150 | 165 [19], 191 [34], 159 [35], 157 [42], 158 [43] | |
| (GPa) | 112 | 83 [19], 120 [34], 90 [35], 123 [42] | |
| (GPa) | 41 | 29 [19], 43 [34], 32 [35], 45 [42] | |
| 0.38 | 0.42 [19], 0.40 [34], 0.41 [35], 0.37 [42] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, F.; Liu, Y. First-Principles Calculations of Structural, Mechanical, and Electronic Properties of the B2-Phase NiTi Shape-Memory Alloy Under High Pressure. Computation 2019, 7, 57. https://doi.org/10.3390/computation7040057
Yu F, Liu Y. First-Principles Calculations of Structural, Mechanical, and Electronic Properties of the B2-Phase NiTi Shape-Memory Alloy Under High Pressure. Computation. 2019; 7(4):57. https://doi.org/10.3390/computation7040057
Chicago/Turabian StyleYu, Fang, and Yu Liu. 2019. "First-Principles Calculations of Structural, Mechanical, and Electronic Properties of the B2-Phase NiTi Shape-Memory Alloy Under High Pressure" Computation 7, no. 4: 57. https://doi.org/10.3390/computation7040057
APA StyleYu, F., & Liu, Y. (2019). First-Principles Calculations of Structural, Mechanical, and Electronic Properties of the B2-Phase NiTi Shape-Memory Alloy Under High Pressure. Computation, 7(4), 57. https://doi.org/10.3390/computation7040057





