Enhanced Feature Subset Selection Using Niche Based Bat Algorithm

Abstract

Redundant and irrelevant features disturb the accuracy of the classifier. In order to avoid redundancy and irrelevancy problems, feature selection techniques are used. Finding the most relevant feature subset that can enhance the accuracy rate of the classifier is one of the most challenging parts. This paper presents a new solution to finding relevant feature subsets by the niche based bat algorithm (NBBA). It is compared with existing state of the art approaches, including evolutionary based approaches. The multi-objective bat algorithm (MOBA) selected 8, 16, and 248 features with 93.33%, 93.54%, and 78.33% accuracy on ionosphere, sonar, and Madelon datasets, respectively. The multi-objective genetic algorithm (MOGA) selected 10, 17, and 256 features with 91.28%, 88.70%, and 75.16% accuracy on same datasets, respectively. Finally, the multi-objective particle swarm optimization (MOPSO) selected 9, 21, and 312 with 89.52%, 91.93%, and 76% accuracy on the above datasets, respectively. In comparison, NBBA selected 6, 19, and 178 features with 93.33%, 95.16%, and 80.16% accuracy on the above datasets, respectively. The niche multi-objective genetic algorithm selected 8, 15, and 196 features with 93.33%, 91.93%, and 79.16 % accuracy on the above datasets, respectively. Finally, the niche multi-objective particle swarm optimization selected 9, 19, and 213 features with 91.42%, 91.93%, and 76.5% accuracy on the above datasets, respectively. Hence, results show that MOBA outperformed MOGA and MOPSO, and NBBA outperformed the niche multi-objective genetic algorithm and the niche multi-objective particle swarm optimization.

1. Introduction

Feature selection is a method that selects features or a subset of relevant features of a dataset to achieve the best accuracy through a certain classifier. There are two main purposes of feature selection. Firstly, it makes training easier, as applying a classifier is now more efficient because it decreases the size of the dataset by reducing features. This is specifically important for classifiers. Secondly, most of the time, feature selection eliminates noise in the dataset, thus increasing the classification accuracy. A noise feature can increase the classification error of that dataset if it is added. The best feature subset selection has proven to be a nondeterministic polynomial (NP)-complete problem [1]. The task is challenging; initially, the features do not seem relevant when selected individually but seem to be highly relevant when selected with other features. Feature subset selection serves as a pre-processing step for the classification process. The higher the relevance of selected features is, the higher the accuracy of the classifier will be. There are several feature selection techniques that are widely used, such as the two-step protocol that uses F-score for ranking features, as F-score reveals the discriminative power of each feature independently. The features with the highest scores are the most discriminative features, therefore they are selected in the feature subset selection process as the resultant dataset [2,3,4,5]. Another method for feature selection is the maximum relevancy minimum redundancy (mRMR); this method selects features with higher relevance or maximum correlation while minimizing subsets with higher redundancy that cause the classification accuracy to decrease [6,7]. Feature selection is a costly process, and to solve this, many non-heuristic and heuristic methods have been applied. These methods include statistical methods that use univariate as well as multivariate methods. Multivariate methods provide better results, even when features are dependent on datasets of a particular area or domain. The multivariate methods are further divided into wrapper, filter, and hybrid approaches [8]. The filter approach does the feature subset selection without the involvement of classifiers, while the wrapper approach includes the classifier, which improves the solutions in every iteration and evaluates the accuracy in multiple iterations. This makes the wrapper approach a better candidate for providing a solution [9].

Many meta-heuristic methods have been used for feature selection (FS), which include genetic algorithm (GA), particle swarm optimization (PSO), ant colony optimization (ACO) etc. However, these algorithms propose a computationally expensive solution for feature subset selection. Many computational intelligence based algorithms [10], such as the GA [11] and the PSO [12,13], have been applied for feature selection problems on certain benchmark datasets. The genetic algorithm is a biologically inspired evolutionary algorithm and can achieve a high classification accuracy, but as it is a computationally expensive algorithm, it leads to less efficient and less optimized solutions. On the other hand, PSO provides efficient solution strategies for feature subset selection problems. Similarly, the bat algorithm has been used for feature subset selection problems and gives better results as compared to GA and PSO.

An improved feature selection method for larger datasets is an ongoing research problem. In addition, the existing proposed solutions are either dependent on the classifier or on the dataset. Moreover, the current feature subset selection approaches result in redundant or unrelated features within the search space, and this causes the classifier’s performance to decrease. However, selecting related and relevant features correctly can enhance the classifier’s performance for a particular dataset. Due to the inconsistencies and the irregularities in the existing methods, the niche based bat algorithm (NBBA) was proposed. It is based on the existing bat algorithm. The k-nearest neighbor (k-NN) [14] algorithm was used as the classifier. Niching is a technique used in multimodal optimization, and it was initially applied on GA [15]. It divides the main population into multiple sub-populations, and each sub-population converges to its local optima. The bat algorithm is inspired by nature, which uses the power of echolocation of micro-bats. Each of the bats symbolize a complete solution, and the classifier is used to evaluate and select the best bat with the highest classification accuracy and the optimum number of feature subsets. Classification accuracy is the fitness of the feature subsets, and in order to evaluate the fitness, a classifier is used. Initially, the bat algorithm (BA) was used in order to optimize the feature subsets, and as this problem is multi-objective in nature, the multi-objective bat algorithm (MOBA) was also tested and compared with the multi-objective genetic algorithm (MOGA) and the multi-objective particle swarm optimization (MOPSO), while the niche based bat algorithm (NBBA) was tested and compared with the niche multi-objective genetic algorithm and the niche multi-objective particle swarm optimization.

1.1. Motivation for Using Bat Algorithm for This Research

The BA [16] was chosen because it possesses the advantages of other biologically inspired algorithms, and mainly because it includes the properties of the PSO and the Harmony Search algorithms [17]. BA automatically changes its parameters as the iterations proceed, in contrast to other algorithms that use fixed parameter settings. Another advantage is that BA is more efficient than other algorithms, as it automatically zooms into the promising regions of the search space and converts its search from exploration of those promising regions, which make its convergence rate faster [17]. Combinatorial problems are really hard to solve, and the feature subset selection is an NP-complete combinatorial problem. Ramesh et al. proposed a comprehensive study of combined economic load and emission dispatch problems using the bat algorithm [17]. They compared the bat algorithm with other algorithms, including ACO and the hybrid genetic algorithm, concluding that the bat algorithm is better than other algorithms in terms of efficiency, accuracy, and ease of implementation. Musikapun and Pongcharoen solved multi-product, multi-machine, and multi-stage scheduling problems using the bat algorithm [18], and they successfully solved a class of NP-hard problems with a detailed parametric study. Therefore, the existing work indicates the reason for selecting BA for optimization of features in the dataset. The bat algorithm is currently being used to solve various kinds of problems, and fortunately it is very adaptive to the new problems, as researchers are creating newer versions of the bat algorithm that fit their needs [19] The objective functions for the algorithm are to select the minimum relevant features of the dataset and to improve the accuracy of the k-nearest neighbor classifier; all of this combined is a complete solution. The experiments were carried out on benchmark datasets using single, multi-objective, and niche based genetic algorithms, single, multi-objective, and niche based particle swarm optimization algorithms, and single, multi-objective, and niche based bat algorithms.

1.2. Paper Division

Section 2 of the paper presents the background of the problem, Section 3 gives the literature review, Section 4 gives the proposed methodology, Section 5 gives the experimentation with results, Section 6 is the discussion section, and finally, Section 7 presents the conclusion and Section 8 presents the future work.

2. Background

2.1. Feature Subset Selection

The feature subset selection method is also known as dimensionality reduction [20] and/or attribute selection [21]. It selects the most relevant features that result in an increased classification accuracy and better time efficiency due to the decreased number of features.

2.1.1. Different Approaches for Feature Subset Selection

Filter Approach

This feature subset selection method is independent of the used classifier. Filter techniques serve as pre-processing techniques of selecting the subset. Filter methods give emphasis to the finding of relevant associations among features and high-level concepts. Filter techniques make use of straightforward statistics as a result of empirical feature distribution. These empirical distribution methods pick strongly related features while filtering out weakly related features at the evaluation process of overall feature selection process.

Wrapper Approach

This approach is very simple and dependent on the classifier involved [22]. It includes the accuracy of the classifier as the optimization function, thus it is highly dependent on the classifier used. In this approach, a variety of feature subsets are evolved and then evaluated on the basis of the classification accuracy of the classifier, and the best feature subset is selected.

Embedded Approach

The embedded approach has a high classifier involvement. The subset search optimizing algorithm is constructed inside the classifier model. Hence, these approaches are highly dependent on the classifier and the search algorithm. In these techniques, the search space and the feature subset space are combined in the search.

2.1.2. Optimization Problem

An optimization probelm is a problem in which the objective is to find a solution in the search space that has the minimum (or the maximum) value of the objective function. It can be categorized as:

Single Objective

A single objective is a problem that has only one objective to optimize, e.g., in a feature selection problem, it can be the classification accuracy or it can be the number of selected features. The focus is only on the optimization of one single objective at one time.

Multi-Objective

A multi-objective is a problem that has multiple objectives to optimize simultaneously. One objective could be to maximize while the other could be to minimize at the same time.

2.1.3. Scalarization

A multi-objective problem is often solved by combining its multiple objectives into one single-objective scalar function, which makes it very simple to solve. In this case, there is only one optimal solution instead of multiple non-dominated optimal solutions. This approach is known as the weighted-sum or the scalarization method. This paper also used the scalarization method for solving multi-objective optimization through the weighted-sum of classification accuracies and the number of features selected by every individual solution.

f = Σw_kf_k

(1)

where k = 1: k, Σ w_k = 1, “f” represents the fitness function, and k represents the number of objectives. Different weights are tried for objective types, accuracy, and number of features. The best results are found on weights w1 = 0.7 and w2 = 0.3 for accuracy and number of features, respectively.

2.1.4. Multi-Objective Feature Subset Selection

Multi-objective feature subset selection selects the minimum number of features from a larger dataset, which improves the accuracy of the classifier and increases the time efficiency, as discussed earlier. Thus, the two main objectives for fitness function are:

• Increase classifier accuracy;
• Decrease number of features.

In multi-objective optimization, there are conflicting objectives; as in the feature subset selection problem, the classification accuracy has to be maximized, and the number of selected features has to be minimized. Optimization of one objective will never provide the best solution, thus there is a need to optimize function and trade-off among all the objectives. The resultant solution will be optimized to give the best results by taking all the objectives into account.

2.1.5. Genetic Algorithm

GA [11] is a nature motivated algorithm that fits within a bigger arrangement of evolutionary algorithms. It emulates the conduct of characteristic development and choice procedure by Charles Darwin, i.e., the idea of survival of the fittest. GA is utilized to make a productive answer for search and optimization problems. The principle parts of the genetic algorithm were fundamentally motivated by the regular evolution process, for example, legacy, change, determination, and hybrid are connected on the person to get upgraded arrangements.

The genetic algorithm begins from the introduction of the initial population. The initial population is randomly created and, after that, the process of evolution is connected to the population to produce the fittest individual (chromosome as a specialized genetic algorithm). The advancement prepared then proceeds until the stopping criteria (objective function criteria) are met.

2.1.6. Particle Swarm Optimization (PSO)

PSO [12] is one of the swarm based intelligent algorithms. The algorithm was inspired by the basis of swarm (of fish and birds) flocking patterns. The algorithm can be understood by a simple example of a bird group in search of food. The bird closest to food has a louder voice, and other birds move towards this bird according to its volume. This particular bird is called the leader of the flock. The leader of the group keeps changing according to the difference of distance from food. The process continues until the leader reaches the food.

3. Literature Review

In recent years, a number of approaches have been proposed for solving feature subset selection and other optimization problems using meta-heuristics algorithms such as GA, PSO, BA, etc. This section reviews those approaches that are relevant to the proposed approach of this paper.

Cheng Fu-Tsai et al. proposed a technique that executes a bat algorithm in a parallel manner [23]. It divides the initial population into multiple subpopulations and runs each single population or group on a separate processor. It shares the information at the information sharing phase of the algorithm. At this stage, each subpopulation shares its information with all other subpopulations. It increases the efficiency of the algorithm and makes the convergence faster as the environments get parallelized altogether. Their proposed algorithm was compared with the naive bat algorithm [24] by running them on four benchmark functions; results show that the parallelized bat algorithm outperforms the simple bat algorithm not only in terms of time but also in terms of quality.

This paper [16] proposes an algorithm that uses the echolocation behavior of natural bats to find its solution/prey. Bats fly randomly with velocity ‘v’ at position ‘x’ with fixed frequency. As the bat approaches its prey, it increases its pulse emission rate while decreasing its loudness. The algorithm was compared with GA and PSO on five benchmark functions, and results show that BA outperforms GA and PSO both in accuracy and efficiency.

This paper [12] presents a feature selection technique that uses PSO and support vector machine (SVM) as a classifier to find the accuracy of selected feature subsets. This method was applied on five different sized benchmark datasets, and results show that the proposed algorithm reduces features while giving high classification accuracy at the same time.

This paper [25] claims to be the first paper on multi-objective feature selection using PSO. It proposes two algorithms to solve the problem. The first approach finds non-dominated solutions using a simple approach to find the Pareto front [25], while the second approach uses mutation, crowding, and dominance to find the Pareto fronts. These two approaches were then compared for single objective and multi-objective feature selection on 12 benchmark datasets, and results show that the first approach outperforms the second approach. This paper proposes an improved PSO in order to perform attribute selection for the task of predicting coronary artery heart disease using the improved fuzzy artificial neural network classifier. A dataset of 7525 diabetic patients was used, out of which 4329 were males and 3196 were females. The research was carried out separately for the male and female patients, and the study achieved maximum accuracies of 88.82% and 88.05% for male and female patients, respectively, using improved PSO as an optimization algorithm for attribute selection [26].

This paper proposes instance selection using filter based and wrapper based bat algorithms as well as the cuckoo search algorithm with an application in e-fraud detection. The classifier used was SVM. The proposed techniques were evaluated on 24 datasets. Filter based techniques improved the training speed on all the datasets using SVM while not compromising the accuracy, whereas the wrapper based approaches improved the accuracy on 74% of the datasets with significant improvement on the training speed of SVM [27].

Brits et al. [28] proposed a niching technique with GA. It is a technique used for finding multiple optimal solutions for a problem at the same time, and the concept itself is called multimodal optimization. This paper proposes that niching can be done using two methods that are given below:

3.1. Fitness Sharing Method

The fitness sharing strategy rewards individuals that can exceptionally search good zones of the area while profoundly debilitating similar individuals in a space [15]. This is the reason the population differs among itself, which keeps up diversity in the population that ultimately avoids local minima.

3.2. Swarming Method

In the swarming strategy, a small amount of the global population indicated by a rate, namely the generation gap, replicates and dies in every iteration of GA [15]. A parent replaces the most comparative individual (as far as genotype correlation) taken from a random sub population of size crowding factor (swarming component) from the global population. The deterministic swarming strategy presents rivalry in the middle of offspring and parents of indistinguishable corners. This system has a tendency to distinguish arrangements with higher fitness and to eliminate solutions with lower fitness.

Gheyas et al. proposed a hybrid algorithm named as SAGA (Simulated Annealing Genetic Algorithm) [1], a name taking into account two meta-heuristic methods, simulated annealing (SA) and GA, that combines various qualities of existing algorithms to select the ideal subsets from an extensive component space. The SAGA algorithm is a hybrid of various wrapper strategies, i.e., an SA, a GA, a GRNN (generalized regression neural network), and a greedy search algorithm. They compared and analyzed the proposed algorithm (SAGA) with the traditional search algorithms (ACO, FW, GA, PSO, SA, SBS, SFBS, SFFS, and SFS) on 30 high dimensional datasets. Their proposed algorithm outperforms other algorithms [1].

This paper [29] proposes a technique that uses the optimum-path forest classifier. It encodes features in binary form where “0” represents a feature’s absence in the solution, and “1” represents a feature’s presence in the solution. The optimum-path forest is considered as a speedy classifier, and the exploration power of the bat algorithm combined with the speed of the optimum-path classifier was applied on five public datasets and yielded results that demonstrate that this method performs better than other swarm based algorithms or meta-heuristics.

Niche PSO [28] does not use social information of the swarm. Instead, it randomly distributes the particles into the whole search space, and particles use their cognitive information and perform local searches instead—these particles are called swarms. Every time a particle comes into the range of radius of any other particle, it gets merged into that swarm and forms a bigger swarm. It was applied on five benchmark functions and compared with the niche based genetic algorithm (NGA), and it gives better results as compared to GA in terms of convergence and finding all maxima points.

4. Proposed Methodology

This research presents a niche based bat algorithm for feature subset selection and compares its results with single objective and multi objective GA, PSO, and bat algorithms. Comparative analysis of niche based BA was performed with niche based GA and niche based PSO algorithms for performance and efficiency.

4.1. Bat Algorithm

Bat Algorithm behaves as a bat, as it incorporates the echolocation behavior of bats. By using this behavior, bats find the location of their prey. Given below is a Bat Algorithm (Algorithm 1) [16]:

Algorithm 1: Bat Algorithm

1. Define Objective function for (x), x = (x1, …,)

2. Initialize population of bat with random position xi and vi, i = 1, 2, …, m.

3. Define frequency for pulse fi at xi, ∀i = 1, 2, …,

4. Initialize rates for pulse ri and the pulse loudness Ai, i = 1, 2, …,

5. While t < T

6.  For every bat bi, generate some new solutions using Equations (1), (2) and (3).

7.   If rand > ri, then

8.    Select a solution from the best solutions.

9.    Create a local solution close to the best solution.

10.   End if

11.   Generate a new solution by flying randomly

12.   If rand < Ai and (xi) < (x*), then

13.    Accept the new solutions.

14.    Increase ri and reduce Ai.

15.   End if

16.  End for

17. Rank the bats and find the current best x*

18. End while.

$$f_i=f_{min}+\left(f_{max}-f_{min}\right)\beta$$

(2)

$$v_i^t=v_i^t-1+\left(x_i^t-x^{*}\right)f_i$$

(3)

$$x_i^t=x_i^t-1+v_i$$

(4)

x* is the current global best solution in the population.

$$x_{new}=x_{old}+\epsilon A^t$$

(5)

where ε belongs to [−1, 1] is a random number, while $A^t$ = < $A_i^t$ > is the average loudness of all the bats at this time step. Equation (5) is used for the random walk in line number 11.

4.2. How Bat Algorithm Works

In the beginning, every bat is initialized with frequency, loudness, pulse rate, velocity, and the random position in the search space in line numbers 2, 3, and 4 of the algorithm. Later, their positions are updated according to the position of the prey. Frequency decreases as the distance decreases. Equation (2) is used for updating the frequency. The algorithm will run until the maximum number of iterations is reached. To enhance the exploration power of the algorithm, random walk is being performed in line number 11. Then, from lines 12 to 15, if any one of the local solutions has a better fitness value than the global best solution, it becomes the global best solution, and pulse rate increases and loudness decreases. Finally, after the maximum number of iterations, the solutions are ranked according to the criteria, and the best solution is selected as a global solution in line number 16 of the algorithm.

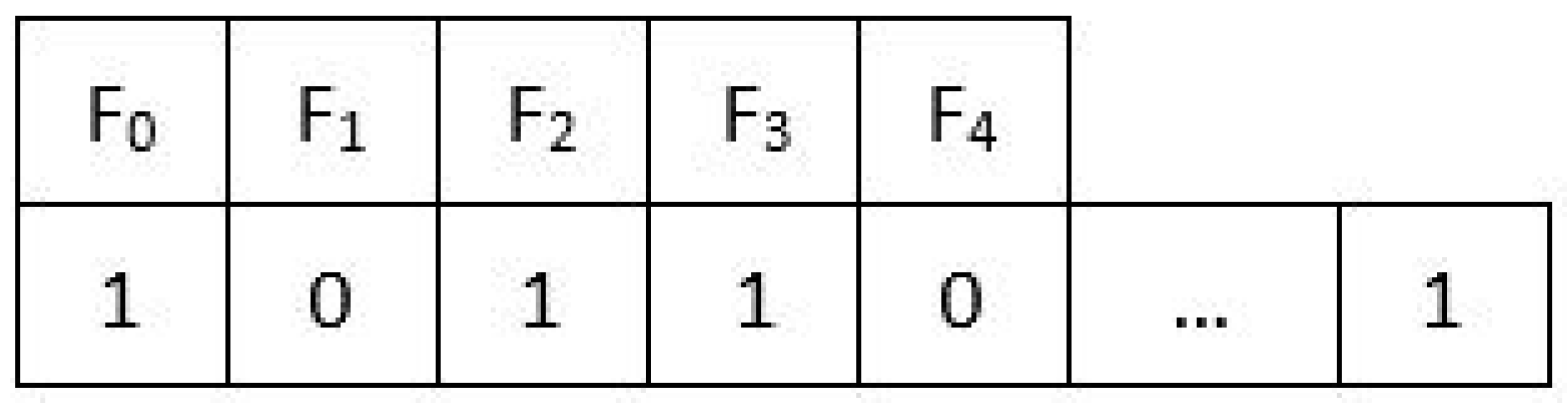
4.3. Bat Representation as a Solution for Feature Selection

Single bat or solution is represented with bits, as shown in Figure 1. The number of bits will be equal to the number of features in the dataset. The first bit represents the first feature, and the second bit represents the second feature in the dataset. The “0” bit value shows that this feature has not been selected, and the “1” bit value shows the existence of a feature in the selection process. The same bat representation is used as the binary version of GA, PSO, MOBA, MOPSO, MOGA, and NBBA. The binary encoding makes the classifier easy to classify and also improves its accuracy and performance. Binary bat is encoded as:

4.4. Evaluation Function

The evaluation function used by NBBA is the weighted sum of the classifier’s accuracy and the number of features that are selected by the solution. The same function is used for MOBA, MOPSO, and MOGA, but not for GA and PSO, which use the classifier’s accuracy or the number of features at any time, as they optimize the single objective problem. The dataset is split into testing and training datasets. The classifier is trained using the training dataset, and the testing dataset shows the accuracy of the classifier. If the bat producing the best fitness value is found, and all the other subsets have been explored, then the algorithm has converged and stops, or the algorithm completes the maximum number of iterations.

4.5. Classifier Used

The K-nearest neighbor (k-NN) was used as a classifier in our proposed technique. This classifier is one of the well-known nonparametric classification methods. The k-NN algorithm is a supervised learning algorithm. The k-NN classifies the input data on the basis of the k-nearest neighbor’s category. k-NN is used for its simplicity in many research problems, such as in [30], where it is used for the prediction of cancer using gene expression data. In our case, the dataset was continuous (integer/real), thus using k-NN was the best choice for our research, as the paper claims that the performance of k-NN on continuous datasets is better than its performance on the text data [31]. It performs equally well with any other statistical machine learning algorithms, as this paper claims [32]. In a recently published paper [33], k-NN was used as a classifier for predicting heart disease with PSO as a feature optimizer, and k-NN predicted heart disease with 100% accuracy.

Classification Measurement

To evaluate the algorithm, the classification accuracy was computed using one of the four evaluation metrics that are widely used to compute the performance of the classifier [4,5]. The accuracy was computed using the following formula:

$$Accuracy={\displaystyle \sum }_{}^{}\frac{TP+TN}{TP+TN+FP+FN}$$

(6)

4.6. Niche Based Bat Algorithm (NBBA), Proposed Algorithm

The input for the Algorithm 2 is: training set T1 with labels and test set T2, number of features n, number of iterations I, population size m, loudness A, pulse emission rate r, α and γ values.

The output consists of: features subset F that gives the maximum accuracy over T2.

Algorithm 2: Niche Based Bat Algorithm

1. Create and initialize an n x-dimensional main bat population, S;

2. repeat

3.  Train the main population, S, for one iteration using the local random walk;

4.  Update the fitness of each bat in main-population, S. xi;

5.  for each sub-population Sk do

6.   Train sub-population of bats, Sk. xi, using main bat algorithm that includes global search;

7.   Update each bat’s fitness;

8.   Update sub-population radius Sk. R;

9.  End For

10.  If possible, merge sub-populations;

11.  Allow sub-populations to absorb solutions/bats from the main population that moved into the radius of any sub-population;

12.  If possible, create new sub-populations;

13. Until stopping condition is true;

14. Return optimal solution Sk. ˆy for each sub-population Sk as a solution.

4.7. How NBBA Works

The niche based bat algorithm (Algorithm 2) initializes the population similarly to the bat algorithm with additional parameters that include the radius of the sub populations and the global best solution of each sub population. The main population is then trained through random walk using Equation (5) in the beginning of the algorithm and again after each iteration to preserve the diversity among the solutions in the main population. Then, their fitness is updated. Initially, there is a single sub population that is also the main population. To identify more sub populations, the algorithm trains the sub populations with the full bat algorithm [9] and updates the fitness of the bats/solutions and finally updates the radius associated with each sub population. Radius ($R_k$) defines the boundary of the sub population. The radius of the sub population $P_k$ ($P_k$ is the kth sub population) is the distance between the global best solution of that sub population and the solution that is farthest from the global best solution of the similar sub population, which is represented by Equation (6) given below. The solutions in the population are the binary strings. Therefore, Hamming distance measure is used for calculating the distance between the two solutions.

$$R_k=\left(\Vert P_k.x_g-P_k.x_i\Vert \right)$$

(7)

P_k.x_g represents the global/best solution/bat in the sub population k, while Pk. xi represents all other particles in that swarm.

The algorithm merges two sub populations ($P_{k1}$ and $P_{k2}$) only if possible (line 9) when the distance between their global solutions is less than the sum of their radii, which is given by Equation (7).

$$\Vert P_{k1}.x_g-P_{k2}.x_g\Vert <\left(R_{k1}+R_{k2}\right)$$

(8)

The algorithm moves the particular solution into the sub populations (line 10) when the solutions move into the radius of the sub population that is given by the Equation (8).

$$\Vert x_i-P_k.x_g\Vert <R_k$$

(9)

The algorithm creates new sub populations in (line 11) when a solution in the main population does not change its fitness significantly after a few iterations (in our case, the number was five). Then, the algorithm combines that solution with the nearest solution in the main population that forms a new sub population, and the algorithm also calculates the radius of the new sub population using Equation (6).

Finally, the algorithm runs until the iterations are complete. After that, all the global best solutions from the sub populations are returned by the algorithm, and the solution with the best fitness (the problem is changed to the minimization problem) among the global solutions from each sub population is considered as the optimal solution by the algorithm.

4.8. Contribution

This paper presents four main contributions: (i) the developed and proposed NBBA; (ii) the NBBA was used for a feature subset selection problem and can be used along with any other classification technique; (iii) use of the niche PSO for feature subset selection problems; (iv) use of the niche GA for feature subset selection problems.

5. Experimentation and Results

5.1. Datasets

The datasets used for classification purposes were Madelon, ionosphere, and sonar datasets taken from the online UCI machine learning data repository [34]. The used datasets were benchmark datasets for classification as shown in

Table 1. Dataset description in detail.

Dataset Name	Total Samples	No. of Attributes	Attribute Characteristics	Train/Test Ratio	No. of Classes
Ionosphere	351	34	integer, real	70/30	2 (Good/Bad)
Sonar	208	60	real	70/30	2 (Mine/Rock)
Madelon	4400	500	real	70/30	2 (+1/−1)

.

5.2. Results

The parameter settings, the classification accuracies, and the number of features selected along with the comparative analyses for GA, PSO, BA, MOGA, MOPSO, MOBA, niche GA, niche PSO, and NBBA are given in

Table 2. Parameter Settings for genetic algorithm (GA), multi-objective genetic algorithm (MOGA), single objective niche GA, and multi-objective niche GA.

Parameters	GA	MOGA	Single Objective Niche GA	Multi-Objective Niche GA
Particle representation	Bit string	Bit string	Bit string	Bit string
Population	30	50	50	50
Selection method	Tournament selection	Tournament selection	Tournament selection	Tournament selection
Elitism	0.3	0.3	0.3	0.3
Generation Gap	0.7	0.7	0.7	0.7
Classifier	k-nearest neighbor (k-NN)	k-nearest neighbor	k-nearest neighbor	k-nearest neighbor
Fitness function	k-NN accuracy	(w1 × k-NN accuracy) + (w2 × no. of features)	k-NN accuracy	(w1 × k-NN accuracy) + (w2 × no. of features)

,

Table 3. Parameter settings for particle swarm optimization (PSO), multi-objective particle swarm optimization (MOPSO), single objective niche PSO, and multi-objective niche PSO.

Parameter	PSO	MOPSO	Single Objective Niche PSO	Multi-Objective Niche PSO
Particle representation	Bit string	Bit string	Bit string	Bit string
Swarm size	30	30	50	50
Inertia Weight	0.8	0.8	0.8	0.8
Classifier	k-nearest neighbor	k-nearest neighbor	k-nearest neighbor	k-nearest neighbor
Fitness function	k-NN accuracy	(w1 × k-NN accuracy) + (w2 × no. of features)	k-NN accuracy	(w1 × k-NN accuracy) + (w2 × no. of features)

,

Table 4. Parameter Settings for bat algorithm (BA), multi-objective bat algorithm (MOBA), single objective niche based BA (NBBA), and multi-objective niche based BA.

Parameter	BA	MOBA	Single Objective NBBA	Multi-Objective NBBA
Particle representation	Bit string	Bit string	Bit string	Bit string
Population	30	30	50	50
Loudness	0.9	0.9	0.9	0.9
Pulse rate	0.3	0.3	0.3	0.3
Fmin	0	0	0	0
Fmax	2	2	2	2
Classifier	k-nearest neighbor	k-nearest neighbor	k-nearest neighbor	k-nearest neighbor
Fitness function	k-NN accuracy	(w1 × k-NN accuracy) + (w2 × no. of features)	k-NN accuracy	(w1 × k-NN accuracy) + (w2 × no. of features)

,

Table 5. Results of single, multi-objective, and niche based genetic algorithm.

		Datasets
		Ionosphere	Sonar	Madelon
Details	Instances	351	208	4400
	Features	34	60	500
Features selected using	GA	12	33	265
	MOGA	10	17	256
	Single-objective Niche GA	16	30	287
	Multi-objective Niche GA	8	15	196
Accuracy	k-NN	80.64%	80.00%	69.50%
	GA + k-NN	92.38%	91.96%	77.83%
	MOGA + k-NN	91.28%	88.70%	75.16%
	Single objective Niche GA + k-NN	90.28%	91.93%	78.50%
	Multi-objective Niche GA + k-NN	93.33%	91.93%	79.16%

,

Table 6. Results of single, multi-objective, and niche based PSO.

		Datasets
		Ionosphere	Sonar	Madelon
Details	Instances	351	351	4400
	Features	34	34	500
Features selected using	PSO	16	16	325
	MOPSO	9	9	312
	Single-objective Niche PSO	26	26	317
	Multi-objective Niche PSO	9	9	213
Accuracy	k-NN	80.64%	80.00%	69.50%
	PSO + k-NN	91.70%	91.70%	75.80%
	MOPSO + k-NN	89.52%	89.52%	76.00%
	Single objective Niche PSO + k-NN	92.38%	92.38%	76.50%
	Multi-objective Niche PSO + k-NN	91.42%	91.42%	76.50%

,

Table 7. Results of single, multi-objective, and niche based BA.

		Datasets
		Ionosphere	Sonar	Madelon
Details	Instances	351	208	4400
	Features	34	60	500
Features selected using	BA	17	34	253
	MOBA	8	16	225
	Single-objective NBBA	19	34	248
	Multi-objective NBBA	6	13	178
Accuracy	k-NN	80.64	80.00	69.50
	BA + k-NN	93.33	91.93	78.33
	MOBA + k-NN	92.38	93.54	78.33
	Single objective NBBA + k-NN	91.70	93.54	79.16
	Multi-objective NBBA + k-NN	93.33	95.16	80.16

,

Table 8. Comparison of number of features selected by single objective GA, PSO, and BA with their classification accuracies.

Dataset	GA		PSO		BA
	Features	Accuracy	Features	Accuracy	Features	Accuracy
Ionosphere	12	92.38%	16	91.7%	17	93.33%
Sonar	33	91.93%	36	88.70%	34	91.93%
Madelon	265	77.83%	325	75.83%	253	78.33%

,

Table 9. Comparison of number of features selected by niche based single objective GA, PSO, and BA with their classification accuracies.

Dataset	GA		PSO		BA
	Features	Accuracy	Features	Accuracy	Features	Accuracy
Ionosphere	16	90.28%	26	92.38%	19	91.7%
Sonar	30	91.93%	36	90.32	34	93.54%
Madelon	287	78.5%	317	76.5%	248	79.16%

,

Table 10. Comparison of number of features selected by multi-objective GA, PSO, and BA with their classification accuracies.

Dataset	MOGA		MOPSO		MOBA
	Features	Accuracy	Features	Accuracy	Features	Accuracy
Ionosphere	10	91.28%	9	89.52%	8	92.38%
Sonar	17	88.7%	21	91.93%	16	93.54%
Madelon	256	75.16%	312	76%	225	78.33%

and

Table 11. Comparison of number of features selected by niche based multi-objective GA, PSO, and BA with their classification accuracies.

Dataset	Niche GA		Niche PSO		Niche BA
	Features	Accuracy	Features	Accuracy	Features	Accuracy
Ionosphere	8	93.33%	9	91.42%	6	93.33%
Sonar	15	91.93%	19	91.93%	13	95.16%
Madelon	196	79.16%	213	76.5%	178	80.16%

below:

6. Discussion

Comparative Analysis

This paper presents purely empirical research in nature. Details are clearly presented about the datasets along with the parameter settings that were selected after conducting experiments on different parameter settings. The parameters with the best settings are listed in Table 1, Table 2 and Table 3. Implementation of the algorithms can be provided on demand through email.

The experiments were conducted in four rounds; the mean accuracy and the mean number of features were calculated by using 10-fold cross validation over five runs of the algorithms on each dataset. In the first round, the accuracies on the dataset were calculated as listed in

Table 12. Resultant accuracy and number of features using different single objective algorithms.

	Ionosphere		Sonar		Madelon
Algorithm	Features	Accuracy	Features	Accuracy	Features	Accuracy
GA	12	92.38%	33	91.93%	265	77.83%
Niche GA	16	90.28%	16	90.28%	287	78.50%
PSO	16	91.7%	36	88.70%	325	75.83%
Niche PSO	26	92.38%	36	90.32	317	76.5%
BA	17	93.33%	34	91.93%	253	78.33%
Niche BA	19	91.7%	34	93.54%	248	79.16%

, using k-NN as a classifier without using any of the algorithms for optimizing the number of features.

In the second round of experiments, accuracies were calculated by retrieving the best features using GA, PSO, and BA, as given in

Table 13. Resultant accuracy and number of features using different multi-objective algorithms.

	Ionosphere		Sonar		Madelon
Algorithm	Features	Accuracy	Features	Accuracy	Features	Accuracy
GA	12	92.38%	17	88.7%	256	75.16%
Niche GA	8	93.33%	15	91.93%	196	79.16%
PSO	9	89.52%	21	91.93%	312	76.00%
Niche PSO	8	93.33%	19	91.93%	213	76.5%
BA	8	92.38%	16	93.54%	225	78.33%
Niche BA	6	93.33%	13	95.16%	178	80.16%

. However, being a single objective (to maximize the classification accuracy) experiment, the number of features selected was not taken into account by the algorithms. BA outperformed GA and PSO on ionosphere and Madelon datasets, while GA outperformed PSO and BA on the sonar dataset.

In the third round of experiments, the problem was multi-objective in nature, thus the scalarization method was used, as given in Equation (1), with the weight of 0.3 for the number of features and the weight of 0.7 for the classification accuracy. The experiments were performed using different weight values, and the values with the best results are quoted in the table. Table 9 shows that MOBA outperformed MOGA and MOPSO in terms of accuracy and number of features selected on all three datasets.

In the fourth round, the experiments were performed with multi-objective niche GA, niche PSO, and NBBA, and the results (as seen in Table 10) show that multi-objective NBBA outperformed multi-objective niche GA and niche PSO in terms of classification accuracy and number of features selected.

The results clearly indicate that adding the niching technique to the bat algorithm can enhance the diversity in the population, ultimately avoiding the local minima. The results show that NBBA outperforms all the other algorithms, including their different variations as well.

7. Conclusions

The proposed algorithm, i.e., NBBA, was compared with niche based GA and niche based PSO. Experiments were carried out to compare the performances of the bat algorithm with the genetic algorithm and the particle swarm optimization algorithm. Implementation results show that single objective and multi-objective bat algorithms yield better results than single and multi-objective genetic algorithm and particle swarm optimization algorithm. Thus, this study presents a direction to explore the bat algorithm with the niching technique.

8. Future Work

8.1. Advantages of NBBA

Single and multi-objective NBBA performs better than the other existing algorithms mentioned in this paper, and, due to the strategy the NBBA adopts, we anticipate that it will also perform better than other state of the art algorithms, such as Non-Dominated Sorting Genetic Algorithm (NSGA II) and Strength Pareto Evolutionary Algorithm (SPEA II). NBBA finds non-dominated solutions or the Pareto front and optimizes with the strategy it builds upon, which is provided in the coming paragraph. Basically, NBBA divides the whole search space into multiple regions called niches by incorporating multiple bats in those regions. By doing this, NBBA avoids the local minima problem because random walk of the bats in the main population moves the bats in different regions of the search space in every iteration of the NBBA, which makes it possible for them to be included in different niches/regions of the search space. This enhances the diversity of the solutions in the search space and ultimately avoids the local minima. Bats/solutions in multiple niches trained with the full BA only explore using random walk and exploits using the global best solution in that particular niche. Similarly, bats in other regions of the search space also explore and exploit those regions and find the best solution in only that region of the search space. Ultimately, the algorithm picks the best solution out of the best solutions of every niche [34].

Table 14. Comparison of NSGA-II with NBBA for their classification accuracies on ionosphere, sonar, and Madelon datasets.

Dataset	NSGA-II				NBBA
	Generation	Population	Features	Accuracy	Features	Accuracy
Ionosphere	100	20	2	96.59	6	93.33
	50	16	2	96.59
Sonar	100	20	6	98.07	13	95.16
	50	16	12	100
Madelon	100	20	149	86	178	80.16
	500	20	123	89.4

shows the comparison of NSGA-II and NBBA for the three datasets used in this paper, i.e., ionosphere, sonar, and Madelon. “Generation” represents the iterations for evolutionary algorithms. The population is the initial set of solutions that begins the optimization problem. These parameters are set, and resultant values of accuracy and number of features selected are reported. The comparison shows the number of features selected with NBBA.

8.2. Limitations

This paper applies a scalarization technique that makes a multi-objective problem into a single objective problem and does not make use of the objectives to optimize independently in order to get the true non-dominated or the Pareto optimal solutions. It compares different weights manually in order to find the true Pareto optimal solutions. In the future, the scalarization technique can be replaced, and NBBA can be implemented in such a way that it finds a non-dominated solution set that must be close to the actual or the true Pareto front. To make the future direction more clear, this paper compares the results of the above mentioned single objective and multi-objective NBBA with NSGA II on the same three datasets. The results show that considering objectives independently and finding non-dominated solutions can give better results.