Abstract
The so-called Relevance Index (RI) metrics are a set of recently-introduced indicators based on information theory principles that can be used to analyze complex systems by detecting the main interacting structures within them. Such structures can be described as subsets of the variables which describe the system status that are strongly statistically correlated with one another and mostly independent of the rest of the system. The goal of the work described in this paper is to apply the same principles to pattern recognition and check whether the RI metrics can also identify, in a high-dimensional feature space, attribute subsets from which it is possible to build new features which can be effectively used for classification. Preliminary results indicating that this is possible have been obtained using the RI metrics in a supervised way, i.e., by separately applying such metrics to homogeneous datasets comprising data instances which all belong to the same class, and iterating the procedure over all possible classes taken into consideration. In this work, we checked whether this would also be possible in a totally unsupervised way, i.e., by considering all data available at the same time, independently of the class to which they belong, under the hypothesis that the peculiarities of the variable sets that the RI metrics can identify correspond to the peculiarities by which data belonging to a certain class are distinguishable from data belonging to different classes. The results we obtained in experiments made with some publicly available real-world datasets show that, especially when coupled to tree-based classifiers, the performance of an RI metrics-based unsupervised feature extraction method can be comparable to or better than other classical supervised or unsupervised feature selection or extraction methods.
1. Introduction
The Relevance Index (RI) metrics are based on information theory and are usually applied to the study of complex systems, since they are able to detect relevant groups of variables, well integrated among one another and well separated from the others, which provide a functional block description of the complex system they describe [1]. In particular, the index of a set V of variables is a standardized version of the integration which measures the relative significance of V within a complex system for which V is a subset of the system state representation. Similar to the other metrics in the same family, its computation relies on the approximation of the statistical distribution of the variables based on the analysis of a sample of the system states observed over a given time interval, possibly in response to a previous perturbation. The higher the , the more relevant V [2].
Intuitively, the properties measured by the RI metrics are not so different from the characteristics, namely relevance and non-redundancy, which are typical of the most discriminating feature sets describing patterns of interest in classification tasks. Moreover, the properties that the metrics highlight in time series, when analyzing the dynamics of complex systems, can be somehow assimilated to the properties of the multivariate distribution of static patterns subject to noise, distortions, etc. Preliminary results indicating that this property can be exploited in pattern recognition applications, in particular for feature extraction, have been obtained in [3], where the attribute subsets which could be detected using the index were shown to be the base for extracting effective features for classification. In that work, the index was used in a supervised way, i.e., it was applied iteratively to homogeneous data subsets of samples belonging to the same class, to extract features capable of summarizing the information content of each class. Despite yielding good results, such a supervised approach is impractical, since it requires that the already resource-demanding phase of computation be repeated, at the same level of complexity, as many times as the number of classes. As a matter of fact, applying the computation to a smaller number of data instances leads only to a negligible reduction of the computation time as the intrinsic complexity of the computation is , where s is the number of features describing the data and not the number of data samples. However, if the analysis based on the metrics is able to detect the peculiarities characterizing the variations within data belonging to the same class, it may also be able to detect the peculiarities characterizing one class with respect to the others. This suggests that an unsupervised approach, where the method is applied to the whole dataset, independently of the classes to which the data belong, may be as successful.
Based on the above considerations and building upon the positive indications of the results reported in [3], the work presented in this paper was aimed at significantly extending that work from two points of view:
- Use an unsupervised approach to extract relevant features that can be used to solve supervised classification problems.
- Perform an in-depth analysis of the results that the -based approach to feature extraction can yield, by applying it to data from different real-world case studies.
Therefore, the main goal of this work was to transfer approaches based on the RI metrics from the domain of complex system analysis to feature extraction. Thus, this work could be considered at least partially successful even if only the hypothesis of direct applicability of a method originally devised for complex system analysis to feature extraction could be experimentally demonstrated to be reasonable.
From now on, in this paper, we refer to the unsupervised -based method we tested as ZIFF (-based Feature Finder). In ZIFF, the computation is carried out by a specifically-designed evolutionary algorithm [4,5], to counteract the curse of dimensionality and find the most relevant variable subsets in reasonable time, given the exponential complexity of an exhaustive search with respect to the number of variables. To further aggregate the variable sets and discard redundant ones, we adopt the iterative sieving procedure described in [6].
Running experiments on three different datasets and using three different families of classifiers (tree-based, distance-based, and support vector machines), we could show that the compressed representations of data which can be obtained using ZIFF, even using possibly the simplest possible feature encoding, can, in some cases, already yield results that are, on average, competitive with other feature extraction method, or even outperform them. As we underline in Section 5, all the feature extraction methods we used as references had, in principle, some a priori advantages over our method, in terms of the information available for constructing the reduced feature sets, being either supervised methods or methods in which each feature is a recombination of the whole set of features by which the original data are represented.
The rest of the paper is structured as follows. In Section 2, we review the state of the art about feature extraction and recent work introducing the metrics. In Section 3, we give details about the theoretical background of such indices. In Section 4, we describe ZIFF, whose experimental evaluation is then described in Section 5 through a comparison, on three datasets corresponding to three different real-world case studies, with other feature extraction/selection techniques. Finally, Section 6 concludes the article with some relevant remarks and the anticipation of possible future developments.
2. State of the Art
Finding algorithms capable of effectively reducing the number of features (attributes) representing data in classification tasks is a central problem in pattern recognition [7]. Theoretically, the presence of many features offers the opportunity to develop classifiers having better discriminating power. However, this is not always true in practice, because not all features are as important for understanding or representing the underlying phenomena of interest. Thus, reducing the number of attributes, or creating new more informative ones, is an essential pre-processing step in classification that may have several beneficial effects, such as lowering the complexity of the classifier model, reducing overfitting, increasing the interpretability of the results, reducing the actual cost of feature collection and pre-processing, resisting noise, and, sometimes, improving the accuracy of a classifier.
There exist three possible approaches to modify the number of features s, typically referred to as feature selection, feature extraction, and feature construction [8]:
- Feature selection chooses a subset of m features out of the original s ones.
- Feature extraction creates a set of new features from the original attributes through some function mappings.
- Feature construction augments the space of features by inferring or creating additional attributes.
These approaches can be further classified into supervised and unsupervised methods. The former include methods that take into account, somehow, information about the classifier or the class to which the training data belong. The latter do not rely on such information but just on the intrinsic properties of the dataset.
In the following, we briefly review articles mainly regarding unsupervised feature extraction methods, with particular emphasis on those based on information theory. Moreover, we briefly summarize previous work on the use of the metrics for detecting relevant subsets in complex systems, along with preliminary attempts to extend them to feature extraction.
Starting with methods which do not rely on Information Theory, the authors of [9] introduced a method for unsupervised feature extraction in time series clustering. This method relies on an orthogonal wavelet transform to perform feature extraction, determining also the appropriate dimension of the optimal feature set in an automated way. The sum of squared errors between the cluster centroids represented according to the new features and the original time series computed on five benchmarks is the criterion used to assess the quality of the resulting clustering.
More recently, in [10], a generic framework for both feature extraction and data classification of hyperspectral images has been presented. The technique tries to jointly optimize the features and the corresponding classifier. In [11], the authors employed Gaussian feature extraction for tracking particles in images produced by CMOS camera sensors. The method is verified on a channel flow, using a boosted regression tree ensemble, and tries to fit generalized Gaussian distributions to particle images. The contribution in [12] uses a projection learning method, namely a low-rank and sparsity preserving embedding for unsupervised learning, which simultaneously learns the graph and the optimum projection by exploiting both global and local information of data. In [13], the authors applied an unsupervised deep-learning framework to reduce the dimensions of a dataset. This is achieved by aligning local features and then transferring them from local coordinates to global coordinates. Jiang et al. [14] tried to apply a novel super Principal Component Analysis method to extract features from hyperspectral images in an unsupervised way, while, in [15], a semi-supervised method, based on deep learning, is used to extract features from colon tissue images. The semi-supervision of the latter derives from the exploitation of domain-specific prior knowledge to identify salient sub-regions in an image, in order to pre-train a deep belief network.
Moving away from methods focused on image analysis, in [16], an extension of Principal Component Analysis, namely a tensor decomposition, is applied to miRNA transfection experiments in order to identify critical genes, whereas, in [17], the same author applied a similar method, together with pure Principal Component Analysis, to represent gene expression in the brains of social insects.
The contribution in [18] compares different linear unsupervised feature extraction methods (Principal Component Analysis, Projection Pursuit and Band Subset Selection) for the classification of high-dimensional multispectral and hyperspectral data. The authors also introduced an optimized version of Projection Pursuit, called Optimized Information Divergence Projection Pursuit (OIPP), which maximizes the information divergence between the probability density function of the projected data and a Gaussian distribution. The aforementioned methods are compared by means of both supervised and unsupervised classifiers over different datasets where OIPP shows good performance in contrasting the Hughes phenomenon as well as the curse of dimensionality.
The usage of Information Theory metrics for unsupervised feature extraction dates back to the the 1980s, when unsupervised feature extraction was employed for face categorization by means of an image compression network [19]. Another example is the work of Fisher and Principe [20], which exploits mutual information for the same aim. Since mutual information is composed of two entropy terms, the algorithm they proposed tries to maximize one entropy term and, at the same time, minimize the other one, seeking a certain parameter that determines the distance of the observed distribution from a uniform distribution. To this aim, the authors employed a Parzen window method as an estimator of the output distribution and the integrated square error as a distance method, as well as an indirect measure of the entropy. In such a way, even if the authors employed mutual information, the method is unsupervised, since it enables entropy manipulation modeled as local interaction between observations in the output space.
In [21], information-theoretic criteria are used for unsupervised image clustering. The method exploits the information bottleneck principle and the mutual information between the clusters and the image content. The principle states that the desired clustering is the one that minimizes the loss of mutual information between the objects and the features extracted from them. The work also exploits a mixture of Gaussian distributions for modeling continuous images and, similar to our work, measures the quality of the resulting clustering by means of supervised classification.
In [22], the authors used, as a criterion, the maximization of an approximation of the mutual information between class labels and feature extractor with the aim to train a feature extractor independently of the classifier. The unsupervised characteristic results from the usage of Renyi’s quadratic entropy in the computation of mutual information and from its nonparametric low-complexity estimation. The information-theoretic criterion employed for the estimation forces the feature extraction matrix to be a rotation matrix.
In [23], the authors studied the problem of unsupervised domain adaptation, trying to detect domain-invariant features and, at the same time, construct the classifier model. This is obtained by optimizing mutual information, using discriminative clustering and simple gradient-based methods. The optimization both maximizes domain similarity (the negated mutual information between all data and their binary domain labels) and minimizes the expected classification error on the target domain (the negated mutual information between the target data and their cluster labels). The proposed solution performs better than other unsupervised methods such as Principal Component Analysis, Structural Correspondence Learning and Transfer Component Analysis.
As regards the Relevance Index metrics, many papers have been published recently. Two seminal papers [1,24] introduced the Dynamical Cluster Index (DCI) as an extension of the Functional Cluster Index (CI) previously defined by Edelman and Tononi [25,26] to detect functional relationships between brain regions. Recently, the DCI has been applied to detecting relevant variable subsets in several kinds of complex systems, including abstract models of gene regulatory networks and simulated chemical [27] and biological systems [28], as well as social networks [29]. In these papers, the DCI was gradually refined and became the so-called Relevance Index (RI); at the same time, its calculation in reasonable time was made possible by the definition of a specific niching genetic algorithm [4] and by the GPU implementation of K-Means PSO [30,31] as well as of the fitness function (RI computation) [5], common to the two approaches.
The most recent advancement related to the use of these metrics is the introduction of an iterative sieving procedure which removes redundant variable sets, i.e., sets between which an inclusion relationship exists while being characterized by different values of the metric taken into consideration. In that case, only the higher-index set is taken into consideration and is considered to represent a single variable from that moment on. The iterative application of the sieve allows one to merge the original variables optimally and to obtain a gradual construction of the compressed representation of the system [6].
The RI metrics have been applied to feature extraction [3], as well as to pattern clustering and classification [2] with promising preliminary results. In [2], one can find the first definition of the index, the metric that we used in this study.
3. Theoretical Background
In this section, we provide an overview of the theoretical aspects of the proposed unsupervised feature extraction method, treating the following points:
- the Integration in the context of the Relevance Index metrics;
- the motivation to use the metric;
- the evolutionary algorithm we implemented to compute the ;
- the sieving procedure used to iterate the computation; and
- the application of the to the unsupervised feature extraction problem.
3.1. Integration as a Relevance Index Metric
Let us consider a system U, composed of N random variables (RVs). The system can be described by its state , i.e., a random vector whose elements are the N random variables, representing the features in the context of this paper. Given this scenario, we consider n independent observations of the state . Therefore, for each RV , we have a sequence of independent observations, identically distributed (). Considering a sufficiently large n, one can consider the empirical entropy of a sequence of RVs, computed through the relative frequencies, to be equal in probability to the real individual entropy [32].
We deal with entropies because they are involved in the definition of the Relevance Index by means of the ratio of two quantities, namely the Integration I and the mutual information , computed over , a subset composed of k variables, with . As a matter of fact, the relevance index RI is defined as:
The mutual information is a well known metric, used also in many feature selection and extraction techniques, which measures the mutual dependence between subset and the remaining part of the system .
Conversely, the use of is usually not so widespread in the context of feature selection/extraction. It measures the mutual dependence among the k elements in . It is defined as the difference between the summation of the entropies of the single variables composing subset and the total entropy of subset itself:
where is the entropy [32] of the sequence . It can be observed that and it is zero when the RVs are independent, such that . On the other hand, the integration increases with the decrease of the second term, i.e., with the correlations among the random variables.
It can be seen from Equation (1) that, in order to have a high Relevance Index, we need a set in which the elements diverge as much as possible from independence among themselves and, at the same time, are as much independent as possible of the rest of the elements in the system. In the context of detecting relevant subsets of complex systems, the idea was to use the value of the RI, which can be computed using empirical entropies, to rank the subsets and consider those having higher index as more relevant. However, a comparison based on the expression given by Equation (1) would be unfair since the RI scales with the size of the considered subset. Moreover, it does not provide information about the significance of the value of the RI itself. To overcome these problems and find a more meaningful expression for the index, a null hypothesis has been usually considered [29,31]: the absence of correlated subsets. In such approaches, the RI was computed as a z-score () as follows:
where and are the sample mean and the sample standard deviation of , the relevance index of a group of k elements computed under the null hypothesis of a cluster-free system.
This approach still has some limitations [2]. First, the definition of the relevance index in Equation (1) is somehow empirical: the choice of dividing the integration by the mutual information is not based on any theory or any specific motivation. The integration alone seems to already provide the majority of the relevant information regarding the tightness of variables in certain subsets. Furthermore, the computation of such a ratio could be sometimes problematic, since the mutual information is zero when the two groups of RVs are independent, which causes the ratio to tend to infinity. Secondly, the z-score form of the RI (Equation (3)) involves the creation of the null system and the computation of its statistics. This direct computation can be avoided if we consider a metric for which the distribution under the null hypothesis is known, such that the z-score can be built without the explicit generation of the null system. In the following subsection, a brief derivation of this new index, called since it is still a sort of z-score, is presented, starting from theoretical considerations about the distributions.
3.2. Motivation to Use the
The metric is defined as follows
where n is the number of observations or instances of the whole system, a subset of k out of N variables and is a subset of dimension k extracted from a null system (i.e., a system within which all N variables are independent).
In other words, using the , it is possible:
- to use only the integration, which, by itself, provides a measure of the tightness of the interaction between variables belonging to the same subset; and
- to adopt a normalization procedure by considering the average value and the standard deviation of the metric, whose computation can be accelerated thanks to the theoretical hints described in the following.
According to Wilks’ theorem [33], and considering as the null hypothesis the case of independent variables and as an alternative hypothesis the case of dependent variables, it is known that the quantity defined as
for n large enough is chi-squared [34] distributed with degrees of freedom () , when the null hypothesis holds. According to Owen [35], this result can be extended to nonparametric likelihood functions, which can be demonstrated to be our case of interest.
Moreover, it can be demonstrated that , with the following implication
under the null hypothesis of independent RVs and with n large enough.
It can be demonstrated that the degrees of freedom for Equation (6) can be expressed as:
where is the cardinality of the alphabet of . The second term of Equation (7) is the number of degrees of freedom under the null hypothesis, while the first term is the number of degrees of freedom in the opposite case, where no RV describing the system is independent of the others.
It is known [34] that the mean and the standard deviation of the chi-squared distribution with g degrees of freedom are
hence, the elements of Equation (4) are now all defined and can be simply computed without relying on the homogeneous system.
3.3. Computation through an Evolutionary Algorithm
The metric expresses the relevance of a group of variables for the system under consideration: the higher the , the more relevant the group. A list of relevant sets can be obtained in principle by enumerating all possible subsets of the system variables and ranking them according to the values. The exhaustive search soon reaches unrealistic requirements for computational resources, because the number of subsets increases exponentially with the number of variables. When large systems are analyzed, this issue makes it impossible to compute the for every possible subset of variables, even using massively parallel hardware such as GPUs.
Therefore, to quickly find the most relevant subsets as well as to counteract the complexity of the exhaustive search, we used a metaheuristic (HyReSS) [4,31], which hybridizes a genetic algorithm with local search strategies. HyReSS maximizes a fitness function corresponding to the computation; moreover, its search procedure is driven by the statistics, computed at runtime, on the results that the algorithm itself is obtaining. HyReSS searches the highest- sets by exploring many peaks in parallel; this happens because the evolutionary search is enhanced by a niching technique introduced to maintain population diversity. HyReSS is first run to address the search towards the basins of attraction of the main local maxima in the search space. Then, the regions identified during the evolutionary process are explored more finely and extensively by a series of local searches to improve the results.
The computation, which is the most computation-intensive module within the algorithm, is parallelized for large blocks of sets through a CUDA (https://developer.nvidia.com) kernel, which fits the computational needs of this problem particularly well [5].
3.4. Iterative Sieving Procedure
As a further and final step, a sieving algorithm [1], performed iteratively, is used to reduce the list of sets found by HyReSS to the most representative ones. The representativeness taken into account by the sieving algorithm is based on the following criterion: if set is a proper subset, or superset, of set and ranks higher than according to the , then is considered more relevant than . Therefore, the algorithm keeps only those sets that are not included in, or do not include, any other higher- set. This sieving action stops when no more eliminations are possible and thus the remaining subsets cannot be decomposed any further.
The sieving procedure allows one to analyze the organization of the variables in terms of its lowest-level subsets; nevertheless, to analyze also the aggregated hierarchical relations among the identified sets, we employed an iterative version of the sieving method, which acts on the data by iteratively grouping one or more sets into a single entity. The simplest, yet effective, way to do so consists in iteratively running the sieving algorithm on the same data, each time using a new representation of the variables, where the top-ranked set, in terms of value, of the previous iteration is considered atomic and is replaced by a single variable (group variable) [6]. In this way, each iteration produces a new representation composed of both single variables and group variables detected in previous iterations.
4. -Based Feature Extraction
Let us consider a dataset whose elements are instances of a schema in which data correspond to a set of k-bit binary features . The class label , if specified, is defined over a finite set of symbols, generalizable as a natural number subspace.
ZIFF derives m () new features from D. It only relies on A, i.e., it does not take the class label into account, and can therefore be termed as unsupervised, as opposed, for example, to the supervised approach we preliminary analyzed in [3].
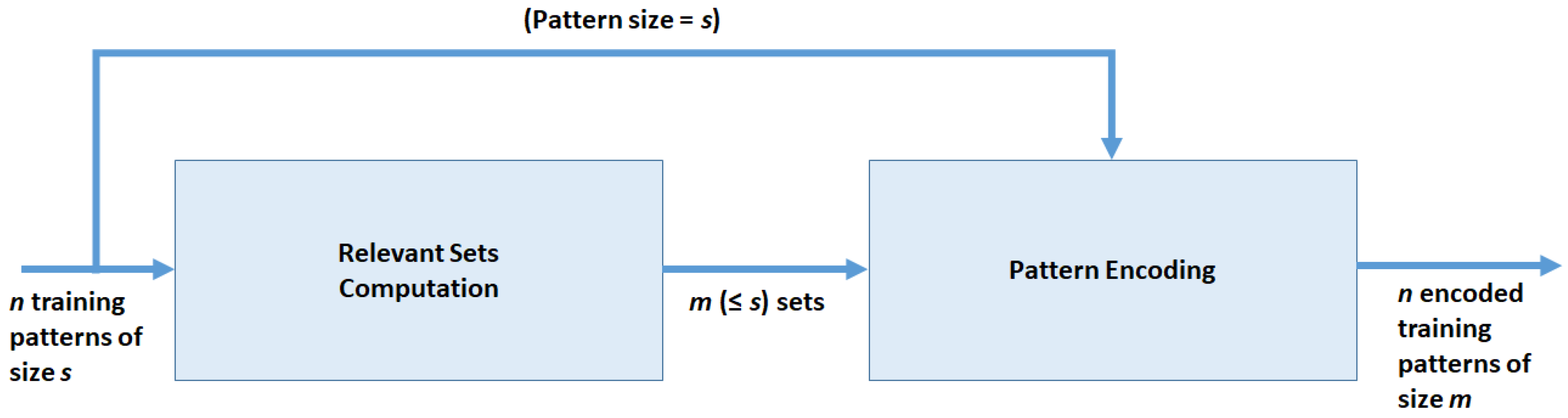
ZIFF is a two-stage method (see Figure 1) which produces as output a new representation of the n input instances in D according to a new schema defined over the m newly created features plus the class label.
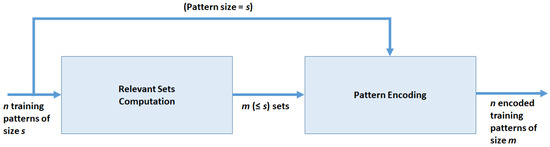
Figure 1.
Data flow of the feature extraction method.
The first stage of the method consists in the -based computation of the relevant variable sets such that for and . The computation is made according to the sieving algorithm described in Section 3.4, whose basic step is the evolutionary algorithm described in Section 3.3. Therefore, each instance of D is decomposed into a set of binary strings , instances of of size , with representing the number of elements in z.
In the second stage, we transform subsets of the original dataset into corresponding numeric features . Therefore, the feature-construction process produces a new dataset, derived from the original one and of lower dimensionality, which is expected to retain as much as possible of the original information content which is useful for developing effective classifiers.
As the results obtained in our experiments show, the feature-encoding phase is critical for the performance of the classifiers which can be generated using the transformed datasets as training and test sets. In the following subsection, we describe the encodings we tested in our experiments. In Section 5, while reporting the experimental results of our tests, we discuss them more in depth, with particular regard to their compliance with the different classifiers we have taken into consideration.
4.1. Possible Encoding Schemata
The most direct (and, possibly, naïvest) way of encoding a binary string into a single numerical feature is transforming it into its corresponding integer representation.
The simplicity and easy applicability of this encoding is compensated by two main drawbacks:
- It depends on the order in which bits are taken into consideration: bits that are remapped as more significant have a larger weight in the final encoding. The ratio between the weight of the most significant bit (MSB) and the least significant bit (LSB) increases exponentially with the number of bits, up to making the LSB virtually irrelevant.
- Topological relationships are not preserved. Neighborhoods of the encoding of a given string S may not (and usually do not) include the encoding of the same elements included in the neighborhood of S.
Despite these drawbacks, some kinds of classifiers, not surprisingly those which are able to “segment” the pattern space into a set of small intervals, such as tree-based classifiers, seem to be mostly insensitive to such problems, as we show in the next section. Because of this good compliance between such an encoding and tree-based classifiers, in the experiments described therein, we report results based on this encoding schema. In fact, the main goal of this paper is showing that the iterated computation of the index is able to identify sets of variables by which one can build features that are relevant to classification as effectively as an exhaustive exploration of the whole space of possible encodings. In using this representation, we only take care of the order in which the variables/features are packed into a bit string, setting as most significant bits the attributes that have been grouped earlier, since, in each iteration, our sieving algorithm extracts the group that is deemed most relevant based on its value.
An immediate amendment of the previous schema consists in normalizing the features obtained as above by dividing each feature by , k being the length in bits of the binary representation of features in the original dataset, such that all new features are bounded within the interval . The more evident and usually positive effect of normalizing a dataset, especially when distance-based classifiers are being used, is mainly guaranteeing that no feature is more relevant than the others just because of its scale. In our approach, this effect can be appreciated (i) as an equalizer between the transformed pattern components, whose scale, and therefore relative weight, depends on the number of elements in the relevant set from which it derives; and (ii) as a partial equalizer between each element in a relevant set, whose relative weight depends on its position within the bit string obtained by packing the values of all elements in the set. Finally, input data normalization is sometimes a requirement for certain kinds of classifiers.
Since normalization actually appears to bring a general improvement of the results, with virtually no negative side effects, we normalized data representations by default in all our experiments.
5. Experimental Evaluation on Real-World Datasets
In this section, we describe the experiments we made to evaluate whether the analysis based on the RI metrics can be effectively extended from the domain of complex system analysis to feature extraction in classification problems. In particular, we compare the results obtained by ZIFF to other supervised or unsupervised feature extraction and selection methods using real-world data from three test problems.
Considering the goals of our research, in setting up our experiments, we expected the results we would obtain to answer the following questions:
- Are the properties of the variable sets detected using the index, which have already been demonstrated to be effective in their original role of detecting functional blocks in complex systems, as relevant when such sets are used to build classification-oriented representations?
- How well do such representations compare with other representations which can be obtained by more classical feature selection/extraction methods?
- How data- or classifier-dependent are the results provided by such representations?
In the rest of this section, we first describe the experimental setup and then we discuss the results of our tests, considering, in particular, the classification accuracy which can be obtained using representations of different dimension provided by ZIFF and by the other feature extraction/selection methods taken as references, when coupled with a selected sample of classifiers of different kinds, both as regards the data types they process and the classification criteria.
5.1. Experimental Setup
The experimental setup was the same for all three tests, in which ZIFF and the reference methods were applied to different datasets. In particular, for each set of features extracted by ZIFF in each iteration: (i) a feature set of the same size was extracted or selected using each reference method; (ii) for each iteration of ZIFF and for each feature extraction or selection method, a corresponding representation of the reference datasets (a training and a test set) was computed; (iii) each training set thus obtained was used to train four classifiers of different kinds; and (iv) the classifiers were finally validated on the corresponding test set by computing their classification accuracy.
5.1.1. Feature Extraction/Selection Methods
We selected the following four feature selection/extraction methods as the references to be compared to ZIFF:
- Principal Component Analysis (PCA) [36], which uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values representing the projection of the data onto an orthogonal base of linearly uncorrelated principal components.
- Information Gain (IG) [37], which is the conditional expected value of the Kullback–Leibler divergence of the univariate probability distribution of one variable from the conditional distribution of such a variable given the other ones.
- Chi-squared test () [38], which is a statistical hypothesis test where the sampling distribution of the test statistic is a chi-squared distribution when the null hypothesis is true.
- Univariate feature selection (F_VAL) [39], which is a feature selection method based on univariate statistical tests.
One should notice, on the one hand, that, except for PCA, all these methods are feature selection methods. This fact offers PCA (and ZIFF) the advantage of being able to create new features that derive from more than one of the original ones, thus having higher potential information content. On the other hand, one should also consider that, while PCA and ZIFF are unsupervised methods, the other methods taken into consideration are all supervised and aimed explicitly at maximizing classification accuracy, which often more than compensates for the above drawback.
5.1.2. Classifiers
As a criterion to compare the five feature selection/extraction methods, we used the classification accuracy of the following four classifiers, trained and tested using, as data representation, the feature sets extracted by each of the above methods and by ZIFF:
Tree-based
- Random Forest (RF) [40], which is an ensemble learning method that constructs a multitude of decision trees at training time and outputs as its final decision (i.e., class) the mode of all the decisions taken by the trees.
- Decision trees (C4.5) [41], which is a tree classifier where nodes hierarchically partition the pattern space, each node based on the values of a single feature, until a leaf node, representing a decision, is reached.
Distance-based
- K-Nearest Neighbors (KNN) [36], which is a non-parametric method where an object is classified by applying a majority vote strategy to the decisions of its neighbors in the training set, resulting in the object being assigned to the class most frequently represented by its K nearest neighbors.
Support Vector Machines (SVM)
- Radial Basis Function (SVM) [36], which is a supervised learning model where the examples, represented as points in the pattern space, are mapped using a Radial Basis Function kernel, such that the margin (distance) between boundary examples representing different classes is maximized.
5.1.3. Datasets
The three different real-world datasets, onto which we focused our attention, are described in the following and summarized in Table 1.

Table 1.
Description of the three datasets used in our tests (B = Binary; N = Nominal).
The first dataset () (ftp://ftp.ce.unipr.it/pub/cagnoni/license_plate) contains low-resolution () binary patterns, representing digits from 0 to 9, collected from license plates at highway toll booths by Società Autostrade SpA. It includes 11034 patterns, roughly uniformly distributed among the ten classes under consideration. The patterns were trivially binarized pixel-wise using a threshold of (considering pixel values normalized between 0 and 1). This resulted in strings of 104 binary features. We used part of the full dataset as a training set with 6024 patterns, and the remaining 5010 patterns, exactly 501 per digit, as a test set.
The second dataset () is the Optical Recognition of Handwritten Digits dataset from the UCI machine learning repository (https://archive.ics.uci.edu/ml/datasets/optical+recognition+of+handwritten+digits). The dataset contains 5620 samples of bitmaps of hand-written digits from 0 to 9: bitmaps were divided into non-overlapping blocks of size and the number of pixels was counted in each block. This quantization produced input patterns of pixels, each of which may have an integer value in the range . In our experiments, we considered a 4-level discretization of the original 16 values; as a consequence, each image of the dataset is an instance with 64 numerical features assuming values in the range , and one class attribute with values in . The training set comprises 3823 instances, while the test set 1797 instances.
The third dataset () regards splice-junctions in gene sequences of the DNA (https://www.openml.org/d/40670). It consists of 3186 data points (instances) described by 180 indicator binary variables (nominal features) and by one class label assuming three possible values (ei, ie, or neither). The classes represent the boundaries between exons (the parts of the DNA sequence retained after splicing) and introns (the parts of the DNA sequence that are spliced out). This dataset is a processed version of the one contained also in the Irvine database (https://archive.ics.uci.edu/ml/datasets/Molecular+Biology+(Splice-junction+Gene+Sequences)) in which the names of the examples, along with the ambiguous instances (only four, actually) were removed. In the dataset we used in our experiments, the four nitrogenous bases (Adenine, Guanine, Thymine, and Cytosine) were replaced by an integer label from the set 0, 1, 2, 3 to make it easier to obtain the numeric encoding of the features extracted by ZIFF. We considered 2230 sequences as a training set and the remaining 956 as a test set.
5.1.4. Evaluation Procedure
The test procedure we adopted to compare the performance of ZIFF to the reference methods can be summarized as follows:
- Compute the Relevant Sets by iteratively applying HyReSS to the training set, as described in Section 3.3 and Section 3.4. Starting from an initial representation in which all correspond to a single feature of the original dataset, in each iteration, we merge into a new set the from the previous iteration whose union has the largest possible value. From then on, and until it is involved in a new merger, HyReSS will treat the newly-created variable set as a single variable (group variable) in the representation of data, which will substitute its components in the list. Thus, after each iteration, the number of variables () used to represent data decreases while the average size of the increases.
- Encode the training and test data, as described in Section 4.1, according to the feature sets extracted up to the current iteration of HyReSS.
- For each of the reference methods, and for each iteration of ZIFF, consider the feature sets, extracted or selected by the method under consideration, having the same size as the number of found by ZIFF, and compute the corresponding representation of the benchmark datasets.
- Apply the classifiers to such representations for testing the effectiveness of the corresponding feature set using the classification accuracy as a quality criterion.
- Stop iterating when the of the new group variable deriving from the merger “proposed” by HyReSS falls below a pre-set threshold.
To perform the computation as efficiently as possible, HyReSS was implemented in C++ and the corresponding GPU-based fitness function, which computes the index, in CUDA C [42]. Instead, the code we used for our tests was written in Python to take advantage of the scikit-learn (https://scikit-learn.org) Python package implementation of all the necessary classifiers and reference feature extraction/selection methods. Notice that, using scikit-learn, the C4.5 algorithm is implemented as an object belonging to the DecisionTreeClassifier (DecisionTreeClassifier(criterion=entropy,...)) class.
Since our goal was to compare the effectiveness of the representations obtained with different feature extraction/selection methods under controlled conditions, and not to obtain the highest possible performance, when applying a classifier to our benchmarks we used the default classifier configuration proposed by scikit-learn. Therefore, when analyzing the results, it is important to mainly focus on the relative ranking between the different methods, independently of the absolute quality of the results.
To take into consideration the intrinsic stochastic nature of Random Forest and a heuristic that has been introduced in the scikit-learn version of C4.5, which makes the results of that classifier stochastic as well, we repeated all experiments using such classifiers five times and computed the average accuracy over the five independent runs.
In this regard, it should also be noticed that the outcome of HyReSS, which is a stochastic optimization algorithm, was stable over the five repetitions, i.e., it always found the same variable sets.
Finally, when considering the KNN classifier, we preliminary tested K values equal to 1, 3, and 5. Since no substantial differences could be observed which would affect the comparison between ZIFF and the references, we only report the graphs related to .
5.2. Results and Comparisons
A preliminary interesting observation which can provide some hints on the sensibility of the features that ZIFF extracts is that, according to the structure of the data from which they have been extracted, they tend to correspond to contiguous regions, and seem to have the same role as focus-of-attention algorithms have in computer vision. This is true for both the data representing two-dimensional patterns ( and ) and one-dimensional DNA sequences (). Figure 2 highlights the variable sets identified by ZIFF after the 70th iteration of the sieving algorithm has been applied to . Different colors represent different groups of pixels identified by ZIFF. As can be seen, the groups represent connected subparts of a digit.

Figure 2.
Relevant variable (pixel) sets identified in the after the 70th iteration of ZIFF. Pixels of the same color belong to the same relevant set.
As regards the quantitative assessment of the quality of the feature sets extracted by ZIFF and by the reference methods, following the procedure described above, the results obtained by ZIFF and by the reference methods can be summarized plotting a curve for each feature extractor/classifier pair. A point of represents the accuracy value which is obtained when classifier i is applied to dataset j represented by the feature set extracted by method f, having a size equal to the number of features extracted by ZIFF in each iteration.
In particular, for each iteration, we collected and plotted the classification accuracy along the y axis of a 2D graph and the size of the feature set (decreasing) or the iteration number (increasing) along the x axis.
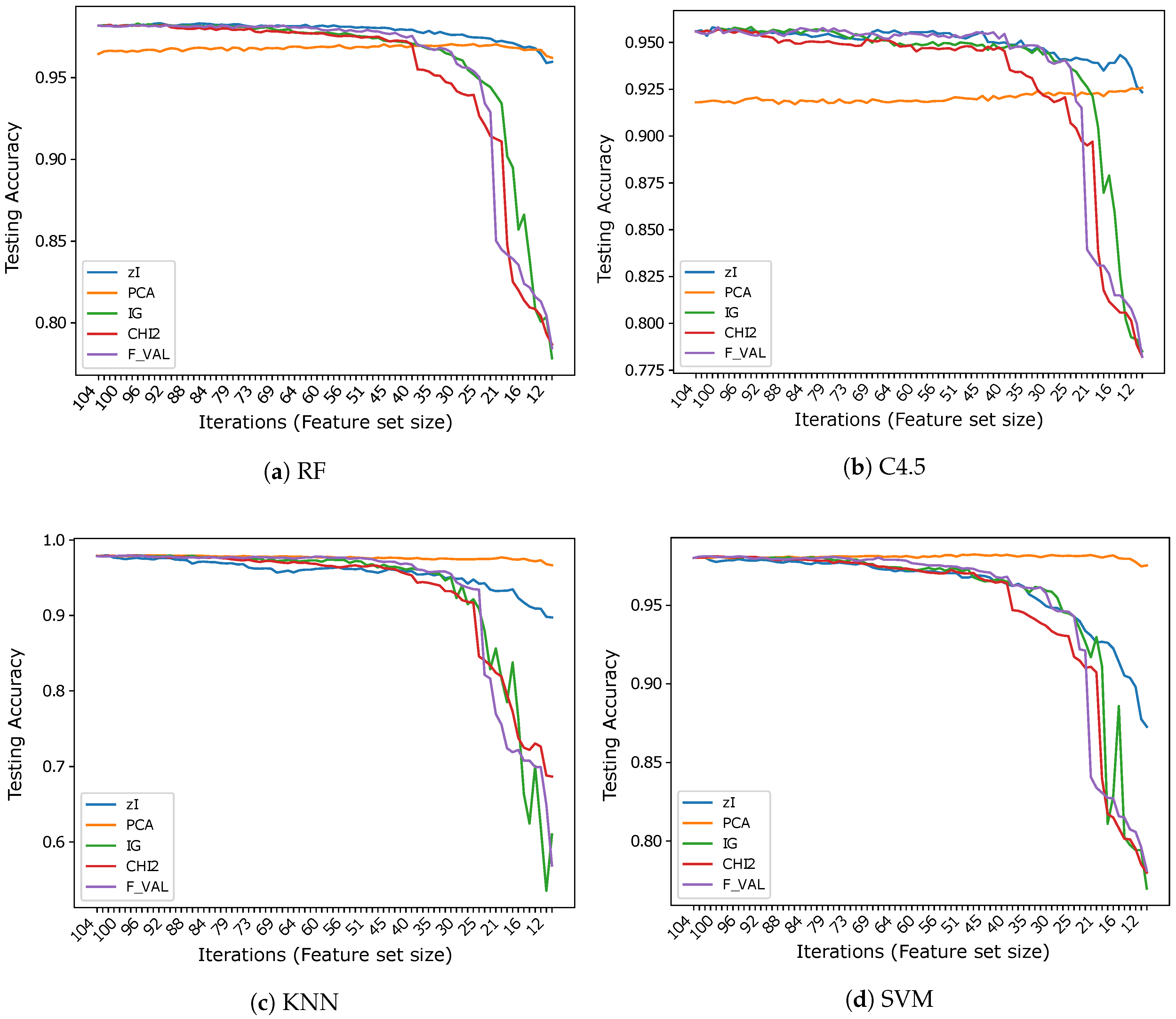
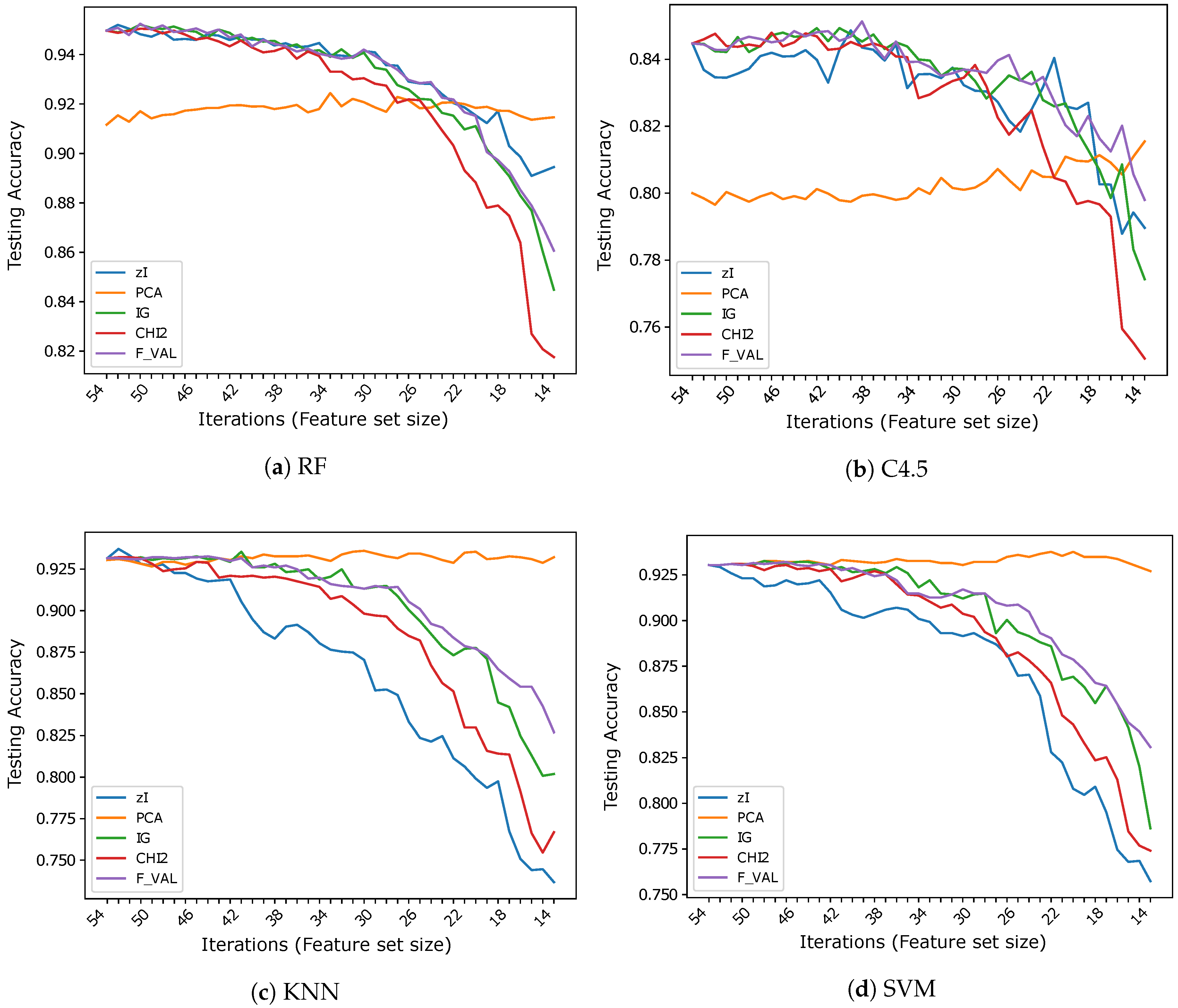
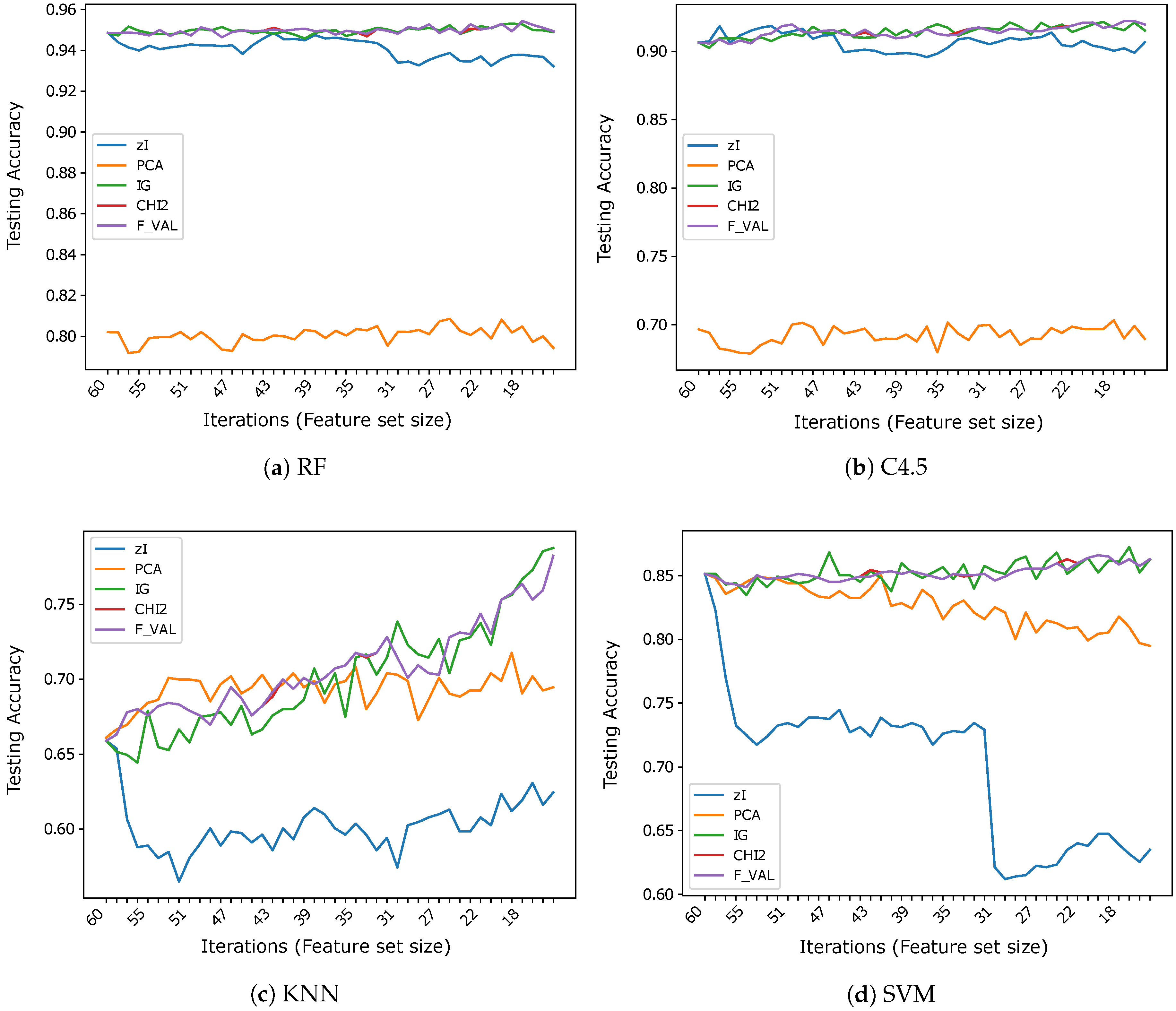
Figure 3, Figure 4 and Figure 5 show the results (accuracies) we obtained in our tests, subdivided by dataset. Ticks on the x-axis represent ZIFF iterations, increasing from left to right, while the corresponding numerical labels represent the number of features extracted in each iteration (the first iteration includes all the original features). These graphs allow one to compare our method and the reference methods over the same data, assessing the capacity of each method to produce representations which preserve the information that is most relevant to classification, as the dimensionality of the representation decreases.
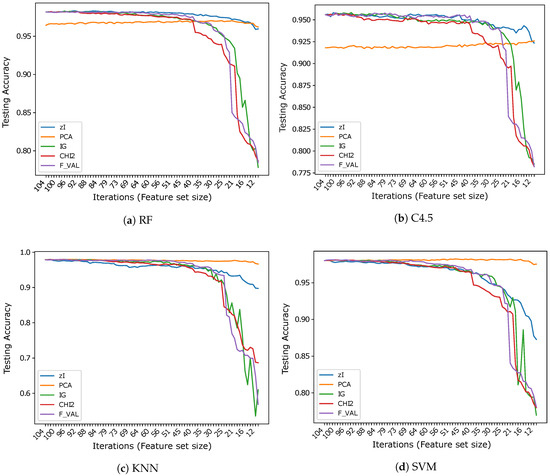
Figure 3.
Accuracy vs. number of iterations (and number of features) for different classifiers using .
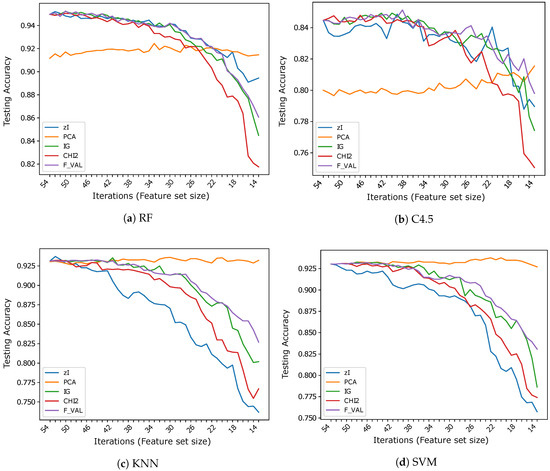
Figure 4.
Accuracy vs. number of iterations (and number of features) for different classifiers using .
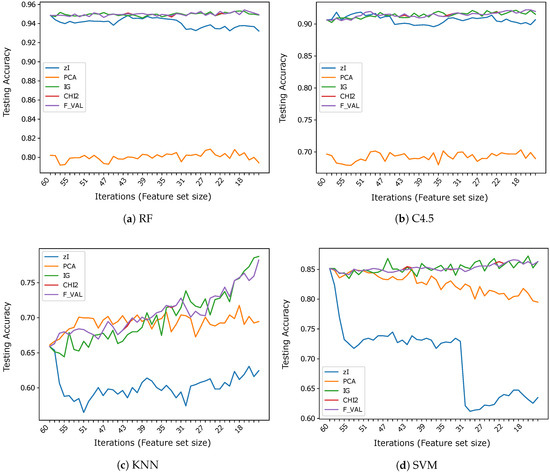
Figure 5.
Accuracy vs. number of iterations (and number of features) for different classifiers using .
Thus, each figure embeds four graphs; each graph within each figure corresponds to a dataset/classifier pair, and each plot within each graph corresponds to a different data representation, given by the specific feature extraction/selection method.
We first provide a straightforward description of the results obtained on each dataset and then comment on them, trying to justify—with regard to ZIFF’s limitations, the nature of data, and the nature of the classifiers – the rather large differences between the performance obtained using different feature extraction and selection methods as well as by different classifiers.
The results obtained on seem to strongly support the hypothesis that the variable (pixel) sets identified by the index actually correspond to features that are relevant for classification. When RF is used as a classifier, ZIFF is the best performing method with virtually all feature set sizes except for the very last few iterations (feature set sizes approximately below 15), where PCA slightly outperforms it (by less than 1% in the very last iteration). The feature-selection methods taken as references perform very closely to ZIFF down to a feature set size of about 40, but show a dramatic decrease soon after that threshold. This decrease is probably “physiological”, considering that the features they select are single bits, with respect to real numbers which condense the information carried by a relevant number of original feature as happens with PCA, whose features combine all the input features, and, to a minor extent, with ZIFF. The results obtained on the other tree-based classifier, C4.5, are very similar, even if generally worse than those obtained by RF, with a performance decrease which is particularly remarkable (4.8% on average on all iterations) for PCA.
Regarding the results which can be obtained using K-NN or SVM classifiers on , the same considerations can be made about the performance of feature extractors versus feature selectors. The accuracy of IG, , and F_VAL is virtually the same as with RF and C4.5 and the critical thresholds under which their performance decreases is also the same. PCA also works as well as before, offering performance that is virtually constant with all feature set sizes, up to the minimum number we considered, which corresponds to the number of sets found in the last iteration of ZIFF. ZIFF, with these classifiers, has a behavior which is intermediate between PCA and the supervised feature selectors, still showing better robustness with respect to feature set size than the latter, but a worse performance than the former.
On , once again, even if less markedly, the features found by ZIFF are the best-performing with RF except for the last iterations (feature size below 20) where PCA is better (of about 2% in the very last iteration), and are very similar to the performance of the feature-selection methods with C4.5. However, on this dataset, RF is much more accurate than C4.5. This is probably caused by the higher intrinsic difficulty of this task (i.e., to the higher variability of data), since RF can create a much finer segmentation of the input domain than C4.5.
ZIFF’s performance is definitely the worst with the classifiers (1-NN and SVM) that usually (or preferably) deal with continuous inputs which reflect data properties for which the computation of Euclidean distances or other topological relationships makes sense.
The inappropriateness of the encoding of ZIFF when used along with K-NN classifiers using the Euclidean distance or SVM is even more clearly highlighted by the results obtained on . In this case, the results obtained using K-NN as a classifier can probably be totally neglected for the incompatibility of such a classifier with data represented by nominal attributes, as we have already remarked. We report such results just for the sake of completeness. Regarding the results obtained with the tree-based classifiers on , the supervised feature selectors are the best representations here, slightly outperforming ZIFF by about on average (roughly versus ). ZIFF still exhibits a remarkable robustness with respect to the feature set size, showing that, when coupled with tree-based classifiers, it is also very robust with respect to the representation of the input data. This is not the case for PCA, whose performance, as could be expected, is very negatively affected by a representation based on nominal features. Only with SVM, PCA accuracy is systematically above , which is still more than worse than the performance of the feature selectors and with RF.
A few observations can be made after analyzing the results reported above, regarding, in particular, the datasets, ZIFF’s encoding, and the classifiers.
A first observation is that results obtained on are generally more “stable” and reproducible. This is probably related to the intrinsic nature of the data, which makes their classification an easier task than classifying the two other datasets, as the best classification results which can be obtained seem to confirm. In fact, quite obviously, although both and represent the same kind of data (two-dimensional patterns representing the figures from 0 to 9), represents handwritten characters which are characterized by an intrinsic variability that is much larger than for data in . Considering also that includes a larger number of samples, our observation finds a rather straightforward justification.
Regarding the intrinsic properties of data, representations based on nominal attributes affect negatively the performance of distance-based classifiers like K-NN. Applying the PCA to such a kind of data by treating the nominal indices as integers actually makes little sense.
In particular, if we consider ZIFF’s problems with K-NN and SVM with respect to the good performance with tree-based classifiers, they may be caused by the lower effectiveness of the features selected by ZIFF, but also by the possible problems related to the compatibility of the encoding scheme with classifiers usually applied to real number representations, as highlighted in Section 4.
The analysis of the results obtained on and seem to support the second hypothesis quite clearly. In fact, ZIFF’s encoding does not preserve distances, and tends to scatter compact neighborhoods in the original representation into a myriad of small intervals in the 1D representation onto which ZIFF maps the original data. This problem affects minimally, if at all, the performance of tree-based classifiers, whose way of working actually corresponds to a partitioning of the input space into a large number of regions, which are labeled after one of the possible classes. The fact that RF performs much better than C4.5 is most probably related with the much higher capacity of RF to identify small regions, owing to the large number of trees (1000 as default value in our tests) of which it is composed with respect to the single, even if larger, decision tree generated by C4.5.
Regarding the problems that ZIFF has with K-NN classifiers based on the Euclidean distance, they are mostly attributable to the distance function adopted, owing to the mentioned lack of topological consistency between the original data representation and the encoding used in ZIFF. This can be shown if we consider datasets that are originally binary, and their K-NN classification based on ZIFF’s encoding and on a distance that can be considered a generalization of the Hamming distance, defined as follows:
where and are N-dimensional vectors and if , 0 otherwise. Therefore, the distance is equal to the number of corresponding elements of the two vectors which are different, and, if x and y are bit strings, it actually corresponds to the Hamming distance between them. However, it can be applied also to integer representations of binary variable sets such as the ones used as encodings by ZIFF.
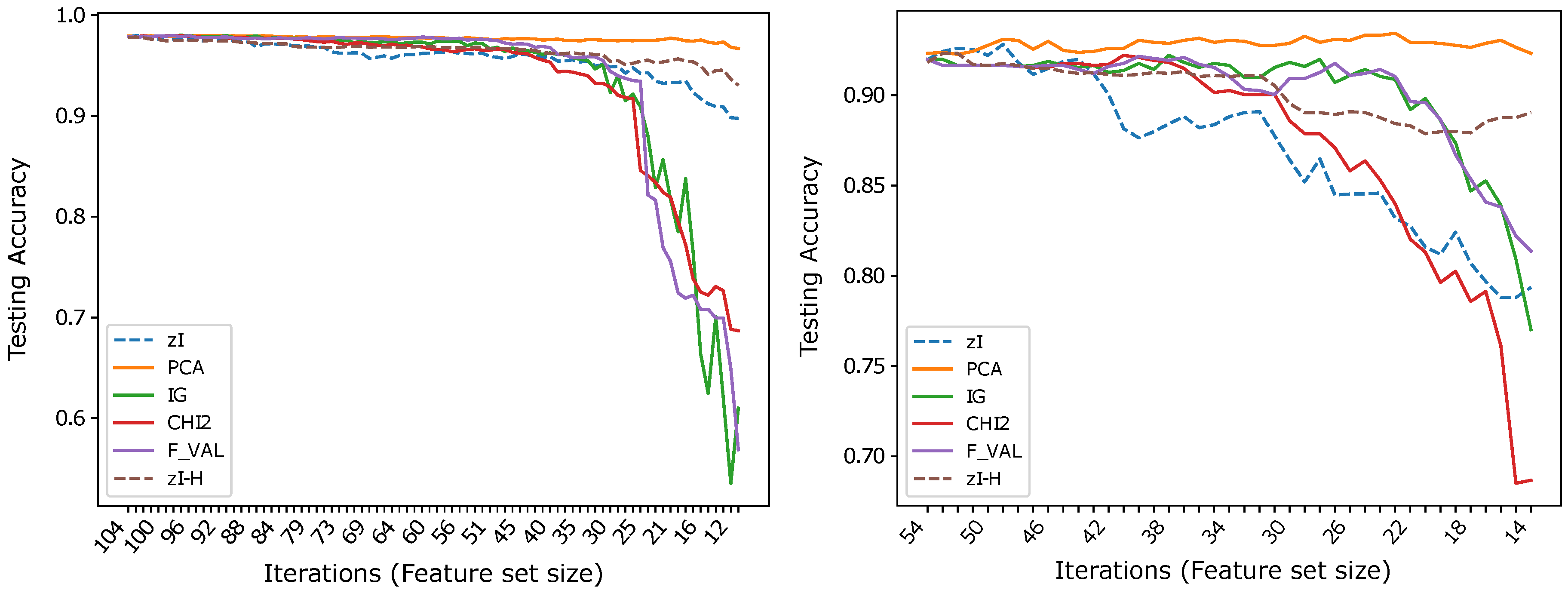
Using 1-NN and as a distance to classify the data representation obtained by applying ZIFF to and, after binarizing the original data, to , we can observe a dramatic improvement of the classification accuracy curves with respect to using the Euclidean distance. In Figure 6, the two dashed lines represent the results of ZIFF using the two distances. Notice that, while for the plots corresponding to the reference methods are the same as in Figure 3, for the results of the reference methods are different from those in Figure 4, since all reference feature extractors/selectors which, in that figure, had been applied based on a four-level discrete representation of the original data, have been applied here to the binary representation of the same data.
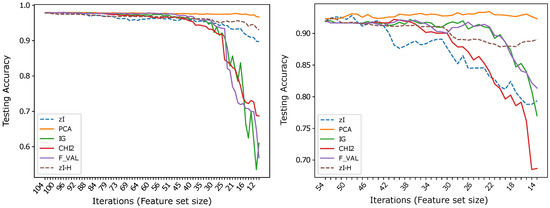
Figure 6.
Results obtained by a 1-NN classifier applied to (left) and to after data binarization (right). The two dashed curves in each plot highlight the improvement that can be obtained computing a generalized Hamming distance to classify -based representations of binary data (-H), with respect to using the Euclidean distance ().
In principle, the distance and, consequently, any K-NN classifier based on it, could be applied to any discrete representation. However, the number of training data necessary for a 1-NN classifier to achieve the same reliability (i.e., necessary for the probability of finding a match between two corresponding components to be the same) increases exponentially with the size of the new feature. Considering, for instance, the representation of a feature derived from M original pixels, the number of possible values that the feature can assume if the original data are binary is , while it becomes if only the original data have a discrete four-value representation. This consideration is the most likely reason for the poor results that can be obtained if we apply 1-NN to the four-level representation of and . It is also almost certainly the reason for the performance decline, with respect to PCA and to some of the other reference methods, which can be observed – even if, on , it is moderate – as the number of iterations increases and, thus, the number of new features decreases and their size, in terms of number of original features included in each of them, increases. Therefore, it is unsurprising that is the dataset on which this effect is less evident, as it contains many more instances than the other datasets, while also being the dataset within which the variance of data within the same class is the lowest (data are printed characters, even if noisy and acquired at a very low resolution).
Therefore, we can say that the distance fits ZIFF’s encoding of features much better than the Euclidean distance for use with distance-based classifiers. The results obtained even suggest that it is optimal for such a representation, when the original features assume discrete values, provided the dataset is large enough. As demonstrated by our tests, this is often the case with binary data representations, but may soon require too many training instances when the number of possible values assumed by the original discrete-valued features increases.
6. Discussion and Conclusions
The work described in this paper was aimed at verifying whether the procedure that uses the metric for detecting relevant functional blocks in complex systems could be applied to classification tasks as well. ZIFF represents possibly the most straightforward adaptation of such a procedure to feature extraction.
In particular, we wanted to assess ZIFF’s performance as an unsupervised extractor of relevant features by which the dimensionality of a dataset representation could be reduced significantly, but with minimum loss of information and, even more importantly, of discrimination power between the different target classes of a supervised classification problem.
Using random forest and decision trees as classifiers, ZIFF obtained results that are competitive with, when not better than, the other feature extractor/selectors taken into consideration. We also showed that, provided that the training dataset size is large enough, ZIFF can also achieve good results using K-NN classifiers based on an appropriate distance. On the contrary, its performance is generally poor when an SVM is used as a classifier.
The results of the tests we performed on three real-world datasets (printed characters, handwritten characters, and DNA sequences) suggest that, even if at the conjecture level, but consistently with the outcome of the tests, we can actually attribute the good results that ZIFF obtained using tree-based classifiers to the relevance of the variable sets ZIFF could identify, the disappointing results obtained using SVMs being most probably related with the inability of our encoding scheme to preserve relationships (such as scale, distance, etc.) which are essential for such classifiers.
A further observation that is worth making is that, in its present implementation, which is exactly the same as the one developed for complex system analysis, for which such a property was not reasonable, ZIFF’s first stage does not allow one to create groups that share the same variable since, in every iteration, the variable sets that are merged are substituted by the new group variable thus obtained. Even though ZIFF obtained good results when applied to binary pattern classification, this can be a rather severe limitation which can be trivially highlighted taking as an example a simple classification problem in which “×” symbols are to be classified against “+” symbols. Considering also the example given in Figure 2, one would expect the relevant variable sets to be represented by horizontal, vertical and oblique segments, possibly having a pixel in common, as happens, for example, with the vertical and horizontal segment of the plus sign. Trivially, considering the features to be equivalent to the segments into which the symbols can be decomposed and the plus symbol as an example, if a feature set represents the vertical bar, then the horizontal bar needs to be split into two segments, one to the right and one to the left of the vertical bar, which, by themselves, are obviously much less relevant than the whole horizontal bar.
Despite these limitations, the results we obtained in our tests confirm that ZIFF, in its version as described in this paper, can represent a viable approach to feature extraction when a good trade-off between classification accuracy and representation size is the goal.
Future Work
Such limitations can be the stimulus and target for future research, summarized in the following.
Firstly, since a mapping between a discrete space into a topologically equivalent continuous one may imply the creation of a higher-dimensional space, which is opposite to the goals with which ZIFF has been devised, the design of new data-dependent encodings seems to be inevitable, to take advantage of local properties of the datasets under consideration and achieve the goal of limiting the dimension of the representation. In particular, we are going to implement and test methods that are specifically aimed at minimizing the distance between adjacent representations, such as Kohonen’s Self-Organizing Maps [43].
Similarly, using global optimization approaches, for instance, genetic programming [44], it would be possibly to find such a (generally non-linear) data-induced mapping also satisfying the requirements for the preservation of topological relationships when moving from the pattern space to the new feature-representation space. Such a property is essential if one wants to apply distance-based classifiers, such as K-NN [45] and Learning Vector Quantization [43] or transformation-based classifiers such as SVM [46] to the new reduced-size representation.
Finally, the feature extraction stage of ZIFF can be modified to enable the re-use of the same original attributes in different feature sets, as happens for example with the PCA, in which all new features are represented by a transformation of the whole set of attributes in the original data representation. We expect this improvement to lead to better final results even if the extension of the number of variable sets to be taken into consideration by HyReSS, the metaheuristic component of ZIFF, could lead to a further increase of the already high demand of computation resources of ZIFF itself.
Author Contributions
Conceptualization, L.S. and S.C.; Data curation, L.S. and R.P.; Formal analysis, L.S., M.M. and S.C.; Investigation, L.S., R.P. and S.C.; Methodology, L.S., R.P. and S.C.; Software, L.S.; Supervision, M.M. and S.C.; Validation, R.P. and S.C.; Writing—original draft, L.S., R.P. and S.C.; and Writing—review and editing, L.S., R.P., M.M., and S.C.
Funding
The work by Laura Sani was co-funded by a grant from Regione Emilia Romagna (“Creazione di valore per imprese e società” con la gestione e l’analisi di BIG DATA”, POR FSE 2014/2020, Obiettivo Tematico 10) within the “Piano triennale alte competenze per la ricerca, il trasferimento tecnologico e l’imprenditorialità” framework, and by Infor srl.
Acknowledgments
The authors would like to thank Chiara Lasagni for the enlightening theoretical details about the derivation of the .
Conflicts of Interest
The authors declare no conflict of interest.
References
- Filisetti, A.; Villani, M.; Roli, A.; Fiorucci, M.; Serra, R. Exploring the organisation of complex systems through the dynamical interactions among their relevant subsets. In Proceedings of the European Conference on Artificial Life 2015; The MIT Press: Cambridge, MA, USA, 2015; pp. 286–293. [Google Scholar]
- Sani, L.; D’Addese, G.; Pecori, R.; Mordonini, M.; Villani, M.; Cagnoni, S. An Integration-Based Approach to Pattern Clustering and Classification. In AI*IA 2018—Advances in Artificial Intelligence; Ghidini, C., Magnini, B., Passerini, A., Traverso, P., Eds.; Springer: Cham, Switzerland, 2018; pp. 362–374. [Google Scholar]
- Sani, L.; Pecori, R.; Vicari, E.; Amoretti, M.; Mordonini, M.; Cagnoni, S. Can the Relevance Index be Used to Evolve Relevant Feature Sets? In International Conference on the Applications of Evolutionary Computation; Sim, K., Kaufmann, P., Eds.; Springer: Cham, Switzerland, 2018; pp. 472–479. [Google Scholar]
- Sani, L.; Amoretti, M.; Vicari, E.; Mordonini, M.; Pecori, R.; Roli, A.; Villani, M.; Cagnoni, S.; Serra, R. Efficient Search of Relevant Structures in Complex Systems. In Conference of the Italian Association for Artificial Intelligence; Springer: Cham, Switzerland, 2016; pp. 35–48. [Google Scholar] [CrossRef]
- Vicari, E.; Amoretti, M.; Sani, L.; Mordonini, M.; Pecori, R.; Roli, A.; Villani, M.; Cagnoni, S.; Serra, R. GPU-based parallel search of relevant variable sets in complex systems. In Italian Workshop on Artificial Life and Evolutionary Computation; Springer: Cham, Switzerland, 2017; pp. 14–25. [Google Scholar] [CrossRef]
- Villani, M.; Sani, L.; Pecori, R.; Amoretti, M.; Roli, A.; Mordonini, M.; Serra, R.; Cagnoni, S. An iterative information-theoretic approach to the detection of structures in complex systems. Complexity 2018, 2018, 3687839. [Google Scholar] [CrossRef]
- Cang, S.; Yu, H. Mutual information based input feature selection for classification problems. Decis. Support Syst. 2012, 54, 691–698. [Google Scholar] [CrossRef]
- Motoda, H.; Liu, H. Feature Selection Extraction and Construction; Communication of IICM; Institute of Information and Computing Machinery: Taipei, Taiwan, 2002. [Google Scholar]
- Zhang, H.; Ho, T.B.; Zhang, Y.; Lin, M.S. Unsupervised Feature Extraction for Time Series Clustering Using Orthogonal Wavelet Transform. Informatica 2006, 30, 305–319. [Google Scholar]
- Qiao, T.; Yang, Z.; Ren, J.; Yuen, P.; Zhao, H.; Sun, G.; Marshall, S.; Benediktsson, J.A. Joint bilateral filtering and spectral similarity-based sparse representation: A generic framework for effective feature extraction and data classification in hyperspectral imaging. Pattern Recognit. 2018, 77, 316–328. [Google Scholar] [CrossRef]
- Franchini, S.; Charogiannis, A.; Markides, C.N.; Blunt, M.J.; Krevor, S. Calibration of astigmatic particle tracking velocimetry based on generalized Gaussian feature extraction. Adv. Water Resour. 2019, 124, 1–8. [Google Scholar] [CrossRef]
- Zhan, S.; Wu, J.; Han, N.; Wen, J.; Fang, X. Unsupervised feature extraction by low-rank and sparsity preserving embedding. Neural Netw. 2019, 109, 56–66. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yu, J.; Tao, D. Local Deep-Feature Alignment for Unsupervised Dimension Reduction. IEEE Trans. Image Process. 2018, 27, 2420–2432. [Google Scholar] [CrossRef]
- Jiang, J.; Ma, J.; Chen, C.; Wang, Z.; Cai, Z.; Wang, L. SuperPCA: A Superpixelwise PCA Approach for Unsupervised Feature Extraction of Hyperspectral Imagery. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4581–4593. [Google Scholar] [CrossRef]
- Sari, C.T.; Gunduz-Demir, C. Unsupervised Feature Extraction via Deep Learning for Histopathological Classification of Colon Tissue Images. IEEE Trans. Med. Imaging 2019, 38, 1139–1149. [Google Scholar] [CrossRef]
- Taguchi, Y.H. Tensor Decomposition-Based Unsupervised Feature Extraction Can Identify the Universal Nature of Sequence-Nonspecific Off-Target Regulation of mRNA Mediated by MicroRNA Transfection. Cells 2018, 7, 54. [Google Scholar] [CrossRef]
- Taguchi, Y.H. Tensor decomposition-based and principal-component-analysis-based unsupervised feature extraction applied to the gene expression and methylation profiles in the brains of social insects with multiple castes. BMC Bioinform. 2018, 19, 99. [Google Scholar] [CrossRef] [PubMed]
- Jimenez-Rodriguez, L.O.; Arzuaga-Cruz, E.; Velez-Reyes, M. Unsupervised Linear Feature-Extraction Methods and Their Effects in the Classification of High-Dimensional Data. IEEE Trans. Geosci. Remote Sens. 2007, 45, 469–483. [Google Scholar] [CrossRef]
- Fleming, M.K.; Cottrell, G.W. Categorization of faces using unsupervised feature extraction. In Proceedings of the 1990 IJCNN International Joint Conference on Neural Networks, San Diego, CA, USA, 17–21 June 1990; Volume 2, pp. 65–70. [Google Scholar]
- Fisher, J.W.; Principe, J.C. A methodology for information theoretic feature extraction. In Proceedings of the 1998 IEEE International Joint Conference on Neural Networks, Anchorage, AK, USA, 4–9 May 1998; Volume 3, pp. 1712–1716. [Google Scholar]
- Goldberger, J.; Gordon, S.; Greenspan, H. Unsupervised image-set clustering using an information theoretic framework. IEEE Trans. Image Process. 2006, 15, 449–458. [Google Scholar] [CrossRef] [PubMed]
- Hild, K.E.; Erdogmus, D.; Torkkola, K.; Principe, J.C. Feature extraction using information-theoretic learning. IEEE Trans. Pattern Anal. Mach. Intell. 2006, 28, 1385–1392. [Google Scholar] [CrossRef] [PubMed]
- Shi, Y.; Sha, F. Information-theoretical Learning of Discriminative Clusters for Unsupervised Domain Adaptation. In Proceedings of the 29th International Conference on Machine Learning, Edinburgh, UK, 26 June–1 July 2012; pp. 1275–1282. [Google Scholar]
- Villani, M.; Roli, A.; Filisetti, A.; Fiorucci, M.; Poli, I.; Serra, R. The Search for Candidate Relevant Subsets of Variables in Complex Systems. Artif. Life 2015, 21, 412–431. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G.; Sporns, O.; Edelman, G.M. A measure for brain complexity: Relating functional segregation and integration in the nervous system. Proc. Natl. Acad. Sci. USA 1994, 91, 5033–5037. [Google Scholar] [CrossRef] [PubMed]
- Tononi, G.; McIntosh, A.; Russel, D.; Edelman, G. Functional clustering: Identifying strongly interactive brain regions in neuroimaging data. Neuroimage 1998, 7, 133–149. [Google Scholar] [CrossRef]
- Villani, M.; Filisetti, A.; Benedettini, S.; Roli, A.; Lane, D.; Serra, R. The detection of intermediate-level emergent structures and patterns. In Artificial Life Conference Proceedings 13; The MIT Press: Cambridge, MA, USA, 2013; pp. 372–378. [Google Scholar]
- Villani, M.; Sani, L.; Amoretti, M.; Vicari, E.; Pecori, R.; Mordonini, M.; Cagnoni, S.; Serra, R. A Relevance Index Method to Infer Global Properties of Biological Networks. In Artificial Life and Evolutionary Computation; Pelillo, M., Poli, I., Roli, A., Serra, R., Slanzi, D., Villani, M., Eds.; Springer: Cham, Switzerland, 2018; pp. 129–141. [Google Scholar]
- Sani, L.; Lombardo, G.; Pecori, R.; Fornacciari, P.; Mordonini, M.; Cagnoni, S. Social Relevance Index for Studying Communities in a Facebook Group of Patients. In Applications of Evolutionary Computation; Sim, K., Kaufmann, P., Eds.; Springer: Cham, Switzerland, 2018; pp. 125–140. [Google Scholar]
- Passaro, A.; Starita, A. Particle Swarm Optimization for Multimodal Functions: A Clustering Approach. J. Artif. Evol. Appl. 2008, 2008, 482032. [Google Scholar] [CrossRef]
- Silvestri, G.; Sani, L.; Amoretti, M.; Pecori, R.; Vicari, E.; Mordonini, M.; Cagnoni, S. Searching Relevant Variable Subsets in Complex Systems Using K-Means PSO. In Artificial Life and Evolutionary Computation; Pelillo, M., Poli, I., Roli, A., Serra, R., Slanzi, D., Villani, M., Eds.; Springer: Cham, Switzerland, 2018; pp. 308–321. [Google Scholar]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory (Wiley Series in Telecommunications and Signal Processing); Wiley-Interscience: Hoboken, NJ, USA, 2006. [Google Scholar]
- Wilks, S.S. The Large-Sample Distribution of the Likelihood Ratio for Testing Composite Hypotheses. Ann. Math. Stat. 1938, 9, 60–62. [Google Scholar] [CrossRef]
- Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes; McGraw-Hill: Boston, MA, USA, 2015. [Google Scholar]
- Owen, A. Empirical Likelihood Ratio Confidence Regions. Ann. Stat. 1990, 18, 90–120. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition And Machine Learning; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Greenwood, C.; Nikulin, M.S. A Guide to Chi-Squared Testing; Wiley: Hoboken, NJ, USA, 1996. [Google Scholar]
- Everitt, B. The Cambridge Dictionary of Statistics; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993. [Google Scholar]
- CUDA Toolkit. Available online: http://developer.nvidia.com/cuda-toolkit (accessed on 6 August 2019).
- Kohonen, T. Self-Organizing Maps, 3rd ed.; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Poli, R.; Langdon, W.B.; McPhee, N.F.; Koza, J.R. A Field Guide to Genetic Programming; Lulu Press: Morrisville, NC, USA, 2008. [Google Scholar]
- Duda, R.O.; Hart, P.E.; Stork, D.G. Pattern Classification; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Scholkopf, B.; Smola, A.J. Learning With Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; MIT Press: Cambridge, MA, USA, 2001. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).