Colebrook’s Flow Friction Explicit Approximations Based on Fixed-Point Iterative Cycles and Symbolic Regression
Abstract
1. Introduction
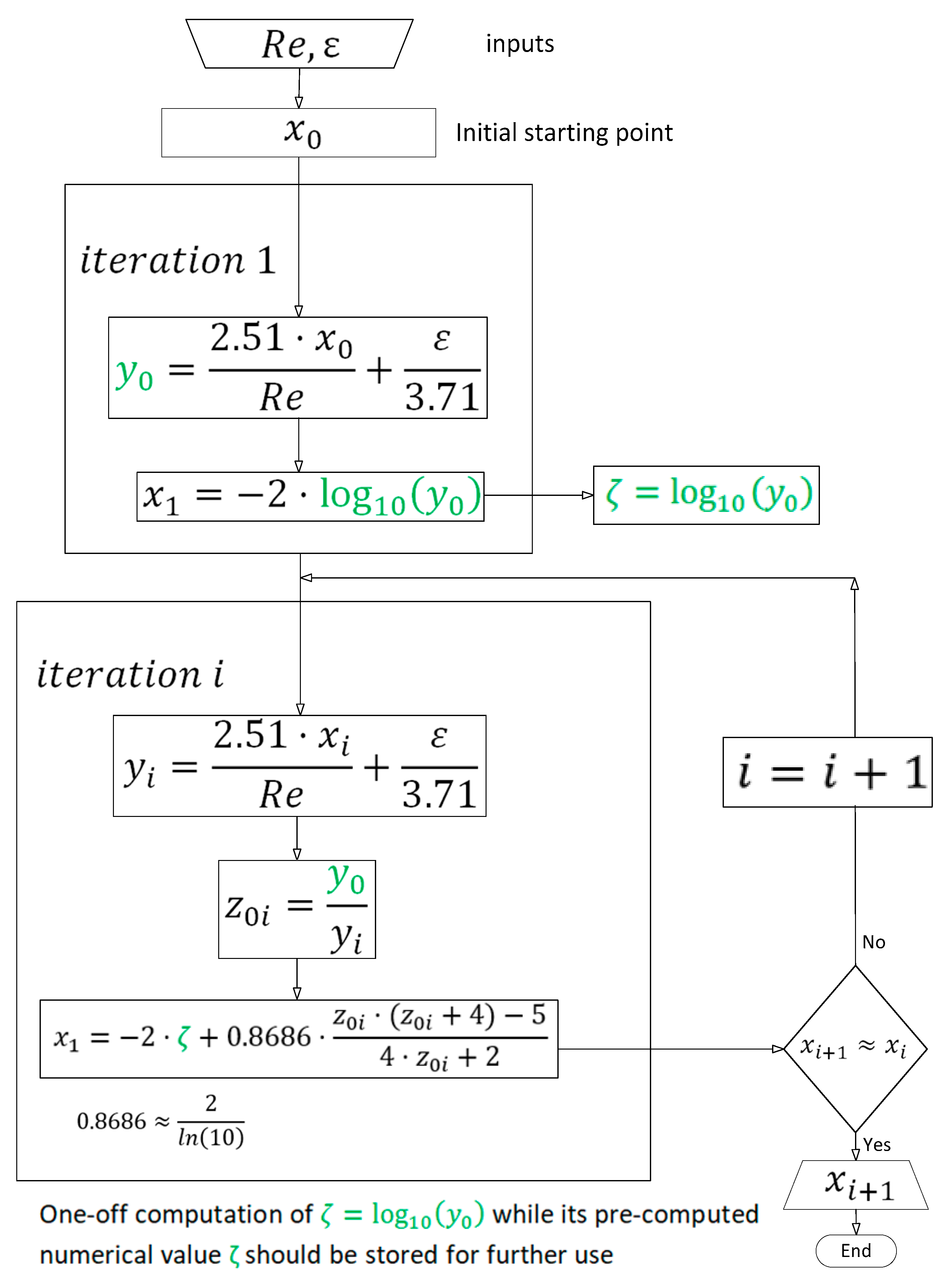
2. A Fixed-Point Iterative Procedure Based on Padé Approximants
3. Explicit Approximations Based on Padé Approximants
3.1. Explicit Approximations with One Internal Iterative Cycle
3.1.1. An Explicit Approximation with One Internal Iterative Cycle and a Numerical Fix-Value Starting Point
3.1.2. An Explicit Approximation with One Internal Iterative Cycle and a Starting Point Given by a Rational Function
3.2. Explicit Approximations with Two Internal Iterative Cycles
3.2.1. An Explicit Approximation with Two Internal Iterative Cycles and a Fixed Starting Point
3.2.2. An Explicit Approximation with Two Internal Iterative Cycles and a Starting Point Given by a Rational Function
3.3. Further Error Analysis and Comparisons
4. Description of Software
y0 = 2.51*x./R + K./3.71;
x1 = −2*log10(y0);
z = y0./((K/3.71) + (2.51*x1./R));
ln11 = @(z) (z.*(z + 4) − 5)./(4*z + 2);
x = x1 + 0.8686*ln11(z);
f = 1./x.^2;
y0 = 2.51*x./R + K./3.71;
x1 = −2*log10(y0);
z = y0./((K/3.71) + (2.51*x1./R));
ln11 = @(z) (z.*(z + 4) − 5)./(4*z + 2);
x = x1 + 0.8686*ln11(z);
z = y0./((K/3.71) + (2.51*x./R));
x = x1 + 0.8686*ln11(z);
f = 1./x.^2;
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Colebrook, C.F. Turbulent flow in pipes with particular reference to the transition region between the smooth and rough pipe laws. J. Inst. Civ. Eng. 1939, 11, 133–156. [Google Scholar] [CrossRef]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.; Jeffrey, D.J.; Knuth, D.E. On the LambertW function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Hayes, B. Why W? On the Lambert W function, a candidate for a new elementary function in mathematics. Am. Sci. 2005, 93, 104–108. [Google Scholar] [CrossRef]
- Keady, G. Colebrook-White formula for pipe flows. J. Hydraul. Eng. 1998, 124, 96–97. [Google Scholar] [CrossRef]
- Sonnad, J.R.; Goudar, C.T. Constraints for using Lambert W function-based explicit Colebrook–White equation. J. Hydraul. Eng. 2004, 130, 929–931. [Google Scholar] [CrossRef]
- More, A.A. Analytical solutions for the Colebrook and White equation and for pressure drop in ideal gas flow in pipes. Chem. Eng. Sci. 2006, 61, 5515–5519. [Google Scholar] [CrossRef]
- Clamond, D. Efficient resolution of the Colebrook equation. Ind. Eng. Chem. Res. 2009, 48, 3665–3671. [Google Scholar] [CrossRef]
- Biberg, D. Fast and accurate approximations for the Colebrook equation. J. Fluids Eng. 2017, 139, 031401. [Google Scholar] [CrossRef]
- Brkić, D.; Praks, P. Accurate and efficient explicit approximations of the Colebrook flow friction equation based on the Wright ω-function. Mathematics 2019, 7, 34. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Choosing the optimal multi-point iterative method for the Colebrook flow friction equation. Processes 2018, 6, 130. [Google Scholar] [CrossRef]
- Zigrang, D.J.; Sylvester, N.D. Explicit approximations to the solution of Colebrook’s friction factor equation. AIChE J. 1982, 28, 514–515. [Google Scholar] [CrossRef]
- Winning, H.K.; Coole, T. Explicit friction factor accuracy and computational efficiency for turbulent flow in pipes. Flow Turbul. Combust. 2013, 90, 1–27. [Google Scholar] [CrossRef]
- Winning, H.K.; Coole, T. Improved method of determining friction factor in pipes. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 941–949. [Google Scholar] [CrossRef]
- Vatankhah, A.R. Approximate analytical solutions for the Colebrook equation. J. Hydraul. Eng. 2018, 144, 06018007. [Google Scholar] [CrossRef]
- Pimenta, B.D.; Robaina, A.D.; Peiter, M.X.; Mezzomo, W.; Kirchner, J.H.; Ben, L.H. Performance of explicit approximations of the coefficient of head loss for pressurized conduits. Rev. Bras. Eng. Agrícola Ambient. 2018, 22, 301–307. [Google Scholar] [CrossRef]
- Colebrook, C.; White, C. Experiments with fluid friction in roughened pipes. Proc. R. Soc. Lond. Ser. A Math. Phys. Sci. 1937, 161, 367–381. [Google Scholar] [CrossRef]
- Díaz-Damacillo, L.; Plascencia, G. A new six parameter model to estimate the friction factor. AIChE J. 2019, 65, 1144–1148. [Google Scholar] [CrossRef]
- McKeon, B.J.; Zagarola, M.V.; Smits, A.J. A new friction factor relationship for fully developed pipe flow. J. Fluid Mech. 2005, 538, 429–443. [Google Scholar] [CrossRef]
- Ekhtiari, A.; Dassios, I.; Liu, M.; Syron, E. A novel approach to model a gas network. Appl. Sci. 2019, 9, 1047. [Google Scholar] [CrossRef]
- Barreras, F.; López, A.M.; Lozano, A.; Barranco, J.E. Experimental study of the pressure drop in the cathode side of air-forced open-cathode proton exchange membrane fuel cells. Int. J. Hydrogen Energy 2011, 36, 7612–7620. [Google Scholar] [CrossRef]
- Stubbs, A.; Stoesser, T.; Bockelmann-Evans, B. Developing an approximation of a natural, rough gravel riverbed both physically and numerically. Geosciences 2018, 8, 449. [Google Scholar] [CrossRef]
- Möws, R.; Koll, K. Roughness Effect of submerged groyne fields with varying length, groyne distance, and groyne types. Water 2019, 11, 1253. [Google Scholar] [CrossRef]
- Mouza, A.A.; Skordia, O.D.; Tzouganatos, I.D.; Paras, S.V. A simplified model for predicting friction factors of laminar blood flow in small-caliber vessels. Fluids 2018, 3, 75. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. One-log call iterative solution of the Colebrook equation for flow friction based on Padé polynomials. Energies 2018, 11, 1825. [Google Scholar] [CrossRef]
- Baker, G.A.; Graves-Morris, P. Padé Approximants, 2nd ed.; Cambridge University Press: Cambridge, UK, 1996. [Google Scholar]
- Copley, L. Padé Approximants. In Mathematics for the Physical Sciences; De Gruyter: Berlin, Germany, 2014; Chapter 7; pp. 163–179. [Google Scholar] [CrossRef]
- Kalateh Bojdi, Z.; Ahmadi-Asl, S.; Aminataei, A. A new extended Padé approximation and its application. Adv. Numer. Anal. 2013, 2013, 263467. [Google Scholar] [CrossRef]
- Peker, H.A.; Karaoğlu, O.; Oturanç, G. The differential transformation method and Padé approximant for a form of Blasius equation. Math. Comput. Appl. 2011, 16, 507–513. [Google Scholar] [CrossRef]
- Li, S.; Liu, X.; Zhang, X. A few iterative methods by using [1,n]-order Padé approximation of function and the improvements. Mathematics 2019, 7, 55. [Google Scholar] [CrossRef]
- Alfaro-Guerra, M.; Guerra-Rojas, R.; Olivares-Gallardo, A. Evaluación experimental de la solución analítica exacta de la ecuación de Colebrook-White (Experimental evaluation of exact analytical solution of the Colebrook-White Equation). Ingeniería Investigación y Tecnología 2019, 20, 1–11. (In Spanish) [Google Scholar] [CrossRef]
- Dubčáková, R. Eureqa: Software review. Genet. Program. Evol. Mach. 2011, 12, 173–178. [Google Scholar] [CrossRef]
- Schmidt, M.; Lipson, H. Distilling free-form natural laws from experimental data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Gholamy, A.; Kreinovich, V. How to use absolute-error-minimizing software to minimize relative error: Practitioner’s guide. Int. Math. Forum 2017, 12, 763–770. [Google Scholar] [CrossRef][Green Version]
- Praks, P.; Brkić, D. Symbolic regression-based genetic approximations of the Colebrook equation for flow friction. Water 2018, 10, 1175. [Google Scholar] [CrossRef]
- Gorkemli, B.; Karaboga, D. A quick semantic artificial bee colony programming (qsABCP) for symbolic regression. Inf. Sci. 2019, 502, 346–362. [Google Scholar] [CrossRef]
- Brkić, D.; Ćojbašić, Ž. Intelligent flow friction estimation. Comput. Intell. Neurosci. 2016, 2016, 5242596. [Google Scholar] [CrossRef] [PubMed]
- Brkić, D.; Ćojbašić, Ž. Evolutionary optimization of Colebrook’s turbulent flow friction approximations. Fluids 2017, 2, 15. [Google Scholar] [CrossRef]
- Praks, P.; Brkić, D. Advanced iterative procedures for solving the implicit Colebrook equation for fluid flow friction. Adv. Civ. Eng. 2018, 2018, 5451034. [Google Scholar] [CrossRef]
- Brkić, D. Review of explicit approximations to the Colebrook relation for flow friction. J. Pet. Sci. Eng. 2011, 77, 34–48. [Google Scholar] [CrossRef]
- Sobol’, I.M.; Turchaninov, V.I.; Levitan, Y.L.; Shukhman, B.V. Quasi-Random Sequence Generators; Distributed by OECD/NEA Data Bank; Keldysh Institute of Applied Mathematics; Russian Academy of Sciences: Moscow, Russia, 1992; Available online: https://europa.eu/ (accessed on 28 August 2019).
- Bratley, P.; Fox, B.L. Algorithm 659: Implementing Sobol’s quasirandom sequence generator. ACM Trans. Math. Softw. 1988, 14, 88–100. [Google Scholar] [CrossRef]
- Brkić, D. Solution of the implicit Colebrook equation for flow friction using Excel. Spreadsheets Educ. 2017, 10, 4663. Available online: https://sie.scholasticahq.com/article/4663.pdf (accessed on 19 August 2019).
- Pérez-Pupo, J.R.; Navarro-Ojeda, M.N.; Pérez-Guerrero, J.N.; Batista-Zaldívar, M.A. On the explicit expressions for the determination of the friction factor in turbulent regime. Rev. Mex. Ing. Chim. 2020, 19, 313–334. [Google Scholar] [CrossRef]
| Padé Approximant | No | /1,1/ | ||
|---|---|---|---|---|
| solution version 1 | x = x1 + 0.8686*log(z) | x = x1 + 0.8686*(z*(z + 4) − 5)/(4*z + 2) | ||
| Iteration | 1 | 2 | 1 | 2 |
| Fixed starting point | 1.81% | −0.317% | 1.81% | −0.317% |
| Starting point by Equation (2) | −0.156% | 0.0259% | −0.156% | 0.0259% |
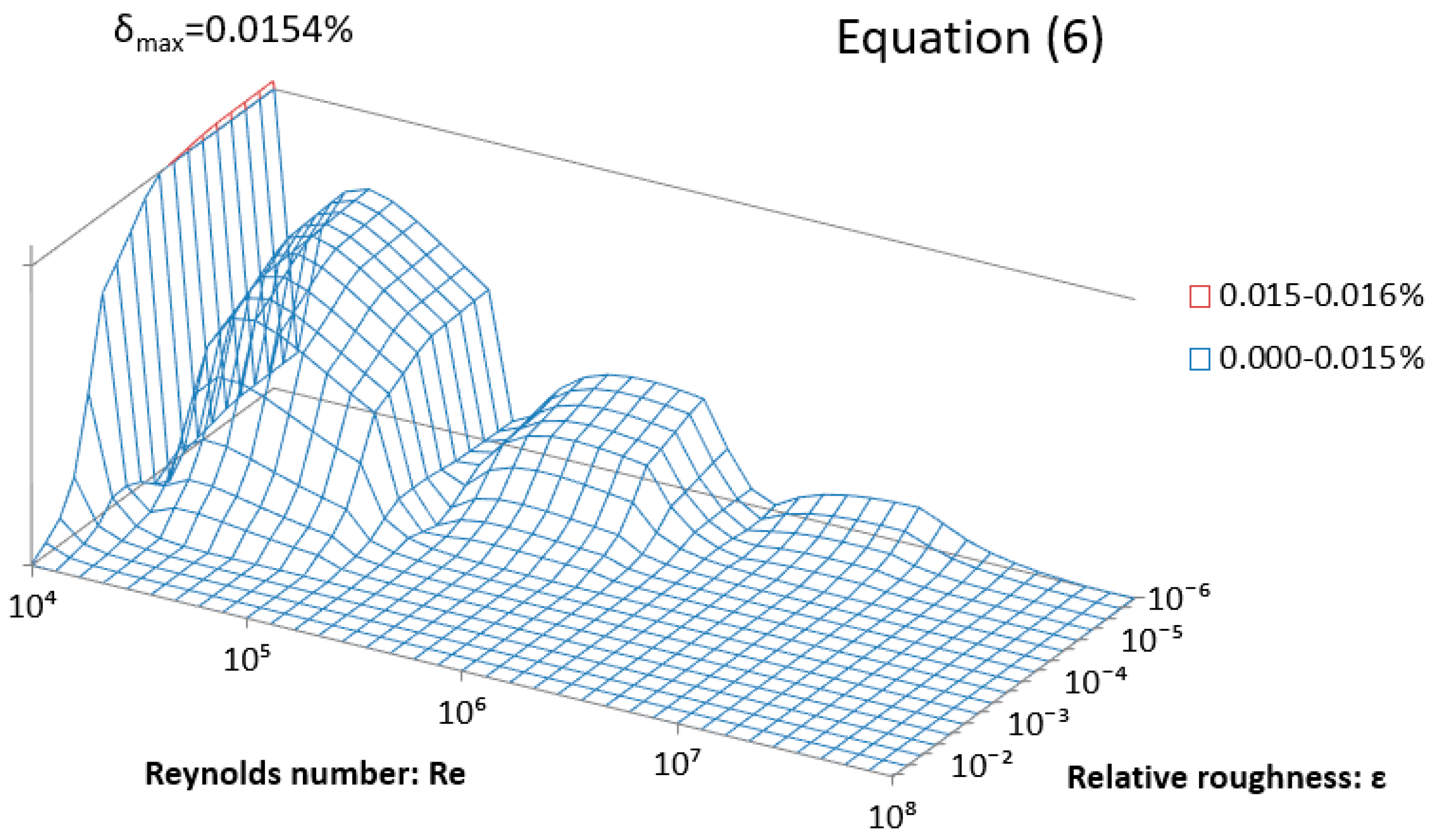
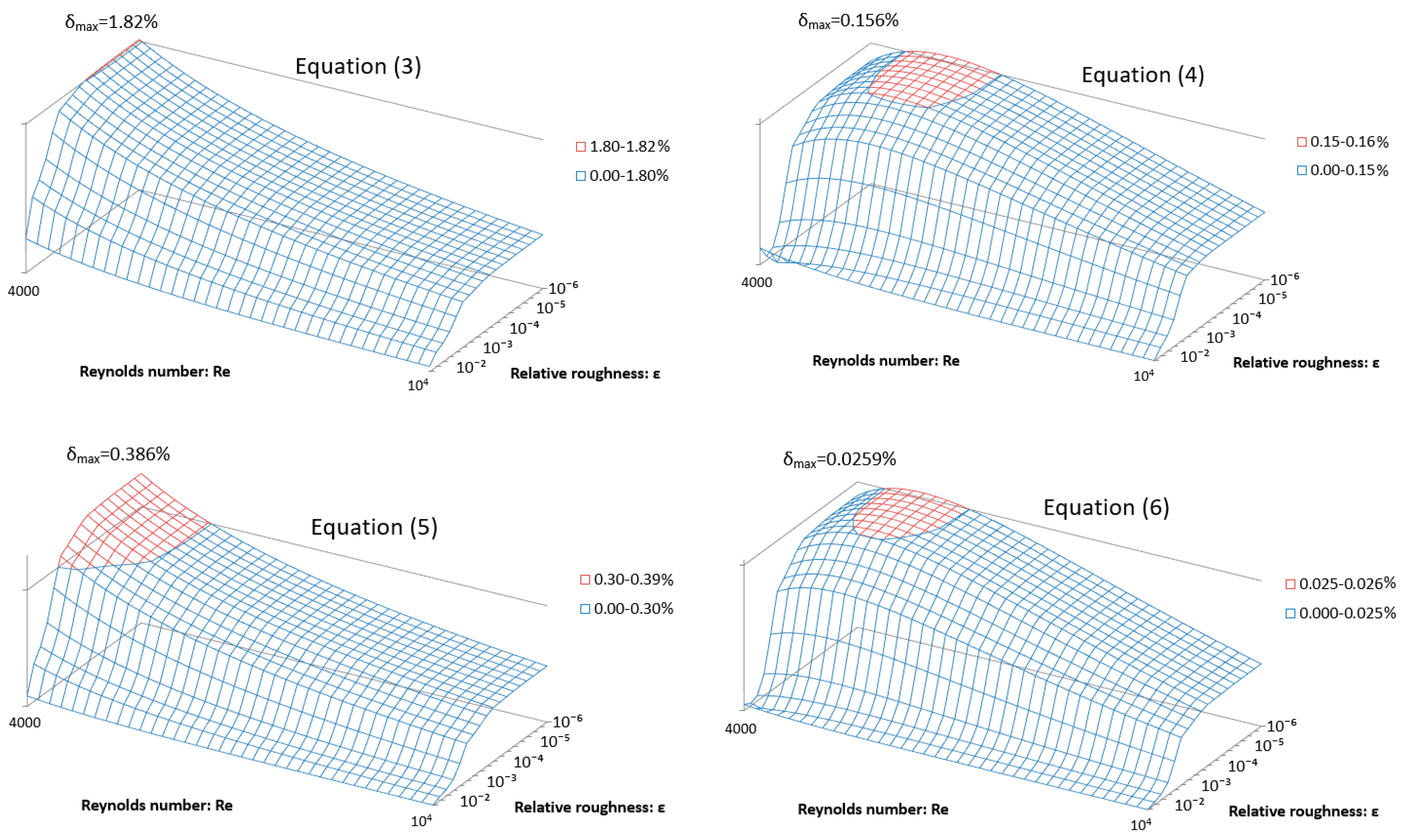
| Max. Rel. Error % | 740 Test Points 1 | 2 Million Test Point 2 |
|---|---|---|
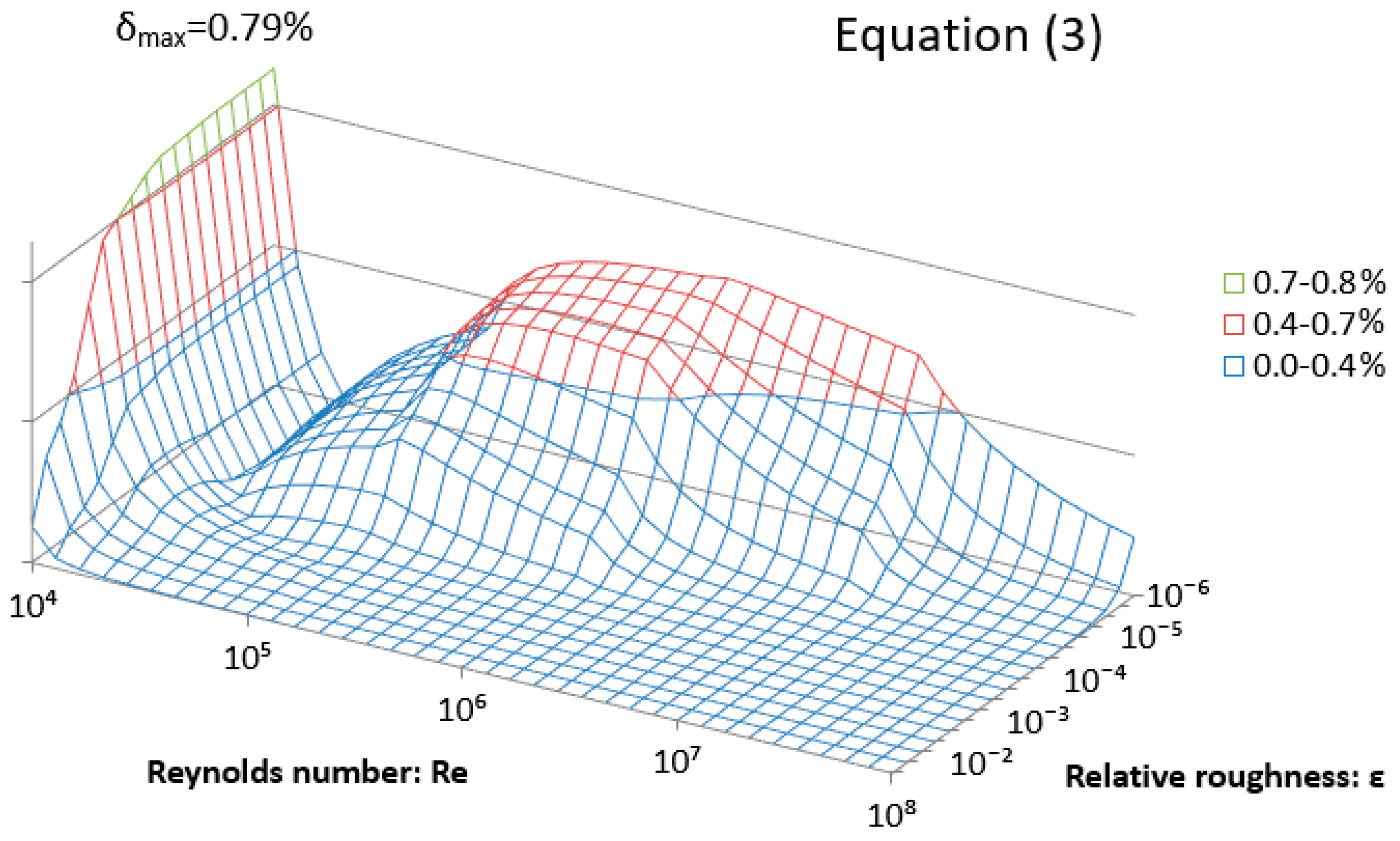
| Equation (3) | 0.79% | 1.81% |
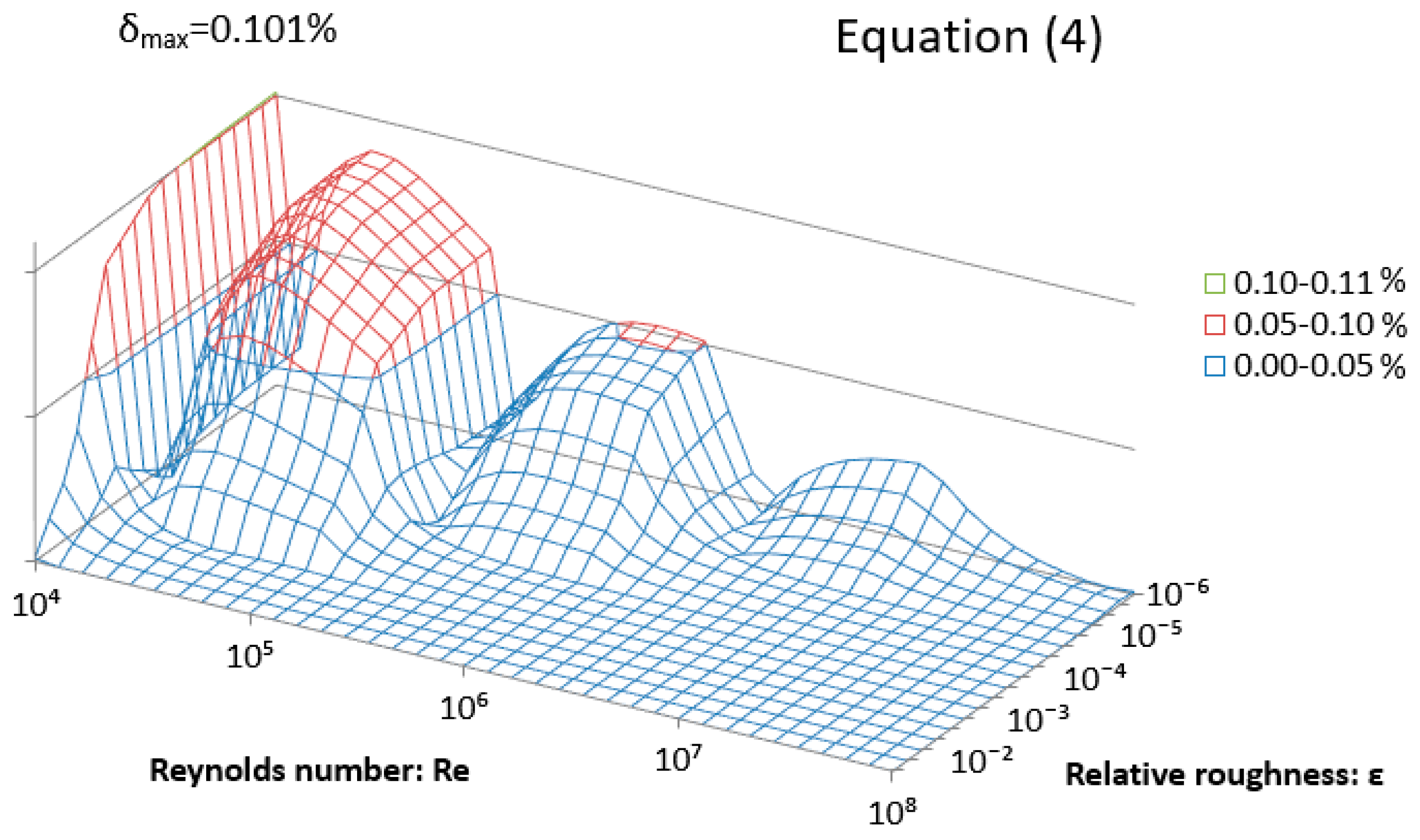
| Equation (4) | 0.101% | 0.156% |
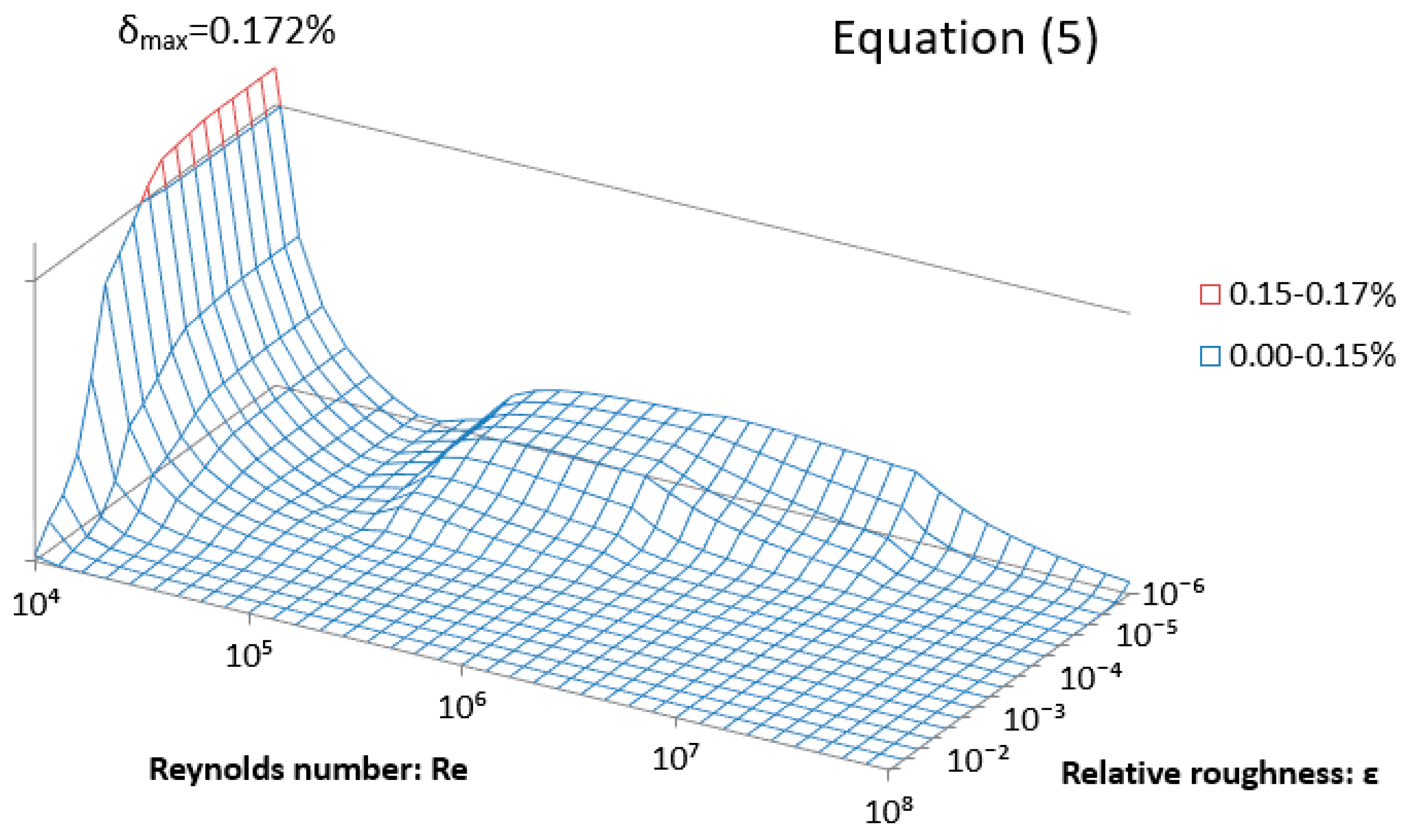
| Equation (5) | 0.172% | 0.317% |
| Equation (6) | 0.0154% | 0.0259% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brkić, D.; Praks, P. Colebrook’s Flow Friction Explicit Approximations Based on Fixed-Point Iterative Cycles and Symbolic Regression. Computation 2019, 7, 48. https://doi.org/10.3390/computation7030048
Brkić D, Praks P. Colebrook’s Flow Friction Explicit Approximations Based on Fixed-Point Iterative Cycles and Symbolic Regression. Computation. 2019; 7(3):48. https://doi.org/10.3390/computation7030048
Chicago/Turabian StyleBrkić, Dejan, and Pavel Praks. 2019. "Colebrook’s Flow Friction Explicit Approximations Based on Fixed-Point Iterative Cycles and Symbolic Regression" Computation 7, no. 3: 48. https://doi.org/10.3390/computation7030048
APA StyleBrkić, D., & Praks, P. (2019). Colebrook’s Flow Friction Explicit Approximations Based on Fixed-Point Iterative Cycles and Symbolic Regression. Computation, 7(3), 48. https://doi.org/10.3390/computation7030048






