Design and Implementation of a Microcontroller Based Active Controller for the Synchronization of the Petrzela Chaotic System
Abstract
1. Introduction
2. Petrzela Chaotic System
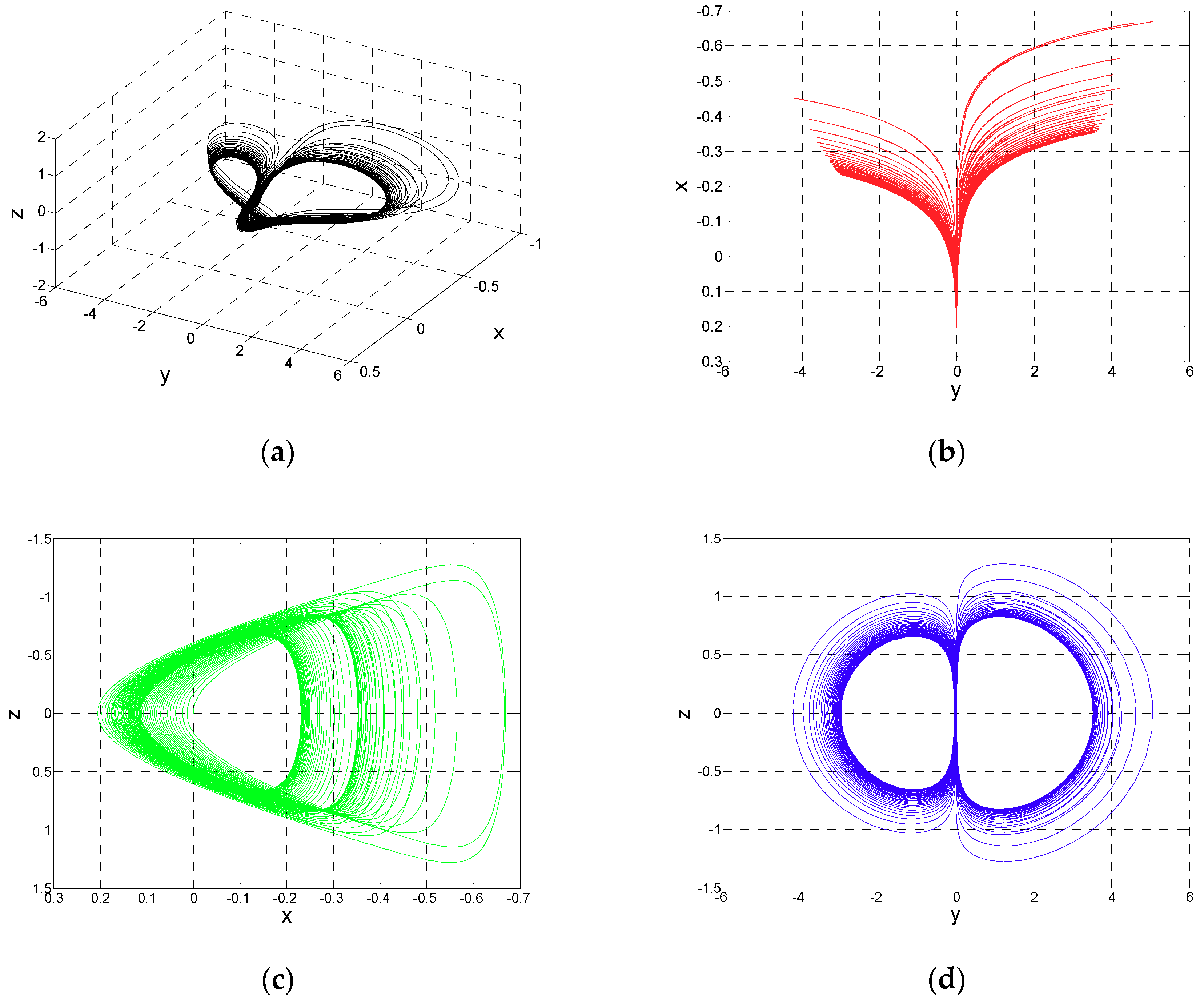
Numerical Analysis of the Chaotic System
3. Synchronization with Active Control
Stability Proof
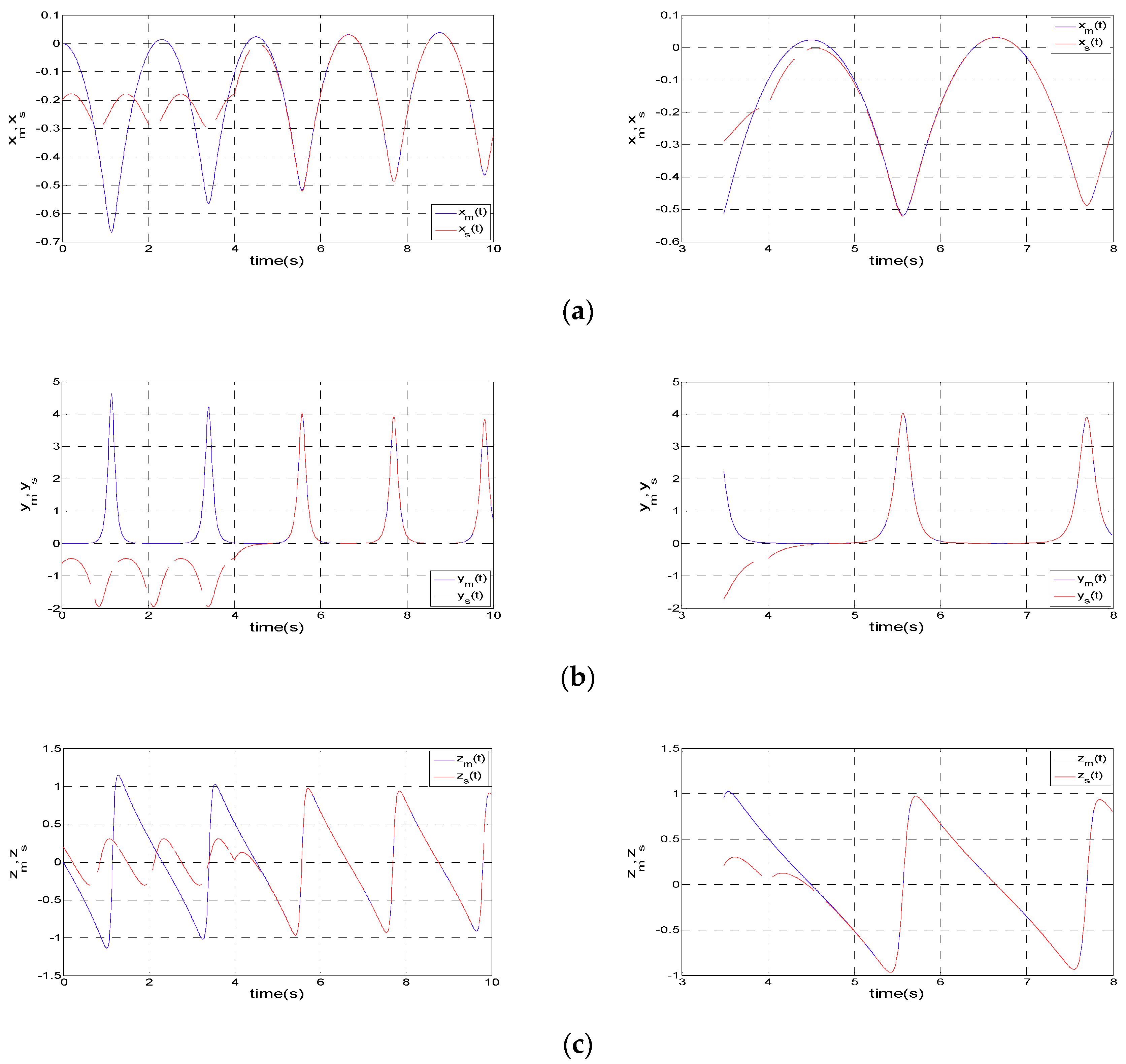
4. Numerical Results
5. Hardware Implementation
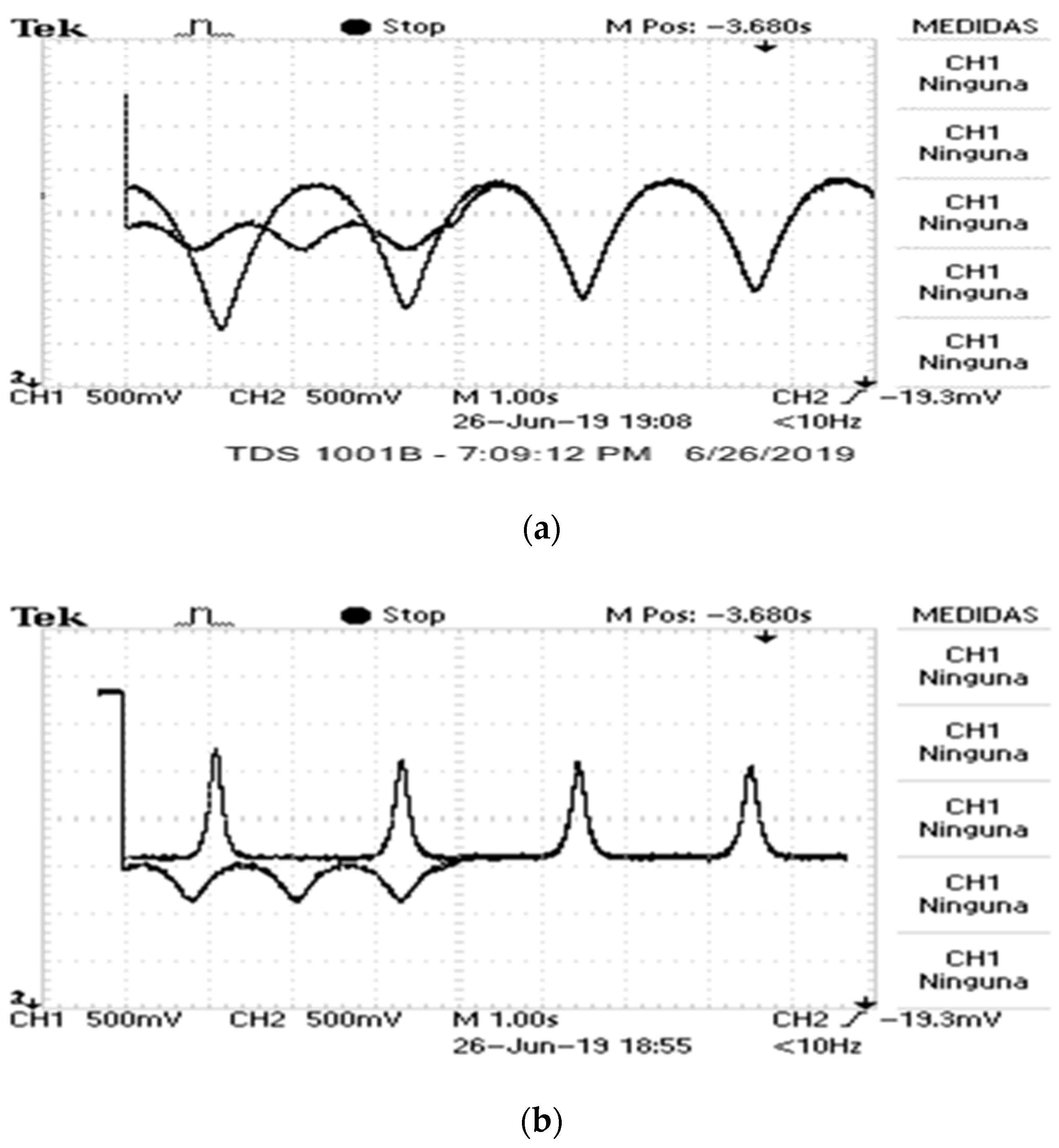
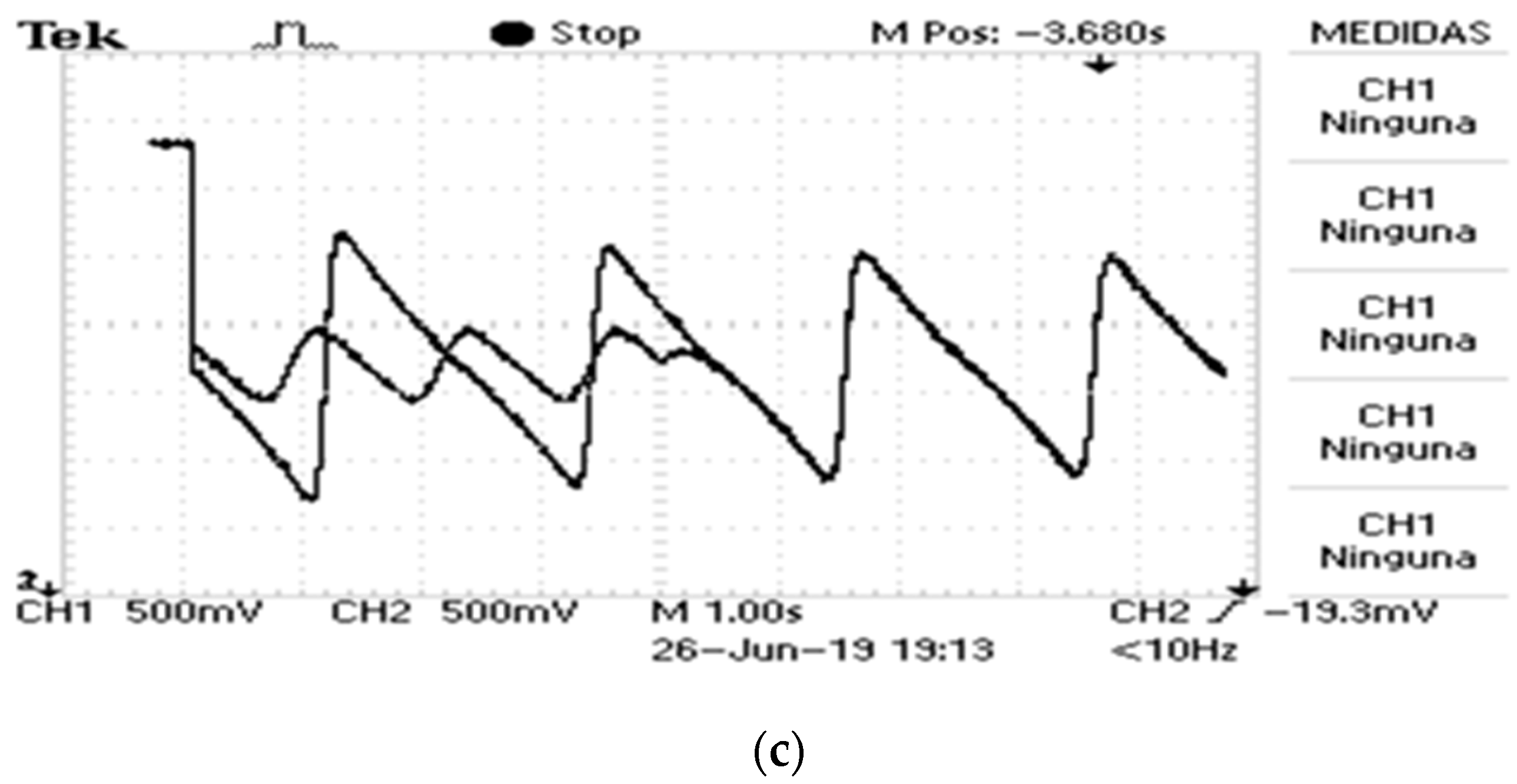
Experimental Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Pecora, L.M.; Carroll, T.L. Synchronization in chaotic systems. Phys. Rev. Lett. 1990, 64, 821–825. [Google Scholar] [CrossRef] [PubMed]
- Pecora, L.M.; Carroll, T.L.; Johnson, G.A.; Mar, D.J.; Heagy, J.F. Fundamentals of synchronization in chaotic systems, concepts, and applications. Chaos Int. J. Nonlinear Sci. 1997, 7, 520–543. [Google Scholar] [CrossRef] [PubMed]
- Feki, M. An adaptive chaos synchronization scheme applied to secure communication. Chaos Solitons Fractals 2003, 18, 141–148. [Google Scholar] [CrossRef]
- Tanougast, C.; Dandache, A.; Azzaz, M.S.; Sadoudi, S. Hardware design of embedded systems for security applications. In Embedded Systems—High Performance Systems, Applications and Projects; Intech: Rijeka Croatia, 2012; pp. 233–260. [Google Scholar]
- Zapateiro De la Hoz, M.; Acho, L.; Vidal, Y. An experimental realization of a chaos-based secure communication using arduino microcontrollers. Sci. World J. 2015, 2015, 123080. [Google Scholar] [CrossRef] [PubMed]
- Yang, T. A survey of chaotic secure communication systems. Int. J. Comput. Cognit. 2004, 2, 81–130. [Google Scholar]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N. Image encryption process based on chaotic synchronization phenomena. Signal Proc. 2013, 93, 1328–1340. [Google Scholar] [CrossRef]
- Nakamura, Y.; Sekiguchi, A. The chaotic mobile robot. IEEE Trans. Robot. Autom. 2001, 17, 898–904. [Google Scholar] [CrossRef]
- Bae, Y.C.; Kim, J.W.; Kim, Y.G. Obstacle avoidance methods in the chaotic mobile robot with integrated some chaos equation. Int. J. Fuzzy Logic Intell. Syst. 2003, 3, 206–214. [Google Scholar] [CrossRef]
- Fallahi, K.; Leung, H. A cooperative mobile robot task assignment and coverage planning based on chaos synchronization. Int. J. Bifurc. Chaos 2010, 20, 161–176. [Google Scholar] [CrossRef]
- Fahmy, A.A. Performance evaluation of chaotic mobile robot controllers. Int. Trans. J. Eng. Manag. Appl. Sci. Technol. 2012, 3, 145–158. [Google Scholar]
- Zang, X.; Iqbal, S.; Zhu, Y.; Liu, X.; Zhao, J. Applications of chaotic dynamics in robotics. Int. J. Adv. Robot. Syst. 2016, 13, 60. [Google Scholar] [CrossRef]
- Volos, C.K.; Kyprianidis, I.M.; Stouboulos, I.N.; Nistazakis, H.E.; Tombras, G.S. Cooperation of autonomous mobile robots for surveillance missions based on hyperchaos synchronization. J. Appl. Math. Bioinf. 2016, 6, 125–143. [Google Scholar]
- Campos, J.M.S. Inducción de trayectorias caóticas mediante acoplamiento de robots móviles para la cobertura de áreas específicas de forma síncrona. Ph.D. Thesis, Manufactura avanzada—CIATEQ, San Luis Potosí, México, January 2019. [Google Scholar]
- Nasr, S.; Mekki, H.; Bouallegue, K. A multi-scroll chaotic system for a higher coverage path planning of a mobile robot using flatness controller. Chaos Solitons Fractals 2019, 118, 366–375. [Google Scholar] [CrossRef]
- Lu, J.; Wu, X.; Han, X.; Lü, J. Adaptive feedback synchronization of a unified chaotic system. Phys. Lett. A 2004, 329, 327–333. [Google Scholar] [CrossRef]
- Han, X.; Lu, J.A.; Wu, X. Adaptive feedback synchronization of Lü system. Chaos Solitons Fractals 2004, 22, 221–227. [Google Scholar] [CrossRef]
- Wang, X.; Wang, Y. Adaptive control for synchronization of a four-dimensional chaotic system via a single variable. Nonlinear Dyn. 2011, 65, 311–316. [Google Scholar] [CrossRef]
- Yang, C.C. Adaptive synchronization of Lü hyperchaotic system with uncertain parameters based on single-input controller. Nonlinear Dyn. 2011, 63, 447–454. [Google Scholar] [CrossRef]
- Wang, F.; Liu, C. A new criterion for chaos and hyperchaos synchronization using linear feedback control. Phys. Lett. A 2006, 360, 274–278. [Google Scholar] [CrossRef]
- Yan, Z.; Yu, P. Linear feedback control, adaptive feedback control and their combination for chaos (lag) synchronization of LC chaotic systems. Chaos Solitons Fractals 2007, 33, 419–435. [Google Scholar] [CrossRef]
- Rafikov, M.; Balthazar, J.M. On control and synchronization in chaotic and hyperchaotic systems via linear feedback control. Commun. Nonlinear Sci. Numer. Simul. 2008, 13, 1246–1255. [Google Scholar] [CrossRef]
- Chen, H.H. Chaos control and global synchronization of Liu chaotic systems using linear balanced feedback control. Chaos Solitons Fractals 2009, 40, 466–473. [Google Scholar] [CrossRef]
- Huang, L.; Feng, R.; Wang, M. Synchronization of chaotic systems via nonlinear control. Phys. Lett. A 2004, 320, 271–275. [Google Scholar] [CrossRef]
- Pérez-Cruz, J.H.; Portilla-Flores, E.A.; Niño-Suárez, P.A.; Rivera-Blas, R. Design of a nonlinear controller and its intelligent optimization for exponential synchronization of a new chaotic system. Optik 2017, 130, 201–212. [Google Scholar] [CrossRef]
- Wang, Y.; Guan, Z.H.; Wang, H.O. Feedback and adaptive control for the synchronization of Chen system via a single variable. Phys. Lett. A 2003, 312, 34–40. [Google Scholar] [CrossRef]
- Pérez-Cruz, J.H. Stabilization and Synchronization of Uncertain Zhang System by Means of Robust Adaptive Control. Complexity 2018, 2018, 4989520. [Google Scholar] [CrossRef]
- Jiang, G.P.; Chen, G.; Tang WK, S. A new criterion for chaos synchronization using linear state feedback control. Int. J. Bifurc. Chaos 2003, 13, 2343–2351. [Google Scholar] [CrossRef]
- Wu, X.; Cai, J.; Wang, M. Master-slave chaos synchronization criteria for the horizontal platform systems via linear state error feedback control. J. Sound Vib. 2006, 295, 378–387. [Google Scholar] [CrossRef]
- Wu, X.; Chen, G.; Cai, J. Chaos synchronization of the master–slave generalized Lorenz systems via linear state error feedback control. Phys. D Nonlinear Phenom. 2007, 229, 52–80. [Google Scholar] [CrossRef]
- Chen, Y.; Wu, X.; Gui, Z. Global synchronization criteria for a class of third-order non-autonomous chaotic systems via linear state error feedback control. Appl. Math Modell. 2010, 34, 4161–4170. [Google Scholar] [CrossRef]
- Lin, Q.; Wu, X. The sufficient criteria for global synchronization of chaotic power systems under linear state-error feedback control. Nonlinear Anal. Real World Appl. 2011, 12, 1500–1509. [Google Scholar] [CrossRef]
- Li, C.; Li, H. Robust control for a class of chaotic and hyperchaotic systems via linear state feedback. Phys. Scr. 2012, 85, 025007. [Google Scholar] [CrossRef]
- Cruz, J.H.P.; Figueroa, M.; Paredes, S.A.R.; Villa, A.L. Synchronization of chaotic Akgul system by means of feedback linearization and pole placement. IEEE Latin Am. Trans. 2017, 15, 249–256. [Google Scholar] [CrossRef]
- Shahverdiev, E.M.; Nuriev, R.A.; Hashimov, R.H.; Shore, K.A. Parameter mismatches, variable delay times and synchronization in time-delayed systems. Chaos Solitons Fractals 2005, 25, 325–331. [Google Scholar] [CrossRef]
- Park, J.H.; Kwon, O.M. A novel criterion for delayed feedback control of time-delay chaotic systems. Chaos Solitons Fractals 2005, 23, 495–501. [Google Scholar] [CrossRef]
- Emelianova, Y.P.; Emelyanov, V.V.; Ryskin, N.M. Synchronization of two coupled multimode oscillators with time-delayed feedback. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 3778–3791. [Google Scholar] [CrossRef]
- Khan, A.; Budhraja, M.; Ibraheem, A. Multiswitching dual combination synchronization of time-delay chaotic systems. Math. Methods Appl. Sci. 2018, 41, 5679–5690. [Google Scholar] [CrossRef]
- Varan, M.; Akgul, A. Control and synchronisation of a novel seven-dimensional hyperchaotic system with active control. Pramana 2018, 90, 54. [Google Scholar] [CrossRef]
- Singh, P.P.; Roy, B.K. Comparative performances of synchronisation between different classes of chaotic systems using three control techniques. Ann. Rev. Control 2018, 45, 152–165. [Google Scholar] [CrossRef]
- Vaidyanathan, S. Generalized projective synchronization of vaidyanathan chaotic system via active and adaptive control. In Advances and Applications in Nonlinear Control Systems; Springer: Cham, Switzerland, 2016; pp. 97–116. [Google Scholar]
- Cicek, S.; Ferikoglu, A.; Pehlivan, I. A new 3D chaotic system: Dynamical analysis, electronic circuit design, active control synchronization and chaotic masking communication application. Optik 2016, 127, 4024–4030. [Google Scholar] [CrossRef]
- Pérez, J.H. Neural control for synchronization of a chaotic Chua-Chen system. IEEE Latin Am. Trans. 2016, 14, 3560–3568. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C. Simple chaotic flows with a line equilibrium. Chaos Solitons Fractals 2013, 57, 79–84. [Google Scholar] [CrossRef]
- Pham, V.T.; Jafari, S.; Volos, C.; Vaidyanathan, S.; Kapitaniak, T. A chaotic system with infinite equilibria located on a piecewise linear curve. Optik 2016, 127, 9111–9117. [Google Scholar] [CrossRef]
- Jafari, S.; Sprott, J.C.; Pham, V.T.; Volos, C.; Li, C. Simple chaotic 3D flows with surfaces of equilibria. Nonlinear Dyn. 2016, 86, 1349–1358. [Google Scholar] [CrossRef]
- Gotthans, T.; Petržela, J. New class of chaotic systems with circular equilibrium. Nonlinear Dyn. 2015, 81, 1143–1149. [Google Scholar] [CrossRef]
- Nwachioma, C.; Pérez-Cruz, J.H. Realization and implementation of polynomial chaotic sun system. Phys. Sci. Int. J. 2017, 16, 1–7. [Google Scholar] [CrossRef]
- Nwachioma, C.; Pérez-Cruz, J.H.; Jiménez, A.; Ezuma, M.; Rivera-Blas, R. A new chaotic oscillator-properties, analog implementation, and secure communication application. IEEE Access 2019, 7, 7510–7521. [Google Scholar] [CrossRef]
- Rajagopal, K.; Cicek, S.; Pham, V.; Jafari, S.; Karthikeyan, A. A novel class of chaotic systems with different shapes of equilibrium and microcontroller-based cost-effective design for digital applications. Eur. Phys. J. Plus 2018, 133, 231. [Google Scholar] [CrossRef]
- Giakoumis, A.E.; Volos, C.K.; Stouboulos, I.N.; Kyprianidis, I.K. Implementation of a hyperchaotic system with hidden attractors into a microcontroller. In Proceedings of the 20th International Conference on Circuits, Systems, Communications and Computers (CSCC 2016), Corfu Island, Greece, 14–17 July 2016. [Google Scholar]
- Castañeda, C.E.; López-Mancilla, D.; Chiu, R.; Villafana-Rauda, E.; Orozco-López, O.; Casillas-Rodríguez, F.; Sevilla-Escoboza, R. Discrete-time neural synchronization between an Arduino microcontroller and a compact development system using multiscroll chaotic signals. Chaos Solitons Fractals 2019, 119, 269–275. [Google Scholar] [CrossRef]
- Janakiraman, S.; Thenmozhi, K.; Rayappan, J.B.B.; Amirtharajan, R. Lightweight chaotic image encryption algorithm for real-time embedded system: Implementation and analysis on 32-bit microcontroller. Microprocess. Microsyst. 2018, 56, 1–12. [Google Scholar] [CrossRef]
- Tlelo-Cuautle, E.; Rangel-Magdaleno, J.J.; Pano-Azucena, A.D.; Obeso-Rodelo, P.J.; Nunez-Perez, J.C. FPGA realization of multi-scroll chaotic oscillators. Commun. Nonlinear Sci. Numer. Simulat. 2015, 27, 66–80. [Google Scholar] [CrossRef]
- Pano-Azucena, A.D.; Tlelo-Cuautle, E.; Rodriguez-Gomez, A.G.; de la Fraga, L.G. FPGA-based implementation of chaotic oscillators by applying the numerical method based on trigonometric polynomials. AIP Adv. 2018, 8, 075217. [Google Scholar] [CrossRef]
- Tuna, M.; Fidan, C.B. Electronic circuit design, implementation and FPGA-based realization of a new 3D chaotic system with single equilibrium point. Optik 2016, 127, 11786–11799. [Google Scholar] [CrossRef]
- Muthuswamy, B.; Banerjee, S. A Route to Chaos Using FPGAs; Springer: Cham, Switzerland, 2015. [Google Scholar]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rivera-Blas, R.; Rodríguez Paredes, S.A.; Flores-Herrera, L.A.; Adrián Romero, I. Design and Implementation of a Microcontroller Based Active Controller for the Synchronization of the Petrzela Chaotic System. Computation 2019, 7, 40. https://doi.org/10.3390/computation7030040
Rivera-Blas R, Rodríguez Paredes SA, Flores-Herrera LA, Adrián Romero I. Design and Implementation of a Microcontroller Based Active Controller for the Synchronization of the Petrzela Chaotic System. Computation. 2019; 7(3):40. https://doi.org/10.3390/computation7030040
Chicago/Turabian StyleRivera-Blas, Raúl, Salvador Antonio Rodríguez Paredes, Luis Armando Flores-Herrera, and Ignacio Adrián Romero. 2019. "Design and Implementation of a Microcontroller Based Active Controller for the Synchronization of the Petrzela Chaotic System" Computation 7, no. 3: 40. https://doi.org/10.3390/computation7030040
APA StyleRivera-Blas, R., Rodríguez Paredes, S. A., Flores-Herrera, L. A., & Adrián Romero, I. (2019). Design and Implementation of a Microcontroller Based Active Controller for the Synchronization of the Petrzela Chaotic System. Computation, 7(3), 40. https://doi.org/10.3390/computation7030040





