Probabilistic Fatigue Life Prediction of Dissimilar Material Weld Using Accelerated Life Method and Neural Network Approach
Abstract
:1. Introduction
2. Dissimilar Material Welding between Alloy 617 and 12 Cr Steel
3. Assessing Fatigue Strength of Dissimilar Material Weld
3.1. Materials and Test Procedure
3.2. Results and Discussion
4. Fatigue Life Prediction Using the Accelerated Life Method
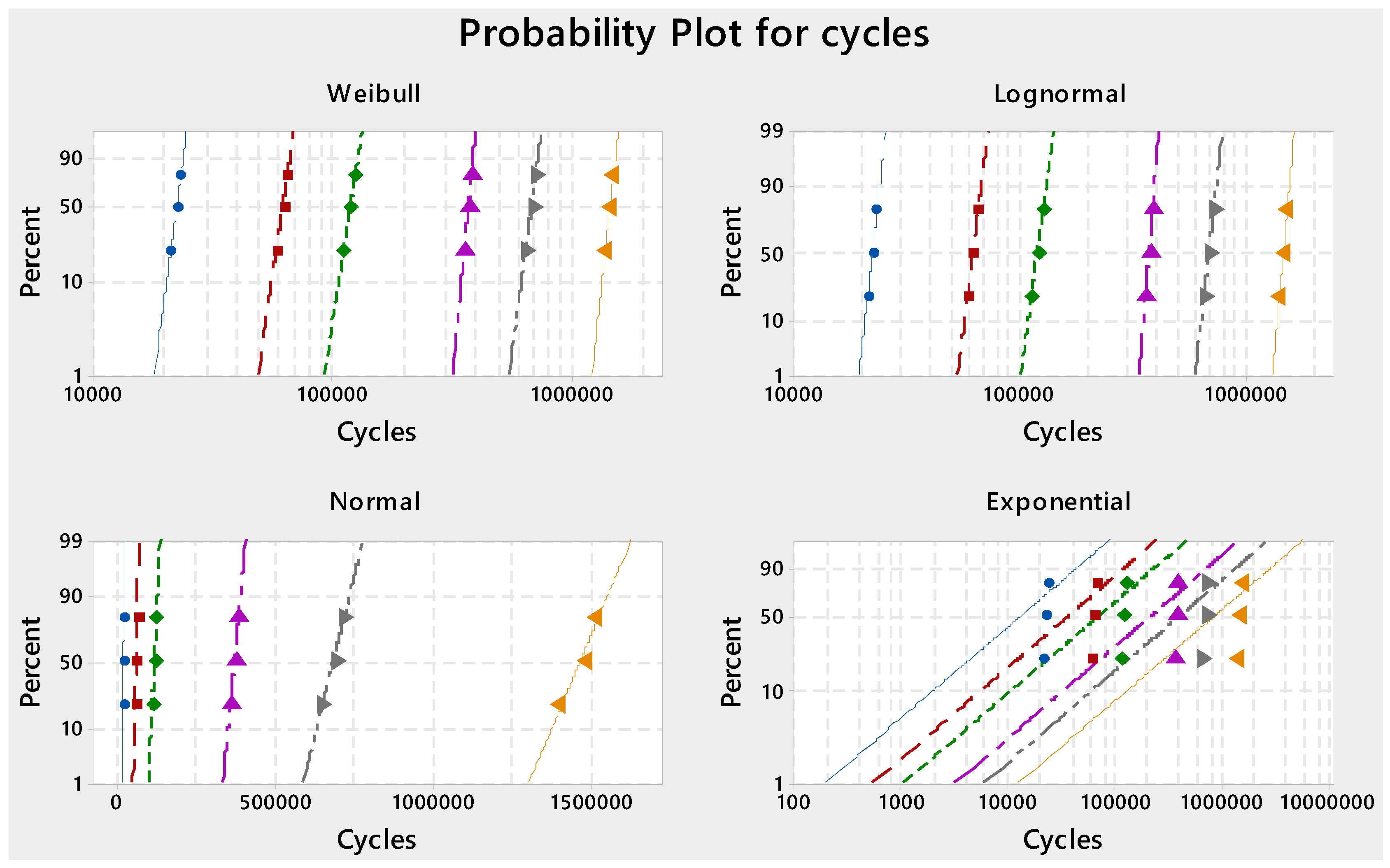
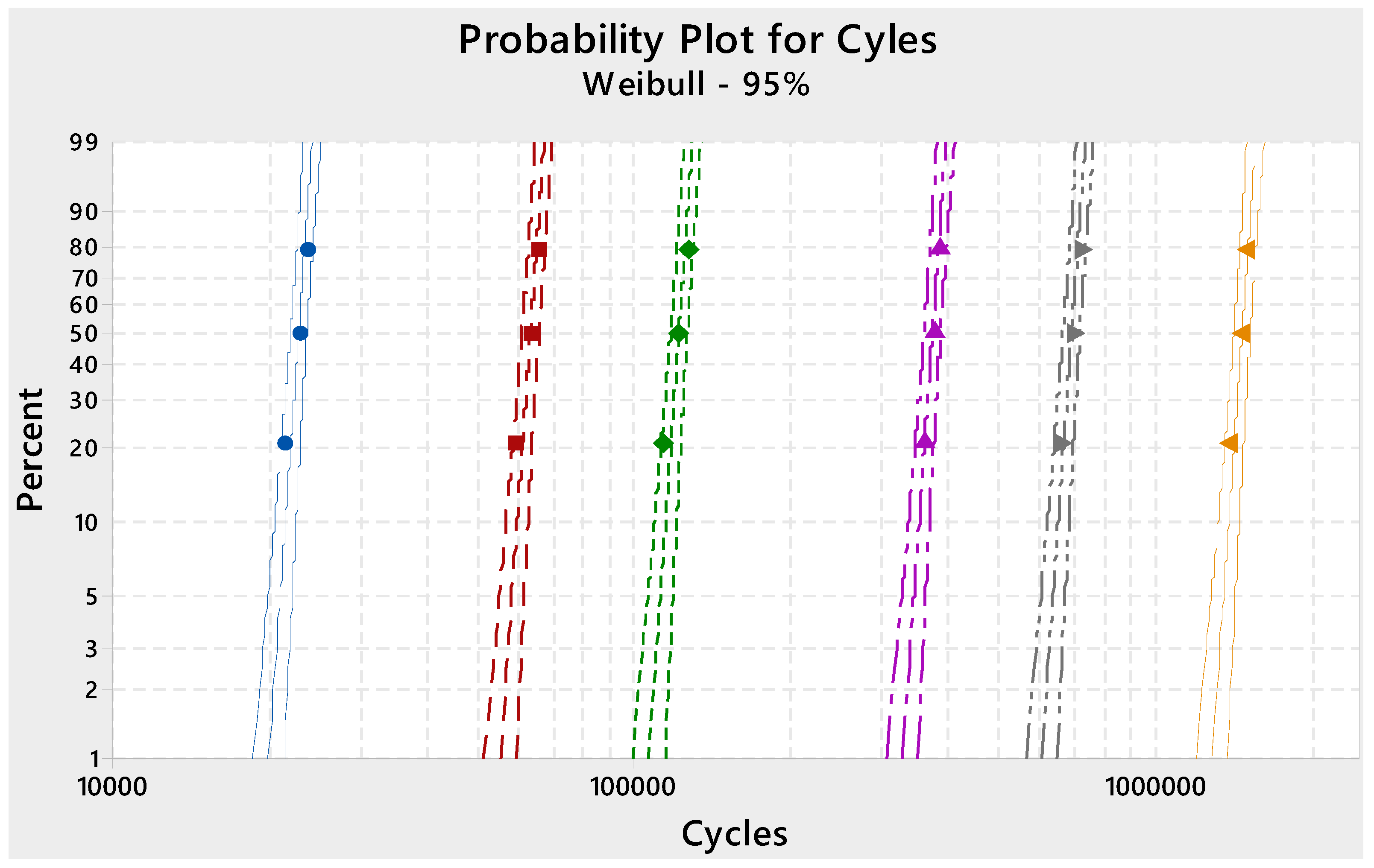
4.1. The Goodness-of-Fit Verification
4.2. Accelerated Fatigue Life Verification
5. Fatigue Life Prediction Using a Neural Network
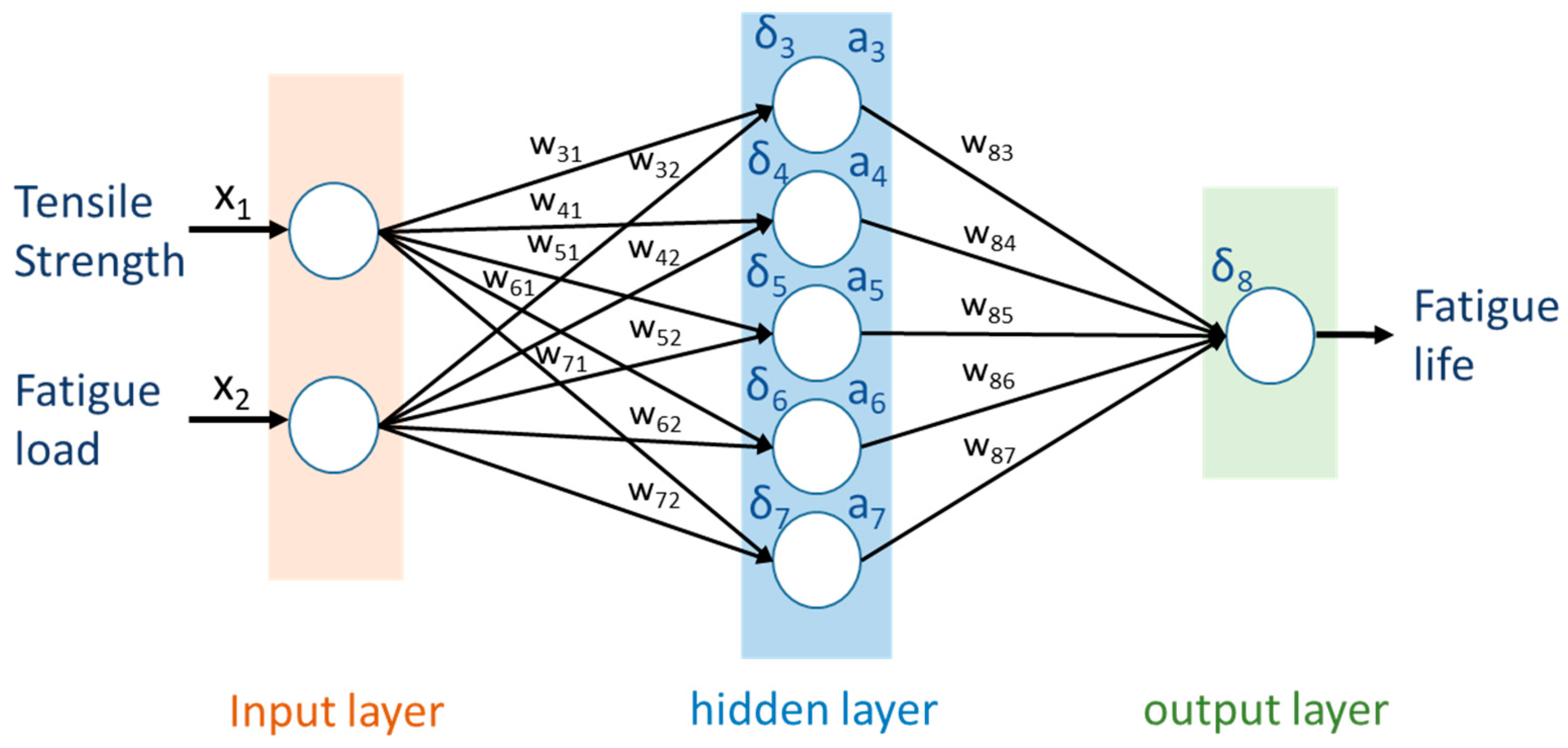
5.1. Artificial Neural Network Architecture
5.2. Dataset for Artificial Neural Network Experiment
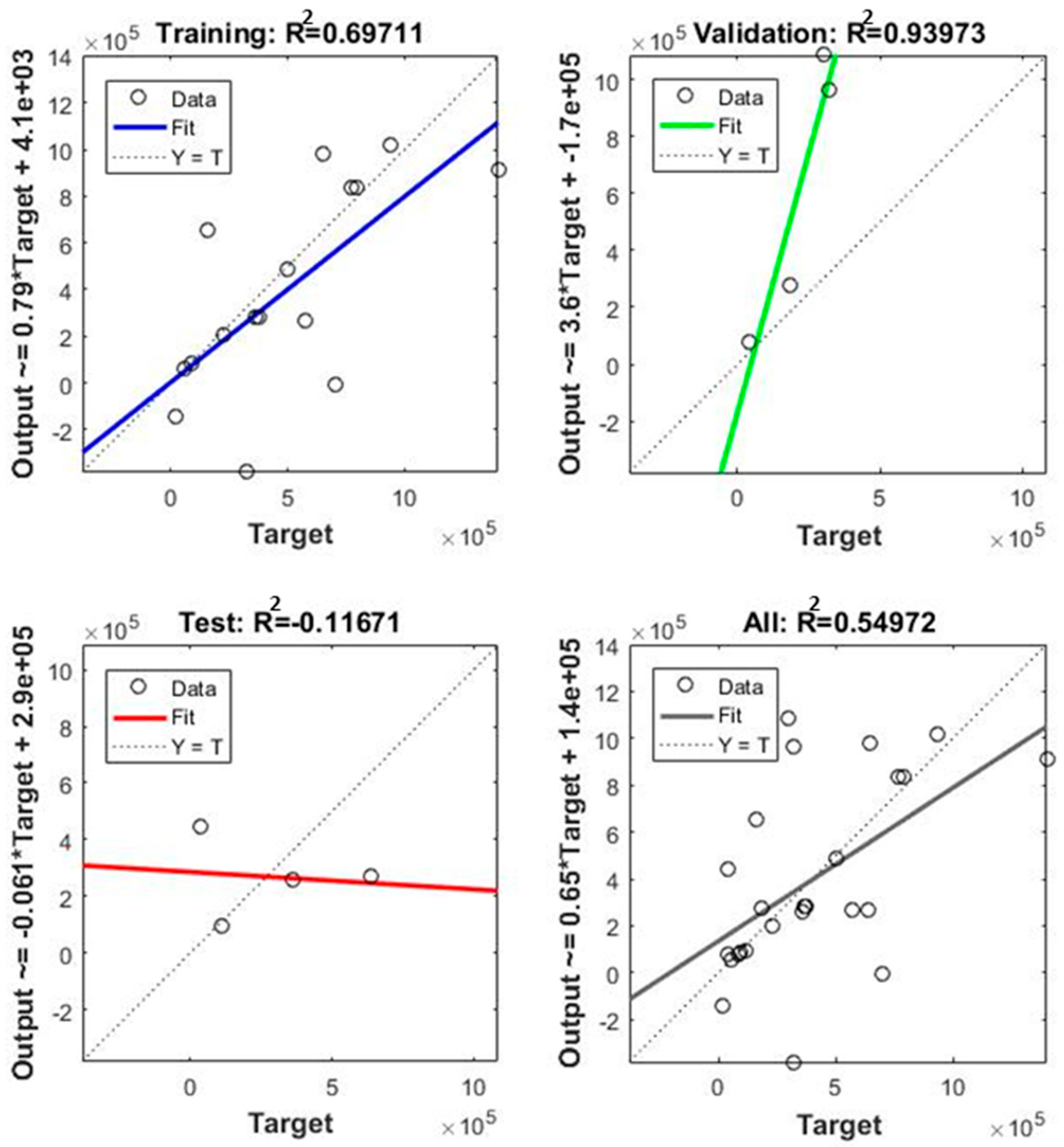
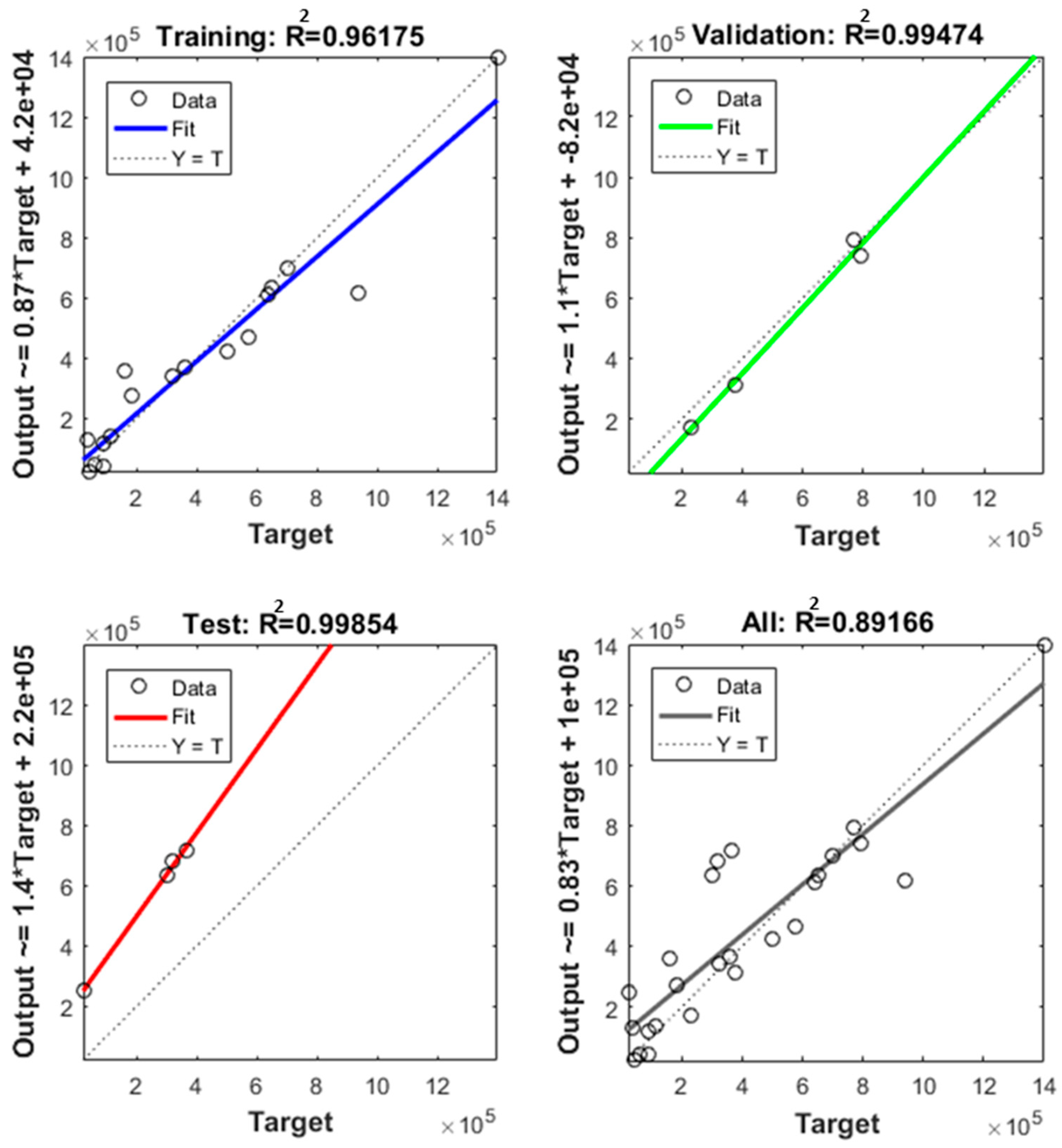
5.3. Training
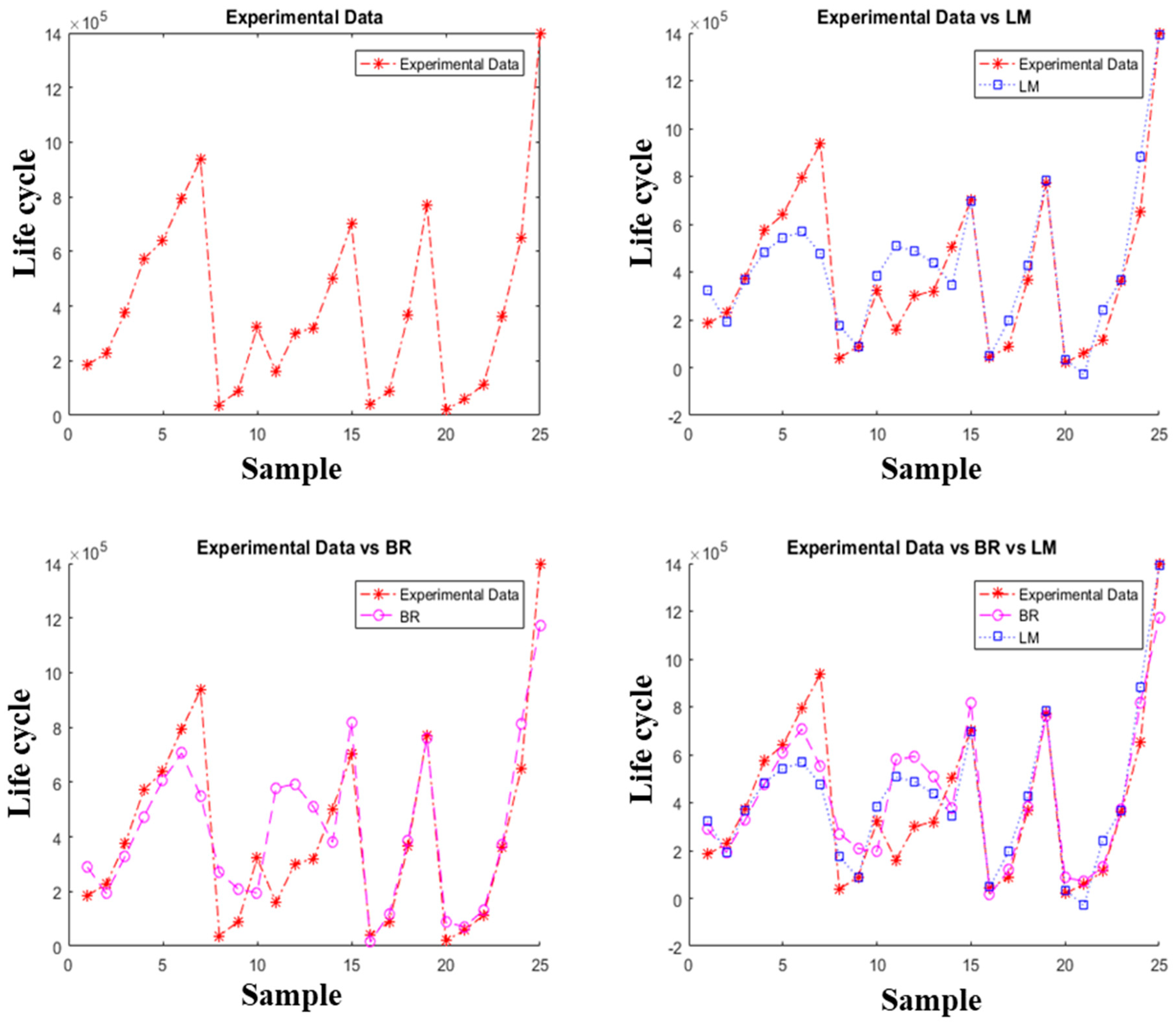
5.4. Fatigue Life Comparison
6. Conclusions
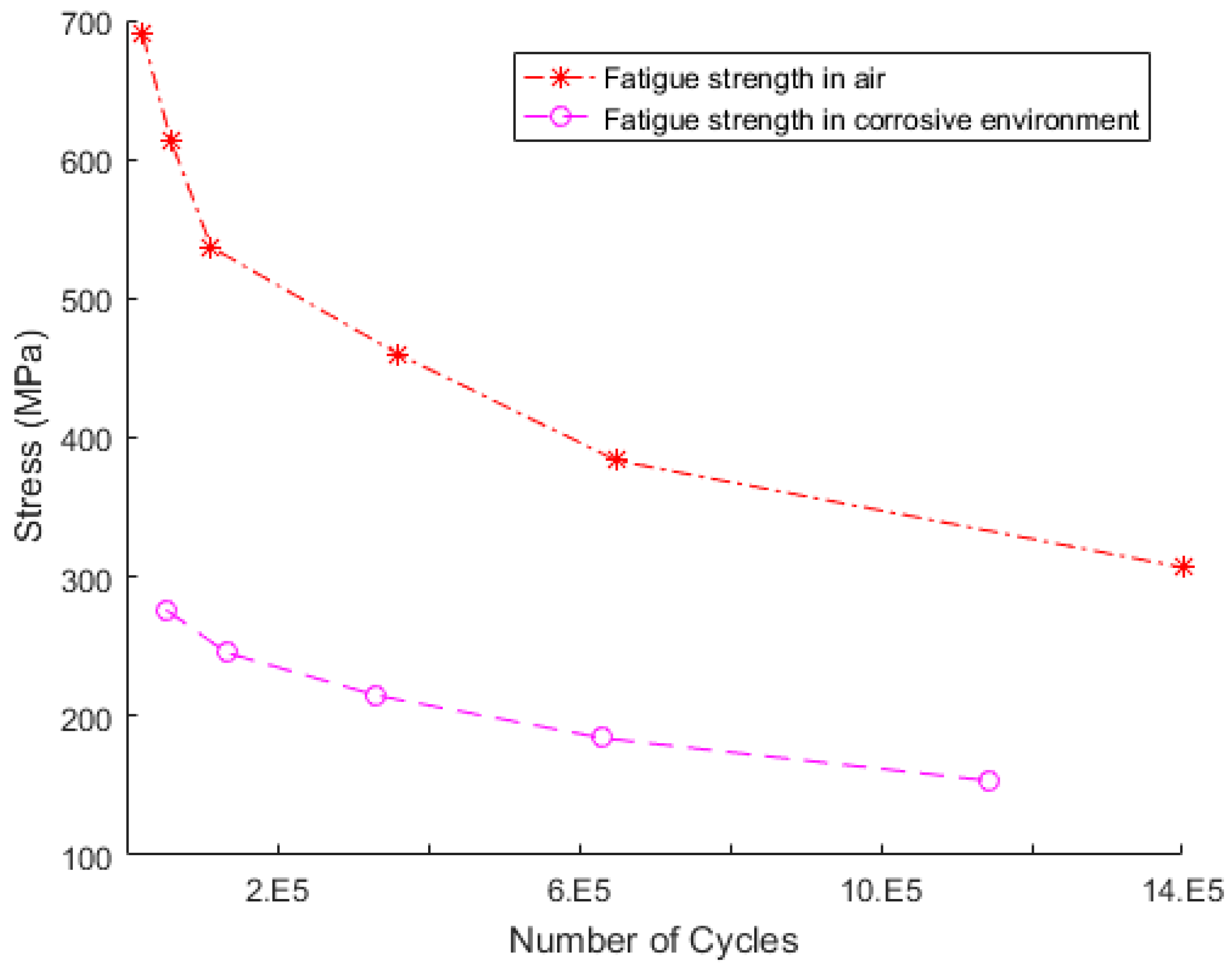
- The fatigue limit of dissimilar material weld was assessed at 306.8 MPa and 153.4 MPa in the air and in a corrosive environment. The electrochemical dissolution in an aggressive environment reduced the fatigue life of dissimilar material weld.
- The Weibull distribution was found to be the most appropriate distribution that fit the fatigue data well. The acceleration of fatigue life test data was attained with 95% reliability for the Weibull distribution. The accuracy of the fatigue life prediction results was higher than 90%.
- The corrosion fatigue life of dissimilar material weld predicted by Bayesian regularization (BR) and Levenberg–Marquardt (LM) was in good agreement with the experimentally-obtained results. It seems the Bayesian regularization training algorithm is more accurate, as it can handle the complex relationship between different parameters.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blackwood, M. Maximum efficiency of a wind turbine. UJMM 2016, 6, 2. [Google Scholar] [CrossRef]
- Green, M.A.; Hishikawa, Y.; Dunlop, E.D.; Levi, D.H.; Hohl-Ebinger, J.; Ho-Baillie, A.W.Y. Solar cell efficiency tables (version 52). Prog. Photovolt. Res. Appl. 2018, 26, 427–436. [Google Scholar] [CrossRef]
- Moon, H.; Zarrouk, S.J. Efficiency of Geothermal Power Plants: A Worldwide Review. Geothermics 2014, 51, 142–153. [Google Scholar]
- Xie, X.; Wu, Y.; Chi, C.; Zhang, M. Superalloys for Advanced Ultra-Super-Critical Fossil Power Plant Application. Superalloys 2015, 51–76. [Google Scholar] [CrossRef]
- Yakup, K. Microstructral, Mechanical and corrosion investigations of ship steel-Aluminium bimetal composites produced by explosive welding. Metals 2018, 8, 554–569. [Google Scholar]
- Corigliano, P.; Crupi, V.; Guglielmino, E.; Sili, A.M. Full-field analysis of Al-Fe explosive welded joints for shipbuilding applications. Mar. Struc. 2018, 57, 207–218. [Google Scholar] [CrossRef]
- Pasqualino, C.; Crupi, V.; Guglielmino, E. Non linear finite element simulation of explosise welded joints of dissimilar metals for shipbuilding applications. Ocean Eng. 2018, 160, 346–353. [Google Scholar]
- Fehim, F. Recent developments in explosive welding. Mat. Des. 2011, 32, 1081–1093. [Google Scholar]
- Escobar, L.A.; Meeker, W.Q. A Review of Accelerated Test Models. Stat. Sci. 2006, 21, 552–577. [Google Scholar] [CrossRef]
- Elsayed, E.A. Overview of reliability testing. IEEE Trans. Reliab. 2012, 61, 282–291. [Google Scholar] [CrossRef]
- Cox, D.R. Regression Models and Life-Tables; Springer: New York, NY, USA, 1992; pp. 527–541. [Google Scholar]
- Ciampi, A.; Etezadi-Amoli, J. A general model for testing the proportional hazards and the accelerated failure time hypotheses in the analysis of censored survival data with covariates. Commun. Stat. Theory Methods 1985, 14, 651–667. [Google Scholar] [CrossRef]
- Elsayed, E.A.; Liao, H.; Wang, X. An extended linear hazard regression model with application to time-dependent dielectric breakdown of thermal oxides. IIE Trans. 2006, 38, 329–340. [Google Scholar] [CrossRef]
- Zhao, W.; Elsayed, E.A.; Zhao, W. International Journal of Systems Science Modelling accelerated life testing based on mean residual life Modelling accelerated life testing based on mean residual life. Int. J. Syst. Sci. 2005, 36, 689–696. [Google Scholar] [CrossRef]
- Brass, W. Mortality models and their uses in demography. Trans. Fac. Actuar. 1974, 33, 123–142. [Google Scholar] [CrossRef]
- Ahmad, H.; Hwang, J.; Lee, J.; Bae, D. An Assessment of the Mechanical Properties and Microstructural Analysis of Dissimilar Material Welded Joint between Alloy 617 and 12Cr Steel. Metals 2016, 6, 242. [Google Scholar] [CrossRef]
- Weldments, T. Determination of Residual Stresses in Structural Shapes. Weld. J. 1992, 29, 305–312. [Google Scholar] [CrossRef]
- Meetham, G. Steel and Nickel Alloys at High Temperatures. Mater. Des. 1989, 10, 77–92. [Google Scholar] [CrossRef]
- Special Metals High–Performance Nickel Alloys Leveraging a Network of Expertise. Available online: http://www.specialmetals.com/assets/smc/documents/pcc-8064-sm-alloy-handbook-v04.pdf (accessed on 18 May 2018).
- ASTM International. Standard Test Methods for Tension Testing of Metallic Materials; ASTM International: West Conshohocken, PA, USA, 2009; Volume I, pp. 1–27. [Google Scholar] [CrossRef]
- Ahmad, H.W.; Lee, J.H.; Hwang, J.H.; Bae, D.H. Welding Residual Stress Analysis and Fatigue Strength Assessment of Multi-Pass Dissimilar Material Welded Joint between Alloy 617 and 12Cr Steel. Metals 2017, 8, 21. [Google Scholar] [CrossRef]
- Sudarshan, T.S.; Srivatsan, T.S.; Harvey, D.P. Fatigue processes in metals—role of aqueous environments. Eng. Fract. Mech. 1990, 36, 827–852. [Google Scholar] [CrossRef]
- Gowda, S.; Manigandan, K.; Patnaika, A.; Srivatsan, T.S. Influence of exposure to an aggressive environment on cyclic fatigue response and life of an alloy steel. J. Eng. Res. 2017, 14, 124–136. [Google Scholar] [CrossRef]
- Seidel, J.M.; Duquette, D.J. Pre-crack fatigue damage and crack initiation under corrosion fatigue conditions. In Proceedings of the HH Uhlig Memorial Symposium; The Electrochemical Society: Pennington, NJ, USA, 1995; Volume 94, p. 229. [Google Scholar]
- Sibi, P.; Jones, S.A.; Siddarth, P. Analysis of different activation functions using back propagation neural networks. J. Theor. Appl. Inf. Technol. 2013, 47, 1264–1268. [Google Scholar]
- Cameron, A.C.; Windmeijer, F.A.G. An R-squared measure of goodness of fit for some common nonlinear regression models. J. Econom. 1997, 77, 329–342. [Google Scholar] [CrossRef]
- Nielsen, M. Neural Networks and Deep Learning; Determination Press, 2015. Available online: http://neuralnetworksanddeeplearning.com/ (accessed on 2 February 2019).
- Kayri, M. Predictive Abilities of Bayesian Regularization and Levenberg–Marquardt Algorithms in Artificial Neural Networks: A Comparative Empirical Study on Social Data. Math. Comput. Appl. 2016, 21, 20. [Google Scholar] [CrossRef]
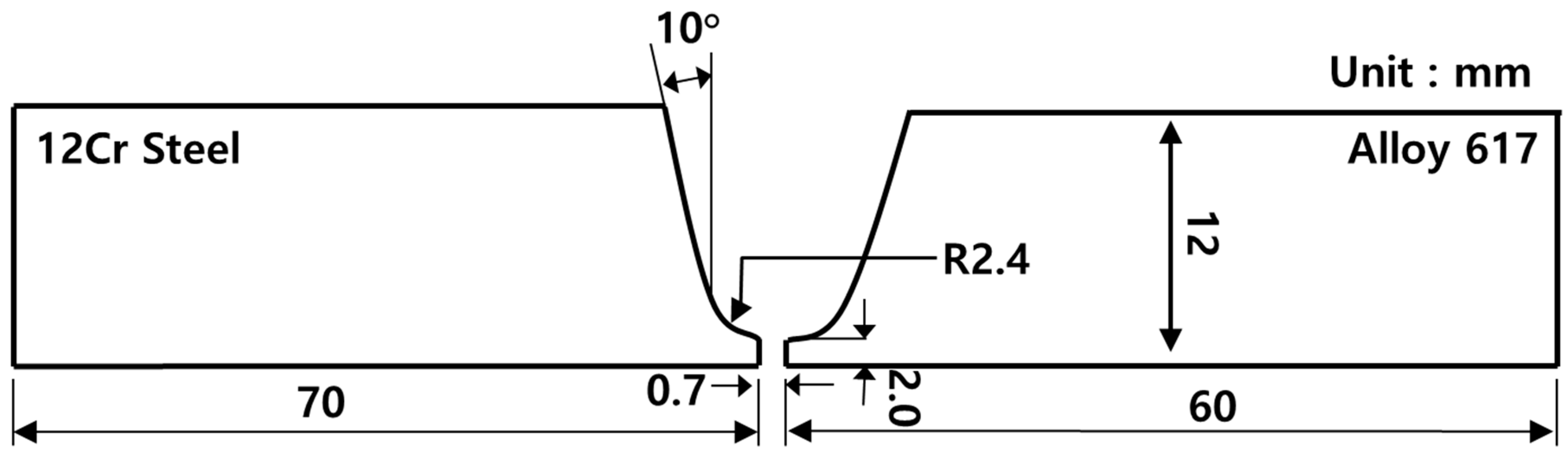

| Base/Filler Metal | Chemical Composition (Weight %) | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ni | Cr | Mo | Co | Al | Fe | C | Si | Mn | Ti | Cu | S | |
| Alloy 617 | 44.3 | 22 | 9.0 | 12.5 | 1.2 | 1.5 | 0.07 | 0.5 | 0.5 | 0.3 | 0.2 | 0.008 |
| 12 Cr | 0.43 | 11.6 | 0.04 | - | - | Bal. | 0.13 | 0.4 | 0.58 | - | 0.1 | - |
| Thyssen 617 | 45.7 | 21.5 | 9.0 | 11.0 | 1.0 | 1.0 | 0.05 | 0.1 | - | 1 | - | - |
| DMW | 46.97 | 21.11 | 9.57 | 10.32 | - | 12.03 | - | - | - | - | - | - |
| Material | Yield Strength (MPa) | Tensile Strength (MPa) | Elongation (%) | Reduction in Area (%) | Melting Point (°C) |
|---|---|---|---|---|---|
| Alloy 617 | 322 | 732 | 62 | 56 | 1330 |
| 12 Cr | 551 | 758 | 18 | 50 | 1375 |
| DMW | 490 | 767 | 48 | - | - |
| σmax = 767MPa (Air) | σL = 306.8 MPa (Corrosive Environment) | Load Ratio(R) |
|---|---|---|
| 0.9σu = 690.3 | 0.9σL = 276.12 | 0.1 |
| 0.8σu = 613.6 | 0.8σL = 245.44 | |
| 0.7σu = 536.9 | 0.7σL = 214.76 | |
| 0.6σu = 460.2 | 0.6σL = 184.08 | |
| 0.5σu = 383.5 | 0.5σL = 153.4 | |
| 0.4σu = 306.8 |
| Stress Max. (MPa) | Anderson–Darling Value for Different Distributions | |||
|---|---|---|---|---|
| Weibull | Log-Normal | Normal | Exponential | |
| 690.3 | 3.46 | 3.492 | 3.488 | 4.552 |
| 613.6 | 3.446 | 3.468 | 3.464 | 4.539 |
| 536.9 | 3.441 | 3.454 | 3.451 | 4.526 |
| 460.2 | 3.441 | 3.451 | 3.45 | 4.58 |
| 383.5 | 3.442 | 3.458 | 3.455 | 4.548 |
| 306.8 | 3.478 | 3.517 | 3.513 | 4.574 |
| No. | Experiment | Prediction | Accuracy (%) | |
|---|---|---|---|---|
| Stress Max. (MPa) | Fatigue Life (Cycles) | Fatigue Life (Cycles) | ||
| 1 | 690.3 | 21,279 | 23,523.83 | 90.5 |
| 2 | 613.6 | 58,846 | 64,778.24 | 90.8 |
| 3 | 536.9 | 112,645 | 123,797.3 | 91.0 |
| 4 | 460.2 | 359,978 | 376,277.9 | 95.7 |
| 5 | 383.5 | 650,000 | 690,486 | 94.1 |
| 6 | 306.8 | 1,400,000 | 1,453,466 | 96.3 |
| Maximum Stress (MPa) | Tensile Strength (MPa) | Life Cycles | Maximum Stress (MPa) | Tensile Strength (MPa) | Life Cycles |
|---|---|---|---|---|---|
| 500.1 | 579.8 | 184,703 | 259.5 | 519 | 502,180 |
| 521.1 | 579.8 | 227,403 | 207.6 | 675 | 701,714 |
| 492.2 | 579.8 | 374,892 | 607.5 | 675 | 41,451 |
| 463.2 | 579.8 | 572,923 | 540 | 675 | 89,208 |
| 434.3 | 579.8 | 639,282 | 472.5 | 675 | 364,802 |
| 405.3 | 579.8 | 792,364 | 405 | 675 | 770,636 |
| 376.4 | 502 | 937,293 | 690.3 | 767 | 21,279 |
| 237.3 | 502 | 38,227 | 613.6 | 767 | 58,846 |
| 211 | 502 | 90,257 | 536.9 | 767 | 112,645 |
| 184.6 | 519 | 321,251 | 460.2 | 767 | 359,978 |
| 415.2 | 519 | 160,140 | 383.5 | 767 | 650,000 |
| 363.3 | 519 | 301,108 | 306.8 | 767 | 1,400,000 |
| 311.4 | 519 | 320,115 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmad, H.W.; Hwang, J.H.; Javed, K.; Chaudry, U.M.; Bae, D.H. Probabilistic Fatigue Life Prediction of Dissimilar Material Weld Using Accelerated Life Method and Neural Network Approach. Computation 2019, 7, 10. https://doi.org/10.3390/computation7010010
Ahmad HW, Hwang JH, Javed K, Chaudry UM, Bae DH. Probabilistic Fatigue Life Prediction of Dissimilar Material Weld Using Accelerated Life Method and Neural Network Approach. Computation. 2019; 7(1):10. https://doi.org/10.3390/computation7010010
Chicago/Turabian StyleAhmad, Hafiz Waqar, Jeong Ho Hwang, Kamran Javed, Umer Masood Chaudry, and Dong Ho Bae. 2019. "Probabilistic Fatigue Life Prediction of Dissimilar Material Weld Using Accelerated Life Method and Neural Network Approach" Computation 7, no. 1: 10. https://doi.org/10.3390/computation7010010
APA StyleAhmad, H. W., Hwang, J. H., Javed, K., Chaudry, U. M., & Bae, D. H. (2019). Probabilistic Fatigue Life Prediction of Dissimilar Material Weld Using Accelerated Life Method and Neural Network Approach. Computation, 7(1), 10. https://doi.org/10.3390/computation7010010





