Wind Pressure Distributions on Buildings Using the Coherent Structure Smagorinsky Model for LES
Abstract
:1. Introduction
2. SGS Models and Numerical Methods
2.1. SGS Models
2.2. Numerical Methods
3. Numerical Simulation for Isolated Buildings in Uniform Flow
3.1. Experiments for Validation
3.2. Computational Model and Calculation Conditions
3.3. Results and Discussion
3.3.1. Pressure Coefficients of Buildings
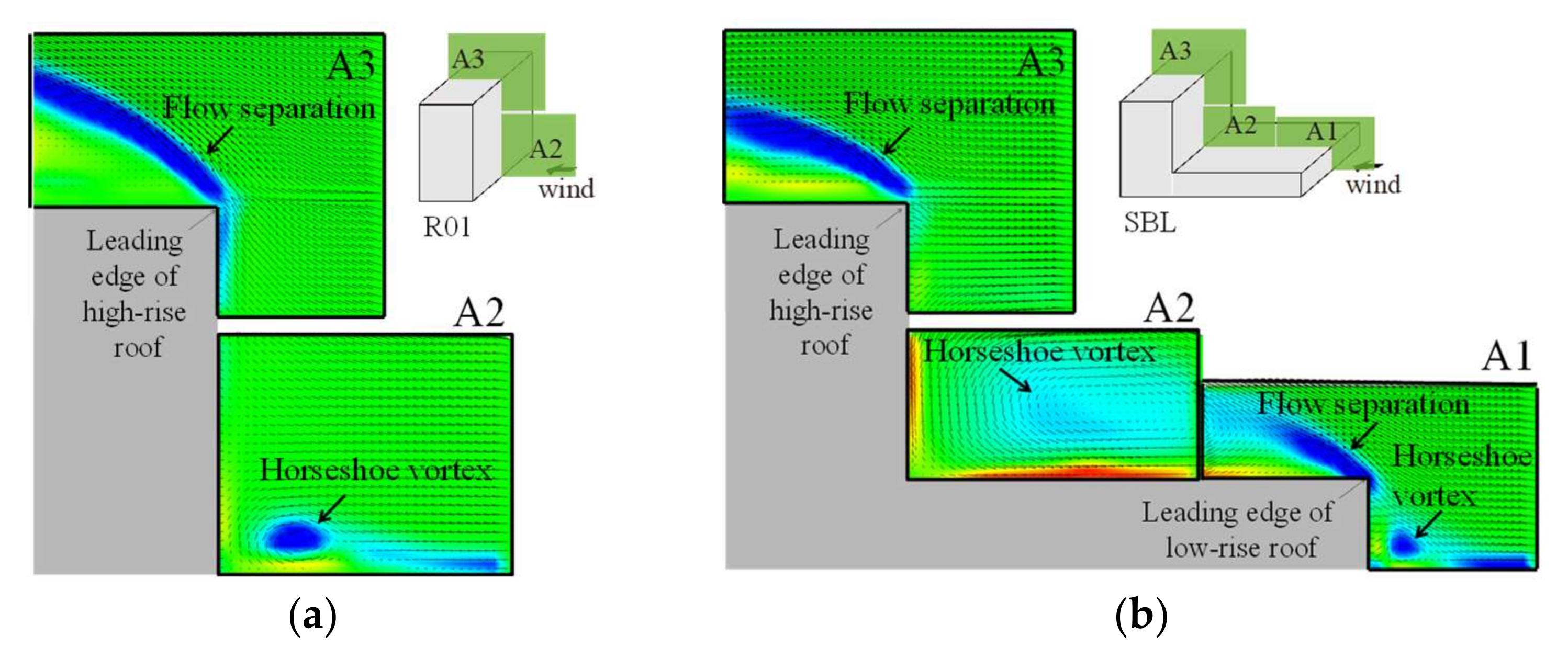
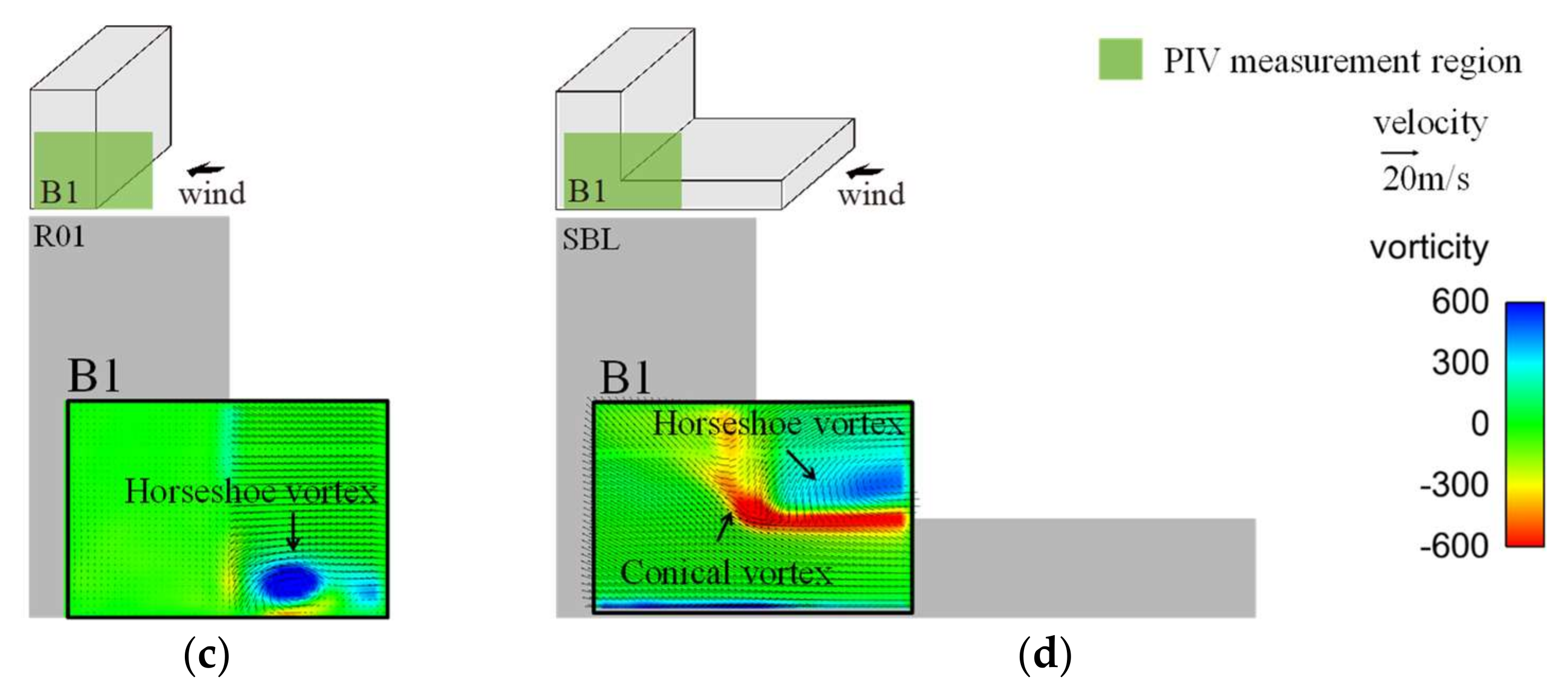
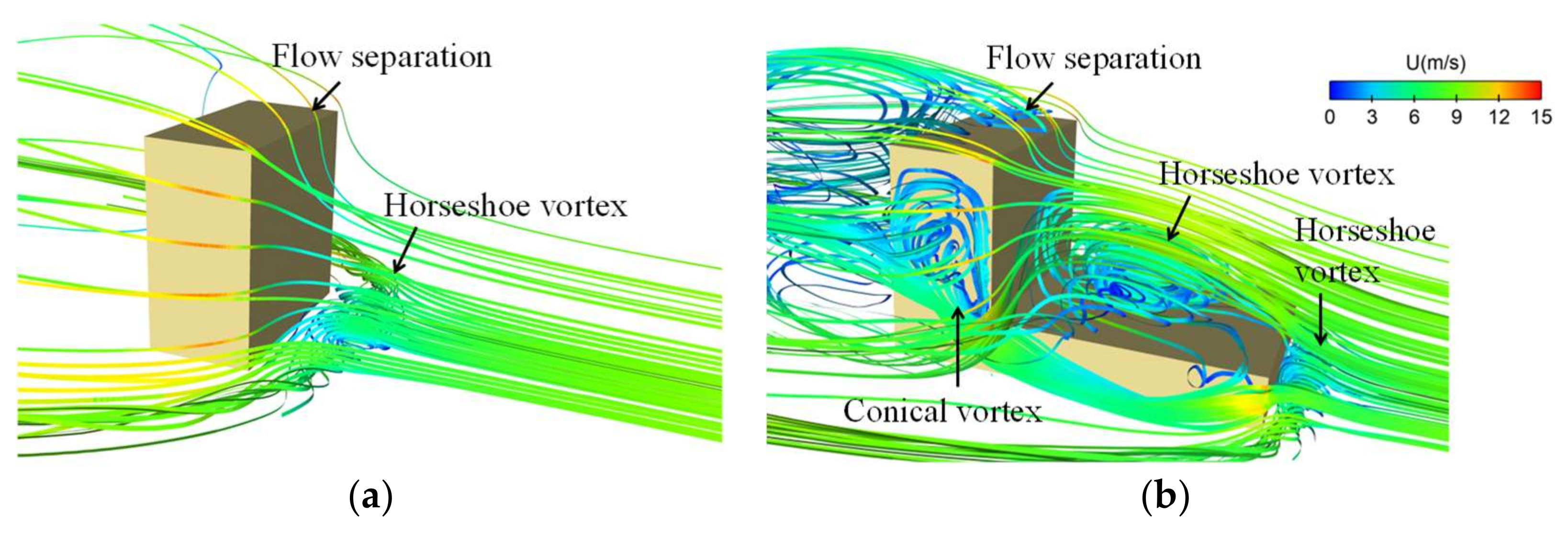
3.3.2. Flow Fields around Buildings
4. Numerical Simulation for a High-Rise Building in an Urban City with Turbulent Flow
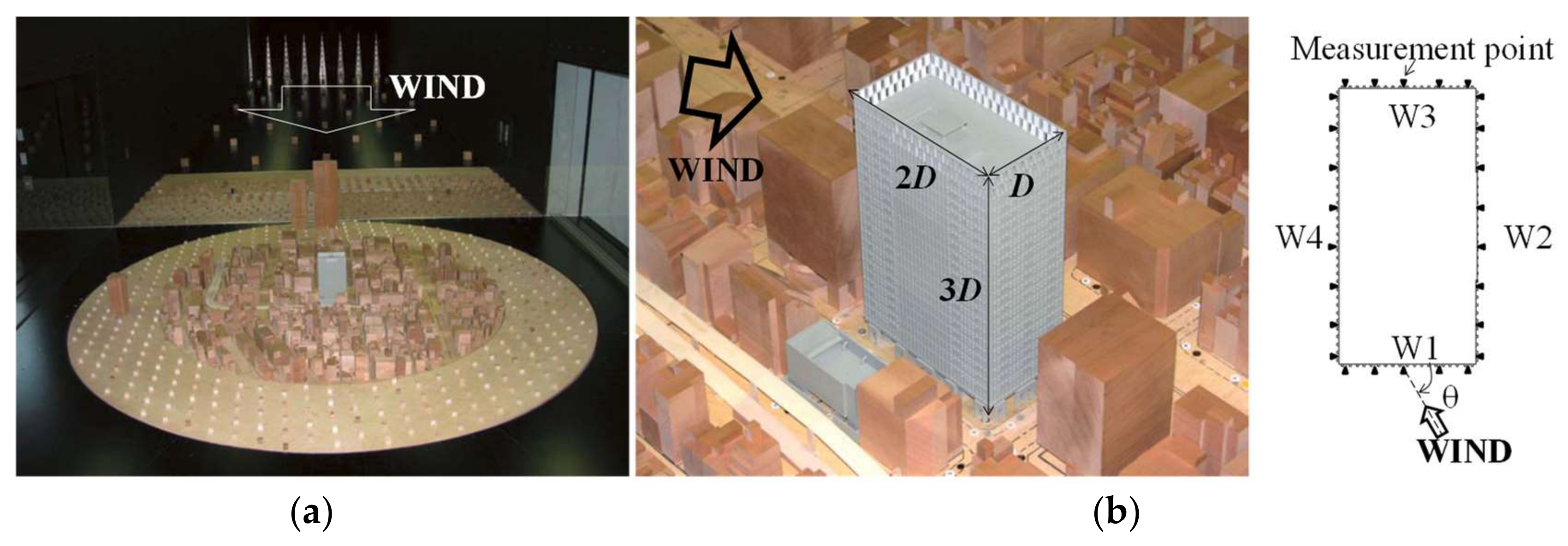
4.1. Validation Experiments
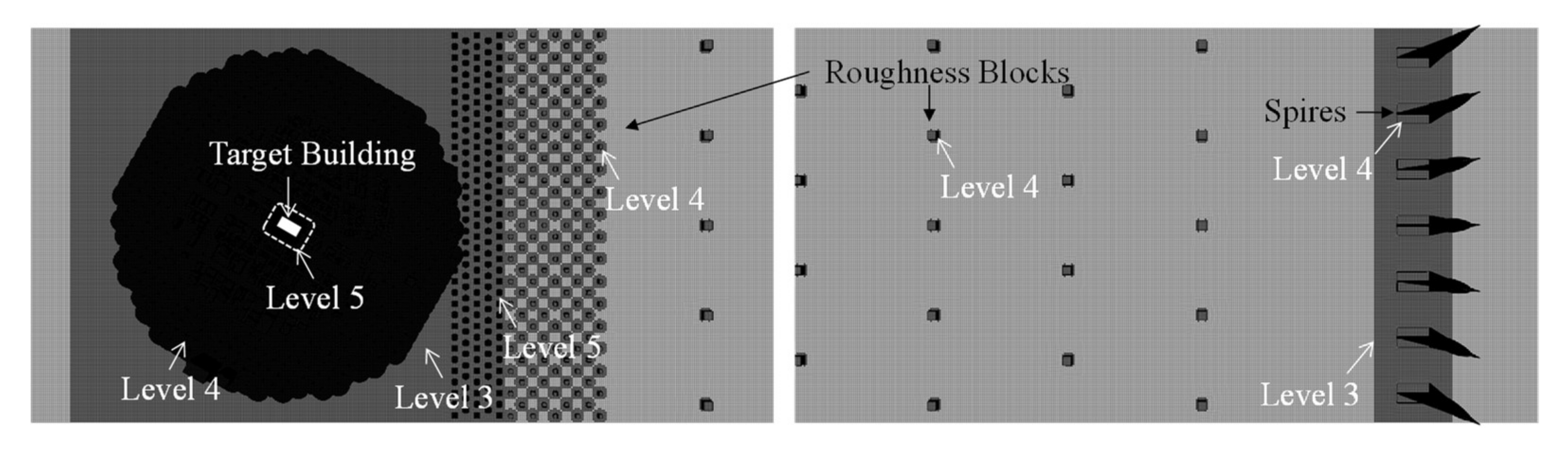
4.2. Computational Models and Calculation Conditions
4.3. Results and Discussion
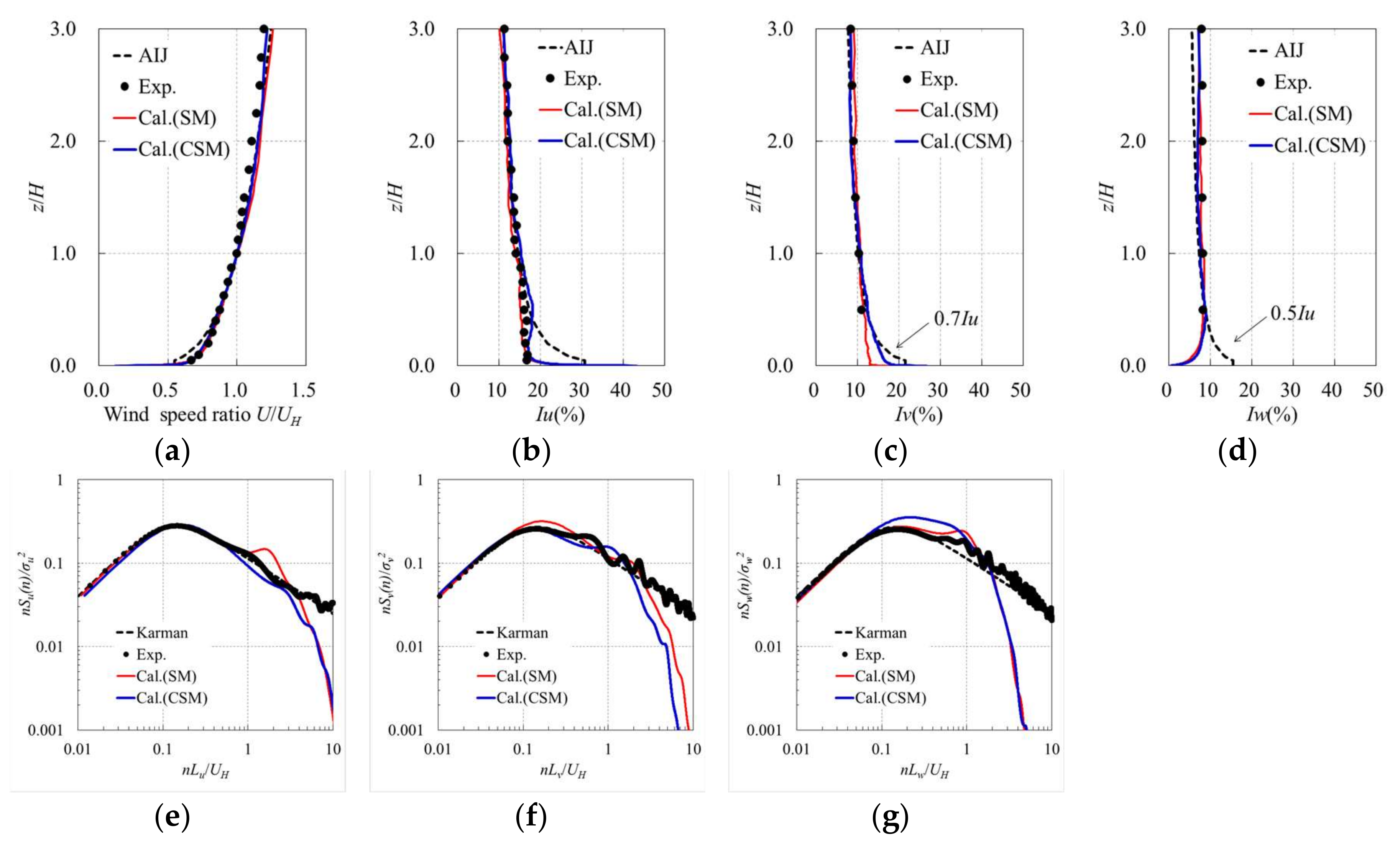
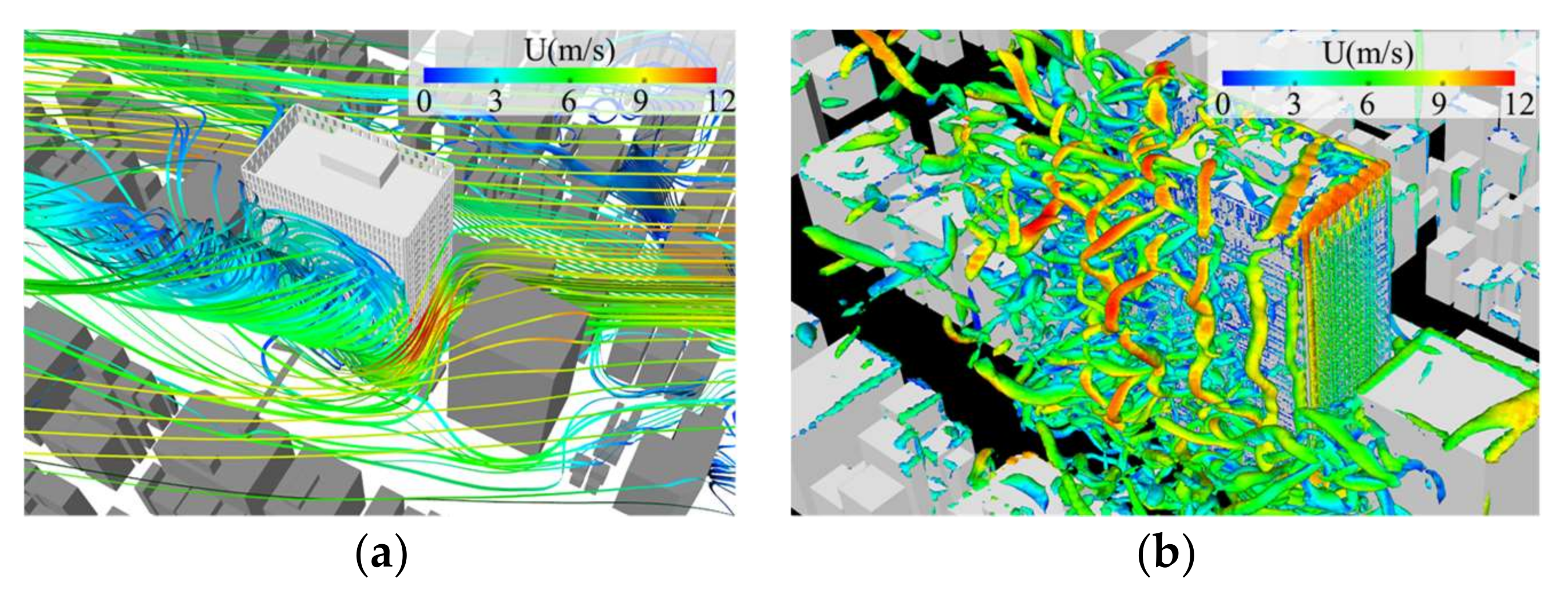
4.3.1. Wind Flow Characteristics
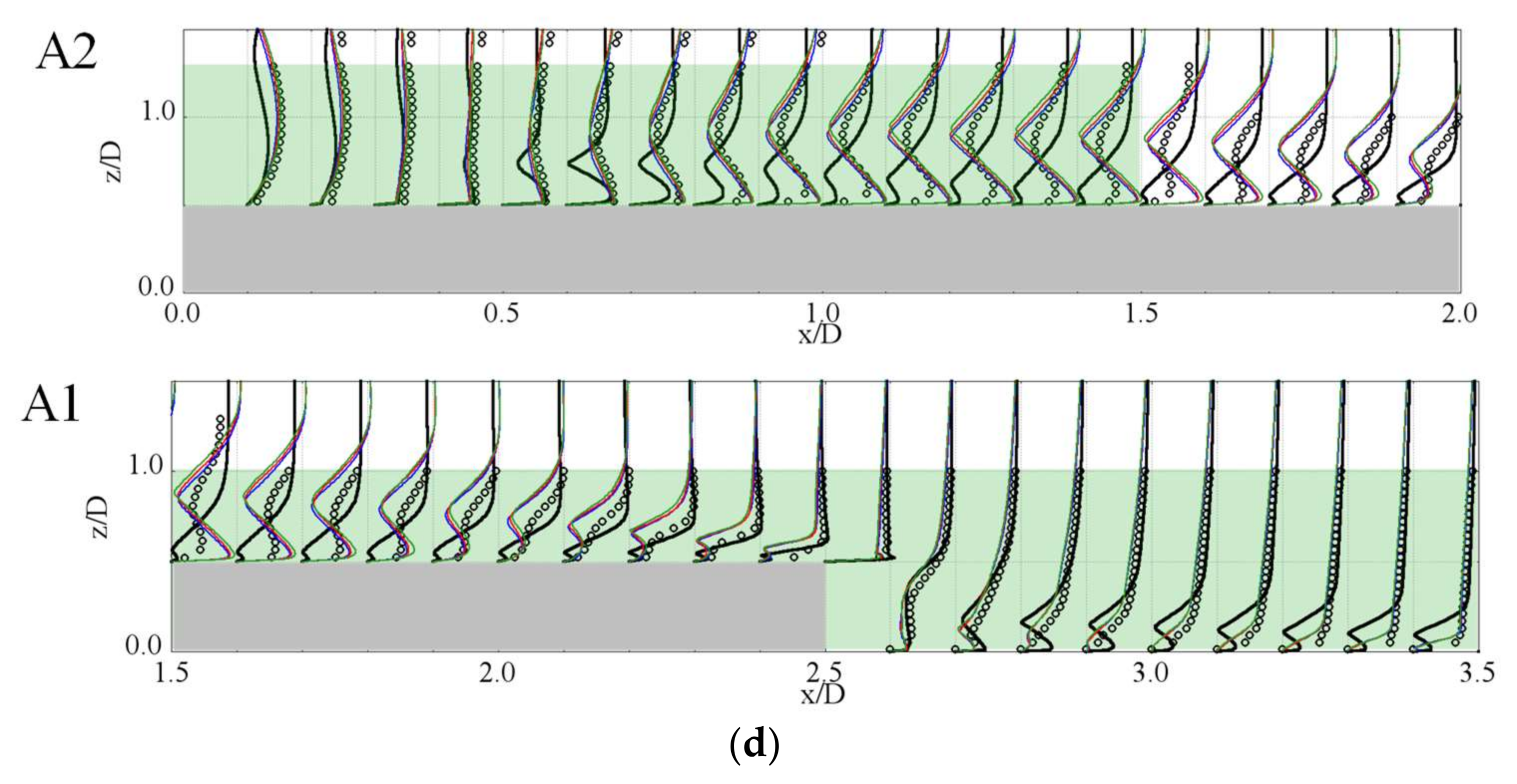
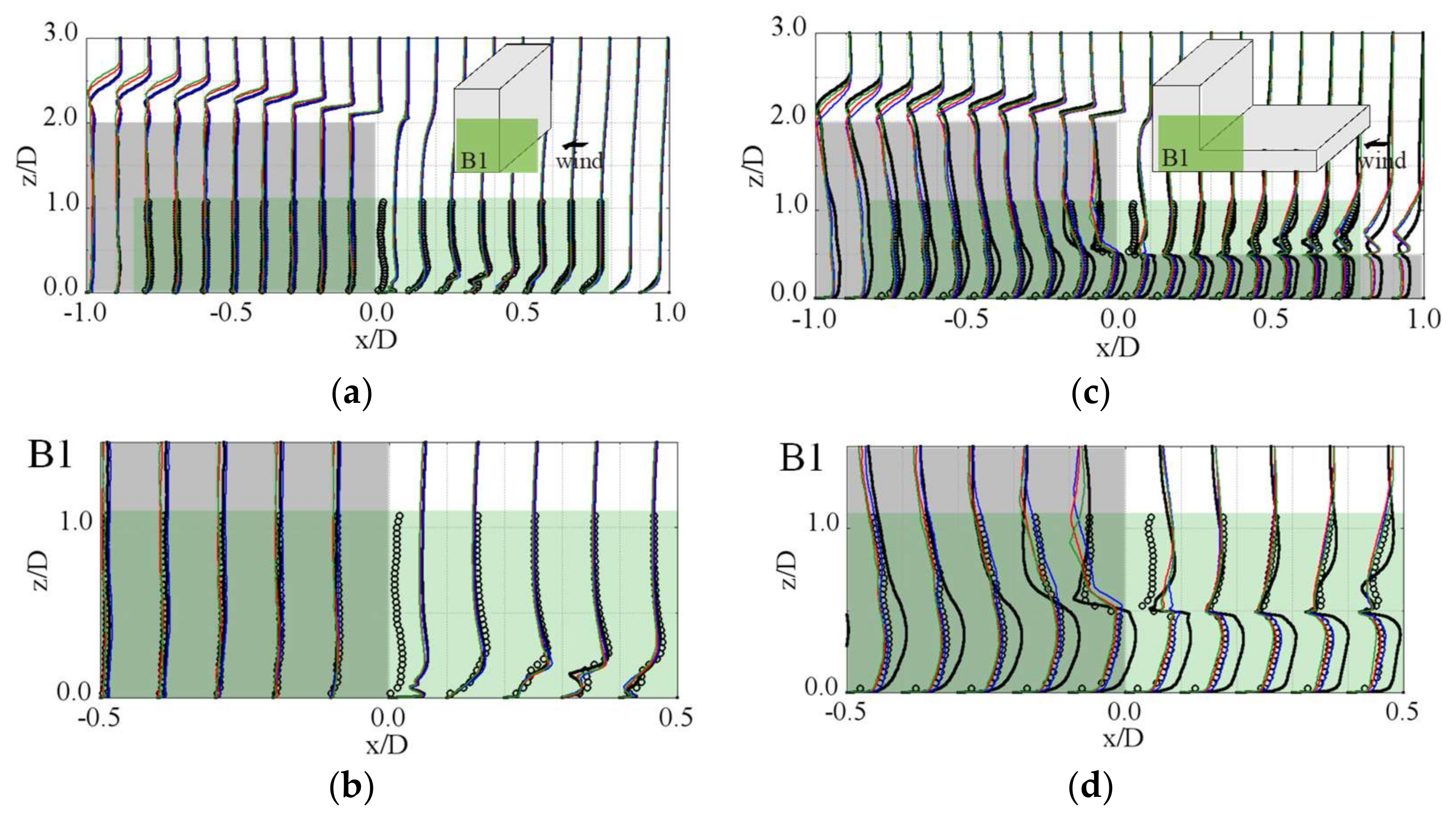
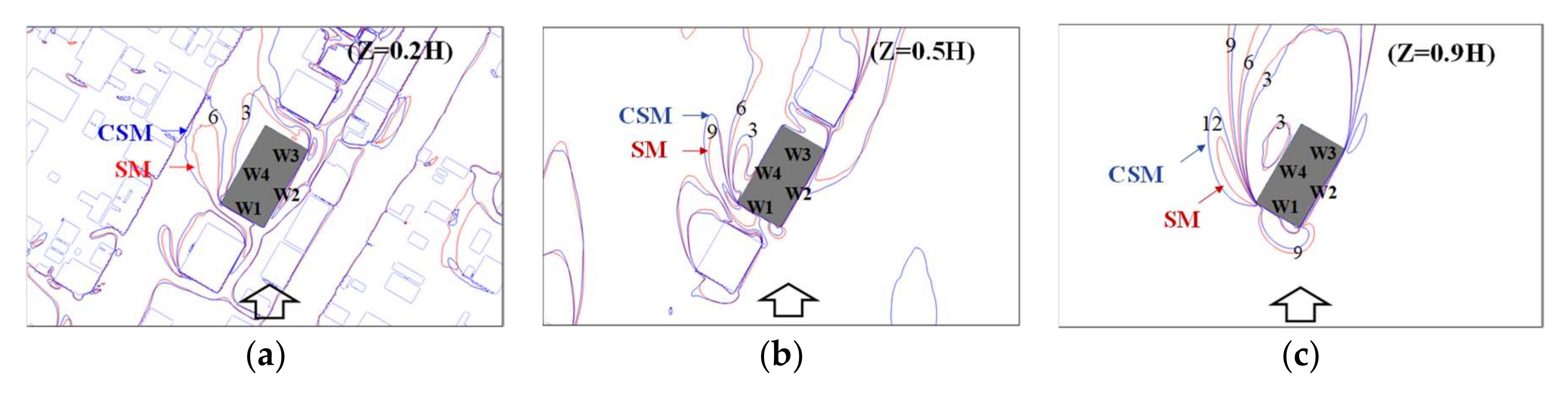
4.3.2. Flow Fields around the Target Building
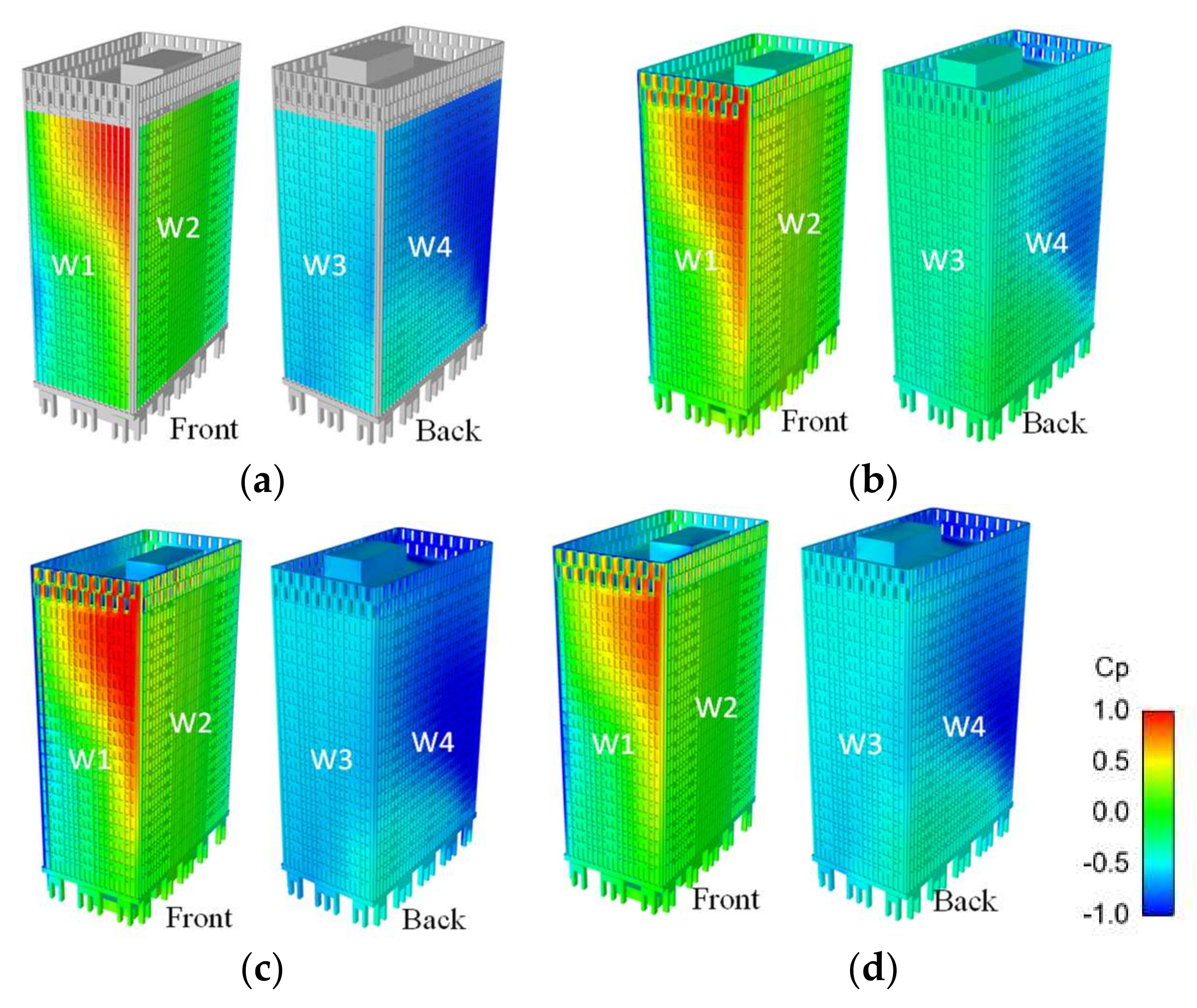
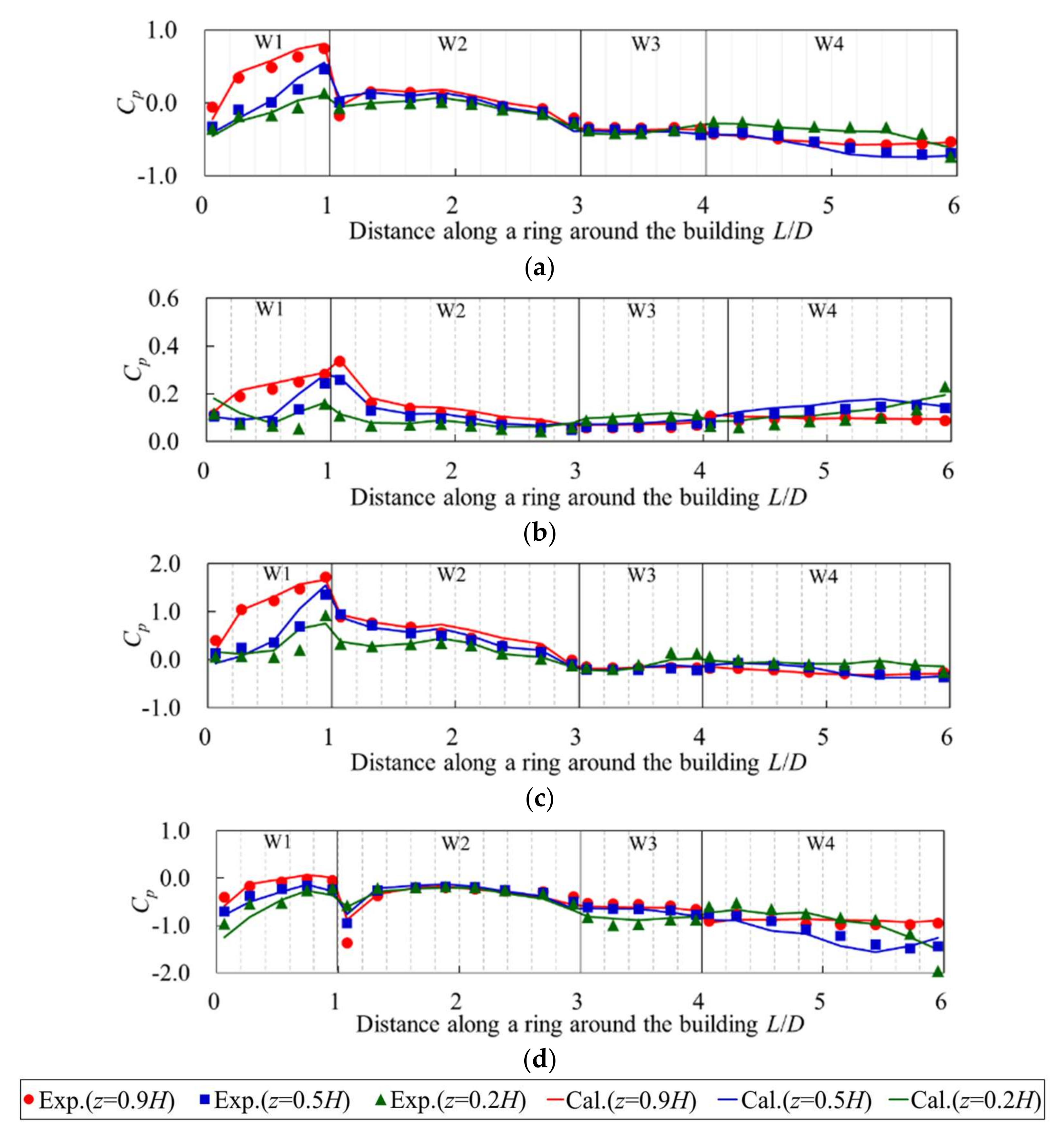
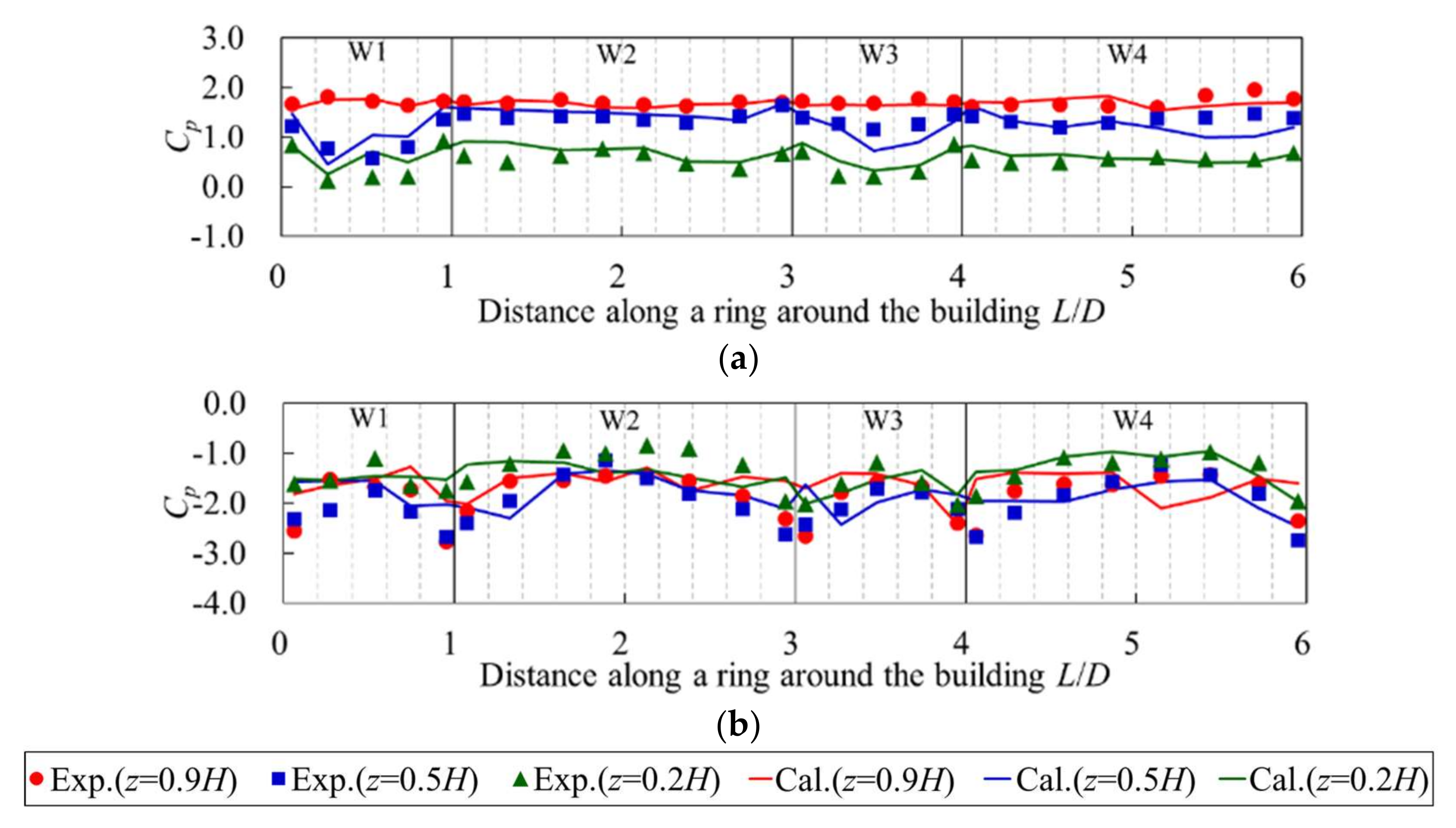
4.3.3. Pressure Coefficients of the Target Building for a Specific Wind Direction
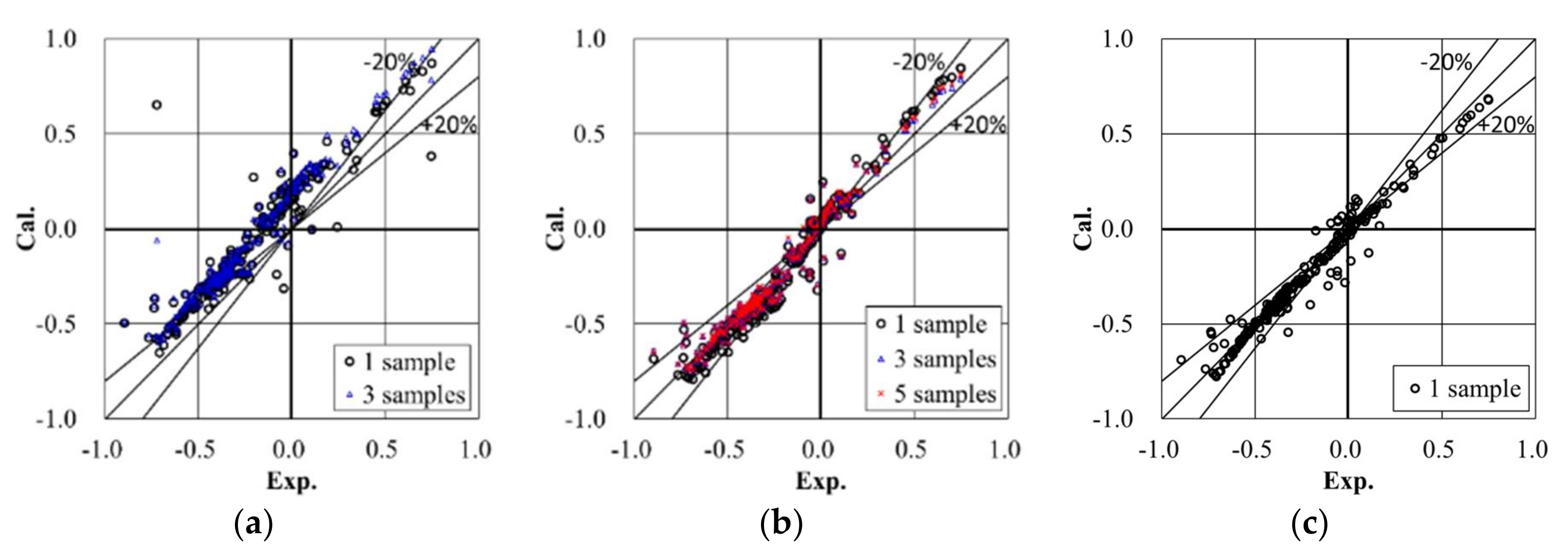
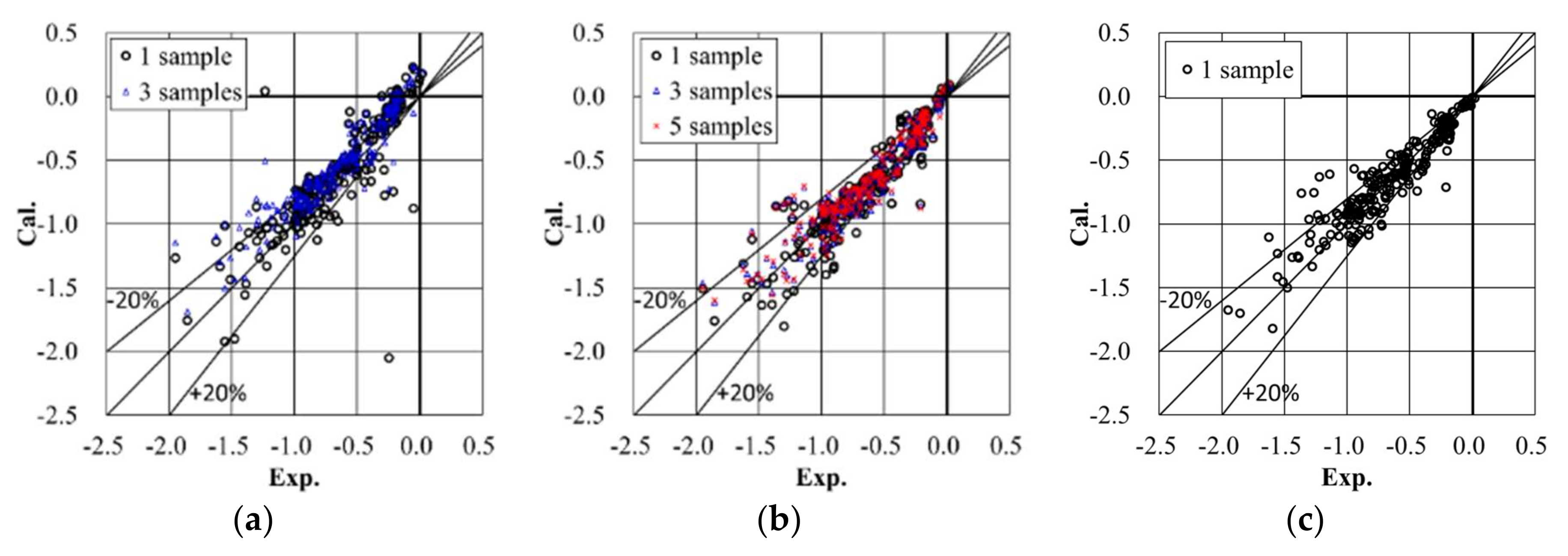
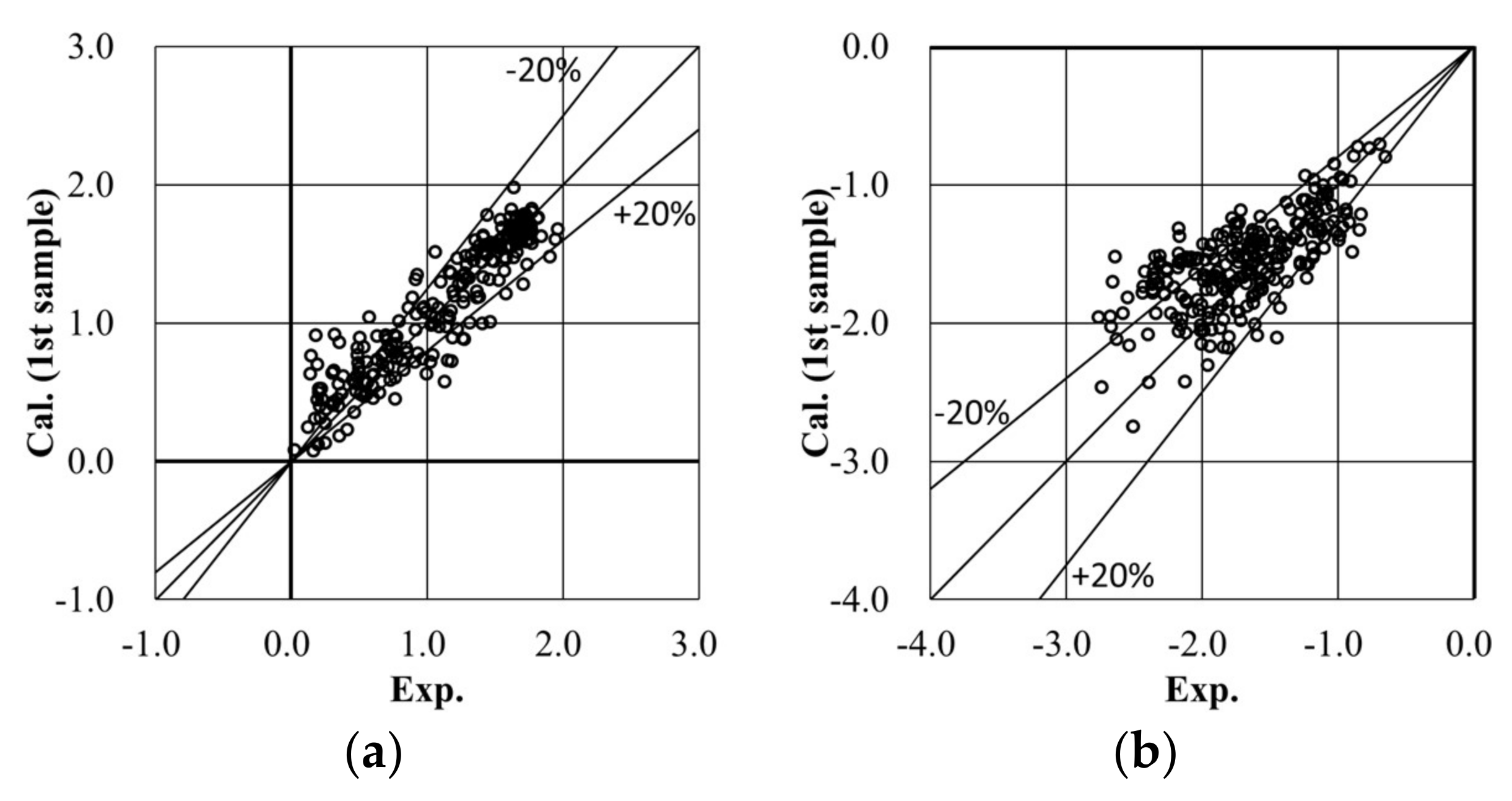
4.3.4. Pressure Coefficients of the Target Building for All Wind Directions
5. Conclusions
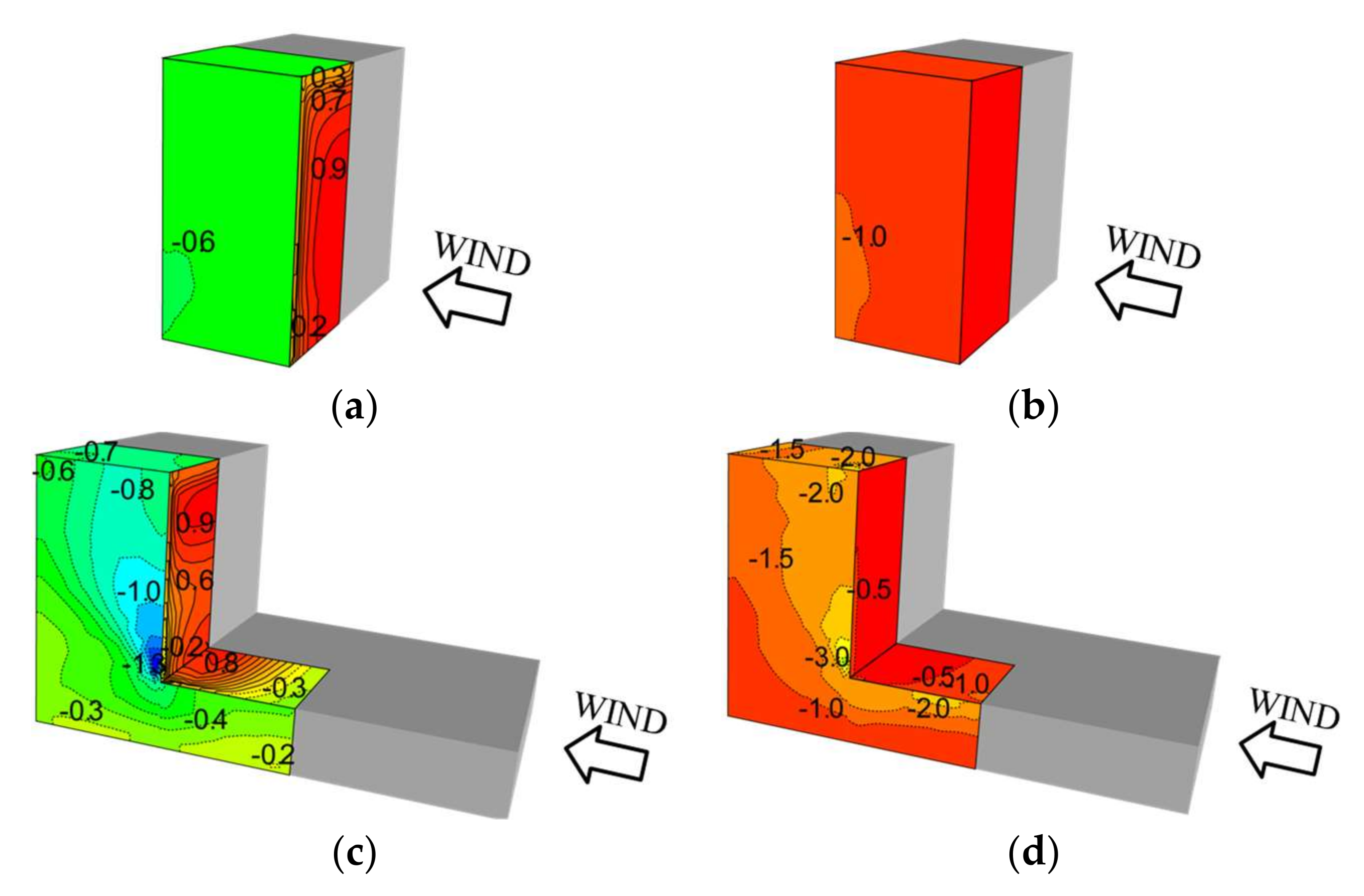
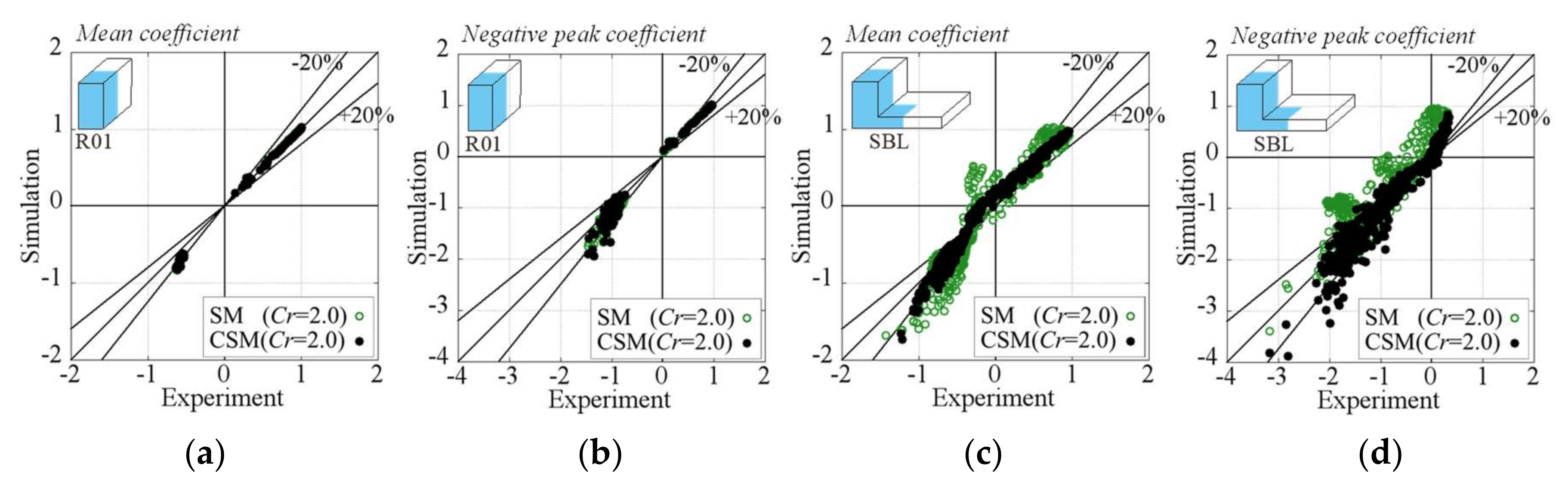
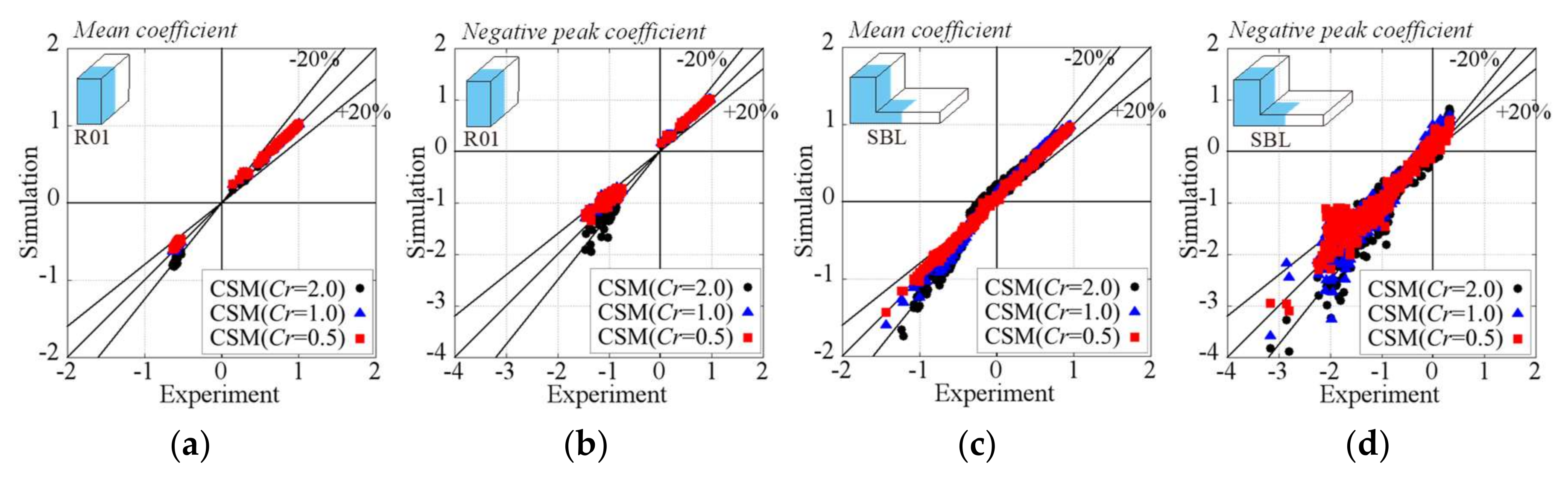
- For an isolated rectangular building in uniform flow, the flow field around the building is generated by the horseshoe vortex and separated flow. Both SM and CSM show good agreement with the PIV results in the flow separation region as well as in the horseshoe vortex regions. The wind pressure coefficients calculated using both SM and CSM consistently agree with the experimental results (values within 20%).
- For an isolated building with a setback in uniform flow, a complex flow field is generated by a distinctive large horseshoe vortex interfering with the separated flow from the lower roof. A large negative pressure coefficient is found at the corner of the sidewall, near the interfered-with area. Although using the SM results in under-prediction, the predictions made using the CSM show good agreement with the PIV results for the flow field. This means that the CSM with the model parameter based on the coherent structure reflects the vortex behaviors and simulates well the complex flow fields due to the strong interference of the vorticities and flow separations. The CSM results also showed much better performance than the SM results for the wind pressure distribution on this building, being within 20% of the experimental results.
- For a high-rise building in an actual urban city with a turbulent boundary layer flow, we found that a strong three-dimensional complex wind flow occurs due to the strong influence of neighboring buildings, including interference of vortices and separated flows. We also found a distinctive wind pressure distribution that had strong positive and negative pressures simultaneously occurring on the front wall of the target building. The CSM also gives more accurate results with less variation than the SM, being within 20% of experimental results. In addition, LES with the CSM was conducted for all wind directions. The calculated largest positive and negative peak pressure coefficients were consistently in good agreement with experimental results (within 20%) in the relatively high-pressure region, at least similar to or less than the COVs of the wind tunnel test results [20].
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Smagorinsky, J. General circulation experiments with the primitive equations I, The basic experiment. Mon. Weather Rev. 1963, 91, 99–164. [Google Scholar] [CrossRef]
- Germano, M.; Piomelli, U.; Moin, P.; Cabot, W.H. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids 1991, 3, 1760–1765. [Google Scholar] [CrossRef]
- Ghosal, S.; Lund, T.S.; Moin, P.; Akselvoll, K. A dynamic localization model for large-eddy simulation of turbulent flows. J. Fluid Mech. 1995, 286, 229–255. [Google Scholar] [CrossRef]
- Meneveau, C.; Lund, T.S.; Cabot, W.H. A lagrangian dynamic subgrid-scale model of turbulence. J. Fluid Mech. 1996, 319, 353–385. [Google Scholar] [CrossRef]
- Murakami, S. Current status and future trends in computational wind engineering. J. Wind Eng. Ind. Aerodyn. 1997, 67–68, 3–34. [Google Scholar] [CrossRef]
- Yoshizawa, A.; Kobayashi, K.; Kobayashi, T.; Taniguchi, N. A nonequilibrium fixed-parameter subgrid-scale model obeying the near-wall asymptotic constraint. Phys. Fluids 2000, 12, 2338–2344. [Google Scholar] [CrossRef]
- Vreman, A.W. An eddy-viscosity subgrid-scale model for turbulent shear flow: Algebraic theory and applications. Phys. Fluids 2004, 16, 3670–3681. [Google Scholar] [CrossRef]
- Park, N.; Lee, S.; Lee, J.; Choi, H. A dynamic subgrid-scale eddy viscosity model with a global model coefficient. Phys. Fluids 2006, 18, 125109. [Google Scholar] [CrossRef]
- Kobayashi, H. The subgrid-scale models based on coherent structures for rotating homogeneous turbulence and turbulent channel flow. Phys. Fluids 2005, 17, 045104. [Google Scholar] [CrossRef]
- Kobayashi, H. Large eddy simulation of magnetohydrodynamic turbulent channel flows with local subgrid-scale model based on coherent structures. Phys. Fluids 2006, 18, 045107. [Google Scholar] [CrossRef]
- Kobayashi, H. Large eddy simulation of magnetohydrodynamic turbulent duct flows turbulent duct flows. Phys. Fluids 2008, 20, 015102. [Google Scholar] [CrossRef]
- Kobayashi, H.; Ham, F.; Wu, X. Application of a local SGS model based on coherent structures to complex geometries. Int. J. Heat Fluid Flow 2008, 29, 640–653. [Google Scholar] [CrossRef]
- Onodera, N.; Aoki, T.; Shimokawabe, T.; Kobayashi, H. Large-scale LES Wind Simulation using Lattice Boltzmann Method for a 10 km × 10 km Area in Metropolitan Tokyo. Tsubame ESJ 2013, 9, 2–8. [Google Scholar]
- Melbourne, W.H. Turbulence and the leading edge phenomenon. J. Wind Eng. Ind. Aerodyn. 1993, 49, 45–63. [Google Scholar] [CrossRef]
- Okuda, Y.; Taniike, Y. Conical vortices over side face of a three dimensional square prism. J. Wind Eng. Ind. Aerodyn. 1993, 50, 163–172. [Google Scholar] [CrossRef]
- Kawai, H. Local peak pressure and conical vortex on building. J. Wind Eng. Ind. Aerodyn. 2002, 90, 251–263. [Google Scholar] [CrossRef]
- Tominaga, Y.; Mochida, A.; Yoshie, R.; Kataoka, H.; Nozu, T.; Yoshikawa, M.; Shirasawa, T. AIJ guidelines for practical applications of CFD to pedestrian wind environment around buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1749–1761. [Google Scholar] [CrossRef]
- Tamura, T.; Miyagi, T.; Kitagishi, T. Numerical prediction of unsteady pressures on a square cylinder with various corner shapes. J. Wind Eng. Ind. Aerodyn. 1998, 74–76, 531–542. [Google Scholar] [CrossRef]
- Tamura, T.; Nozawa, K.; Kondo, K. AIJ guide for numerical prediction of wind loads on buildings. J. Wind Eng. Ind. Aerodyn. 2008, 96, 1974–1984. [Google Scholar] [CrossRef]
- Tamura, Y.; Phuc, P.V. Development of CFD and applications: Monologue by a non-CFD-expert. J. Wind Eng. Ind. Aerodyn. 2015, 144, 3–13. [Google Scholar] [CrossRef]
- Yoshikawa, M. Wind load for cladding. In Material of Panel Discussion of Steering Committee for Loads on Buildings at Annual Meeting of AIJ in Tokai; Architectural Institute of Japan: Nagoya, Japan, 2012; pp. 21–24. (In Japanese) [Google Scholar]
- Nozu, T.; Tamura, T.; Takeshi, K.; Akira, K. Mesh-adaptive LES for wind load estimation of a high-rise building in a city. J. Wind Eng. Ind. Aerodyn. 2015, 144, 62–69. [Google Scholar] [CrossRef]
- Architectural Institute of Japan. Guidebook of Recommendations for Loads on Buildings 2; Wind-Induce Response and Load Estimation/Practical Guide of CFD for Wind Resistant Design; Architectural Institute of Japan: Tokyo, Japan, 2017; pp. 381–434. (In Japanese) [Google Scholar]
- OpenFOAM. User Guide. Available online: https://www.openfoam.com/documentation/user-guide/ (accessed on 22 January 2018).
- Rafei, M.E.; Könözsy, L.; Rana, Z. Investigation of Numerical Dissipation in Classical and Implicit Large Eddy Simulations. Aerospace 2017, 4, 59. [Google Scholar] [CrossRef]
- Phuc, V.P.; Nozu, T.; Kikuchi, H.; Hibi, K.; Tamura, Y. Wind pressure distributions on a high-rise building in the actual urban area using Coherent-structure Smagorinsky model for LES. In Proceedings of the 24th National Symposium on Wind Engineering, Tokyo, Japan, 6 December 2016; pp. 241–246. (In Japanese). [Google Scholar]
- Architectural Institute of Japan. Recommendations for Loads on Buildings; Architectural Institute of Japan: Tokyo, Japan, 2015. [Google Scholar]

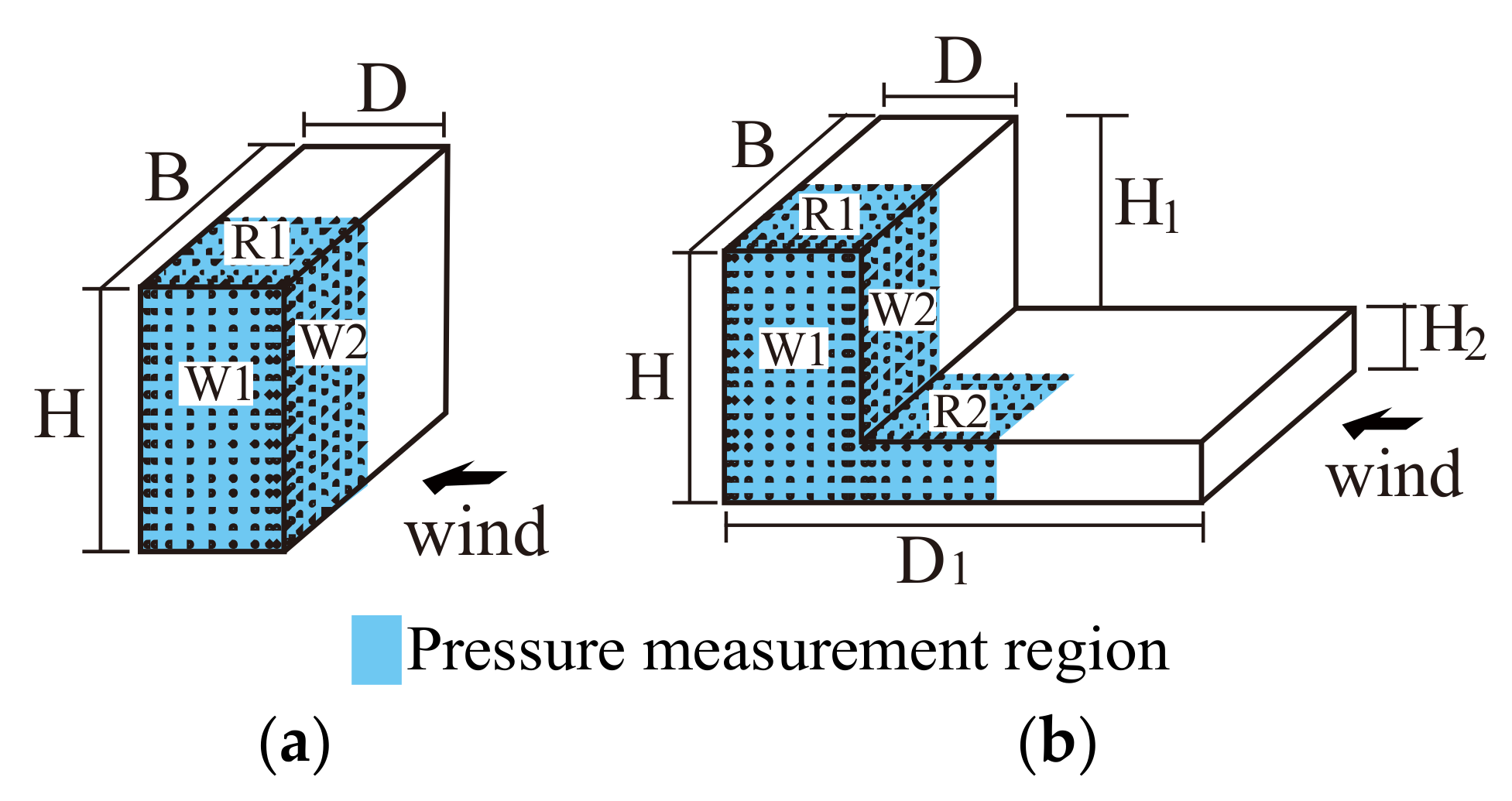
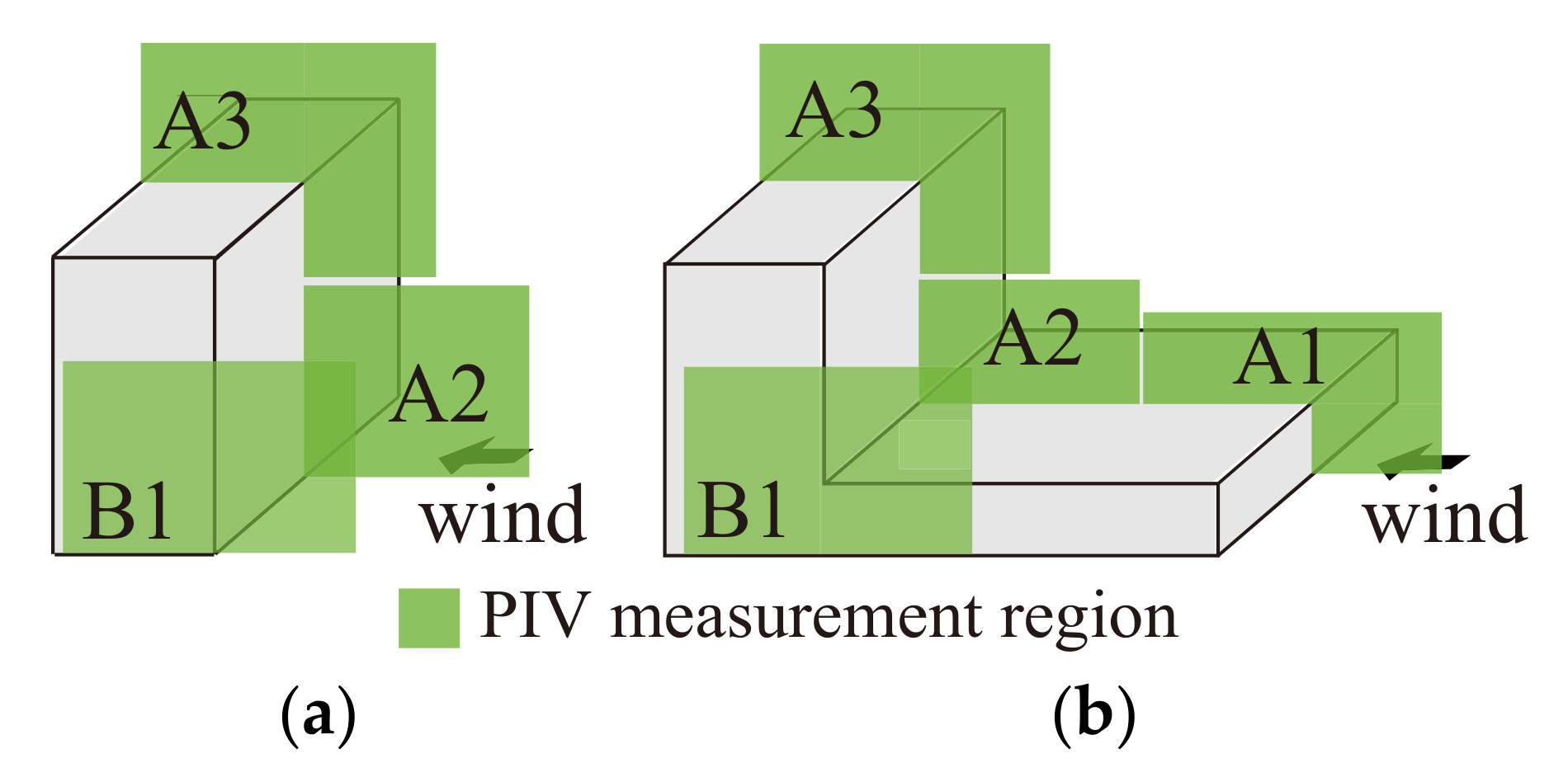
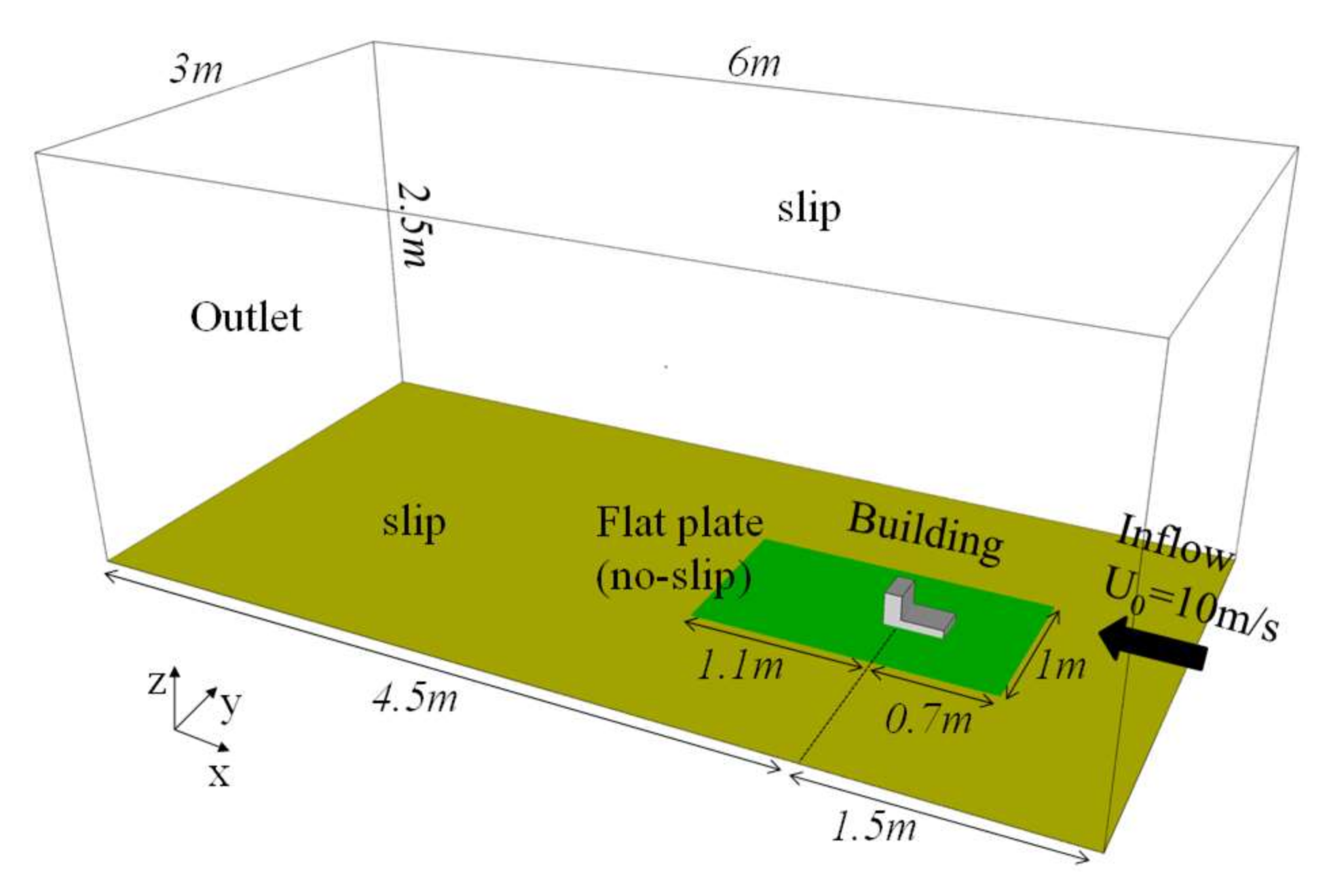



| Type | B | D | H | H1 | H2 | D1 |
|---|---|---|---|---|---|---|
| R01 | 0.20 | 0.10 | 0.20 | |||
| SBL | 0.20 | 0.10 | 0.20 | 0.15 | 0.05 | 0.35 |
| Subgrid-Scale (SGS) Model | Smagorinsky Model (SM) | Coherent Structure Smagorinsky Model (CSM) |
|---|---|---|
| Mesh cells (millions) | 570 | 570 |
| Time increment Δt (s) | 10−4 | 10−4, 5 × 10−5, 2.5 × 10−5 |
| Courant number Cr | 2.0 | 2.0, 1.0, 0.5 |
| Initial run-up time (s) | 3 | 3 |
| Evaluation time (s) | 8 | 8 |
| Number of parallel CPUs | 6144 | 6144 |
| SGS Model Use in Large Eddy Simulation (LES) | SM | CSM | CSM |
|---|---|---|---|
| Mesh type | A | A | B |
| Mesh cells (millions) | 140 | 140 | 1100 |
| Wind direction θ (degree) | 60 | 60 (0, .., 350) | 60 |
| Time increment Δt (s) | 2.5 × 10−5 | 2.5 × 10−5 | 1.25 × 10−5 |
| Courant number Cr | 1 | 1 | 1 |
| Initial run-up time (s) | 3 | 3 | 3 |
| Evaluation time (s) | 18 | 30 (6) | 6 |
| Number of samples in ten-minute record in real-time conversion for evaluation | 3 | 5 (1) | 1 |
| Number of parallel CPUs | 768 | 768 | 6144 |
| Computational time for one sample (days) | 40 | 20 | 20 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phuc, P.V.; Nozu, T.; Kikuchi, H.; Hibi, K.; Tamura, Y. Wind Pressure Distributions on Buildings Using the Coherent Structure Smagorinsky Model for LES. Computation 2018, 6, 32. https://doi.org/10.3390/computation6020032
Phuc PV, Nozu T, Kikuchi H, Hibi K, Tamura Y. Wind Pressure Distributions on Buildings Using the Coherent Structure Smagorinsky Model for LES. Computation. 2018; 6(2):32. https://doi.org/10.3390/computation6020032
Chicago/Turabian StylePhuc, Pham Van, Tsuyoshi Nozu, Hirotoshi Kikuchi, Kazuki Hibi, and Yukio Tamura. 2018. "Wind Pressure Distributions on Buildings Using the Coherent Structure Smagorinsky Model for LES" Computation 6, no. 2: 32. https://doi.org/10.3390/computation6020032
APA StylePhuc, P. V., Nozu, T., Kikuchi, H., Hibi, K., & Tamura, Y. (2018). Wind Pressure Distributions on Buildings Using the Coherent Structure Smagorinsky Model for LES. Computation, 6(2), 32. https://doi.org/10.3390/computation6020032





