1. Introduction
Non-covalent interactions, especially of the van der Waals type, have been nowadays recognized as fundamental ingredients of any correct and accurate description of complex materials [
1,
2,
3,
4,
5,
6,
7,
8,
9]. In fact, even if the magnitude of non-covalent forces is typically much smaller than that of iono-covalent bonds, the ubiquity of such interactions makes them significant in large systems. Moreover, for non-polar complexes and/or at large intermolecular distances, where covalent interactions are negligible, they play a dominant role. For these reasons, the proper description of dispersion as well as other non-covalent forces has gained a prominent role in computational chemistry [
6,
10,
11,
12,
13,
14,
15,
16]. Even more important is the role they play in solid-state applications where extended systems are involved, whose cohesion is not mainly determined by iono-covalent interactions [
3,
5,
8,
9,
17,
18,
19,
20,
21], e.g., layered or molecular solids.
One of the most popular computational approaches used in solid-state calculations is Kohn–Sham (KS) density functional theory (DFT) [
22]. In this context, in fact, unlike for chemical applications, Hartree–Fock based, perturbative, and high-level correlated methods show often an excessive computational cost. On the other hand, using DFT, even rather simple semilocal approximations of the exchange-correlation (XC) functional [
23,
24], such as generalized gradient approximation (GGA) functionals, work fairly well allowing for an efficient description of many solid-state systems [
24,
25,
26,
27,
28,
29]. Nevertheless, one main drawback of semilocal DFT is the poor description of van der Waals interactions [
30,
31,
32]. Thus, to be able to apply it to a wide range of solid-state problems (including e.g., layered materials, organic crystals, molecular absorption on surfaces) it is necessary to correct this limitation of the DFT methods, without losing the computational efficiency.
Over the years, several different strategies have been developed to realize “dispersion corrections” for DFT methods [
2,
33,
34,
35,
36,
37,
38,
39,
40,
41,
42,
43,
44,
45,
46]. In the solid-state context, one of the most popular of such strategies is to complement the semilocal functional with a non-local correlation term [
19,
20,
47,
48,
49]. This has the advantage of yielding a true density functional approach (unlike for some of the pairwise dispersion corrections [
37,
40]), gives a realistic XC hole model [
50], which improves over the semilocal XC hole [
51], and, under periodic boundary conditions, it can be implemented in a relatively efficient way. The first non-local functional was derived within the adiabatic-coupling fluctuation-dissipation formalism, using a simplified treatment of the electronic polarizability [
50]. Since then, several simplifications and improvements have been proposed to simplify and optimize the functional [
44,
45,
48,
52,
53,
54]. One of the most popular, for solid-state applications, is the revised VV10 (rVV10) non-local functional [
54].
Recently, a properly reparameterized rVV10 functional has been coupled to several semilocal XC functionals. Very promising results have been found at the meta-GGA level of theory, e.g., considering the SCAN + rVV10 functional [
55]. However, meta-GGA calculations on extended systems (with periodic boundary conditions) are still not routine. On the other hand, relatively good results can be obtained, with a reduced computational effort, using rVV10 in combination with GGAs. Recently, in particular, a reparameterization of rVV10 has been coupled to the Perdew–Burke–Ernzerhof (PBE) GGA functional [
56] to yield the PBE + rVV10L functional [
57]. This approach has been shown to be quite successful for the description of layered materials, suggesting that well-designed dispersion-corrected GGA functionals can indeed be important tools for general solid-state applications, joining efficiency and accuracy. However, in the case of PBE + rVV10L, the good performance for layered materials is not paired by a similar good performance for standard iono-covalent solids because of the intrinsic limitations of the PBE functional in these cases [
58,
59]. Thus, the method cannot be considered for broad use in solid-state calculations.
To overcome this limitation, we consider a slightly different strategy and we look at coupling a reparameterized rVV10 functional to the recently developed SG4 functional [
26], derived in the context of the semiclassical atom theory. The SG4 functional performs remarkably well for iono-covalent bulk solids [
26,
27], yielding accurate equilibrium lattice constants, bulk moduli, cohesive, surface, and monovacancy energies. On the other hand, unlike some other good-performing functionals for solids [
58,
60,
61,
62], it yields an important underestimation of the interaction energy in various van der Waals dominated solids (see, e.g., Tables III and IV of Reference [
27]). Therefore, it appears to be a good choice to construct a dispersion-corrected DFT method, with the aim of obtaining an accurate, broadly applicable, and efficient computational tool for the solid-state framework.
In this work, we carry on this plan and we construct the SG4 + rVV10m functional, using a reparameterized rVV10m functional to complement the SG4 GGA. Hence, we show that this method is indeed generally able to describe with good accuracy the cohesive and structural properties of a broad range of solid-state systems, ranging from bulk insulators to layered materials and molecular crystals. However, our assessment also highlights a few cases where the SG4 + rVV10m functional shows a limited accuracy, whereas the bare SG4 functional works better. A density analysis is then used to characterize these cases and rationalize the performance of the two functionals.
2. Method and Computational Details
To combine the SG4 GGA with the rVV10m non-local functional, we needed to fit the two free parameters of the latter (i.e.,
b and
C, controlling the damping and the long-range functional behavior respectively; see Reference [
54]). To perform this task, we have considered the lattice constants and cohesive energies of two possible training sets: NOB4, i.e., bulk crystals of noble-gas atoms (Ne, Ar, Kr, Xe) and ALK5, i.e., bulk crystals of five alkali metals (Li, Na, K, Rb, Cs). As reference lattice constants, we have used the zero-point anharmonic expansion corrected values reported in References [
63,
64,
65]. The choice of the NOB4 as a training set is rather obvious as this is one of the most classical collections of dispersion-dominated bulk materials. On the other hand, this choice may lead to an over-consideration of dispersion interactions; then, pure dispersion-dominated materials might be favored too much at the expense of other materials (e.g., layered materials or even iono-covalent solids). Thus, the selection of ALK5 as a second possible training set was motivated by fact that this set, despite the fact that it includes only five free-electron metals of the same group, provides a collection of systems characterized by different magnitudes of dispersion effects (the heavy alkali metals (Rb, Cs) contain long-range dispersion effects, whereas the light alkali metals (Li, Na, K) show less or no dispersion effects [
66]). Thus, it constitutes a minimal training set of rather broad representativity as concerns the dispersion.
As a result of the fitting, we have obtained
for the NOB4 case and
for ALK5. In both cases, the parameter
C turned out to have the value
that was our cut-off for low-values. Note that such a low value of
C implies some overestimation of the asymptotic atomic
coefficients, but this appears not to be a big issue for solid-state problems; indeed, our value is in line with the one found for the AM05-VV10sol functional [
19], also fitted to solid-state references.
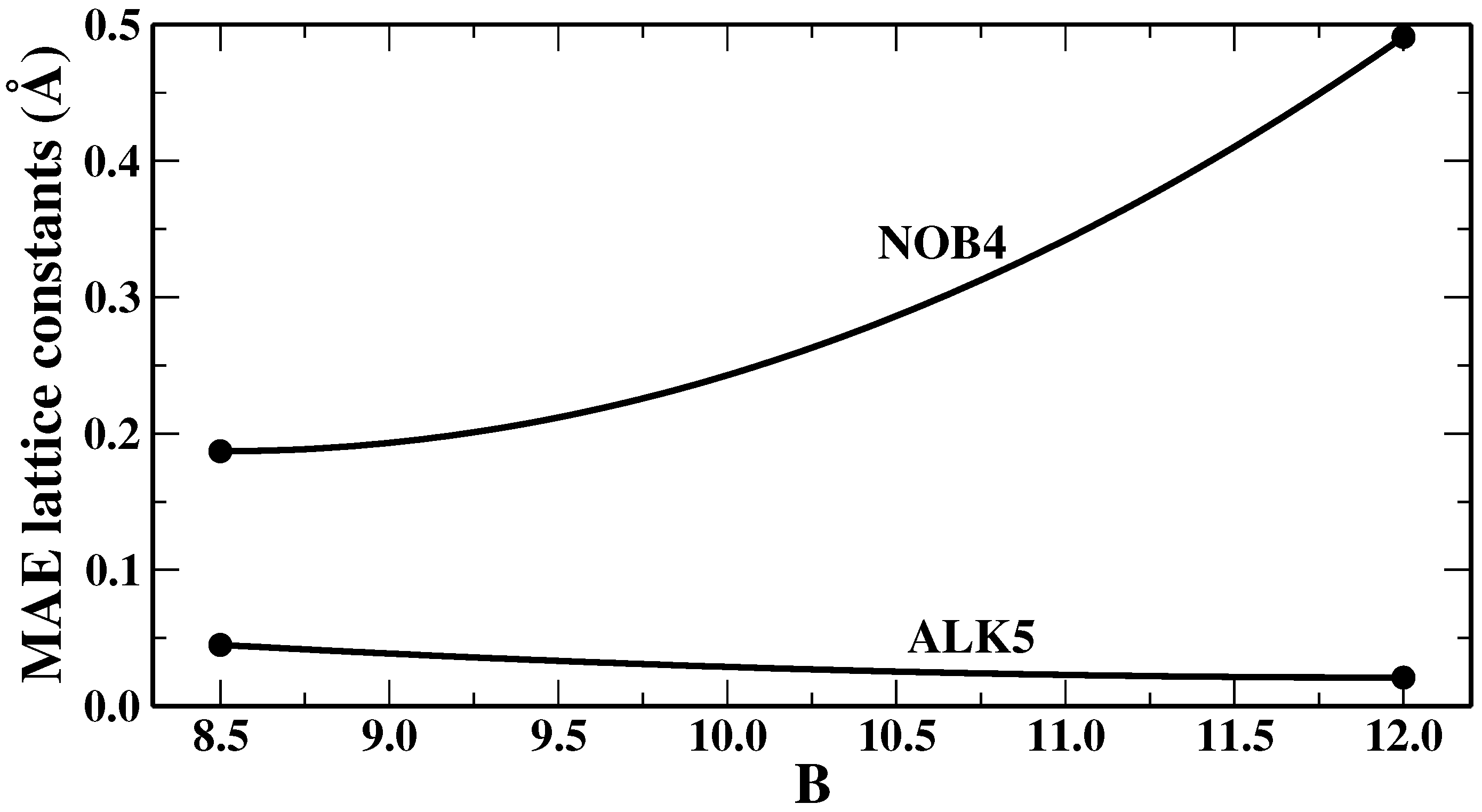
We remark that, as in any fitting, the values that we found for the parameters represent only a best compromise for the lattice constants of the NOB4 or ALK5 training sets (although we will show in the next section that this “good compromise” also holds quite well in general), whereas various properties of different systems can be improved by specific ad hoc choices of the parameters. This depends on the fact that different systems or properties require in general different amounts of non-local correlation to correct the description provided by the semilocal functional. This is shown, for example, in
Figure 1, where we report the mean absolute errors, obtained from SG4 + rVV10m as functions of the value of the parameter
b in the rVV10m non-local term, for the lattice constants of the two training sets we have employed, i.e., NOB4 and ALK5. It can be seen that the two sets display an opposite behavior. Therefore, ALK5 systems are slightly overbound when
while NOB4 materials are underbound using
. Hence, no absolute best value can be identified for the
b parameter. This shows that, in general, obtaining a uniformly good performance is a very hard task.
To test the functional, we have considered a set of layered materials (Graphite, h-BN, MoS
, MoTe
, VS
, VSe
, PdTe
, WS
, NbTe
, and NbSe
; reference data were obtained from References [
20,
21]), and a set of molecular crystals (ammonia and urea [hydrogen-bond], CO
, naphthalene, and pyrazine [van der Waals]; reference data were obtained from Refences [
67,
68,
69,
70,
71]). In addition, we have considered a set of iono-covalent bulk materials (named SET27) including subsets of different characters. In more detail: Al, Ca, K, Li, Na, Sr, Ba (simple metals); Ag, Cu, Pd, Rh , Pt (transition metals); GaAs, GaP, GaN, Si, SiC, Ge (semiconductors); LiCl, LiF, MgO, NaCl, NaF (ionic solids); AlN, BN, BP, C (insulators). Reference data were taken from References [
64,
72,
73,
74,
75]. Finally, we have performed some calculations on the S22 test set [
76,
77], in order to verify the performance on non-covalent molecular complexes.
The S22 calculations have been performed using a local version of the TURBOMOLE program package (V7.0, TURBOMOLE GmbH, Karlsruhe, Germany) [
78,
79] and a def2-TZVPP basis set [
80,
81]. All solid-state calculations have been carried out with a locally modified version of the Quantum Espresso program package (V6.0, Quantum Espresso Foundation, Cambridge, UK) [
82], implementing the SG4functional and the modified rVV10m parameters. An energy cutoff 140 Ry was used for molecular crystals while it was fixed to 120 Ry for all other materials. The following values have been considered for the Monkhorst–Pack
k-point meshes: for SET27 and ALK5 16 × 16 × 16, for Graphite and h-BN 16 × 16 × 8, for 2H-materials (MoS
, MoTe
, WS
, NbSe
) 8 × 8 × 4, for 1T-materials (VS
, VSe
, PdTe
, NbTe
) 8 × 8 × 6, for the molecular crystals of ammonia, urea, CO
, and naphthalene 8 × 8 × 8, for pyrazine 6 × 8 × 8. The bulk moduli have been computed applying the Murnaghan equation of state [
83]. For layered materials, the bulk modulus in the direction perpendicular to the layers has been considered. Interaction energies have been calculated as
where
is the energy of the unit cell of a bulk,
is the sum of the energies of the unit elements (molecule, atom, or monolayer) in the cell, and
n is number of the unit elements in the unit cell of the bulk. Cohesive energies are defined as the opposite of the interaction energies. The energies of the unit elements have been obtained placing them into large boxes, so that interactions between periodic replicas were negligible. In more detail, for SET27 and ALK5, atoms have been placed in a box with dimensions 13 × 14 × 15 Å; for layered materials, the monolayer calculations have been performed at fixed relaxed bulk geometry with vacuum space of about 33 Å for Graphite and h-BN, and 37 Å for all other materials; for the molecular crystals, the minimum distance between molecular unit elements has been set to about 14 Å. The atomic data sets required by projected augmented wave (PAW) calculations [
84] have been generated by the ATOMPAW code [
85], using the input files provided on the ABINIT program web site [
86]. The SG4 exchange and correlation functionals have been implemented in a local version of the libXC library [
87]. We recall that libXC can be linked to ATOMPAW.
3. Results
In this section, we show the results of our assessment of the SG4-rVV10m functional for different solid-state tests. For comparison, we also report the results of the PBE + rVV10L [
57] and rVV10 [
54] functionals, which are examples of state-of-the-art DFT approaches using an rVV10-like non local term for treating dispersion in the solid-state framework.
To start our survey of the results, we report in
Table 1 the lattice constants, bulk moduli, and cohesive energies computed for the NOB4 test set with different functionals.
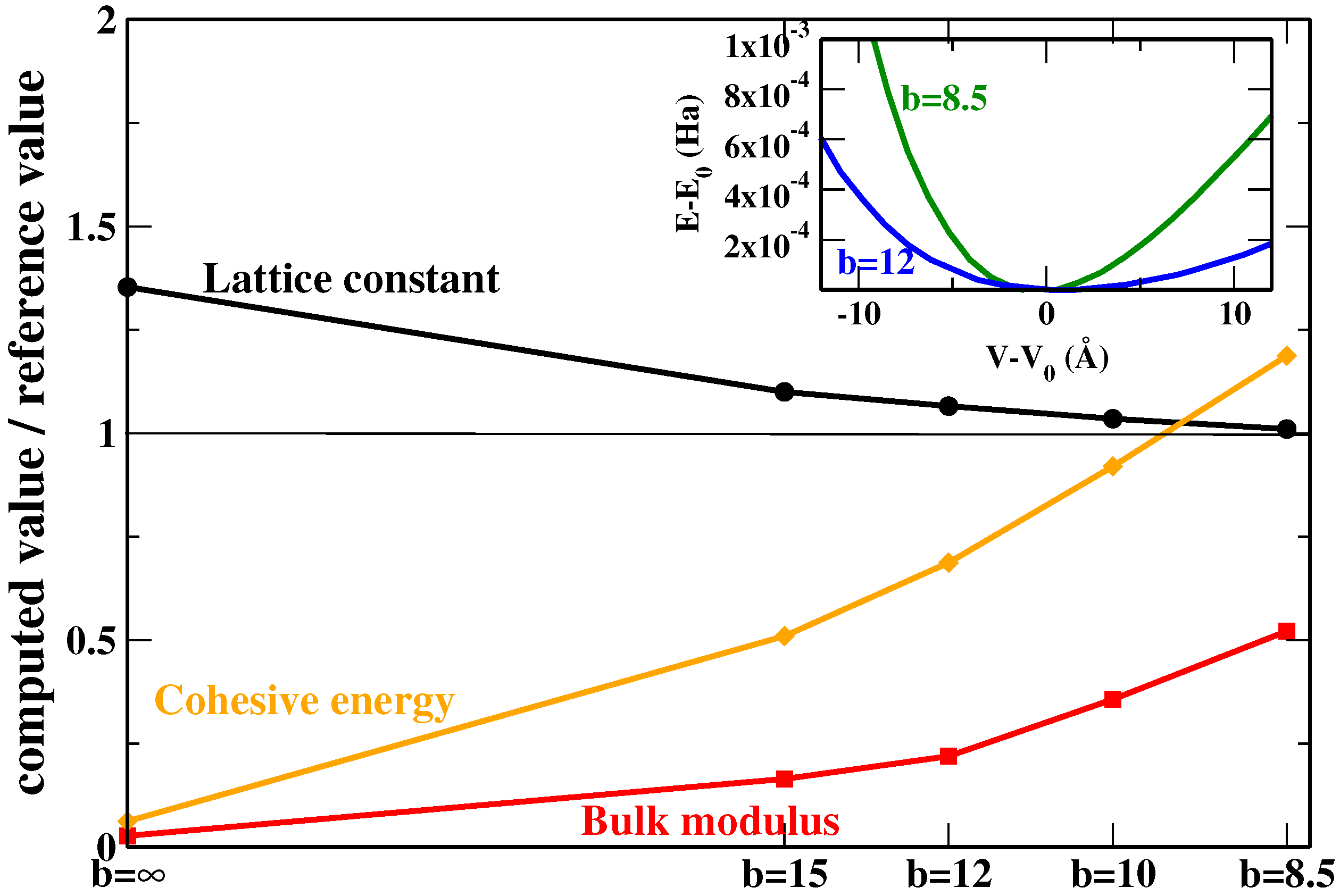
We see that, of course, the inclusion of non-local rVV10m corrections helps to highly improve with respect to the original SG4 results, especially for lattice constants where SG4 yields a strong overestimation (even with respect to other GGAs; for example, the mean absolute error (MAE) of PBE in this case is 0.674 Å), while a more contained improvement is observed for bulk moduli and interaction energies. Concerning the differences between the two parameterizations of SG4-rVV10m, the use of
, which has been fitted to this set, provides a small improvement but not a very relevant one. This traces back to the fact that by reducing the value of the parameter
b (hence, increasing the dispersion correction), the change in the interaction energies is faster than for the lattice constants while, at the same time, the latter is faster than the change in the bulk modulus (see
Figure 2 where the Xe case is reported as an example; in the inset, we have reported the energy vs. volume curves for two values of
b in order to show how the bulk modulus increases by increasing the amount of dispersion correction).
Thus, it is not possible to find a value of the parameter that yields at the same time very accurate lattice constants and interaction energies. Instead, our optimal value, , yields a small underestimation of lattice constants and a small overestimation of interaction energies. On the other hand, the use of , derived from the ALK5 fitting, gives an overestimation of the lattice constants but only a small underestimation of interaction energies (except for Ne). Thus, finally the overall performance is not much worse than with the optimized parameter.
The situation is somehow different considering the ALK5 set, whose results are reported in
Table 2.
In this case, in fact, the use of always gives an overestimation of the dispersion, while a good description of all properties can be achieved by fitting (which gives ), although all materials are predicted to be slightly softer than they should be (bulk moduli are slightly underestimated). This behavior can be traced back to the fact that the bare SG4, even if it is always underestimating the interaction strength, already describes relatively well the lattice constants of ALK5 (e.g., better than PBE, which has a MAE of 0.065 Å), and thus only a relatively small dispersion correction is needed. As a consequence, the SG4-rVV10m functional (using ) is competitive with the other state-of-the-art approaches for the description the ALK5 materials.
Another important class of solid-state materials characterized by dispersion interactions is that of layered materials. The results for a selection of these are reported in
Table 3.
Inspection of the data shows that the bare SG4 functional does not perform very well for these systems (compare the MAEs for inter- and intra-layer lattice constants to those of PBE which are 1.417 Å and 0.034 Å, respectively). Thus, a consistent improvement can be expected after applying a dispersion correction. However, using
, the SG4-rVV10m functional gives a non-negligible overestimation of the dispersion interaction, leading to underestimated lattice constants and overestimated interaction energies. On the opposite, for
, it performs overall well for the layered materials, being the best method for lattice constants (both interlayer and intralayer ones) and being competitive with rVV10 and PBE + rVV10L for bulk moduli and cohesive energies (note that PBE + rVV10L has been fitted to layered materials [
57]). Note, however, that on these latter properties a proper quantitative comparison is not possible since the reference values are not experimental results but are obtained from different computational methods whose accuracy cannot be verified exactly.
Despite this good performance, we must note that there are also a few cases where the SG4-rVV10m functional does not yield accurate results and instead bare SG4 results are better (MoTe, PdTe, NbSe). In these cases, in fact, the SG4 functional is already describing quite well the lattice constants (even slightly underestimating them) and does not give too much pronounced underestimation of the interaction energy. Thus, when the rVV10m correction is plugged in, the results are not improved. This drawback is clearly related to the fact that, unlike in most of the other cases, for these particular systems, the SG4 functional already includes a significant amount of dispersion interaction. Thus, the addition of rVV10m results in a sort of double counting of this effects. The reason for this behavior of the SG4 functional is discussed in the next section.
As a further test, we consider, in
Table 4, the lattice constants and interaction energies of some molecular crystals. These are in fact important systems for materials science but also difficult cases for conventional DFT approaches due to the relevant role of dispersion in determining the intermolecular interactions and the crystal packing [
8,
18,
88].
Also in this case, the SG4-rVV10m functional, with , gives a significant improvement over SG4 and is overall competitive with other dispersion-corrected DFT methods. In particular, it yields the best performance for interaction energies and a similar mean absolute error as rVV10 for lattice constants (note that, however, the rVV10 mean absolute error for interaction energies is more than twice as large as the SG4-rVV10m one). When the NOB4 parameterization () is considered, a slight but not systematic improvement with respect to the ALK5 parameterization () can be obtained for lattice constants. However, interaction energies are generally overestimated (in absolute value).
To conclude our assessment, we consider in
Table 5 the mean absolute errors for the lattice constants, bulk moduli, and cohesive energies of several classes of iono-covalent bulk solids (simple metals, transition metals, semiconductors, ionic crystals, and insulators). These systems are not dominated by dispersion effects and they are well described by the original SG4 functional [
26,
27]. Nevertheless, it is important to check that the addition of the rVV10m correction is not worsening this accuracy for these materials, in order to verify the broad applicability of the method.
Inspection of the table shows that indeed the SG4-rVV10m functional performs quite similarly to the parent SG4 functional (except for cohesive energies; see below). This happens especially for the parameterization using
, while using the value
derived from the fitting to the NOB4 training set, the dispersion correction is stronger and thus the results are slightly more different from the SG4 ones. In more details, we see that the rVV10m correction has little impact on the lattice constants of transition metals, semiconductors, and insulators, whereas it produces a small worsening for simple metals and a slight improvement for ionic crystals. Hence, the overall mean absolute error is comparable to the SG4 one and clearly smaller than for PBE + VV10L and rVV10. For the bulk moduli, the effect of the addition of the rVV10m correction is even more positive, since only the transition metals results are somehow worsened while improvements are observed in all other cases. Thus, for this property, the SG4-rVV10m functional performs definitely better than PBE+VV10L and rVV10 and even slightly better than the SG4 functional itself. An opposite behavior is found instead concerning the cohesive energies. In this case, the SG4 functional is already generally slightly overestimating the correct energy, thus the addition of the rVV10m correction leads to a worsening of the results. The only exception is for ionic crystals, where a clear improvement is observed. Consequently, the SG4-rVV10m performance is worse than for the parent SG4 and than both PBE+VV10L and rVV10. We remark, anyway, that the overall mean absolute error on cohesive energies of the SG4-rVV10m functional using
is similar to that of other popular solid-state XC functionals such as PBEsol [
26].
4. Discussion
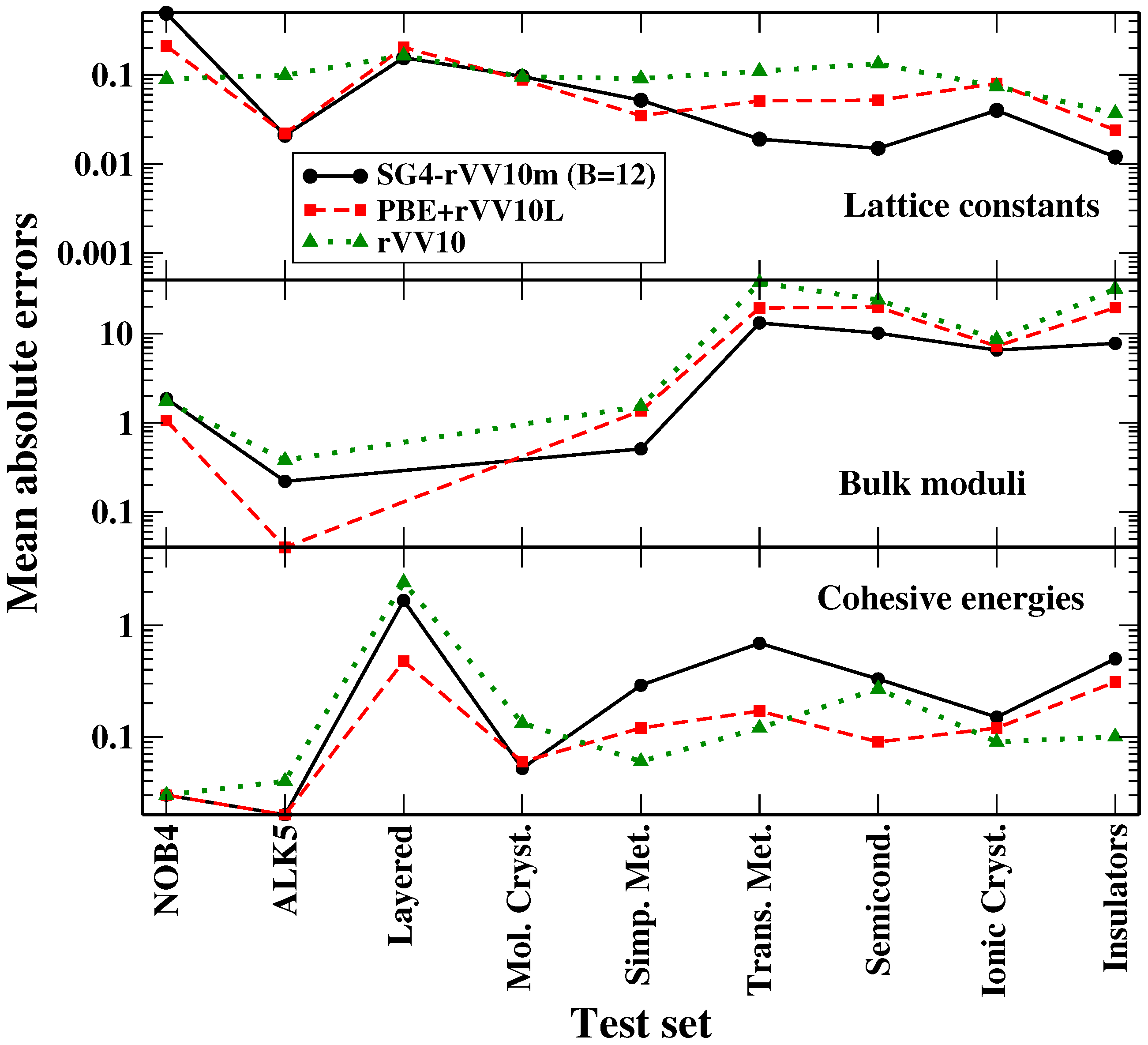
In the previous section, we have discussed the assessment of the SG4-rVV10m functional for different problems in solid-state physics. In
Figure 3, we summarize these results to obtain an overall picture of the performance of the functional.
One can see that, for lattice constants and bulk moduli, the SG4-rVV10m functional (with
) is competitive with the PBE + VV10L and rVV10 methods for all the dispersion tests (NOB4, ALK5, layered materials, molecular crystals) and better than the latter for iono-covalent solids. When cohesive or interaction energies are considered, SG4-rVV10m yields a good performance for dispersion tests, being almost comparable to PBE + rVV10L and better than rVV10, but shows some limitations for iono-covalent systems, in particular for transition metals (that are anyway a known difficult case for DFT [
75]). As mentioned, the accuracy for these latter cases is anyway in line with that of other popular approaches for iono-covalent solids and it is thus not preventing the application of the functional in these situations (even though, if only these kinds of systems and properties are considered, other functionals may be a better choice). Thus, we can conclude that the SG4-rVV10m functional displays a broad applicability for solid-state simulations, being able to yield reasonably accurate results for a large palette of systems and properties.
Hence, we saw that the SG4-rVV10m functional is generally performing well for the description of dispersion in different solid-state systems. This depends on the fact that in most cases the original SG4 functional is not including dispersion contributions, thus the addition of a dispersion correction via the rVV10m non-local term is correctly patching the XC contribution. In this way, the systematic underbinding of dispersion-dominated systems can be corrected and, within some limits due to the parameterization, accurate results can be achieved. Nonetheless, we have also observed that in some cases (e.g., MoTe) the SG4 functional is not displaying any underbinding. Consequently, the SG4-rVV10m functional provides quite underestimated lattice constants and overestimated interaction energies. The origin of this peculiar behavior for some systems can be understood considering the gradient contributions of the particular system and the features of the SG4 functional form.
Before doing this, however, to put the whole discussion into the right perspective, we need to shortly discuss the common underestimation of the dispersion interaction by GGA functionals. We recall that this is not only an important practical feature, which allows the functional to be more easily compatible with a van der Waals corrections [
89], but also an important theoretical result. In fact, in principle, all GGA functionals should not describe dispersion interactions, especially the long-range ones. Nevertheless, in practice, all of them partially include (short range) dispersion forces via an error compensation effect. This effect is related to the shape of the XC enhancement factor, which is defined as
where
is the XC energy per particle of the given functional,
is the exchange energy per particle of the spin-unpolarized uniform electron gas,
,
, and
is the spin polarization. It is found that GGA functionals, which have smaller values of the enhancement factor at large values of the reduced gradient
s, generally favor an overestimation of interaction energy in low density regions. This traces back to the fact that the dispersion bonds occur in regions of small density, which are characterized by a relatively large value of the reduced gradient
s, we can denote this value with
, but at the bond the reduced gradient is zero. Hence, the XC contribution to the interaction energy due to the dispersion is approximately proportional to
. This implies that the more
is larger than
the more non-bonding is the XC contribution to the interaction energy (a positive contribution is added to the negative interaction energy). In fact, some semilocal functionals obtain a fairly good description of dispersion interaction via a de-enhancement at large reduced gradient values [
90,
91,
92].
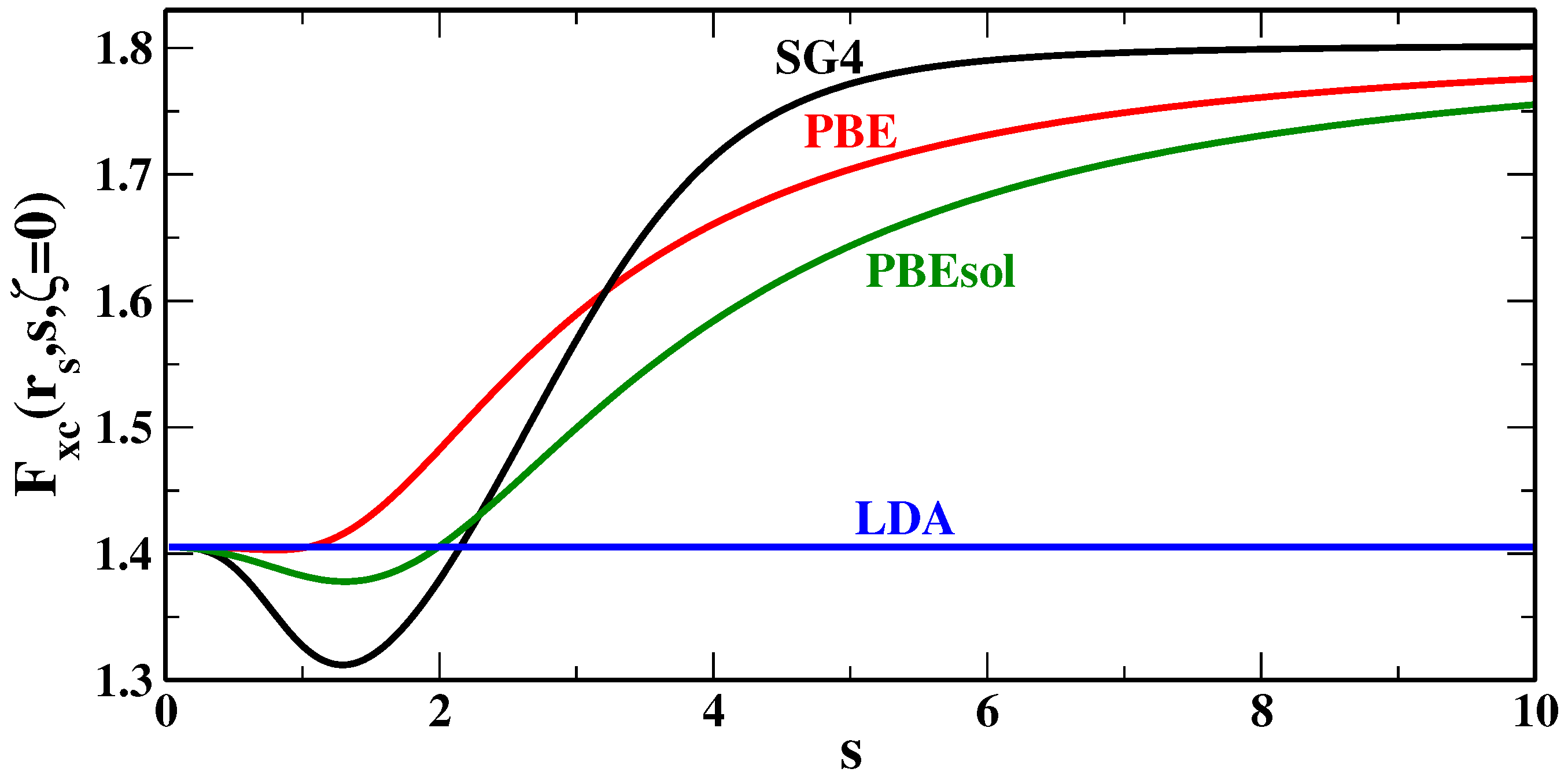
Figure 4 reports the XC enhancement factors of several GGA functionals, for the spin-unpolarized case (
) and the bulk parameter
, which corresponds to a small density case, often found in van der Waals bonding regions. Looking at the plots, we see that, for
, the SG4 functional has indeed a larger enhancement factor than other functionals, especially if we compare it to functionals of common use in solid state (e.g., PBEsol [
58]).
Thus, we can infer that, in most cases (i.e., those where
), SG4 can be expected to give smaller dispersion interaction energies with respect to other GGAs (e.g., PBE [
56], and PBEsol [
58]). Evidence for this fact can be found in the previous section, and it is especially perceptible considering the S22 test [
76,
77] reported in
Table 6. In fact, for molecular systems, due to the exponential decay of the density in the tail, the dispersion bond concerns regions with especially large values
of the reduced gradient. On the other hand, in some solids, the value of
may be relatively small because the electron density diminishes only slowly in the interstitial regions. This is the case, for example, of MoTe
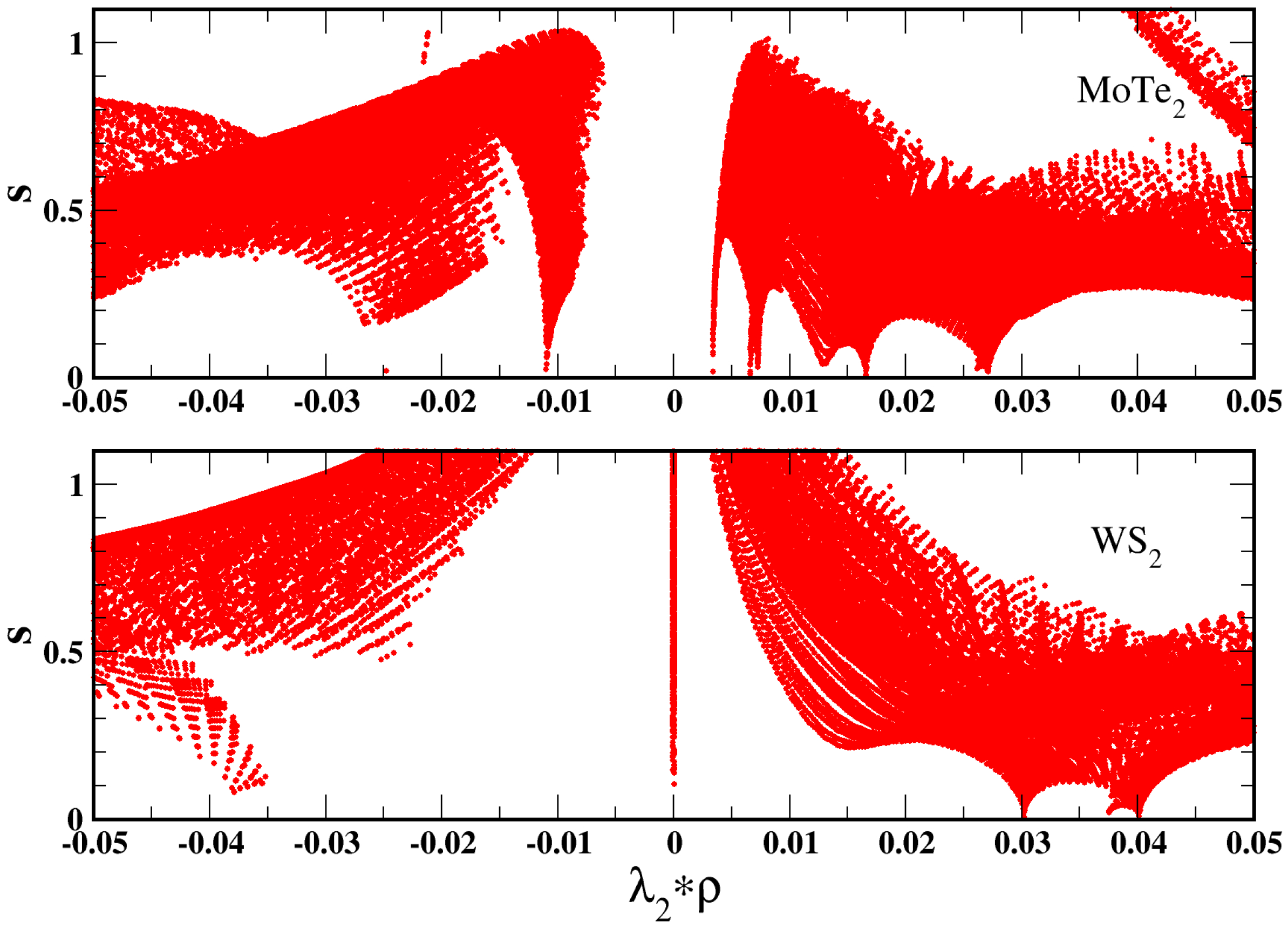
, whose density versus gradient plot is reported in
Figure 5. In this case, we can observe indeed that the reduced gradient is barely exceeding the value
. At such small values of
s, the SG4 enhancement factor shows, however, a significant de-enhancement. Consequently, the functional provides a bonding contribution from the dispersion bond (this can be also noted in the plot of the non-covalent interaction (NCI) indicator [
93] (
Figure 5) where peaks at negative values of
indicate bonding interactions (whereas positive values indicate repulsive interactions); thus, the downwards peak at
indicates the presence of a van der Waals bond).
Thus, the reduced gradient analysis, together with the inspection of the XC enhancement factor, provides a rationalization for the drawbacks observed for the SG4-rVV10m functional. Moreover, it gives a hint on understanding why, when using the NOB4 training set, the resulting b value is generally too small to assure a good description of dispersion in other materials. This depends on the fact that, for bulk solids, made of noble-gas atoms the relevant reduced gradient values are quite large, due to the very weak interaction in such solids. Therefore, the SG4 functional displays almost no dispersion contributions and a rather strong correction is required by the non-local rVV10m term. However, in the case of other more conventional solids, the values of the reduced gradient are not so high and thus a smaller correction is required. For this reason, the parameterization based on the ALK5 set gives a more balanced contribution, even though it is too underbinding for the noble-gas bulk solids.
Finally, the shape of the SG4 enhancement factor also helps to understand the general slight overestimation of cohesive energies by this functional, which causes the SG4-rVV10m to perform not very accurately for these properties in covalent-solids. In fact, the origin of the problem traces back to the underestimation of the atomic energies by SG4, which in turn originates on the discussed deenhancement. This underestimation causes the overestimation of the computed cohesive energy. For the case of dispersion solids, however, the problem is hidden by an even larger underestimation of the energy of the solid (as it should be in any GGA to be corrected via dispersion corrections).