The Role of Conformational Entropy in the Determination of Structural-Kinetic Relationships for Helix-Coil Transitions
Abstract
1. Introduction
2. Computational Methods
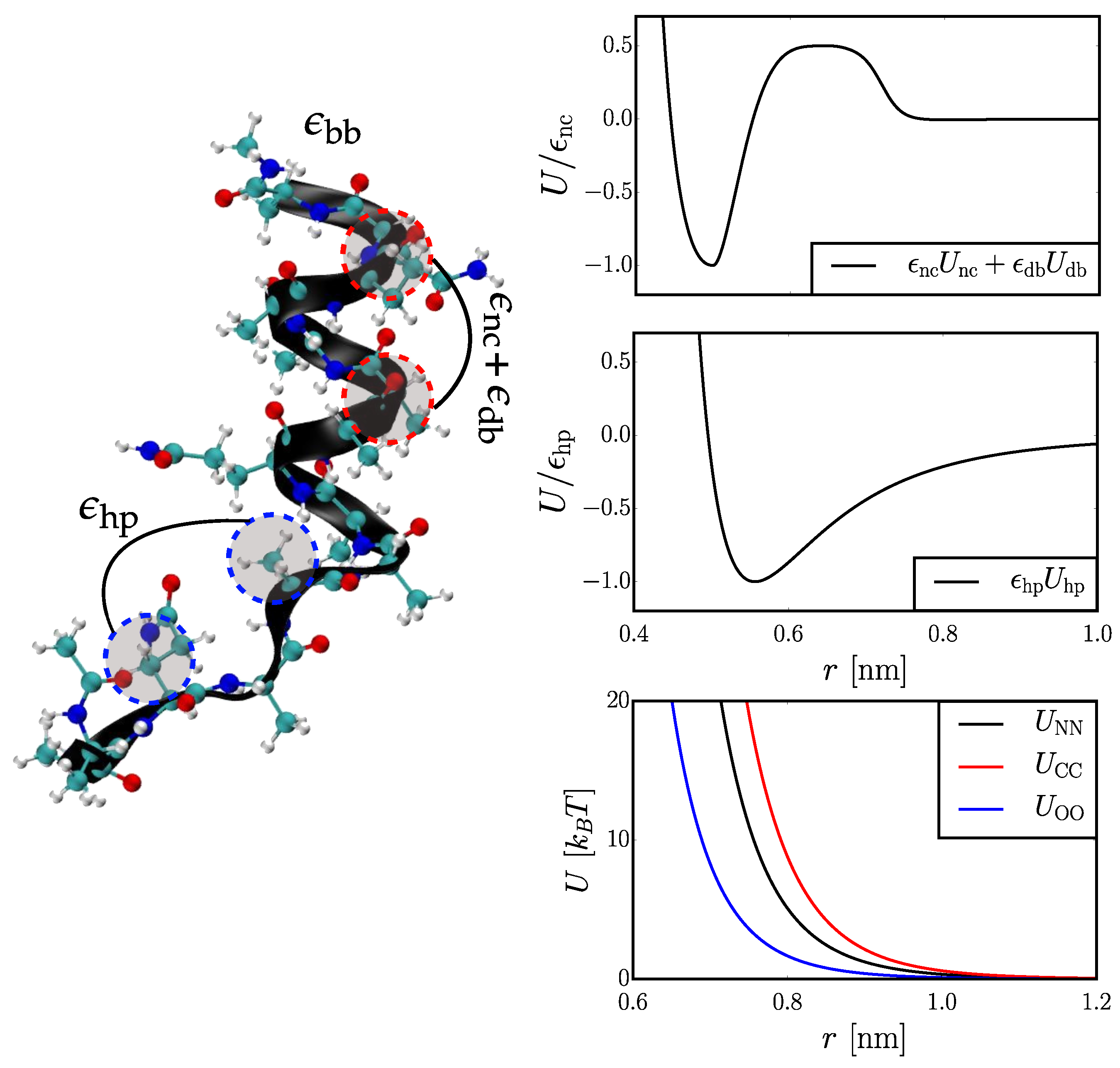
2.1. Coarse-Grained (CG) Models
2.1.1. Hybrid Gō (Hy-Gō)
2.1.2. PLUM
- the side chain van der Waals radius is decreased to 90% of its original value [20].
- the hydrogen-bonding interaction strength is decreased to 94.5% of its original value [30].
- the hydrogren-bonding interaction strength is decreased to 90% of its original value.
- the side chain interaction interaction strength is decreased to 95% of its original value.
2.2. Simulation Details
2.2.1. Hy-Gō
2.2.2. PLUM
2.3. Lifson-Roig Models
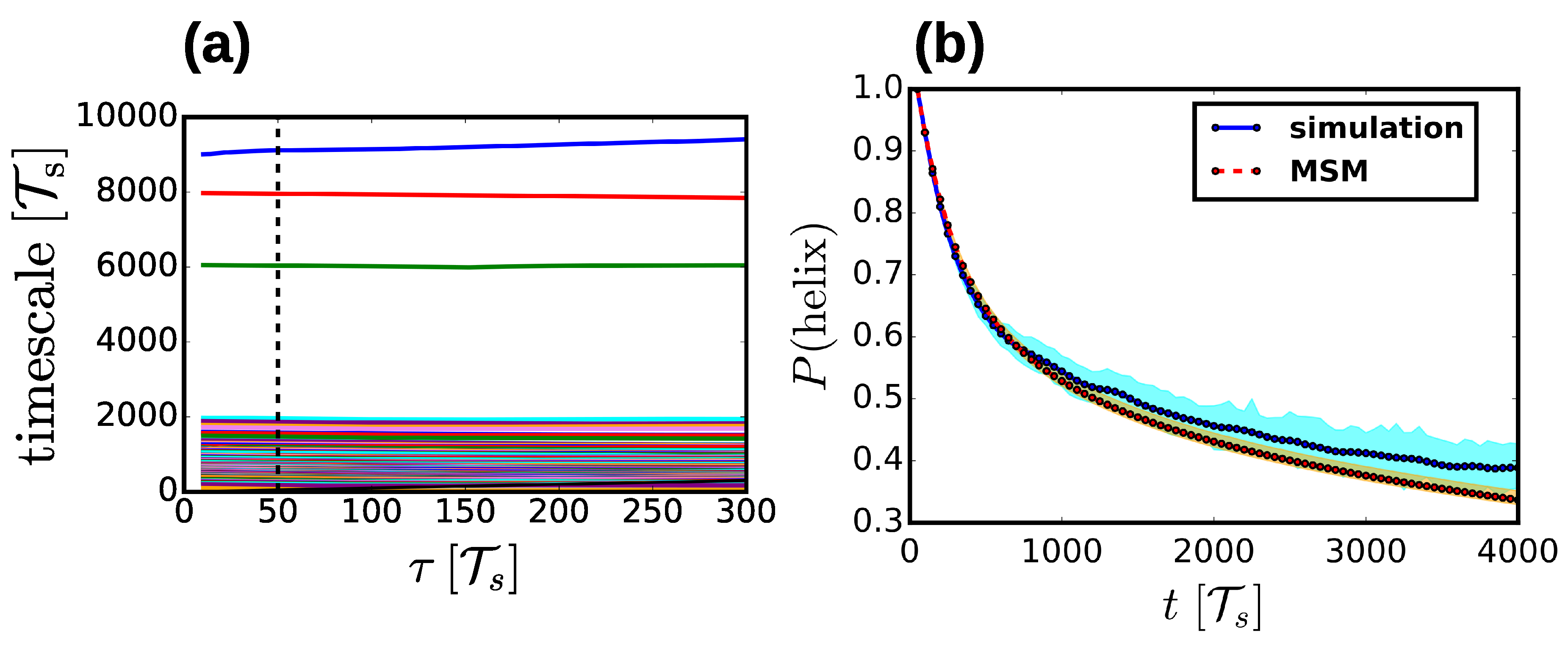
2.4. Markov State Models
3. Results and Discussion
3.1. Properties of the Helix-Coil Transition
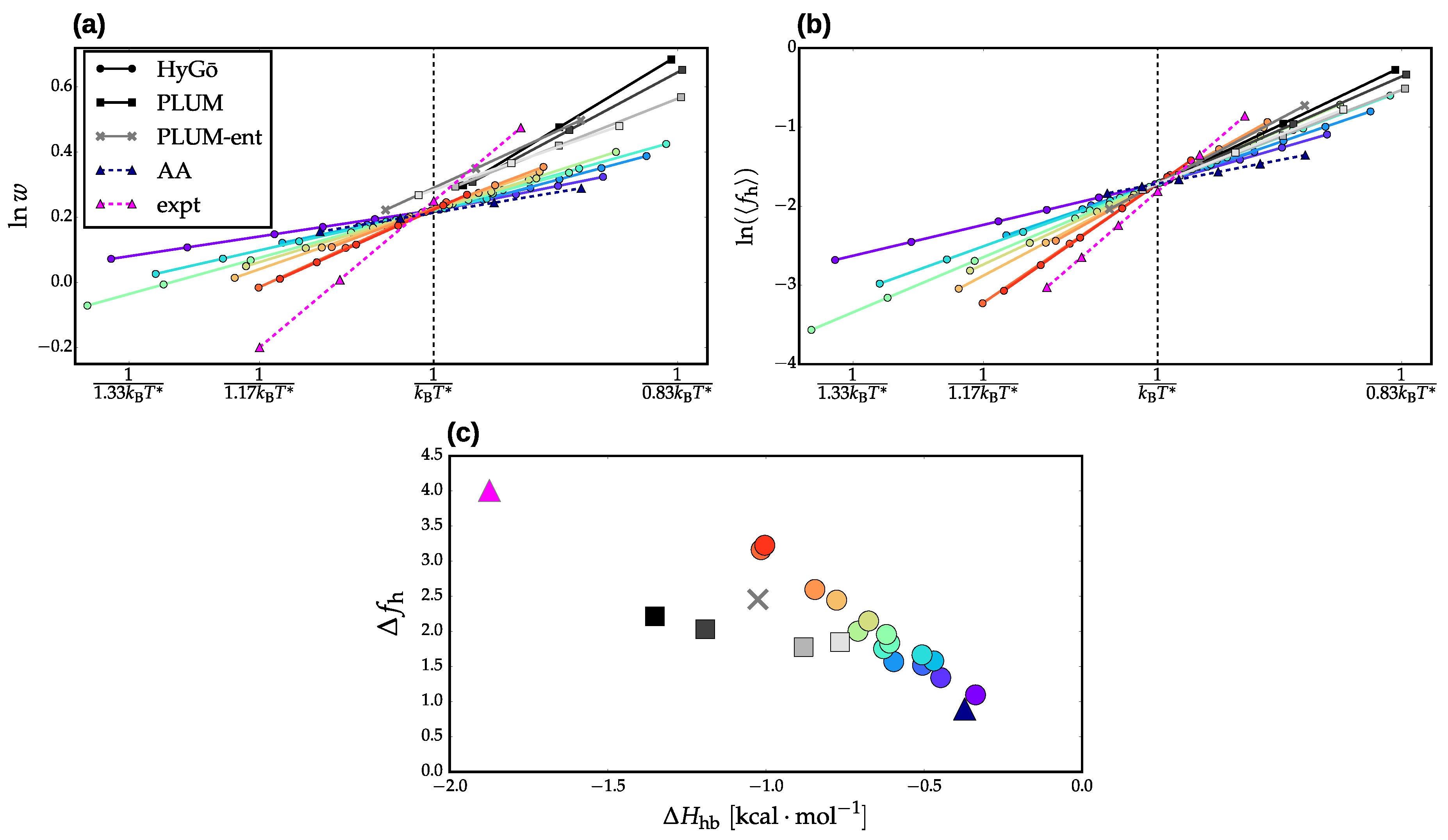
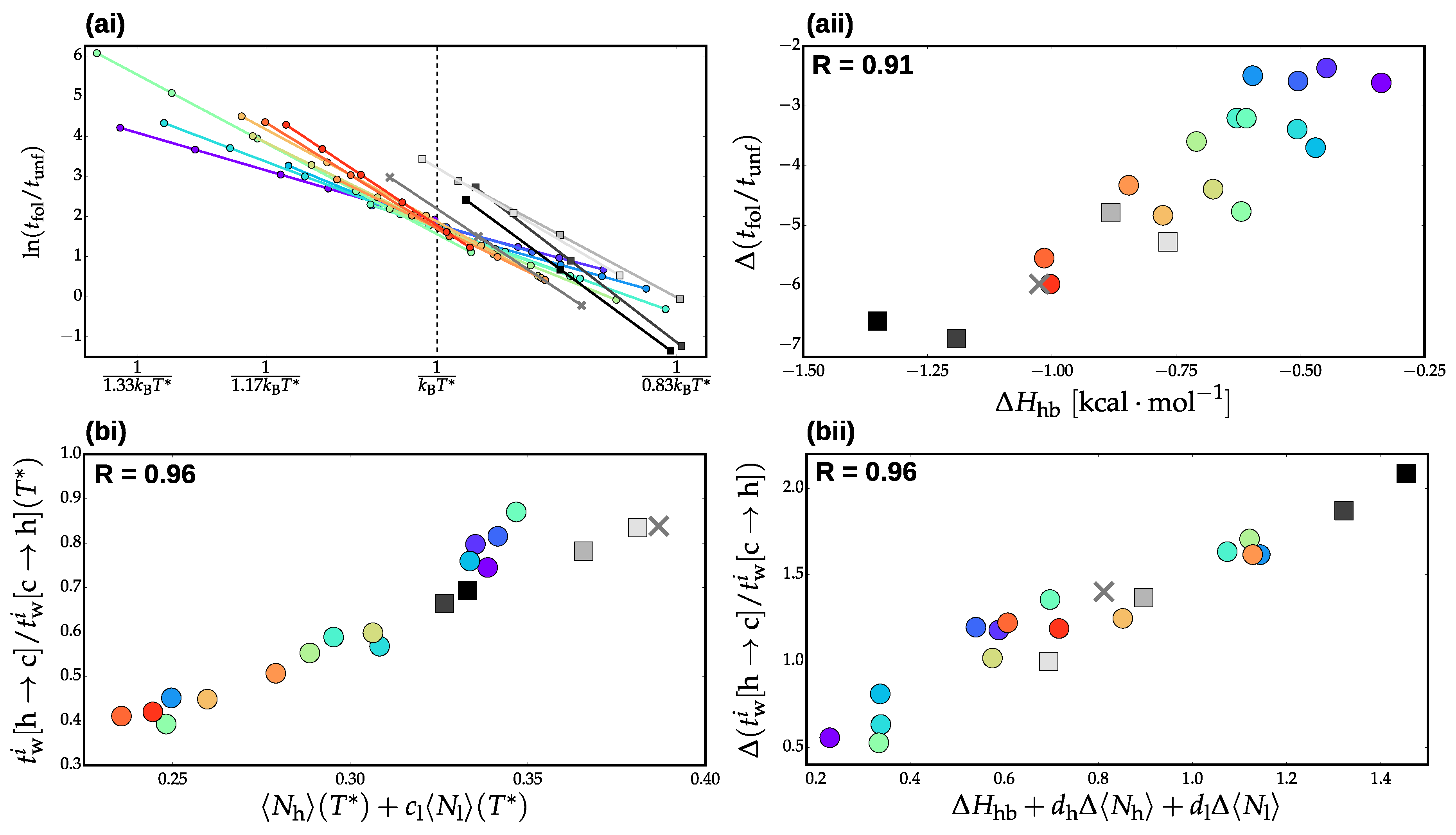
3.2. Validation of Structural-Kinetic Relationships for
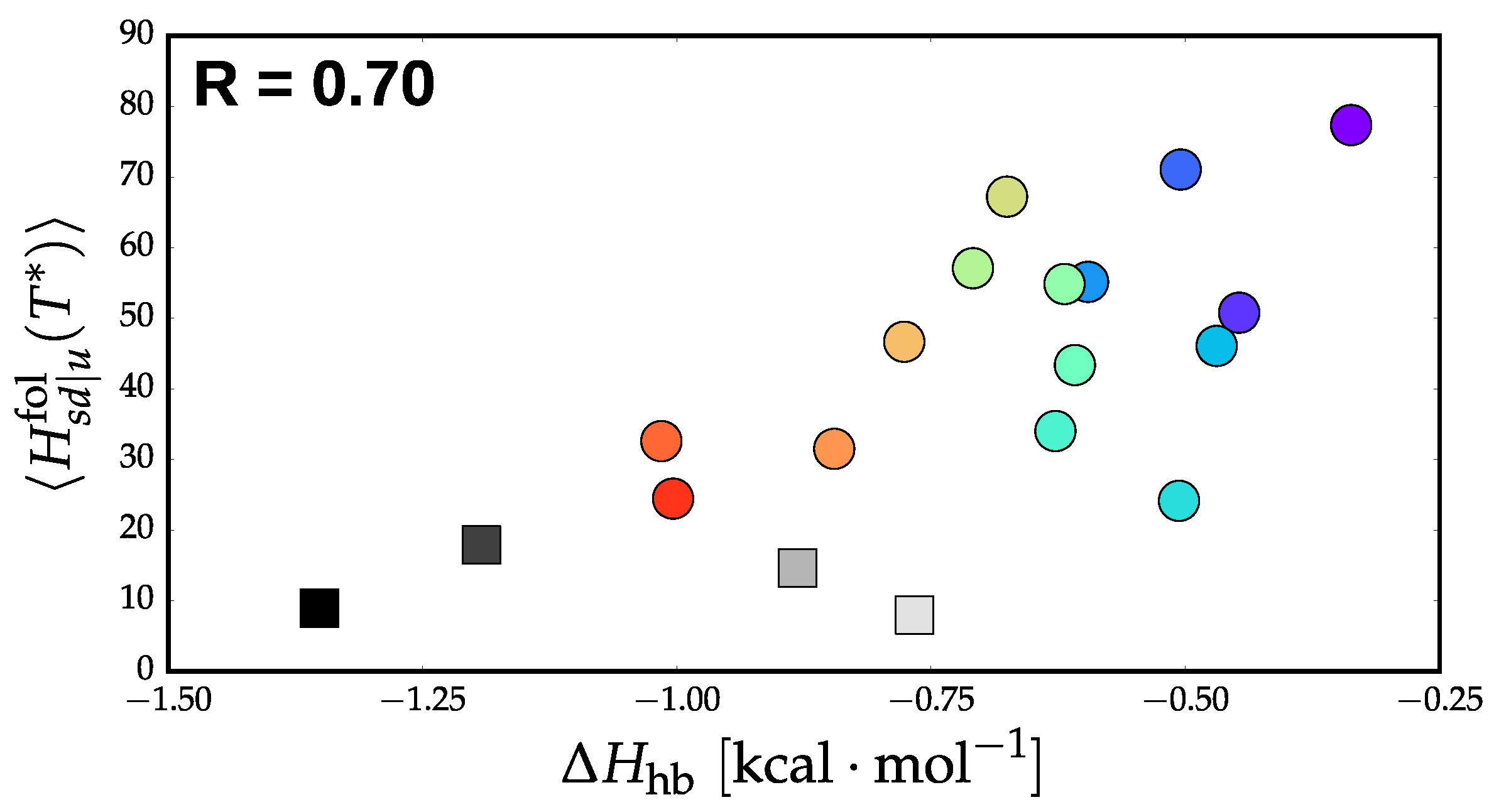
3.3. Thermodynamics and Transition Network Topology
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| CG | coarse-grained |
| MSM | Markov state model |
| AA | all-atom |
| LR | Lifson-Roig |
| Hy-Gō | Hybrid Gō |
References
- Dill, K.A.; Chan, H.S. From Levinthal to Pathways to Funnels. Nat. Struct. Biol. 1997, 4, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Kmiecik, S.; Gront, D.; Kolinski, M.; Wieteska, L.; Dawid, A.E.; Kolinski, A. Coarse-Grained Protein Models and Their Applications. Chem. Rev. 2016, 116, 7898–7936. [Google Scholar] [CrossRef] [PubMed]
- Schuler, B.; Soranno, A.; Hofmann, H.; Nettels, D. Single-Molecule FRET Spectroscopy and the Polymer Physics of Unfolded and Intrinsically Disordered Proteins. Ann. Rev. Biochem. 2016, 45, 207–231. [Google Scholar] [CrossRef] [PubMed]
- Liwo, A.; Oldziej, S.; Czaplewski, C.; Kozlowska, U.; Scheraga, H.A. Parametrization of Backbone-Electrostatic and Multibody Contributions to the UNRES Force Field for Protein-Structure Prediction from Ab Initio Energy Surfaces of Model Systems. J. Phys. Chem. B 2004, 108, 9421–9438. [Google Scholar] [CrossRef]
- Maupetit, J.; Tuffery, P.; Derreumaux, P. A Coarse-Grained Protein Force Field for Folding and Structure Prediction. Proteins Struct. Funct. Bioinf. 2007, 69, 394–408. [Google Scholar] [CrossRef] [PubMed]
- Bereau, T.; Deserno, M. Generic Coarse-Grained Model for Protein Folding and Aggregation. J. Chem. Phys. 2009, 130, 235106. [Google Scholar] [CrossRef] [PubMed]
- Davtyan, A.; Schafer, N.P.; Zheng, W.; Clementi, C.; Wolynes, P.G.; Papoian, G.A. AWSEM-MD: Protein Structure Prediction Using Coarse-Grained Physical Potentials and Bioinformatically Based Local Structure Biasing. J. Phys. Chem. B 2012, 116, 8494–8503. [Google Scholar] [CrossRef] [PubMed]
- Habibi, M.; Rottler, J.; Plotkin, S.S. As Simple as Possible, but not Simpler: Exploring the Fidelity of Coarse-Grained Protein Models for Simulated Force Spectroscopy. PLoS Comput. Biol. 2016, 12. [Google Scholar] [CrossRef] [PubMed]
- Rudzinski, J.F.; Kremer, K.; Bereau, T. Communication: Consistent Interpretation of Molecular Simulation Kinetics Using Markov State Models Biased with External Information. J. Chem. Phys. 2016, 144, 051102. [Google Scholar] [CrossRef] [PubMed]
- Harmandaris, V.A.; Kremer, K. Predicting Polymer Dynamics at Multiple Length and Time Scales. Soft Matter 2009, 5, 3920–3926. [Google Scholar] [CrossRef]
- Salerno, K.; Agrawal, A.; Perahia, D.; Grest, G. Resolving Dynamic Properties of Polymers through Coarse-Grained Computational Studies. Phys. Rev. Lett. 2016, 116, 058302. [Google Scholar] [CrossRef] [PubMed]
- Hijón, C.; Español, P.; Vanden-Eijnden, E.; Delgado-Buscalioni, R. Mori–Zwanzig Formalism as a Practical Computational Tool. Fold. Des. 2010, 144, 301–322. [Google Scholar] [CrossRef]
- Rudzinski, J.F.; Bereau, T. Structural-Kinetic-Thermodynamic Relationships for Peptide Secondary Structure Formation Identified from Transition Network Properties. bioRxiv. 2017. Available online: https://www.biorxiv.org/content/early/2017/12/18/183053 (accessed on 31 August 2017).
- Cheung, M.; Garcia, A.; Onuchic, J. Protein Folding Mediated by Solvation: Water Expulsion and Formation of the Hydrophobic Core Occur after the Structural Collapse. Proc. Natl. Acad. Sci. USA 2002, 99, 685–690. [Google Scholar] [CrossRef] [PubMed]
- Clementi, C.; Plotkin, S.S. The Effects of Nonnative Interactions on Protein Folding Rates: Theory and Simulation. Protein Sci. 2004, 13, 1750–1766. [Google Scholar] [CrossRef] [PubMed]
- Chan, H.S.; Zhang, Z.; Wallin, S.; Liu, Z. Cooperativity, Local-Nonlocal Coupling, and Nonnative Interactions: Principles of Protein Folding from Coarse-Grained Models. Ann. Rev. Phys. Chem. 2011, 62, 301–326. [Google Scholar] [CrossRef] [PubMed]
- Taketomi, H.; Ueda, Y.; Gō, N. Studies on Protein Folding, Unfolding and Fluctuations by Computer-Simulation. I. Effect of Specific Amino-Acid Sequence Represented by Specific Inter-Unit Interactions. Int. J. Pept. Protein Res. 1975, 7, 445–459. [Google Scholar] [CrossRef] [PubMed]
- Hornak, V.; Abel, R.; Okur, A.; Strockbine, B.; Roitberg, A.; Simmerling, C. Comparison of Multiple Amber Force Fields and Development of Improved Protein Backbone Parameters. Proteins Struct. Funct. Bioinf. 2006, 65, 712–725. [Google Scholar] [CrossRef] [PubMed]
- Weeks, J.; Chandler, D.; Andersen, H. Role of Repulsive Forces in Determining Equilibrium Structure of Simple Liquids. J. Chem. Phys. 1971, 54, 5237. [Google Scholar] [CrossRef]
- Rudzinski, J.F.; Bereau, T. Concurrent Parametrization Against Static and Kinetic Information Leads to More Robust Coarse-Grained Force Fields. Eur. Phys. J. Spec. Top. 2016, 225, 1373–1389. [Google Scholar] [CrossRef][Green Version]
- Whitford, P.C.; Noel, J.K.; Gosavi, S.; Schug, A.; Sanbonmatsu, K.Y.; Onuchic, J.N. An All-Atom Structure-Based Potential for Proteins: Bridging Minimal Models with All-Atom Empirical Forcefields. Proteins Struct. Funct. Bioinf. 2009, 75, 430–441. [Google Scholar] [CrossRef] [PubMed]
- Bereau, T.; Bachmann, M.; Deserno, M. Interplay Between Secondary and Tertiary Structure Formation in Protein Folding Cooperativity. J. Am. Chem. Soc. 2010, 132, 13129–13131. [Google Scholar] [CrossRef] [PubMed]
- Bereau, T.; Deserno, M.; Bachmann, M. Structural Basis of Folding Cooperativity in Model Proteins: Insights from a Microcanonical Perspective. Biophys. J. 2011, 100, 2764–2772. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Bereau, T.; Wang, Z.J.; Deserno, M. More than the Sum of its Parts: Coarse-Grained Peptide-Lipid Interactions from a Simple Cross-Parametrization. J. Chem. Phys. 2014, 140, 115101. [Google Scholar] [CrossRef] [PubMed]
- Bereau, T.; Bennett, W.F.D.; Pfaendtner, J.; Deserno, M.; Karttunen, M. Folding and Insertion Thermodynamics of the Transmembrane WALP Peptide. J. Chem. Phys. 2015, 143, 1. [Google Scholar] [CrossRef] [PubMed]
- Bereau, T.; Globisch, C.; Deserno, M.; Peter, C. Coarse-Grained and Atomistic Simulations of the Salt-Stable Cowpea Chlorotic Mottle Virus (SS-CCMV) Subunit 26-49: Beta-Barrel Stability of the Hexamer and Pentamer Geometries. J. Chem. Theory Comput. 2012, 8, 3750–3758. [Google Scholar] [CrossRef] [PubMed]
- Osborne, K.L.; Bachmann, M.; Strodel, B. From Computational Biophysics to Systems Biology. In Proceedings of the CBSB11, Julich, Germany, 20–22 July 2011; p. 151. [Google Scholar]
- Osborne, K.L.; Bachmann, M.; Strodel, B. Thermodynamic Analysis of Structural Transitions during GNNQQNY Aggregation. Proteins Struct. Funct. Bioinf. 2013, 81, 1141–1155. [Google Scholar] [CrossRef] [PubMed]
- Osborne, K.L.; Barz, B.; Bachmann, M.; Strodel, B. Thermodynamics of protein aggregation. Phys. Procedia 2014, 53, 90. [Google Scholar] [CrossRef]
- Rutter, G.O.; Brown, A.H.; Quigley, D.; Walsh, T.R.; Allen, M.P. Testing the Transferability of a Coarse-Grained Model to Intrinsically Disordered Proteins. Phys. Chem. Chem. Phys. 2015, 17, 31741–31749. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Hummer, G. Optimized Molecular Dynamics Force Fields Applied to the Helix-Coil Transition of Polypeptides. J. Phys. Chem. B 2009, 113, 9004–9015. [Google Scholar] [CrossRef] [PubMed]
- Hess, B.; Kutzner, C.; van der Spoel, D.; Lindahl, E. GROMACS 4: Algorithms for Highly Efficient, Load-Balanced, and Scalable Molecular Simulation. J. Chem. Theory Comput. 2008, 4, 435–447. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.J.; Deserno, M. A Systematically Coarse-Grained Solvent-Free Model for Quantitative Phospholipid Bilayer Simulations. J. Phys. Chem. B 2010, 114, 11207–11220. [Google Scholar] [CrossRef] [PubMed]
- Limbach, H.; Arnold, A.; Mann, B.; Holm, C. ESPResSo - An Extensible Simulation Package for Research on Soft Matter Systems. Comput. Phys. Commun. 2006, 174, 704–727. [Google Scholar] [CrossRef]
- Lifson, S.; Roig, A. On the Theory of Helix-Coil Transition in Polypeptides. J. Chem. Phys. 1961, 34, 1963–1974. [Google Scholar] [CrossRef]
- Vitalis, A.; Caflisch, A. 50 Years of Lifson-Roig Models: Application to Molecular Simulation Data. J. Chem. Theory Comput. 2012, 8, 363–373. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Swope, W.C.; Pitera, J.W.; Dill, K.A. Long-Time Protein Folding Dynamics from Short-Time Molecular Dynamics Simulations. Multiscale Model. Simul. 2006, 5, 1214–1226. [Google Scholar] [CrossRef]
- Noé, F. Probability Distributions of Molecular Observables Computed from Markov Models. J. Chem. Phys. 2008, 28, 244103. [Google Scholar] [CrossRef] [PubMed]
- Bowman, G.R.; Pande, V.S.; Noé, F. An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation; Springer Science and Business Media: Dordrecht, The Netherlands, 2014. [Google Scholar]
- Prinz, J.H.; Wu, H.; Sarich, M.; Keller, B.; Senne, M.; Held, M.; Chodera, J.D.; Schütte, C.; Noé, F. Markov Models of Molecular Kinetics: Generation and Validation. J. Chem. Phys. 2011, 134, 174105. [Google Scholar] [CrossRef] [PubMed]
- Perez-Hernandez, G.; Paul, F.; Giorgino, T.; De Fabritiis, G.; Noé, F. Identification of Slow Molecular Order Parameters for Markov Model Construction. J. Chem. Phys. 2013, 139, 015102. [Google Scholar] [CrossRef] [PubMed]
- Sittel, F.; Stock, G. Robust Density-Based Clustering to Identify Metastable Conformational States of Proteins. J. Chem. Theory Comput. 2016, 12, 2426–2435. [Google Scholar] [CrossRef] [PubMed]
- Jain, A.; Stock, G. Identifying Metastable States of Folding Proteins. J. Chem. Theory Comput. 2012, 8, 3810–3819. [Google Scholar] [CrossRef] [PubMed]
- Scherer, M.K.; Trendelkamp-Schroer, B.; Paul, F.; Perez-Hernandez, G.; Hoffmann, M.; Plattner, N.; Wehmeyer, C.; Prinz, J.H.; Noé, F. PyEMMA 2: A Software Package for Estimation, Validation, and Analysis of Markov Models. J. Chem. Theory Comput. 2015, 11, 5525–5542. [Google Scholar] [CrossRef] [PubMed]
- Schwarz, G. On Kinetics of Helix-coil Transition of Polypeptides in Solution. J. Mol. Biol. 1965, 11, 64–77. [Google Scholar] [CrossRef]
- Thompson, P.; Eaton, W.; Hofrichter, J. Laser Temperature Jump Study of the Helix Reversible Arrow Coil Kinetics of an Alanine Peptide Interpreted with a ‘Kinetic Zipper’ Model. Biochemistry 1997, 36, 9200–9210. [Google Scholar] [CrossRef] [PubMed]
- Frauenfelder, Hans. The Physics of Proteins: An Introduction to Biological Physics and Molecular Biophysics; Springer Science and Business Media: New York, NY, USA, 2010. [Google Scholar]
- Kafsi, M.; Grossglauser, M.; Thiran, P. The Entropy of Conditional Markov Trajectories. IEEE Trans. Inf. Theory 2013, 59, 5577–5583. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rudzinski, J.F.; Bereau, T. The Role of Conformational Entropy in the Determination of Structural-Kinetic Relationships for Helix-Coil Transitions. Computation 2018, 6, 21. https://doi.org/10.3390/computation6010021
Rudzinski JF, Bereau T. The Role of Conformational Entropy in the Determination of Structural-Kinetic Relationships for Helix-Coil Transitions. Computation. 2018; 6(1):21. https://doi.org/10.3390/computation6010021
Chicago/Turabian StyleRudzinski, Joseph F., and Tristan Bereau. 2018. "The Role of Conformational Entropy in the Determination of Structural-Kinetic Relationships for Helix-Coil Transitions" Computation 6, no. 1: 21. https://doi.org/10.3390/computation6010021
APA StyleRudzinski, J. F., & Bereau, T. (2018). The Role of Conformational Entropy in the Determination of Structural-Kinetic Relationships for Helix-Coil Transitions. Computation, 6(1), 21. https://doi.org/10.3390/computation6010021




