Optimal Data-Driven Estimation of Generalized Markov State Models for Non-Equilibrium Dynamics
Abstract
:1. Introduction
- (i)
- Time-inhomogeneous dynamics, e.g., the system feels a time-dependent external force, for instance due to an electromagnetic field or force probing.
- (ii)
- Time-homogeneous non-reversible dynamics, i.e., where the governing laws of the system do not change in time, but the system does not obey detailed balance, and, additionally we might want to consider the system in a non-stationary regime.
- (iii)
- Reversible dynamics but non-stationary data, i.e., the system possesses a stationary distribution with respect to which it is in detailed balance, but the empirical distribution of the available data did not converge to this stationary distribution.
2. Studying Dynamics with Functions
2.1. Transfer Operators
- (a)
- The Perron–Frobenius operator (also called propagator),evolves probability distributions.
- (b)
- The Perron–Frobenius operator with respect to the equilibrium density (also called transfer operator, simply),evolves densities with respect to .
- (c)
- The Koopman operatorevolves observables.
2.2. Reversible Equilibrium Dynamics and Spectral Decomposition
3. Markov State Models for Reversible Systems in Equilibrium
3.1. Preliminaries on Equilibrium Markov State Models
- is a positive operator ⟷ all entries of are non-negative;
- is probability-preserving ⟷ each column sum of is 1.
3.2. Metastable Sets
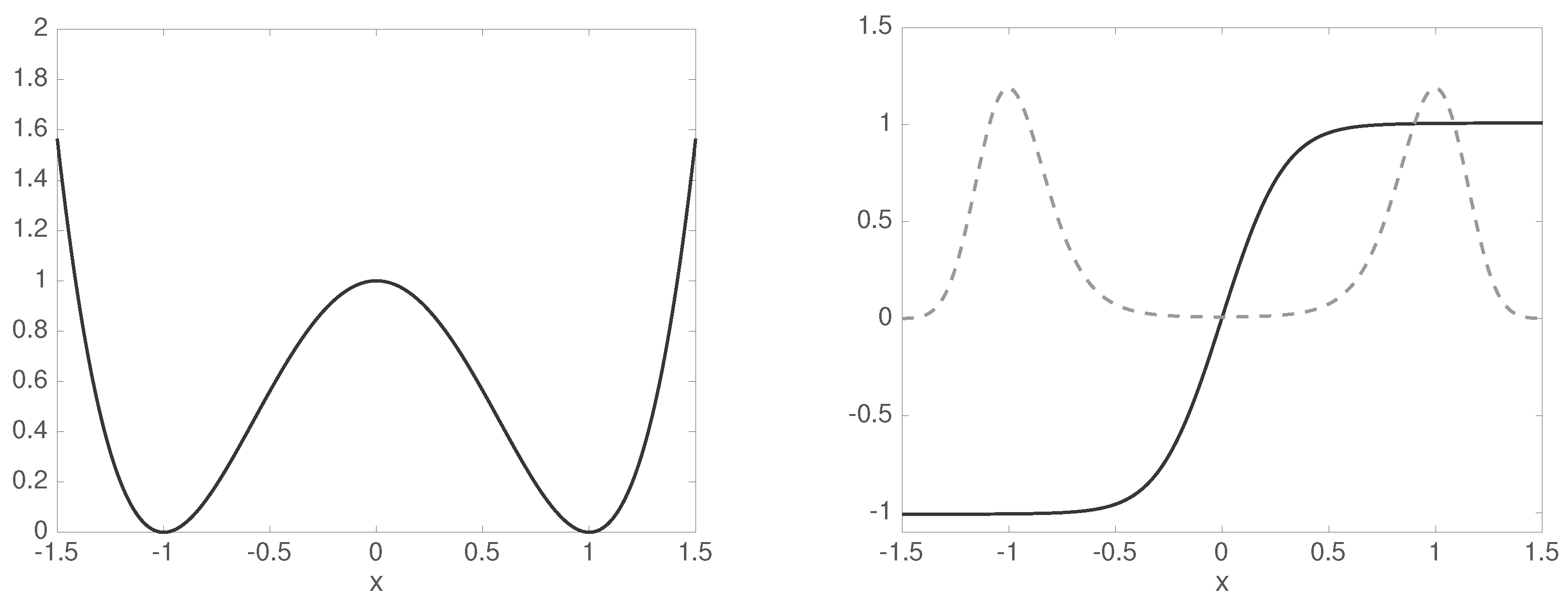
3.3. Example: Stationary Diffusion in Double-Well Potential
4. Markov State Models for Time-Inhomogeneous Systems
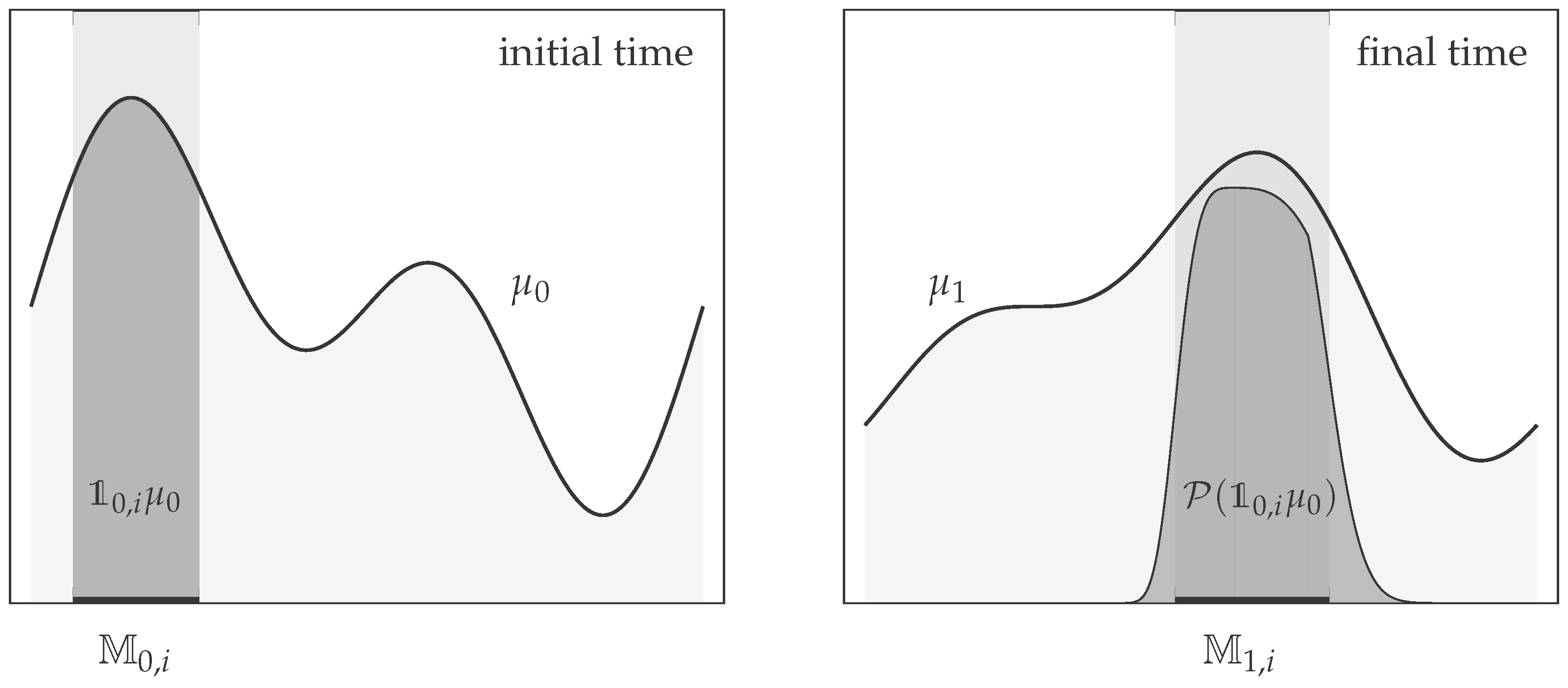
4.1. Minimal Propagation Error by Projections
4.1.1. Conceptual Changes
4.1.2. Adapted Transfer Operators
- , encoding the property that is mapped to by the propagator .
- is positive and integral-preserving, thus .
- Its adjoint is the Koopman operator , .
4.1.3. An Optimal Non-Stationary GMSM
4.2. Coherent Sets
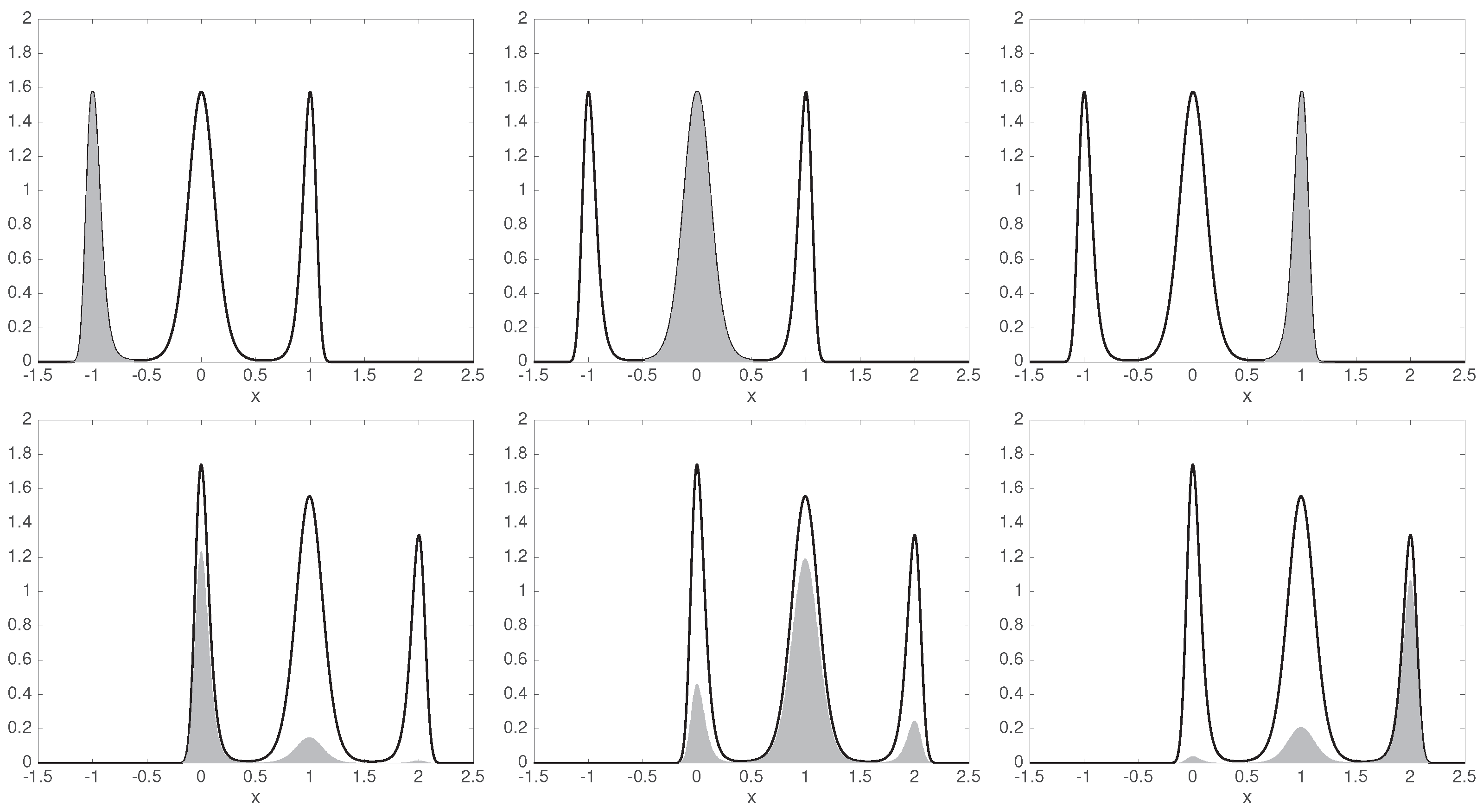
4.3. Example: Diffusion in Shifting Triple-Well Potential
5. Data-Based Approximation
5.1. Setting and Auxiliary Objects
5.2. Projection on the Basis Functions
5.3. Best Low-Rank Approximation
| Algorithm 1 TCCA algorithm to estimate a rank-k GMSM. |
|
6. Time-Homogeneous Systems and Non-Stationary Data
6.1. Equilibrium MSM from Non-Equilibrium Data
6.2. A Non-Reversible System with Non-Stationary Data
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| EDMD | extended dynamic mode decomposition |
| (G)MSM | (generalized) Markov state model |
| SDE | stochastic differential equation |
| TCCA | time-lagged canonical correlation algorithm |
| VAMP | variational approach for Markov processes |
Appendix A. Optimal Low-Rank Approximation of Compact Operators
References
- Schütte, C.; Sarich, M. Metastability and Markov State Models in Molecular Dynamics: Modeling, Analysis, Algorithmic Approaches; American Mathematical Society: Providence, RI, USA, 2013; Volume 24. [Google Scholar]
- Prinz, J.; Wu, H.; Sarich, M.; Keller, B.; Senne, M.; Held, M.; Chodera, J.; Schütte, C.; Noé, F. Markov models of molecular kinetics: Generation and validation. J. Chem. Phys. 2011, 134, 174105. [Google Scholar] [CrossRef] [PubMed]
- Bowman, G.R.; Pande, V.S.; Noé, F. (Eds.) An Introduction to Markov State Models and Their Application to Long Timescale Molecular Simulation. In Advances in Experimental Medicine and Biology; Springer: New York, NY, USA, 2014; Volume 797. [Google Scholar]
- Scherer, M.K.; Trendelkamp-Schroer, B.; Paul, F.; Pérez-Hernández, G.; Hoffmann, M.; Plattner, N.; Wehmeyer, C.; Prinz, J.H.; Noé, F. PyEMMA 2: A software package for estimation, validation, and analysis of Markov models. J. Chem. Theory Comput. 2015, 11, 5525–5542. [Google Scholar] [CrossRef] [PubMed]
- Harrigan, M.P.; Sultan, M.M.; Hernández, C.X.; Husic, B.E.; Eastman, P.; Schwantes, C.R.; Beauchamp, K.A.; McGibbon, R.T.; Pande, V.S. MSMBuilder: Statistical Models for Biomolecular Dynamics. Biophys. J. 2017, 112, 10–15. [Google Scholar] [CrossRef] [PubMed]
- Schütte, C.; Noé, F.; Lu, J.; Sarich, M.; Vanden-Eijnden, E. Markov State Models based on Milestoning. J. Chem. Phys. 2011, 134, 204105. [Google Scholar] [CrossRef] [PubMed]
- Sarich, M.; Noé, F.; Schütte, C. On the approximation quality of Markov state models. Multiscale Model. Simul. 2010, 8, 1154–1177. [Google Scholar] [CrossRef]
- Djurdjevac, N.; Sarich, M.; Schütte, C. Estimating the eigenvalue error of Markov State Models. Multiscale Model. Simul. 2012, 10, 61–81. [Google Scholar] [CrossRef]
- Noé, F.; Nüske, F. A variational approach to modeling slow processes in stochastic dynamical systems. Multiscale Model. Simul. 2013, 11, 635–655. [Google Scholar] [CrossRef]
- Nüske, F.; Keller, B.G.; Pérez-Hernández, G.; Mey, A.S.; Noé, F. Variational approach to molecular kinetics. J. Chem. Theory Comput. 2014, 10, 1739–1752. [Google Scholar] [CrossRef] [PubMed]
- Schütte, C.; Fischer, A.; Huisinga, W.; Deuflhard, P. A direct approach to conformational dynamics based on hybrid Monte Carlo. J. Comput. Phys. 1999, 151, 146–168. [Google Scholar] [CrossRef]
- Deuflhard, P.; Weber, M. Robust Perron cluster analysis in conformation dynamics. Linear Algebra Its Appl. 2005, 398, 161–184. [Google Scholar] [CrossRef]
- Wu, H.; Paul, F.; Wehmeyer, C.; Noé, F. Multiensemble Markov models of molecular thermodynamics and kinetics. Proc. Natl. Acad. Sci. USA 2016, 113, E3221–E3230. [Google Scholar] [CrossRef] [PubMed]
- Chodera, J.D.; Swope, W.C.; Noé, F.; Prinz, J.; Shirts, M.R.; Pande, V.S. Dynamical reweighting: Improved estimates of dynamical properties from simulations at multiple temperatures. J. Chem. Phys. 2011, 134, 06B612. [Google Scholar] [CrossRef] [PubMed]
- Froyland, G.; Santitissadeekorn, N.; Monahan, A. Transport in time-dependent dynamical systems: Finite-time coherent sets. Chaos Interdiscip. J. Nonlinear Sci. 2010, 20, 043116. [Google Scholar] [CrossRef] [PubMed]
- Froyland, G. An analytic framework for identifying finite-time coherent sets in time-dependent dynamical systems. Phys. D Nonlinear Phenom. 2013, 250, 1–19. [Google Scholar] [CrossRef]
- Koltai, P.; Ciccotti, G.; Schütte, C. On metastability and Markov state models for non-stationary molecular dynamics. J. Chem. Phys. 2016, 145, 174103. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Nüske, F.; Paul, F.; Klus, S.; Koltai, P.; Noé, F. Variational Koopman models: Slow collective variables and molecular kinetics from short off-equilibrium simulations. J. Chem. Phys. 2017, 146, 154104. [Google Scholar] [CrossRef] [PubMed]
- Schütte, C.; Wang, H. Building Markov State Models for Periodically Driven Non-Equilibrium Systems. J. Chem. Theory Comput. 2015, 11, 1819–1831. [Google Scholar]
- Froyland, G.; Koltai, P. Estimating long-term behavior of periodically driven flows without trajectory integration. Nonlinearity 2017, 30, 1948–1986. [Google Scholar] [CrossRef]
- Seifert, U.; Speck, T. Fluctuation-dissipation theorem in nonequilibrium steady states. EPL Europhys. Lett. 2010, 89, 10007. [Google Scholar] [CrossRef]
- Lee, H.K.; Lahiri, S.; Park, H. Nonequilibrium steady states in Langevin thermal systems. Phys. Rev. E 2017, 96, 022134. [Google Scholar] [CrossRef] [PubMed]
- Yao, Y.; Cui, R.; Bowman, G.; Silva, D.; Sun, J.; Huang, X. Hierarchical Nystroem methods for constructing Markov state models for conformational dynamics. J. Chem. Phys. 2013, 138, 174106. [Google Scholar] [CrossRef] [PubMed]
- Bowman, G.; Meng, L.; Huang, X. Quantitative comparison of alternative methods for coarse-graining biological networks. J. Chem. Phys. 2013, 139, 121905. [Google Scholar] [CrossRef] [PubMed]
- Knoch, F.; Speck, T. Cycle representatives for the coarse-graining of systems driven into a non-equilibrium steady state. New J. Phys. 2015, 17, 115004. [Google Scholar] [CrossRef]
- Mori, H. Transport, collective motion, and Brownian motion. Prog. Theor. Phys. 1965, 33, 423–455. [Google Scholar] [CrossRef]
- Zwanzig, R. Nonlinear generalized Langevin equations. J. Stat. Phys. 1973, 9, 215–220. [Google Scholar] [CrossRef]
- Chorin, A.J.; Hald, O.H.; Kupferman, R. Optimal prediction and the Mori–Zwanzig representation of irreversible processes. Proc. Natl. Acad. Sci. USA 2000, 97, 2968–2973. [Google Scholar] [CrossRef] [PubMed]
- Chorin, A.J.; Hald, O.H.; Kupferman, R. Optimal prediction with memory. Phys. D Nonlinear Phenom. 2002, 166, 239–257. [Google Scholar] [CrossRef]
- Wu, H.; Noé, F. Variational approach for learning Markov processes from time series data. arXiv, 2017; arXiv:1707.04659. [Google Scholar]
- Baxter, J.R.; Rosenthal, J.S. Rates of convergence for everywhere-positive Markov chains. Stat. Probab. Lett. 1995, 22, 333–338. [Google Scholar] [CrossRef]
- Schervish, M.J.; Carlin, B.P. On the convergence of successive substitution sampling. J. Comput. Graph. Stat. 1992, 1, 111–127. [Google Scholar]
- Klus, S.; Nüske, F.; Koltai, P.; Wu, H.; Kevrekidis, I.; Schütte, C.; Noé, F. Data-Driven Model Reduction and Transfer Operator Approximation. J. Nonlinear Sci. 2018, 1–26. [Google Scholar] [CrossRef]
- Mattingly, J.C.; Stuart, A.M. Geometric ergodicity of some hypo-elliptic diffusions for particle motions. Markov Process. Relat. Fields 2002, 8, 199–214. [Google Scholar]
- Mattingly, J.C.; Stuart, A.M.; Higham, D.J. Ergodicity for SDEs and approximations: Locally Lipschitz vector fields and degenerate noise. Stoch. Process. Their Appl. 2002, 101, 185–232. [Google Scholar] [CrossRef]
- Bittracher, A.; Koltai, P.; Klus, S.; Banisch, R.; Dellnitz, M.; Schütte, C. Transition Manifolds of Complex Metastable Systems. J. Nonlinear Sci. 2017, 1–42. [Google Scholar] [CrossRef]
- Denner, A. Coherent Structures and Transfer Operators. Ph.D. Thesis, Technische Universität München, München, Germany, 2017. [Google Scholar]
- Hsing, T.; Eubank, R. Theoretical Foundations of Functional Data Analysis, with an Introduction to Linear Operators; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Froyland, G.; Horenkamp, C.; Rossi, V.; Santitissadeekorn, N.; Gupta, A.S. Three-dimensional characterization and tracking of an Agulhas Ring. Ocean Model. 2012, 52–53, 69–75. [Google Scholar] [CrossRef]
- Froyland, G.; Horenkamp, C.; Rossi, V.; van Sebille, E. Studying an Agulhas ring’s long-term pathway and decay with finite-time coherent sets. Chaos 2015, 25, 083119. [Google Scholar] [CrossRef] [PubMed]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A data–driven approximation of the Koopman operator: Extending dynamic mode decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef]
- Klus, S.; Koltai, P.; Schütte, C. On the numerical approximation of the Perron–Frobenius and Koopman operator. J. Comput. Dyn. 2016, 3, 51–79. [Google Scholar]
- Korda, M.; Mezić, I. On convergence of extended dynamic mode decomposition to the Koopman operator. J. Nonlinear Sci. 2017, 1–24. [Google Scholar] [CrossRef]
- Pérez-Hernández, G.; Paul, F.; Giorgino, T.; Fabritiis, G.D.; Noé, F. Identification of slow molecular order parameters for Markov model construction. J. Chem. Phys. 2013, 139, 015102. [Google Scholar] [CrossRef] [PubMed]
- Schwantes, C.R.; Pande, V.S. Improvements in Markov state model construction reveal many non-native interactions in the folding of NTL9. J. Chem. Theory Comput. 2013, 9, 2000–2009. [Google Scholar] [CrossRef] [PubMed]
- Molgedey, L.; Schuster, H.G. Separation of a mixture of independent signals using time delayed correlations. Phys. Rev. Lett. 1994, 72, 3634–3637. [Google Scholar] [CrossRef] [PubMed]
- Hammersley, J.M.; Morton, K.W. Poor man’s Monte Carlo. J. R. Stat. Soc. Ser. B Methodol. 1954, 16, 23–38. [Google Scholar]
- Rosenbluth, M.N.; Rosenbluth, A.W. Monte Carlo calculation of the average extension of molecular chains. J. Chem. Phys. 1955, 23, 356–359. [Google Scholar] [CrossRef]
- Jarzynski, C. Nonequilibrium equality for free energy differences. Phys. Rev. Lett. 1997, 78, 2690. [Google Scholar] [CrossRef]
- Crooks, G.E. Entropy production fluctuation theorem and the nonequilibrium work relation for free energy differences. Phys. Rev. E 1999, 60, 2721. [Google Scholar] [CrossRef]
- Bucklew, J. Introduction to Rare Event Simulation; Springer Science & Business Media: New York, NY, USA, 2013. [Google Scholar]
- Hartmann, C.; Schütte, C. Efficient rare event simulation by optimal nonequilibrium forcing. J. Stat. Mech. Theory Exp. 2012, 2012, P11004. [Google Scholar] [CrossRef]
- Hartmann, C.; Richter, L.; Schütte, C.; Zhang, W. Variational Characterization of Free Energy: Theory and Algorithms. Entropy 2017, 19, 626. [Google Scholar] [CrossRef]
- Dellnitz, M.; Junge, O. On the approximation of complicated dynamical behavior. SIAM J. Numer. Anal. 1999, 36, 491–515. [Google Scholar] [CrossRef]
- Djurdjevac Conrad, N.; Weber, M.; Schütte, C. Finding dominant structures of nonreversible Markov processes. Multiscale Model. Simul. 2016, 14, 1319–1340. [Google Scholar] [CrossRef]
- Conrad, N.D.; Banisch, R.; Schütte, C. Modularity of directed networks: Cycle decomposition approach. J. Comput. Dyn. 2015, 2, 1–24. [Google Scholar]
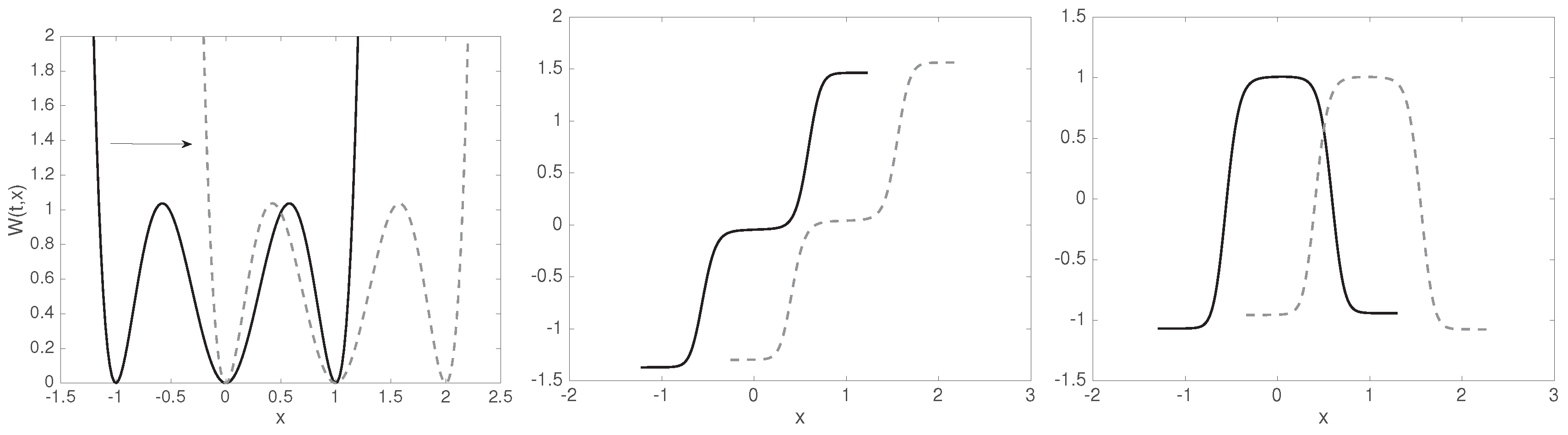
| A Stochastic (Markov) Process Is Called | |
|---|---|
| time-homogeneous | if the transition probabilities from time s to time t depend only on (in analogy to the evolution of an autonomous ordinary differential equation). |
| stationary | if the distribution of the process does not change in time (such a distribution is also called invariant, cf. (2)). |
| reversible | if it is stationary and the detailed balance condition (5) holds (reversibility means that time series are statistically indistinguishable in forward and backward time). |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koltai, P.; Wu, H.; Noé, F.; Schütte, C. Optimal Data-Driven Estimation of Generalized Markov State Models for Non-Equilibrium Dynamics. Computation 2018, 6, 22. https://doi.org/10.3390/computation6010022
Koltai P, Wu H, Noé F, Schütte C. Optimal Data-Driven Estimation of Generalized Markov State Models for Non-Equilibrium Dynamics. Computation. 2018; 6(1):22. https://doi.org/10.3390/computation6010022
Chicago/Turabian StyleKoltai, Péter, Hao Wu, Frank Noé, and Christof Schütte. 2018. "Optimal Data-Driven Estimation of Generalized Markov State Models for Non-Equilibrium Dynamics" Computation 6, no. 1: 22. https://doi.org/10.3390/computation6010022
APA StyleKoltai, P., Wu, H., Noé, F., & Schütte, C. (2018). Optimal Data-Driven Estimation of Generalized Markov State Models for Non-Equilibrium Dynamics. Computation, 6(1), 22. https://doi.org/10.3390/computation6010022





