Seismic Response of Adjacent Unequal Buildings Subjected to Double Pounding Considering Soil-Structure Interaction
Abstract
1. Introduction
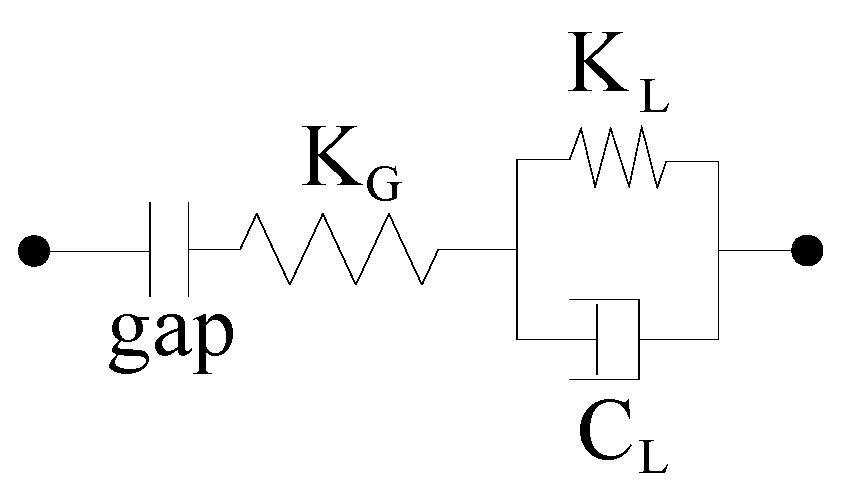
2. Impact Elements
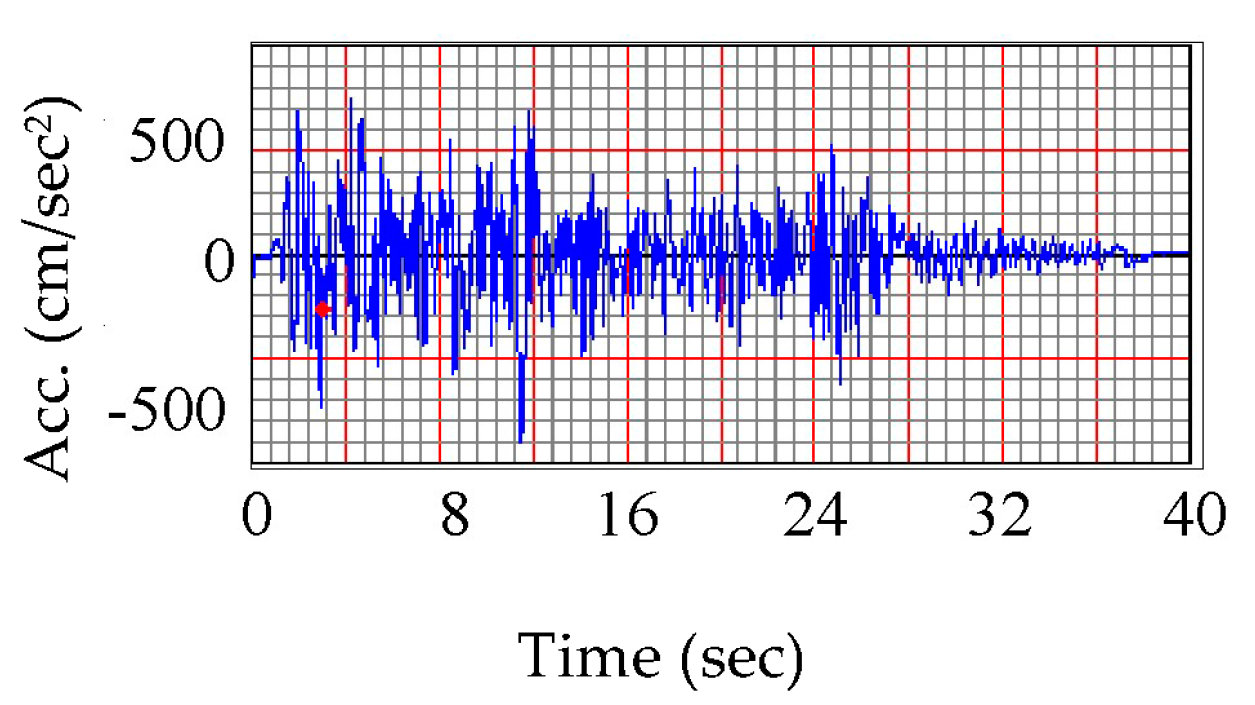
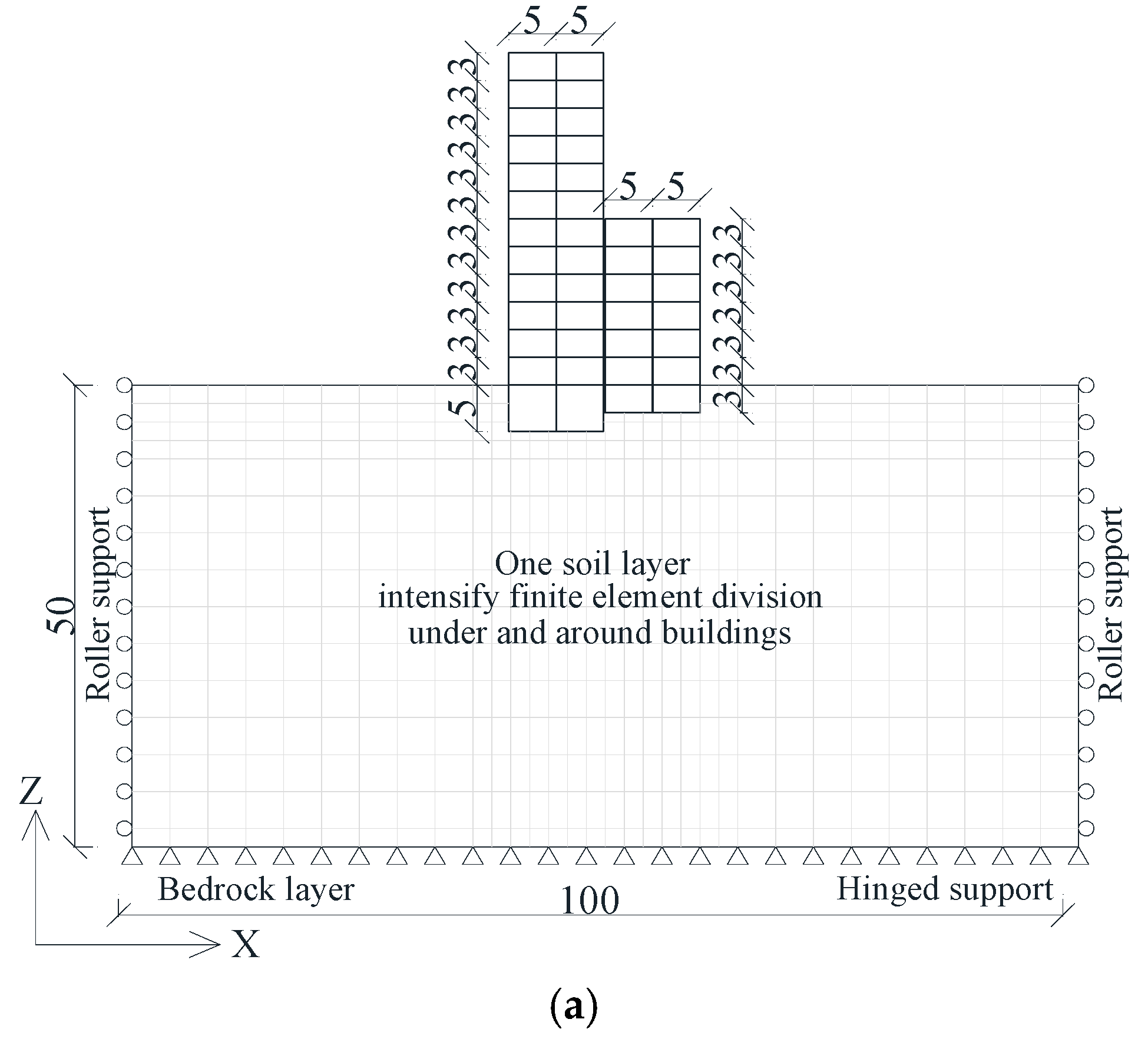
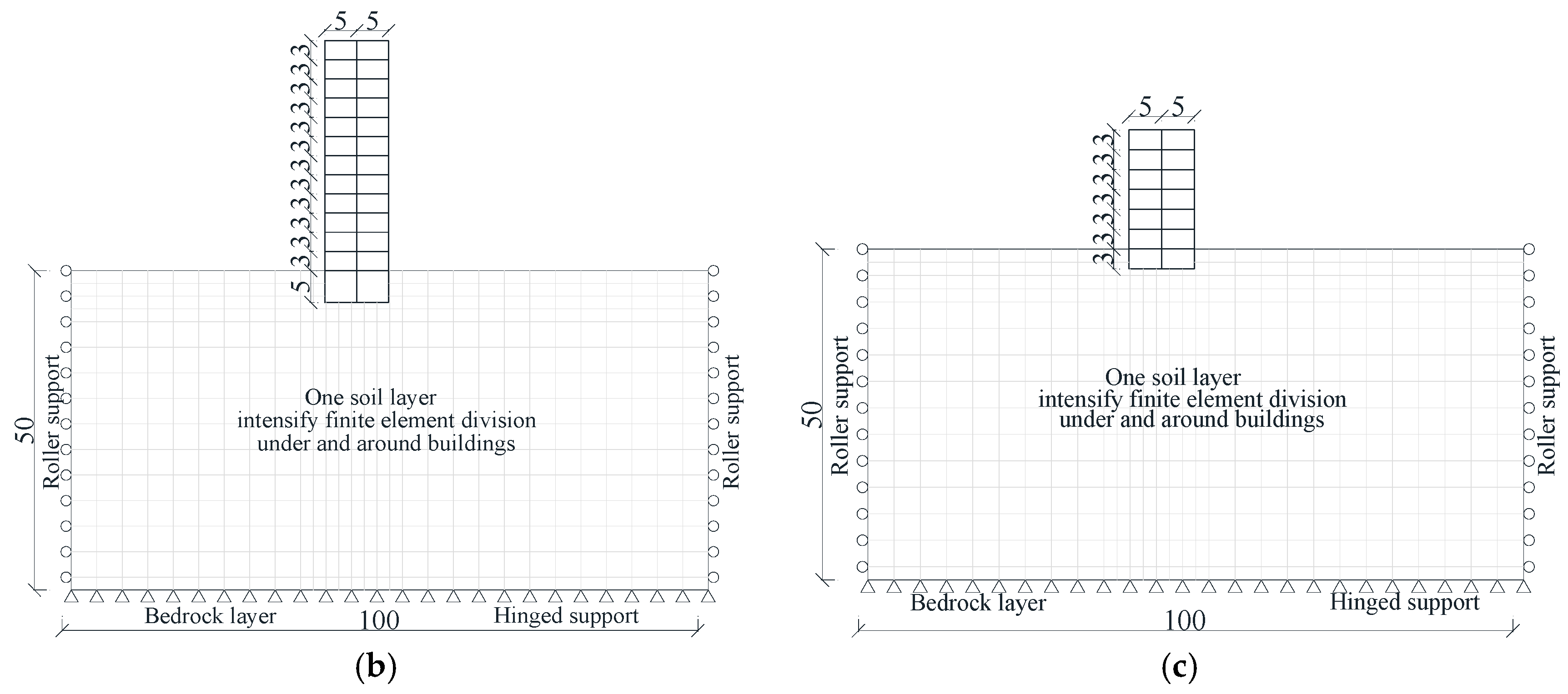
3. Model Description
4. Results and Discussion
4.1. Adjacent Buildings with Equal Foundation Levels
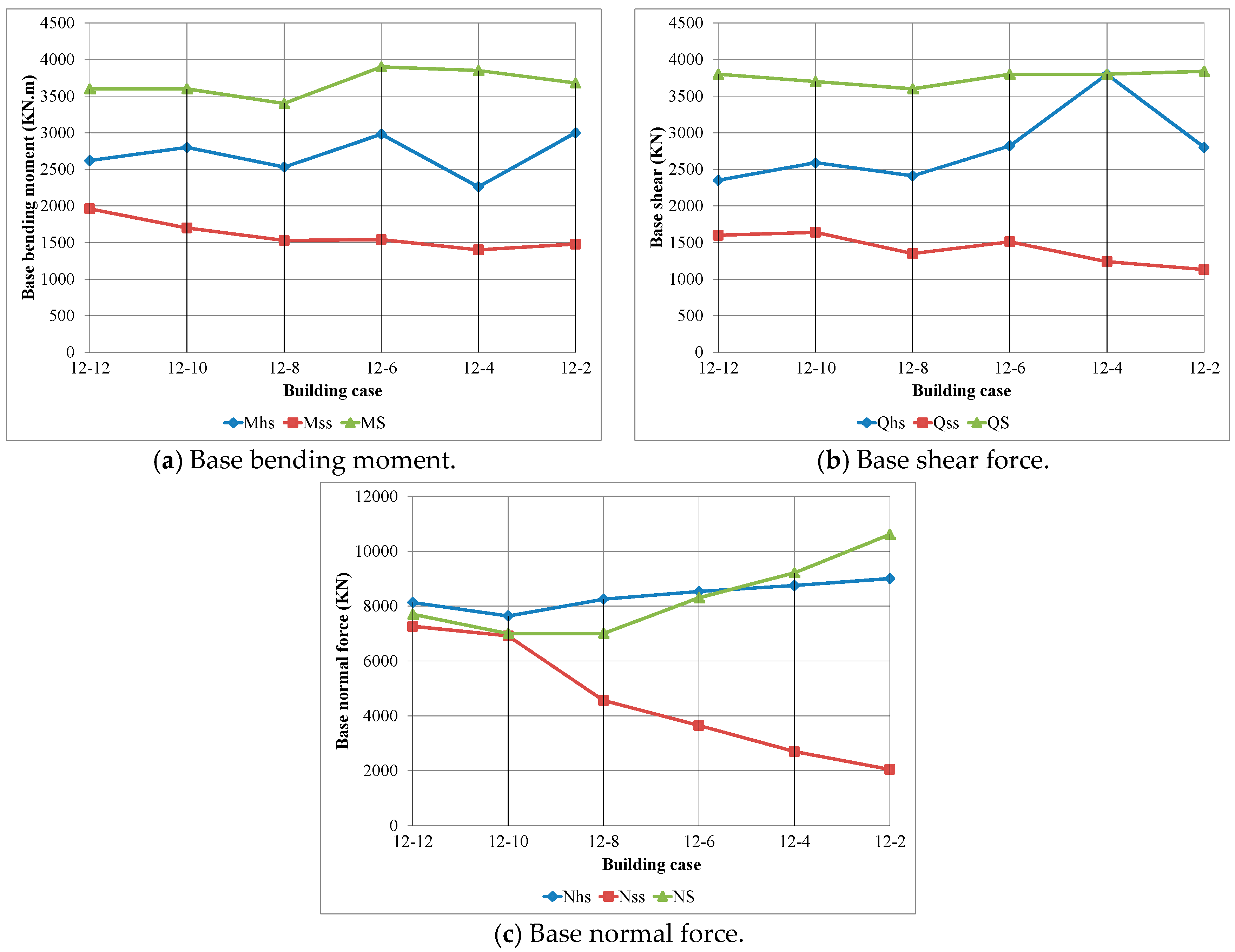
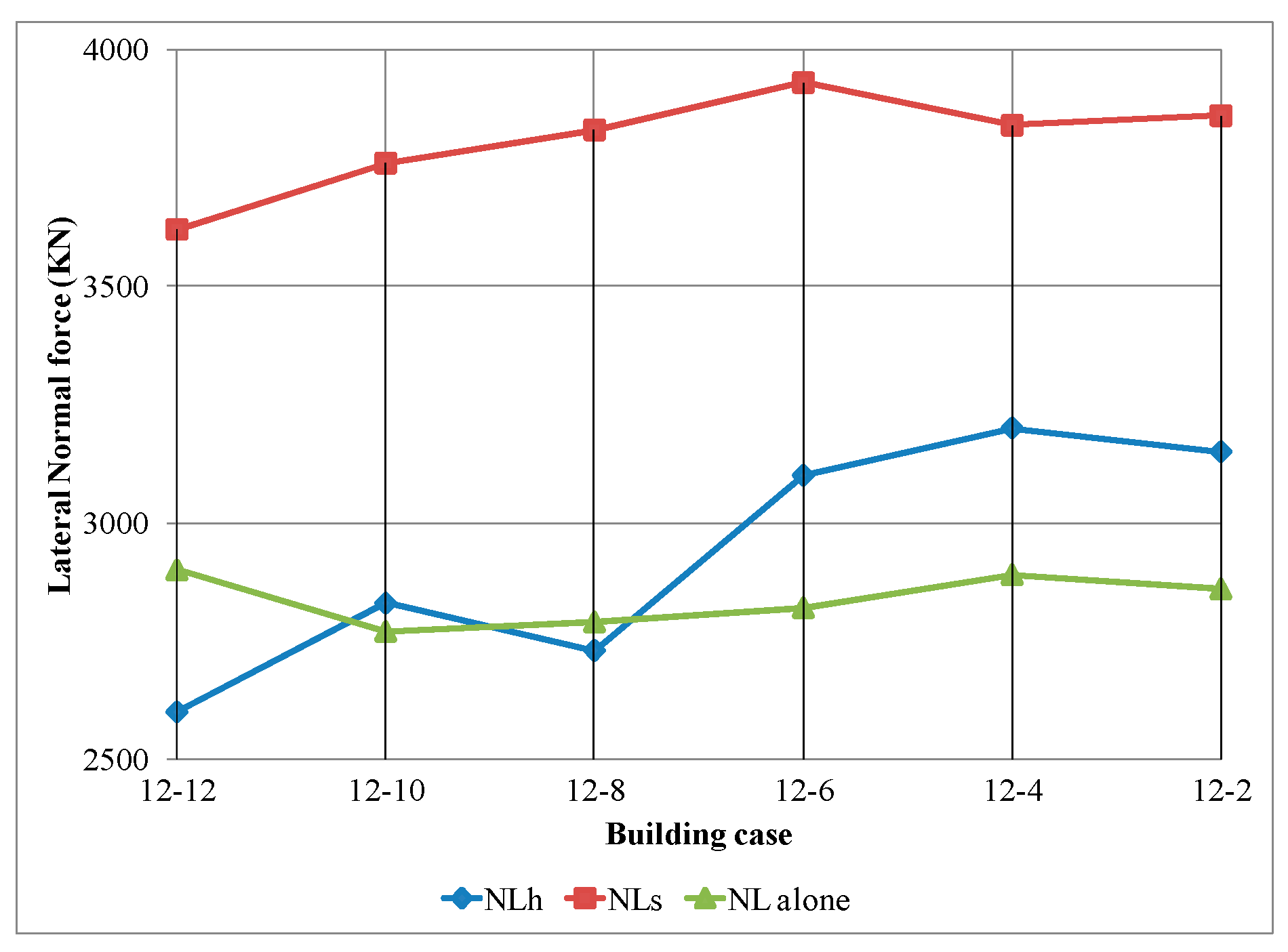
4.2. Adjacent Buildings with Unequal Foundation Levels
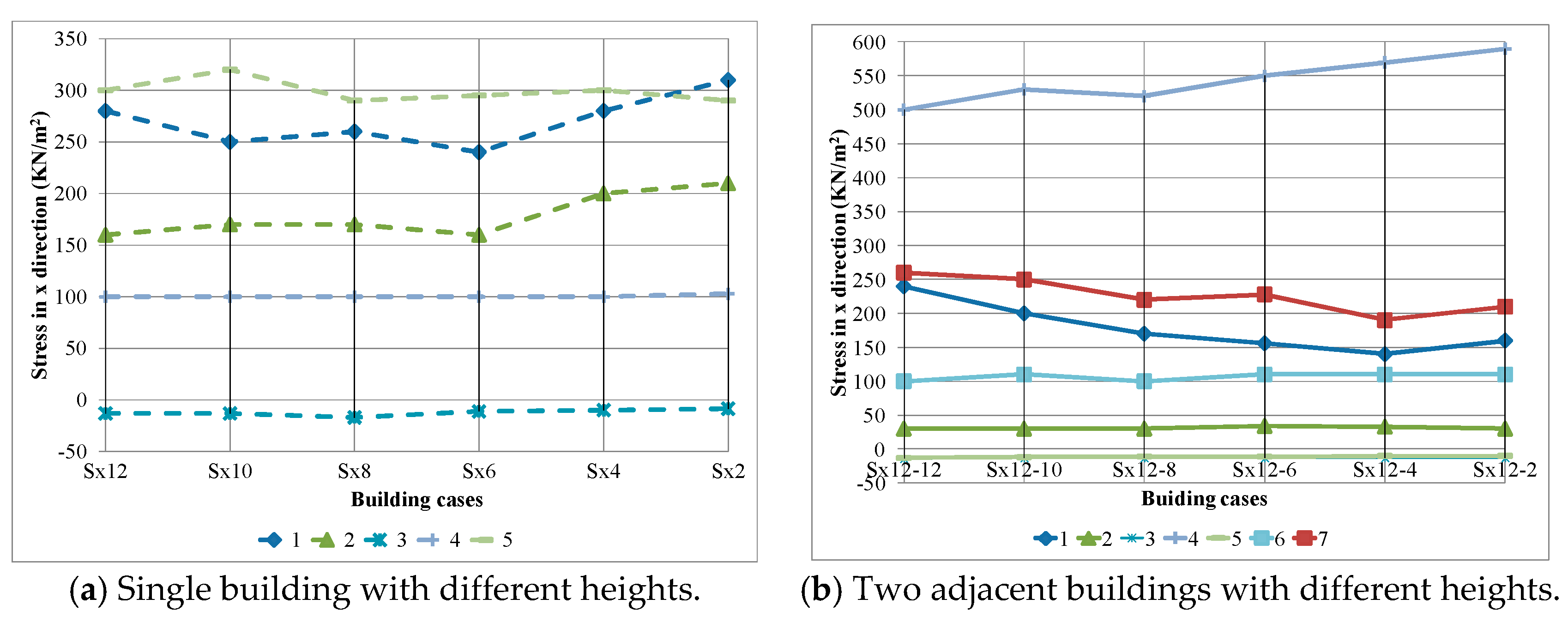
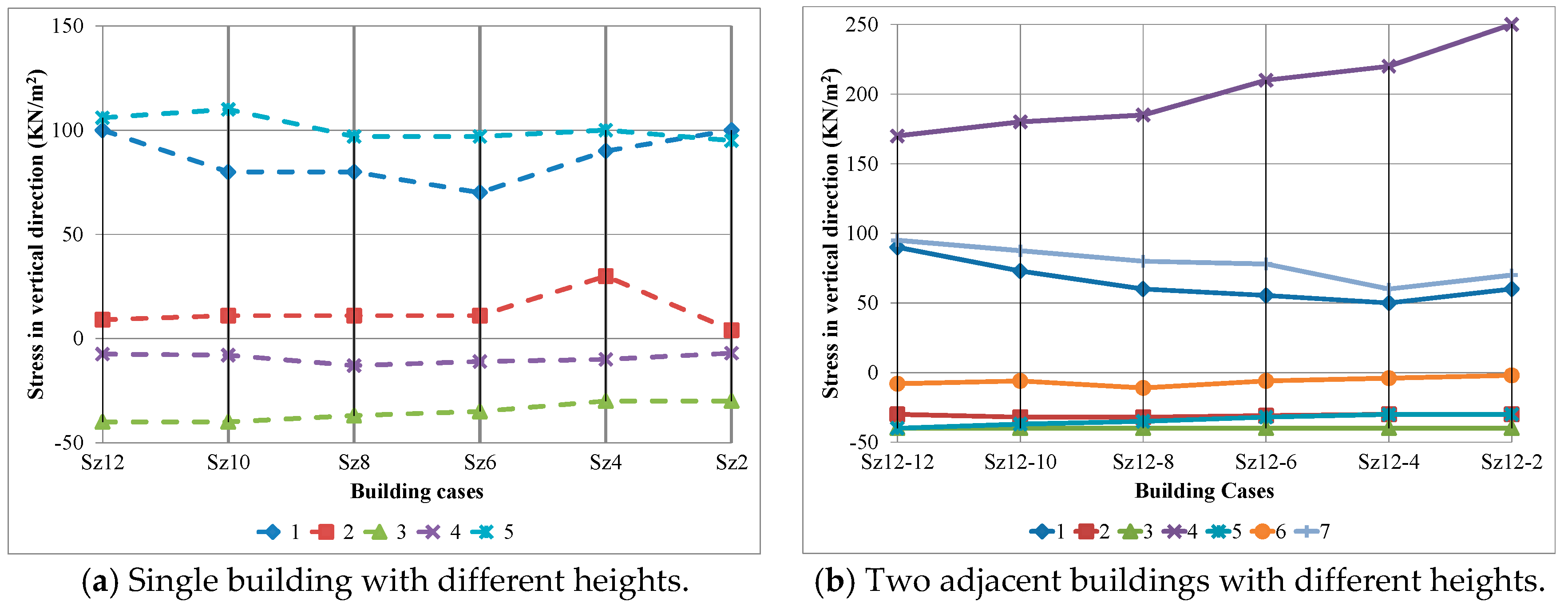
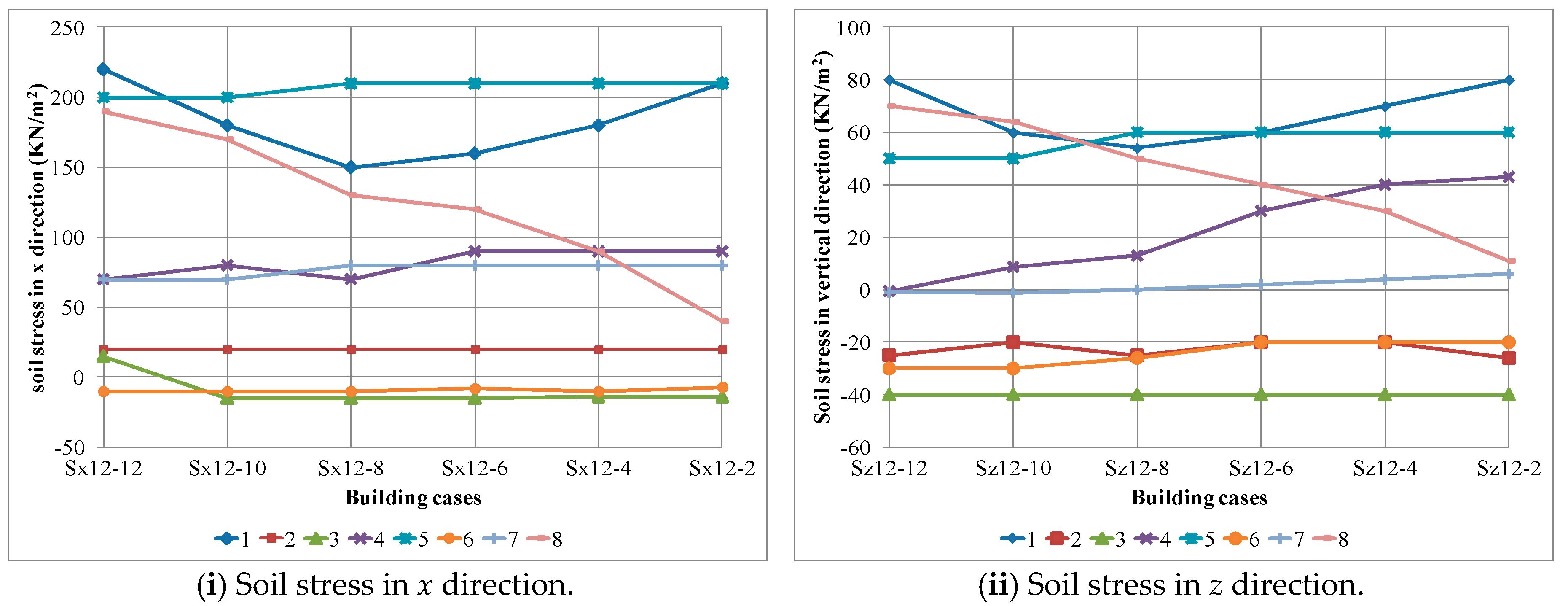
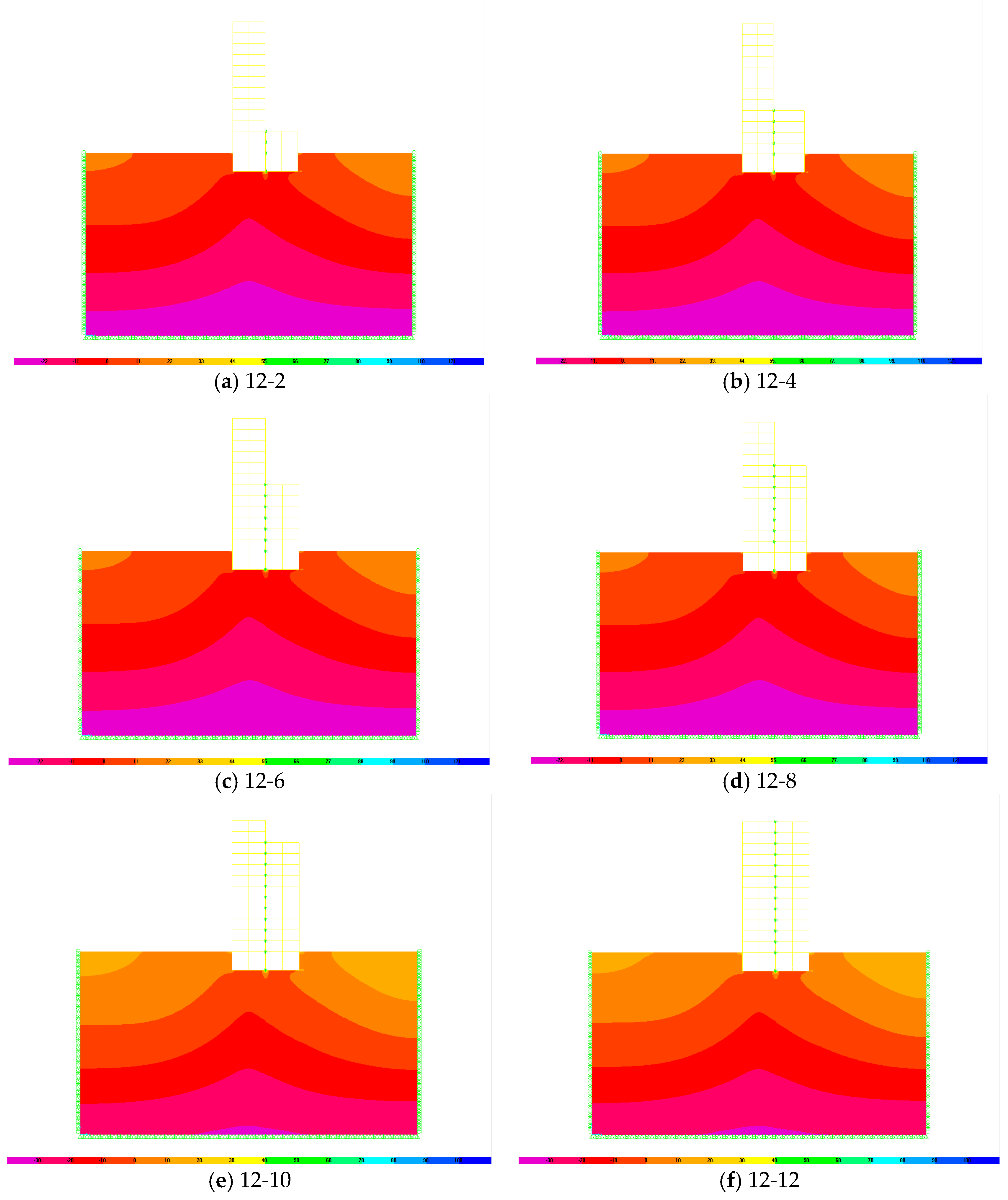
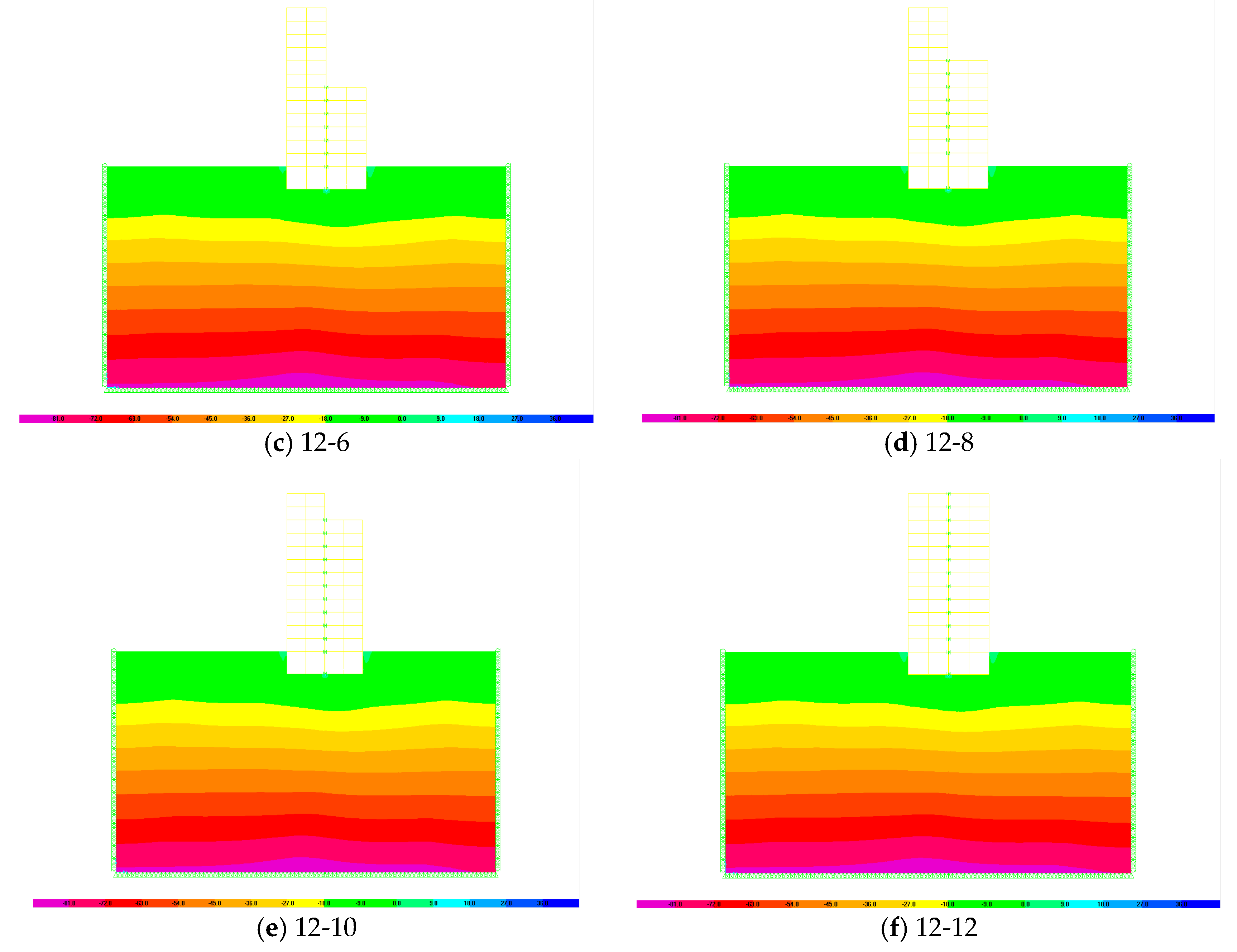
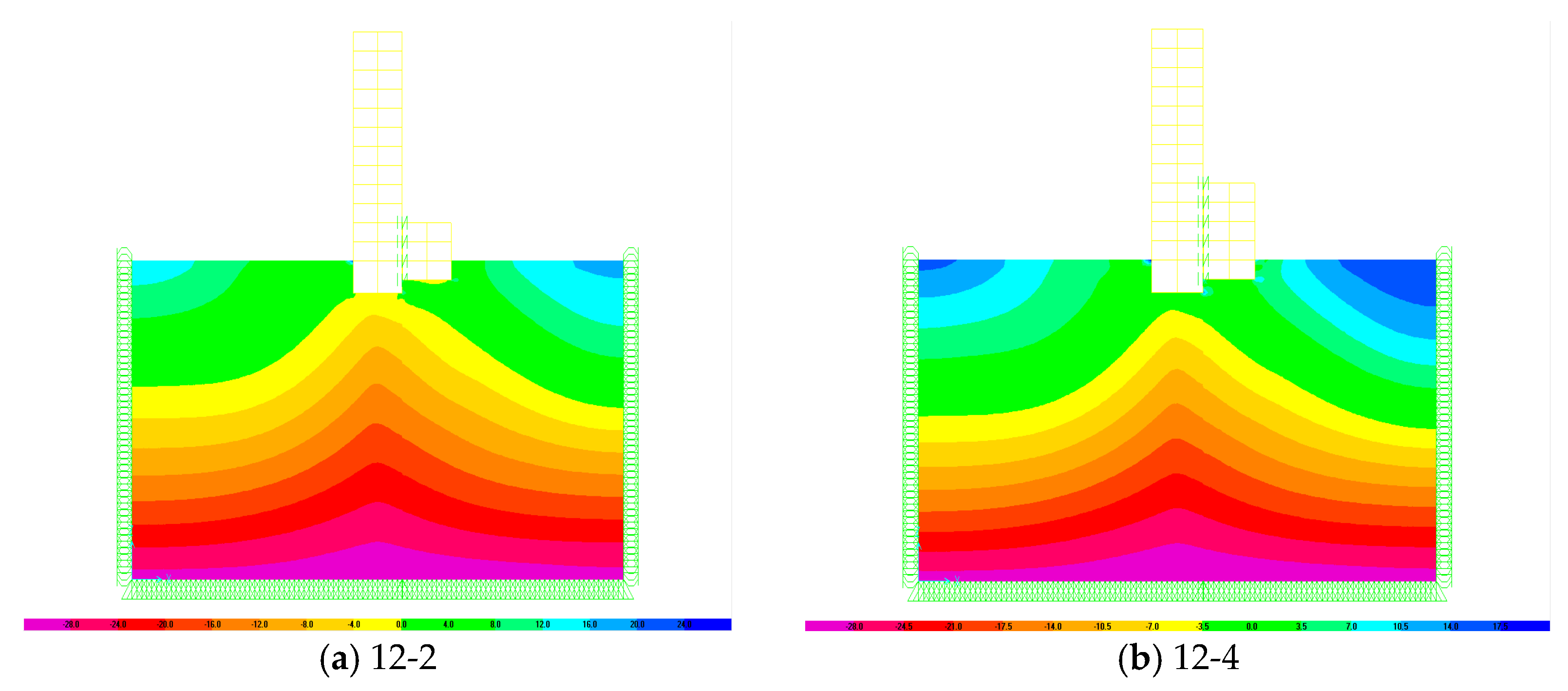
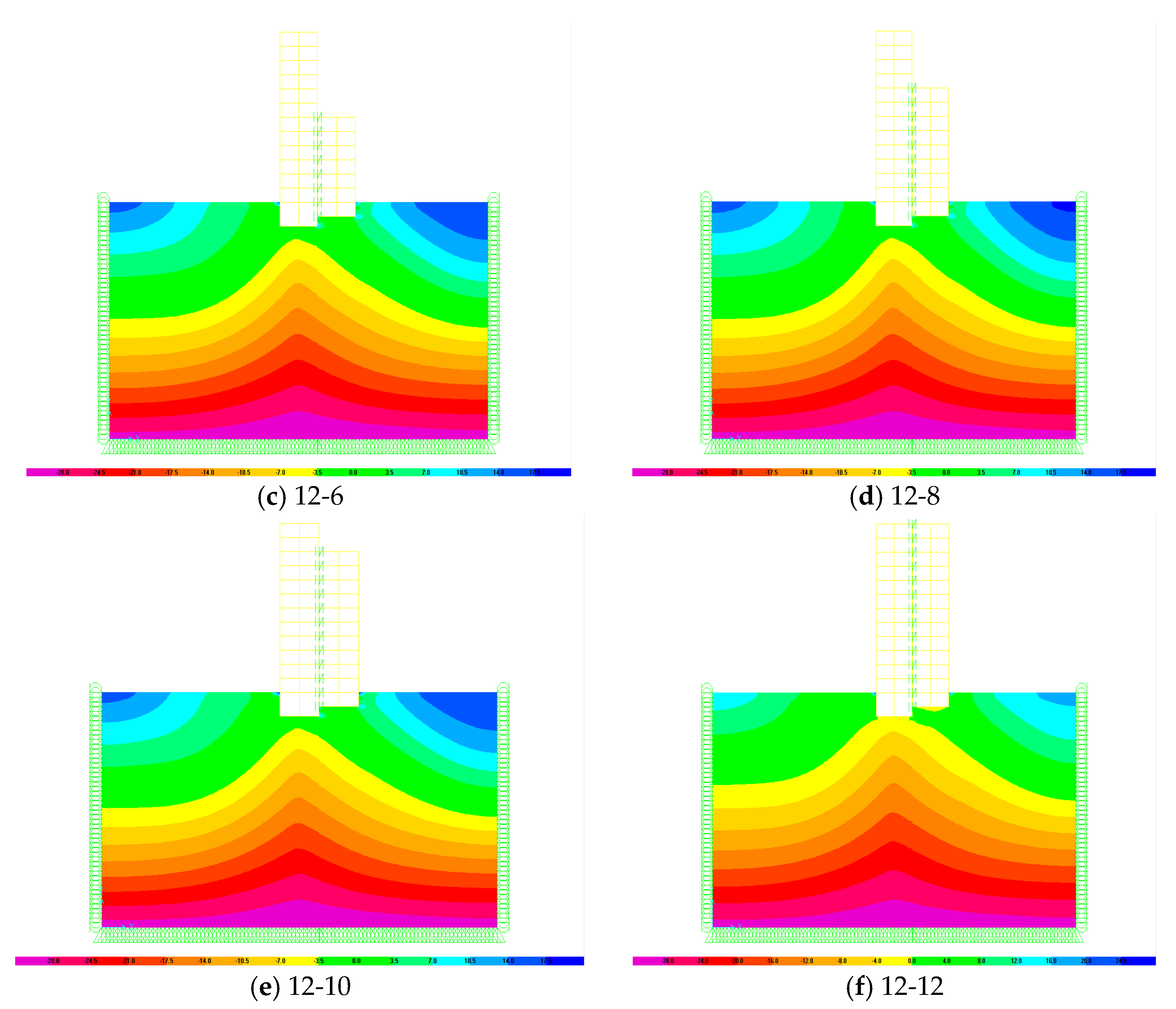
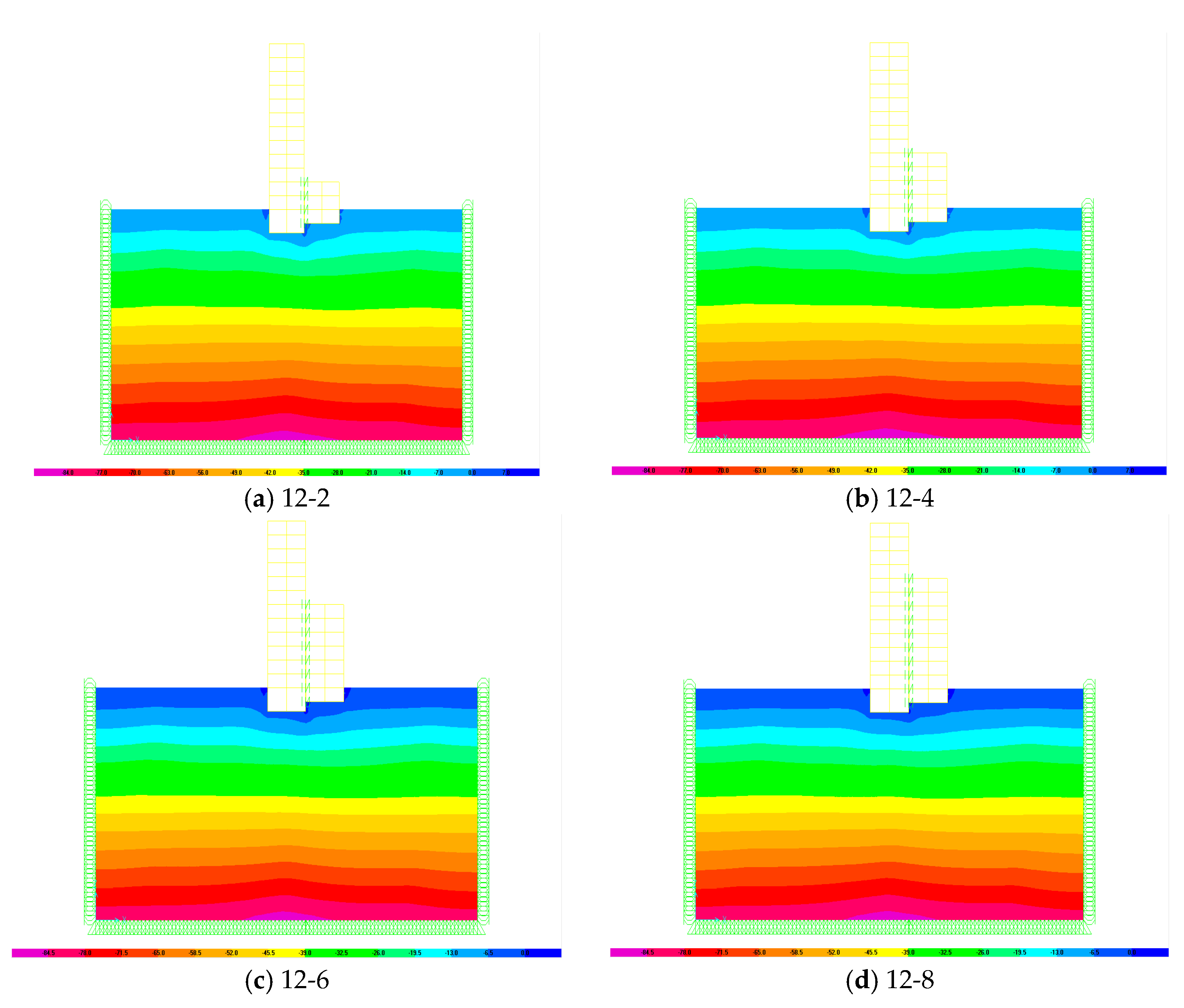
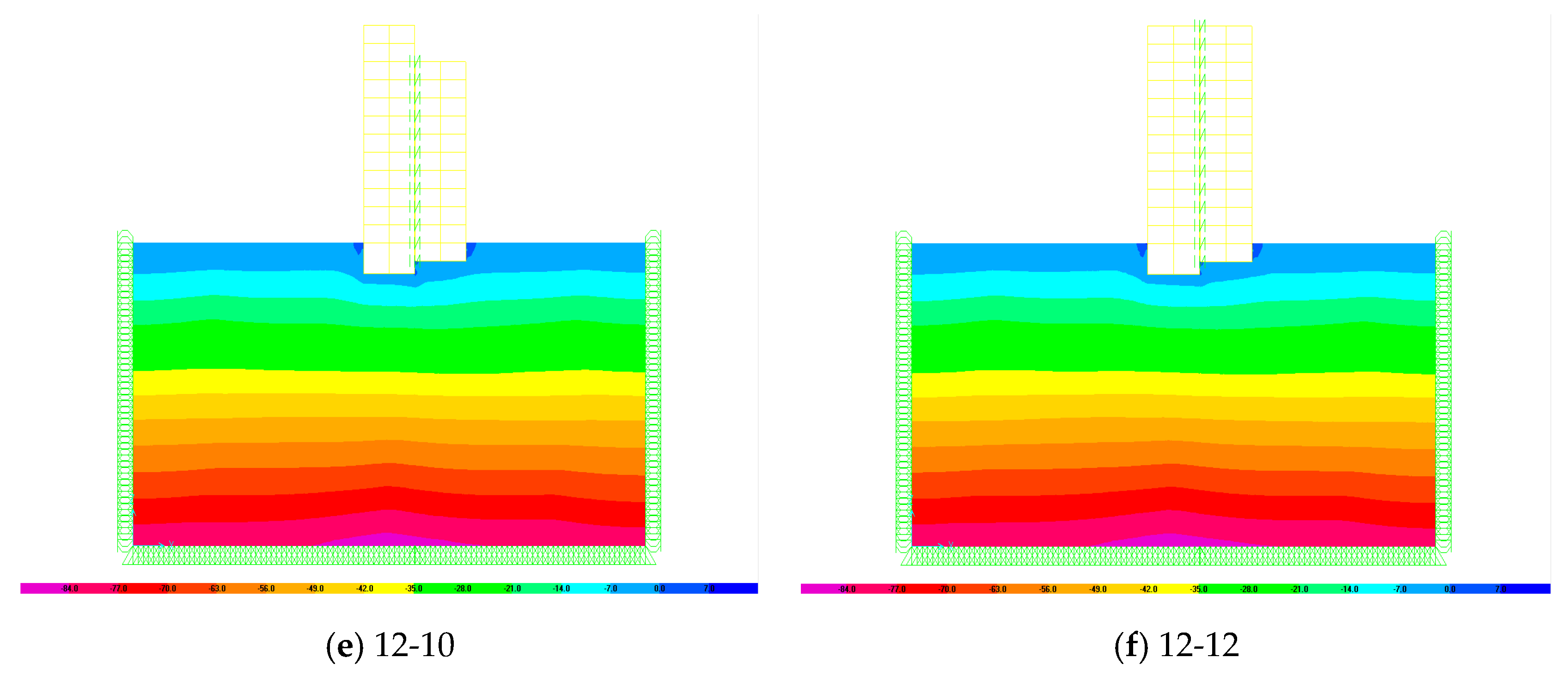
4.3. Soil Response
5. Conclusions
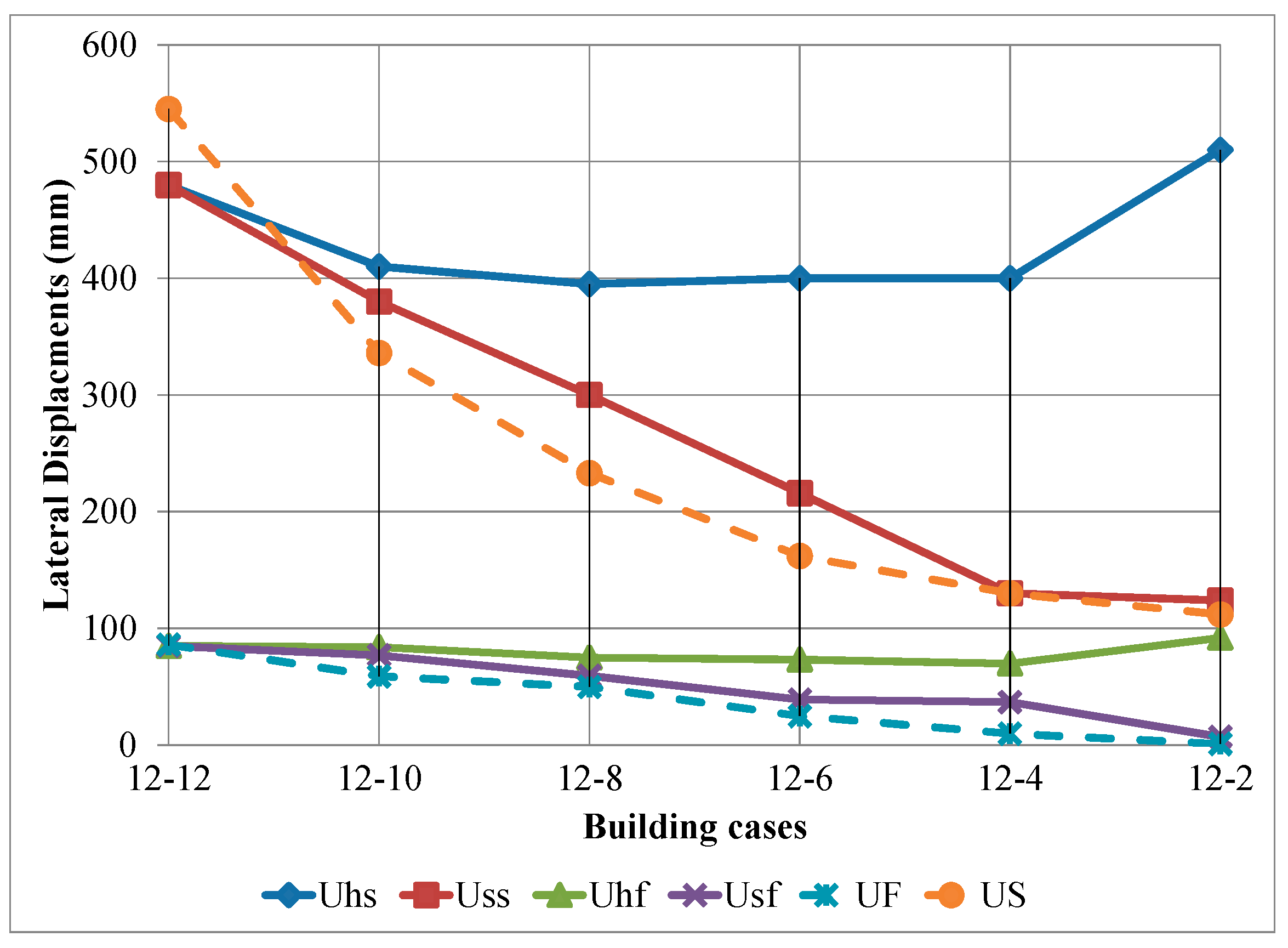
- The top lateral displacement in the single and the two adjacent buildings is bigger in the SSI effect case than in the fixed base case.
- When considering the SSI effect, the top acceleration of the short building in the two adjacent buildings decreases with the decrease of its height, while the top acceleration in the tall building is not strongly affected by the height of the short building.
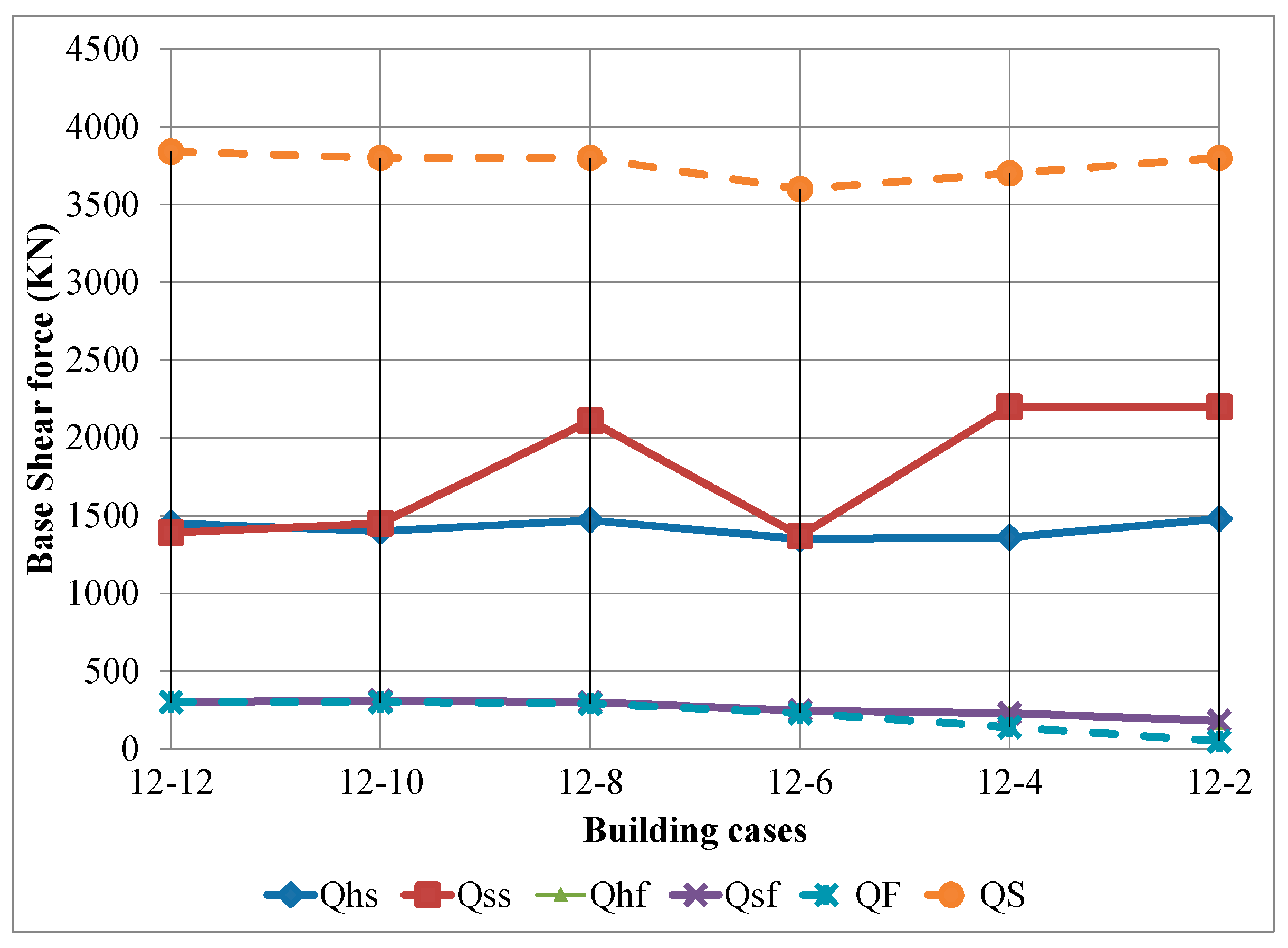
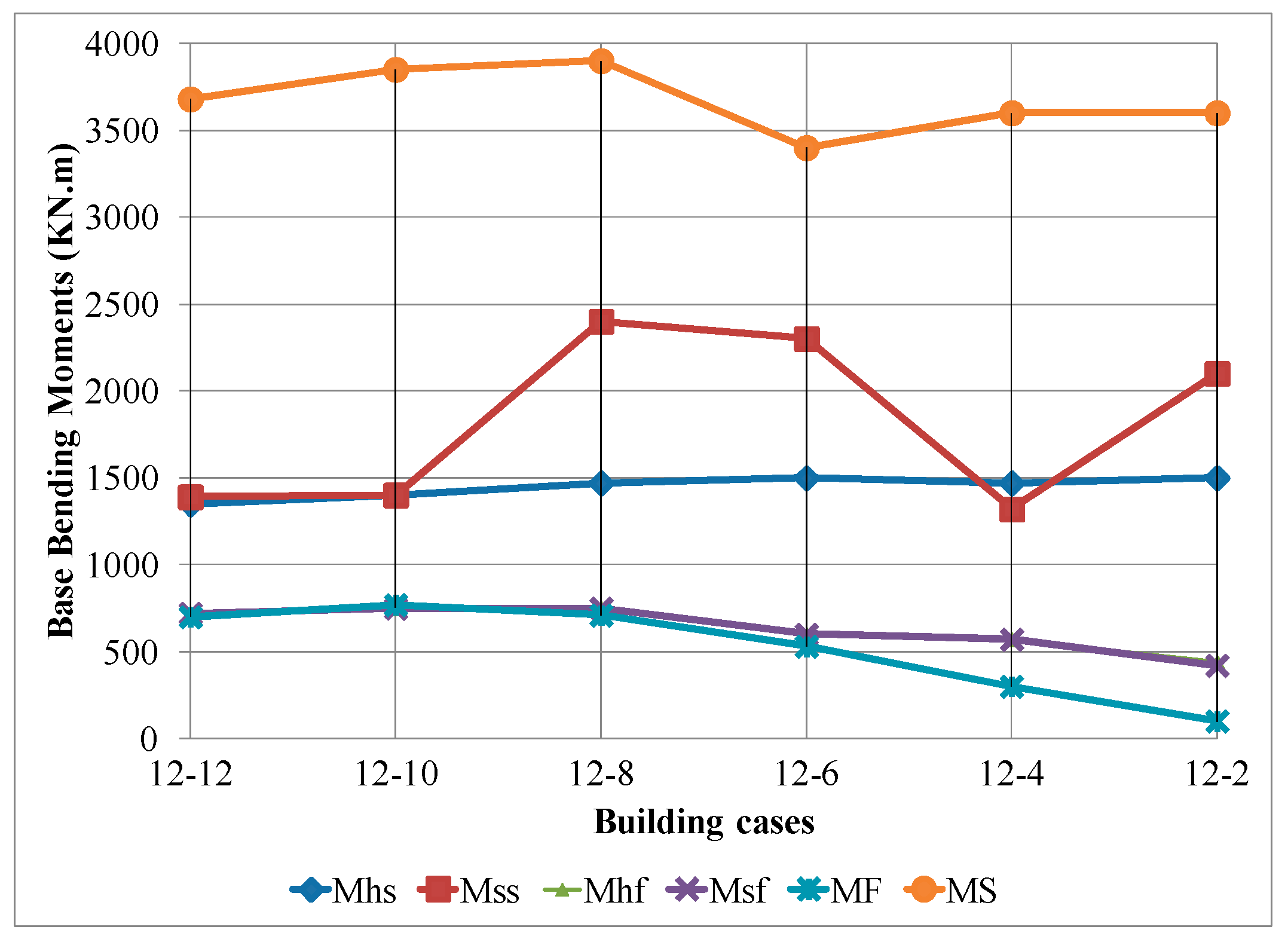
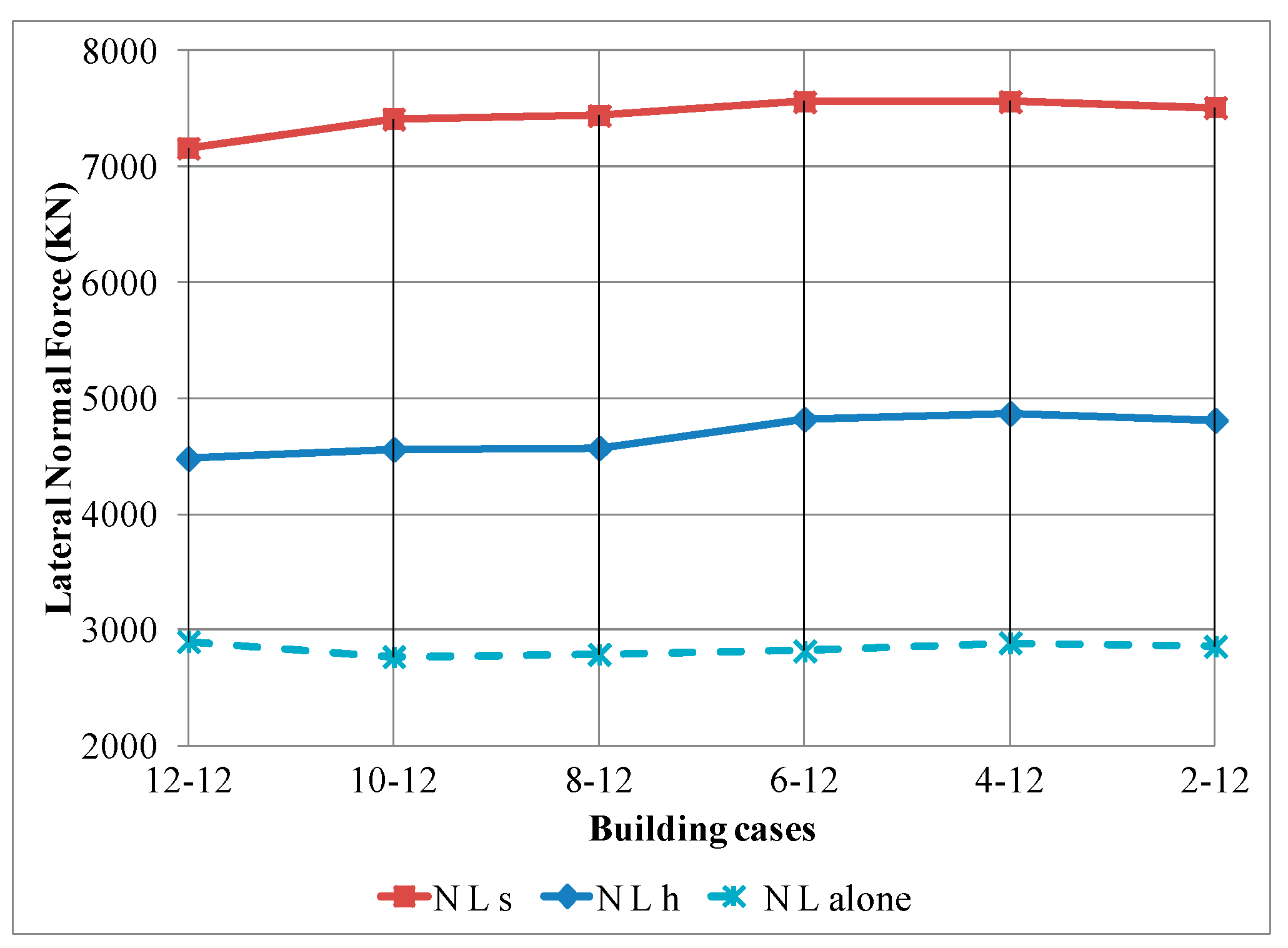
- The base shear forces, the bending moments and the base normal forces in the two adjacent buildings are bigger when considering the SSI effect than in the fixed base case.
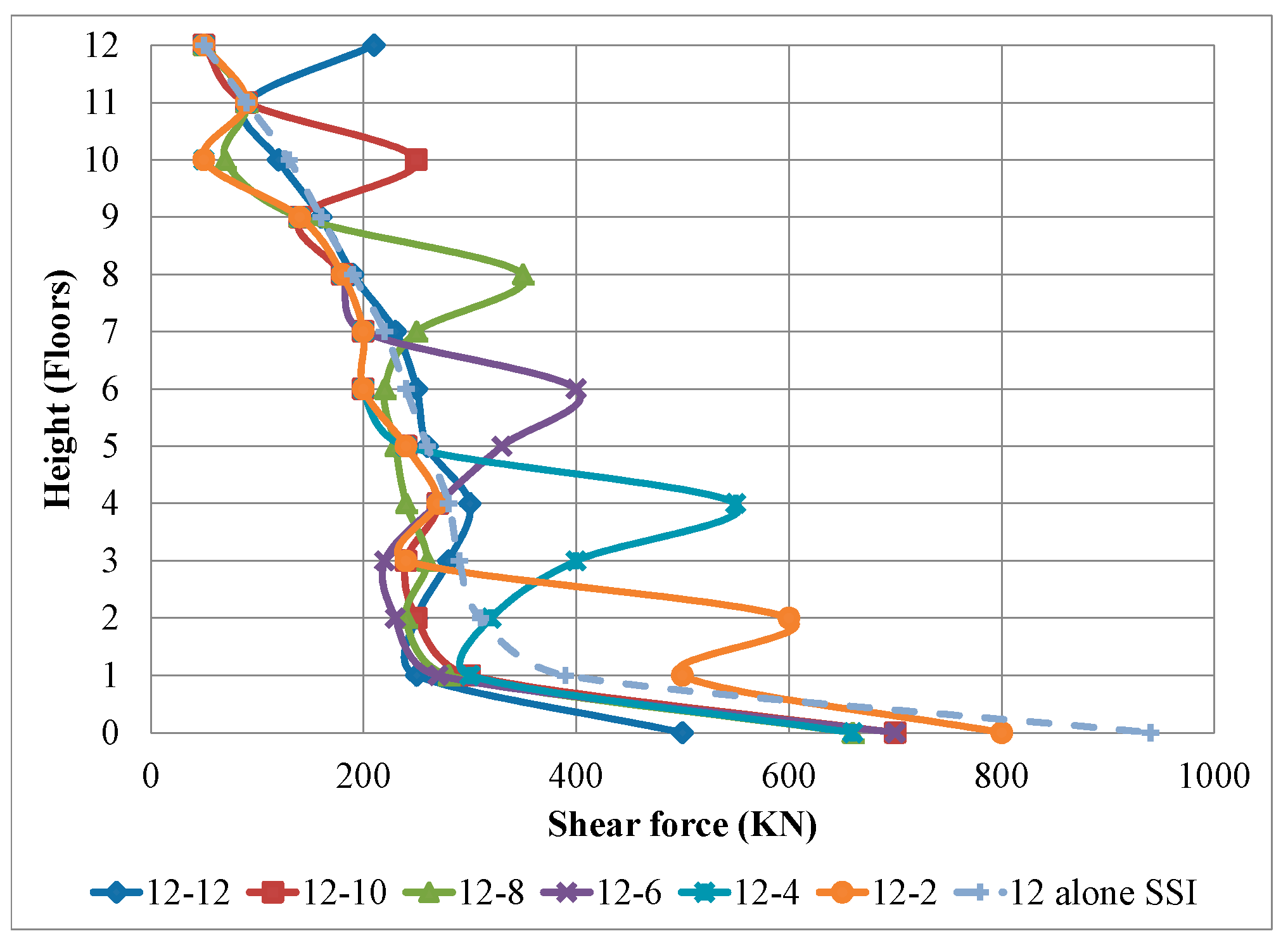
- The shear force in the column in the basement level is bigger than in the floor levels for the different heights of the two adjacent buildings.
- The results of the straining actions on the two adjacent buildings subjected to earthquake considering SSI reveal the double pounding at top of the low building and at foundation level.
- The importance of equal foundation levels should be considered for adjacent buildings even if they have not the same number of floors.
- The soil-structure interaction (SSI) and the double pounding effects should be taken into consideration in the building design and the seismic analysis of adjacent buildings especially those with different heights and different foundation levels.
Author Contributions
Conflicts of Interest
References
- Anagnostopoulos, S.A. Pounding of Buildings in Series during Earthquakes. Earthq. Eng. Struct. Dyn. 1988, 16, 443–456. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A. Equivalent viscous damping for modeling inelastic impacts in earthquake pounding problems. Earthq. Eng. Struct. Dyn. 2004, 33, 897–902. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A.; Spiliopoulos, K.V. An investigation of earthquake induced pounding between adjacent buildings. Earthq. Eng. Struct. Dyn. 1992, 21, 289–302. [Google Scholar] [CrossRef]
- Karayannis, C.G.; Favvata, M.J. Earthquake-induced interaction between adjacent reinforced concrete structures with non-equal heights. Earthq. Eng. Struct. Dyn. 2005, 34, 1–20. [Google Scholar] [CrossRef]
- Karayannis, C.G.; Favvata, M.J. Inter-story pounding between multistory reinforced concrete structures. Struct. Eng. Mech. 2005, 20, 505–526. [Google Scholar] [CrossRef]
- Anagnostopoulos, S.A.; Karamaneas, C.E. Use of collision shear walls to minimize seismic separation and to protect adjacent buildings from collapse due to earthquake-induced pounding. Earthq. Eng. Struct. Dyn. 2008, 37, 1371–1388. [Google Scholar] [CrossRef]
- Efraimiadou, S.; Hatzigeorgiou, G.D.; Beskos, D.E. Structural pounding between adjacent buildings subjected to strong ground motions. Part I: The effect of different structures arrangement. Earthq. Eng. Struct. Dyn. 2013, 42, 1509–1528. [Google Scholar] [CrossRef]
- Efraimiadou, S.; Hatzigeorgiou, G.D.; Beskos, D.E. Structural pounding between adjacent buildings subjected to strong ground motions. Part II: The effect of multiple earthquakes. Earthq. Eng. Struct. Dyn. 2013, 42, 1529–1545. [Google Scholar] [CrossRef]
- Cole, G.; Dhakal, R.; Carr, A.; Bull, D. An Investigation of the Effects of Mass Distribution on Pounding Structures. Earthq. Eng. Struct. Dyn. 2011, 40, 641–659. [Google Scholar] [CrossRef]
- Polycarpou, P.C.; Komodromos, P. Earthquake-induced poundings of a seismically isolated building with adjacent structures. Eng. Struct. 2010, 32, 1937–1951. [Google Scholar] [CrossRef]
- Polycarpou, P.C.; Papaloizou, L.; Komodromos, P. An efficient methodology for simulating earthquake-induced 3D pounding of buildings. Earthq. Eng. Struct. Dyn. 2014, 43, 985–1003. [Google Scholar] [CrossRef]
- Polycarpou, P.C.; Papaloizou, L.; Komodromos, P.; Charmpis, D.C. Effect of the seismic excitation angle on the dynamic response of adjacent buildings during pounding. Earthq. Struct. 2015, 8, 1127–1146. [Google Scholar] [CrossRef]
- Wang, L.X.; Chau, K.T.; Wei, X.X. Numerical Simulations of Nonlinear Seismic Torsional Pounding between Two Single-Story Structures. Adv. Struct. Eng. 2009, 12, 87–101. [Google Scholar] [CrossRef]
- Jankowski, R. Earthquake-Induced Pounding between Equal Height Buildings with substantially different dynamic properties. Eng. Struct. 2008, 30, 2818–2829. [Google Scholar] [CrossRef]
- Papadrakakis, M.; Apostopoulou, C.; Zacharopoulos, A.; Bitzarakis, S. Three Dimensional Simulation of Structural Pounding during Earthquakes. J. Eng. Mech. 1996, 122, 423–431. [Google Scholar] [CrossRef]
- Hao, H.; Liu, X.Y.; Shen, J. Pounding Response of Adjacent Buildings Subjected to Spatial Earthquake Ground Excitations. Adv. Struct. Eng. 2000, 3, 145–162. [Google Scholar] [CrossRef]
- Hao, H.; Gong, L. Analysis of Coupled Lateral-Torsional-Pounding Responses of One-Storey Asymmetric Adjacent Structures Subjected to Bidirectional Ground Motions, Part II: Spatially Varying Ground Motion Input. Adv. Struct. Eng. 2005, 8, 481–496. [Google Scholar] [CrossRef]
- Rahman, A.M.; Carr, A.J.; Moss, P.J. Seismic pounding of a case of adjacent multiple-story buildings of different total heights considering soil flexibility effects. Bull. N. Z. Soc. Earthq. Eng. 2001, 34, 40–59. [Google Scholar]
- Shakya, K.; Wijeyewickrema, A.C. Mid column Pounding of Multi-Story Reinforced Concrete Buildings considering Soil Effects. Adv. Struct. Eng. 2009, 12, 71–85. [Google Scholar] [CrossRef]
- Naserkhaki, S.; Pourmohammad, H. SSI and SSSI effects in seismic analysis of twin buildings: Discrete model concept. J. Civil Eng. Manag. 2012, 18, 890–898. [Google Scholar] [CrossRef]
- Naserkhaki, S.; Abdul Aziz Farah, N.A.; Pourmohammad, H. Earthquake induced pounding between adjacent buildings considering soil-structure interaction. Earthq. Eng. Eng. Vib. 2012, 11, 343–358. [Google Scholar] [CrossRef]
- Mahmoud, S.; Abd-Elhamed, A.; Jankowski, R. Earthquake-induced pounding between equal heights multi-storey buildings considering soil-structure interaction. Bull. Earthq. Eng. 2013, 11, 1021–1048. [Google Scholar] [CrossRef]
- Qin, X.; Chouw, N. Numerical investigation of seismic gap between adjacent structures with SFSI. In Proceedings of the 2013 World Congress on Advances in Structural Engineering and Mechanics (ASEM13), ICC-Jeju, Jeju, Korea, 8–12 September 2013; pp. 4179–4189. [Google Scholar]
- Naserkhaki, S.; El-Richa, M.; Abdul Aziz, F.N.A.; Pourmohammad, H. Separation Gap, A Critical Factor in Earthquake Induced Pounding between Adjacent Buildings. Asian J. Civil Eng. 2013, 14, 881–898. [Google Scholar]
- Behnamfar, F.; Madani, B. Effects of mutual cross interaction and pounding on nonlinear seismic response of adjacent buildings. In Proceedings of the Second European Conference on Earthquake Engineering and Seismology, Istanbul, Turkey, 25–29 August 2014; pp. 1–10. [Google Scholar]
- Alam, M.I.; Kim, D. Spatially Varying Ground Motion Effects on Seismic Response of Adjacent Structures considering Soil Structure Interaction. Adv. Struct. Eng. 2014, 17, 131–142. [Google Scholar] [CrossRef]
- Pawar, P.D.; Murnal, P.B. Effect of Seismic Pounding on Adjacent Blocks of Unsymmetrical Buildings Considering Soil-Structure Interaction. Int. J. Emerg. Technol. Adv. Eng. 2014, 4, 391–395. [Google Scholar]
- Madani, B.; Behnamfar, F.; Tajmir Riahi, H. Dynamic response of structures subjected to pounding and structure-soil-structure interaction. Soil Dyn. Earthq. Eng. 2015, 78, 46–60. [Google Scholar] [CrossRef]
- Ghandil, M.; Behnamfar, F.; Vafaeian, M. Dynamic responses of structure-soil-structure systems with an extension of the equivalent linear soil modelling. Soil Dyn. Earthq. Eng. 2016, 80, 149–162. [Google Scholar] [CrossRef]
- Farghaly, A.A. Seismic analysis of adjacent buildings subjected to double pounding considering soil–structure interaction. Int. J. Adv. Struct. Eng. 2017, 9, 51–62. [Google Scholar] [CrossRef]
- Kharazian, A.; Lopez-Almansa, F. State-of-the-Art of Research on Seismic Pounding Between Buildings with Aligned Slabs. Arch. Comput. Methods Eng. 2017, 1–19. [Google Scholar] [CrossRef]
- Ghandil, M.; Aldaikh, H. Damage-based seismic planar pounding analysis of adjacent symmetric buildings considering inelastic structure–soil–structure interaction. Earthq. Eng. Struct. Dyn. 2017, 46, 1141–1159. [Google Scholar] [CrossRef]
- Li, P.; Liu, S.; Lu, Z. Studies on Pounding Response Considering Structure-Soil-Structure Interaction under Seismic Loads. Sustainability 2017, 9, 2219. [Google Scholar] [CrossRef]
- Jankowski, R. Non-linear viscoelastic modelling of earthquake-induced structural pounding. Earthq. Eng. Struct. Dyn. 2005, 34, 595–611. [Google Scholar] [CrossRef]
- Van Mier, J.G.M.; Preuijssers, A.F.; Reinhardt, H.W.; Monnier, T. Load-Time Response of Colliding Concrete Bodies. J. Struct. Eng. 1991, 117, 354–374. [Google Scholar] [CrossRef]
- SAP2000® Version 17. Integrated Software for Structural Analysis and Design, Computers and Structures, Inc.: Walnut Creek, CA, USA; New York, NY, USA, 2015.
- Egyptian Code of Practice for Reinforced Concrete (ECP-203). In Egyptian Code for Design and Construction of Reinforced Concrete Structures, ECPCS-203; Housing and Building National Research Center, Ministry of Housing, Utilities and Urban Planning: Cairo, Egypt, 2007.
- Egyptian Code of Practice for loading (ECP-201). In Egyptian Code for Calculating Loads and Forces in Structural Work and Masonry, ECP-201; Housing and Building National Research Center, Ministry of Housing, Utilities and Urban Planning: Cairo, Egypt, 2008.
- Nascimbene, R. An Arbitrary Cross Section, Locking Free Shear-flexible Curved Beam Finite Element. Int. J. Comput. Methods Eng. Sci. Mech. 2013, 14, 90–103. [Google Scholar] [CrossRef]
- Nascimbene, R. Towards Non-Standard Numerical Modeling of Thin-Shell Structures: Geometrically Linear Formulation. Int. J. Comput. Methods Eng. Sci. Mech. 2014, 15, 126–141. [Google Scholar] [CrossRef]



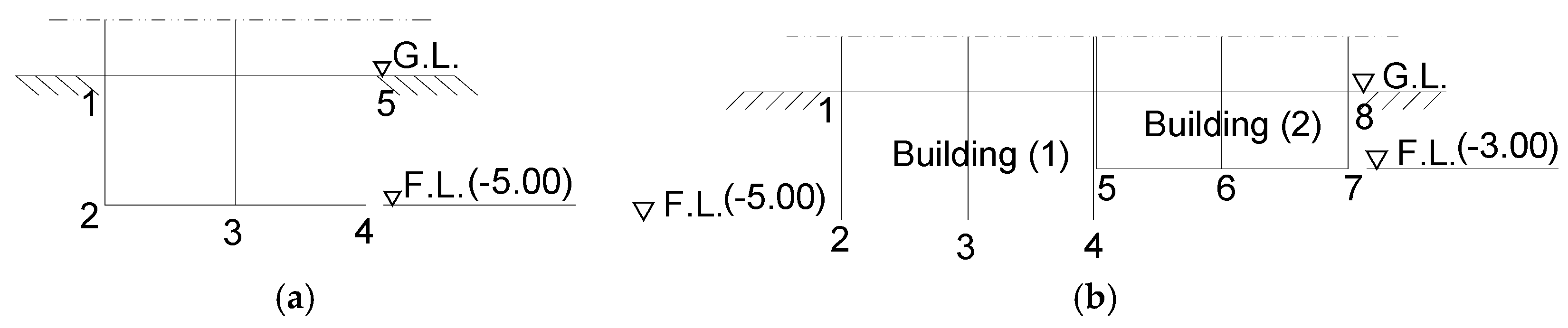



| Elastic Modulus, E (KN/m2) | 30,000 |
| Soil shear modulus, G (KN/m2) | 14,350 |
| Poisson’s ratio, ν | 0.40 |
| Weight per unit volume, γ (KN/m3) | 16 |
| Symbol | Definition | Symbol | Definition |
|---|---|---|---|
| F.L. | Foundation Level. | s | Building considering SSI. |
| G.L. | Ground Level. | S | Single building considering SSI. |
| 12-12 | Two adjacent buildings: both with 12 floors. | f | Fixed base building. |
| 12-10 | Two adjacent buildings: one with 12 floors and the other with 10 floors. | F | Fixed base single building. |
| 12-8 | Two adjacent buildings: one with 12 floors and the other with 8 floors. | U | Displacement. |
| 12-6 | Two adjacent buildings: one with 12 floors and the other with 6 floors. | a | Acceleration. |
| 12-4 | Two adjacent buildings: one with 12 floors and the other with 4 floors. | Q | Base shear force. |
| 12-2 | Two adjacent buildings: one with 12 floors and the other with 2 floors. | M | Base bending moment. |
| h | High (tall) building with 12 floors. | N | Base normal force. |
| s | Short (low) building. | Sx | Lateral soil stress. |
| alone | Single building. | Sz | Vertical soil stress. |
| SSI | Soil Structure Interaction effect. | N L | Lateral normal force at foundation. |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kontoni, D.-P.N.; Farghaly, A.A. Seismic Response of Adjacent Unequal Buildings Subjected to Double Pounding Considering Soil-Structure Interaction. Computation 2018, 6, 10. https://doi.org/10.3390/computation6010010
Kontoni D-PN, Farghaly AA. Seismic Response of Adjacent Unequal Buildings Subjected to Double Pounding Considering Soil-Structure Interaction. Computation. 2018; 6(1):10. https://doi.org/10.3390/computation6010010
Chicago/Turabian StyleKontoni, Denise-Penelope N., and Ahmed Abdelraheem Farghaly. 2018. "Seismic Response of Adjacent Unequal Buildings Subjected to Double Pounding Considering Soil-Structure Interaction" Computation 6, no. 1: 10. https://doi.org/10.3390/computation6010010
APA StyleKontoni, D.-P. N., & Farghaly, A. A. (2018). Seismic Response of Adjacent Unequal Buildings Subjected to Double Pounding Considering Soil-Structure Interaction. Computation, 6(1), 10. https://doi.org/10.3390/computation6010010






