An Overview of Network-Based and -Free Approaches for Stochastic Simulation of Biochemical Systems
Abstract
1. Introduction
2. Network-Based Approach
- Initialize: Set the time and set up the initial state vector, propensities, and random number generators.
- Execute: Using a suitable sampling procedure, generate random numbers and, on the basis of these, determine the next reaction to occur and the time interval.
- Update: Update the molecule count, and if needed, recalculate the propensities. Output the system state.
- Iterate: If simulation end time is not reached, go to step 2.
3. Network-Free Approach
4. Benchmarking Stochastic Simulation
4.1. Simulators
4.2. Models
5. Results
5.1. Increasing Numbers of Particles
5.2. Dependency on the Simulation End Time
6. Discussion
7. Methods
7.1. Model Construction
7.2. Simulations
7.3. Analysis
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Supplementary Figures
Appendix A.1. Multi-State Model
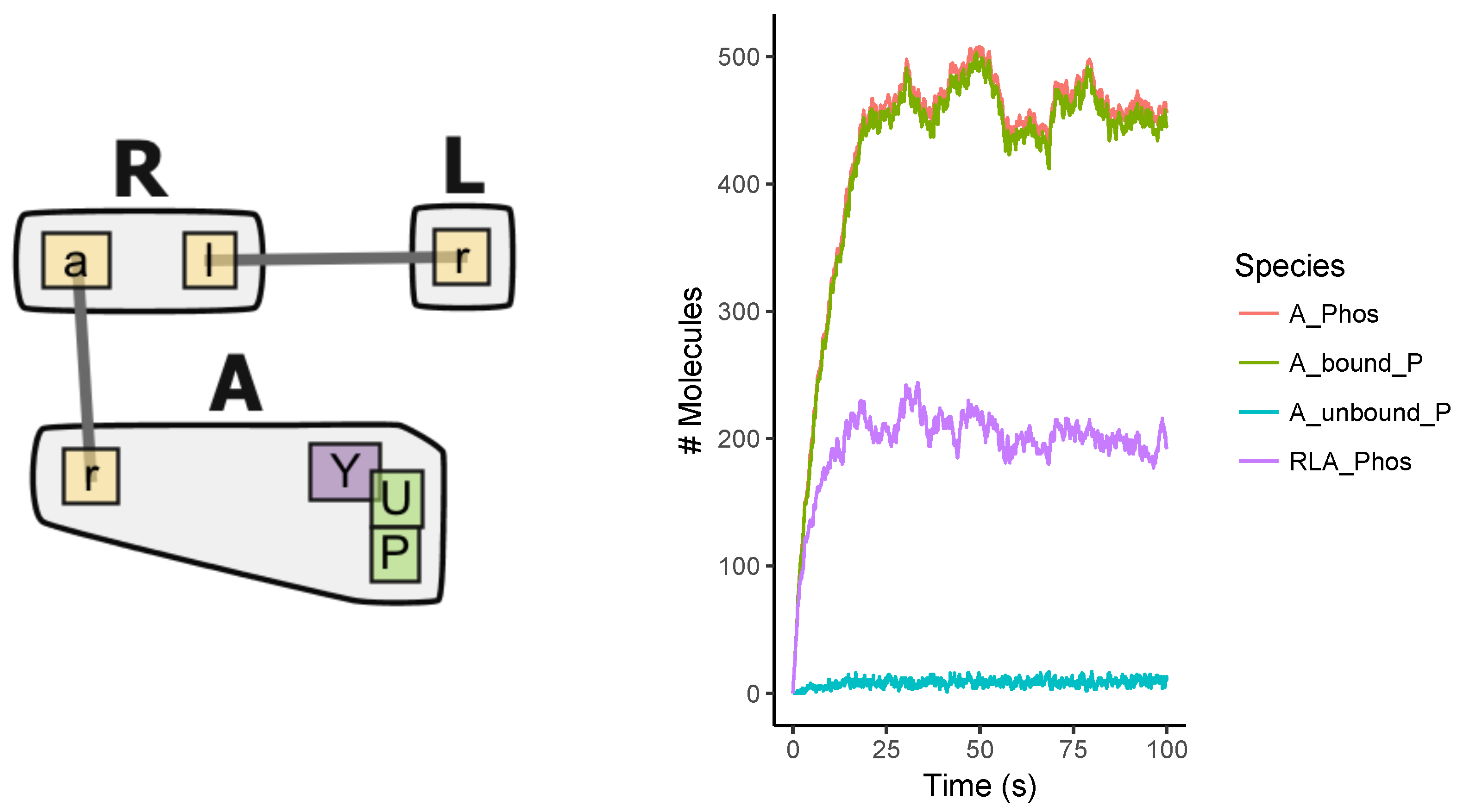
Appendix A.2. Multi-Site Model
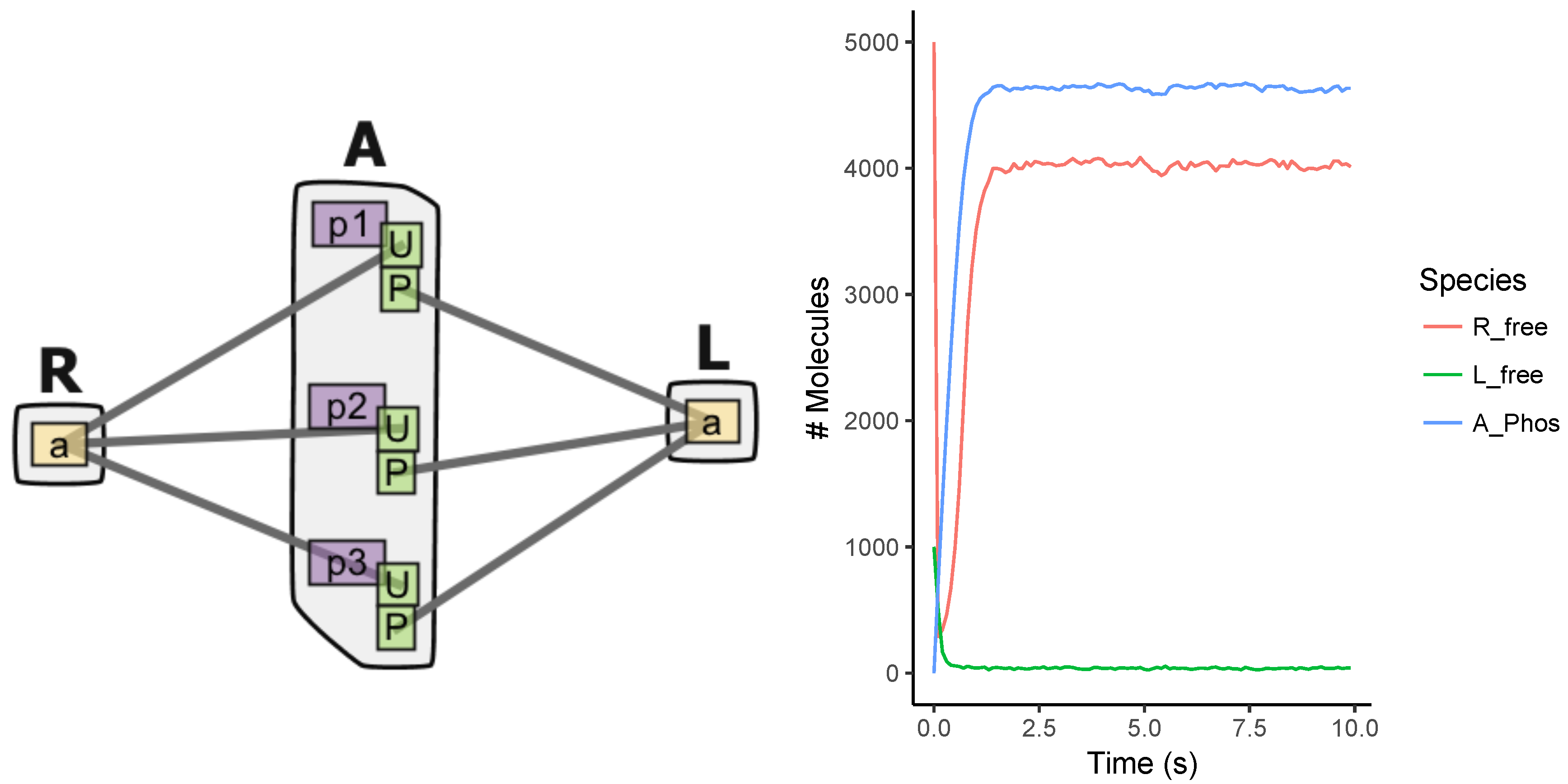
Appendix A.3. EGFR Signaling Model
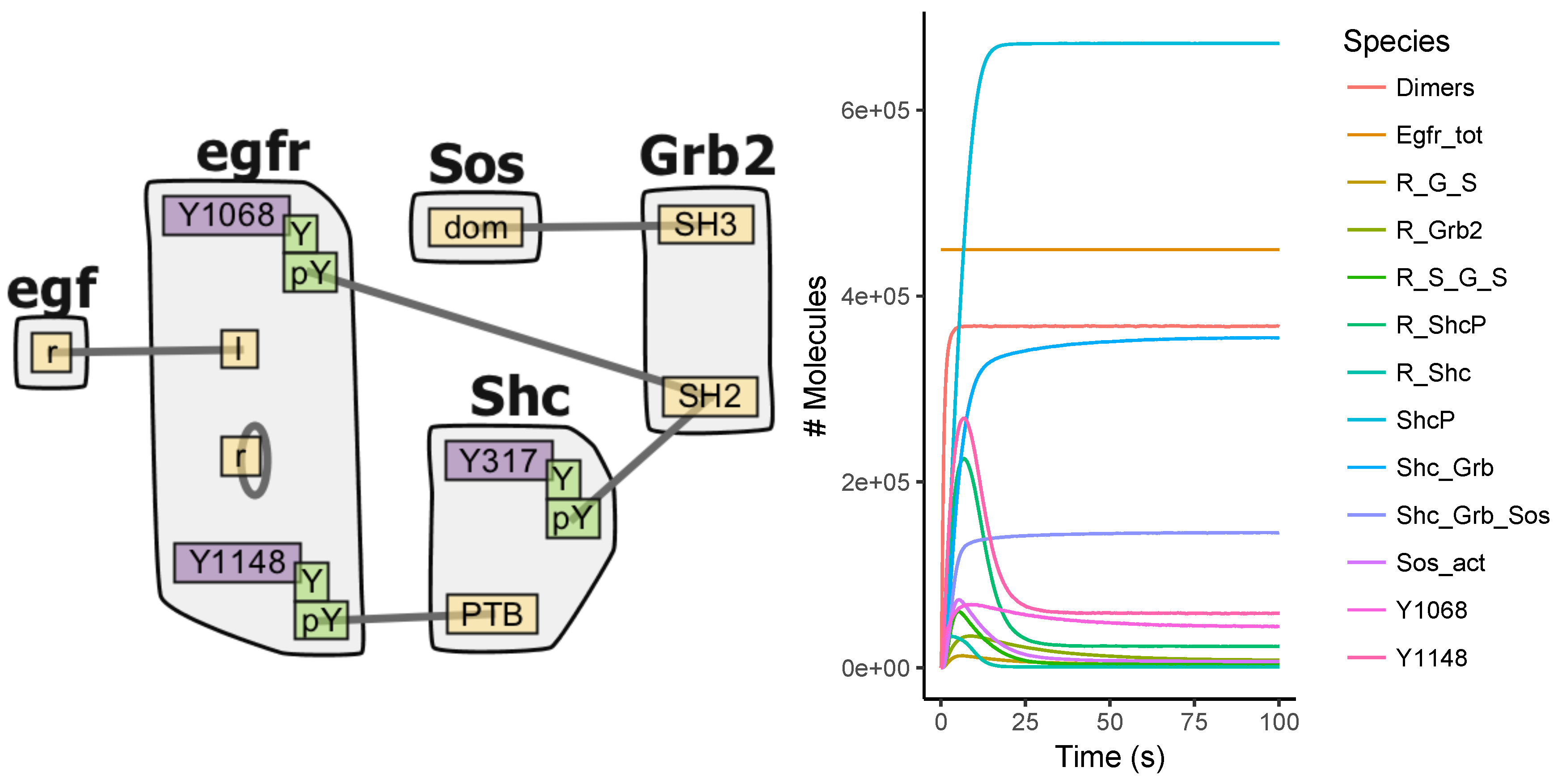
Appendix A.4. BCR Signaling Model
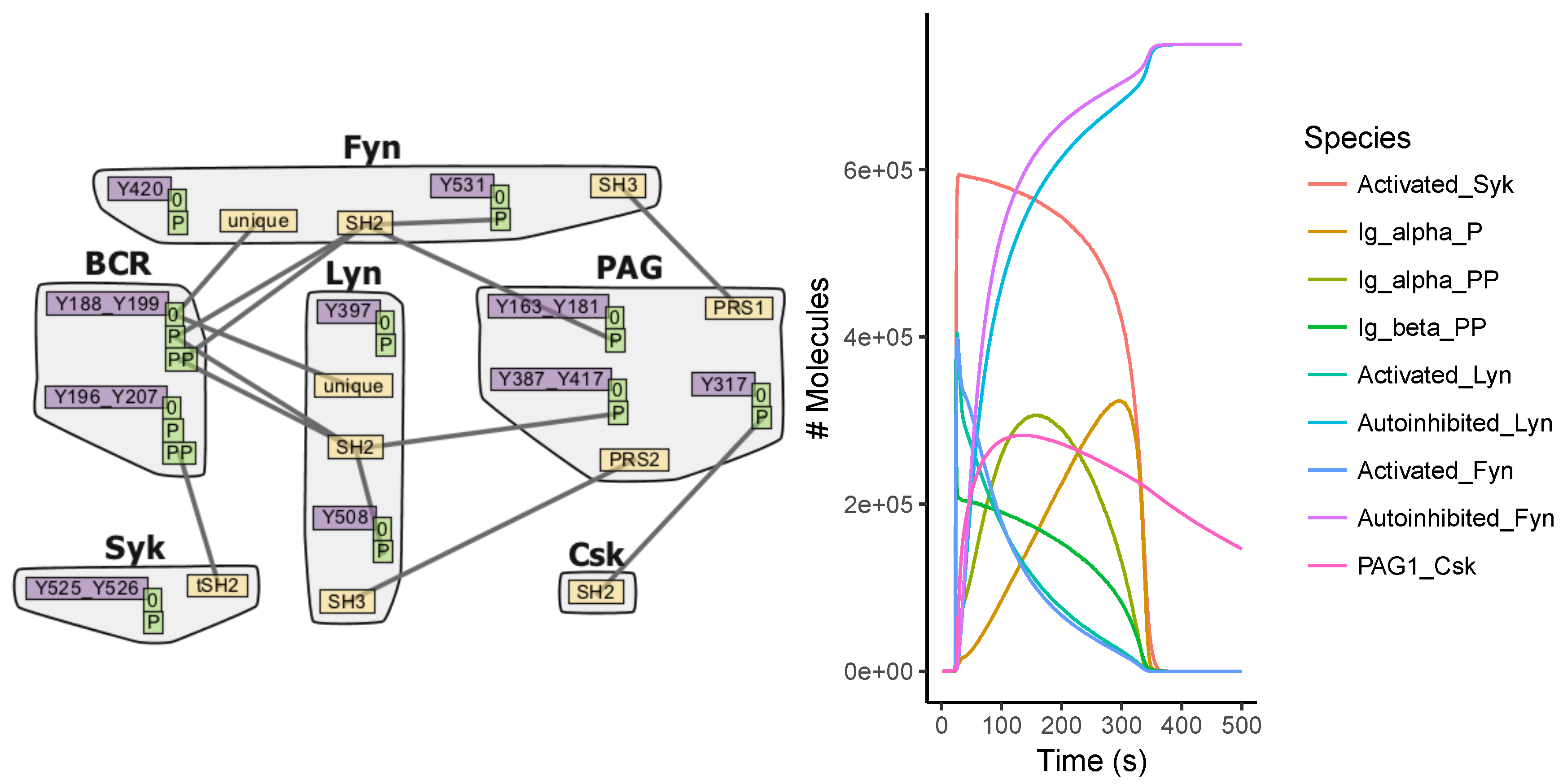
Appendix A.5. FcϵRI Signaling Model
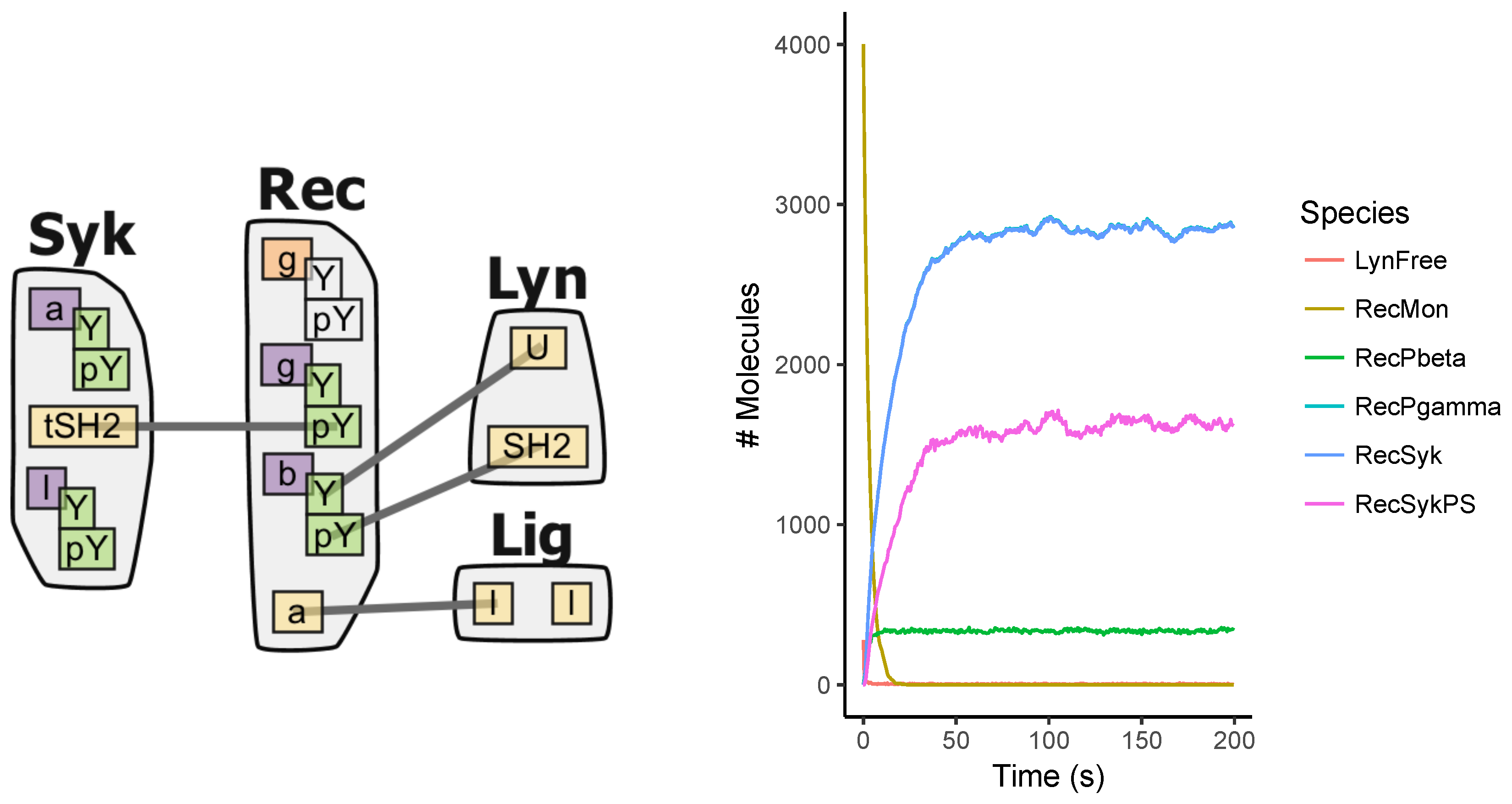
Appendix A.6. Fastest Simulators under the Tested Scenarios

Appendix A.7. Performance Differences between Random Number Generators
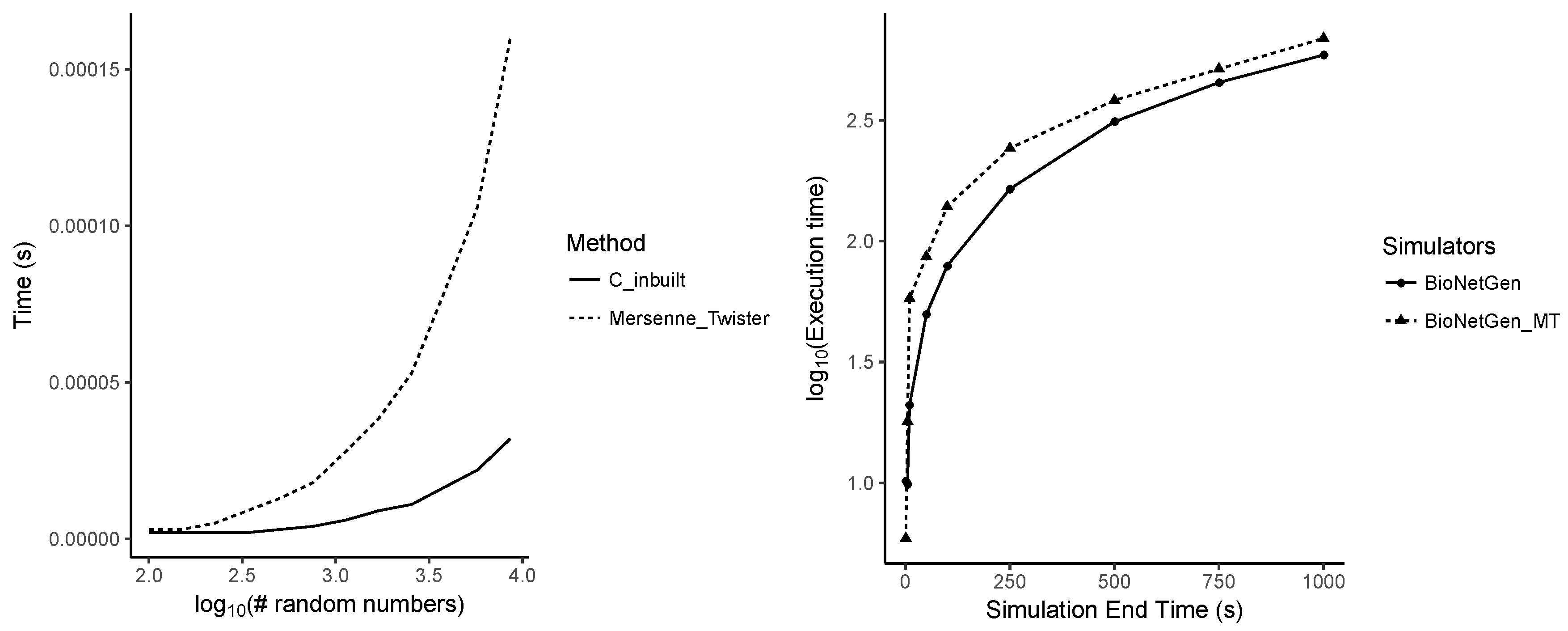
Appendix B. Supplementary Table
| Model | Test Scenario | Number of Molecules | Simulation End Time (s) |
|---|---|---|---|
| Multi-state | Different molecule numbers | R = 500 to 25,000 | 100 |
| L = 100 to 10,000 | |||
| A = 500 to 25,000 | |||
| Different simulation end times | R = 5000, L = 1000, A = 5000 | 1 to 10,000 | |
| Multi-site | Different molecule numbers | R = 500 to 25,000 | 100 |
| L = 100 to 10,000 | |||
| A = 500 to 25,000 | |||
| Different simulation end times | R = 5000, L = 1000, A = 5000 | 1 to 10,000 | |
| EGFR | Different molecule numbers | = 1.2 to 6.0 | 100 |
| = 1800 to 9.0 | |||
| = 1000 to 5.0 | |||
| = 2700 to 1.35 | |||
| = 130 to 6.5 | |||
| = 490 to 2.45 | |||
| Different simulation end times | = 1.2 | 1 to 1000 | |
| = 1.8 | |||
| = 1.0 | |||
| = 2.7 | |||
| = 1.3 | |||
| = 4.9 | |||
| BCR | Different molecule numbers | = 3000 to 7.5 | 100 |
| Different simulation end times | = 30,000 | 1 to 1000 | |
| FcϵRI | Different molecule numbers | = 6000 to 600,000 | 100 |
| = 400 to 40,000 | |||
| = 30 to 3000 | |||
| = 400 to 40,000 | |||
| Different simulation end times | = 60,000 | 1 to 1000 | |
| = 4000 | |||
| = 300 | |||
| = 4000 |
References
- McQuarrie, D. Stochastic approach to chemical kinetics. J. Appl. Probab. 1967, 4, 413–478. [Google Scholar] [CrossRef]
- Gillespie, D.T. A general method for numerically simulating coupled chemical reactions. J. Comput. Phys. 1976, 22, 403–434. [Google Scholar] [CrossRef]
- Gillespie, D.T. Exact Stochastic Simulation of Coupled Chemical Reactions. J. Phys. Chem. 1977, 81, 2340–2361. [Google Scholar] [CrossRef]
- Gibson, M.A.; Bruck, J. Efficient Exact Stochastic Simulation of Chemical Systems with Many Species and Many Channels. J. Phys. Chem. 2000, 104, 1876–1889. [Google Scholar] [CrossRef]
- Cao, Y.; Li, H.; Petzold, L.; Bruck, J. Efficient formulation of the stochastic simulation algorithm for chemically reacting systems. J. Chem. Phys. 2004, 121, 4059–4067. [Google Scholar] [CrossRef] [PubMed]
- Hoops, S.; Sahle, S.; Gauges, R.; Lee, C.; Pahle, J.; Simus, N.; Singhal, M.; Xu, L.; Mendes, P.; Kummer, U. COPASI—A COmplex PAthway SImulator. Bioinformatics 2006, 22, 3067–3074. [Google Scholar] [CrossRef] [PubMed]
- Blinov, M.L.; Schaff, J.C.; Vasilescu, D.; Moraru, I.I.; Bloom, J.E.; Loew, L.M. Compartmental and Spatial Rule-Based Modeling with Virtual Cell. Biophys. J. 2017, 113, 1365–1372. [Google Scholar] [CrossRef] [PubMed]
- Maarleveld, T.R.; Olivier, B.G.; Bruggeman, F.J. StochPy: A Comprehensive, User-Friendly Tool for Simulating Stochastic Biological Processes. PLoS ONE 2013, 8, e79345. [Google Scholar] [CrossRef] [PubMed]
- Ramsey, S.; Orrell, D.; Bolouri, H. Dizzy: Stochastic simulation of large-scale genetic regulatory networks. J. Bioinform. Comput. Biol. 2005, 3, 415–436. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, C.S.; Wilkinson, D.J.; Proctor, C.J.; Shanley, D.P.; Boys, R.J.; Kirkwood, T.B.L. Tools for the SBML Community. Bioinformatics 2006, 22, 628–629. [Google Scholar] [CrossRef] [PubMed]
- Lloyd-Price, J.; Gupta, A.; Ribeiro, A.S. SGNS2: A compartmentalized stochastic chemical kinetics simulator for dynamic cell populations. Bioinformatics 2012, 28, 3004–3005. [Google Scholar] [CrossRef] [PubMed]
- Somogyi, E.T.; Bouteiller, J.M.; Glazier, J.A.; König, M.; Medley, J.K.; Swat, M.H.; Sauro, H.M. libRoadRunner: A high performance SBML simulation and analysis library. Bioinformatics 2015, 31, 3315–3321. [Google Scholar] [CrossRef] [PubMed]
- Ostrenko, O.; Incardona, P.; Ramaswamy, R.; Brusch, L.; Sbalzarini, I.F. pSSAlib: The partial-propensity stochastic chemical network simulator. PLoS Comput. Biol. 2017, 13, e1005865. [Google Scholar]
- Hlavacek, W.S.; Faeder, J.R.; Blinov, M.L.; Perelson, A.S.; Goldstein, B. The complexity of complexes in signal transduction. Biotechnol. Bioeng. 2003, 84, 783–794. [Google Scholar] [CrossRef] [PubMed]
- Hlavacek, W.S.; Faeder, J.R.; Blinov, M.L.; Posner, R.G.; Hucka, M.; Fontana, W. Rules for Modeling Signal-Transduction Systems. Sci. Signal. 2006, 2006. [Google Scholar] [CrossRef] [PubMed]
- Stefan, M.I.; Bartol, T.M.; Sejnowski, T.J.; Kennedy, M.B. Multi-state Modeling of Biomolecules. PLoS Comput. Biol. 2014, 10, e1003844. [Google Scholar] [CrossRef] [PubMed]
- Blinov, M.L.; Faeder, J.R.; Goldstein, B.; Hlavacek, W.S. BioNetGen: Software for rule-based modeling of signal transduction based on the interactions of molecular domains. Bioinformatics 2004, 20, 3289–3291. [Google Scholar] [CrossRef] [PubMed]
- Danos, V.; Laneve, C. Formal molecular biology. Theor. Comput. Sci. 2004, 325, 69–110. [Google Scholar] [CrossRef]
- Sneddon, M.W.; Faeder, J.R.; Emonet, T. Efficient modeling, simulation and coarse-graining of biological complexity with NFsim. Nat. Methods 2010, 8, 177–183. [Google Scholar] [PubMed]
- Chylek, L.A.; Harris, L.A.; Tung, C.S.; Faeder, J.R.; Lopez, C.F.; Hlavacek, W.S. Rule-based modeling: A computational approach for studying biomolecular site dynamics in cell signaling systems. Wiley Interdiscip. Rev. Syst. Biol. Med. 2014, 6, 13–36. [Google Scholar] [CrossRef] [PubMed]
- Chylek, L.A.; Harris, L.A.; Faeder, J.R.; Hlavacek, W.S. Modeling for (physical) biologists: An introduction to the rule-based approach. Phys. Biol. 2015, 12, 045007. [Google Scholar] [CrossRef] [PubMed]
- Danos, V.; Feret, J.; Fontana, W.; Krivine, J. Scalable Simulation of Cellular Signaling Networks. Lect. Notes Comput. Sci. 2007, 4807, 139–157. [Google Scholar]
- Harris, L.A.; Hogg, J.S.; Tapia, J.J.; Sekar, J.A.P.; Gupta, S.; Korsunsky, I.; Arora, A.; Barua, D.; Sheehan, R.P.; Faeder, J.R. BioNetGen 2.2: Advances in rule-based modeling. Bioinformatics 2016, 32, 3366–3368. [Google Scholar] [CrossRef] [PubMed]
- Lopez, C.F.; Muhlich, J.L.; Bachman, J.A.; Sorger, P.K. Programming biological models in Python using PySB. Mol. Syst. Biol. 2013, 9. [Google Scholar] [CrossRef] [PubMed]
- Colvin, J.; Monine, M.I.; Faeder, J.R.; Hlavacek, W.S.; Von Hoff, D.D.; Posner, R.G. Simulation of large-scale rule-based models. Bioinformatics 2009, 25, 910–917. [Google Scholar] [CrossRef] [PubMed]
- McCollum, J.M.; Peterson, G.D.; Cox, C.D.; Simpson, M.L.; Samatova, N.F. The sorting direct method for stochastic simulation of biochemical systems with varying reaction execution behavior. Comput. Biol. Chem. 2006, 30, 39–49. [Google Scholar] [CrossRef] [PubMed]
- Ramaswamy, R.; González-Segredo, N.; Sbalzarini, I.F. A new class of highly efficient exact stochastic simulation algorithms for chemical reaction networks. J. Chem. Phys. 2009, 130, 244104. [Google Scholar] [CrossRef] [PubMed]
- Slepoy, A.; Thompson, A.P.; Plimpton, S.J. A constant-time kinetic Monte Carlo algorithm for simulation of large biochemical reaction networks. J. Chem. Phys. 2008, 128, 205101. [Google Scholar] [CrossRef] [PubMed]
- Ramaswamy, R.; Sbalzarini, I.F. A partial-propensity variant of the composition-rejection stochastic simulation algorithm for chemical reaction networks. J. Chem. Phys. 2010, 132, 044102. [Google Scholar] [CrossRef] [PubMed]
- Thanh, V.H.; Zunino, R.; Priami, C. On the rejection-based algorithm for simulation and analysis of large-scale reaction networks. J. Chem. Phys. 2015, 142, 244106. [Google Scholar] [CrossRef] [PubMed]
- Gillespie, D.T. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 2001, 115, 1716–1733. [Google Scholar] [CrossRef]
- Pahle, J. Biochemical simulations: stochastic, approximate and hybrid approaches. Brief. Bioinform. 2009, 10, 53–64. [Google Scholar] [CrossRef] [PubMed]
- Sanft, K.R.; Wu, S.; Roh, M.; Fu, J.; Lim, R.K.; Petzold, L.R. StochKit2: Software for discrete stochastic simulation of biochemical systems with events. Bioinformatics 2011, 27, 2457–2458. [Google Scholar] [CrossRef] [PubMed]
- Palmisano, A.; Hoops, S.; Watson, L.T.; Jones, T.C., Jr.; Tyson, J.J.; Shaffer, C.A. Multistate Model Builder (MSMB): A flexible editor for compact biochemical models. BMC Syst. Biol. 2014, 8. [Google Scholar] [CrossRef] [PubMed]
- Faeder, J.R.; Blinov, M.L.; Goldstein, B.; Hlavacek, W.S. Rule-based modeling of biochemical networks. Complexity 2005, 10, 22–41. [Google Scholar] [CrossRef]
- Blinov, M.L.; Yang, J.; Faeder, J.R.; Hlavacek, W.S. Graph Theory for Rule-Based Modeling of Biochemical Networks. Trans. Comput. Syst. Biol. 2006, 7, 89–106. [Google Scholar]
- Hogg, J.S.; Harris, L.A.; Stover, L.J.; Nair, N.S.; Faeder, J.R. Exact Hybrid Particle/Population Simulation of Rule-Based Models of Biochemical Systems. PLoS Comput. Biol. 2014, 10, e1003544. [Google Scholar] [CrossRef] [PubMed]
- Andrei, O.; Kirchner, H. A Rewriting Calculus for Multigraphs with Ports. Electron. Notes Theor. Comput. Sci. 2008, 219, 67–82. [Google Scholar] [CrossRef]
- Colvin, J.; Monine, I.M.; Gutenkunst, R.N.; Hlavacek, W.S.; Hoff, D.D.V.; Posner, R.G. RuleMonkey: Software for stochastic simulation of rule-based models. BMC Bioinform. 2010, 11, 404. [Google Scholar] [CrossRef] [PubMed]
- Novere, N.L.; Shimizu, T.S. STOCHSIM: Modelling of stochastic biomolecular processes. Bioinformatics 2001, 17, 575–576. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Hlavacek, W.S. Efficiency of reactant site sampling in network-free simulation of rule-based models for biochemical systems. Phys. Biol. 2011, 8. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Monine, M.I.; Faeder, J.R.; Hlavacek, W.S. Kinetic Monte Carlo method for rule-based modeling of biochemical networks. Phys. Rev. E 2008, 78, 031910. [Google Scholar] [CrossRef] [PubMed]
- Falkenberg, C.V.; Blinov, M.L.; Loew, L.M. Pleomorphic Ensembles: Formation of Large Clusters Composed of Weakly Interacting Multivalent Molecules. Biophys. J. 2013, 105, 2451–2460. [Google Scholar] [CrossRef] [PubMed]
- Lok, L.; Brent, R. Automatic generation of cellular reaction networks with Moleculizer 1.0. Nat. Biotechnol. 2005, 23, 131–136. [Google Scholar] [CrossRef] [PubMed]
- Blinov, M.L.; Faeder, J.R.; Yang, J.; Goldstein, B.; Hlavacek, W.S. ‘On-the-fly’ or ‘generate-first’ modeling? Nat. Biotechnol. 2005, 23, 1344–1345. [Google Scholar] [CrossRef] [PubMed]
- Hucka, M.; Finney, A.; Sauro, H.M.; Bolouri, H.; Doyle, J.C.; Kitano, H.; Arkin, A.P.; Bornstein, B.J.; Bray, D.; Cornish-Bowden, A.; et al. The systems biology markup language (SBML): A medium for representation and exchange of biochemical network models. Bioinformatics 2003, 19, 524–531. [Google Scholar] [CrossRef] [PubMed]
- Blinov, M.L.; Faeder, J.R.; Goldstein, B.; Hlavacek, W.S. A network model of early events in epidermal growth factor receptor signaling that accounts for combinatorial complexity. Biosystems 2006, 83, 136–151. [Google Scholar] [CrossRef] [PubMed]
- Barua, D.; Hlavacek, W.S.; Lipniacki, T. A Computational Model for Early Events in B Cell Antigen Receptor Signaling: Analysis of the Roles of Lyn and Fyn. J. Immunol. 2012, 189, 646–658. [Google Scholar] [CrossRef] [PubMed]
- Faeder, J.R.; Hlavacek, W.S.; Reischl, I.; Blinov, M.L.; Metzger, H.; Redondo, A.; Wofsy, C.; Goldstein, B. Investigation of Early Events in FcϵRI-Mediated Signaling Using a Detailed Mathematical Model. J. Immunol. 2003, 170, 3769–3781. [Google Scholar] [CrossRef] [PubMed]
- Creamer, M.S.; Stites, E.C.; Aziz, M.; Cahill, J.A.; Tan, C.W.; Berens, M.E.; Han, H.; Bussey, K.J.; Von Hoff, D.D.; Hlavacek, W.S.; et al. Specification, annotation, visualization and simulation of a large rule-based model for ERBB receptor signaling. BMC Syst. Biol. 2012, 6. [Google Scholar] [CrossRef] [PubMed]
- Chylek, L.A.; Akimov, V.; Dengjel, J.; Rigbolt, K.T.G.; Hu, B.; Hlavacek, W.S.; Blagoev, B. Phosphorylation Site Dynamics of Early T-cell Receptor Signaling. PLoS ONE 2014, 9, e104240. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, M.; Nishimura, T. Mersenne Twister: A 623-Dimensionally Equidistributed Uniform Pseudo-Random Number Generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef]
- Marsaglia, G. Random Numbers Fall Mostly in the Planes. Proc. Natl. Acad. Sci. USA 1968, 61, 25–28. [Google Scholar] [CrossRef] [PubMed]
- Park, S.K.; Miller, K.W. Random Numbers Generators: Good Ones Are Hard To Find. Commun. Assoc. Comput. Mach. 1988, 31, 1192–1201. [Google Scholar] [CrossRef]
- Selivanov, V.A.; Votyakova, T.V.; Zeak, J.A.; Trucco, M.; Roca, J.; Cascante, M. Bistability of Mitochondrial Respiration Underlies Paradoxical Reactive Oxygen Species Generation Induced by Anoxia. PLoS Comput. Biol. 2009, 5, e1000619. [Google Scholar] [CrossRef] [PubMed]
- Meng, X.; Firczuk, H.; Pietroni, P.; Westbrook, R.; Dacheux, E.; Mendes, P.; McCarthy, J.E. Minimum-noise production of translation factor eIF4G maps to a mechanistically determined optimal rate control window for protein synthesis. Nucleic Acids Res. 2017, 45, 1015–1025. [Google Scholar] [CrossRef] [PubMed]
- Evans, T.W.; Gillespie, C.S.; Wilkinson, D.J. The SBML discrete stochastic models test suite. Bioinformatics 2008, 24, 285–286. [Google Scholar] [CrossRef] [PubMed]
- GNU Implementation of Time. Available online: https://www.gnu.org/software/time/ (accessed on 22 October 2017).
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017. [Google Scholar]
- Wickham, H. Tidyverse: Easily Install and Load the ‘Tidyverse’, version 1.2.1 R Package; Available online: https://www.tidyverse.org/ (accessed on 15 November 2017).
- Xu, W.; Smith, A.M.; Faeder, J.R.; Marai, G.E. RuleBender: A visual interface for rule-based modeling. Bioinformatics 2011, 27, 1721–1722. [Google Scholar] [CrossRef] [PubMed]
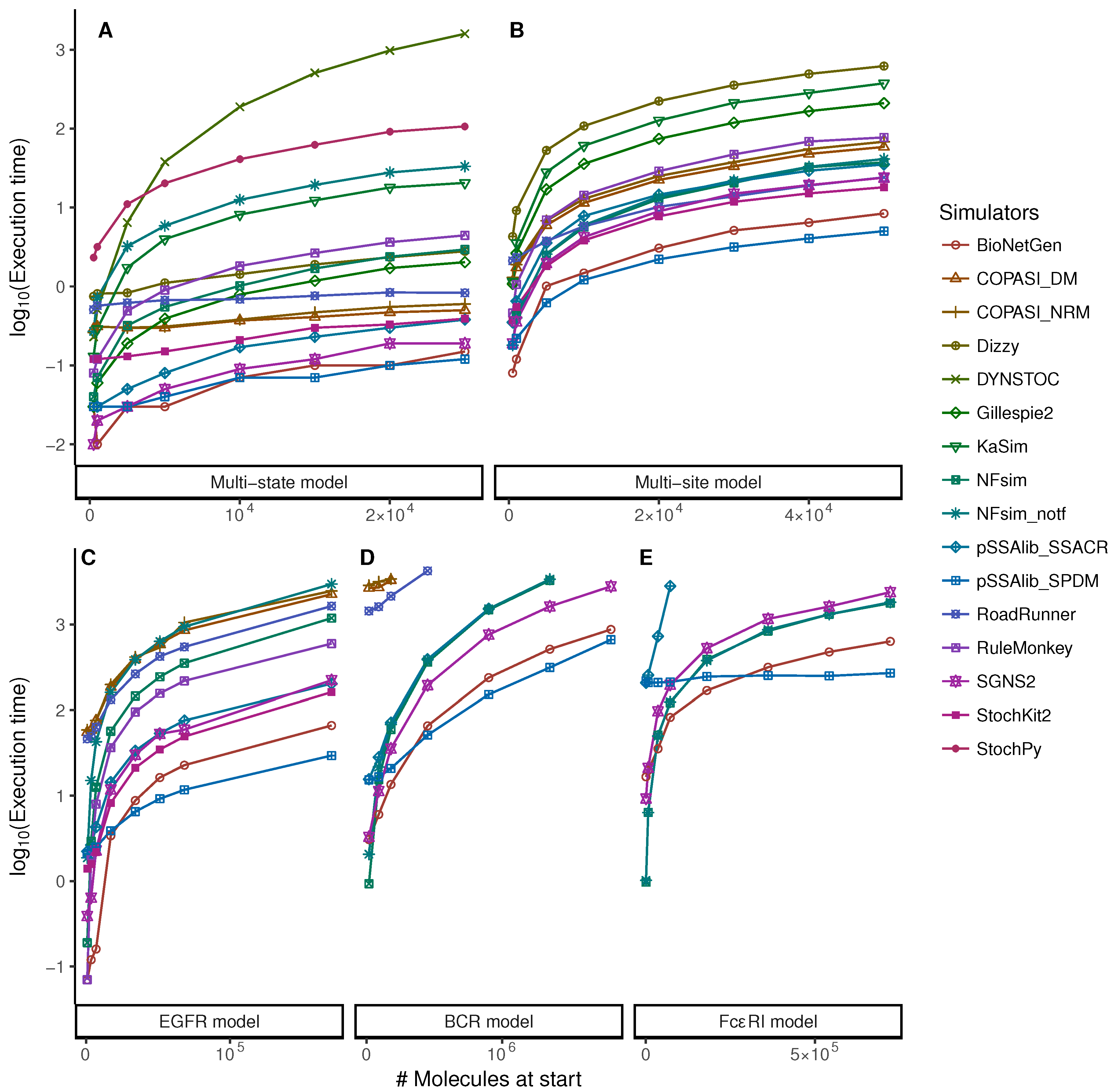
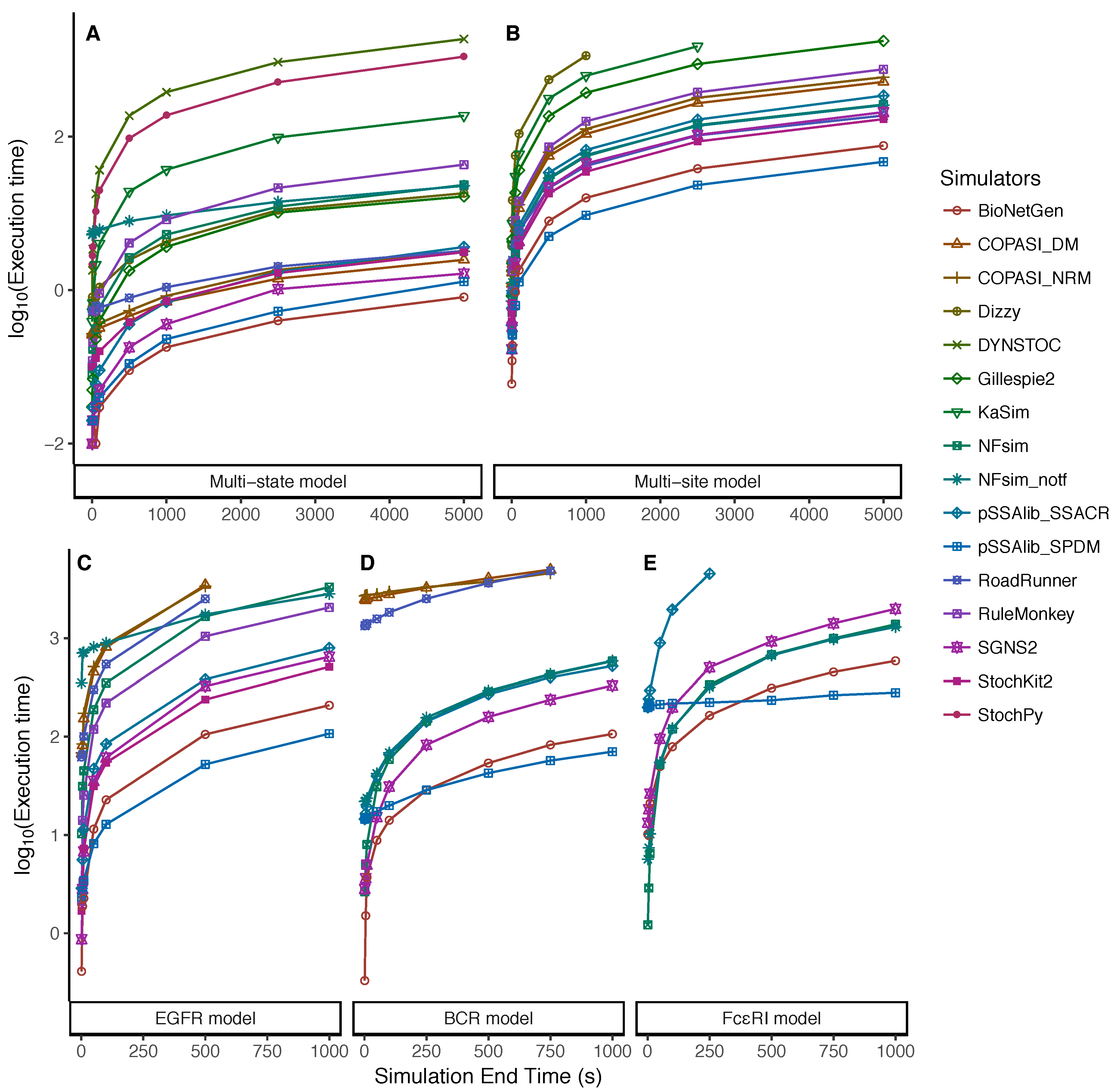
| Approach | Simulator | SSA Method | Language | Version | Reference |
|---|---|---|---|---|---|
| Network-based | BioNetGen | SDM * | Perl and C++ | 2.3.1 | [17] |
| COPASI_D | DM ** | C++ | 4.21 (Build 166) | [6] | |
| COPASI_GB | NRM *** | C++ | 4.21 (Build 166) | [6] | |
| Dizzy | DM | Java | 1.11.4 | [9] | |
| Gillespie2 | DM | C | Rev: 56 | [10] | |
| pSSAlib_SPDM | SPDM # | C++ | 2.0.0 | [13] | |
| pSSAlib_SSACR | CR ## | C++ | 2.0.0 | [13] | |
| RoadRunner | DM | C | 1.4.24 | [12] | |
| SGNS2 | NRM | C++ | 2.1.170 | [11] | |
| StochKit2 | CR | C++ | 2.0.13 | [33] | |
| StochPy | DM | Python | 2.3 | [8] | |
| Network-free | DYNSTOC | — | C | 1.2.0 | [25] |
| KaSim | — | OCaml | 3.5 | [22] | |
| NFsim | — | C++ | 1.11 | [19] | |
| RuleMonkey | — | C | 2.0.25 | [39] |
| Model | No. of Species | No. of Rules | No. of Reactions | Derivation Time (s) |
|---|---|---|---|---|
| Multi-state [17,25] | 6 | 4 | 8 | 0.0 |
| Multi-site [39] | 66 | 12 | 288 | 0.3 |
| EGFR * signaling [47] | 356 | 23 | 3749 | 11.6 |
| BCR ** signaling [48] | 1122 | 72 | 24,388 | 33.17 |
| FcϵRI *** signaling () [49] | 3744 | 24 | 58,276 | 163.8 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gupta, A.; Mendes, P. An Overview of Network-Based and -Free Approaches for Stochastic Simulation of Biochemical Systems. Computation 2018, 6, 9. https://doi.org/10.3390/computation6010009
Gupta A, Mendes P. An Overview of Network-Based and -Free Approaches for Stochastic Simulation of Biochemical Systems. Computation. 2018; 6(1):9. https://doi.org/10.3390/computation6010009
Chicago/Turabian StyleGupta, Abhishekh, and Pedro Mendes. 2018. "An Overview of Network-Based and -Free Approaches for Stochastic Simulation of Biochemical Systems" Computation 6, no. 1: 9. https://doi.org/10.3390/computation6010009
APA StyleGupta, A., & Mendes, P. (2018). An Overview of Network-Based and -Free Approaches for Stochastic Simulation of Biochemical Systems. Computation, 6(1), 9. https://doi.org/10.3390/computation6010009





