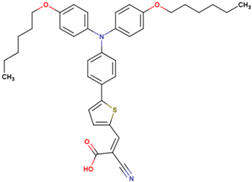
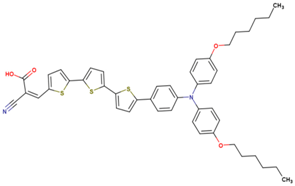
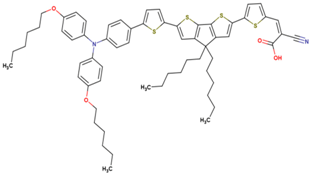
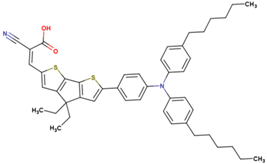
Abstract
Post silicon solar cell era involves light-absorbing dyes for dye-sensitized solar systems (DSSCs). Therefore, there is great interest in the design of competent organic dyes for DSSCs with high power conversion efficiency (PCE) to bypass some of the disadvantages of silicon-based solar cell technologies, such as high cost, heavy weight, limited silicon resources, and production methods that lead to high environmental pollution. The DSSC has the unique feature of a distance-dependent electron transfer step. This depends on the relative position of the sensitized organic dye in the metal oxide composite system. In the present work, we developed quantitative structure-property relationship (QSPR) models to set up the quantitative relationship between the overall PCE and quantum chemical molecular descriptors. They were calculated from density functional theory (DFT) and time-dependent DFT (TD-DFT) methods as well as from DRAGON software. This allows for understanding the basic electron transfer mechanism along with the structural attributes of arylamine-organic dye sensitizers for the DSSCs explicit to cobalt electrolyte. The identified properties and structural fragments are particularly valuable for guiding time-saving synthetic efforts for development of efficient arylamine organic dyes with improved power conversion efficiency.
1. Introduction
Research into renewable energy has become one of the most imperative issues in global energy strategy due to increasing energy consumption and limited fossil resources. The incident solar energy on earth per hour exceeds the current consumption of the energy of the world per year. The necessity of cultivating renewable energy sources is growing day by day [1]. Therefore, efficient solar energy conversion provides a promising technology for balancing the increasing energy demand due to fast industrial development [2]. In general, industrial photovoltaic cells are made of monocrystalline silicon, polycrystalline silicon, amorphous silicon, cadmium telluride, copper indium selenide/sulfide, or GaAs-based multi-junction material systems [3].
The possibility of using devices based on molecular components for the construction of a large-scale solar electricity production facility became reality after O’Regan and Grätzel reported the invention of their efficient dye solar cell [4]. Emerging research topics and pre-industrial technology in solar cells, which involve light-absorbing dyes for dye-sensitized solar systems (DSSCs), quantum dot solar devices (QDSCs), Perovskite solar cell, and organic/polymer solar cells, are still below the performance of silicon devices, with the highest efficiency still below 13% for DSSC [5]. The estimated theoretical QDSC performance is close to that of silicon-based devices; however, at present those record efficiencies only amount to 4.5% [6]. Despite the present low efficiency and stability, organic solar cell applications are intensively studied due to the potential low cost of production [7,8]. Specifically, the development of efficient DSSCs by O’Regan and Grätzel in 1991 [4] has put the solid-state technology on a challenge by devices operating at molecular or nanoscale levels.
The intricate relationship between the electron injection and dye regeneration processes in DSSCs is governed by redox reactions. The central constituent of the dye regeneration reaction is electrolytes where a classic I−/I3− redox couple has been considered one of the high-performance organic solvents in DSSCs [9]. However, the I−/I3− redox couple reduces the rate of open-circuit potential, VOC, during the dye-regeneration process due to its complex redox chemistry. A better reduction potential redox mediator than I3− is the cobalt (CoII/CoIII) complexes (polypyridyl), which can be used to increase the efficiency of DSSCs [10,11]. The redox chemistry of cobalt complexes can be fine-tuned by varying the ligand environment. To increase the efficiency of DSSCs, it is better to keep CoIII away from the surface of the semiconductor. In the case of organic dyes, this can be accomplished by using longer/bulky substituents in the donor group [12,13]. A cobalt complex has been used in Zn-based [10], Ru-based [11], and organic dye-based [12,13] solar cells with very good efficiency. Therefore, in our study we have considered DSSCs as necessary to cobalt electrolytes.
Arylamine organic dyes (AOD) with donor (D), π-bridge (π), and acceptor (A) moieties for DSSCs have received great attention in the last decade because of their high molar absorption coefficient, low cost, and structural variety. In the case of DSSCs, a large number of experimental works are available [8], together with some theoretical studies [14]; joint experimental and theoretical [15,16,17] work is becoming the common research strategy. However, the development and optimization of materials for organic solar cells is, in general, not yet rational, but rather empirical. The aim of the present work is to determine the macroscopic characteristics of arylamine organic dyes of DSSCs from computed molecular properties and to elucidate the elementary mechanistic steps of electron transfer in such solar cells through DFT and TD-DFT studies, followed by quantitative structure-property relationship (QSPR) study. The use of in silico methods for chemical property prediction is well established and the QSPR method emerged as an important computational tool with a diverse range of applications [18]. Robust and validated QSPR models can predict properties of new or untested molecular structures and provide insights that expedite the design of new compounds with enhanced desired properties [18]. When applied to the property and energy efficiency of compounds, regulatory agencies worldwide have already accepted the implications of QSPR models that can explore the central relationship between organic dyes and the composite system of DSSCs. This kind of study not only saves resources but also provides some guidance for the synthesis of more efficient dye sensitizers in the future.
A limited number of QSPR models have been developed to model the power conversion efficiency (PCE) value of solar cells to date. Though few QSPR models were developed for the modeling of PCE of DSSCs, the only global QSPR model was reported by our group for Fullerene derivatives (FDs) as an acceptor for polymer-based solar cells (PSCs). We have revealed nine FDs with promising PCE values through QSPR models from virtual screening with a 200% increase in PCE value, compared to existing FDs as acceptors [19]. Venkatraman et al. [20] reported the first successful application of comparative molecular field analysis (CoMFA) and vibrational frequency-based eigenvalue (EVA) descriptors to model molecular structure-photovoltaic performance relationships for a set of 40 coumarin derivatives as dyes for DSSCs. The obtained models provided statistically robust predictions of PCE values for all studied dyes. In another study, Venkatraman et al. [21] investigated de novo computational design methodology to design a coumarin-based dye sensitizer with improved properties for use in DSSCs. Ip et al. [22] performed successful prediction through in silico modeling of a set of new dyes on the basis of the known performance of existing dyes. In a recent work, Li et al. [23] investigated organic dyes from diverse classes of chemicals to model PCE with a QSPR tool. They reported an acceptable cascade QSPR model to model PCE.
Here we have considered 21 arylamine organic dyes on which experiments have been performed with a TiO2 film and liquid cobalt electrolyte for DSSCs. This allows us to strictly maintain OECD Principle 1 to model PCE with computed descriptors directly from the dyes’ structures without considering any experimental properties of DSSCs. The constructed QSPR model enables the identification of the essential structural attributes necessary for quantifying the molecular prerequisites of diverse dyes, chiefly responsible for the high PCE of DSSCs. The identified properties and structural fragments are particularly valuable for guiding future synthetic efforts for development of new organic dyes with improved power conversion efficiency.
2. Methods and Materials
2.1. Dataset
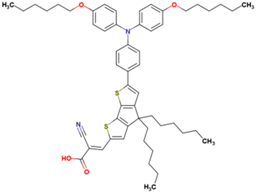
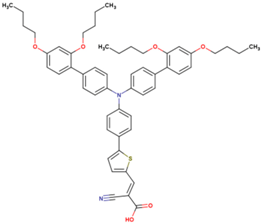
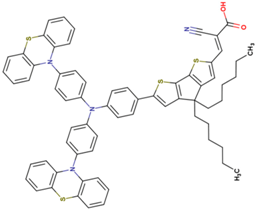
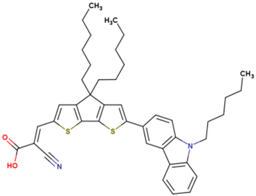
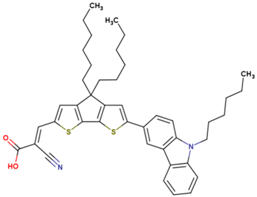
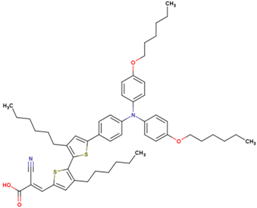
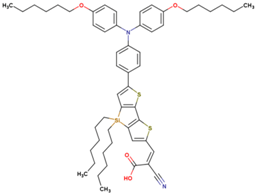
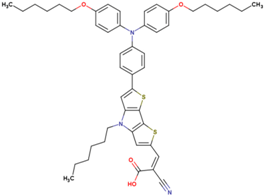
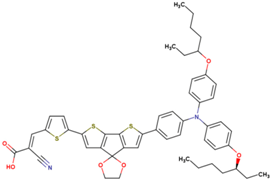
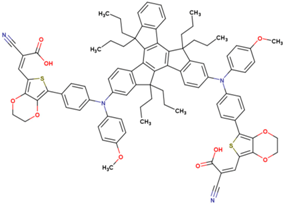
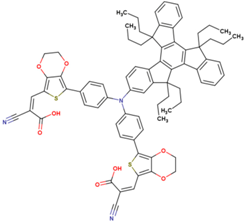
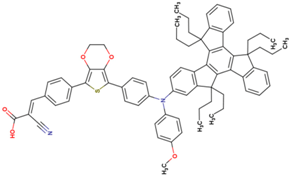
The dataset includes 21 organic arylamine dyes as sensitizers with a TiO2 film and liquid cobalt electrolyte for solar cells with experimental PCE values collected from the literature [24,25,26,27,28,29,30,31,32,33]. This dataset covers all possible arylamines available in the literature considering the experimental conditions. Therefore, although the dataset is small it is the only one available. The complete workflow of the study is addressed in Figure 1 and molecular structures with observed parameters are represented in Table 1.
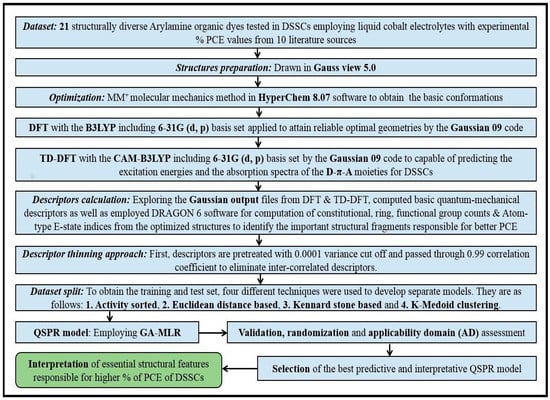
Figure 1.
A complete scheme of the present study.

Table 1.
Chemical structure of arylamine organic dyes tested in DSSCs employing liquid cobalt electrolytes with their experimental and predicted %PCE values.
2.2. Structure Preparation, Molecular and Quantum Chemical Calculations (DFT/TD-DFT)
Li et al. [23] suggested the importance of quantum-mechanical descriptors in the modeling of AOD. Therefore, the molecular geometries of Dye structures considered here were first prepared by molecular mechanics (MM). The MM+ molecular mechanics method, as implemented in the HyperChem 8.07 software package [34], was applied and subsequently geometry optimizations were performed in the gas phase using DFT and TD-DFT methods with B3LYP and CAM-B3LYP exchange correlation functionals, respectively, as implemented in GAUSSIAN 09 software package [35]. In both cases we choose the same basis set 6-31G (d, p). The CAM-B3LYP functional for the TD-DFT method is selected as its long-range coulomb-attenuating method comprises 19% of HF and 81% of B88 exchange interaction at short range; and 65% of HF plus 35% of B88 at long range [36]. Furthermore, the literature suggested that the CAM-B3LYP method provides reasonable prediction for the excitation energies and the absorption spectra of the D-π-A molecules [37,38]. Therefore, the vertical excitation energy and electronic absorption spectra were simulated using the TD-CAM-B3LYP method. Again, Magyar and Tretiak [39] study showed that to describe charge transfer states one should include 50% or more HF exchange for more reliability.
The effects of the solvents (the experimental solvents for the studied compounds were acetonitrile, dichloromethane, dimethylforamide) on the absorption spectra of the studied dyes have been simulated by the conductor-like polarizable continuum model (C-PCM) method at the TD CAM-B3LYP/6-31G (d, p) level of theory to compare the computed spectrum with the experimental spectrum of the dyes.
2.3. Descriptor Selection
Exploring the Gaussian output files from DFT and TD-DFT, we computed 32 basic quantum-mechanical descriptors. In addition, DRAGON 6 [40] software was used for computation of a total of 132 constitutional, ring, functional group counts & Atom-type E-state indices from the optimized structures to identify the important structural fragments responsible for better PCE. All the quantities related to DFT/TD-DFT properties are extracted for building QSPR models. Quantum-mechanical descriptors such as energy of HOMO and LUMO, difference of HOMO and LUMO energy, valence band, conduction band, hardness, Mulliken electronegativity, electronic chemical potential, and dipole moment are considered important, as suggested by the literature. Properties from DFT study such as absorption spectrum, ability to interacting with semiconductor oxide surface, excitation energy level, and stability are also considered as they significantly affect PCE. On the other hand, from TD-DFT calculations one can get energy descriptors that indicate the stability of molecules and electron transition property; the excited state properties, like maximum absorption wavelength and width of spectrum, give parameters related to sunlight absorption. The complete list of computed descriptors for the study is illustrated in Table S1 in the Supplementary Materials.
2.4. Data Pre-Processing
The complete pool of descriptors was initially pretreated with a 0.0001 variance cutoff and passed through a 0.99 correlation coefficient to eliminate correlations between them and reduce the noise level among input descriptors. Then, a genetic algorithm (GA) was applied to select the best possible set of descriptors for QSPR modeling from the pretreated pool consists of 139 descriptors [41]. Such a “descriptor-thinning” procedure led us to identify 10 common descriptors from the pool of 139 from 100 equations generated by GA for the complete dataset. Therefore, the identified ones are the most relevant for our study as they can reflect the required properties of all studied dyes.
2.5. Dataset Splitting
Selection of the training and test sets plays a crucial role in the construction of a statistically significant QSAR model. The selection should be such that the test set molecules lie within the chemical space occupied by the training set molecules. To nullify the bias of splitting the dataset, we have employed four different techniques to split the dataset into training and test sets with a 3:1 ratio [41]. The techniques are as follows: (1) Activity sorted; (2) Euclidean distance based; (3) Kennard stone based; and (4) K-Medoid clustering.
2.6. Model Development and Validation
We employed the genetic algorithm (GA) technique [41] as the selection statistical tool implemented in the Genetic Algorithm 1.4 software package [41]. Next, multiple linear regression (MLR) analysis was performed by MLR Plus Validation GUI 1.2 software [41], using the training set compounds to develop the QSPR model, which was followed by validation of the model using the test set compounds. We used the following steering parameters for the GA algorithm: total number of iterations 100, cross-over probability 1, mutation probability 0.5, and smoothing parameter (LOF calculation) 1.
2.7. Model Validation and Metrics
Different statistical metrics were employed to ensure the fitness of the in silico models, and internal and external validation methodologies were subsequently employed for model validation. The goodness-of-fit of the equation was judged by the quality metric determination coefficient (R2), as well as by using the following internal validation metrics: the leave-one-out cross-validation parameter, Q2LOO, and external validation metrics, R2pred. The rm2 metric [42,43] was also calculated for the present work. The developed QSPR models were also subjected to additional validation tests like Q2ext(F2); and Golbraikh and Tropsha’s criteria were used to check each model’s reliability [43].
2.8. Y-Randomization
The robustness of the models was checked based on the Y-randomization technique. For a robust model, the determination coefficient (R2) of the non-random model should exceed the squared average correlation coefficient of the randomized models (Rr2). The model randomization was performed 100 times via shuffling the dependent variables while maintaining the original independent variables. The average R2 of 100 random models was computed and defined as Rr2 followed by calculation of the cRp2 parameter [41,43] that penalizes model R2 for small differences in the values of R2 and Rr2.
For an acceptable model, the value of cRp2 should be greater than 0.5.
2.9. Applicability Domain Study
According to OECD Principle 3, an acceptable QSPR model should possess a defined AD, which represents the chemical space defined by the structural information extracted from the chemicals used in model development, i.e., the training set compounds in a QSAR analysis. Here, the AD of the QSPR model was checked using two different approaches: (a) the Euclidean distance approach [41]; and (b) the standardization-based technique [44].
3. Results and Discussion
3.1. Computational Results
Based on the experimental PCE data and thinned descriptors, we developed four separate QSPR models employing the hybrid GA-MLR tool. The statistical validation metrics data are provided in Table 2. Here, it is interesting to say that only acceptable internal validation does not provide the ultimate criteria to choose the best QSPR model. Rather, external validation is equally important to balance the quality as well as the predictability of any model to confirm the accurate prediction for new compounds. If we compare the numerical values, the least effective model is developed from the Kennard–Stone-based division (Model 3) as the basic external prediction metric R2ped (0.41) completely failed; Q2ext(F2) and rm2 metrics for the test set, though internal validation data, are acceptable. As for the remaining three models, the activity-based model (Model 1) failed in rm2 metrics for the test set and the Euclidean-based model (Model 2) bearing rm2 metrics values below the stipulated threshold for both training and test sets though all internal validation metrics is acceptable. Therefore, Model 4, based on K-Medoid clustering, emerged as the best QSPR model considering the acceptable values for internal as well as external validation metrics to prove the models’ quality as well as the predictability of new test compounds that are not considered in the model development.

Table 2.
Statistical quality of QSPR models developed based on different division tools.
The Y-randomization (Figure 2) study was performed to ensure that the model was not the outcome of mere chance alone, and all four models passed as their internal qualities are acceptable. However, except for the model developed based on K-Medoid clustering, the other models lack predictability. Again, a scatter plot (Figure 3) strongly supports the fact that Model 4 is the best among all four models as not a single test compound fell outside of the mean normalized distance of the training set compounds. Additionally, the AD study with the Euclidean distance approach and the standardization-based technique concludes that all test compounds were inside of the AD and their predictions are completely reliable for Model 4. Therefore, we can confidently predict 100% of test compounds based on the developed model after rigorous testing for validation and AD. The Euclidean distance plot is provided in Figure 4. For the comparison of all models’ quality, scatter plots and Euclidean distance plots for other three models are also provided in Figure 3 and Figure 4, respectively.
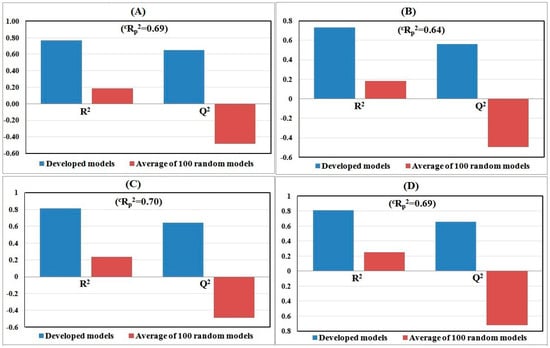
Figure 2.
Randomization plots of QSPR models developed with the following dataset splitting methods: (A) Activity sorted; (B) Euclidean distance based; (C) Kennard–Stone based; and (D) K-Medoid clustering.
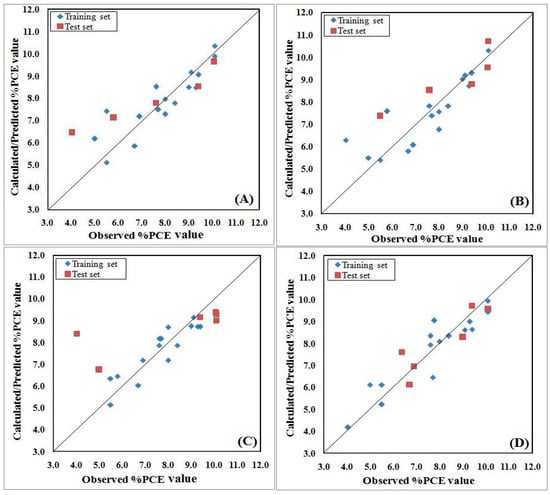
Figure 3.
Scatter plots of QSPR models developed with the following dataset splitting methods: (A) Activity sorted; (B) Euclidean distance based; (C) Kennard–Stone based; and (D) K-Medoid clustering.
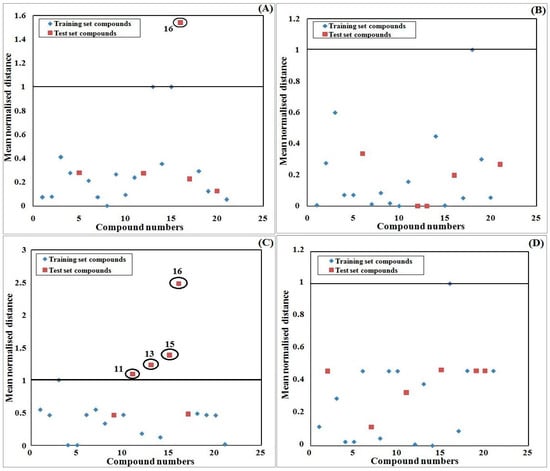
Figure 4.
Euclidean distance plots of the developed QSPR model for the AD study. Models were developed with the following dataset splitting methods: (A) Activity sorted; (B) Euclidean distance based; (C) Kennard–Stone based; and (D) K-Medoid clustering.
The statistical data as well as all graphical illustrations prove that QSPR Model 4 is well fitted and robust to reliably predict the PCE of untested compounds. The predicted PCE value for all studied molecules is illustrated in Table 1. So, for the interpretation and further discussions we have considered only Model 4. The developed equation for Model 4 is as follows:
Equation (2) involves three descriptors and explains 81.0% of the variance. Equation (2) was obtained in compliance with OECD principles, although the complete dataset is extremely diverse in terms of the structural variability of the molecules. However, satisfactory measures of goodness-of-fit, robustness, and predictability were achieved. Moreover, the least possible deviation of the predicted activity data from the corresponding observed ones is further implied from the satisfactory values of all the rm2 metrics. Almost identical values for the Q2(F1) (0.63) and Q2(F2) (0.62) metrics indicate that the test and training sets selected for the development of the QSPR model have similar response distributions. External predictability was further assessed according to Golbraikh and Tropsha’s criteria, which are highly satisfactory.
To check the model’s quality further, we employed another stringent criterion to check the quality and predictability of the model together, developed by Roy et al. [45]: error-based judgment of test set predictions. The obtained Mean Absolute Error (MAE) value is 0.43027, the Standard Deviation of Absolute Error (SD) is 0.25567, and the suggested model quality based on MAE-based criteria showed ‘GOOD’ prediction.
Further, simulated absorption spectra for the investigated dyes calculated at TD CAM-B3LYP/6-31G (d, p) level of theory in reported experimental solvents by the C-PCM methods. One has to note that the experimental spectra are completely comparable with the computed ones (see Table S2 and Figure S1 in the Supplementary Materials), suggesting that the choice of functional for the present study is quite reliable.
3.2. Interpretation of the Developed Model
The descriptors thus appearing in Equation (2) obey the following order of significance based on their standardized coefficients: (a) ; (b) ; and (c) ; and the standardized coefficient values are 1.45, 1.20, and 1.12, respectively. All the modeled descriptors make a positive and almost equivalent contribution to PCE values. Pearson correlation (Table 3) between descriptors is checked to avoid correlation and, interestingly, there is no correlation at all. One has to note that the training set is small in comparison to the number of parameters used for producing the QSPR models, but our model completely maintains the descriptors usage rule for the QSPR model considering the number of compounds (rule of 5:1 :: Sample size : Descriptors) [18].

Table 3.
Calculated square correlation among the modeled descriptors for Model 4.
To comply with OECD Principle 5, a mechanistic interpretation should be given for any predictive QSPR model. Here we provide the interpretation, with suitable examples, and justify the importance of each descriptor appearing in the GA-MLR equation:
is an atom-type E-state index that defines the sum of E-state values for the presence of 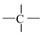 fragments in a molecule, and is a functional group count related to the number of total quaternary C(sp3). Although they are different descriptors, their impact on PCE is the same. A higher number of alkyl substitutions results in a high E-state () value along with the increment of count of sp3 carbon atoms. Structure and the orientation of dyes mostly dictate the efficiency of the solar cell via electron injection dynamics. In this regard, carboxyl plays the role of an anchor group and the longer alkyl chain is one of the most important entities in the dyes. The literature suggests [46] that J-aggregates formation becomes easier with the increasing length of the alkyl chain. Not only that, but the intrinsic sensitization or quantum efficiency is increased with the length of the alkyl chain due to the bathochromic shift of the absorption band [47]. Moreover, longer alkyl chains attached to the sensitizer dyes allow the dye to bind normally to the TiO2 surface [48]. Therefore, our findings are completely in agreement with the literature.
fragments in a molecule, and is a functional group count related to the number of total quaternary C(sp3). Although they are different descriptors, their impact on PCE is the same. A higher number of alkyl substitutions results in a high E-state () value along with the increment of count of sp3 carbon atoms. Structure and the orientation of dyes mostly dictate the efficiency of the solar cell via electron injection dynamics. In this regard, carboxyl plays the role of an anchor group and the longer alkyl chain is one of the most important entities in the dyes. The literature suggests [46] that J-aggregates formation becomes easier with the increasing length of the alkyl chain. Not only that, but the intrinsic sensitization or quantum efficiency is increased with the length of the alkyl chain due to the bathochromic shift of the absorption band [47]. Moreover, longer alkyl chains attached to the sensitizer dyes allow the dye to bind normally to the TiO2 surface [48]. Therefore, our findings are completely in agreement with the literature.
 fragments in a molecule, and is a functional group count related to the number of total quaternary C(sp3). Although they are different descriptors, their impact on PCE is the same. A higher number of alkyl substitutions results in a high E-state () value along with the increment of count of sp3 carbon atoms. Structure and the orientation of dyes mostly dictate the efficiency of the solar cell via electron injection dynamics. In this regard, carboxyl plays the role of an anchor group and the longer alkyl chain is one of the most important entities in the dyes. The literature suggests [46] that J-aggregates formation becomes easier with the increasing length of the alkyl chain. Not only that, but the intrinsic sensitization or quantum efficiency is increased with the length of the alkyl chain due to the bathochromic shift of the absorption band [47]. Moreover, longer alkyl chains attached to the sensitizer dyes allow the dye to bind normally to the TiO2 surface [48]. Therefore, our findings are completely in agreement with the literature.
fragments in a molecule, and is a functional group count related to the number of total quaternary C(sp3). Although they are different descriptors, their impact on PCE is the same. A higher number of alkyl substitutions results in a high E-state () value along with the increment of count of sp3 carbon atoms. Structure and the orientation of dyes mostly dictate the efficiency of the solar cell via electron injection dynamics. In this regard, carboxyl plays the role of an anchor group and the longer alkyl chain is one of the most important entities in the dyes. The literature suggests [46] that J-aggregates formation becomes easier with the increasing length of the alkyl chain. Not only that, but the intrinsic sensitization or quantum efficiency is increased with the length of the alkyl chain due to the bathochromic shift of the absorption band [47]. Moreover, longer alkyl chains attached to the sensitizer dyes allow the dye to bind normally to the TiO2 surface [48]. Therefore, our findings are completely in agreement with the literature.Another property is a ring descriptor that defines the distance/detour ring index of order 11. This descriptor can be best defined with the fragment illustrated in Figure 5. Compounds like 1, 13, 16, etc. have this fragment, along with a higher value for other descriptors showing very high PCE (see Table 1). On the contrary, compounds like 6, 9, and 18 lack this fragment, resulting in lower PCE values (see Table 1). Again, compound 17 has the ring fragment but due to the lowest value for the other two descriptors it generates the lowest PCE value among the studied dyes (see Table 1). This fragment will help to make a composite fused structure dye system where favorable molecular orbital energy enables rapid electron injection into the semiconductor and allows efficient regeneration of the oxidized dye. As the effectiveness of the DSSCs is influenced by the amount of solar energy absorbed by the dye and the kinetics of the charge transfer across the semiconductor network, the abovementioned fragment affects performance immensely to gain a higher PCE value for DSSCs, along with the abovementioned descriptors and .
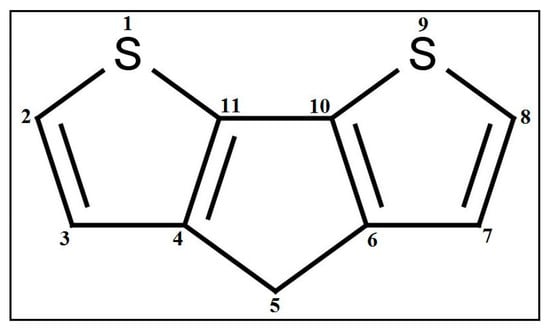
Figure 5.
Fragment defines D/Dtr11 descriptor.
4. Conclusions
We have introduced a QSPR model that allowed us to identify the essential fragments and structural features of AOD that are most responsible for the high PCE of DSSCs explicit to cobalt electrolytes through a stringent validation approach. Our findings can be summarized as follows:
- The QSPR model enables identification of the essential structural attributes necessary for quantifying the prime molecular prerequisites of a diverse AOD system that could guide the design and synthesis of more efficient dyes in the near future. The interpretation of the model revealed that a higher number of alkyl substitutions, along with the increment of count of sp3 carbon atoms and the combination of a distance/detour ring index of order 11 fragment, enable rapid electron injection into the semiconductor. This dynamic step allows efficient regeneration of the oxidized dye and helps to achieve a higher PCE value for an arylamine dye-sensitized solar cell explicit to cobalt electrolytes.
- The QSPR model, developed from a set of 21 diverse AOD, is an efficient tool to screen a wide range of AOD, allowing for the identification of dyes with high PCE in a time- and cost-effective manner.
- The developed QSPR model is particularly valuable for predicting and characterizing the nature of the donor:π-bridge:acceptor relationships critical for photoconversion.
Our calculations provide a set of data that will enable scientists to reduce their experimental effort, time, and resources. In addition, the exploratory features may assist in designing more efficient units. In our future work, we are working to develop global QSPR models for a huge number of AOD for DSSCs explicit to iodine electrolytes, followed by designing new AOD with their first principle study with emphasis on electron transfer rates and an experimental analysis that could further validate our QSPR models.
Supplementary Materials
The following are available online at http://www.mdpi.com/2079-3197/5/1/2/s1.
Acknowledgments
S.K., J.K.R., D.L., and J.L. thank the National Science Foundation (NSF/CREST HRD-1547754, and EPSCoR (Award#: 362492-190200-01/NSFEPS-0903787) for financial support. The authors want to acknowledge the Extreme Science and Engineering Discovery Environment (XSEDE) by National Science Foundation grant number OCI-1053575 and XSEDE award allocation number DMR110088 and the Mississippi Center for Supercomputing Research (MCSR) for providing state-of-the-art, high-performance computing facilities and outstanding services for supporting this research.
Author Contributions
S.K. conceived and designed the experiments; S.K. and J.K.R. performed the experiments; S.K., J.K.R., D.L. and J.L. analyzed the data; S.K. contributed analysis tools; S.K., J.K.R., D.L. and J.L wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kohn, W.; Heeger, A. The Power of the Sun. 2005. Available online: http:/powerofthesun.ucsb.edu (accessed on 10 September 2016).
- Kammen, D.M. The rise of renewable energy. Sci. Am. 2006, 295, 84–93. [Google Scholar] [CrossRef] [PubMed]
- Chiba, Y.; Islam, A.; Watanabe, Y.; Komiya, R.; Koide, N.; Han, L. Dye-Sensitized Solar Cells with Conversion Efficiency of 11.1%. Jpn. J. Appl. Phys. 2006, 45, L638–L640. [Google Scholar] [CrossRef]
- Regan, B.O.; Grätzel, M. A low-cost, high-efficiency solar cell based on dye-sensitized colloidal TiO2 films. Nature 1991, 353, 737–740. [Google Scholar] [CrossRef]
- Yella, A.; Lee, H.W.; Tsao, H.N.; Yi, C.; Chandiran, A.K.; Nazeeruddin, M.K.; Diau, E.W.; Yeh, C.Y.; Zakeeruddin, S.M.; Grätzel, M. Porphyrin-sensitized solar cells with cobalt(II/III)-based redox electrolyte exceed 12 percent efficiency. Science 2011, 334, 629–634. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.L.; Lo, Y.S. Highly Efficient Quantum-Dot-Sensitized Solar Cell Based on Co-Sensitization of CdS/CdSe. Adv. Funct. Mater. 2009, 19, 604–609. [Google Scholar] [CrossRef]
- Cheng, Y.J.; Yang, S.H.; Hsu, C.S. Synthesis of conjugated polymers for organic solar cell applications. Chem. Rev. 2009, 109, 5868–5923. [Google Scholar] [CrossRef] [PubMed]
- Hagfeldt, H.; Boschloo, G.; Sun, L.; Kloo, L.; Pettersson, H. Dye-sensitized solar cells. Chem. Rev. 2010, 110, 6595–6663. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Islam, A.; Chen, H.; Malapaka, C.; Chiranjeevi, B.; Zhang, S.; Yang, X.; Yanagida, M. High-efficiency dye-sensitized solar cell with a novel Co-adsorbent. Energy Environ. Sci. 2012, 5, 6057–6060. [Google Scholar] [CrossRef]
- Wang, M.; Chamberland, N.; Breau, L.; Moser, J.E.; Baker, R.H.; Marsan, B.; Zakeeruddin, S.M.; Grätzel, M. An organic redox electrolyte to rival triiodide/iodide in dye-sensitized solar cells. Nat. Chem. 2010, 2, 385–389. [Google Scholar] [CrossRef] [PubMed]
- Nusbaumer, H.; Zakeeruddin, S.M.; Moser, J.-E.; Grätzel, M. An Alternative Efficient Redox Couple for the Dye-Sensitized Solar Cell System. Chem. Eur. J. 2003, 9, 3756–3763. [Google Scholar] [CrossRef] [PubMed]
- Mosconi, E.; Yum, J.-H.; Kessler, F.; Gómez García, C.J.; Zuccaccia, C.; Cinti, A.; Nazeeruddin, M.K.; Grätzel, M.; De Angelis, F. Cobalt Electrolyte/Dye Interactions in Dye-Sensitized Solar Cells: A Combined Computational and Experimental Study. J. Am. Chem. Soc. 2012, 134, 19438–19453. [Google Scholar] [CrossRef] [PubMed]
- Nelson, J.J.; Amick, T.J.; Elliott, C.M. Mass Transport of Polypyridyl Cobalt Complexes in Dye-Sensitized Solar Cells with Mesoporous TiO2 Photoanodes. J. Phys. Chem. C 2008, 112, 18255–18263. [Google Scholar] [CrossRef]
- Zhang, J.; Kan, Y.-H.; Li, H.-B.; Geng, Y.; Wu, Y.; Su, Z.-M. How to design proper π-spacer order of the D-π-A dyes for DSSCs? A density functional response. Dyes Pigments 2012, 95, 313–321. [Google Scholar] [CrossRef]
- Le Bahers, T.; Labat, F.; Pauporté, T.; Lainé, P.P.; Ciofini, I. Theoretical Procedure for Optimizing Dye-Sensitized Solar Cells: From Electronic Structure to Photovoltaic Efficiency. J. Am. Chem. Soc. 2011, 133, 8005–8013. [Google Scholar] [CrossRef] [PubMed]
- Labat, F.; Le Bahers, T.; Ciofini, I.; Adamo, C. First-principles modeling of dye-sensitized solar cells: Challenges and perspectives. Acc. Chem. Res. 2012, 45, 1268–1277. [Google Scholar] [CrossRef] [PubMed]
- Le Bahers, T.; Pauporté, T.; Lainé, P.P.; Labat, F.; Adamo, C.; Ciofini, I. Modeling Dye-Sensitized Solar Cells: From Theory to Experiment. J. Phys. Chem. Lett. 2013, 4, 1044–1050. [Google Scholar] [CrossRef] [PubMed]
- Roy, K.; Kar, S.; Das, R.N. Understanding the Basics of QSAR for Applications in Pharmaceutical Sciences and Risk Assessment; Academic Press: San Diego, CA, USA, 2015. [Google Scholar]
- Kar, S.; Sizochenko, N.; Ahmed, L.; Batista, V.S.; Leszczynski, J. Quantitative structure-property relationship model leading to virtual screening of fullerene derivatives: Exploring structural attributes critical for photoconversion efficiency of polymer solar cell acceptors. Nano Energy 2016, 26, 677–691. [Google Scholar] [CrossRef]
- Venkatraman, V.; Åstrand, P.-O.; Alsberg, B.K. Quantitative Structure-Property Relationship Modeling of Grätzel Solar Cell Dyes. J. Comput. Chem. 2014, 35, 214–226. [Google Scholar] [CrossRef] [PubMed]
- Venkatraman, V.; Abburu, S.; Alsberg, B.K. Artificial evolution of coumarin dyes for dye sensitized solar cells. Phys. Chem. Chem. Phys. 2015, 17, 27672–27682. [Google Scholar] [CrossRef] [PubMed]
- Venkatraman, V.; Alsberg, B.K. A quantitative structure-property relationship study of the photovoltaic performance of phenothiazine dyes. Dyes Pigments 2015, 114, 69–77. [Google Scholar] [CrossRef]
- Li, H.; Zhong, Z.; Li, L.; Gao, R.; Cui, J.; Gao, T.; Hu, L.H.; Lu, Y.; Su, Z.M.; Li, H. A Cascaded QSAR Model for Efficient Prediction of Overall Power Conversion Efficiency of All-Organic Dye-Sensitized Solar Cells. J. Comput. Chem. 2015, 36, 1036–1046. [Google Scholar] [CrossRef] [PubMed]
- Feldt, S.M.; Gibson, E.A.; Gabrielsson, E.; Sun, L.; Boschloo, G.; Hagfeldt, A. Design of organic dyes and cobalt polypyridine redox mediators for high-efficiency dye-sensitized solar cells. J. Am. Chem. Soc. 2010, 132, 16714–16724. [Google Scholar] [CrossRef] [PubMed]
- Xu, M.; Zhou, D.; Cai, N.; Liu, J.; Li, R.; Wang, P. Electrical and photophysical analyses on the impacts of arylamine electron donors in cyclopentadithiophene dye-sensitized solar cells. Energy Environ. Sci. 2011, 4, 4735–4742. [Google Scholar] [CrossRef]
- Xu, M.; Zhang, M.; Pastore, M.; Li, R.Z.; Angelis, F.D.; Wang, P. Joint electrical, photophysical and computational studies on D-π-A dye sensitized solar cells: The impacts of dithiophene rigidification. Chem. Sci. 2012, 3, 976–983. [Google Scholar] [CrossRef]
- Zhang, M.; Liu, J.Y.; Wang, Y.H.; Zhou, D.F.; Wang, P. Redox couple related influences of π-conjugation extension in organic dye-sensitized mesoscopic solar cells. Chem. Sci. 2011, 2, 1401–1406. [Google Scholar] [CrossRef]
- Bai, Y.; Zhang, J.; Zhou, D.; Wang, Y.; Zhang, M.; Wang, P. Engineering Organic Sensitizers for Iodine-Free Dye-Sensitized Solar Cells: Red-Shifted Current Response Concomitant with Attenuated Charge Recombination. J. Am. Chem. Soc. 2011, 133, 11442–11445. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.M.; Cai, N.; Wang, Y.L.; Li, R.Z.; Yuan, Y.; Wang, P. Modulating the assembly of organic dye molecules on titania nanocrystals via alkyl chain elongation for efficient mesoscopic cobalt solar cells. Phys. Chem. Chem. Phys. 2012, 14, 8282–8286. [Google Scholar] [CrossRef] [PubMed]
- Yum, J.H.; Baranoff, E.; Kessler, F.; Mmoehl, T.; Ahmad, S.; Bessho, T.; Mmarchioro, A.; Ghadiri, E.; Mmoser, J.E.; Yi, C.Y.; et al. A cobalt complex redox shuttle for dye-sensitized solar cells with high open-circuit potentials. Nat. Commun. 2012, 3, 631–638. [Google Scholar] [CrossRef] [PubMed]
- Qin, C.; Peng, W.; Zhang, K.; Islam, A.; Han, L. A novel organic sensitizer combined with a cobalt complex redox shuttle for dye-sensitized solar cells. Org. Lett. 2012, 14, 2532–2535. [Google Scholar] [CrossRef] [PubMed]
- Zong, X.P.; Liang, M.; Fan, C.R.; Tang, K.; Li, G.; Sun, Z.; Xue, S. Design of Truxene-Based Organic Dyes for High-Efficiency Dye-Sensitized Solar Cells Employing Cobalt Redox Shuttle. J. Phys. Chem. C 2012, 116, 11241–11250. [Google Scholar] [CrossRef]
- Zong, X.P.; Liang, M.; Chen, T.; Jia, J.N.; Wang, L.N.; Sun, Z.; Xue, S. Efficient iodine-free dye-sensitized solar cells employing truxene-based organic dyes. Chem. Commun. 2012, 48, 6645–6647. [Google Scholar] [CrossRef] [PubMed]
- HyperChem (TM), Hypercube, Inc.: Gainesville, FL, USA.
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09; Gaussian Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Yanai, T.; Tew, D.P.; Handy, N.C. A New Hybrid Exchange-Correlation Functional Using the Coulomb-Attenuating Method (CAM-B3LYP). Chem. Phys. Lett. 2004, 393, 51–57. [Google Scholar] [CrossRef]
- Preat, J. Photoinduced Energy-Transfer and Electron-Transfer Processes in Dye-Sensitized Solar Cells: TDDFT Insights for Triphenylamine Dyes. J. Phys. Chem. C 2010, 114, 16716–16725. [Google Scholar] [CrossRef]
- Irfan, A.; Jin, R.; Al-Sehemi, A.G.; Asiri, A.M. Quantum Chemical Study of the Donor-Bridge-Acceptor Triphenylamine Based Sensitizers. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2013, 110, 60–66. [Google Scholar] [CrossRef] [PubMed]
- Magyar, R.J.; Tretiak, S. Dependence of Spurious Charge-Transfer Excited States on Orbital Exchange in TDDFT: Large Molecules and Clusters. J. Chem. Theory Comput. 2007, 3, 976–987. [Google Scholar] [CrossRef] [PubMed]
- Dragon Molecular Descriptors. Available online: http://www.talete.mi.it/products/dragon_molecular_descriptors.htm (accessed on 20 December 2016).
- Software Tools. Available online: http://teqip.jdvu.ac.in/QSAR_Tools/ (accessed on 20 December 2016).
- Roy, K.; Mitra, I.; Kar, S.; Ojha, P.; Das, R.N.; Kabir, H. Comparative studies on some metrics for external validation of QSPR models. J. Chem. Inf. Model. 2012, 52, 396–408. [Google Scholar] [CrossRef] [PubMed]
- Roy, K.; Kar, S. How to Judge Predictive Quality of Classification and Regression Based QSAR Models? In Frontiers of Computational Chemistry; Haq, Z.U., Madura, J., Eds.; Bentham Science Publishers: Sharjah, UAE, 2015; pp. 71–120. [Google Scholar]
- Roy, K.; Kar, S.; Ambure, P. On a simple approach for determining applicability domain of QSAR models. Chemom. Intell. Lab. Syst. 2015, 145, 22–29. [Google Scholar] [CrossRef]
- Roy, K.; Das, R.N.; Ambure, P.; Aher, R.B. Be aware of error measures. Further studies on validation of predictive QSAR models. Chemom. Intell. Lab. Syst. 2016, 152, 18–33. [Google Scholar] [CrossRef]
- Iriyama, K.; Mizutani, F.; Yoshiura, M. Enhancement of Photocurrent at a Merocyanine-Coated Electrode due to Chromophore Aggregation. Chem. Lett. 1980, 11, 1399–1402. [Google Scholar] [CrossRef]
- Sayama, K.; Hara, K.; Sugihara, H.; Arakawa, H.; Mori, N.; Satsuki, M.; Suga, S.; Tsukagoshi, S.; Abe, Y.; O’Regan, B.; et al. Photosensitization of a Porous TiO2 Electrode with Merocyanine Dyes Containing a Carboxyl Group and a Long Alkyl Chain. Chem. Commun. 2000, 353, 1173–1174. [Google Scholar] [CrossRef]
- Kroeze, J.E.; Hirata, N.; Koops, S.; Nazeeruddin, M.K.; Schmidt-Mende, L.; Grätzel, M.; Durrant, J.R. Alkyl Chain Barriers for Kinetic Optimization in Dye-Sensitized Solar Cells. J. Am. Chem. Soc. 2006, 128, 16376–16383. [Google Scholar] [CrossRef] [PubMed]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).