Abstract
The frequency response function is a quantitative measure used in structural analysis and engineering design; hence, it is targeted for accuracy. For a large structure, a high number of substructures, also called cells, must be considered, which will lead to a high amount of computational time. In this paper, the recursive method, a finite element method, is used for computing the frequency response function, independent of the number of cells with much lesser time costs. The fundamental principle is eliminating the internal degrees of freedom that are at the interface between a cell and its succeeding one. The method is applied solely for free (no load) nodes. Based on the boundary and interior degrees of freedom, the global dynamic stiffness matrix is computed by means of products and inverses resulting with a dimension the same as that for one cell. The recursive method is demonstrated on periodic structures (cranes and buildings) under harmonic vibrations. The method yielded a satisfying time decrease with a maximum time ratio of and a percentage difference of 19%, in comparison with the conventional finite element method. Close values were attained at low and very high frequencies; the analysis is supported for two types of materials (steel and plastic). The method maintained its efficiency with a high number of forces, excluding the case when all of the nodes are under loads.
1. Introduction
The study of structural dynamics is essential for understanding and evaluating the performance of any engineering structure. Most structures vibrate. In operation, all machines, vehicles and buildings are subjected to dynamic forces that cause vibrations. Very often, the vibrations have to be investigated because they may cause an immediate problem. Whatever the reason, we need to quantify the structural response in some way, so that its implication on factors such as performance and fatigue can be evaluated. The frequency response function (FRF) will then be considered. These structures may have a uniform geometry or a periodic one. The frequency response function has acquired much consideration for high frequencies, since at small values, the system can be analyzed statically. Getting this function for the structures and system mentioned under a high range of angular frequencies will lead to a large amount of computation time, since solving for the displacement vector requires inversing the dynamic stiffness matrix at each angular frequency. As the number of substructures, also called cells, increases the computational cost increases. Hence, the approach emphasized in this research presents a solution for this time issue.
Various methods were inspected to determine the frequency response for one-dimensional structures and their behavior as assembled for a two-dimensional element as a truss or frame. Original numerical approaches were done by Dong and Aalami [1,2] to estimate the deformations on each point on the cross-section by finite element analysis (conventional FEM).
One approach for structural analysis is the spectral finite element method (SFEM) that was mainly used by Finnveden [3,4]. It considers general uniform structures with complex cross-sections and handles all types of boundary conditions. The displacements in the cross-section are described by the finite element method (FEM), while ordinary differential equations for 2D structures will express the variation along the axis of symmetry (x-axis) with a solution of the form , where y and z are cross-sectional coordinates. A similar approach as SFEM called the dynamic stiffness method (DSM) is notably efficient for the study of excited structures under high frequencies [5]. It provides an economical solution with a much higher accuracy, since it divides the member into distinct elements. Both methods include similar steps till the extent of obtaining the dynamic stiffness matrix. DSM defines a relationship between the nodal displacement and forces of the element using shape functions, in order to derive the dynamic stiffness matrix; whereas the SFEM uses the virtual work method to obtain the stiffness matrix, and the dynamic matrix will have a more laborious presentation, being a function of the wave number. Structures made of plates and shells were examined by the SFEM approach by Nilsson [6]. Birgersson [7,8,9] studied plane wave and fluid structure interaction. Gry and Gavric [10,11] applied similar approaches for the detection of wave propagation on rails, where they calculated the relative dispersion relations. Similar techniques were interpreted by Bartoli and Marzani [12,13] for the purpose of computing the dispersion relations for damped structures of arbitrary cross-sections and with symmetric elements.
Duhamel et al. [14] established a combined method between wave and finite element approaches for investigating periodic structures; it has an advantage over the SFEM by its ease of operations for complex geometries and scattered materials. Lee et al. [15] utilized a compounded method using finite element and boundary element (FEBE) methods for studying periodic structures meshed non-periodically.
Reduced order models (ROMs) are mainly mathematically-inexpensive methods for solving complex and large-scale dynamic problems by decreasing the model’s degrees of freedom. It gathers the system’s responses under excitations, providing near real-life analysis, however with low accuracy. ROM was applied on mistuned bladed disks by Castanier et al. [16] for capturing localized modes and producing low order models with modest memory storage; it calculated relatively acceptable results in comparison with FEM. The method was later improved by employing the Craig–Bampton component mode synthesis (CMS), which is an ROM-based technique yielding better mode accuracy; it required that at least one subspace iteration is executed (Bathe et al. [17]). CMS was then applied by Zhou et al. [18] on dynamics analysis using non-uniform rational B-spline (NURBS) finite elements to generate appropriate constructions of interfaced substructures. The method obtained a complete structural model consistent with the original model.
Duhamel [19,20] analyzed the frequency response by the recursive method (RM), on waveguide structures, as beams, plates and tires. The beam was divided into two substructures. As the division number increases, a higher accuracy in the frequency response is obtained. He also studied some plates excited in the mid x and y positions. A simply supported plate is meshed, and then, its mass and stiffness matrices are extracted from ABAQUS and then inserted in MATLAB to obtain the frequency response using the method studied. A similar method aiming to reduce the number of degrees of freedom under zero forces called the Guyan method is commonly used; however, it had been employed mainly for static analysis. Further, it neglects the inertia at the omitted DOF, hence being obsolete for structures of high mass to stiffness ratios [21].
The paper provides a computational solving method for periodic structures that cannot be designed as waveguides, where the recursive method is studied for its efficiency. The recursive method tends to ease the study of finite element analysis for complex structures. It is a computational method that computes the global dynamic stiffness matrix by products and inverses of matrices, resulting with the same dimension as that of one cell. For a complex cross-section, the structure is sectioned and modeled in the conventional finite element software and then post-processed in MATLAB. RM tends to eliminate any degrees of freedom (DOF) on the nodes that are not under study. Thus, a structure of two elements can be examined as one, on account of omitting the DOF at the boundaries between two consecutive cells, if there were no internal loads.
Two applications were examined under the illustrated method. The first application is where the RM is applied on 1D bar structures and demonstrating their manner as assembled in a crane under harmonic and seismic loadings. The crane will be dealt with as a truss. A real-life example will be considered, with a conservative number of elements. For the second application, the RM will be applied on a building modeled as a frame. The seismic load will be designed as harmonic displacement at its base end. The truss and the frame are considered as 2D periodic structures.
Modal analysis is used to assess the dynamic properties of a structure by assessing the natural frequencies and their corresponding mode shapes. It was employed to determine the range of frequencies to be examined. FEM works on the full modes when computing the FRF, while RM will only work on the modes that include the studied nodes. For example, in the presented study, the structure has no internal nodes for examination; hence, RM will consider the first mode only with the two end nodes. Using the recursive method, a few computations are needed for finding a close response compared to the number of computations used in the finite element analysis.
2. Recursive Method
2.1. Review
The recursive method is used to calculate the forced response of various types of structures, which might lead to a high consumption of computation. This method is used to compute the general dynamic stiffness matrix with a much lower amount of computational time. Generally, the recursive method is a purely computational method, which computes the global dynamic stiffness matrix by products and inverses of matrices with the same dimensions as the dynamic stiffness matrix of a cell.
For a complex cross-section, the structure is sectioned and modeled in the conventional finite element software (ANSYS). Then, the mass, stiffness and damping matrices are extracted from ANSYS.
These matrices will be post-processed to give the dynamic stiffness matrix of the section under study, after which, the global dynamic stiffness matrix of the whole structure will be figured from the recursive method. It will be obtained by means of products and inverses of the matrices with the dimension equal to that of the dynamic stiffness matrix of the section. This method tends to eliminate any degrees of freedom (DOF) on the nodes that are not under study. Thus, a structure of two elements can be examined as one, on account of omitting the DOF at the boundaries between two consecutive cells, if there were no internal loads. In general, this method is applicable and effective when the structure is not under a large number of forces.
The periodic structure that is divided into N cells is considered. The problem studied is under a point force excitation, having a response . Following is a demonstration for the recursive method, numerically [14].
2.2. Behavior of One Cell
First, consider a one-cell element. The discrete dynamic stiffness matrix of a cell for a time-dependent is given by:
where , is the angular frequency, is the stiffness matrix, is the damping matrix, is the mass matrix, is the displacement vector and is the loading vector.
Thus, the dynamic stiffness matrix is:
Decomposing the degrees of freedom into the boundary (B) and interior (I), the resulting dynamic equation is:
Then, eliminate the second row of Equation (3):
The first row in Equation (3) will be:
Thus, boundary conditions are only considered in the study. These conditions can be decomposed into left (L) and right (R) for the relative nodes.
Equation (5) becomes:
where is the dynamic stiffness matrix of a single cell.
Since matrices , and are symmetric, matrix will also be symmetric.
2.3. Behavior of Two Cells
For the assembly of two cells, consider the dynamic stiffness matrices A and B for Cell 1 and Cell 2, respectively, as shown in Figure 1. The dynamic stiffness matrix is now denoted with , which relates the DOF between the two sides (left and right). The dynamic stiffness matrix of the structure is calculated using:
since the interior side is taken with free loading . Thus, solving for the second row in the matrix:

Figure 1.
Two-cell element.
The global dynamic stiffness matrix will then be:
where is the dynamic stiffness matrix of the two cells’ structure.
Since matrices and are symmetric, matrix will also be symmetric. Therefore, we can write:
2.4. General Case
Consider now a general case of a structure made of N cells, where it is under no load at its internal nodes. Denote its total dynamic stiffness matrix as . Note that the structure is periodic and is isotropic. Firstly, consider a structure with identical cells; omit the internal degrees of freedom that are under no load. As stated in the foregoing method, the element of two cells is subsequently modeled as one cell. Hence, the current one-cell element will be assembled with a one-cell element that was previously a two-cell element. Proceeding with the N-cell structure, the outcome is a one-cell element that holds the nodes that are of interest for the assessment. For no restriction on the number of cells, the procedure is computed for steps. This accustomed number of steps will have a high effectiveness on saving the number of computations, when comparing with the conventional finite element analysis; since it is no longer required for the global assembly of the whole structure. The complete analysis is reviewed in Figure 2.
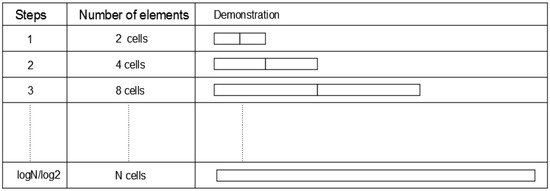
Figure 2.
Element assembly in the recursive method.
In case the number of cells was not as a power of two, a binary representation will be used to model the system. For example, for N number of cells where N is not equal to a number with a power of two, it can be written in binary representation as .
The system is solved as follows:
- Calculate the dynamic stiffness matrix for a structure of eight cells, decomposing them into four of two cells each.
- The studied structure is then assembled with a structure of two cells, studied previously.
- The resulting matrix is assembled with a structure of one cell.
This approach can be resumed by:
This method provides an easy approach for the computations of a structure with a large number of cells under harmonic vibrations. After applying the force and displacement boundary conditions, the response for the node subjected to forced vibrations is studied and detected for the frequency response function.
3. Applications
Periodic structures were examined in this paper. For the first application, 1D bar structures are assembled in a crane. Excitation and seismic loading will be examined on cranes, where it will be dealt with as a truss. On the other hand, the application of the recursive method will be on 2D frame, where a harmonic displacement is loaded at its base nodes (model of seismic load). The frame is considered as a 2D periodic structure.
After computing the FRF conventionally (using harmonic analysis in ANSYS), the response will be compared to that determined from the recursive method. Note that a FULL analysis method was used in ANSYS, where it uses the full system’s matrices for computing the response; this will lead to a more comprehensive and detailed approach. RM is defined by a self-written MATLAB code where it takes the K, M and C matrices of a one cell from ANSYS for the frame structure. However, these matrices will be calculated manually for the truss application. Then, the matrices will be assembled reaching N cells, recursively. The dynamic stiffness matrix will be obtained by products and inverses of matrices with the same dimension as the dynamic stiffness matrix of one cell. Nodes that are under no load or not under study will be omitted using this method. Hence, internal degrees of freedom between the adjacent cells will be removed using the RM.
3.1. Truss Application
A truss is an element structure consisting of two or more bar elements, connected to each other by pins, by which each pin will support rotations around its axis only. Cranes are modeled as a truss, where this will be studied under forced vibrations and seismic loading. A freestanding crane is considered as a periodic structure where the repeated cell is shown in Figure 3. The global nodes are numbered as in the displayed order in ANSYS.
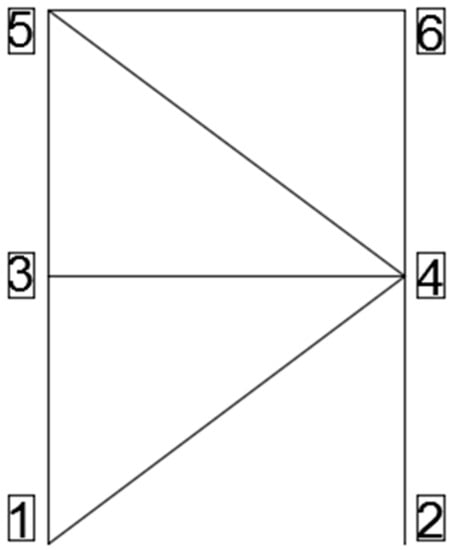
Figure 3.
Repeated cell in the truss.
The bar elements will differ by their cross-sectional areas, since the vertical bars hold larger loads; then, its cross-sectional area is larger than those of the horizontal and inclined bars. Hence, each element is oriented differently relative to the global coordinate system.
The element equation is expressed as:
where , is the angular velocity, is the local stiffness matrix, is the local damping matrix, is the local mass matrix, is the local displacement vector and is the local loading vector.
The truss element will have two degrees of freedom (DOF) at each node: translations in the nodal x and y directions.
The bar element under study is a steel bar with characteristics represented in Table 1.

Table 1.
Bar element characteristics.
Referenced to real-life applications, freestanding tower cranes with fixed foundations and no undercarriage supports are modeled as cranes with the repeated cell mentioned before, and they are only repeated 16 times with a total length of , including the foundation height. All dimensions are assumed relative to actual values.
Both types of loadings will be applied to the same crane structure presented, with the same repeated cell and type of material employed. Hence, the structures relative to the two different loadings will have equal stiffness, mass and damping matrices. The dynamic stiffness matrix is obtained due to the discussed approach, without the need for global assembly.
3.1.1. Truss under Forced Vibration at the Last Node
is taken for two different types of damping:
- Rayleigh damping:where and are calculated from the natural frequencies and the relative damping ratio. The natural frequencies taken are the first two natural frequencies, with their relative mode shapes shown in Figure 4; determined by modal analysis. The damping ratio for steel material used in a footbridge damping is [22].
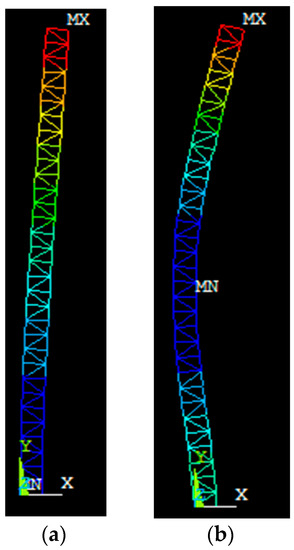 Figure 4. Mode shapes for the natural frequencies. (a) The first mode shape with a modal frequency of ; (b) the second mode shape with a modal frequency of .
Figure 4. Mode shapes for the natural frequencies. (a) The first mode shape with a modal frequency of ; (b) the second mode shape with a modal frequency of . - Hysteretic damping:The dynamic stiffness matrix is demonstrated as:
The crane interpreted is illustrated in Figure 5. The last nodes of interest are under harmonic vibrations for , where . The fixed foundation will remove the degrees of freedom on the first two nodes in the global system, and the matrix is assembled upon a relationship between a cell and its consecutive one. The periodic structure is computed under a range of driving frequencies, for the purpose of estimating the frequency response function at the excited node.
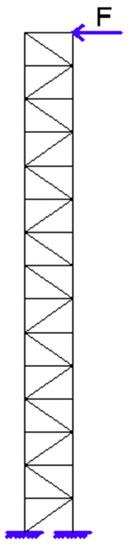
Figure 5.
Crane under forced excitation.
3.1.2. Truss under Seismic Load
The truss application is applied under a second type of loading for the investigation of the frequency response function under a range of frequencies. The crane structure will be studied under hysteretic damping solely, represented by the previously shown dynamic stiffness matrix (14). The first two nodes are subjected to seismic load, which is modeled as a harmonic displacement of , where on the base of the structure, as shown in Figure 6.

Figure 6.
Crane under seismic load.
3.2. Frame Application under Seismic Load
Frames are structures that have a combination of beams resisting loads. Such structures are modeled to overcome large moments developed due to the applied loading. The connected node acquires three DOF, preventing displacement in the y-direction and rotations in the x- and z-direction. A building under seismic load is modeled as a frame. Timoshenko beams will be studied, having four degrees of freedom. The cross-sectional dimensions of all frame elements and the repeated cell are illustrated in Figure 7 and Figure 8, respectively. The cell will be repeated 16 times with a total length of .
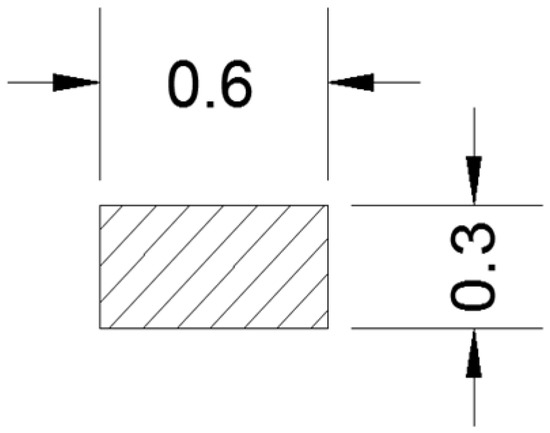
Figure 7.
Cross-section of the frame; dimensions are in meters.
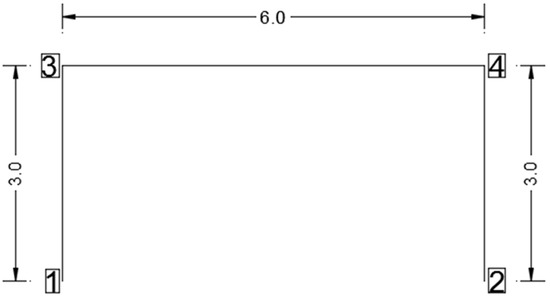
Figure 8.
Repeated cell in the frame; dimensions are in meters.
Frame analysis for the local element is similar to the truss element. Stiffness and mass matrices ( and ) are found from the ANSYS program, and the damping matrix () is established using hysteretic damping, as mentioned for the truss; where the dynamic stiffness matrix is represented as:
The beam used is made up of steel with a modulus of elasticity and density similar to that of the bar element; where Young’s modulus of elasticity is and the density is . The nodes at the base are under a harmonic displacement of , where , as shown in Figure 9. The periodic structure will be examined for a range of frequencies for computing the frequency response function.

Figure 9.
Frame model under seismic load.
4. Results
The FRF obtained from the recursive method will be compared to that using a conventional finite element program (ANSYS). The elapsed time for each application is measured and collated between the FEM and RM. The PC machine utilized for finite element analysis runs on an Intel Core i7-4500U with a clk (clock) speed of 2.40 GHz and 8.00 GB of RAM.
4.1. Truss Application under Forced Vibration
The results for the crane structure made up of 16 repeated cells under Rayleigh damping is demonstrated in Figure 10, and a zoomed-in presentation was done to illustrate the difference in achieving close results between low and high frequencies. The results represent the variation of the modulus of displacement logarithmically with respect to the range of frequencies for the last node, excited under harmonic forced vibration.
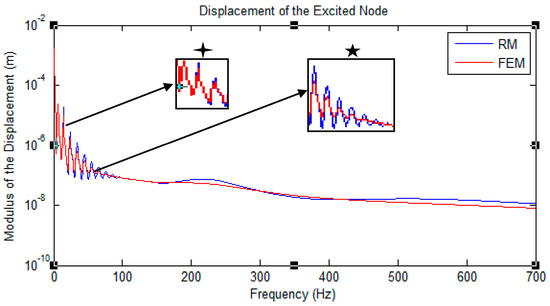
Figure 10.
Displacement of the excited node under Rayleigh damping for the truss application that is applied to forced vibration. The graph is logarithmically scaled.  : low frequencies;
: low frequencies;  : high frequencies. RM, recursive method.
: high frequencies. RM, recursive method.
 : low frequencies;
: low frequencies;  : high frequencies. RM, recursive method.
: high frequencies. RM, recursive method.
Figure 11 illustrates the normalized percentage error between the RM and FEM methods in the low and high frequencies domains, evaluating approximate low frequencies as values less than 50 Hz. In the low frequency domain, the structure most likely behaves as in the static equilibrium, where the effect of the driving frequencies is still minimal on the response (low effect as if ). The evaluated percentages were very small for . However, for , the structure is most likely showing dynamic behavior. High frequencies will estimate a larger percentage range since then, the effect of becomes recognizable and influential, increasing the mass effect . Very high frequencies estimated better results since beyond that for cases where the structure’s properties (mass and stiffness) are high (complete structure estimated recursively), the inverse of the dynamic stiffness matrix will result in closer FRF. The response under hysteretic damping is shown in Figure 12.
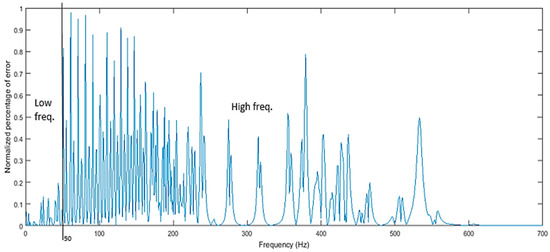
Figure 11.
Normalized percentage of error between FEM and RM for a range of frequencies.
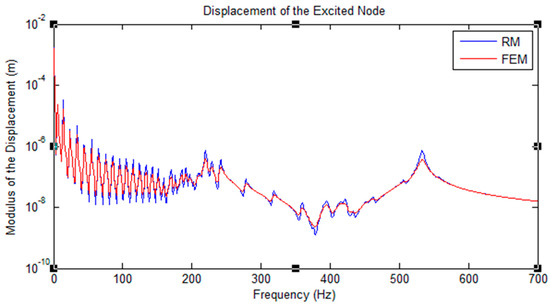
Figure 12.
Displacement of the excited node under hysteretic damping for the truss application that is applied to forced vibration. The graph is logarithmically scaled.
The difference in the elapsed time for each method is presented in Table 2. The time elapsed for getting the frequency response in both damping cases is much higher using the finite element method than that of the recursive method. The finite element analysis took approximately 18-times more than the recursive method. Larger time differences between the two damping types are anticipated to be calculated for more complex structures where the number of DOF is very large.

Table 2.
Time comparison between the two methods, for the truss application under forced vibrations.
More high frequency peaks are shown for hysteretic damping, due to its complete material dependency. The peaks are caused by imperfections in material elasticity, in which the reaction of the material to changes is dependent on its past reactions to change.
4.2. Truss Application under Seismic Load
The frequency response function found from the recursive method using hysteretic damping will be compared to that using the conventional finite element program (ANSYS), and the results are shown in Figure 13. The values calculated demonstrate the variation of the displacement under a range of frequencies for the first node that is applied to harmonic displacement. Hysteretic damping is known to be completely material dependent. This is due to some imperfection of the elasticity of the material, in which the reaction of the material to changes is dependent on its past reactions to change.
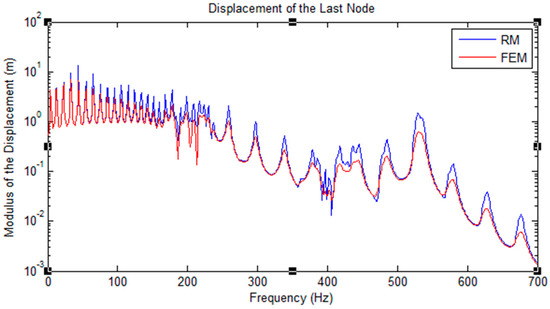
Figure 13.
Displacement of the last top node of the truss structure under seismic load, applied to hysteretic damping. The graph is logarithmically scaled.
The time ratio calculated between the two methods is approximately 1:22, as in Table 3. The calculated elapsed time shows that the finite element method took approximately 22-times more than the recursive method to compute the FRF for the crane structure under hysteretic damping.

Table 3.
Time comparison between the two methods, for the truss application under seismic load.
4.3. Frame Application under Seismic Load
The results found using the recursive method and the conventional finite element software (ANSYS) for determining the frequency response function are presented in Figure 14. It displays the logarithmic varying displacement of the first bottom node that is excited under harmonic displacement. The modulus of displacement is studied for a range of frequencies.
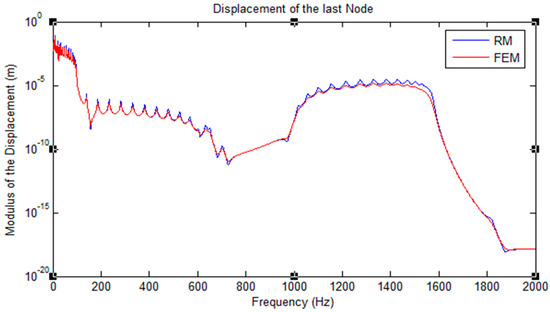
Figure 14.
Displacement of the last top node for the frame application under seismic loading, applied to hysteretic damping. The graph is logarithmically scaled.
The time ratio calculated between two methods is approximately 1/31.6, as shown in Table 4. The measured time elapsed for the two comparing methods reveals that the FEM took approximately 32-times more than the RM to compute the FRF for the frame structure under seismic load.

Table 4.
Time comparison between the two methods for the frame application.
4.4. Analysis
4.4.1. Periodic Structures Having Steel Material
The results for the two different applications under harmonic vibrations showed that RM calculated values are close, but slightly higher than the values of the FEM. For low and high frequencies, the modulus of displacement of the RM showed nearer values than at frequencies that cannot be considered as high. Note that the finite element analysis was taken as the reference method. The percentage difference between the two approaches for the two applications is established in Table 5.

Table 5.
Percentage difference.
Rayleigh damping is defined as the type of damping that is frequency dependent, and it depends on the natural frequencies for defining its equation. However, hysteretic damping is a material-dependent type of damping; thus, it has the advantage of minimizing the effect of the driving frequency on the response. These two types of damping were studied on the truss application under forced excitations, solely. The graph relative to the Rayleigh damping demonstrates that the response was damped at lower frequency than that of the other type of damping.
The maximum natural frequency is defined as the greatest value of the frequency that can illustrate a physical understanding of the structure’s response via the mode shape demonstrated by modal analysis. Further, this value of the natural frequency will determine the maximum range of frequencies to be examined. Concerning the truss structure, for natural frequencies greater than , the crane structure could not be interpreted physically. Nevertheless, for the frame structure, the maximum natural frequency was , beyond which it will not acquire major interest. The mode shapes relative to these frequencies are observed in Figure 15. Hence, the range of frequencies considered for both applications compensates for this frequency and beyond.
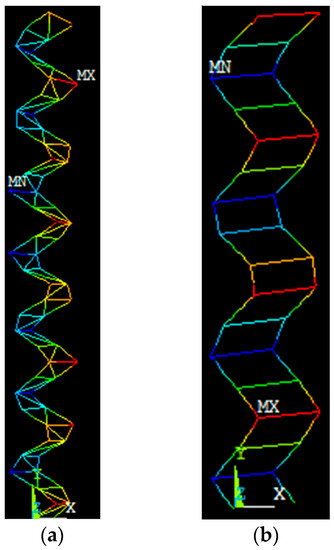
Figure 15.
Mode shapes for the natural frequencies. (a) The mode shapes relative to the modal frequency for the truss application of ; (b) the mode shape for the frame application of .
The modulus of displacement at the excited node for the truss application under forced vibrations was examined upon altering the repeated cell, leading to a change in the total number of cells used. RM was studied when enlarging the repeated cell, by making the new total number of cells as , where is the total number of cells in the previous step. Hence, will initially be 16. The study was done at the most critical case, resonance, where the driving frequencies are equal to the natural frequencies of the structure. This is demonstrated in Figure 16, and the results are presented in Table 6, where it represents the modulus of displacement in the x-direction for the studied node. This test was applied on the two applications (truss and frame) under the studied types of loadings, and they all evaluated the same analysis. The table showed that the response is not affected by the number of cells used, as long as the same structure is studied. The structure is the same when changing the repeated cell, since the total number of the cells was modified correspondingly.
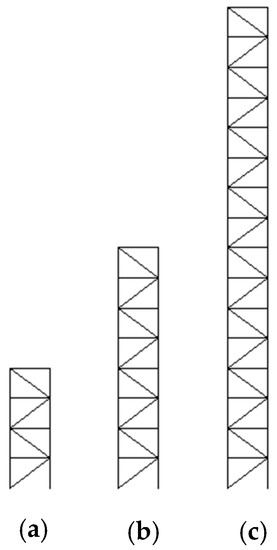
Figure 16.
The repeated cells are presented where: (a) the new repeated cell is double the previous one and it is repeated eight times; (b) the new repeated cell consists of four-times the old cell, and it is repeated four times; (c) the cell will be repeated two times.

Table 6.
The modulus of displacement in the x-direction for the excited node under three different natural frequencies, for a truss application under forced vibrations.
4.4.2. Periodic Structures Having Plastic Material
This was also investigated for a plastic material (PVC: polyvinyl chloride) having Young’s modulus of elasticity of and a density of for the two applications under forced excitation and seismic loading. The results are shown in Table 7. The values measured had the same inspection, determining the acceptance of the analysis deduced, by which for low and high driving frequencies, the response was more acceptable than intermediate frequencies in comparison with FEM. The percentage difference between the two approaches for the two applications when PVC material is assigned are established in Table 8. The table shows that the measured elapsed time for the FEM took approximately 22× more time than the RM to compute the FRF for the truss structure under the two types of loadings. Moreover, FEM consumed a high amount of time in the computations during the implementations of the frame structure under seismic load, where it took 150× more time than the RM to compute the FRF.

Table 7.
The modulus of displacement in the x-direction for the excited node under three different natural frequencies, for a truss application under forced vibrations, upon assignment of PVC.

Table 8.
Percentage difference for the PVC material.
4.4.3. The Effect of the Number of Forces Applied
The first study on the crane included behavioral examination of the excited node under forced vibrations. Loads were applied on one node exclusively. This section includes studying the effectiveness of this approach for periodic structures under a large number of forces. The effect of the number of forces is investigated in three different cases, in an increasing order of multiplying by two. A force is added at the mid-span of the truss structure in addition to the load exerted at its top. Then, the number of loads increases to four, after applying two excitations at and . Further increasing includes the addition of four more forces, resulting in a periodic structure applied to eight loads that are equal in magnitude and uniformly distanced. Table 9 presents the resultant outcomes for the relevant test.

Table 9.
Results upon adding different numbers of forces distributed equally over the periodic structure.
The elapsed times consumed by the FEM and the RM are displayed and compared; the time ratio shows the high efficacy of applying this method on a high number of forces. The percentage difference was measured at each excited node, and the results show a low difference between the two methods. However, there were two excited nodes that showed a high difference upon interpretations. The two nodes are the last excited node when four forces were applied, and the other is the mid-excited node upon eight force excitations, where the percentage difference exceeded 50%. Farther studies should be employed to illustrate a relation between the numbers of forces that can be applied with the length of the periodic structure, while maintaining significant effectiveness. Supplementary expectations are that when the forces are engaged with every node, the method will not be feasible for calculating the frequency response function, since the advantage of removing the internal nodes recursively will be obsolete.
5. Conclusions
In this paper, a further study was done on structures that cannot be designed as waveguides. Cranes and buildings were modeled as trusses and frames, respectively, under various loading. Trusses and frames have in their structural composition the inability to guide waves along their longitudinal axis. Waveguides are used in various types of applications and have different methods for accurate computations. However, structures that are not considered as waveguides consume various applications, as well, but there are no different numerical methods for easier, faster and precise computations.
The recursive method is an approach used for calculating the frequency response function of general periodic structures. In spite of the element’s complexity, a recursive method can be employed on all types of periodic structures, as long as the internal nodes are under no load. For finding a satisfying result, a high number of cells must be considered, which will lead to a large number of computations. This method provides a solution close to that obtained from the reference method (FEM), and it decreases the time consumption. The time consumed for a steel material was observed to a have a range of ratios between 1:18 and 1:31, depending on the type of cells and the load exerted. Displacement values were nearer to that of the finite element method at low and very high frequencies. The percentage difference for the structures studied under various types of loading does not exceed 19%. Nevertheless, different materials were studied to have further support of the analysis. The plastic material had much lower time ratios, in the range between 1:22 and 1:151, while the relative percentage difference did not exceed 17%. This difference is due to the inverse of the dynamic stiffness matrix, which will lead to a slight numerical difference between the finite element method and the recursive method. Upon varying the number of forces, the time ratio lied in the range of 1:106 till 1:172, with a low percentage difference.
Future examinations include studying the effectiveness of this approach for periodic structures under a large number of forces. Expectations are that when the forces are engaged with every node, the method will not be feasible for calculating the frequency response function, since the advantage of removing the internal nodes recursively will be obsolete. Further studies include the types of cells to be repeated and the effect on the frequency response function. Moreover, a more applicable solution may be calculated by changing the type of element from linear to quadratic; therefore, vibrations at internal nodes can be computed. Otherwise, an element with a greater mesh size should be examined, since the increase in the mesh size will display the response for the internal nodes. The effect of the frequency on the modulus of displacement will be also inspected, and more complex periodic structures will be interpreted. Unsteady states in heat transfer problems may be evaluated for complex fin geometries.
Author Contributions
Reem Yassine and Faten Salman wrote most of this paper. Ali Al Shaer and Mohammad Hammoud contributed to the numerical simulations. Denis Duhamel contributed to the finalizing of the paper and the reviewing process.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Dong, S.B.; Nelson, R.B. On natural vibrations and waves in laminated orthotropic plates. J. Appl. Mech. 1972, 39, 739–745. [Google Scholar] [CrossRef]
- Aalami, B. Waves in prismatic guides of arbitrary cross section. J. Appl. Mech. 1973, 40, 1067–1072. [Google Scholar] [CrossRef]
- Finnveden, S. Finite Element Techniques for the Evaluation of Energy Flow Parameters: Keynote Lecture. In Proceedings of the Novem2000 Conference, Lyon, France, 2–4 November 2000.
- Finnveden, S. Evaluation of modal density and group velocity by a finite element method. J. Sound Vib. 2004, 273, 51–75. [Google Scholar] [CrossRef]
- Yu, C.P.; Roesset, J.M. Dynamic stiffness matrices for linear members with distributed mass. J. Appl. Sci. Eng. 2001, 4, 253–264. [Google Scholar]
- Nilsson, C.M. Waveguide Finite Elements for Thin-Waled Structures. Licentiate Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2002. [Google Scholar]
- Birgersson, F. Prediction of Random Vibration Using Spectral Methods. Ph.D. Thesis, KTH Royal Institute of Technology, TRITA-AVE, Stockholm, Sweden, 2003; p. 30. [Google Scholar]
- Birgersson, F.; Finnveden, S.; Nilsson, C.M. A spectral super element for modelling of plate vibration. Part 1: General theory. J. Sound Vib. 2005, 287, 297–314. [Google Scholar] [CrossRef]
- Birgersson, F.; Finnveden, S. A spectral super element for modelling of plate vibration. Part 2: Turbulence excitation. J. Sound Vib. 2005, 287, 315–328. [Google Scholar] [CrossRef]
- Gry, L. Dynamic modelling of railway track based on wave propagation. J. Sound Vib. 1996, 195, 477–505. [Google Scholar] [CrossRef]
- Gavric, L. Computation of propagative waves in free rail using finite element technique. J. Sound Vib. 1995, 185, 531–543. [Google Scholar] [CrossRef]
- Bartoli, I.; Marzani, A.; Lanza di Scalea, F.; Viola, E. Modelling wave propagation in damed waveguide of arbitrary cross-section. J. Sound Vib. 2006, 295, 685–707. [Google Scholar] [CrossRef]
- Marzani, A.; Viola, E.; Bartoli, I.; Lanza di Scalea, F.; Rizzo, P. A semi-analytical finite element formulation for modelling stress wave propagation in axisymmertic damped waveguides. J. Sound Vib. 2008, 318, 488–505. [Google Scholar] [CrossRef]
- Duhamel, D.; Mace, B.R.; Brennan, M.J. Finite element analysis of the vibrations of waveguides and periodic structures. J. Sound Vib. 2004, 294, 205–220. [Google Scholar] [CrossRef]
- Lee, S.C.; Rawatt, V.; Lee, J.F. A hybrid finite/boundary element method for periodic structures on non-periodic meshes using an interior penalty formulation for Maxwell’s equations. J. Comput. Phys. 2010, 229, 4934–4951. [Google Scholar] [CrossRef]
- Castanier, M.P.; Ottarsson, G.; Pierre, C. A Reduced Order Modeling Technique for Mistuned Bladed Disks. J. Vib. Acoust. 1997, 119, 439–447. [Google Scholar] [CrossRef]
- Bathe, K.J.; Dong, J. Component mode synthesis with subspace iterations for controlled accuracy of frequency and mode shape solutions. Comput. Struct. 2014, 139, 28–32. [Google Scholar] [CrossRef]
- Zhou, K.; Liang, G.; Tang, J. Component mode synthesis order-reduction for dynamic analysis of structure modeled with NURBS finite element. J. Vib. Acoust. 2016, 138, 021016. [Google Scholar] [CrossRef]
- Duhamel, D. A recursive approach for the finite element computation of waveguides. J. Sound Vib. 2009, 323, 163–172. [Google Scholar] [CrossRef]
- Duhamel, D.; Erlicher, S.; Nguyen, H.H. A recursive finite element method for comuting tyre vibrations. Eur. J. Comput. Mech. 2011, 20, 9–27. [Google Scholar]
- Guyan, R.J. Reduction of stiffness and mass matrices. AIAA J. 1965, 3, 380–387. [Google Scholar] [CrossRef]
- Bachmann, H.; Ammann, W.J.; Deischl, F.; Eisenmann, J.; Floegl, J.; Hirsch, G.H.; Klein, G.K.; Lande, G.J.; Mahrenholtz, O.; Natke, H.G.; et al. Vibration Problems in Structures: Practical Guidelines; Institut für Baustatik und Konstruktion (IBK): Basel, Switzerland, 1995. [Google Scholar]
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).