Abstract
Nowadays, density functional theory (DFT)-based high-throughput computational approach is becoming more efficient and, thus, attractive for finding advanced materials for electrochemical applications. In this work, we illustrate how theoretical models, computational methods, and informatics techniques can be put together to form a simple DFT-based throughput computational workflow for predicting physicochemical properties of room-temperature ionic liquids. The developed workflow has been used for screening a set of 48 ionic pairs and for analyzing the gathered data. The predicted relative electrochemical stabilities, ionic charges and dynamic properties of the investigated ionic liquids are discussed in the light of their potential practical applications.
1. Introduction
Over the past few decades, ionic liquids have been thoroughly investigated as potential solvents for electrochemical applications [,]. Such attention is due to a tunable combination of ionic liquids’ physicochemical properties that are superior to the ones typical for traditional aqueous and organic solvent electrolytes. Density functional theory (DFT) computational methods are widely applied to calculate the electronic properties of ionic liquids on the case-by-case basis. Meanwhile, the so-called high-throughput approach is applied to conduct screening of components of aqueous and organic solvent electrolytes in search for the best candidates for their practical applications [,,,,,,], for example, in the so-called electrolyte genome project []. However, this approach has not yet been fully applied for screening ionic liquids.
The aim of high-throughput screening is to process a large set of candidates to find those that match given criteria. Subsequently, the pool of candidates is downsized using several descriptors corresponding to desirable properties. Then, the process is repeated on a smaller number of candidates, and usually using accurate methods. The high-throughput approach was used to find the best components for energy storage systems [,,,,,,,]. Cheng et al. screened 1400 organic molecules for use in non-aqueous redox-flow batteries []; they down-selected the candidates using DFT-based descriptors for redox potentials, solubility, and stability. For instance, in the latter, and some similar studies, the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) energy was used as a descriptor for the redox potentials.
In the case of ionic liquids, the appropriateness of common DFT methods was benchmarked by Zahn et al. against coupled-cluster with single, double and triple excitations (CCSD(T)) results for 236 ionic pairs []. Lage-Estebanez et al. investigated the effect of the self-interaction error on the DFT results of 24 ionic pairs and 48 ionic associates []. These two works [,] can be classified as low-throughput computational studies. On the path to scaling up to the high-throughput computational screening of ionic liquids for electrochemical applications, we have developed and tested a DFT-based workflow, presented below.
2. Materials and Methods
A workflow for screening a set of ionic liquid pairs (Figure 1) and for automated data analysis was constructed using NaRIBaS (Nanomaterials and Room-temperature Ionic liquids in Bulk and Slab) framework [] with additional Python scripts.
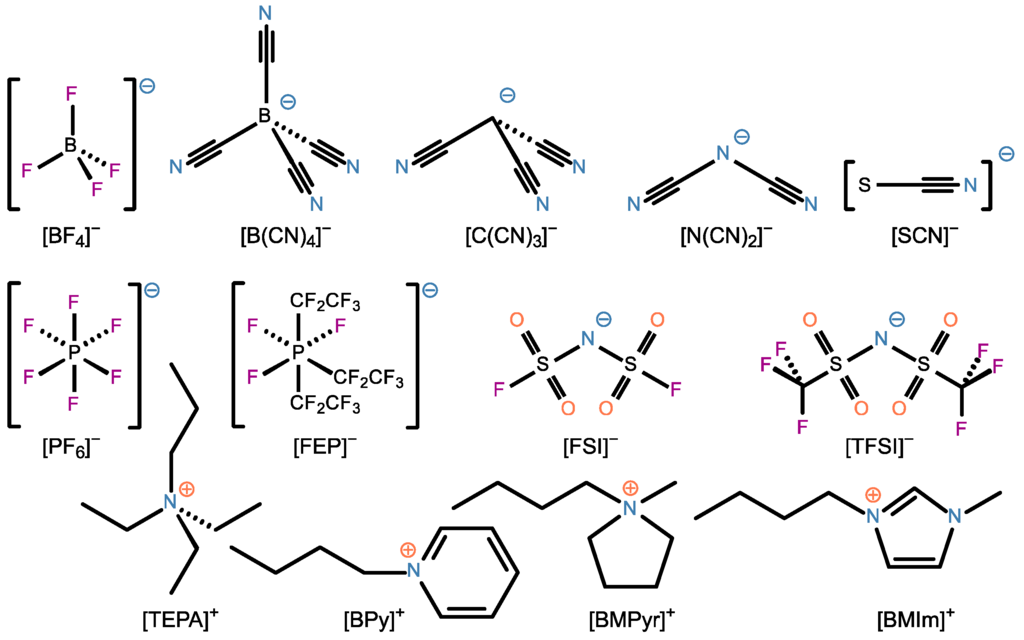
Figure 1.
The individual anions and cations that are combined to make up the 48 ionic pairs. Starting from the top left: tetrafluoroborate, tetracyanoborate, tricyanomethanide, dicyanimide, isocyanate, hexafluorophosphate, tris(pentafluoroethyl)trifluorophosphate, bis(fluorosulfonyl)imide, bis(trifluoromethylsulfonyl)imide, triethylpropylammonium, 1-butylpyridinium, 1-butyl-1-methylpyrrolidinium, 1-butyl-3-methylimidazolium. Chloride, bromide, and iodide ions were also employed but are not shown in the figure.
All calculations were carried out using the Orca 3.0.3 program package []. The starting geometries of the ionic liquids were obtained from a git-hub repository [] and optimized using Becke’s 88 exchange functional [] and Lee, Yang and Parr’s correlation functional [] (BLYP) using the Ahlrics’ style triple-zeta basis set (Def2-TZVP) [], Grimme’s dispersion correction (D3) [,] and geometrical counterpoise correction (gCP) []. Previously, Zahn et al. verified that among other functionals the BLYP functional with a basis set superposition error correction and a dispersion correction gives fairly good results for ionic pair interaction energies []. In previous work [], we showed that application of the hybrid Becke’s three parameter exchange functional [] with Lee, Yang and Parr’s correlation functional [] (B3LYP) to a certain extent suppresses the self-interaction error. Therefore, in this work, single point calculations were carried out with the hybrid B3LYP functional, which contains Hartree–Fock exchange energy to deal with the self-interaction error, again using the Def2-TZVP basis set as well as D3 and gCP corrections.
In Section 3.1 we estimated the electrochemical stabilities of the ionic pairs. The electrochemical stability of ionic liquids was extensively studied before using DFT methods [,]. The simplest approach is to correlate the cathodic stability with the LUMO energy value and the anodic stability with the HOMO energy value of ions forming an ionic liquid []. A more accurate approach is the delta self-consistent field (ΔSCF) method, in which the electron affinities and ionization energies are calculated from the electronic energy differences of reduced and oxidized species [,]. According to the ΔSCF method, the ionization energy (IEion) of a cation is defined as the difference between the electronic energies of the cation and its reduced form. Similarly, electron affinity (EAion) for an anion is defined the difference between the electronic energies of the anion and the oxidized anion:
For more exact analysis, solvation has to be accounted for either by a continuum model or specifically in a more expensive molecular dynamics simulation []. Furthermore, in molecular dynamics simulations, an electrode can be modeled, which allows more realistic circumstances for the cathodic or anodic decomposition. However, in this work, the aim was to reproduce experimental properties with simple and robust DFT calculations, which enable scaling up. For this reason, we used a modified ΔSCF method. Note, the ΔSCF method applied to single ions tends to underestimate the electrochemical stability [], because only ions in vacuo are simulated, while in a realistic system inter-ionic and interfacial interactions are important []. At the first approximation, taking into account the inter-ionic interactions and neglecting the interfacial interactions, we carried out the ΔSCF procedure with the ionic pair, therefore, accounting the solvation of an ion with its counter-ion:
By combining the ¼IEpair with ¾IEion and ¼EApair with ¾EAion, the electron affinities (EA) and ionization energies (IE) for the ionic liquids were calculated, respectively. The scaling factors ¼ and ¾ were chosen by fitting the computed values against the experimental electrochemical window values (see Table 6 in Reference []). The physical meaning of this scaling factor is closely related to the Madelung constant difference (Appendix A). Effectively, the approach applied takes into account the solvation energy of the species involved in the redox reactions at the interface.
The calculated electron affinities and ionization energies of the ionic pairs were used to estimate the relative electrochemical stabilities of the ionic liquids in terms of electrochemical potential window (EW):
In Section 3.2, we discuss the relation between ionic charges, energetics, and electronic density distribution by observing the correlation between dipole moments and interaction energies of ionic pairs. Dipole moment (μ) is a value that describes the charge separation of a system, and is equal to the multiplication of the distance between the centers of the charges (r) and the absolute value of the charge (q):
The ionic charges were estimated (i) by evaluating deviations on the interaction energy–dipole moment plot; and (ii) with the help of the Charges from Electrostatic Potentials using a Grid based method (CHELPG) []. Note, a detailed assessment of ionic charges by several computational methods, including CHELPG, is given in Reference [].
The interaction energy of the ionic pair is:
where EIP is the total energy of an ionic pair, and EAnion and ECation are the energies of the anion and the cation in their separately optimized geometries, respectively. Note, the energies are given with the gCP correction; the D3 correction was calculated and used to estimate the dispersion energy (Edisp) similar to Equation (5).
In Section 3.3, we discuss the dynamic properties of ionic liquids. The core dynamic property is the diffusion of ions, and it is commonly utilized as a litmus test for the ability of computational methods to predict this experimental quantity []. Tsuzuki identified several important molecular level quantities that have an influence on the dynamic properties, such as the size of the ions, the attraction between the ions and the conformational flexibility of the ions []. Zhang and Maginn showed that the diffusion of ions is proportional to the lifetime of an ionic associate implying that the interaction energy of an ionic pair is an important factor in the diffusive movement of the ions []. Therefore, it can be suggested to choose ionic liquids, which have lower calculated ionic pair lifetimes corresponding to higher diffusion coefficients and, thus, lower viscosity and higher conductivity. Instead of evaluating the diffusion coefficients, in this work, we focused on viscosities, simply because there are more experimental data on the latter. In Appendix A, we provide some further discussion about the diffusional movement of ionic liquids and show how it is related to viscosity. In Section 3.3, we turn the readers’ attention to the novel relation between ionic liquid viscosity and the ionic pair interaction energy that has been found in this study.
We chose relative electrochemical stability, charge density distribution and estimated activation energy of viscosity, as the descriptors for selecting ionic liquids for electrochemical applications.
3. Results
3.1. Relative Electrochemical Stability
For electrochemical applications, one of the most important properties of an ionic liquid is its electrochemical stability. The ΔSCF method enables estimating the IE and EA values, which, in combination, provide an estimation to the electrochemical potential windows as discussed in Section 2. EA and IE values estimated for 48 ionic pairs are presented in Figure 2.
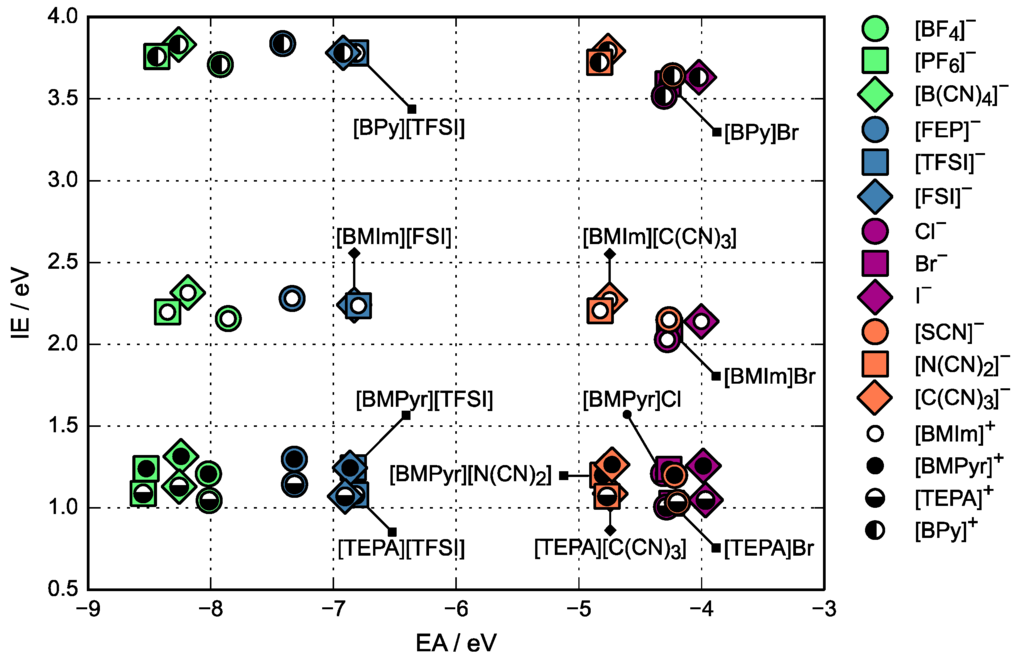
Figure 2.
Electron affinities and ionization energies of 48 ionic pairs, determined with the ΔSCF method. Each of the inner circles indicates a cation and the surrounding marker indicates an anion of an ionic pair.
As can be seen in Figure 2, the straightforward DFT-based approach provides a map of the relative stabilities of the ionic pairs towards reduction and oxidation. In Figure 2 the most stable ionic pairs reside on the bottom left part of the plot and the stability decreases when moving right and upwards on the plot. A better approach, comparable to experiment, would require modeling of the interface and exploring all possible reaction pathways, which would make the simulations more complicated and less scalable. The simpler DFT method gives the stability row for ions: [TEPA]+ ≈ [BMPyr]+ > [BMIm]+ > [BPy]+ and [PF6]− > [B(CN)4]− > [BF4]− > [FEP]− > [FSI]− ≈ [TFSI]− >> [N(CN)2]− ≈ [C(CN)3]− > Cl− > Br− ≈ [SCN]− > I− that is in agreement with the experiment (see Refs in []).
3.2. Charge Density Distribution
Figure 3 illustrates the dipole moment dependence on interaction energy of ionic pair for the 48 ionic pairs. The most important component of the ionic interaction energy is Coulomb interaction; which corresponds to the equation:
where q is the absolute ionic charge, r is the distance between the charge centers, and constant k, which is derived from the permittivity of vacuum and appropriate unit conversion factors, equals 1389.35 kJ·Å·mol−1.
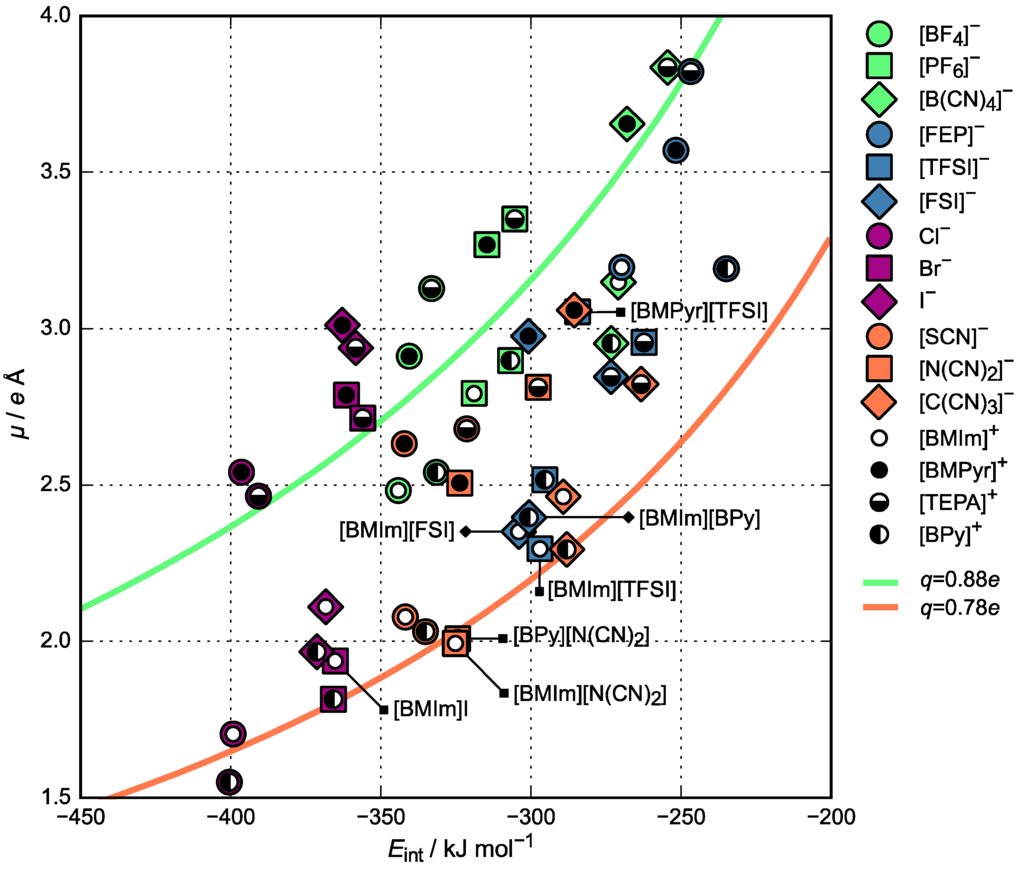
Figure 3.
Dipole moment dependence on the interaction energies of ionic pairs. Each of the inner circles indicates a cation and the surrounding marker indicates an anion of an ionic pair.
Combination of Equations (4) and (6) gives:
The two lines shown in Figure 3 were calculated using Equation (7) with arbitrarily chosen ionic charge values of 0.88e and 0.78e. The larger is the charge transfer from an anion to a cation, the lower is the corresponding point located in Figure 3. Dipole moment decreases with an increasing charge transfer, because of the effective charge of ions that decreases as well. In Figure 3, points are scattered which implies that the extent of charge transfer is not the same for the different ionic pairs. It is worth noting that the data points indicating [BMPyr]+ and [TEPA]+ cations are located systematically higher in Figure 3 than those corresponding to [BMIm]+ or [BPy]+ cations. In addition, fluorine-containing anions have higher dipole moments while cyanide and halide anions have lower dipole moments, except [B(CN)4]−. According to Figure 2, ionic liquids containing [BMIm]+ and [BPy]+ cations have higher IE, and those containing cyanide and halide anions have higher EA. Taking EA = ε(HOMO) and IE = −ε(LUMO), one can observe that the proximity of the HOMO and LUMO levels leads to the charge transfer between ions and lower dipole values. Figure 4 illustrates that charge transfer values calculated using CHELPG method are between 0.05e and 0.45e. Apparently, the CHELPG values of absolute ionic charges are slightly lower than those estimated using Equation (7) (see Figure 3). This implies that the interaction between ions is not purely Coulomb-type but, for instance, includes hydrogen bonding.
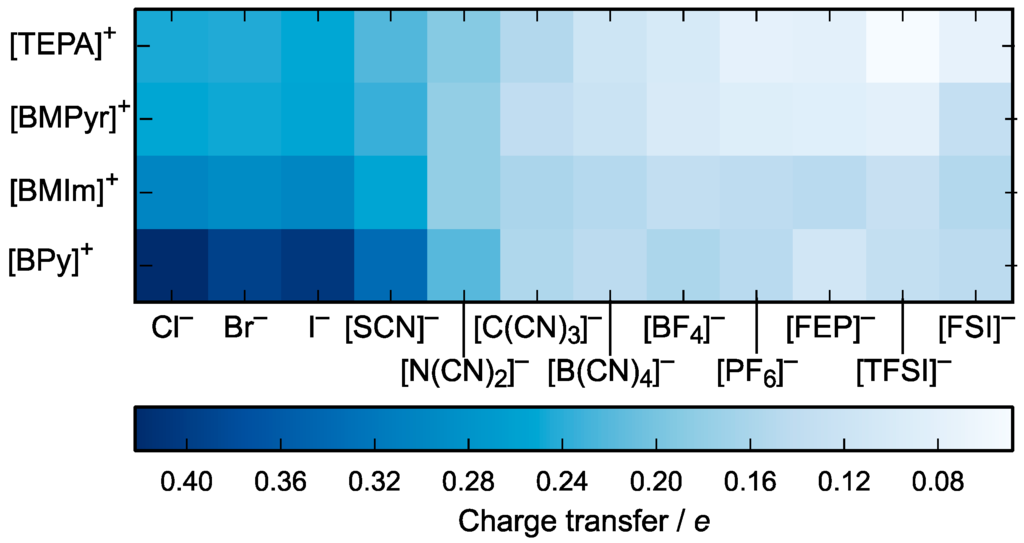
Figure 4.
Charge transfer in the ionic pairs from anion to cation calculated using CHELPG method.
3.3. Activation Energy of Viscosity
Experimental viscosity temperature dependences of ionic liquids were investigated before with various methods summarized by de Riva et al. []. Due to the limited time- and size-scales, the DFT methods are not perfect in predicting collective properties, such as viscosity. Intrinsically, this property can be evaluated with the help of molecular dynamics simulations. However, the force fields used in molecular dynamics simulations do not fully describe the charge transfer between ions, thus leading to underestimated dynamics of ions and, therefore, overestimated viscosity []. Consequently, the DFT methods are used to estimate dynamic properties extrinsically.
Below we present the correlation between the interaction energy of the ionic pairs and the activation energy of viscosity of the corresponding ionic liquid. Firstly, a symbolic activation energy of viscosity was derived using Arrhenius equation to tie a macroscopic phenomenon such as viscosity to an energetic parameter. The viscosity–temperature dependence data were taken from the references listed in Table B1 (see Appendix B). We calculated the activation energy (Eacalc) by linearizing the experimental viscosity (η) temperature dependences of ionic liquids:
where A is a constant and R is the ideal gas constant.
To obtain a linear relationship, the interaction energies were scaled by a factor ai, which includes a difference between two Madelung-type constants (ΔM = 0.165, see Appendix A) and an effective charge component’s square:
The effective charge for ionic pairs was fitted by minimizing the root-mean-square deviation of the Eaest – Eacalc linear dependence. The effective charge was fitted to 0.85e and to 0.74e for the ionic pairs with smaller and larger charge transfer, respectively. The obtained absolute values are in agreement with the ionic charge values estimated using the CHELPG method and are expectedly lower than expected from Figure 3. The dispersion energy (Edisp) was subtracted from the Eint, taking into account the promoting effect of the dispersion forces, as well as hydrogen bonding on the diffusional movement of ions. The effect of dispersion was normalized with another factor (b) which was taken to be half of the ΔM value. The normalization factors ai and b were defined as follows:
As can be seen in Figure 5a, the normalized interaction energy (Eaest) found with Equation (9) is in a good correlation with the activation energy of viscosity (Eacalc) calculated using the experimental data and Equation (8). Thus, the DFT-based approach, though simplified, represents a fast and efficient way of estimating the activation energy of viscosity of a pure ionic liquid. Figure 5b illustrates a diffusional jump potential energy profile regarding Eint. Assuming that the mass transport mechanism (as discussed in Appendix A) is the same for different ionic liquids, by Figure 5b, Eacalc is directly related to Eint.
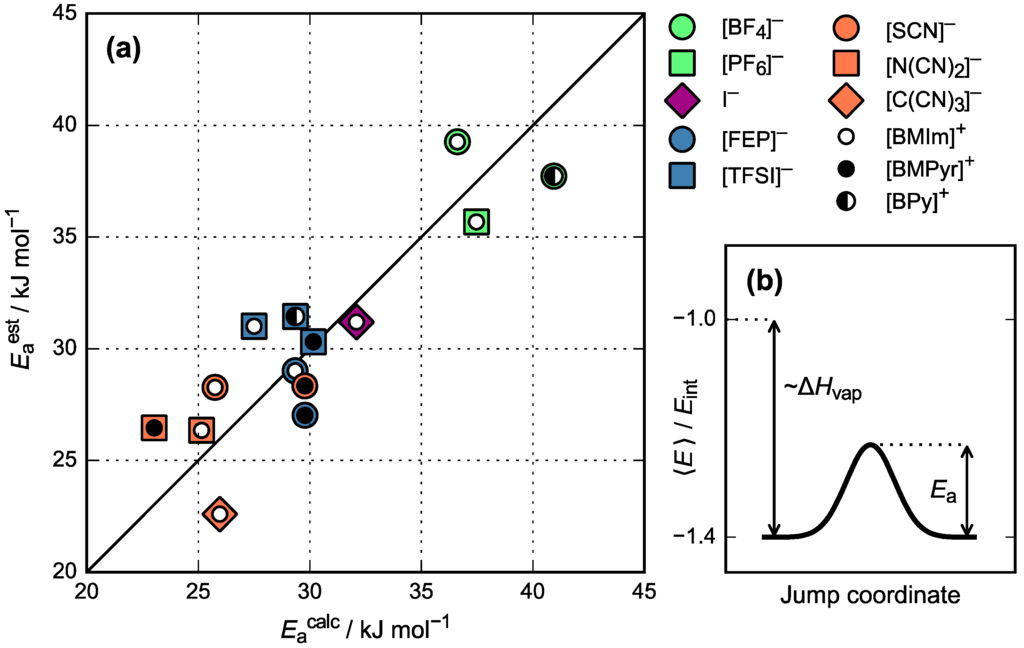
Figure 5.
(a) The relation between the interaction energies and the activation energies of viscosity. Each of the inner circles indicates a cation and the surrounding marker indicates an anion of an ionic pair; (b) Potential energy profile of a diffusional jump.
In Figure 6, we plotted the estimated activation energies of viscosity vs. the calculated electrochemical potential windows (Equation (3)) of ionic pairs. Both quantities are related to Eint (Equations (1)–(3) and (9)), yet the EW is largely determined by the electronic structure. It is known that the more stable ionic pairs, such as those containing the [BF4]− and [PF6]−, are very viscous, while those that are less stable also tend to be less viscous, e.g., ionic pairs containing cyanide-based anions have both low stability and low activation energy of viscosity. The exception to this is [B(CN)4]−, which is relatively stable and has a low activation energy of viscosity, and thus represents an interest for electrochemical applications. On the contrary, it can be seen that ionic pairs containing halogen anions have a high activation energy of viscosity due to their strong interactions with cation and are also relatively unstable. Nevertheless, the conclusion that more stable ionic pairs have higher viscosities and vice versa can be drawn from the plot. The trade-off can be found by choosing ionic liquids with EW >3 V and Eaest < 30 kJ·mol−1. These criteria satisfy ammonium- and pyrrolidinium-based ionic liquids combined with [B(CN)4]−, [C(CN)3]−, [C(CN)2]−, [TFSI]−, [FSI]−, and [FEP]−, which were all previously proposed as possible electrolytes for electrochemical applications [].
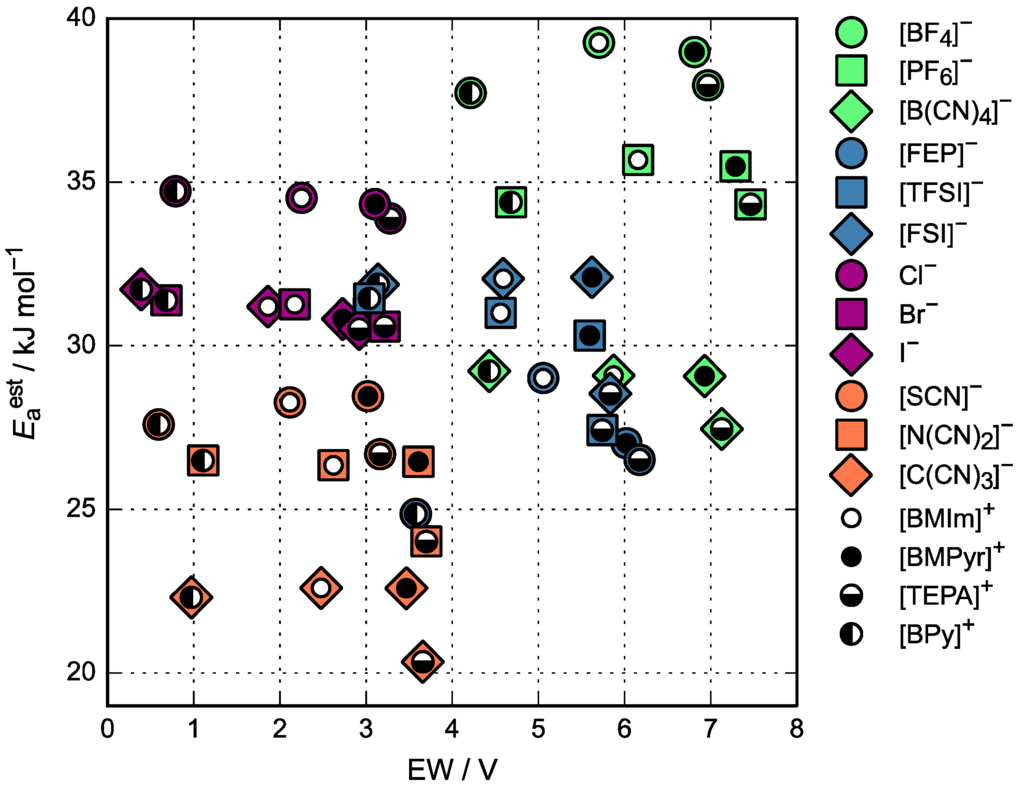
Figure 6.
The relation between the electrochemical stability window (EW) and the estimated activation energy of viscosity (Eaest).
4. Discussion
A number of studies focused previously on finding correlations between the interaction energy (Eint) and physicochemical properties of ionic liquids. Borodin et al. [] investigated some correlations between the heat of vaporization (ΔHvap), Eint, molar volume (Vm), self-diffusion coefficient (D), and ionic conductivity of 29 ionic liquids using molecular dynamics simulations. Investigation of the relation between D and ΔHvap for improving a correlation between −log(D) and ΔHvap revealed that adding 0.18 of the gas-phase cation–anion binding energy to ΔHvap improves the relationship. Borodin et al. suggested that the sum ΔHvap + 0.18Eint could be thought of as a cohesive energy that reflects contributions due to removing an ionic pair from the ionic liquid and therefore breaking it apart []. Further endeavors of those authors to correlate a product of the volume of the ionic pair in power n and the average self-diffusion coefficient revealed that the best correlation is obtained for (VmD)−1 vs. ΔHvap + 0.28Eint. Deviations of some ionic liquids from the reported curve were explained on the basis of ion packing and diffusion pathways.
Bernard et al. [] observed a linear correlation between the proposed ratio of the total Eint to its dispersion component and melting point, especially when considering trends for individual anions, indicating the anion dependence of the melting point in ionic liquids. Their results also suggested that the inclusion of contributions from all possible ion-pair conformations close in energy to the lowest energy conformation through the Boltzmann average of their Eint at a given temperature can improve the correlations. In addition, some limitations are noted. The ratio is based on the Eint and, therefore it will only be able to predict trends where cation–anion interactions dominate thermodynamic properties. Moreover, they found that the dispersion component of Eint correlated better with viscosities and conductivities than the total Eint or its electrostatic component. It was suggested that the dispersion component correlates linearly with conductivity and viscosity because dispersion interactions are the first to be disrupted to allow ions to move.
Bernard et al. [] also suggested that Eint not always correlates with the observed physical properties due to entropy effects. In a study by Hunt et al. [] investigated why an ionic liquid, which had a weaker Eint had a higher melting point than another ionic liquid with higher Eint. It was found that the ionic liquid with weaker Eint had a smaller number of stable ion-pair conformations, thus suggesting that it has lower entropy. Lower entropy would favor the solid state and therefore, would be consistent with a higher melting point [].
In this study, we have found a linear correlation between Eint and viscosity activation energy. This illustrates how DFT can be utilized to predict not only the static but also the dynamic properties basing on calculations of the simplest models-ionic pairs. Moreover, DFT calculations provide insight into the relative electrochemical stability and the charge density distribution of ionic pairs, which are among the most important properties of ionic liquids for their practical applications. We emphasize that the charge transfer between ions has an opposite effect on electrochemical stability and viscosity. On the one hand, a larger charge transfer in ionic pairs correlates with a lower resistance of anions and cations towards oxidation and reduction, respectively. On the other hand, a larger charge transfer is associated with lower viscosity and, therefore, with higher ionic conductivity.
Overall, quick DFT calculations allow the screening of numerous ionic liquid pairs to evaluate the essential properties, such as electrochemical stability and viscosity of the corresponding ionic liquids. It can then be judged adequately which ionic liquids are the most suitable candidates for given practical applications.
Acknowledgments
We acknowledge “Ministerio de Ciencia e Innovación” (Project: CTQ2010-19232) and “Comunidad de Madrid” (Project: LIQUORGAS-CM S2013_MAE-2800) for the financial support. This research was supported by the EU through the European Regional Development Fund (Centre of Excellence, 2014-2020.4.01.15-0011), Institutional Research Grant IUT20-13, and Estonian Personal Research Project PUT1107.
Author Contributions
Vladislav Ivaništšev, Isabel Lage-Estebanez, and José M. García de la Vega conceived and designed the work; Karl Karu developed the computational workflow, ran all calculations, and performed the data analysis; Anton Ruzanov and Heigo Ers assisted in the analysis and contributed to the paper writing.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HOMO | Highest occupied molecular orbital |
| LUMO | Lowest unoccupied molecular orbital |
| DFT | Density functional theory |
| BLYP | Becke’s 88 exchange functional and Lee, Yang and Parr’s correlation functional |
| Def2-TZVP | Ahlrics’ style triple-zeta basis set |
| D3 | Grimme’s dispersion correction |
| gCP | Grimme’s counterpoise correction |
| B3LYP | Hybrid Becke’s three parameter exchange functional and Lee, Yang and Parr’s correlation functional |
| ΔSCF | method to estimate electron affinities and ionization energies |
| EA | Electron Affinity |
| IE | Ionization Energy |
| Eint | Interaction energy of an ionic pair |
| CHELPG | Charges from Electrostatic Potentials using a Grid based method |
| ΔHvap | Heat of vaporization |
| Vm | Molar volume |
| D | Self-diffusion coefficient |
Appendix A
For the interpretation of the diffusional behavior of ionic liquids, the Bahe–Varela pseudolattice formalism proves to be useful []. Because of the long-range nature of ionic interactions, the longer-range order, i.e., pseudolattice, is expected in ionic liquids than in other types of electrolyte solutions. Among some assumptions of this simple model approach, we will highlight that the energy calculation errors, stemming from the approximation of a liquid by an ordered lattice, are expected effectively canceled. Therefore, the free energy difference coming from strong Coulomb and van der Waals interactions can be approximated:
where MCoulomb and MvdW are multiplications of Madelung-like constants for Coulomb (E ∝ r−1) and van der Waals (E ∝ r−6) interactions, respectively, by a number of specific physical variables and constants which are omitted to retain clarity; R is the pseudolattice constant. The Madelung constant relates the structural features of a crystal with the interaction energy of the neighboring ions in the unit cells to give the corresponding lattice energy. As was shown by Izgorodina et al. it can be also applied to organic salts []. Within the pseudolattice formalism, we use the Madelung-like constants to define the free energy difference for an ion in both stable and transition states (Equation (A1)), when jumping from one cage to another (illustrated in Figure 5b). The rate of the successful jumps (ω) over the rate-limiting energy barriers (E#) can be quantified:
where kB is Boltzmann constant, h is Planck’s constant, P is the probability of a cavity formation with a radius larger than r/2, and r is the jump-length proportional to the anion–cation distance. Note, for the self-diffusion coefficient (D) applies: D ~ ω/r2. Experimentally it was confirmed that ω is proportional to the conductivity (σ) for a set of 14 ionic liquids []. In simulations of 29 ionic liquids it was shown that the ion pair lifetime (t ~ ω−1) is inversely proportional to the conductivity []. As shown in Appendix B, through the Stokes–Einstein and Nernst–Einstein equations the conductivity is related to the diffusion coefficient and viscosity of an ionic liquid as σ ~ D and σ ~ η−1, respectively. Therefore, the interaction between the cation and anion plays a significant role in controlling the ion dynamics in ionic liquids. We suggest that the activation energy can be expressed as the difference between Madelung-like constants (ΔM) for ion in a stable and transition states. Consequently, under the approximations described above, the interaction energy of an ionic pair is theoretically related to the activation energy and the probability for the ion jump between two pseudolattice cages. The elegance of such approach is that ΔM serves as proportionality coefficient in Equation (9), and is roughly the same for the investigated set of data. Moreover, taking into account that during the vaporization an ionic pair evaporates from the ionic liquid surface, the heat of vaporization can be approximated as: ΔHvap ≈ (M − 1)Eint. The latter expression provides an explanation to a number of derived D vs. ΔHvap relations, discussed in Section 4.
Appendix B
In this work, we operate with viscosities instead of the diffusion coefficients, because there are more experimental data on the former. Ren et al. investigated ionic liquids with ultrafast two-dimensional IR spectroscopy []. Their results suggested that breaking up of the local ion-cage is the key event for activating translational diffusion and hence viscosity in ionic liquids. More generally, in substance with no chemical or electrical gradients (i.e., pure ionic liquid at potential of zero charge) the viscosity (η) is inversely proportional to the self-diffusion coefficient (D):
where λ1 and λ2 are the pseudo-lattice constants in the plane parallel to where the observed diffusional movement takes place and λ3 is the pseudo-lattice constant normal to the diffusional plane [], kB is the Boltzmann constant, and T is absolute temperature.
When describing classical electrolyte solutions, the mobile charge carrier is related to its diffusion coefficient (D) through the Nernst–Einstein equation:
where, z is the valence of the charge carrier, e0 corresponds to the elementary charge, NA is the Avogadro number.
Also, the diffusion coefficient of a model spherical species of an effective radius r is inversely proportional to the medium viscosity, according to the Stokes–Einstein equation:
The Nernst–Einstein relation was derived for non-interacting ions, such as in an infinitely dilute electrolyte solution. In real ionic liquids mass, momentum, charge and energy transport processes which involve correlated collisions, caging, and vortex motions can also be taken into account []. In fragile ionic liquids where the structure is dominated by packing effects, the structural relaxation, which determines the transport properties, is that of the cage around each particle []. Nevertheless, from Equations (B2) and (B3) the following equation can be derived when taking into account that N = nNA and σ = Λn/V:
Therefore, the conductivity (σ) of a classical electrolyte solution is inversely proportional to the medium viscosity. The same applies to the ionic liquids, thus can be used in high-throughput calculations to evaluate conductivity values from the estimated viscosity values.

Table B1.
The range of temperatures (T) of the fitted experimental viscosities, experimental viscosities (η) at the lowest temperature of the corresponding temperature range, and the activation energies (Eacalc) calculated from the experimental viscosity–temperature dependence using Equation (8).
| Ionic Liquid | T Range/K | Max. η/Pa·s | Eacalc/kJ·mol−1 |
|---|---|---|---|
| [BMIm]BF4 | 278.15−338.15 | 0.36 [] | 36.62 |
| [BMIm]PF6 | 288.15−373.15 | 0.533 [] | 37.47 |
| [BMIm]TFSI | 278.15−373.15 | 0.143 [] | 27.50 |
| [BMIm]I | 353.15−388.15 | 0.0365 [] | 32.09 |
| [BMIm]N(CN)2 | 293.15−343.15 | 0.03679 [] | 25.15 |
| [BMIm]SCN | 313.15−353.15 | 0.0322 [] | 25.75 |
| [BMIm]C(CN)3 | 298.15−338.15 | 0.02784 [] | 25.96 |
| [BMIm]FAP | 293.15−373.15 | 0.1003 [] | 29.34 |
| [BMPyr]SCN | 298.15−348.15 | 0.109 [] | 29.84 |
| [BMPyr]N(CN)2 | 293.15−343.15 | 0.0413 [] | 23.02 |
| [BMPyr]FAP | 290−365 | 0.355 [] | 29.78 |
| [BMPyr]TFSI | 283.15−353.15 | 0.168 [] | 30.16 |
| [BPy]BF4 | 298.15−343.15 | 0.145 [] | 40.94 |
| [BPy]TFSI | 303.15−328.15 | 0.04915 [] | 29.36 |
References
- Fedorov, M.V.; Kornyshev, A.A. Ionic Liquids at Electrified Interfaces. Chem. Rev. 2014, 114, 2978–3036. [Google Scholar] [CrossRef] [PubMed]
- MacFarlane, D.R.; Tachikawa, N.; Forsyth, M.; Pringle, J.M.; Howlett, P.C.; Elliott, G.D.; Davis, J.H.; Watanabe, M.; Simon, P.; Angell, C.A. Energy applications of ionic liquids. Energy Environ. Sci. 2014, 7, 232–250. [Google Scholar] [CrossRef]
- Korth, M. Large-scale virtual high-throughput screening for the identification of new battery electrolyte solvents: Evaluation of electronic structure theory methods. Phys. Chem. Chem. Phys. 2014, 16, 7919–7926. [Google Scholar] [CrossRef] [PubMed]
- Borodin, O.; Olguin, M.; Spear, C.E.; Leiter, K.W.; Knap, J. Towards high throughput screening of electrochemical stability of battery electrolytes. Nanotechnology 2015, 26, 354003. [Google Scholar] [CrossRef] [PubMed]
- Schütter, C.; Husch, T.; Korth, M.; Balducci, A. Toward New Solvents for EDLCs: From Computational Screening to Electrochemical Validation. J. Phys. Chem. C 2015, 119, 13413–13424. [Google Scholar] [CrossRef]
- Husch, T.; Yilmazer, N.D.; Balducci, A.; Korth, M. Large-scale virtual high-throughput screening for the identification of new battery electrolyte solvents: Computing infrastructure and collective properties. Phys. Chem. Chem. Phys. 2015, 17, 3394–3401. [Google Scholar] [CrossRef] [PubMed]
- Husch, T.; Korth, M. Charting the known chemical space for non-aqueous lithium-air battery electrolyte solvents. Phys. Chem. Chem. Phys. 2015, 17, 22596–22603. [Google Scholar] [CrossRef] [PubMed]
- Husch, T.; Korth, M. How to estimate solid-electrolyte-interphase features when screening electrolyte materials. Phys. Chem. Chem. Phys. 2015, 17, 22799–22808. [Google Scholar] [CrossRef] [PubMed]
- Borodin, O.; Olguin, M.; Spear, C.; Leiter, K.; Knap, J.; Yushin, G.; Childs, A.; Xu, K. Challenges with Quantum Chemistry-Based Screening of Electrochemical Stability of Lithium Battery Electrolytes. ECS Trans. 2015, 69, 113–123. [Google Scholar] [CrossRef]
- Qu, X.; Jain, A.; Rajput, N.N.; Cheng, L.; Zhang, Y.; Ong, S.P.; Brafman, M.; Maginn, E.; Curtiss, L.A.; Persson, K.A. The Electrolyte Genome project: A big data approach in battery materials discovery. Comput. Mater. Sci. 2015, 103, 56–67. [Google Scholar] [CrossRef]
- Cheng, L.; Assary, R.S.; Qu, X.; Jain, A.; Ong, S.P.; Rajput, N.N.; Persson, K.; Curtiss, L.A. Accelerating Electrolyte Discovery for Energy Storage with High-Throughput Screening. J. Phys. Chem. Lett. 2015, 6, 283–291. [Google Scholar] [CrossRef] [PubMed]
- Zahn, S.; MacFarlane, D.; Izgorodina, E.I. Assessment of Kohn-Sham Density Functional Theory and Moller-Plesset Perturbation Theory for Ionic Liquids. Phys. Chem. Chem. Phys. 2013, 15, 13664–13675. [Google Scholar] [CrossRef] [PubMed]
- Lage-Estebanez, I.; Ruzanov, A.; de la Vega, J.M.G.; Fedorov, M.V.; Ivaništšev, V.B. Self-interaction error in DFT-based modelling of ionic liquids. Phys. Chem. Chem. Phys. 2016, 18, 2175–2182. [Google Scholar] [CrossRef] [PubMed]
- Ivaništšev, V.; Kirchner, K. NaRIBaS: A Scripting Framework for Computational Modelling of Nanomaterials and Room Temperature Ionic Liquids in Bulk and Slab. 2015. Available online: www.github.com/vladislavivanistsev/NaRIBaS (accessed on 15 July 2016).
- Neese, F. The ORCA program system. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Grimme, S. Density functional theory with London dispersion corrections. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2011, 1, 211–228. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [PubMed]
- Kruse, H.; Grimme, S. A geometrical correction for the inter- and intra-molecular basis set superposition error in Hartree-Fock and density functional theory calculations for large systems. J. Chem. Phys. 2012, 136, 154101. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Ong, S.P.; Andreussi, O.; Wu, Y.; Marzari, N.; Ceder, G. Electrochemical Windows of Room-Temperature Ionic Liquids from Molecular Dynamics and Density Functional Theory Calculations. Chem. Mater. 2011, 23, 2979–2986. [Google Scholar] [CrossRef]
- Pandian, S.; Raju, S.G.; Hariharan, K.S.; Kolake, S.M.; Park, D.-H.; Lee, M.-J. Functionalized ionic liquids as electrolytes for lithium-ion batteries. J. Power Sources 2015, 286, 204–209. [Google Scholar] [CrossRef]
- Ivaništšev, V.; O’Connor, S.; Fedorov, M.V. Poly(a)morphic portrait of the electrical double layer in ionic liquids. Electrochem. Commun. 2014, 48, 61–64. [Google Scholar] [CrossRef]
- Galiński, M.; Lewandowski, A.; Stępniak, I. Ionic liquids as electrolytes. Electrochim. Acta 2006, 51, 5567–5580. [Google Scholar] [CrossRef]
- Breneman, C.M.; Wiberg, K.B. Determining atom-centered monopoles from molecular electrostatic potentials. The need for high sampling density in formamide conformational analysis. J. Comput. Chem. 1990, 11, 361–373. [Google Scholar] [CrossRef]
- Kirchner, B.; Malberg, F.; Firaha, D.S.; Hollóczki, O. Ion pairing in ionic liquids. J. Phys. Condens. Matter 2015, 27, 463002. [Google Scholar] [CrossRef] [PubMed]
- Schröder, C. Comparing reduced partial charge models with polarizable simulations of ionic liquids. Phys. Chem. Chem. Phys. 2012, 14, 3089–3102. [Google Scholar] [CrossRef] [PubMed]
- Tsuzuki, S. Factors Controlling the Diffusion of Ions in Ionic Liquids. ChemPhysChem 2012, 13, 1664–1670. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Maginn, E.J. Direct Correlation between Ionic Liquid Transport Properties and Ion Pair Lifetimes: A Molecular Dynamics Study. J. Phys. Chem. Lett. 2015, 6, 700–705. [Google Scholar] [CrossRef] [PubMed]
- De Riva, J.; Ferro, V.R.; del Olmo, L.; Ruiz, E.; Lopez, R.; Palomar, J. Statistical Refinement and Fitting of Experimental Viscosity-to-Temperature Data in Ionic Liquids. Ind. Eng. Chem. Res. 2014, 53, 10475–10484. [Google Scholar] [CrossRef]
- Batista, M.L.; Coutinho, J.A.; Gomes, J.R. Prediction of Ionic Liquids Properties through Molecular Dynamics Simulations. Curr. Phys. Chem. 2014, 4, 151–172. [Google Scholar] [CrossRef]
- Borodin, O. Relation between Heat of Vaporization, Ion Transport, Molar Volume, and Cation- Anion Binding Energy for Ionic Liquids. J. Phys. Chem. B 2009, 113, 12353–12357. [Google Scholar] [CrossRef] [PubMed]
- Borodin, O.; Vatamanu, J.; Smith, G. Bulk and Interfacial Behavior of Ionic Liquids from Molecular Dynamics Simulations. ECS Trans. 2010, 33, 583–599. [Google Scholar]
- Bernard, U.L.; Izgorodina, E.I.; MacFarlane, D.R. New Insights into the Relationship between Ion-Pair Binding Energy and Thermodynamic and Transport Properties of Ionic Liquids. J. Phys. Chem. C 2010, 114, 20472–20478. [Google Scholar] [CrossRef]
- Hunt, P.A. Why does a reduction in hydrogen bonding lead to an increase in viscosity for the 1-butyl-2, 3-dimethyl-imidazolium-based ionic liquids? J. Phys. Chem. B 2007, 111, 4844–4853. [Google Scholar] [CrossRef] [PubMed]
- Varela, L.M.; Carrete, J.; García, M.; Rodríguez, J.R.; Gallego, L.J.; Turmine, M.; Cabeza, O. Pseudolattice theory of ionic liquids. In Ionic Liquids: Theory, Properties, New Approaches; Kokorin, A., Ed.; InTech: Shanghai, China, 2011; pp. 347–366. [Google Scholar]
- Izgorodina, E.I.; Bernard, U.L.; Dean, P.M.; Pringle, J.M.; MacFarlane, D.R. The Madelung Constant of Organic Salts. Cryst. Growth Des. 2009, 9, 4834–4839. [Google Scholar] [CrossRef]
- Sangoro, J.R.; Iacob, C.; Serghei, A.; Friedrich, C.; Kremer, F. Universal scaling of charge transport in glass-forming ionic liquids. Phys. Chem. Chem. Phys. 2009, 11, 913–916. [Google Scholar] [CrossRef] [PubMed]
- Ren, Z.; Ivanova, A.S.; Couchot-Vore, D.; Garrett-Roe, S. Ultrafast structure and dynamics in ionic liquids: 2D-IR spectroscopy probes the molecular origin of viscosity. J. Phys. Chem. Lett. 2014, 5, 1541–1546. [Google Scholar] [CrossRef] [PubMed]
- Kincaid, J.F.; Eyring, H.; Stearn, A.E. The Theory of Absolute Reaction Rates and its Application to Viscosity and Diffusion in the Liquid State. Chem. Rev. 1941, 28, 301–365. [Google Scholar] [CrossRef]
- Cohen, E. Fifty years of kinetic theory. Phys. Stat. Mech. Its Appl. 1993, 194, 229–257. [Google Scholar] [CrossRef]
- Madden, P.A.; Wilson, M. Covalent effects in ionic liquids. J. Phys. Condens. Matter 2000, 12, A95. [Google Scholar] [CrossRef]
- Salgado, J.; Regueira, T.; Lugo, L.; Vijande, J.; Fernández, J.; García, J. Density and viscosity of three (2,2,2-trifluoroethanol + 1-butyl-3-methylimidazolium) ionic liquid binary systems. J. Chem. Thermodyn. 2014, 70, 101–110. [Google Scholar] [CrossRef]
- Ghatee, M.H.; Zare, M.; Moosavi, F.; Zolghadr, A.R. Temperature-Dependent Density and Viscosity of the Ionic Liquids 1-Alkyl-3-methylimidazolium Iodides: Experiment and Molecular Dynamics Simulation. J. Chem. Eng. Data 2010, 55, 3084–3088. [Google Scholar] [CrossRef]
- Seoane, R.G.; Corderí, S.; Gómez, E.; Calvar, N.; González, E.J.; Macedo, E.A.; Domínguez, Á. Temperature Dependence and Structural Influence on the Thermophysical Properties of Eleven Commercial Ionic Liquids. Ind. Eng. Chem. Res. 2012, 51, 2492–2504. [Google Scholar] [CrossRef]
- Larriba, M.; Navarro, P.; García, J.; Rodríguez, F. Selective extraction of toluene from n-heptane using [emim][SCN] and [bmim][SCN] ionic liquids as solvents. J. Chem. Thermodyn. 2014, 79, 266–271. [Google Scholar] [CrossRef]
- Zubeir, L.F.; Romanos, G.E.; Weggemans, W.M.A.; Iliev, B.; Schubert, T.J.S.; Kroon, M.C. Solubility and Diffusivity of CO2 in the Ionic Liquid 1-Butyl-3-methylimidazolium Tricyanomethanide within a Large Pressure Range (0.01 MPa to 10 MPa). J. Chem. Eng. Data 2015, 60, 1544–1562. [Google Scholar] [CrossRef]
- Almantariotis, D.; Stevanovic, S.; Fandiño, O.; Pensado, A.S.; Padua, A. a. H.; Coxam, J.-Y.; Costa Gomes, M.F. Absorption of carbon dioxide, nitrous oxide, ethane and nitrogen by 1-alkyl-3-methylimidazolium (C(n)mim, n = 2,4,6) tris(pentafluoroethyl)trifluorophosphate ionic liquids (eFAP). J. Phys. Chem. B 2012, 116, 7728–7738. [Google Scholar] [CrossRef] [PubMed]
- Domańska, U.; Królikowska, M. Density and Viscosity of Binary Mixtures of Thiocyanate Ionic Liquids + Water as a Function of Temperature. J. Solut. Chem. 2012, 41, 1422–1445. [Google Scholar] [CrossRef] [PubMed]
- González, E.J.; González, B.; Macedo, E.A. Thermophysical Properties of the Pure Ionic Liquid 1-Butyl-1-methylpyrrolidinium Dicyanamide and Its Binary Mixtures with Alcohols. J. Chem. Eng. Data 2013, 58, 1440–1448. [Google Scholar] [CrossRef]
- Fletcher, S.I.; Sillars, F.B.; Hudson, N.E.; Hall, P.J. Physical Properties of Selected Ionic Liquids for Use as Electrolytes and Other Industrial Applications. J. Chem. Eng. Data 2010, 55, 778–782. [Google Scholar] [CrossRef]
- Tokuda, H.; Tsuzuki, S.; Susan, M.A.B.H.; Hayamizu, K.; Watanabe, M. How Ionic Are Room-Temperature Ionic Liquids? An Indicator of the Physicochemical Properties. J. Phys. Chem. B 2006, 110, 19593–19600. [Google Scholar] [CrossRef] [PubMed]
- Khupse, N.D.; Kumar, A. Dramatic Change in Viscosities of Pure Ionic Liquids upon Addition of Molecular Solvents. J. Solut. Chem. 2009, 38, 589–600. [Google Scholar] [CrossRef]
- Oliveira, F.S.; Freire, M.G.; Carvalho, P.J.; Coutinho, J.A.P.; Lopes, J.N.C.; Rebelo, L.P.N.; Marrucho, I.M. Structural and Positional Isomerism Influence in the Physical Properties of Pyridinium NTf2-Based Ionic Liquids: Pure and Water-Saturated Mixtures. J. Chem. Eng. Data 2010, 55, 4514–4520. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).