Orbital Energy-Based Reaction Analysis of SN2 Reactions
Abstract
:1. Introduction
2. Orbital Energy-Based Reaction Analysis Theory
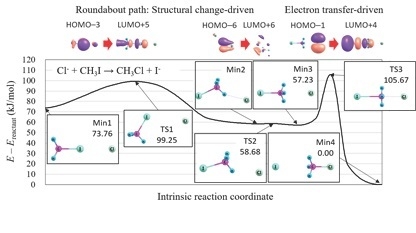
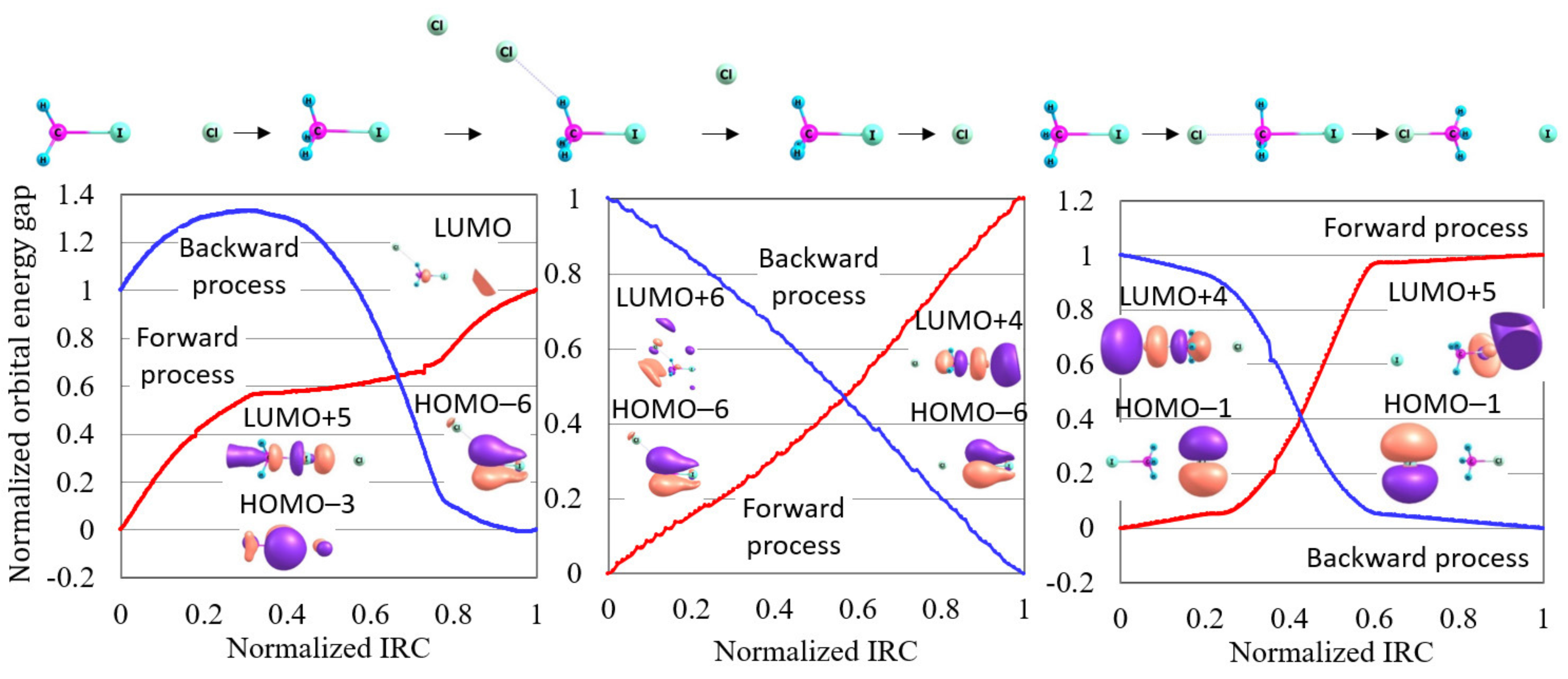
- Then, the target orbitals are selected to be the occupied and unoccupied orbitals giving the most varied valence orbital energies. This selection is based on the concept of Equation (7) that reactions proceed to maximize the variation of chemical potentials, i.e., outermost orbital energies.
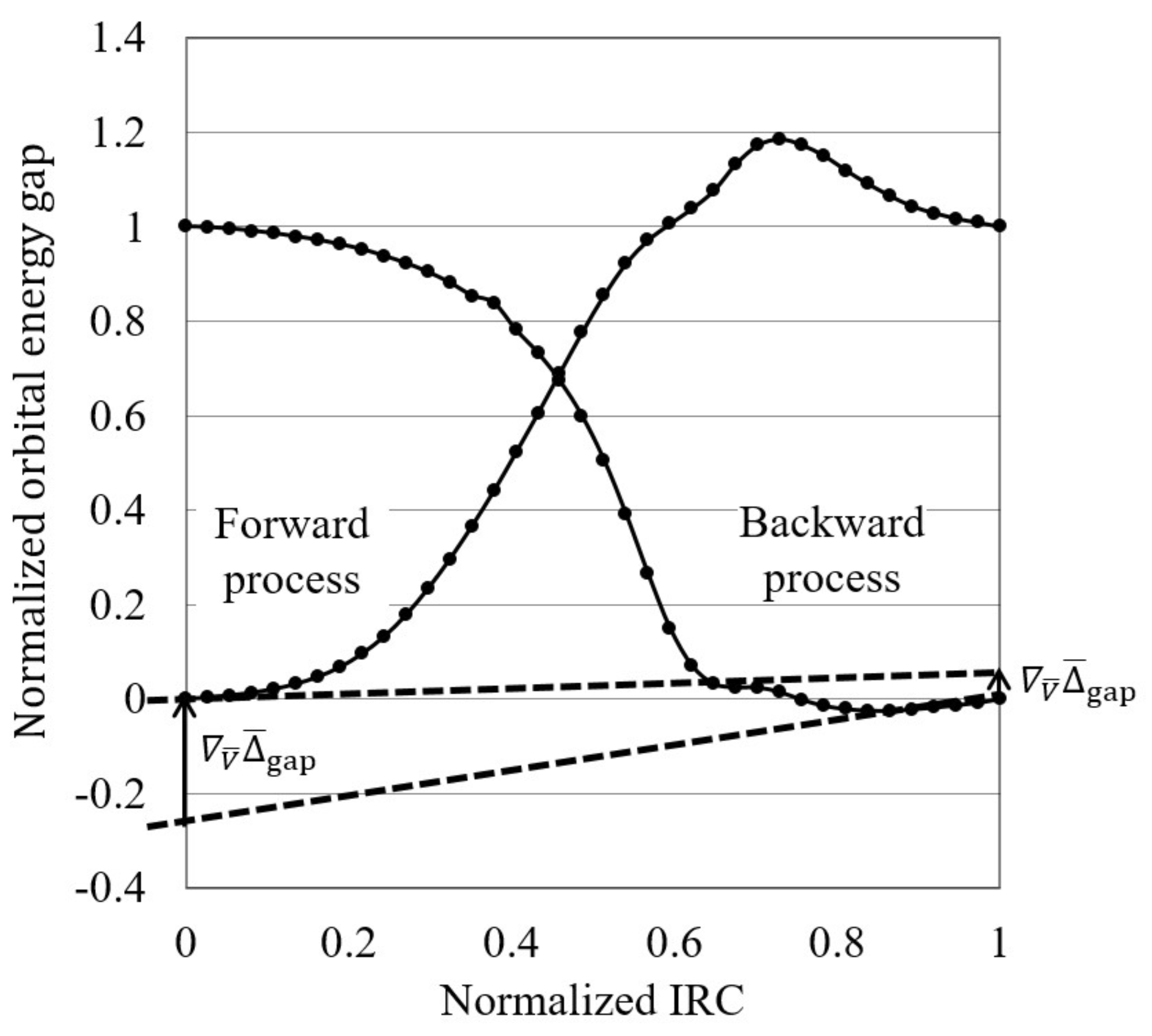
- The normalized reaction diagram is illustrated by plotting the normalized orbital energy gap:where and are the target orbital energy gaps at the initial and terminal steps of each process, on the normalized IRCs, , as shown in Figure 1.
- Finally, the orbital energy gap gradient in terms of the normalized IRCs, , is calculated at the initial reaction stage as a “reactivity index”. Reactions are interpreted to be electron transfer-driven when the orbital energy gap gradient is less than a threshold value, which is temporarily 0.250 in this study.
3. Computational Details
4. Results and Discussion
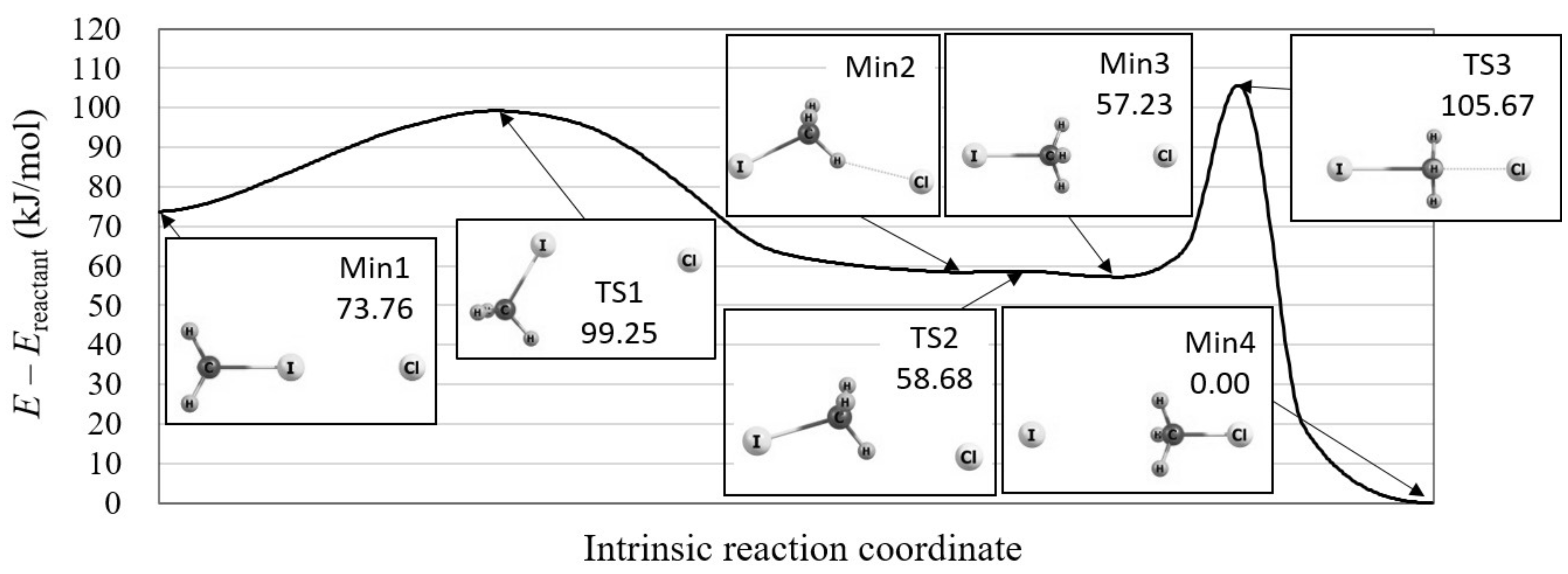
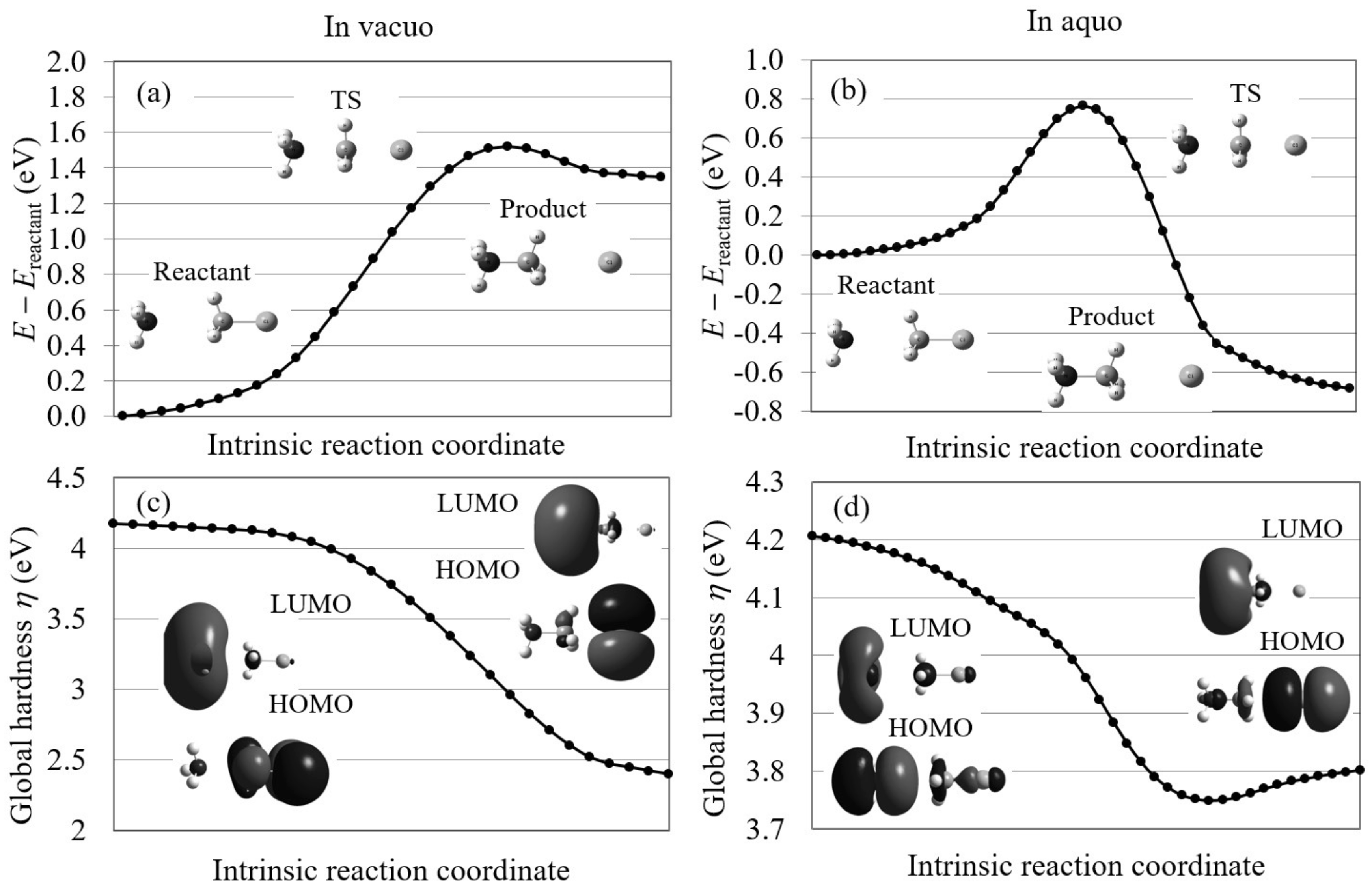
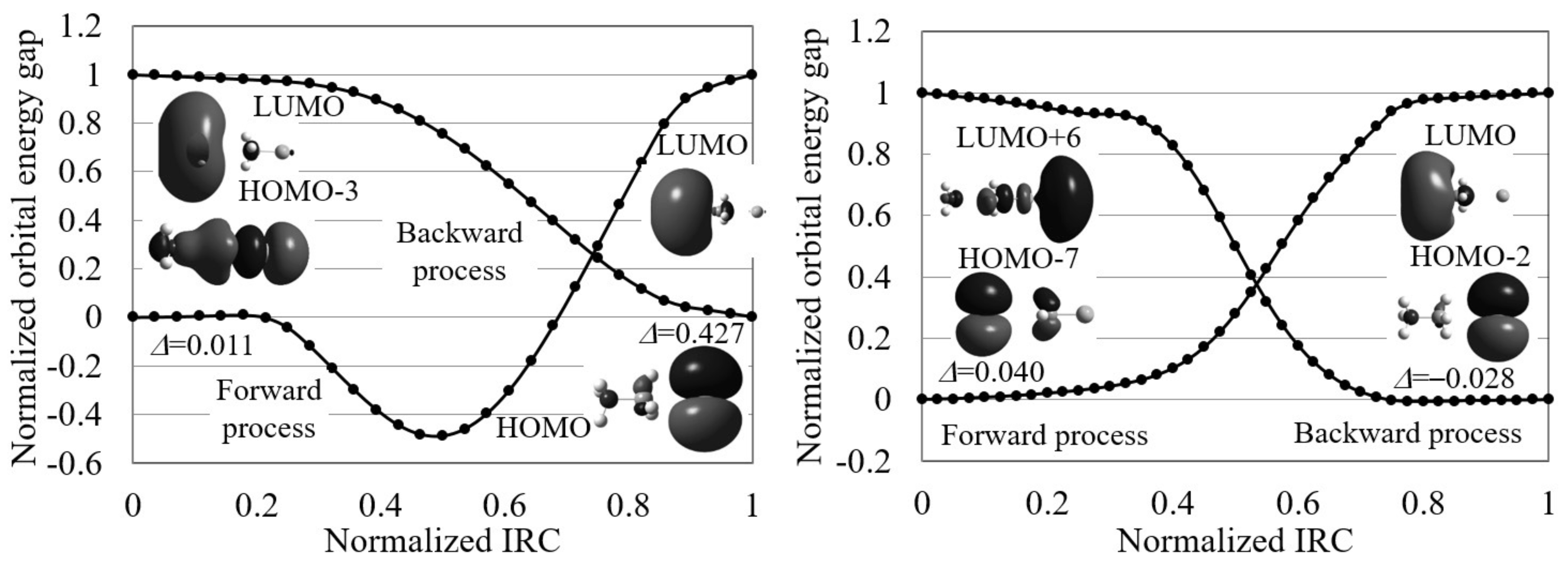
4.1. Orbital Energy-Based Reaction Analysis of Cl + CHI → CHCl + I Reaction
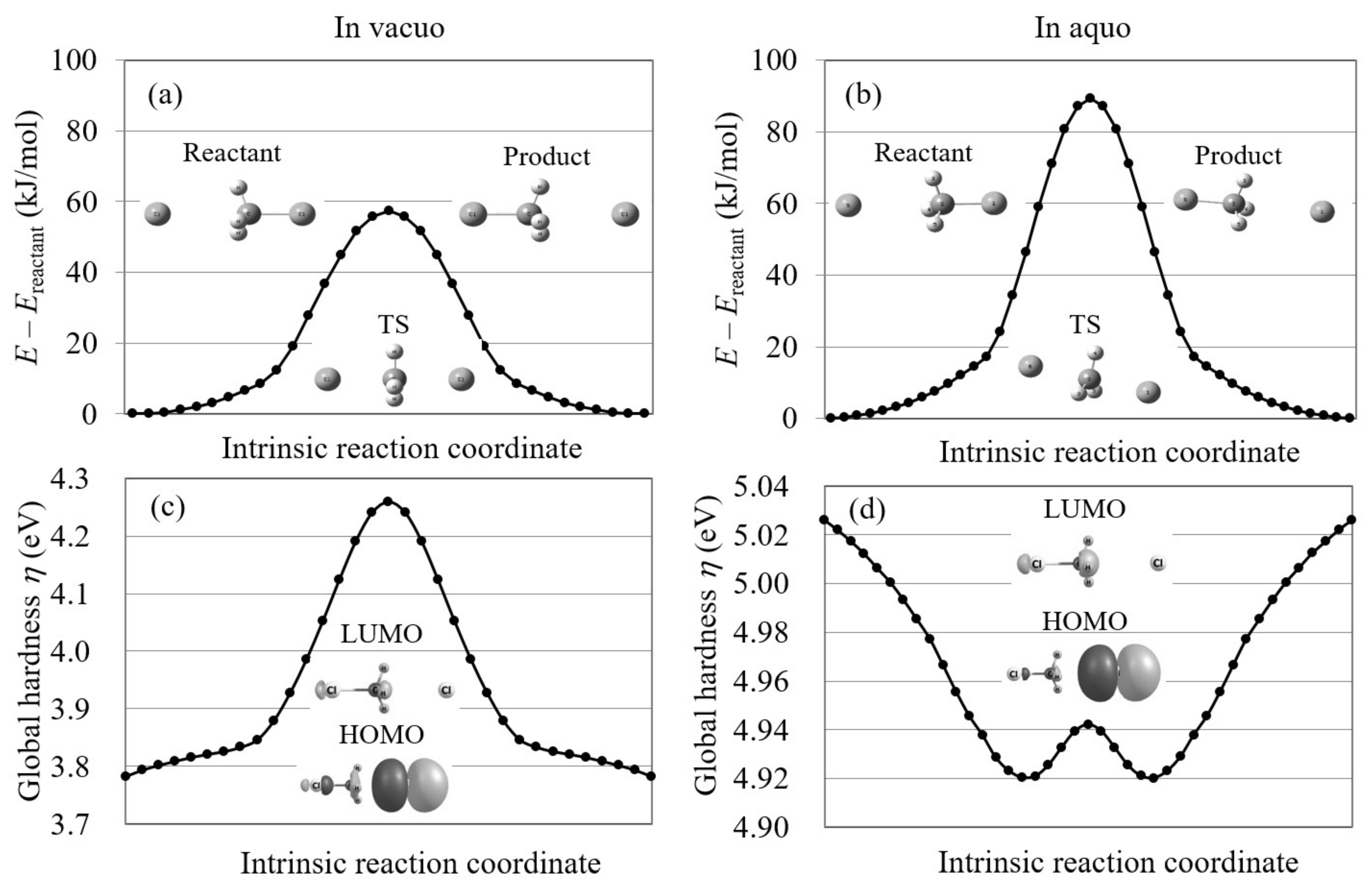
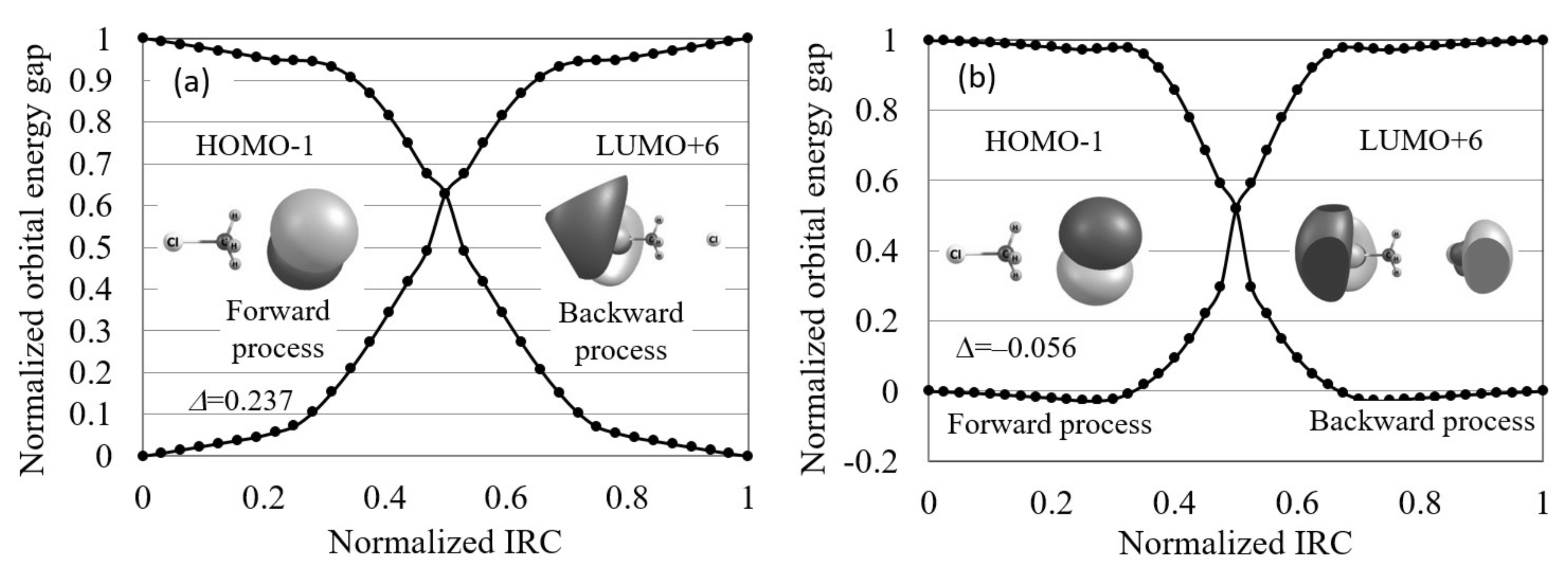
4.2. Reaction Path Search for Cl + CHI → ClCH + I Reaction
4.3. S2 Reactions in Aqueous Solution
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Itatani, J.; Levesque, J.; Zeidler, D.; Niikura, H.; Pepin, H.; Kieffer, J.C.; Corkum, P.B.; Vileneuve, D.M. Tomographic imaging of molecular orbitals. Nature 2004, 432, 867–871. [Google Scholar] [CrossRef] [PubMed]
- Fukui, K.; Yonezawa, T.; Shingu, H. A molecular orbital theory of reactivity in aromatic hydrocarbons. J. Chem. Phys. 1952, 20, 722–725. [Google Scholar] [CrossRef]
- Nalewajski, R.F.; Parr, R.G. Legendre transforms and Maxwell relations in density functional theory. J. Chem. Phys. 1982, 77, 399–407. [Google Scholar] [CrossRef]
- Tsuneda, T.; Singh, R.K. Reactivity index based on orbital energies. J. Comput. Chem. 2014, 35, 1093–1100. [Google Scholar] [CrossRef] [PubMed]
- Tsuneda, T. Density Functional Theory in Quantum Chemistry; Springer: Tokyo, Japan, 2014. [Google Scholar]
- Iikura, H.; Tsuneda, T.; Yanai, T.; Hirao, K. A long-range correction scheme for generalized-gradient-approximation exchange functionals. J. Chem. Phys. 2001, 115, 3540–3544. [Google Scholar] [CrossRef]
- Tawada, Y.; Tsuneda, T.; Yanagisawa, S.; Yanai, T.; Hirao, K. A long-range-corrected time-dependent density functional theory. J. Chem. Phys. 2004, 120, 8425–8433. [Google Scholar] [CrossRef] [PubMed]
- Tsuneda, T.; Song, J.W.; Suzuki, S.; Hirao, K. On Koopmans’ theorem in density functional theory. J. Chem. Phys. 2010, 133, 174101. [Google Scholar] [CrossRef] [PubMed]
- Tsuneda, T.; Kamiya, M.; Hirao, K. Regional self-interaction correction of density functional theory. J. Comput. Chem. 2003, 24, 1592–1598. [Google Scholar] [CrossRef] [PubMed]
- Nakata, A.; Tsuneda, T.; Hirao, K. Modified Regional Self-Interaction Correction Method Based on the Pseudospectral Method. J. Phys. Chem. A 2010, 114, 8521–8528. [Google Scholar] [CrossRef] [PubMed]
- Nakata, A.; Tsuneda, T. Density functional theory for comprehensive orbital energy calculations. J. Chem. Phys. 2013, 139, 064102. [Google Scholar] [CrossRef] [PubMed]
- Singh, R.K.; Tsuneda, T. Reaction energetics on long-range corrected density functional theory: Diels–Alder reactions. J. Comput. Chem. 2013, 34, 379–386. [Google Scholar] [CrossRef] [PubMed]
- Sham, L.J.; Schlüter, M. Density-functional theory of the band gap. Phys. Rev. B 1985, 32, 3883–3889. [Google Scholar] [CrossRef]
- Hase, W.L. Simulations of Gas-Phase Chemical Reactions: Applications to SN2 Nucleophilic Substitution. Science 1994, 266, 998–1002. [Google Scholar] [CrossRef] [PubMed]
- Mikosch, J.; Trippel, S.; Eichhorn, C.; Otto, R.; Lourderaj, U.; Zhang, J.X.; Hase, W.L.; Weidemuller, M.; Wester, R. Imaging nucleophilic substitution dynamics. Science 2008, 319, 183–186. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Mikosch, J.; Trippel, S.; Otto, R.; Weidemüller, M.; Wester, R.; Hase, W.L. F− + CH3I → FCH3 + I− reaction dynamics. Nontraditional atomistic mechanisms and formation of a hydrogen-bonded complex. J. Phys. Chem. Lett. 2010, 1, 2747–2752. [Google Scholar] [CrossRef]
- Zhang, J.; Lourderaj, U.; Sun, R.; Mikosch, J.; Wester, R.; Hase, W.L. Simulation studies of the Cl− + CH3I SN2 nucleophilic substitution reaction: Comparison with ion imaging experiments. J. Chem. Phys. 2013, 138, 114309. [Google Scholar] [CrossRef] [PubMed]
- Szabó, I.; Császár, A.G.; Czakó, G. Dynamics of the F− + CH3Cl → Cl− + CH3F SN2 reaction on a chemically accurate potential energy surface. Chem. Sci. 2013, 4, 4362–4370. [Google Scholar] [CrossRef]
- Szabó, I.; Czakó, G. Revealing a double-inversion mechanism for the F−+ CH3Cl SN2 reaction. Nat. Commun. 2015, 6, 5972–5977. [Google Scholar] [CrossRef] [PubMed]
- Stei, M.; Carrascosa, E.; Kainz, M.A.; Kelkar, A.H.; Meyer, J.; Szabó, I.; Czakó, G.; Wester, R. Influence of the leaving group on the dynamics of a gas-phase SN2 reaction. Nat. Chem. 2016, 8, 151–156. [Google Scholar] [CrossRef] [PubMed]
- Hohenberg, P.; Kohn, W. Inhomogeneous electron gas. Phys. Rev. B 1964, 136, 864–871. [Google Scholar] [CrossRef]
- Levy, M. Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem. Proc. Natl. Acad. Sci. USA 1979, 76, 6062–6065. [Google Scholar] [CrossRef] [PubMed]
- Tsuneda, T. Chemical Reaction Analyses Based on Orbitals and Orbital Energies. Int. J. Quantum Chem. 2015, 115, 270–282. [Google Scholar] [CrossRef]
- Janak, J.F. Proof that ∂E/∂ni = ϵ in density-functional theory. Phys. Rev. B 1978, 18, 7165–7168. [Google Scholar] [CrossRef]
- Hratchian, H.P.; Schlegel, H.B. Accurate reaction paths using a Hessian based predictor-corrector integrator. J. Chem. Phys. 2004, 120, 9918–9924. [Google Scholar] [CrossRef] [PubMed]
- Hratchian, H.P.; Schlegel, H.B. Using Hessian updating to increase the efficiency of a Hessian based predictor-corrector reaction path following method. J. Chem. Theory Comput. 2005, 1, 61–69. [Google Scholar] [CrossRef] [PubMed]
- Kohn, W.; Sham, L.J. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
- Weigend, F.; Ahlrichs, R. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef] [PubMed]
- Weigend, F. Accurate Coulomb-fitting basis sets for H to Rn. Phys. Chem. Chem. Phys. 2006, 8, 1057–1065. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Ohno, K.; Morokuma, K. Systematic exploration of the mechanism of chemical reactions: The global reaction route mapping (GRRM) strategy using the ADDF and AFIR methods. Phys. Chem. Chem. Phys. 2013, 15, 3683–3701. [Google Scholar] [CrossRef] [PubMed]
- Maeda, S.; Taketsugu, T.; Morokuma, K. Exploring transition state structures for intramolecular pathways by the artificial force induced reaction method. J. Comput. Chem. 2014, 35, 166–173. [Google Scholar] [CrossRef] [PubMed]
- Kamiya, M.; Tsuneda, T.; Hirao, K. A density functional study of van der Waals interactions. J. Chem. Phys. 2002, 117, 6010–6015. [Google Scholar] [CrossRef]
- Sato, T.; Tsuneda, T.; Hirao, K. Van der Waals interactions studied by density functional theory. Mol. Phys. 2005, 103, 1151–1164. [Google Scholar] [CrossRef]
- Sato, T.; Tsuneda, T.; Hirao, K. Long-range corrected density functional study on weakly bound systems: Balanced descriptions of various types of molecular interactions. J. Chem. Phys. 2007, 126, 1402–1406. [Google Scholar] [CrossRef] [PubMed]
- Sato, T.; Nakai, H. Density functional method including weak interactions: Dispersion coefficients based on the local response approximation. J. Chem. Phys. 2009, 131, 224104. [Google Scholar] [CrossRef] [PubMed]
- Becke, A.D. Density-functional exchange-energy approximation with correct asymptotic behavior. Phys. Rev. A 1988, 38, 3098–3100. [Google Scholar] [CrossRef]
- Tsuneda, T.; Suzumura, T.; Hirao, K. A new one-parameter progressive Colle-Salvetti-type correlation functional. J. Chem. Phys. 1999, 110, 10664–10678. [Google Scholar] [CrossRef]
- Barone, V.; Cossi, M. Quantum calculation of molecular energies and energy gradients in solution by a conductor solvent model. J. Phys. Chem. A 1998, 102, 1995–2001. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Schmidt, M.W.; Baldridge, K.K.; Boatz, J.A.; Elbert, S.T.; Gordon, M.S.; Jensen, J.H.; Koseki, S.; Matsunaga, N.; Nguyen, K.A.; Su, S.; et al. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. [Google Scholar] [CrossRef]
- Parr, R.G.; Chattaraj, P.K. Principle of maximum hardness. J. Am. Chem. Soc. 1991, 113, 1854–1855. [Google Scholar] [CrossRef]

© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsuneda, T.; Maeda, S.; Harabuchi, Y.; Singh, R.K. Orbital Energy-Based Reaction Analysis of SN2 Reactions. Computation 2016, 4, 23. https://doi.org/10.3390/computation4030023
Tsuneda T, Maeda S, Harabuchi Y, Singh RK. Orbital Energy-Based Reaction Analysis of SN2 Reactions. Computation. 2016; 4(3):23. https://doi.org/10.3390/computation4030023
Chicago/Turabian StyleTsuneda, Takao, Satoshi Maeda, Yu Harabuchi, and Raman K. Singh. 2016. "Orbital Energy-Based Reaction Analysis of SN2 Reactions" Computation 4, no. 3: 23. https://doi.org/10.3390/computation4030023
APA StyleTsuneda, T., Maeda, S., Harabuchi, Y., & Singh, R. K. (2016). Orbital Energy-Based Reaction Analysis of SN2 Reactions. Computation, 4(3), 23. https://doi.org/10.3390/computation4030023