Interaction of Hydrogen with Au Modified by Pd and Rh in View of Electrochemical Applications
Abstract
:1. Introduction
2. Computational Details
3. Results and Discussion
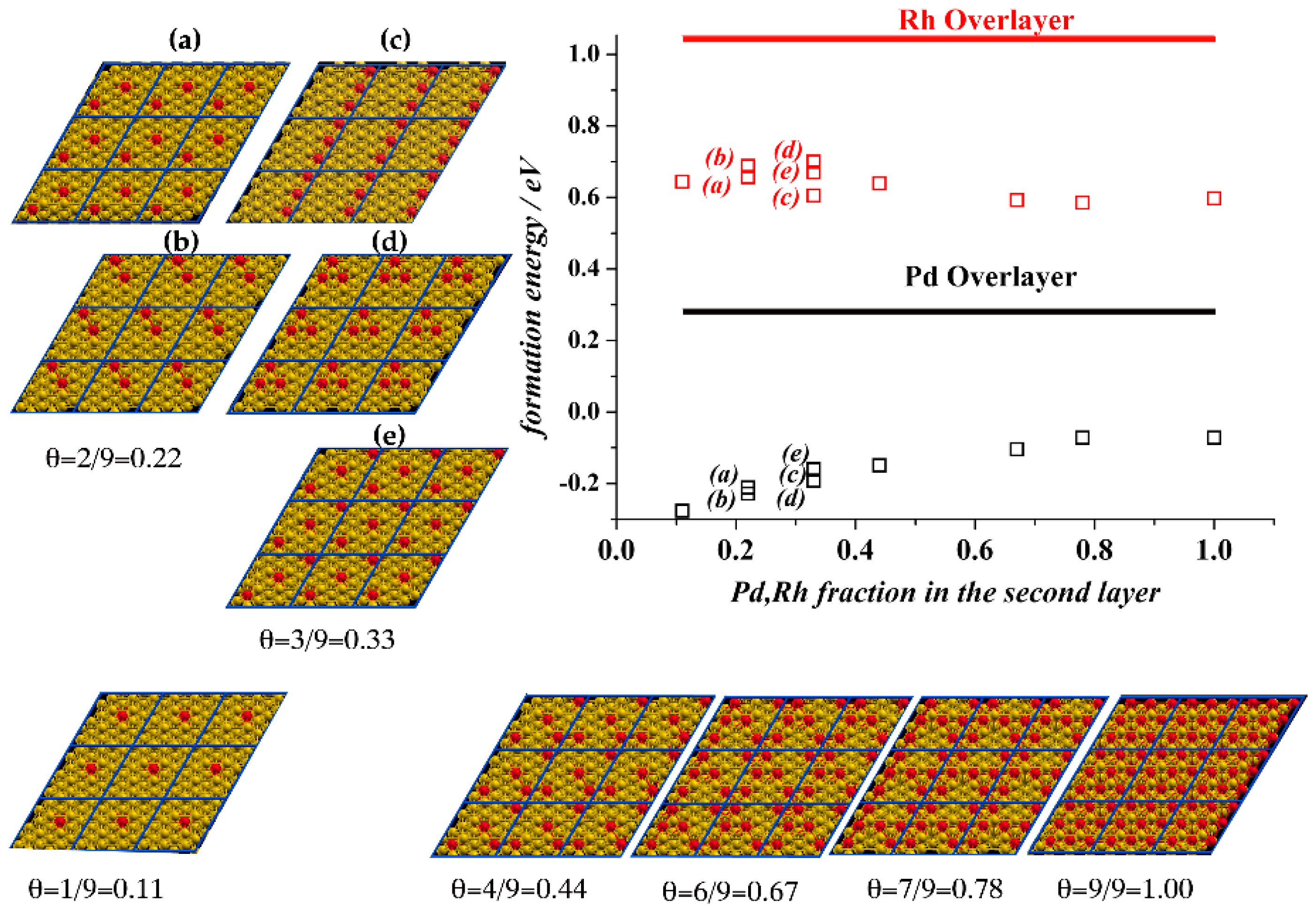
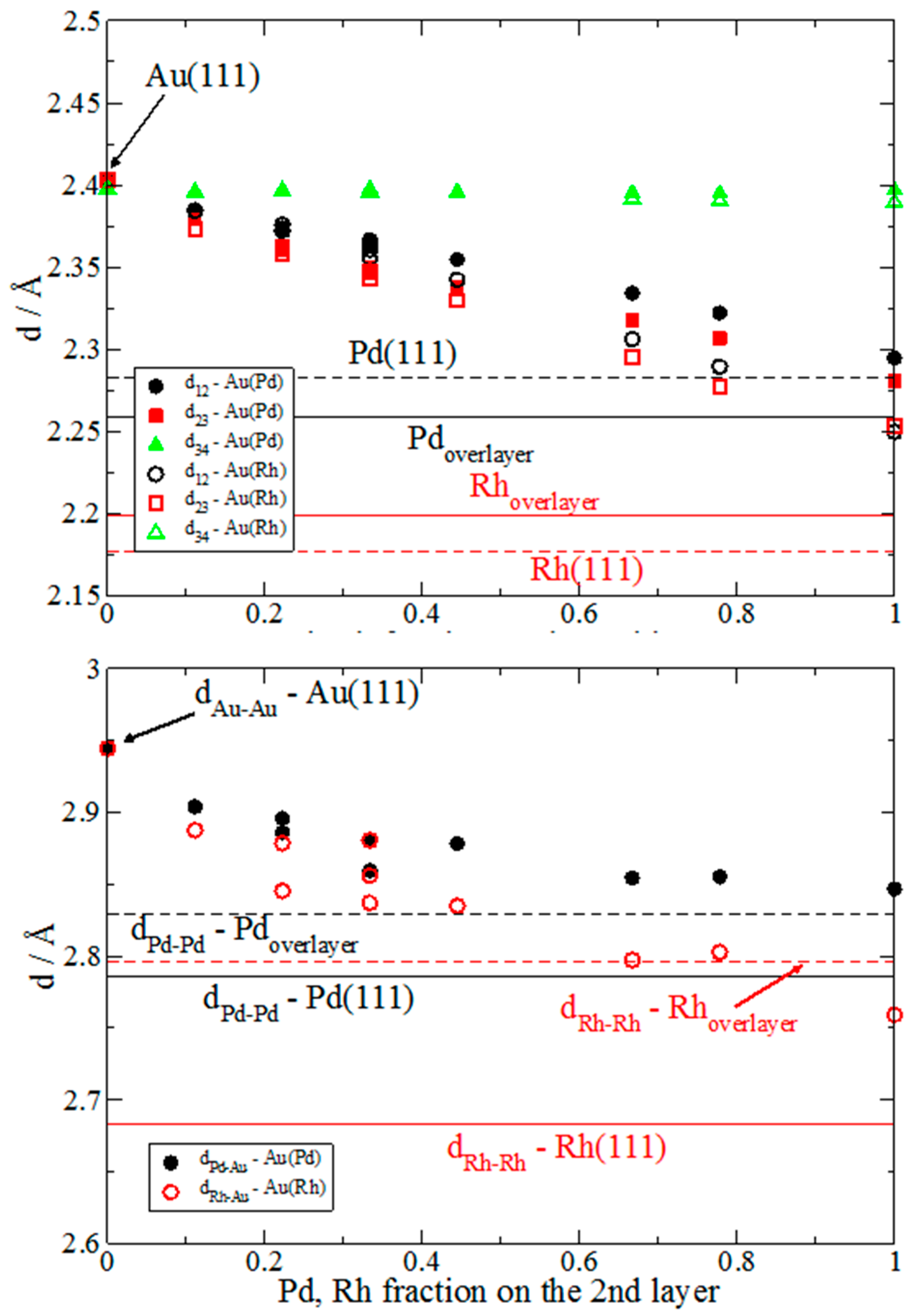
3.1. Pd and Rh Induced Structural, Electronic, and Energetic Property Modifications of Au(111)
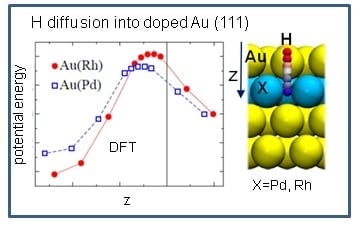
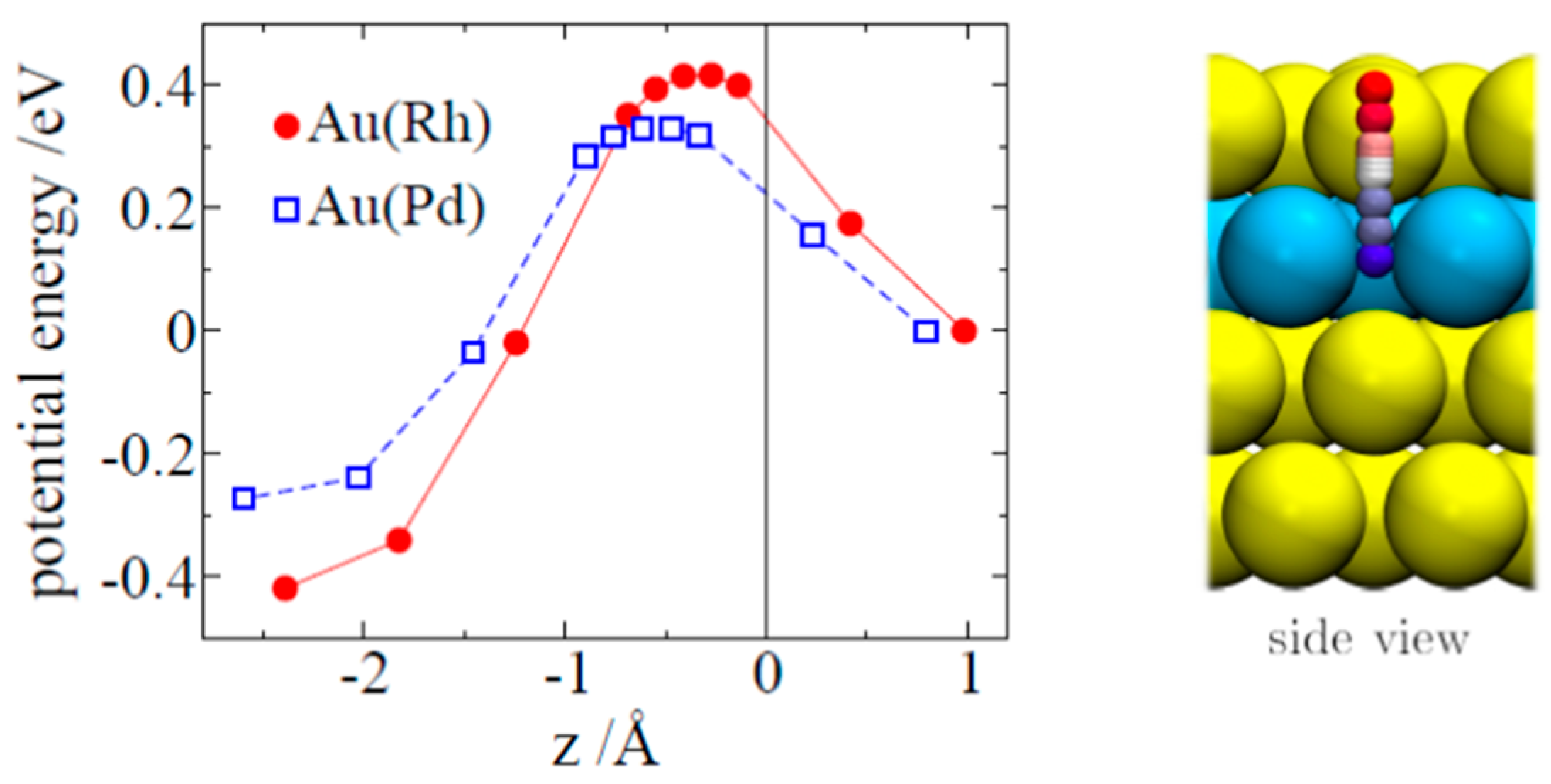
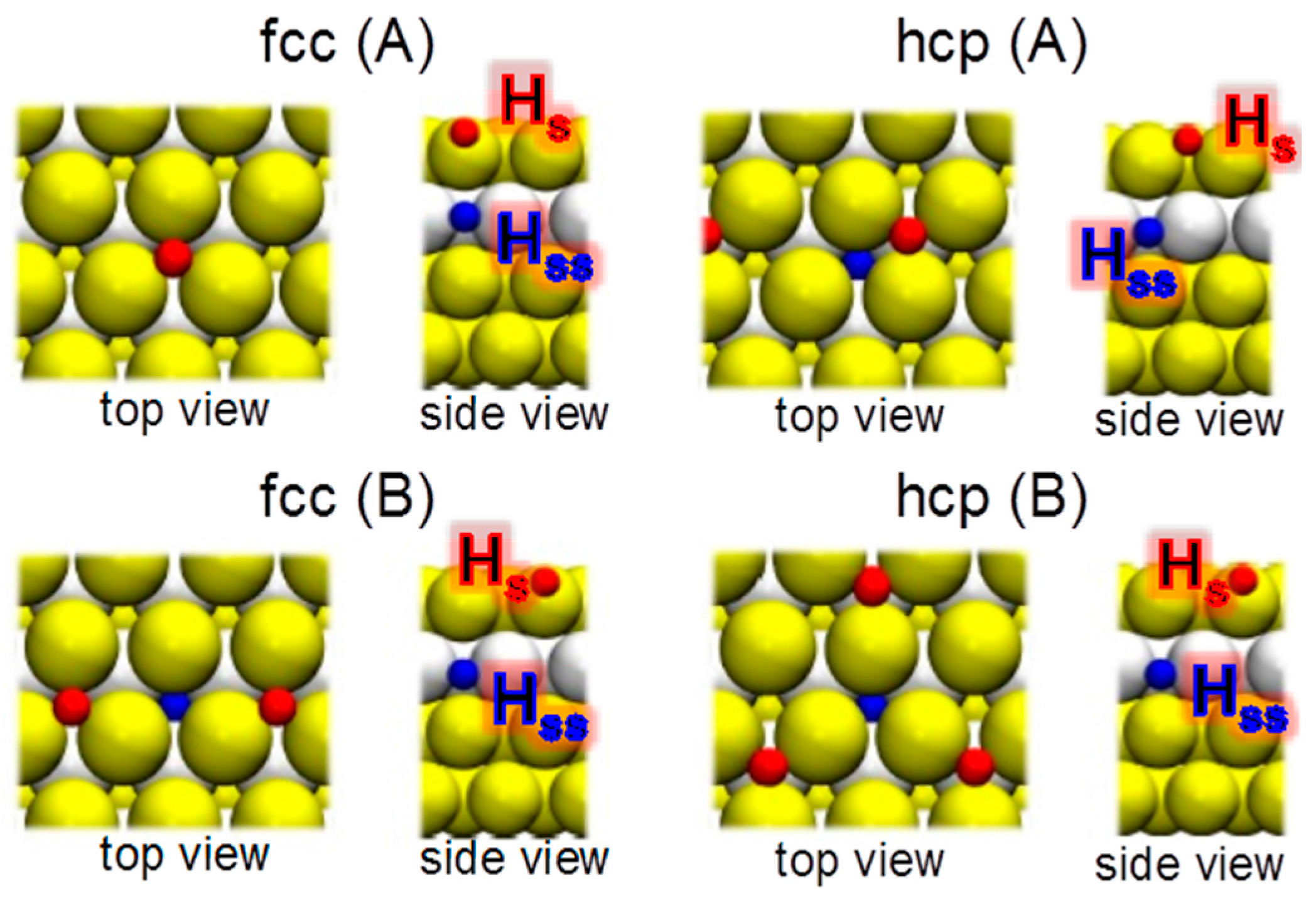
3.2. Hydrogen Ab- and Adsorption
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, J.H.; Wang, A.Q.; Chi, Y.S.; Lin, H.P.; Mou, C.Y. Synergistic Effect in an Au-Ag Alloy Nanocatalyst: Co Oxidation. J. Phys. Chem. B 2005, 109, 40–43. [Google Scholar] [CrossRef] [PubMed]
- Wang, D.; Villa, A.; Porta, F.; Prati, L.; Su, D. Bimetallic Gold/Palladium Catalysts: Correlation between Nanostructure and Synergistic Effects. J. Phys. Chem. C 2008, 112, 8617–8622. [Google Scholar] [CrossRef]
- Mott, D.; Luo, J.; Njoki, P.N.; Lin, Y.; Wang, L.; Zhong, C.-J. Synergistic Activity of Gold-Platinum Alloy Nanoparticle Catalysts. Catal. Today 2007, 122, 378–385. [Google Scholar] [CrossRef]
- Zhang, L.; Iyyamperumal, R.; Yancey, D.F.; Crooks, R.M.; Henkelman, G. Design of Pt-Shell Nanoparticles with Alloy Cores for the Oxygen Reduction Reaction. ACS Nano 2013, 7, 9168–9172. [Google Scholar] [CrossRef] [PubMed]
- Chen, M.S.; Kumar, D.; Yi, C.W.; Goodman, D.W. The Promotional Effect of Gold in Catalysis by Palladium-Gold. Science 2005, 310, 291–293. [Google Scholar] [CrossRef] [PubMed]
- Hugon, A.; El Kolli, N.; Louis, C. Advances in the Preparation of Supported Gold Catalysts: Mechanism of Deposition, Simplification of the Procedures and Relevance of the Elimination of Chlorine. J. Catal. 2010, 274, 239–250. [Google Scholar] [CrossRef]
- Gao, F.; Wang, Y.; Goodman, D.W. Co Oxidation over Aupd(100) from Ultrahigh Vacuum to near-Atmospheric Pressures: The Critical Role of Contiguous Pd Atoms. J. Am. Chem. Soc. 2009, 131, 5734–5735. [Google Scholar] [CrossRef] [PubMed]
- Garcia, S.; Zhang, L.; Piburn, G.W.; Henkelman, G.; Humphrey, S.M. Microwave Synthesis of Classically Immiscible Rhodium-Silver and Rhodium-Gold Alloy Nanoparticles: Highly Active Hydrogenation Catalysts. ACS Nano 2014, 8, 11512–11521. [Google Scholar] [CrossRef] [PubMed]
- Garcia-Mota, M.; Lopez, N. The Role of Long-Lived Oxygen Precursors on Aum Alloys (M = Ni, Pd, Pt) in Co Oxidation. Phys. Chem. Chem. Phys. 2011, 13, 5790–5797. [Google Scholar] [CrossRef] [PubMed]
- Tenney, S.A.; He, W.; Roberts, C.C.; Ratliff, J.S.; Shah, S.I.; Shafai, G.S.; Turkowski, V.; Rahman, T.S.; Chen, D.A. Co-Induced Diffusion of Ni Atoms to the Surface of Ni-Au Clusters on Tio2(110). J. Phys. Chem. C 2011, 115, 11112–11123. [Google Scholar] [CrossRef]
- Guesmi, H.; Louis, C.; Delannoy, L. Chemisorbed Atomic Oxygen Inducing Pd Segregation in Pdau(111) Alloy: Energetic and Electronic DFT Analysis. Chem. Phys. Lett. 2011, 503, 97–100. [Google Scholar] [CrossRef]
- Dhouib, A.; Guesmi, H. DFT Study of the M Segregation on Mau Alloys (M = Ni, Pd, Pt) in Presence of Adsorbed Oxygen O and O2. Chem. Phys. Lett. 2012, 521, 98–103. [Google Scholar] [CrossRef]
- Pittaway, F.; Paz-Borbon, L.O.; Johnston, R.L.; Arslan, H.; Ferrando, R.; Mottet, C.; Barcaro, G.; Fortunelli, A. Theoretical Studies of Palladium-Gold Nanoclusters: Pd-Au Clusters with up to 50 Atoms. J. Phys. Chem. C 2009, 113, 9141–9152. [Google Scholar] [CrossRef]
- Guesmi, H. Theoretical Insights on the Effect of Reactive Gas on the Chemical Ordering of Gold-Based Alloys. Gold Bull. 2013, 46, 213–219. [Google Scholar] [CrossRef]
- Zhu, B.; Guesmi, H.; Creuze, J.; Legrand, B.; Mottet, C. Crossover among Structural Motifs in Pd-Au Nanoalloys. Phys. Chem. Chem. Phys. 2015, 17, 28129–28136. [Google Scholar] [CrossRef] [PubMed]
- Ferrando, R.; Jellinek, J.; Johnston, R.L. Nanoalloys: From Theory to Applications of Alloy Clusters and Nanoparticles. Chem. Rev. 2008, 108, 845–910. [Google Scholar] [CrossRef] [PubMed]
- Visart de Bocarme, T.; Chau, T.D.; Tielens, F.; Andres, J.; Gaspard, P.; Wang, R.L.C.; Kreuzer, H.J.; Kruse, N. Oxygen Adsorption on Gold Nanofacets and Model Clusters. J. Chem. Phys. 2006, 125, 054703. [Google Scholar] [CrossRef] [PubMed]
- Tielens, F.; Andrés, J.; Chau, T.-D.; Visart de Bocarmé, T.; Kruse, N.; Geerlings, P. Molecular Oxygen Adsorption on Electropositive Nano Gold Tips. Chem. Phys. Lett. 2006, 421, 433–438. [Google Scholar] [CrossRef]
- Juarez, M.F.; Soldano, G.; Guesmi, H.; Tielens, F.; Santos, E. Catalytic Properties of Au Electrodes Modified by an Underlayer of Pd. Surf. Sci. 2015, 631, 235–247. [Google Scholar] [CrossRef]
- Quaino, P.M.; Nazmutdinov, R.; Peiretti, L.F.; Santos, E. Unravelling the Hydrogen Absorption Process in Pd Overlayers on a Au(111) Surface. Phys. Chem. Chem. Phys. 2016, 18, 3659–3668. [Google Scholar] [CrossRef] [PubMed]
- Hammer, B.; Hansen, L.B.; Norskov, J.K. Improved Adsorption Energetics within Density-Functional Theory Using Revised Perdew-Burke-Ernzerhof Functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab-Initio Molecular-Dynamics for Liquid-Metals. Phys. Rev. B 1993, 47, 558–561. [Google Scholar] [CrossRef]
- Kresse, G.; Hafner, J. Ab-Initio Molecular-Dynamics Simulation of the Liquid-Metal Amorphous-Semiconductor Transition in Germanium. Phys. Rev. B 1994, 49, 14251–14269. [Google Scholar] [CrossRef]
- Perdew, J.P.; Chevary, J.A.; Vosko, S.H.; Jackson, K.A.; Pederson, M.R.; Singh, D.J.; Fiolhais, C. Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation. Phys. Rev. B 1992, 46, 6671–6687. [Google Scholar] [CrossRef]
- Tielens, F.; Andres, J. Prediction of Gold Zigzag Nanotube-Like Structure Based on Au-32 Units: A Quantum Chemical Study. J. Phys. Chem. C 2007, 111, 10342–10346. [Google Scholar] [CrossRef]
- Rodriguez-Castillo, M.; Laurencin, D.; Tielens, F.; van der Lee, A.; Clement, S.; Guari, Y.; Richeter, S. Reactivity of Gold Nanoparticles Towards N-Heterocyclic Carbenes. Dalton Trans. 2014, 43, 5978–5982. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple (Vol 77, Pg 3865, 1996). Phys. Rev. Lett. 1997, 78, 1396–1396. [Google Scholar] [CrossRef]
- Blochl, P.E.; Jepsen, O.; Andersen, O.K. Improved Tetrahedron Method for Brillouin-Zone Integrations. Phys. Rev. B 1994, 49, 16223–16233. [Google Scholar] [CrossRef]
- Monkhorst, H.J.; Pack, J.D. Special Points for Brillouin-Zone Integrations. Phys. Rev. B 1976, 13, 5188–5192. [Google Scholar] [CrossRef]
- Kittel, C. Introduction to Solid State Physics, 3rd ed.; Wiley: New York, NY, USA, 1967. [Google Scholar]
- Sluiter, M.H.F.; Colinet, C.; Pasturel, A. Ab Initio Calculation of the Phase Stability in Au-Pd and Ag-Pt Alloys. Phys. Rev. B 2006, 73, 174204. [Google Scholar] [CrossRef]
- Skriver, H.L.; Rosengaard, N.M. Surface Energy and Work Function of Elemental Metals. Phys. Rev. B Condens. Matter Mater. Phys. 1992, 46, 7157–7168. [Google Scholar] [CrossRef]
- Yanagita, H.; Fujioka, H.; Aruga, T.; Takagi, N.; Nishijima, M. Vibrational Spectra of Hydrogen on the Rh(111) Surface. Surf. Sci. 1999, 441, 507–514. [Google Scholar] [CrossRef]
- Mann, S.S.; Seto, T.; Barnes, C.J.; King, D.A. Coverage Dependence of Surface-Diffusion of Hydrogen and Deuterium on Rh(111) by Laser-Induced Thermal-Desorption. Surf. Sci. 1992, 261, 155–163. [Google Scholar] [CrossRef]
- Soldano, G.; Schulz, E.N.; Salinas, D.R.; Santos, E.; Schmickler, W. Hydrogen Electrocatalysis on Overlayers of Rhodium over Gold and Palladium Substrates-More Active Than Platinum? Phys. Chem. Chem. Phys. 2011, 13, 16437–16443. [Google Scholar] [CrossRef] [PubMed]
- Wilke, S.; Natoli, V.; Cohen, M.H. Theoretical Investigation of Water Formation on Rh and Pt Surfaces. J. Chem. Phys. 2000, 112, 9986–9995. [Google Scholar] [CrossRef]
- Quaino, P.; Santos, E.; Wolfschmidt, H.; Montero, M.A.; Stimming, U. Theory Meets Experiment: Electrocatalysis of Hydrogen Oxidation/Evolution at Pd-Au Nanostructures. Catal. Today 2011, 177, 55–63. [Google Scholar] [CrossRef]
- Ferrin, P.; Kandoi, S.; Nilekar, A.U.; Mavrikakis, M. Hydrogen Adsorption, Absorption and Diffusion on and in Transition Metal Surfaces: A DFT Study. Surf. Sci. 2012, 606, 679–689. [Google Scholar] [CrossRef]

| Au | Rh | Pd | |
|---|---|---|---|
| a | 4.17 | 3.84 | 3.96 |
| a (exp.) [31] | 4.08 | 3.80 | 3.89 |
| ΔEcoh | −2.98 | −5.77 | −3.72 |
| ΔEcoh (exp.) [31] | −3.81 | −5.75 | −3.89 |
| ΔEsurf | 0.30 | 0.87 | 0.56 |
| ΔEsurf (exp.) [33] | 0.88 | 1.1 | 0.95 |
| X | ΔEbind(Au-X)/eV |
|---|---|
| Pd | −2.055 |
| Rh | −2.477 |
| Au | −0.973 |
| θ(Hs) = 0.25 ML | θ(Hs) = 1.00 ML | ||||
|---|---|---|---|---|---|
| fcc | hcp | fcc | hcp | ||
| Pd(111) | −0.61 | ||||
| Rh(111) | −0.56 | ||||
| Au(111) | 0.10 | ||||
| Clean surfaces (θ(Hss) = 0.00 ML) | Au(Pd) | 0.10 | 0.17 | 0.27 | 0.31 |
| Au(Rh) | 0.01 | 0.11 | 0.20 | 0.27 | |
| Surfaces containing H (θ(Hss) = 0.25 ML) | Au(Pd) | (A) 0.10 | 0.19 | ||
| (B) 0.15 | 0.24 | ||||
| Au(Rh) | (A) 0.01 | 0.12 | |||
| (B) 0.04 | 0.20 | ||||
| Surfaces containing H (θ(Hss) = 1.00 ML) | Au(Pd) | 0.007 | 0.03 | 0.18 | 0.18 |
| Au(Rh) | 0.01 | 0.08 | 0.20 | 0.23 | |
| θ(Hss) = 0.25 ML | θ(Hss) = 1.00 ML | ||||
|---|---|---|---|---|---|
| fcc | hcp | fcc | hcp | ||
| Pd(111) | −0.28 | ||||
| Rh(111) | 0.18 | ||||
| Au(111) | 0.89 | ||||
| Clean surfaces (θ(Hss) = 0.00 ML) | Au(Pd) | −0.17 | 0.36 | 0.05 | 0.51 |
| Au(Rh) | −0.40 | 0.25 | −0.31 | 0.41 | |
| ΔE(Hs➔Hss) | Eact(Hs➔Hss) | Eact(Hss➔Hs) | |
|---|---|---|---|
| Pd(111) | 0.30 | 0.40 | 0.10 |
| Rh(111) | 0.76 | 0.84 | 0.09 |
| Au(111) | 0.64 | 0.76 | 0.12 |
| Au(Pd) | −0.26 | 0.33 | 0.59 |
| Au(Rh) | −0.41 | 0.42 | 0.83 |
| θ(Hss) (ML) | θ(Hs) (ML) | Site | Au(Rh) | Au(Pd) |
|---|---|---|---|---|
| 0.00 | 1.00 | fcc | −0.43 | −0.41 |
| hcp | −0.32 | −0.32 | ||
| 1.00 | 0.00 | fcc | 0.25 | 0.35 |
| hcp | 0.27 | 0.16 | ||
| 1.00 | 1.00 | fcc | −0.36 | −0.45 |
| hcp | −0.33 | −0.44 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Juarez, F.; Soldano, G.; Santos, E.; Guesmi, H.; Tielens, F.; Mineva, T. Interaction of Hydrogen with Au Modified by Pd and Rh in View of Electrochemical Applications. Computation 2016, 4, 26. https://doi.org/10.3390/computation4030026
Juarez F, Soldano G, Santos E, Guesmi H, Tielens F, Mineva T. Interaction of Hydrogen with Au Modified by Pd and Rh in View of Electrochemical Applications. Computation. 2016; 4(3):26. https://doi.org/10.3390/computation4030026
Chicago/Turabian StyleJuarez, Fernanda, German Soldano, Elizabeth Santos, Hazar Guesmi, Frederik Tielens, and Tzonka Mineva. 2016. "Interaction of Hydrogen with Au Modified by Pd and Rh in View of Electrochemical Applications" Computation 4, no. 3: 26. https://doi.org/10.3390/computation4030026
APA StyleJuarez, F., Soldano, G., Santos, E., Guesmi, H., Tielens, F., & Mineva, T. (2016). Interaction of Hydrogen with Au Modified by Pd and Rh in View of Electrochemical Applications. Computation, 4(3), 26. https://doi.org/10.3390/computation4030026