Artificial Intelligence Optimization of Polyaluminum Chloride (PAC) Dosage in Drinking Water Treatment: A Hybrid Genetic Algorithm–Neural Network Approach
Abstract
1. Introduction
2. Materials and Methods
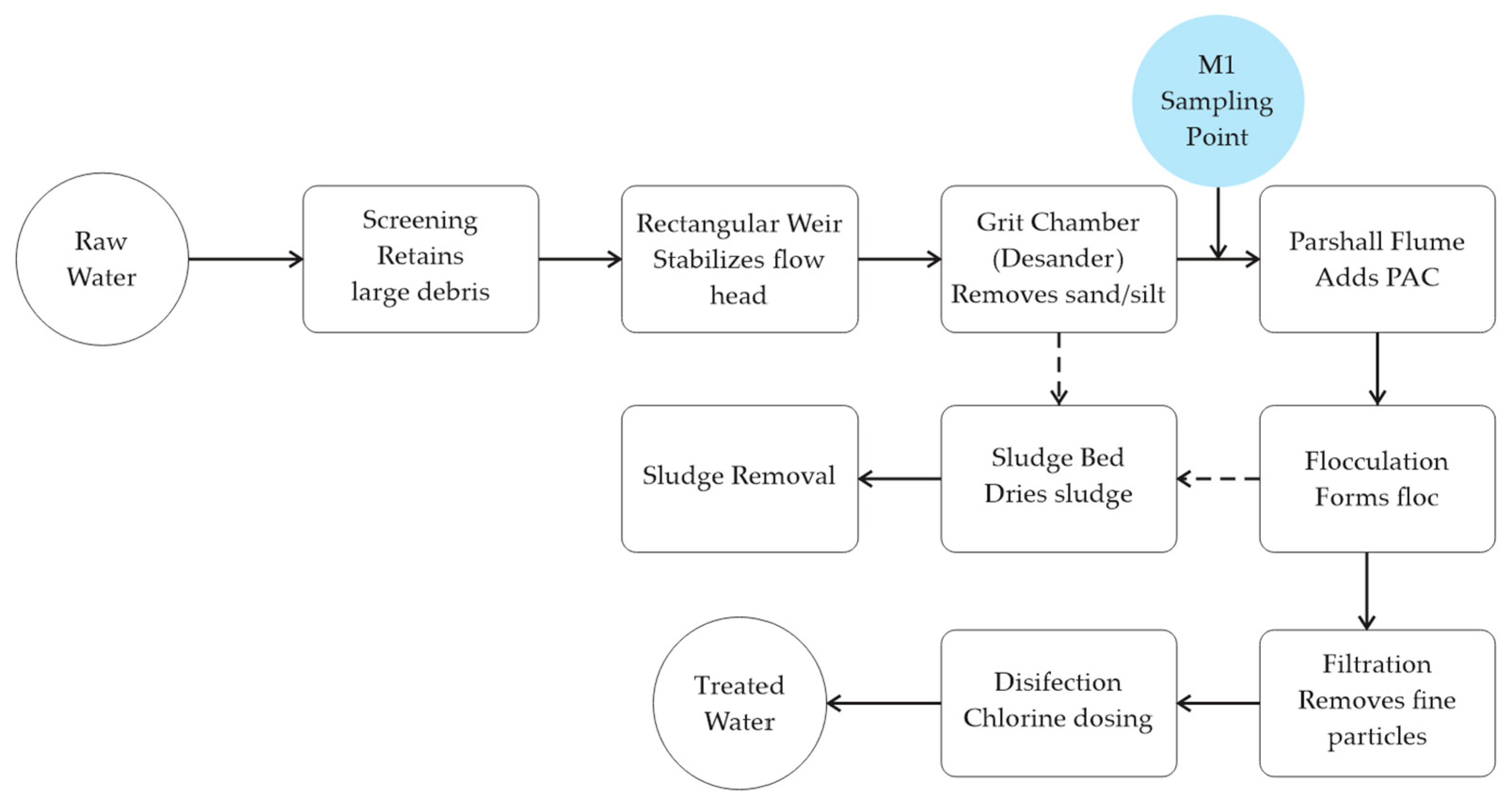
2.1. Site Description and Process Layout
2.2. Data Collection
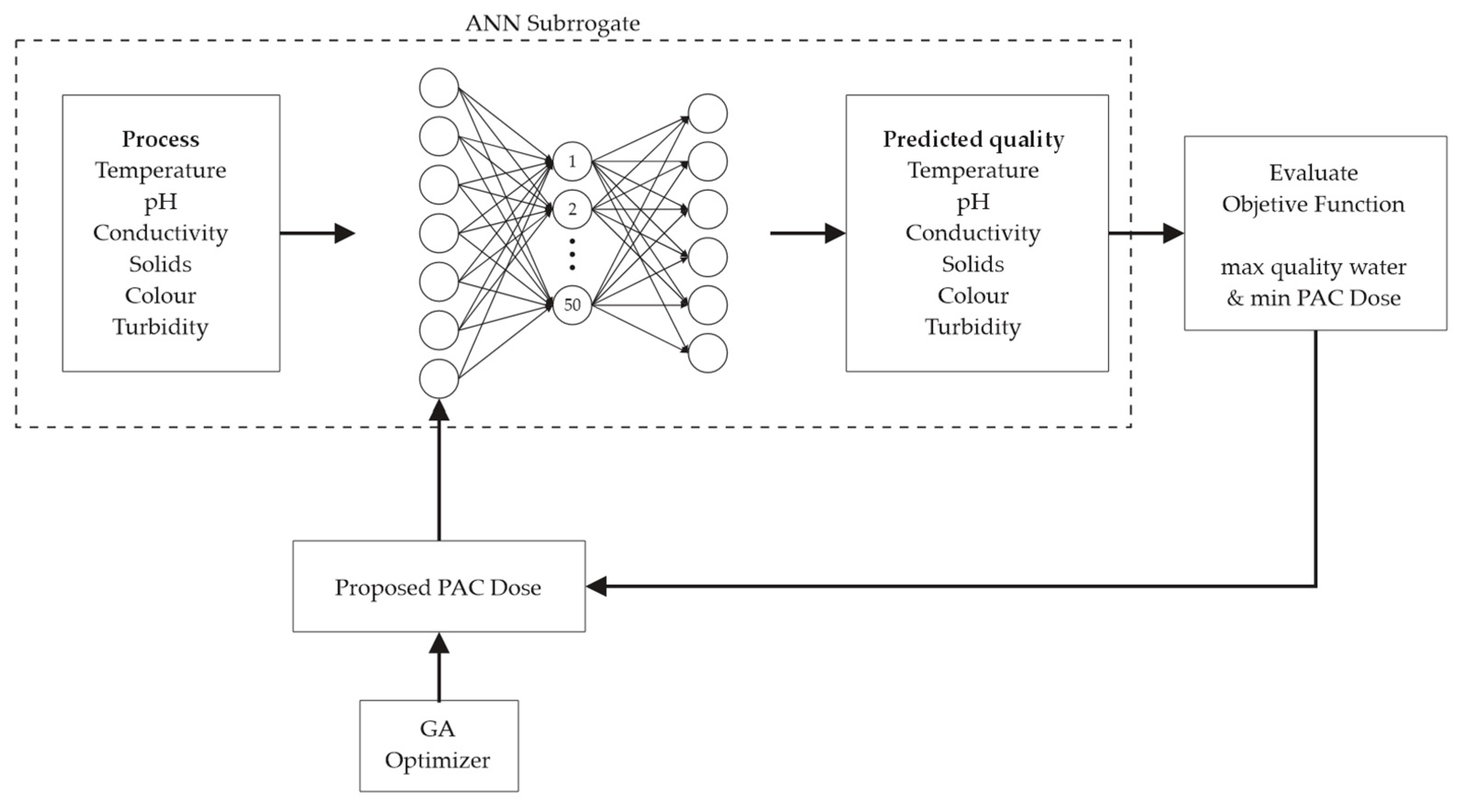
2.3. Data Analysis and Artificial Neural Network Development
- —
- Y_Color (Pt-Co units);
- —
- Y_Turbidity (NTU);
- —
- Y_pH (dimensionless);
- —
- Y_Conductivity (μS/cm);
- —
- Y_Temperature (°C);
- —
- Y_TDS (mg/L).
2.3.1. ANN Architecture and Training Protocol
2.3.2. Genetic Algorithm Optimization
- —
- Color exceeds 1.5 Pt-Co;
- —
- Turbidity exceeds 0.8 NTU;
- —
- pH falls outside the range 6.4–7.0.
- —
- λ = 3, to emphasize minimizing PAC cost;
- —
- α = 0.10, to penalize large deviations from the historical average dosage;
- —
- A hard penalty P of 5 × 104 for non-compliance with regulatory limits.
3. Results and Discussion
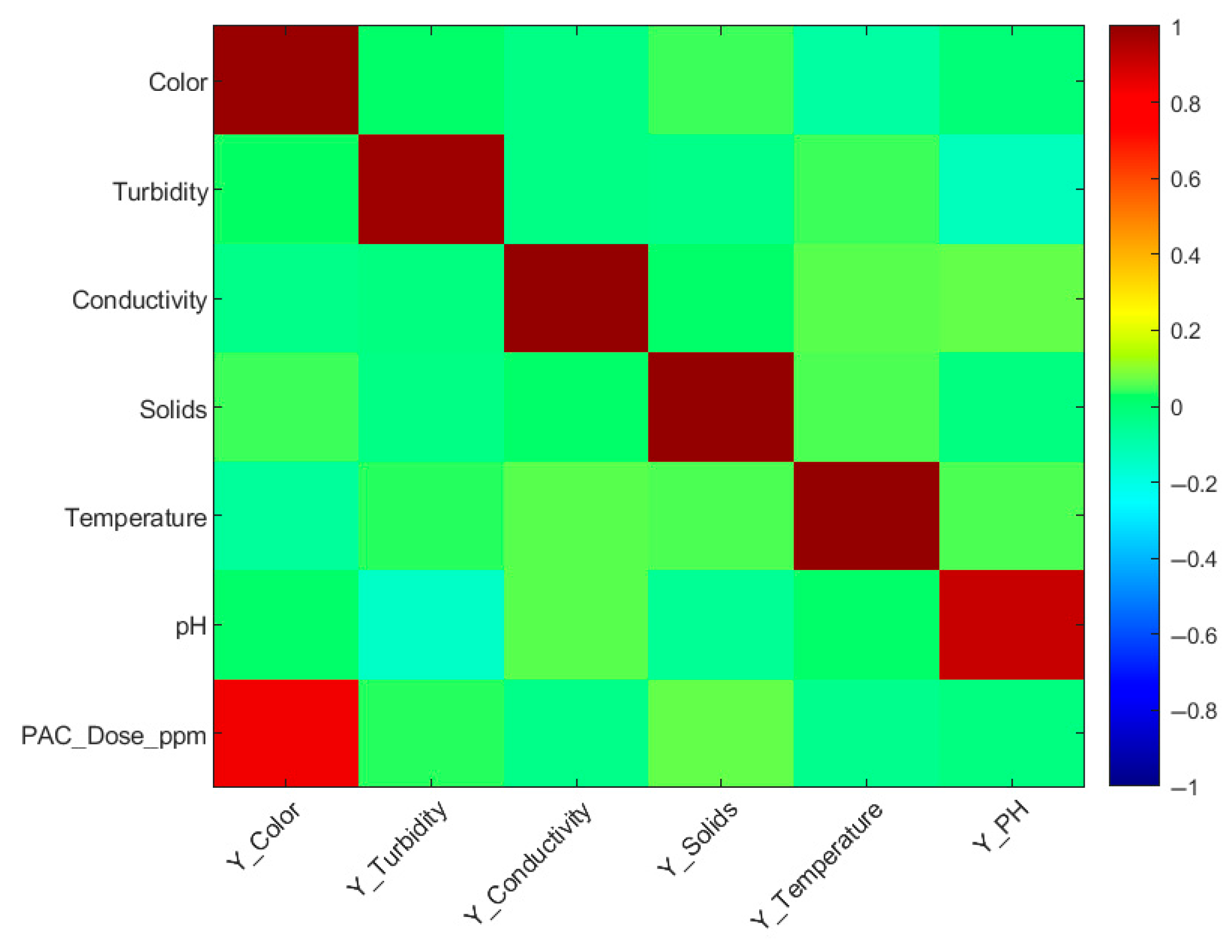
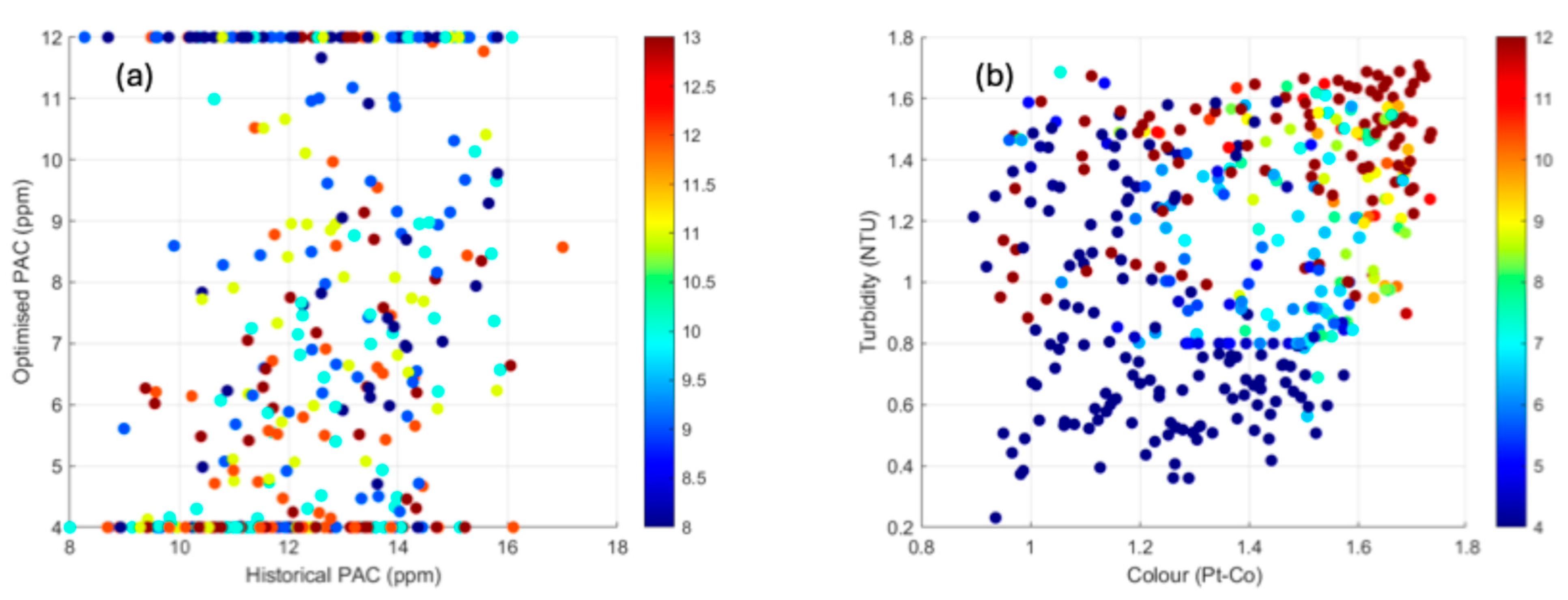
3.1. Exploratory Insight
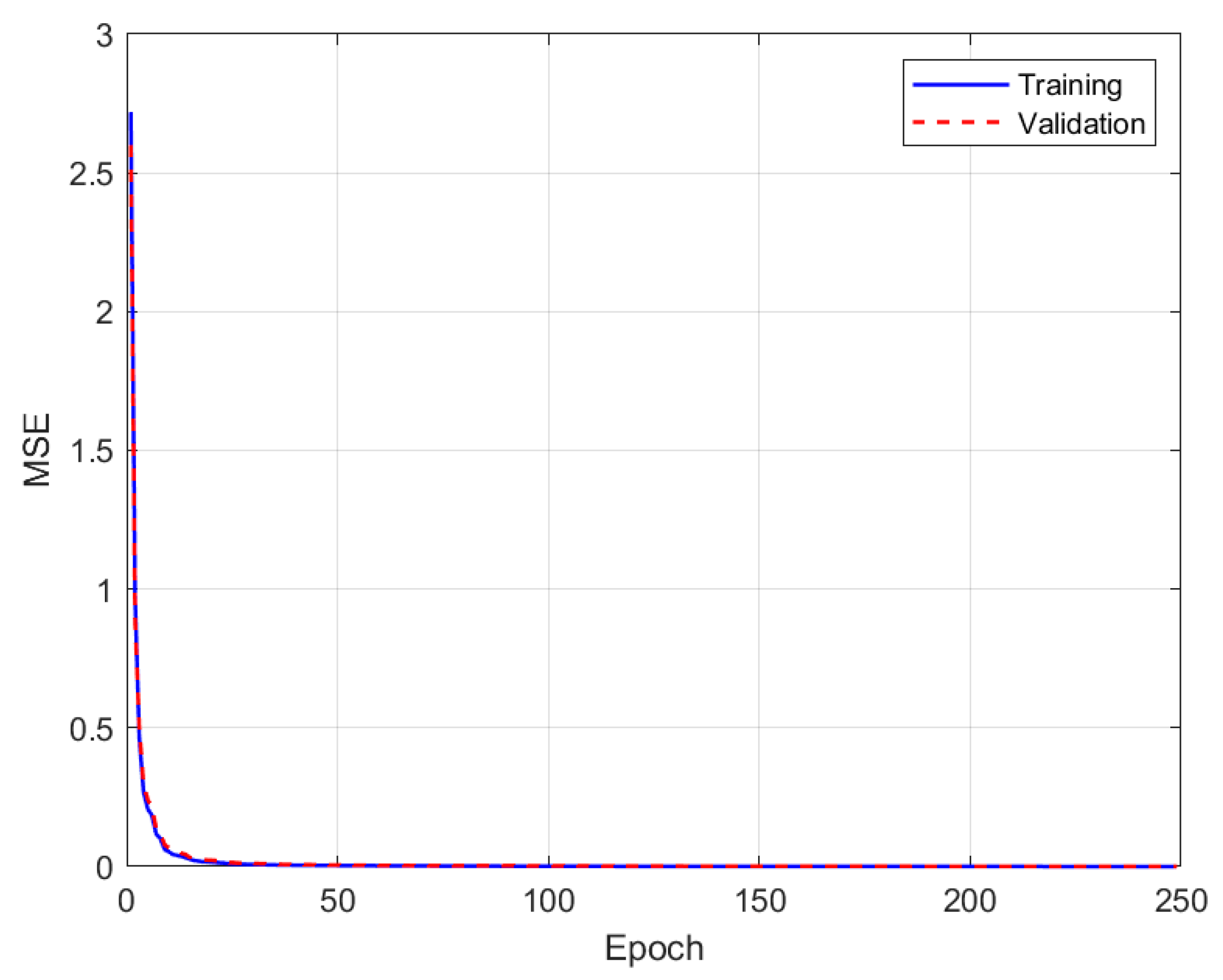
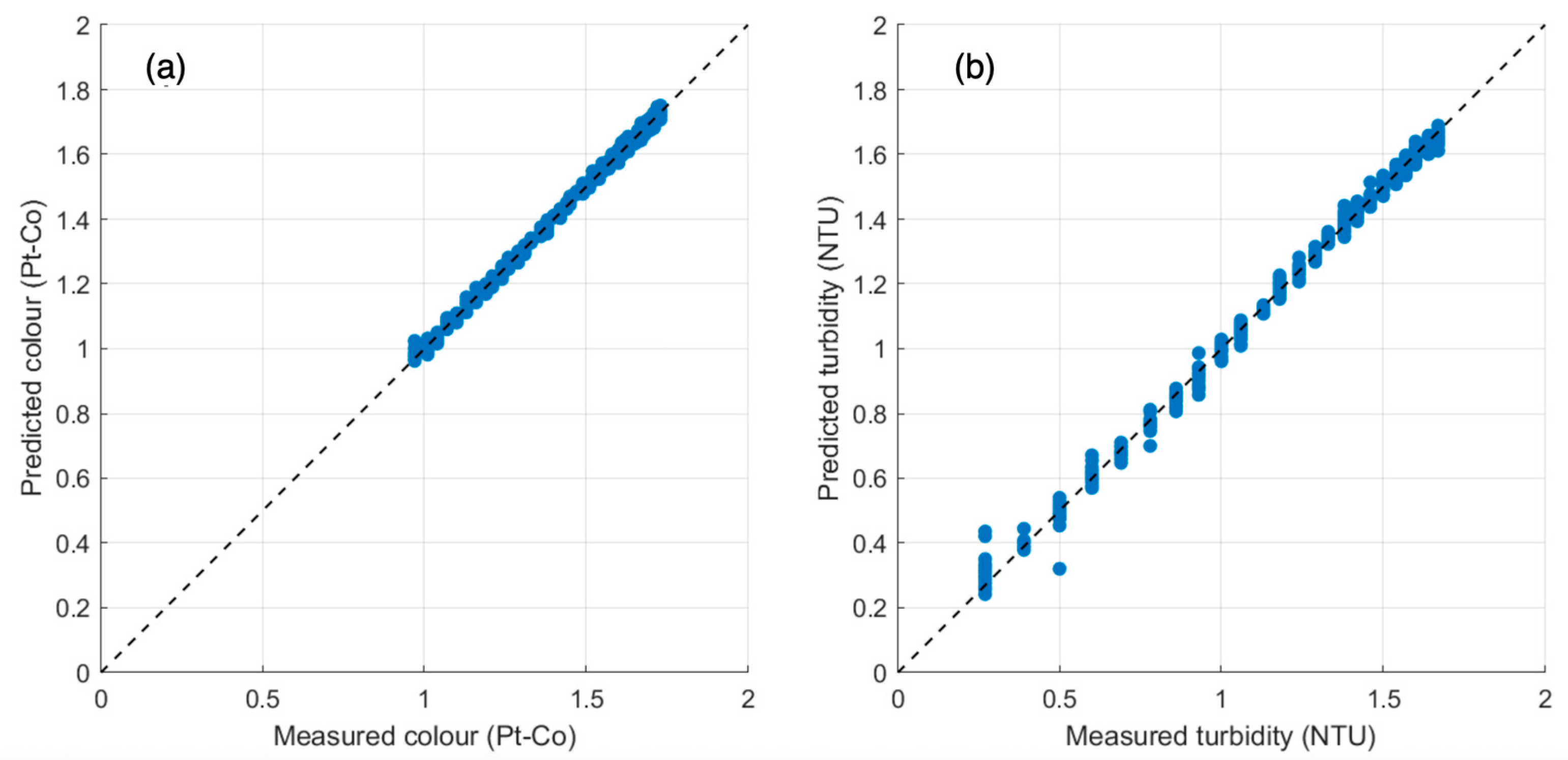
3.2. ANN Predictive Performance
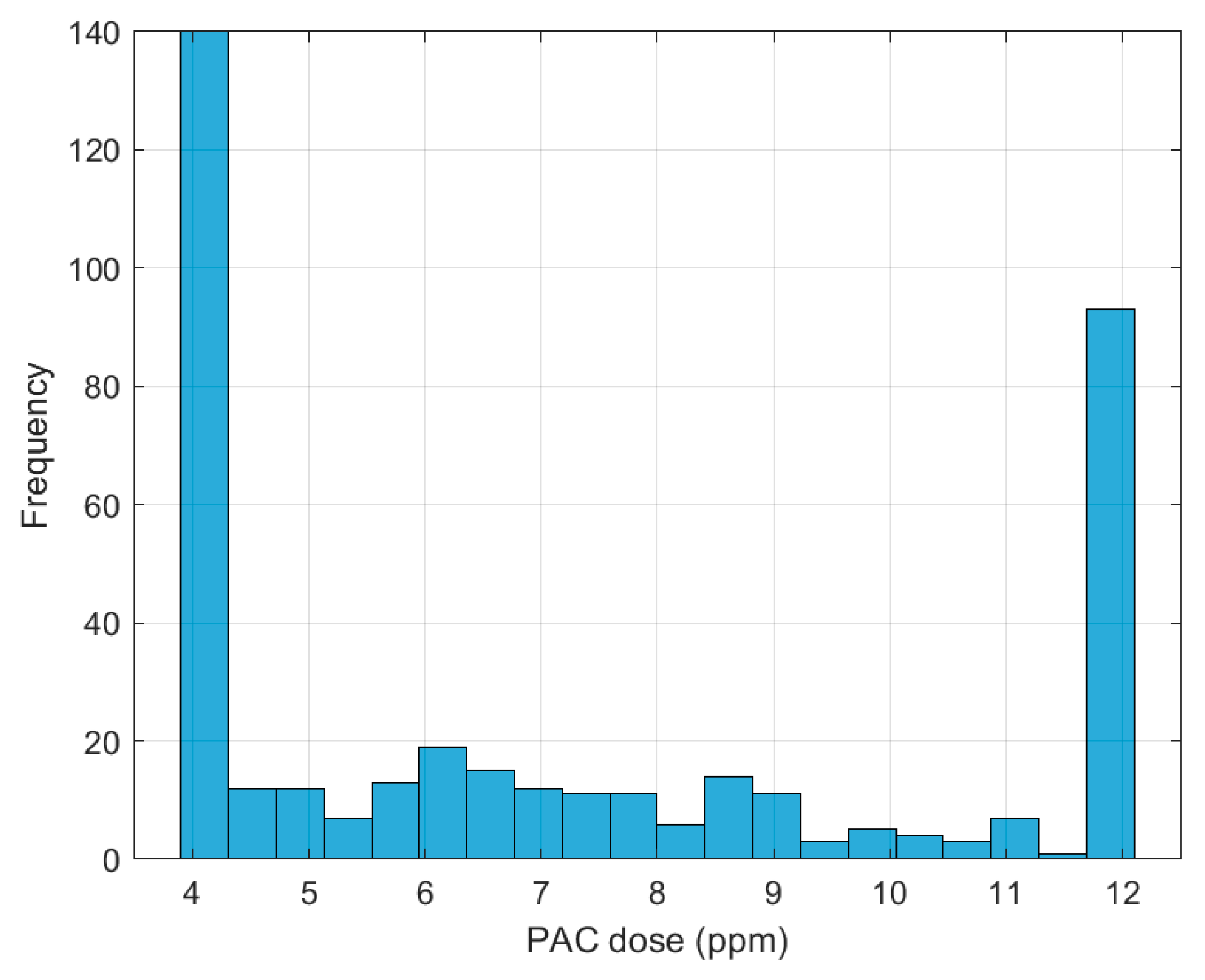
3.3. Optimized PAC Dose Distribution
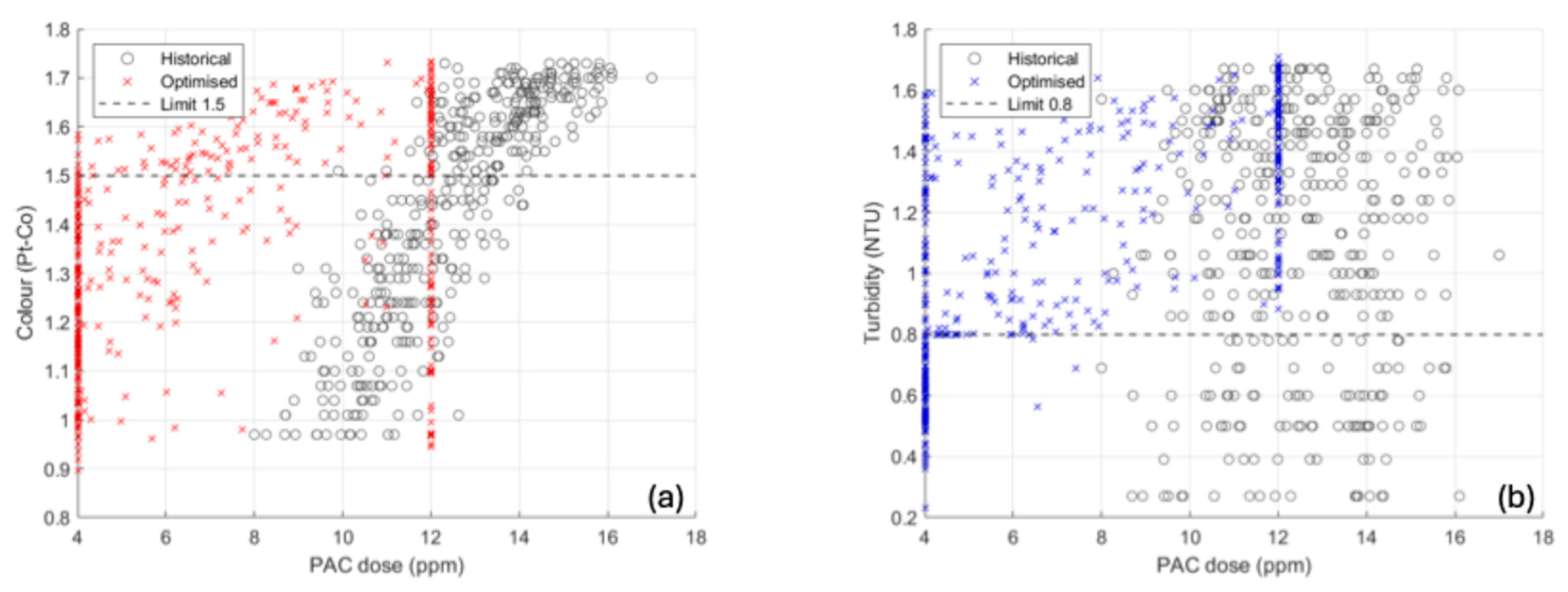
3.4. Dose–Response Relationships
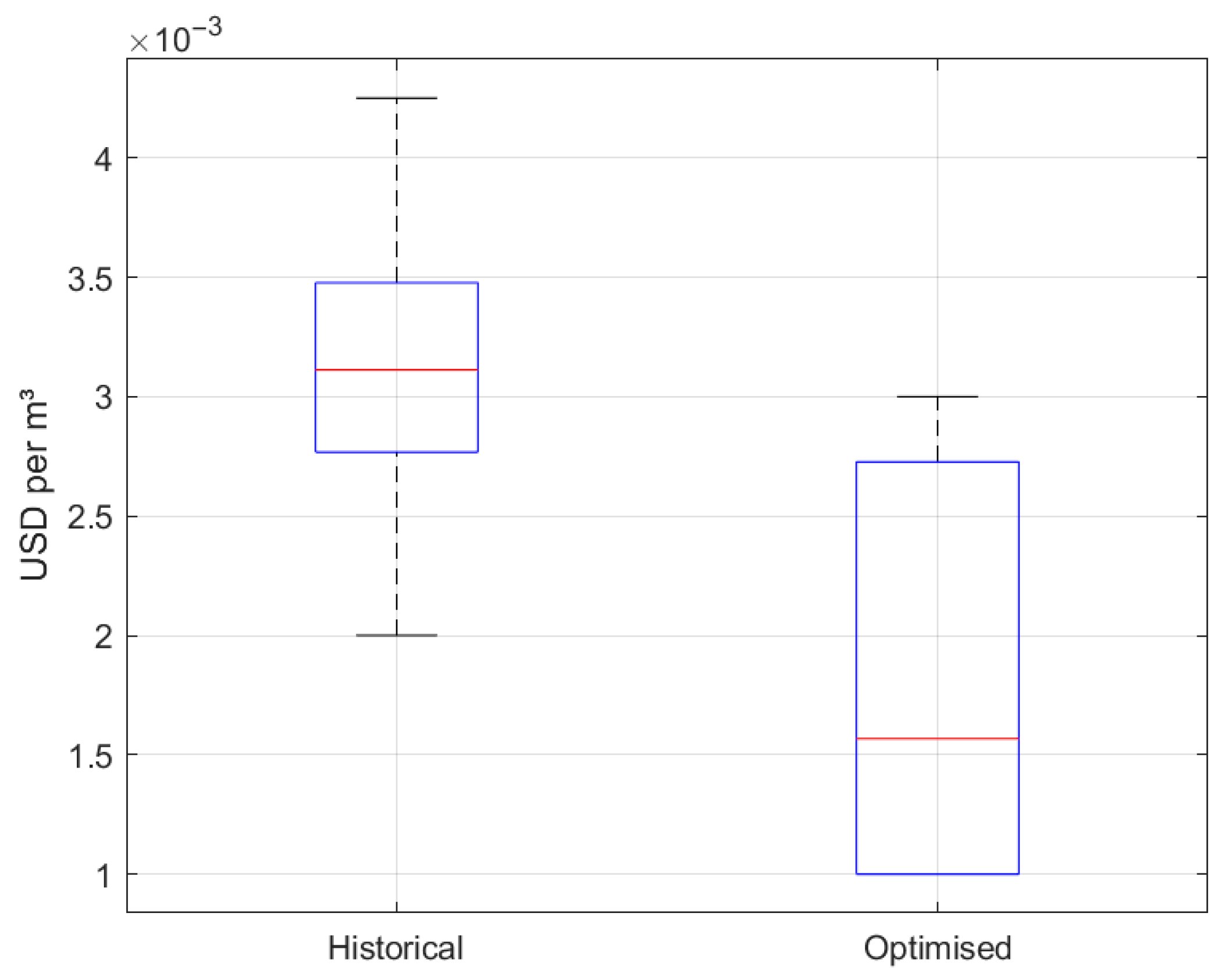
3.5. Economic Impact
3.6. Regulatory Compliance
3.7. Drivers of Dose Variability
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Assembly, U.G. Resolution Adopted by the General Assembly on 25 September 2015. Transforming Our World: The 2030 Agenda for Sustainable Development. 2015. Available online: http://www.un.org/en/development/desa/population/migration/generalassembly/docs/globalcompact/A_RES_70_1_E.pdf (accessed on 21 June 2025).
- Tubon-Usca, G.; Centeno, C.; Pomasqui, S.; Beneduci, A.; Arias, F.A. Enhanced Adsorption of Methylene Blue in Wastewater Using Natural Zeolite Impregnated with Graphene Oxide. Appl. Sci. 2025, 15, 2824. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, X.; Smith, K.; Inial, G.; Liu, S.; Conil, L.B.; Pan, B. Integrating water quality and operation into prediction of water production in drinking water treatment plants by genetic algorithm enhanced artificial neural network. Water Res. 2019, 164, 114888. [Google Scholar] [CrossRef] [PubMed]
- Igwegbe, C.A.; Ovuoraye, P.E.; Białowiec, A.; Onukwuli, O.D.; Balogun, P.A. Green flocculation for sustainable remediation of municipal landfill leachate using Parkia biglobosa extract: Optimization, mechanistic insights and implication for design. Clean Technol. Environ. Policy 2024, 26, 3429–3456. [Google Scholar] [CrossRef]
- Izquierdo, C.; Pezántes, B.; Ayala, E. Prediction of the Optimal Dosage of Poly Aluminum Chloride for Coagulation in Drinking Water Treatment using Artificial Neural Networks. Rev. Técnica Energía 2023, 20, 93–99. [Google Scholar] [CrossRef]
- Shen, Y.-H.; Dempsey, B.A. synthesis and speciation of polyaluminum chloride for water treatment. Environ. Int. 1998, 24, 899–910. [Google Scholar] [CrossRef]
- Ebrahimzade, H.; Khayati, G.R.; Schaffie, M. PSO–ANN-based prediction of cobalt leaching rate from waste lithium-ion batteries. J. Mater. Cycles Waste Manag. 2020, 22, 228–239. [Google Scholar] [CrossRef]
- Gyparakis, S.; Trichakis, I.; Diamadopoulos, E. Using Artificial Neural Networks to Predict Operational Parameters of a Drinking Water Treatment Plant (DWTP). Water 2024, 16, 2863. [Google Scholar] [CrossRef]
- Kassa, A.E.; Shibeshi, N.T.; Tizazu, B.Z. Synthesis of polyaluminum chloride: Optimization of process parameters, characterization and performance investigation for water treatment. J. Water Process. Eng. 2024, 57, 104700. [Google Scholar] [CrossRef]
- Yateh, M.; Lartey-Young, G.; Li, F.; Li, M.; Tang, Y. Application of Response Surface Methodology to Optimize Coagulation Treatment Process of Urban Drinking Water Using Polyaluminium Chloride. Water 2023, 15, 853. [Google Scholar] [CrossRef]
- Gyparakis, S.; Trichakis, I.; Daras, T.; Diamadopoulos, E. Artificial Neural Networks (ANNs) and Multiple Linear Regression (MLR) Analysis Modelling for Predicting Chemical Dosages of a Water Treatment Plant (WTP) of Drinking Water. Water 2025, 17, 227. [Google Scholar] [CrossRef]
- Wu, G.-D.; Lo, S.-L. Predicting real-time coagulant dosage in water treatment by artificial neural networks and adaptive network-based fuzzy inference system. Eng. Appl. Artif. Intell. 2008, 21, 1189–1195. [Google Scholar] [CrossRef]
- Guamán-Lozada, D.; Heredia, M.J.T.; Zambrano-Vinueza, M.; Ortiz, R.A.P.; Moscoso-Martínez, M.; Pinto, P.M.M. Predictive Modeling and Optimization of Plywood Drying: An Artificial Neural Network Approach. Recent Innov. Chem. Eng. (Former. Recent Pat. Chem. Eng.) 2024, 17, 208–220. [Google Scholar] [CrossRef]
- Vinitha, E.V.; Ahammed, M.M.; Gadekar, M.R. Chemical coagulation of greywater: Modelling using artificial neural networks. Water Sci. Technol. 2018, 2017, 869–877. [Google Scholar] [CrossRef] [PubMed]
- Narges, S.; Ghorban, A.; Hassan, K.; Mohammad, K. Prediction of the optimal dosage of coagulants in water treatment plants through developing models based on artificial neural network fuzzy inference system (ANFIS). J. Environ. Health Sci. Eng. 2021, 19, 1543–1553. [Google Scholar] [CrossRef] [PubMed]
- Wu, G.D.; Lo, S.L. Effects of data normalization and inherent-factor on decision of optimal coagulant dosage in water treatment by artificial neural network. Expert Syst. Appl. 2010, 37, 4974–4983. [Google Scholar] [CrossRef]
- Tariq, R.; Abatal, M.; Vargas, J.; Vázquez-Sánchez, A.Y. Deep learning artificial neural network framework to optimize the adsorption capacity of 3-nitrophenol using carbonaceous material obtained from biomass waste. Sci. Rep. 2024, 14, 20250. [Google Scholar] [CrossRef] [PubMed]
- Sutherland, C.; Chittoo, B.S.; Venkobachar, C. Application of an artificial neural network–genetic algorithm methodology for modelling and optimization of the improved biosorption of a chemically modified peat moss: Kinetic studies. Desalination Water Treat. 2017, 84, 69–84. [Google Scholar] [CrossRef]
- Shirkoohi, M.G.; Tyagi, R.D.; Vanrolleghem, P.A.; Drogui, P. Artificial neural networks and genetic algorithms: An efficient modelling and optimization methodology for active chlorine production using the electrolysis process. Can. J. Chem. Eng. 2021, 99, S389–S403. [Google Scholar] [CrossRef]
- Achite, M.; Samadianfard, S.; Elshaboury, N.; Sharafi, M. Modeling and optimization of coagulant dosage in water treatment plants using hybridized random forest model with genetic algorithm optimization. Environ. Dev. Sustain. 2023, 25, 11189–11207. [Google Scholar] [CrossRef]
- Yel, E.; Onen, V.; Tezel, G.; Yilmazturk, D. Performance prediction modeling of andesite processing wastewater physicochemical treatment via artificial neural network. Arab. J. Geosci. 2020, 13, 985. [Google Scholar] [CrossRef]
- Dharshini, S.D.; Anurag; Kumar, A.; Satpal; Kumar, M.; Priyanka, P.; Pugazenthi, K. Evaluation of machine-learning algorithms in estimation of relative water content of sorghum under different irrigated environments. J. Arid Environ. 2025, 229, 105390. [Google Scholar] [CrossRef]
- Ji, X.; Li, Z.; Wang, M.; Yuan, Z.; Jin, L. Response Surface Methodology Approach to Optimize Parameters for Coagulation Process Using Polyaluminum Chloride (PAC). Water 2024, 16, 1470. [Google Scholar] [CrossRef]
- Li, L.; Rong, S.; Wang, R.; Yu, S. Recent advances in artificial intelligence and machine learning for nonlinear relationship analysis and process control in drinking water treatment: A review. Chem. Eng. J. 2021, 405, 126673. [Google Scholar] [CrossRef]
- Wang, D.; Chang, X.; Ma, K. Predicting flocculant dosage in the drinking water treatment process using Elman neural network. Environ. Sci. Pollut. Res. 2022, 29, 7014–7024. [Google Scholar] [CrossRef] [PubMed]
- Instituto Ecuatoriano de Normalización (INEN). Drinking Water. Requirements, NTE INEN 1108:2014, 5th rev., Quito, Ecuador. 2014. Available online: https://www.insistec.ec/images/insistec/02-cliente/07-descargas/NTE%20INEN%201108%20-%20AGUA%20POTABLE.%20REQUISITOS.pdf (accessed on 23 June 2025).
- Maier, H.R.; Dandy, G.C. Neural networks for the prediction and forecasting of water resources variables: A review of modelling issues and applications. Environ. Model. Softw. 2000, 15, 101–124. [Google Scholar] [CrossRef]
- Huang, C.Y.; Chen, Y.Y.; Chuang, S.H.; Hsu, Y.S.; Wu, R.S.; Ko, K.Y. A precise dosing system based on a coagulation reaction model for water treatment. J. Water Process Eng. 2025, 70, 106962. [Google Scholar] [CrossRef]
- Chatterjee, S.; Sarkar, S.; Dey, N.; Sen, S.; Goto, T.; Debnath, N.C. Water quality prediction: Multi objective genetic algorithm coupled artificial neural network based approach. In Proceedings of the 2017 IEEE 15th International Conference on Industrial Informatics, INDIN 2017, Emden, Germany, 24–26 July 2017; pp. 963–968. [Google Scholar] [CrossRef]
- Mohadesi, M.; Aghel, B. Use of ANFIS/Genetic Algorithm and Neural Network to Predict Inorganic Indicators of Water Quality. J. Chem. Pet. Eng. 2020, 54, 155–164. [Google Scholar] [CrossRef]
- Ding, Y.R.; Cai, Y.J.; Sun, P.D.; Chen, B. The Use of Combined Neural Networks and Genetic Algorithms for Prediction of River Water Quality. J. Appl. Res. Technol. 2014, 12, 493–499. [Google Scholar] [CrossRef]
- Gholami, V.; Sahour, H.; Khaleghi, M.R.; Ghajari, Y.E.; Sahour, S. Combining artificial neural networks and genetic algorithms to model nitrate contamination in groundwater. Nat. Hazards 2024, 120, 4789–4809. [Google Scholar] [CrossRef]
- Achite, M.; Farzin, S.; Elshaboury, N.; Anaraki, M.V.; Amamra, M.; Toubal, A.K. Modeling the optimal dosage of coagulants in water treatment plants using various machine learning models. Environ. Dev. Sustain. 2024, 26, 3395–3421. [Google Scholar] [CrossRef]
- Sharafi, M.; Rezaverdinejad, V.; Behmanesh, J.; Samadianfard, S. Development of long short-term memory along with differential optimization and neural networks for coagulant dosage prediction in water treatment plant. J. Water Process Eng. 2024, 65, 105784. [Google Scholar] [CrossRef]
- Kim, C.M.; Parnichkun, M. Prediction of settled water turbidity and optimal coagulant dosage in drinking water treatment plant using a hybrid model of k-means clustering and adaptive neuro-fuzzy inference system. Appl. Water Sci. 2017, 7, 3885–3902. [Google Scholar] [CrossRef]
- Wang, W.-F.; Ruan, R. Study of PFS and PAC coagulation effect on Pi River Water. E3S Web Conf. 2021, 272, 01012. [Google Scholar] [CrossRef]
- Jia, R.-S.; Weng, C.H. Experimental Research on Removal of Turbidity and UV254 by Poly-aluminum Chloride (PAC). E3S Web Conf. 2018, 53, 04006. [Google Scholar] [CrossRef]
- Campinas, M.; Viegas, R.M.C.; Coelho, R.; Lucas, H.; Rosa, M.J. Adsorption/Coagulation/Ceramic Microfiltration for Treating Challenging Waters for Drinking Water Production. Membranes 2021, 11, 91. [Google Scholar] [CrossRef] [PubMed]
- Nakazawa, Y.; Abe, T.; Matsui, Y.; Shinno, K.; Kobayashi, S.; Shirasaki, N.; Matsushita, T. Differences in removal rates of virgin/decayed microplastics, viruses, activated carbon, and kaolin/montmorillonite clay particles by coagulation, flocculation, sedimentation, and rapid sand filtration during water treatment. Water Res. 2021, 203, 117550. [Google Scholar] [CrossRef] [PubMed]
- Kirchen, F.; Fundneider, T.; Gimmel, L.; Thomann, M.; Pulfer, M.; Lackner, S. Scattered and transmitted light as surrogates for activated carbon residual in advanced wastewater treatment processes: Investigating the influence of particle size. Water Res. X 2024, 23, 100222. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Zhou, Y.; Du, M.; Du, Z. Enhanced Removal of Refractory Organic Compounds from Coking Wastewater Using Polyaluminum Chloride with Coagulant Aids. Water 2024, 16, 2662. [Google Scholar] [CrossRef]
- Yan, M.; Wang, D.; Ni, J.; Qu, J.; Yan, Y.; Chow, C.W. Effect of polyaluminum chloride on enhanced softening for the typical organic-polluted high hardness North-China surface waters. Sep. Purif. Technol. 2008, 62, 401–406. [Google Scholar] [CrossRef]
- Balbinoti, J.R.; Jorge, R.M.M.; Junior, R.E.d.S.; Balbinoti, T.C.V.; Coral, L.A.d.A.; Bassetti, F.d.J. Treatment of low-turbidity water by coagulation combining Moringa oleifera Lam and polyaluminium chloride (PAC). J. Environ. Chem. Eng. 2024, 12, 111624. [Google Scholar] [CrossRef]
- Wu, L.; Deng, J.; Liu, H.; Yu, H.; Zhang, H.; Tong, Y.; Sun, L.; Meng, F.; Zhao, L. Understanding synergistic mechanisms of silicate decorated polyaluminium chloride and organic polymer flocculation for enhancing polymer-flooding wastewater treatment. Process Saf. Environ. Prot. 2023, 170, 1–10. [Google Scholar] [CrossRef]
- Olukowi, O.M.; Xie, Y.; Zhou, Z.; Adebayo, I.O.; Zhang, Y. Performance improvement and mechanism of composite PAC/PDMDAAC coagulant via enhanced coagulation coupled with rapid sand filtration in the treatment of micro-polluted surface water. J. Environ. Chem. Eng. 2022, 10, 108450. [Google Scholar] [CrossRef]
- Al-Jadabi, N.; Laaouan, M.; El Hajjaji, S.; Mabrouki, J.; Benbouzid, M.; Dhiba, D. The Dual Performance of Moringa Oleifera Seeds as Eco-Friendly Natural Coagulant and as an Antimicrobial for Wastewater Treatment: A Review. Sustainability 2023, 15, 4280. [Google Scholar] [CrossRef]
- Alenezi, A.; Alabaiadly, Y. Artificial Intelligence Applications in Water Treatment and Desalination: A Comprehensive Review. Water 2025, 17, 1169. [Google Scholar] [CrossRef]
- Dalibard, A.; Kriem, L.S.; Beckett, M.; Scherle, S.; Yeh, Y.-C.; Schließmann, U. Challenges and requirements of AI-based waste water treatment systems. At-Automatisierungstechnik 2025, 73, 40–49. [Google Scholar] [CrossRef]
- Ojadi, J.O.; Owulade, O.A.; Researcher, N.I.; Odionu, C.S.; Researcher, U.I.; Onukwulu, E.C.; Researcher, L.I. AI-Driven Optimization of Water Usage and Waste Management in Smart Cities for Environmental Sustainability. Eng. Technol. J. 2025, 10, 4284–4306. [Google Scholar] [CrossRef]
- Lowe, M.; Qin, R.; Mao, X. A Review on Machine Learning, Artificial Intelligence, and Smart Technology in Water Treatment and Monitoring. Water 2022, 14, 1384. [Google Scholar] [CrossRef]
- Ghafari, S.; Aziz, H.A.; Isa, M.H.; Zinatizadeh, A.A. Application of response surface methodology (RSM) to optimize coagulation–flocculation treatment of leachate using poly-aluminum chloride (PAC) and alum. J. Hazard. Mater. 2009, 163, 650–656. [Google Scholar] [CrossRef] [PubMed]
- Mahmudabadi, T.Z.; Ebrahimi, A.A.; Eslami, H.; Mokhtari, M.; Salmani, M.H.; Ghaneian, M.T.; Mohamadzadeh, M.; Pakdaman, M. Optimization and economic evaluation of modified coagulation–flocculation process for enhanced treatment of ceramic-tile industry wastewater. AMB Express 2018, 8, 172. [Google Scholar] [CrossRef] [PubMed]
- Yanza-López, J.; Rivera-Hernández, R.; Gómez-Torres, L.; Zafra-Mejía, C. Evaluación de FeCl3 y PAC para la potabilización de agua con alto contenido de color y baja turbiedad. TecnoLógicas 2019, 22, 9–21. [Google Scholar] [CrossRef]
- Fernández, J.; Montenegro, S.; Ledezma, C.; Yanza, J. Sedimentabilidad de partículas floculentas en aguas con alto contenido de color y baja turbiedad, coaguladas con FeCl3 + PAC versus PAC. TecnoLógicas 2021, 24, e1789. [Google Scholar] [CrossRef]



| Parameters | Unit | Media | Minimum | Maximum | Standard Deviation | Permissible Limits INEN 1108 2014 |
|---|---|---|---|---|---|---|
| Color | Pt-Co | 39.9 | 20 | 60 | 12.2 | 15 |
| Turbidity | NTU | 13.4 | 2 | 25 | 6.9 | 5 |
| Conductivity | μm/S | 130.3 | 40 | 220 | 55 | <1000 |
| Solids | mg/L | 9.8 | 0 | 20 | 6.3 | <500 |
| Temperature | °C | 10.3 | 8 | 13 | 1.7 | 5–15 |
| pH | - | 6.6 | 6 | 7 | 0.4 | 6.5–8.5 |
| Dosage PAC | mg/L | 12.2 | 8 | 17 | 3.2 | -- |
| Dataset | Color | Turbidity | Conductivity | Solids | Temperature | pH |
|---|---|---|---|---|---|---|
| Train | 0.015/0.998 | 0.014/0.998 | 0.014/0.998 | 0.015/0.998 | 0.014/0.998 | 0.025/0.994 |
| Validation | 0.019/0.995 | 0.032/0.988 | 0.020/0.995 | 0.019/0.996 | 0.017/0.998 | 0.039/0.988 |
| Test | 0.017/0.997 | 0.022/0.995 | 0.020/0.996 | 0.019/0.996 | 0.022/0.996 | 0.040/0.982 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guamán-Lozada, D.F.; Orozco Cantos, L.S.; Santillán Lima, G.P.; Arias Arias, F. Artificial Intelligence Optimization of Polyaluminum Chloride (PAC) Dosage in Drinking Water Treatment: A Hybrid Genetic Algorithm–Neural Network Approach. Computation 2025, 13, 179. https://doi.org/10.3390/computation13080179
Guamán-Lozada DF, Orozco Cantos LS, Santillán Lima GP, Arias Arias F. Artificial Intelligence Optimization of Polyaluminum Chloride (PAC) Dosage in Drinking Water Treatment: A Hybrid Genetic Algorithm–Neural Network Approach. Computation. 2025; 13(8):179. https://doi.org/10.3390/computation13080179
Chicago/Turabian StyleGuamán-Lozada, Darío Fernando, Lenin Santiago Orozco Cantos, Guido Patricio Santillán Lima, and Fabian Arias Arias. 2025. "Artificial Intelligence Optimization of Polyaluminum Chloride (PAC) Dosage in Drinking Water Treatment: A Hybrid Genetic Algorithm–Neural Network Approach" Computation 13, no. 8: 179. https://doi.org/10.3390/computation13080179
APA StyleGuamán-Lozada, D. F., Orozco Cantos, L. S., Santillán Lima, G. P., & Arias Arias, F. (2025). Artificial Intelligence Optimization of Polyaluminum Chloride (PAC) Dosage in Drinking Water Treatment: A Hybrid Genetic Algorithm–Neural Network Approach. Computation, 13(8), 179. https://doi.org/10.3390/computation13080179








