Implementing Astronomical Potential and Wavelet Analysis to Improve Regional Tide Modeling
Abstract
1. Introduction
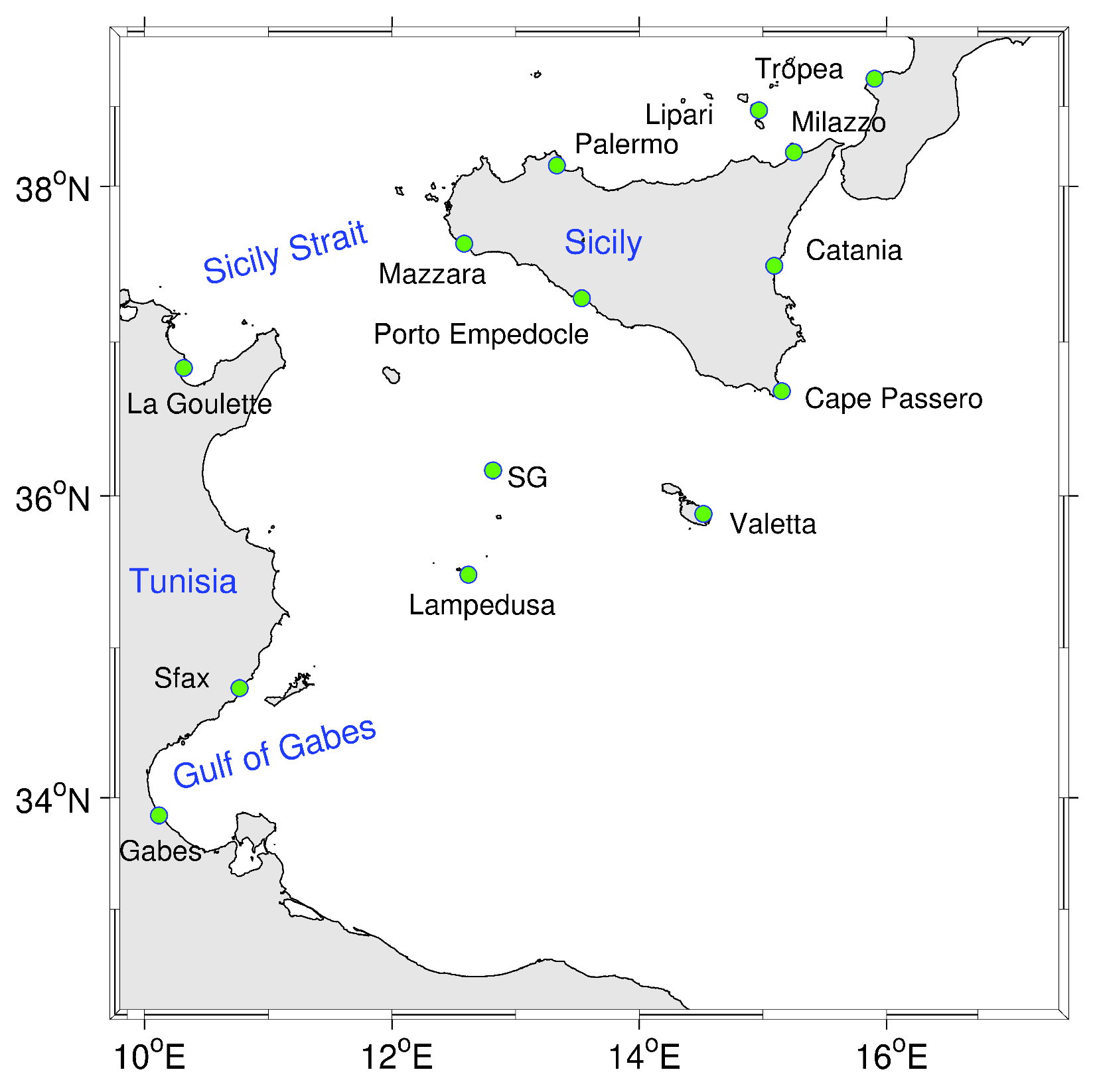
2. Materials and Methods
2.1. Numerical Modeling Approach
2.2. Simulation Strategy
2.3. Potential Tide Implementation
- is the tidal equilibrium amplitude for a given constituent n;
- is the phase of the disturbing celestial body (to which the tidal constituent pulsation is attributed) relative to the Greenwich meridian at the origin time ;
- and are the nodal correction factors for amplitude and phase relative to the tidal constituent n, respectively;
- is equal to 0 for long waves, 1 for diurnal waves, and 2 for semi-diurnal ones;
- is the longitude and the latitude of a given point;
- is a function of latitude that is equal to:
2.4. Wavelet Implementation
3. Results
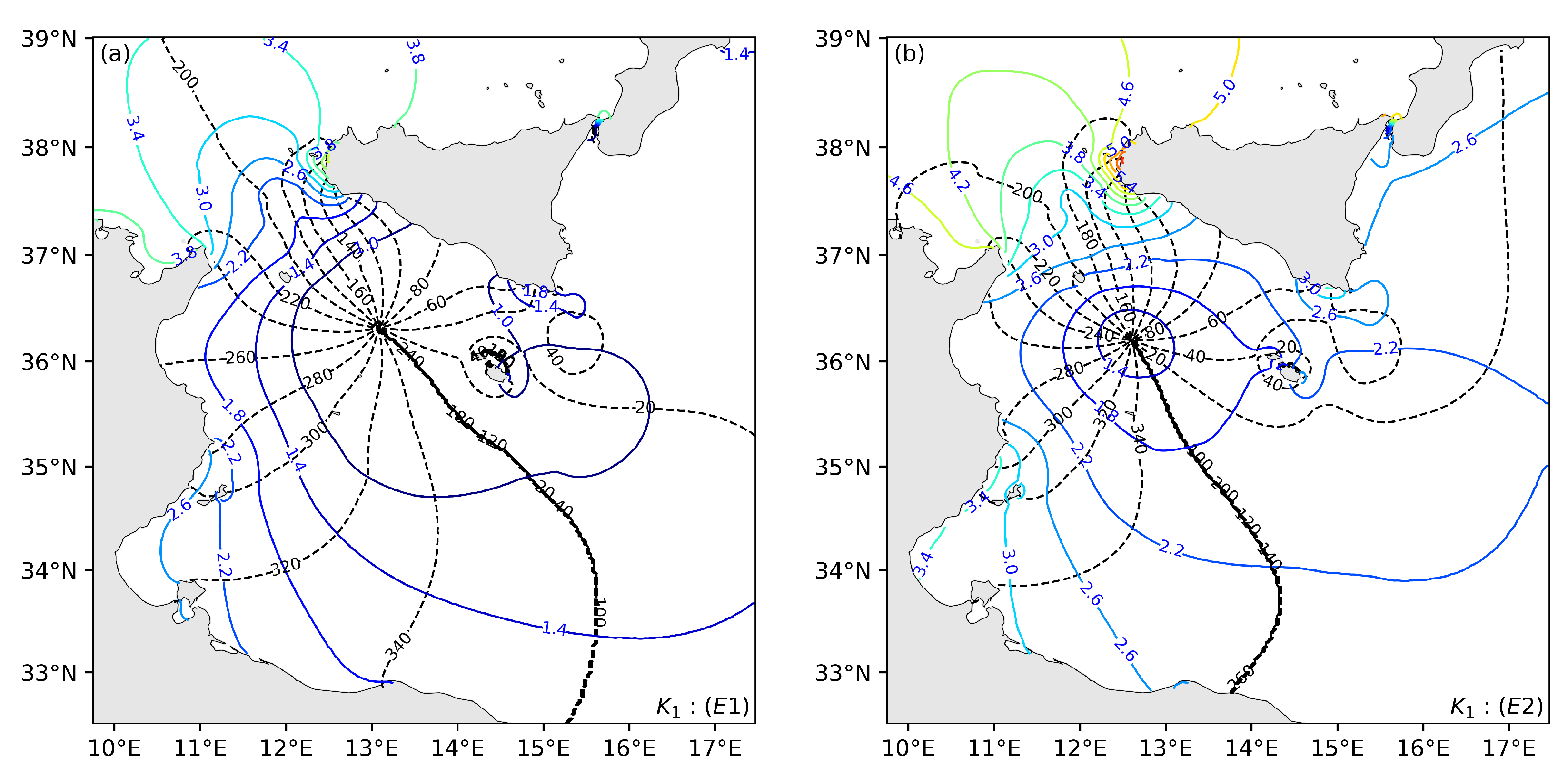
3.1. Impact of the Astronomical Tide-Generating Potential
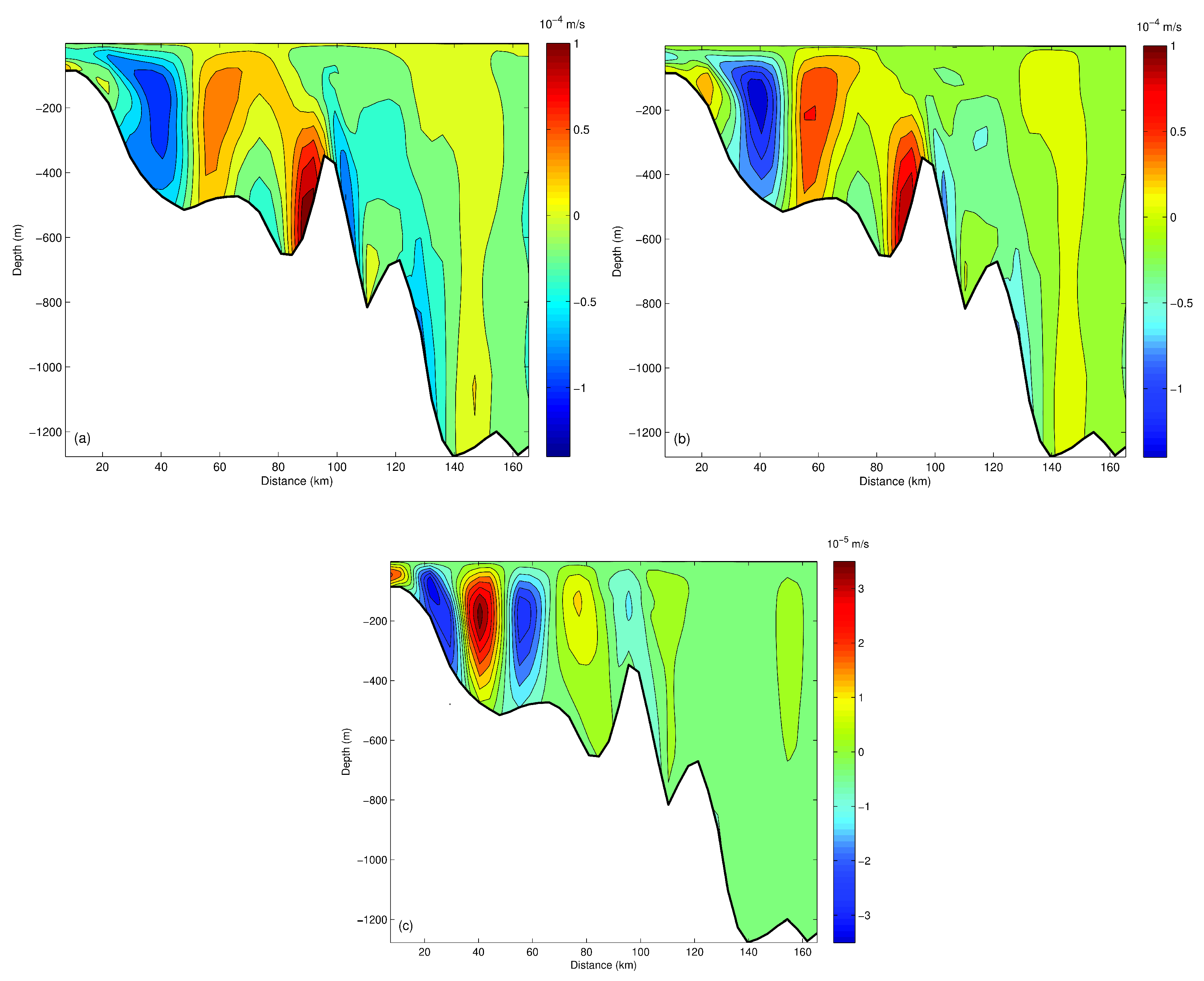
3.2. WEOF Analysis of Internal Tides
3.2.1. Wavelet Decomposition
3.2.2. WEOFs and Internal Tide Propagation
4. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lozano, C.J.; Candela, J. The M2 tide in the Mediterranean Sea: Dynamic analysis and data assimilation. Oceanol. Acta 1995, 18, 419–441. [Google Scholar]
- Sammari, C.; Koutitonsky, V.; Moussa, M. Sea level variability and tidal resonance in the Gulf of Gabes, Tunisia. Cont. Shelf Res. 2006, 26, 338–350. [Google Scholar] [CrossRef]
- Sanchez, B.V.; Ray, R.D.; Cartwright, D.E. A Proudman-function expansion of the M2 tide in the Mediterranean Sea from satellite altimetry and coastal gauges. Oceanol. Acta 1992, 15, 325–337. [Google Scholar]
- Tsimplis, M.N.; Proctor, R.; Flather, R.A. A two-dimensional tidal model for the Mediterranean Sea. J. Geophys. Res. 1995, 100, 16223–16239. [Google Scholar] [CrossRef]
- McDonagh, B.; Clementi, E.; Goglio, A.C.; Pinardi, N. The characteristics of tides and their effects on the general circulation of the Mediterranean Sea. Ocean Sci. 2024, 20, 1051–1066. [Google Scholar] [CrossRef]
- Candela, J.; Winant, C.; Ruiz, A. Tides in the Strait of Gibraltar. J. Geophys. Res. 1990, 95, 7313–7335. [Google Scholar] [CrossRef]
- Lyard, F.H.; Allain, D.J.; Cancet, M.; Carrère, L.; Picot, N. FES2014 global ocean tide atlas: Design and performance. Ocean Sci. 2021, 17, 615–649. [Google Scholar] [CrossRef]
- Carrere, L.; Lyard, F. Modeling the barotropic response of the global ocean to atmospheric wind and pressure forcing—Comparisons with observations. Geophys. Res. Lett. 2003, 30, 1275. [Google Scholar] [CrossRef]
- Egbert, G.D.; Erofeeva, S.Y. Efficient inverse modeling of barotropic ocean tides. J. Atmos. Ocean. Technol. 2002, 19, 183–204. [Google Scholar] [CrossRef]
- Stammer, D.; Ray, R.D.; Andersen, O.B.; Arbic, B.K.; Bosch, W.; Carrère, L.; Cheng, Y.; Chinn, D.S.; Dushaw, B.D.; Egbert, G.D.; et al. Accuracy assessment of global barotropic ocean tide models. Rev. Geophys. 2014, 52, 243–282. [Google Scholar] [CrossRef]
- Lefèvre, F.; Lyard, F.H.; Le Provost, C.; Schrama, E.J.O. FES99: A Global Tide Finite Element Solution Assimilating Tide Gauge and Altimetric Information. J. Atmos. Ocean. Technol. 2002, 19, 1345–1356. [Google Scholar] [CrossRef]
- Letellier, T. Etude des Ondes de Marée sur les Plateaux Continentaux. Ph.D. Thesis, Université Toulouse III-Paul Sabatier, Toulouse, France, 2004. [Google Scholar]
- Shchepetkin, A.F.; McWilliams, J.C. The regional oceanic modeling system (ROMS): A split-explicit, free-surface, topography-following-coordinate oceanic model. Ocean Modell. 2005, 9, 347–404. [Google Scholar] [CrossRef]
- Purga, N.; Mosetti, F.; Accerboni, E. Tidal harmonic constants for some Mediterranean harbours. Boll. Geofis. Teor. Appl. 1979, XXI, 72–81. [Google Scholar]
- Ray, R.D. A Global Ocean Tide Model from Topex/Poseidon Altimetry: GOT99.2; NASA Technical Memo. 209478; Goddard Space Flight Center: Greenbelt, MD, USA, 1999; 58p. [Google Scholar]
- Munk, W.; Wunsch, C. Abyssal recipes II: Energetics of tidal and wind mixing. Deep. Sea Res. Part I Oceanogr. Res. Pap. 1998, 45, 1977–2010. [Google Scholar] [CrossRef]
- Van der Molen, J. The influence of tides, wind and waves on the net sand transport in the North Sea. Cont. Shelf. Res. 2002, 22, 2739–2762. [Google Scholar] [CrossRef]
- Pairaud, I.; Auclair, F. Combined wavelet and principal component analysis (WEof) of a scale-oriented model of coastal ocean gravity waves. Dyn. Atmos. Oceans. 2005, 40, 254–282. [Google Scholar] [CrossRef]
- Meyers, S.D.; O’Brien, J.J. Spatial and temporal 26-day SST variations in the equatorial Indian Ocean using wavelet analysis. Geophys. Res. Lett. 1994, 21, 777–780. [Google Scholar] [CrossRef]
- Lau, K.-M.; Weng, H. Climate Signal Detection Using Wavelet Transform: How to Make a Time Series Sing. Bull. Am. Meteorol. Soc. 1995, 76, 2391–2402. [Google Scholar] [CrossRef]
- Torrence, C.; Compo, G.P. A Practical Guide to Wavelet Analysis. Bull. Am. Meteorol. Soc. 1998, 79, 61–78. [Google Scholar] [CrossRef]
- Liu, Y.; Liang, X.S.; Weisberg, R.H. Rectification Bias Wavelet Power Spectrum. J. Atmos. Ocean. Technol. 2007, 24, 2093–2102. [Google Scholar] [CrossRef]
- Liu, Y.; Weisberg, R.H.; Vignudelli, S.; Mitchum, G.T. Patterns of the Loop Current system and regions of sea surface height variability in the eastern Gulf of Mexico revealed by the Self-Organizing Maps. J. Geophys. Res. Oceans 2016, 121, 2347–2366. [Google Scholar] [CrossRef]
- Haidvogel, D.B.; Arango, H.; Budgell, W.P.; Cornuelle, B.D.; Curchitser, E.; Di Lorenzo, E.; Fennel, K.; Geyer, W.R.; Hermann, A.J.; Lanerolle, L.; et al. Ocean forecasting in terrain-following coordinates: Formulation and skill assessment of the Regional Ocean Modeling System. J. Comput. Phys. 2008, 227, 3595–3624. [Google Scholar] [CrossRef]
- Send, U.; Font, J.; Krahmann, G.; Millot, C.; Rhein, M.; Tintor, J. Recent advances in observing the physical oceanography of the western Mediterranean. Prog. Oceanogr. 1999, 44, 37–64. [Google Scholar] [CrossRef]
- Fichaut, M.; Garcia, M.J.; Giorgetti, A.; Iona, A.; Kuznetsov, A.; Rixen, M.; Medar Group. MEDAR/MEDATLAS 2002: A Mediterranean and Black Sea Database for Operational Oceanography. Elsevier Oceanogr. Ser. 2003, 69, 645–648. [Google Scholar] [CrossRef]
- Gallagher, B.S.; Munk, W.H. Tides in shallow water: Spectroscopy. Tellus Dyn. Meteorol. Oceanogr. 1971, 23, 346–363. [Google Scholar] [CrossRef]
- Le Provost, C.; Genco, M.L.; Lyard, F.; Vincent, P.; Canceil, P. Spectroscopy of the world ocean tides from a finite element hydrodynamic model. J. Geophys. Res. 1994, 99, 777–797. [Google Scholar] [CrossRef]
- Parker, B.B. Tidal Hydrodynamics; John Wiley and Sons: New York, NY, USA, 1991; 883p. [Google Scholar]
- International Hydrographic Organisation. IHO Tidal Constituent Bank, Station Catalogue, 3rd ed.; Special Publication No. 50; International Hydrographic Organisation: Ottawa, ON, Canada, 1994; 30p. [Google Scholar]
- Astraldi, M.; Galli, C.; Gasparini, G.P.; Lazzoni, E.; Manzella, G.M.R. The Janus Experiment; Internal report, TR 140; CNR/CREA: La Spezia, Italy, 1987; 38p. [Google Scholar]
- Lyard, F.; Lefevre, F.; Letellier, T.; Francis, O. Modelling the global ocean tides: Modern insights from FES2004. Ocean Dyn. 2006, 56, 394–415. [Google Scholar] [CrossRef]

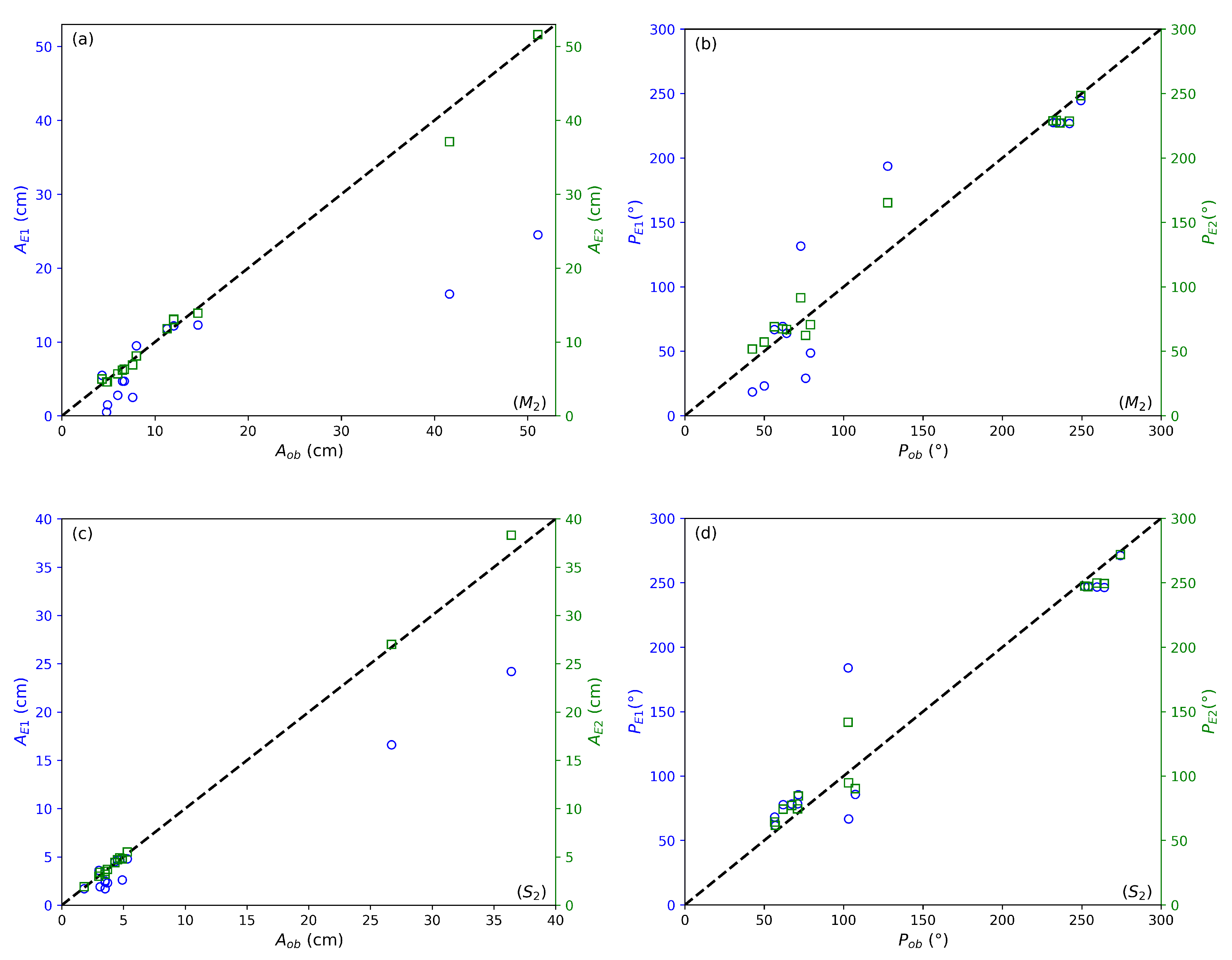




| Stations | (cm) | (cm) | (cm) | (°) | (°) | (°) |
|---|---|---|---|---|---|---|
| La goulette | 8 | 9.5 | 8.1 | 249.4 | 244.6 | 248.4 |
| Sfax | 41.6 | 16.5 | 37.1 | 76.1 | 29.1 | 62.3 |
| Gabes | 51.1 | 24.5 | 51.6 | 79.1 | 48.6 | 70.7 |
| SG | 4.8 | 0.5 | 4.6 | 50 | 23.1 | 57.1 |
| Palermo | 11.3 | 11.8 | 11.8 | 236.3 | 227.3 | 227.2 |
| Mazzara | 4.3 | 5.5 | 5.0 | 127.8 | 193.7 | 165.3 |
| Po.Emp | 4.9 | 1.5 | 4.6 | 73 | 131.6 | 91.5 |
| Valetta | 6 | 2.8 | 5.7 | 64 | 63.9 | 66.9 |
| C.passero | 6.7 | 4.7 | 6.3 | 61.6 | 69.3 | 67.3 |
| Lampedusa | 7.6 | 2.5 | 6.9 | 42.5 | 18.5 | 51.7 |
| Catania | 6.5 | 4.7 | 6.2 | 56.4 | 66.8 | 69.0 |
| Tropea | 14.6 | 12.3 | 13.9 | 242.2 | 226.8 | 228.6 |
| Milazzo | 12 | 12.2 | 13.0 | 234 | 227.4 | 229.2 |
| Lipari | 12 | 12.2 | 13.1 | 232 | 227.5 | 228.8 |
| Stations | (cm) | (cm) | (cm) | (°) | (°) | (°) |
|---|---|---|---|---|---|---|
| La goulette | 3.0 | 3.6 | 3.0 | 274.4 | 271.1 | 271.9 |
| Sfax | 26.7 | 16.6 | 27.0 | 103.1 | 66.7 | 94.8 |
| Gabes | 36.4 | 24.2 | 38.3 | 107.3 | 85.8 | 90.2 |
| SG | 3.1 | 1.9 | 3.4 | 57 | 61.6 | 61.8 |
| Palermo | 4.3 | 4.5 | 4.4 | 259.6 | 246.7 | 249.8 |
| Mazzara | 1.8 | 1.7 | 1.9 | 102.8 | 184 | 141.7 |
| Po.Emp | 3.5 | 1.7 | 3.5 | 71.4 | 85.6 | 84.6 |
| Valetta | 3.7 | 2.3 | 3.7 | 71 | 78.5 | 74.5 |
| C.passero | 3.5 | 2.4 | 3.2 | 67.3 | 78.4 | 77.2 |
| Lampedusa | 4.9 | 2.6 | 4.8 | 56.6 | 68.2 | 64.3 |
| Catania | 3.5 | 2.5 | 3.2 | 61.9 | 77.8 | 74.3 |
| Tropea | 5.3 | 4.8 | 5.5 | 264.2 | 246.4 | 249.4 |
| Milazzo | 4.7 | 4.7 | 4.9 | 252.0 | 247.0 | 247.3 |
| Lipari | 4.5 | 4.7 | 4.7 | 254.0 | 247.0 | 247.0 |
| Stations | (cm) | (cm) | (cm) | (°) | (°) | (°) |
|---|---|---|---|---|---|---|
| La goulette | 3.0 | 3.8 | 3.7 | 195.7 | 215 | 210.8 |
| Sfax | 1.8 | 2.5 | 1.9 | 4.5 | 56.2 | 23.5 |
| Gabes | 2.5 | 2.6 | 2.2 | 349.3 | 316.9 | 356.3 |
| SG | 0.5 | 0.2 | 0.4 | 78 | 83.2 | 69.1 |
| Palermo | 2.9 | 3.8 | 4.1 | 199.2 | 185.6 | 187.5 |
| Mazzara | 3.5 | 3.2 | 4.2 | 85.5 | 118.5 | 114.9 |
| Po.Emp | 1.5 | 1 | 1.8 | 88.7 | 85.8 | 85.4 |
| Valetta | 1.1 | 1.1 | 1.4 | 28.5 | 14.5 | 16.7 |
| C.passero | 1.9 | 1.3 | 1.8 | 52.2 | 18.2 | 31.2 |
| Lampedusa | 0.6 | 0.9 | 0.9 | 346.6 | 309.8 | 359.1 |
| Catania | 1.6 | 1.3 | 1.8 | 42.1 | 27.8 | 37.6 |
| Tropea | 4.1 | 4.0 | 4.3 | 203.1 | 186.7 | 190.8 |
| Milazzo | 3.3 | 4.0 | 4.3 | 200 | 186.7 | 189.7 |
| Lipari | 3.1 | 4.0 | 4.3 | 199 | 187 | 189.6 |
| (cm) | 10.3 | 1.5 | 4.6 | 0.5 | 2.2 | 0.7 | 0.6 | 0.5 |
| (°) | 30.2 | 13.7 | 26.4 | 14.1 | 92.5 | 20.0 | 25.2 | 14.2 |
| (cm) | 9.1 | 2.7 | 4.6 | 2.3 | 2.0 | 0.7 | 0.8 | 0.6 |
| Mode | (Variance, %) | (Variance, %) |
|---|---|---|
| Mode 1 | 98.8% | 78% |
| Mode 2 | 1% | 19% |
| Mode 3 | 0.2% | 3% |
| Mode | (Wavelength, km) | (Wavelength, km) |
|---|---|---|
| Mode 1 | 72 | 30 |
| Mode 2 | 36 | 15 |
| Mode 3 | 24 | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdennadher, J.; Boukthir, M. Implementing Astronomical Potential and Wavelet Analysis to Improve Regional Tide Modeling. Computation 2025, 13, 145. https://doi.org/10.3390/computation13060145
Abdennadher J, Boukthir M. Implementing Astronomical Potential and Wavelet Analysis to Improve Regional Tide Modeling. Computation. 2025; 13(6):145. https://doi.org/10.3390/computation13060145
Chicago/Turabian StyleAbdennadher, Jihene, and Moncef Boukthir. 2025. "Implementing Astronomical Potential and Wavelet Analysis to Improve Regional Tide Modeling" Computation 13, no. 6: 145. https://doi.org/10.3390/computation13060145
APA StyleAbdennadher, J., & Boukthir, M. (2025). Implementing Astronomical Potential and Wavelet Analysis to Improve Regional Tide Modeling. Computation, 13(6), 145. https://doi.org/10.3390/computation13060145







