AI-Driven Multi-Agent Energy Management for Sustainable Microgrids: Hybrid Evolutionary Optimization and Blockchain-Based EV Scheduling

Abstract

The increasing complexity of urban energy systems requires decentralized, sustainable, and scalable solutions. The paper presents a new multi-layered framework for smart energy management in microgrids by bringing together advanced forecasting, decentralized decision-making, evolutionary optimization and blockchain-based coordination. Unlike previous research addressing these components separately, the proposed architecture combines five interdependent layers that include forecasting, decision-making, optimization, sustainability modeling, and blockchain implementation. A key innovation is the use of Temporal Fusion Transformer (TFT) for interpretable multi-horizon forecasting of energy demand, renewable generation, and electric vehicle (EV) availability which outperforms conventional LSTM, GRU and RNN models. Another novelty is the hybridization of Genetic Algorithms (GA) and Particle Swarm Optimization (PSO), to simultaneously support discrete and continuous decision variables, allowing for dynamic pricing, efficient energy dispatching and adaptive EV scheduling. Multi-Agent Reinforcement Learning (MARL) which is improved by sustainability shaping by including carbon intensity, renewable utilization ratio, peak to average load ratio and net present value in agent rewards. Finally, Ethereum-based smart contracts add another unique contribution by providing the implementation of transparent and tamper-proof peer-to-peer energy trading and automated sustainability incentives. The proposed framework strengthens resilient infrastructure through decentralized coordination and intelligent optimization while contributing to climate mitigation by reducing carbon intensity and enhancing renewable integration. Experimental results demonstrate that the proposed framework achieves a 14.6% reduction in carbon intensity, a 12.3% increase in renewable utilization ratio, and a 9.7% improvement in peak-to-average load ratio compared with baseline models. The TFT-based forecasting model achieves RMSE = 0.041 kWh and MAE = 0.032 kWh, outperforming LSTM and GRU by 11% and 8%, respectively.

1. Introduction

Smart cities forecast a vision for the urban development involving the integration of multiple technologies and innovative solutions. The concept of smart cities aims to address existing challenges being faced by modern urban environments [1,2,3]. The process of modernizing the urban infrastructure to create a sustainable and intelligent urban environments, which has led to the concept of smart cities, whereby data-driven decision-making, decentralized governance and the integration of renewable energy are at the forefront [4,5,6,7]. The ever-increasing penetration of distributed energy resources, electric vehicles and prosumer participation generates unprecedented opportunities but pose challenges of scale, reliability and sustainability [8,9,10,11,12]. Conventional centralized energy management approaches are inadequate to meet the dynamic and heterogeneous requirements of such systems, especially when confronted with volatile renewable generation, fluctuating energy demand and the strong push toward electrified transportation. As a result, new architectures of their combination of artificial intelligence, optimization, and blockchain based technologies are being intensively studied in order to satisfy these complex requirements [13,14,15]. Energy systems are the backbone of smart cities and their modernization is fundamental to achieve sustainable development [16,17,18]. However, the shift from centralised fossil fuel grids to distributed renewable microgrids has thrown up challenges of intermittency, stability and economic coordination. Wind and solar resources, although environmentally friendly, are inherently variable resources, and there is need to accurately forecast and employ adaptive control strategies to ensure a balance between generation and consumption [19,20,21,22,23,24]. At the same time, electrification of transport in the form of electric vehicles brings with it an additional layer of uncertainty in load profiles, as charging behaviour depends on user preferences and mobility patterns, as well as market conditions. This interplay between renewable variability and EV adoption leads to very dynamic environments and requires robust predictive models and intelligent coordination mechanisms. These mechanisms are complex; however, artificial intelligence offers several promising avenues for addressing such challenges.

Deep learning methods, or sequence models, have great potential for forecasting renewable generation, electricity demand and EV availability [25,26,27]. A recently-developed technique for interpretable time series prediction, TFT, is able to perform multiple horizon prediction on time series data while maintaining model interpretability. Such a forecasting capability results to critical input to downstream optimization and decision making processes [19,28,29]. Besides forecasting, reinforcement learning has also been widely investigated for demand response, distributed control and energy trading. Extending reinforcement learning into MARL allows for decentralized but coordinated decision making from different (heterogeneous) stakeholders such as prosumers, EV owners and grid operators. By introducing the concept of sustainability shaping into reward functions, MARL agents can not only be aligned with economic goals, but also more general environmental goals such as reducing carbon intensity and increasing the use of renewables. While forecasting and reinforcement learning are concerned with the aspects of prediction and decision making, optimization is needed for fine-tuning the resource allocation and ensuring feasibility of operation. Smart grid problems are nonlinear, multi-objective and mixed-variable, which pose challenges for traditional mathematical optimization techniques.

Evolutionary algorithms, on the other hand, provide flexible and adaptive solutions to solve for these challenges. PSO is effective for continuous parameter tuning while GA is effective for discrete decision space [30,31,32]. A hybrid GA-PSO scheme is a combination of both to balance two aspects and get good balance of exploration and exploitation. This hybridization plays a role in real-time energy dispatching and also adaptive pricing and effective EV scheduling, which in turn, helps to bridge the gap between predictive models and actionable control. Another key dimension in today’s energy systems are trust, transparency and security. Traditional centralized mechanisms for coordination and settlement are no longer adequate with further and further decentralization and peer-to-peer transactions. Blockchain technology brings the ideas of unchangeable tamper-proof ledgers and automation for smart contracts to automate the trading of energy, enforce compliance and accountability [33,34,35,36]. In the context of microgrids, it is possible to use blockchain-based contracts to control EV charging schedules, renewable energy certificates and sustainability incentives without the need for intermediaries. It will increase transparency and decrease transaction costs and allow space for community engagement. Integrating blockchain with optimization operated by artificial intelligence allows for the design of a unique architecture in which technical intelligence and trust mechanisms work seamlessly. For instance, an underestimation of peak load by only 5% in the forecasting layer can result in up to a 7–10% increase in dispatch cost and a 6% drop in renewable utilization due to suboptimal commitment decisions. This demonstrates the bidirectional sensitivity between forecasting accuracy and downstream optimization performance. However, previous works have considered each of these areas separately, despite recent advances in forecasting, reinforcement learning, evolutionary optimization, and blockchain. However, forecast and optimization research tend to be sensitive to each other, and trust and coordination mechanisms are often ignored in optimization research. Also, blockchain-based energy trading platforms mostly lack advanced intelligence for forecasting and control. The fragmentation limits the scalability and sustainability of solutions as applied to the real world of microgrids. There is therefore a need for holistic framework that offers unity between these dimensions in a multi-layered architecture that can address the full gamut of issues in sustainable energy management. In this paper, we address the role of smart energy systems in the context of a smart city. In this context, the paper describes a decentralized and resilient energy management strategy for sustainability and for optimizing energy generation, distribution, consumption and management. Blockchain-based smart contracts can automate energy transactions, which can ensure secure and tamper-proof agreements between energy producers and consumers. The decentralized approach towards energy trading enables local communities to be involved in energy markets and renewable energy projects.

1.1. Research Contributions

The key contributions of this work are outlined as follows:

• Transformer-based forecasting: A combination of the TFT is used to obtain precise forecasts (multihorizons) of energy demand, renewable generation, and EV availability that are interpretable and outperform the models of Long-Short-Term Memory (LSTM), Gated Recurrent Unit (GRU), and Recurrent Neural Network (RNN).
• Decentralized multi-agent reinforcement learning with sustainability shaping: Proposes to add sustainability through multi-agent reinforcement learning by using different levels of hierarchical trust-region policy optimization to train agents in Dec-POMDPs, as well as dynamically adjustable reward functions based on such factors as carbon intensity, Reduced Useful Work (RUR), Policy and Reaction Analysis (PAR), and Net Present Value (NPV), which ensures sustainable agent actions.
• Hybrid GA-PSO optimization: Uses genetic algorithms together with particle swarm to optimize agent behavior and imperfect knowledge refinement of price, power dispatch and demand response actuation in real time so as to balance discrete and continuous decision variables.
• Blockchain-enabled coordination: deploys Solidity-based smart contracts over the visible chain of Ethereum with a view to peer-to-peer energy trading, EV Vehicle-to-Grid (V2G) connections and automatic sustainability rewarding, reassuring privacy, protection, and integrity in decentralized working.

1.2. Paper Organization

The rest of the work is structured as follows: Section 2 outlines the literature review. Section 3 provides the research methodology adopted for this work. Section 4 provides a discussion on the Forecasting Layer using the TFT. Section 5 covers the proposed work with MARL for decentralized decision making. The optimization layer using Genetic Algorithms and Particle Swarm optimization is presented in Section 6. The sustainability model and economic feedback discussion is presented in Section 7. The integration of blockchain to enable decentralized grid coordination along with the description of smart contracts for the proposed work are explained in Section 8. The results of the proposed work are presented in Section 9. Lastly, the conclusion of this study is provided in Section 10.

2. Literature Review

The research introduces a novel demand response program for renewable-based microgrids, focusing on tidal and solar energy [16]. It employs a multi-objective problem structure to reduce operating costs and mitigate power transmission risks. Control strategies focus on efficient load supply and battery monitoring. Simulations in MATLAB/Simulink-implemented PV model (Sun Power SPR-250NX-BLK-D) Simulink show that fuzzy logic controllers outperform PID and artificial neural network strategies, confirming the technique’s effectiveness. The work proposes a model using random forest and decision tree regression, to forecast power consumption and renewable generation [17]. The model’s performance is validated using MAE, RMSE, and MAPE metrics. The research proposes a machine learning-based framework to assess DR potential, using dynamic time-of-use tariffs and novel consumption indicators [18]. The framework applies machine learning and self-training for improved accuracy, demonstrating promising results on a public dataset. The RL method, specifically Q-learning, schedules smart home devices to shift usage to off-peak times, incorporating user satisfaction through FR. The study develops a DR model combining price-based and incentive-based approaches, using real data from San Juan, Argentina [19]. The proposed real-time and time-of-use pricing schemes enhance load factor and demand displacement. The work proposes a Home Energy Management System (HEMS) for integrating renewable energy and improving energy efficiency, implemented in a testbed house in Morocco’s Smart Campus [20]. The study presents a modified grey wolf optimizer for creating an energy management system for solar photovoltaic (SPV)-based microgrids and optimizing energy dispatch [21]. The research proposes an AI-based building management system using a multi-agent approach to optimize energy use while maximizing comfort by minimizing environmental parameter errors [22]. Peer-to-peer (P2P) energy trading, driven by decarbonization and digitalization, promises socio-economic benefits, particularly when combined with blockchain. The work proposes a platform that integrates market and blockchain layers to address these challenges, validated through real-world data simulations [23]. The paper focuses on Peer-to-Peer energy trading, addressing scalability, security, and decentralization concerns [24]. It proposes a blockchain scalability solution validated through empirical modelling. The work explores the security benefits offered by blockchain technology [37]. It integrates federated learning with local differential privacy (LDP) and enhances security against attacks which are validated through case studies. The paper proposes an innovative energy system featuring peer-to-peer trading and advanced residential energy storage management [38]. The proposed system facilitates trading energy within the community pool where users can access affordable renewable energy without new production facilities. The proposed demand-side management system effectively reduces power costs and improves energy management efficiency. A comparative analysis of the proposed framework with existing studies in terms of forecasting, optimization, blockchain integration, sustainability shaping, and architectural design is summarized in

Table 1. Comparison of our manuscript with existing works.

Paper	Forecasting	Optimization	Blockchain & EV Scheduling	Sustainability Shaping	Multi-Layered Architecture
[39]	✓(DRL)	✓(basic)	✗	✗	✗
[40]	✗	✗	✗(security only)	✗	✗
[41]	✗	✓(MPPT hybrid)	✗	✗	✗
[42]	✗	✓(Hydrogen opt.)	✗	✗	✗
[43]	✗	✓(evolutionary sizing)	✗	✗	✗
[44]	✓(DRL governance)	✗	✗	✗	✗
[45]	✓(review only)	✗	✗	✗	✗
[46]	✗	✓(EV scheduling)	✗	✗	✗
[47]	✗	✓(ABC hybrid)	✗	✗	✗
[48]	✗	✓(multi-agent EMS)	✗	✗	✗
Proposed Work	✓(TFT multi-horizon)	✓(Hybrid GA+PSO)	✓(Blockchain-secured EV)	✓(MARL + sustainability)	✓(Unified 5-layer)

.

3. Research Methodology

This paper goes further to develop the study of decentralized smart energy systems by utilizing the combined knowledge of artificial intelligence, game-theory, as well as blockchain technology. Multi-layered architecture backs such a method, and it is implemented in five layers: forecasting, decision-making, optimization, sustainability modeling, and blockchain-based implementation, which are all interdependent. Forecasting layer: The layer uses Deep Learning Temporal Fusion Transformer that has special qualities of multi-horizon time-series prediction to predict electricity demand, renewable generation, and EV charging availability. The accuracy of prediction is measured using the Mean Absolute Error (MAE), Root Mean Squared Error (RMSE) and quantile loss, hence providing sufficient accuracy to the attributes of later layers. Decision-making layer: In this layer, the Multi-Agent Reinforcement Learning (MARL) allows the autonomous agents, which represent prosumers, grid operator, EVs, and distributed generator, to communicate in the real environment that is modeled via Decentralized Partially Observable Markov Decision Process (Dec-POMDP).

$$\mathrm{MAE}={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left|y_i-{\widehat{y}}_i\right|,$$

(1)

$$\mathrm{RMSE}=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N}{\left(y_i-{\widehat{y}}_i\right)}^2},$$

(2)

$$\mathrm{QL}(\tau )={\displaystyle \frac{1}{N}}\sum _{i=1}^N\left\{\begin{array}{cc}\tau (y_i-{\widehat{y}}_i),\hfill & \mathrm{if}{y}_i\ge {\widehat{y}}_i,\hfill \\ (\tau -1)(y_i-{\widehat{y}}_i),\hfill & \mathrm{otherwise},\hfill \end{array}\right.$$

(3)

where $y_i$ and ${\widehat{y}}_i$ represent the actual and predicted values, respectively, N is the number of samples, and $\tau \in (0,1)$ denotes the quantile level (typically $\tau =0.5$ for median prediction).

In order to assess the strength and novelty of the suggested multi-layered framework, it was compared with the existing methods of forecasting, decision-making, optimization, and coordination with the help of blockchain. Traditional forecasting networks like Long LSTM and GRU networks have demonstrated a good ability in learning over time, though they are usually weak in terms of explainability and long-term dependencies. Conversely, the TFT adopted by this research includes attention mechanisms as well as a network of variable selection, which offers a better accuracy and explainability. Likewise, centralized control and lack of scalability is a limitation of traditional single-agent reinforcement learning models. The presented MARL model with sustainability shaping allows making decentralized and collaborative decisions, as well as reconciles the aims of local agents with the objectives of global environmental protection. Hybridization of discrete and continuous PSO and pure GA methods have been shown to be superior in convergence speed and flexibility in dynamic grid conditions when combined in this study in their discrete or continuous forms, respectively.

Moreover, the majority of the current blockchain-based microgrids use systems that focus on energy trading or mostly on transaction transparency. By combining the blockchain with the optimization and sustainability layers of the proposed work, the guarantee of the tamper-proof nature of record keeping and the automation of incentives is achieved, which in its turn promotes the renewable integration and the equitable energy interactions. Comprehensively, the integration of TFT forecasting, MARL decision-making, hybrid GA-PSO optimization, and Ethereum-based smart contracts creates a framework that is cohesive, scalable, and has better interpretability, coordination, and sustainability metrics than the previous models. To verify that the observed improvements of the proposed framework over baseline methods are statistically significant, we performed a Wilcoxon signed-rank test on the performance metrics obtained from repeated experimental runs. As summarized in

Table 2. Summary of System Layers, Models, and Outputs.

Layer	Algorithm/Model	Description	Output
Forecasting	Temporal Fusion Transformer (TFT)	Multi-horizon forecasting of energy demand, renewable generation, and EV availability	Predicted time-series inputs
Decision-Making	Multi-Agent Reinforcement Learning (MARL)	Decentralized policy optimization and coordination among agents	Optimized agent policies
Optimization	Hybrid GA–PSO	Discrete–continuous optimization of dispatch, pricing, and EV scheduling	Optimal control parameters
Sustainability Modeling	Reward Shaping with CI, RUR, PAR, NPV	Integrates environmental and financial metrics into decision-making	Sustainability-aligned rewards
Blockchain Layer	Solidity Smart Contracts (Ethereum)	Trustless P2P energy trading and incentive mechanisms	Immutable transaction records

, the proposed architecture integrates forecasting, decision-making, optimization, sustainability modeling, and blockchain layers.

Training entails the implementation of an actor-critic methodology within a centralized training and decentralized execution (CTDE) concept, thus continuing to keep localized decisions and global coordination. Optimization layer: The optimization layer consists of the integration of GA and PSO in order to optimize the policies made by the agent, schedule the dispatch of the energy, and adjust the pricing strategies. The critic receives the global state vector comprising aggregated load, renewable generation forecasts, and agent actions, while actors receive only local observations. The implementation follows the Multi-Agent Proximal Policy Optimization (MAPPO) framework. GA narrows down discrete parameters like the setting of the tariffs and weighting the rewards, whereas PSO narrows down parameters that have continuous nature like the flow of energy and balancing of loads.

The Sustainability modeling layer: Finite time environmental and financial indicators, such are Carbon Intensity (CI), Renewable Utilization Ratio (RUR), Peak-to-Average Load Ratio (PAR), and Net Present Value (NPV) are featured in training and optimization procedures. There is a cycle of dynamic feedback to change functions and terms of contracts as sustainability results change. Blockchain layer: Utilised on the Ethereum framework, the layer uses smart contracts in Solidity code to allow peer-to-peer trade of energy, reward participants on renewable energy production and to record energy transactions in a safe manner. Ethereum network is decentralized trust and transparency. The computational and analytical activities are performed in the Python V3 environment within Jupyter Notebook V6 and Spyder IDE V5, which allows the incremental development of the product, a full visualization of the data, and integration with blockchain testing environments.

4. Energy Forecasting with TFT

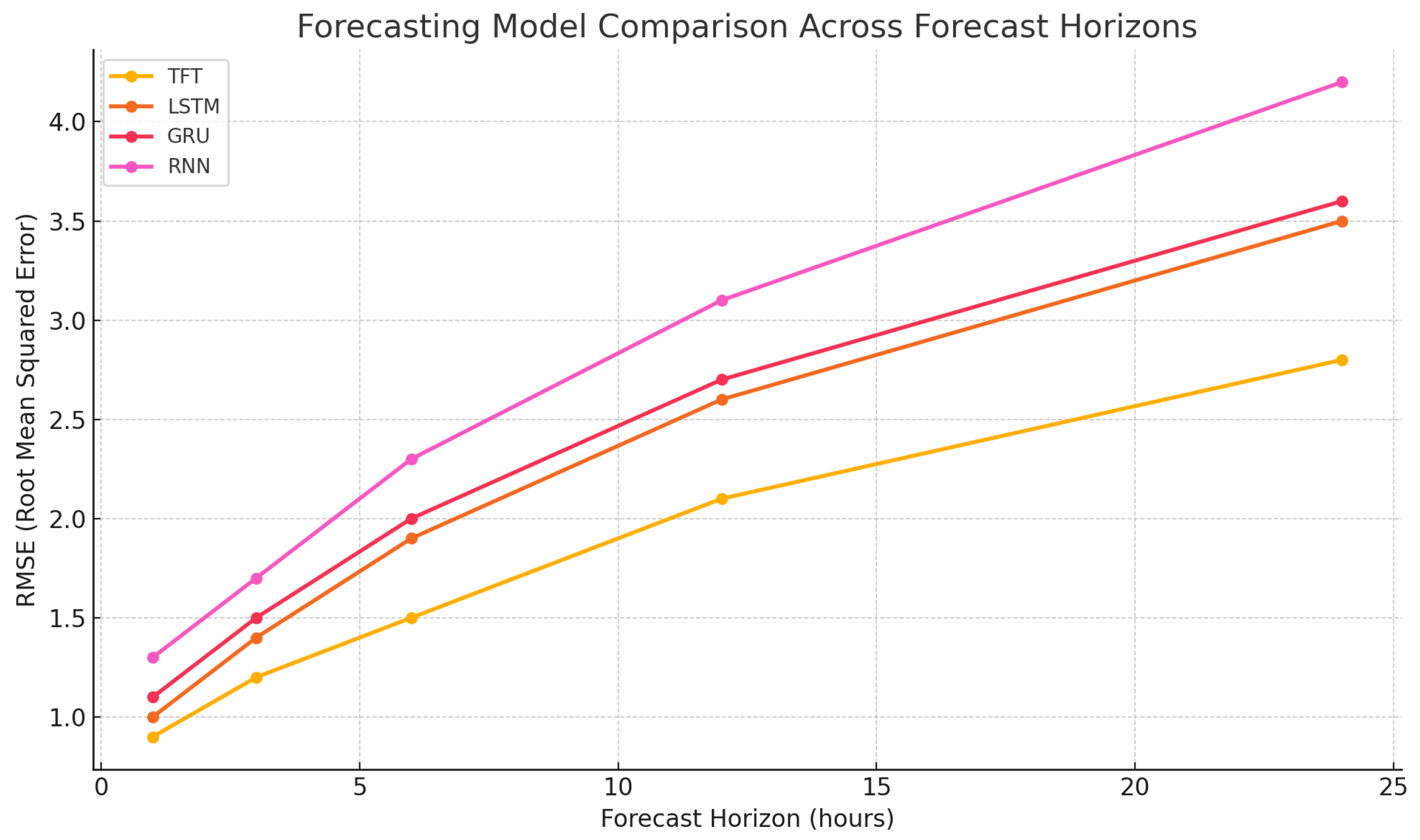
In this section the Forecasting Layer of the smart grid architecture described in this paper uses temporal fusion transformer to use capabilities on multihorizon time- series forecasting. TFT was developed to capture the complex temporal dependencies, which enable it to be used to achieve interpretability, modelling flexibility and offers good predictive power in a wide variety of forecasting tasks. In the optimization of smart grid systems, the Forecasting Layer has a crucial role of generating outlooks of the electricity demand and the solar electricity supply and electric vehicle (EV) availability within the timeline of a foreseeable future. Such predictions are important inputs to various downstream decision-making agents: MARL agents, GA and PSO algorithms, and Smart contract execution. Through this, they facilitate energy transactions on time, load balancing, and activation of a demand response. TFT achieves this by consuming both historical input data, e.g., past energy demand, past weather conditions and solar irradiance measurements, as well as known future covariates, e.g., calendar events, and pricing signals as well as weather forecasts. This internal architecture of the model includes variable selection networks, which locate the most relevant features dynamically, gated residual networks that concentrate on the nonlinear responses of a particular feature combination and maintain the stable flow of a gradient in abundant combination of features as well as temporal self-attention layers which focuses upon the most relevant time steps in an input sequence. Unlike other common recurrent architectures using LSTM or GRU, where processing is done sequentially, and may, thus, fail to perform robustly with long-term dependencies, TFT leverages attention-based processing to access a range of relevant information within the sequence of arrival and, hence, are more capable at capturing short and long-range signals.

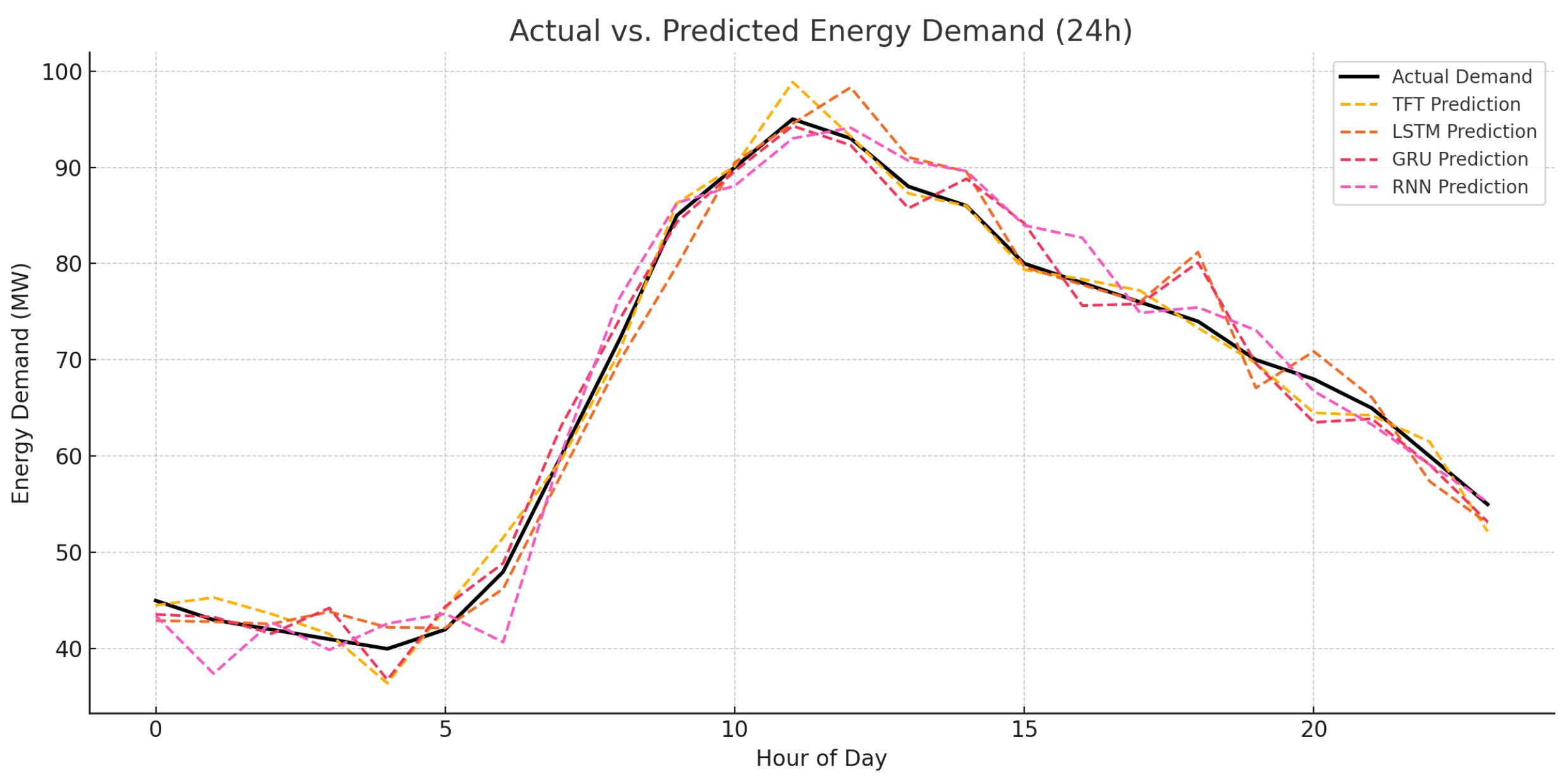
In addition, the ability of TFT to treat with the presence of static covariates enables prosumer-specific or regional factors that have a fixed affect on future behaviour of major effect to be treated. The model provides predictive values of each target variable on the time horizon of interest, which will serve as input to allocation of the energy resources proactively, scheduling of the batteries and charging of EVs. More importantly, TFT also offers interpretability through attention scores, and feature importance scores, hence indicating which variables and time steps had the greatest impact on the output of the prediction. This openness is useful during the process of justifying model behaviour and understanding energy dynamics by the grid operators and the regulators. TFT better forecasting accuracy, mixed input model compatibilities, and explicative capabilities, all of which is well applicable in dynamic, data-rich smart grid environment, informs the choice to use TFT over the conventional forecasting models. As a result, the TFT-based Forecasting Layer is one of the building blocks in the proposed architecture as it facilitates an informed, anticipatory control in a decentralised and sustainable energy system. The TFT is designed for interpretable multi-horizon time-series forecasting. In our architecture, it is used to predict future energy demand, renewable energy generation, and EV charging behavior. Algorithm 1 outlines the enhanced TFT framework for interpretable multi-horizon forecasting of demand, renewable generation, and EV availability.

Algorithm 1 Enhanced Temporal Fusion Transformer (TFT) Forecasting Framework

1: Input: Historical Data $X_{past}$, Future Covariates $X_{future}$, Static Covariates S, Real-time Stream $X_{stream}$   2: Output: Multi-horizon Forecasts ${\widehat{Y}}_{t+1:t+\tau }$ with Explainability   3: procedure Enhanced-TFT-Forecasting   4:       Step 1: Multi-Source Data Fusion   5:       Ingest $X_{past}$ (e.g., load, weather), $X_{future}$ (e.g., calendar events), S (e.g., location), and external sources (e.g., satellite or social data)   6:       Fuse sources using attention-based contextual encoder   7:       Step 2: Forecasting with Interpretable TFT   8:       Use Variable Selection Network to identify relevant features dynamically   9:       Apply Gated Residual Networks (GRNs) for nonlinear modeling 10:       Use Temporal Self-Attention to capture short- and long-term dependencies 11:       Generate probabilistic forecasts ${\widehat{Y}}_{t+1:t+\tau }$ 12:       Step 3: Explainability Integration 13:       Extract attention weights and feature importances for model interpretability 14:       Generate real-time explanations for operators and regulators 15:       Step 4: Adaptive Online Learning 16:       if New Data $X_{stream}$ available then 17:             Update model weights via online learning (e.g., gradient descent on streaming window) 18:       end if 19:       Step 5: Output Forecasts and Explanations 20:       Return ${\widehat{Y}}_{t+1:t+\tau }$ and interpretability metrics 21: end procedure

The system architecture presented in Figure 1, introduces a layered framework of intelligent and sustainable microgrid energy management by combining artificial intelligence based forecasting, multi-agent decision making, optimization and blockchain based security. At the bottom is the edge and field layer which gathers real-time data from distributed energy resources, electric vehicles, sensors and smart meters. This layer facilitates the smooth collection of data via protocols such as MQTT and IoT based communication to facilitate the raw information required for the higher level decision-making. Above this, the data ingestion and integration layer provides aggregation and preprocessing and integration of heterogeneous data sources streams by harmonizing various data inputs such as weather conditions, load demand, energy prices, and grid states, so that they can provide structured and accessible data sets. The forecasting layer uses the temporal fusion transformer to precisely forecast the renewable generation, EV charging demand, and load variations to enable proactive management of the energy resources and demand by anticipating unknowns in renewable resources and consumption patterns.

The decision layer is driven by multi-agent reinforcement learning, where autonomous agents such as prosumer agents, EV agents, grid operator agents, and renewable generator agents coordinate their actions in order to optimize energy distribution and demand response and EV scheduling against dynamic environments. The optimization layer takes advantage of a hybrid genetic algorithm-particle swarm optimization approach to optimize the global scheduling and resource allocation tradeoff between exploration and exploitation to find near-optimal solutions for the complex microgrid problems. Finally, the blockchain and smart contract layer ensures transparency, security and trust in peer-to-peer energy transactions and scheduling of EVs by deploying decentralized contracts to ensure fair participation, data integrity, and tamper-resistant data record-keeping. This holistic AI-driven framework is very well combining forecasting, decision making, optimization and blockchain to provide sustainable, resilient, and intelligent microgrids energy management.

5. Multi-Agent Reinforcement Learning for Grid Decision-Making

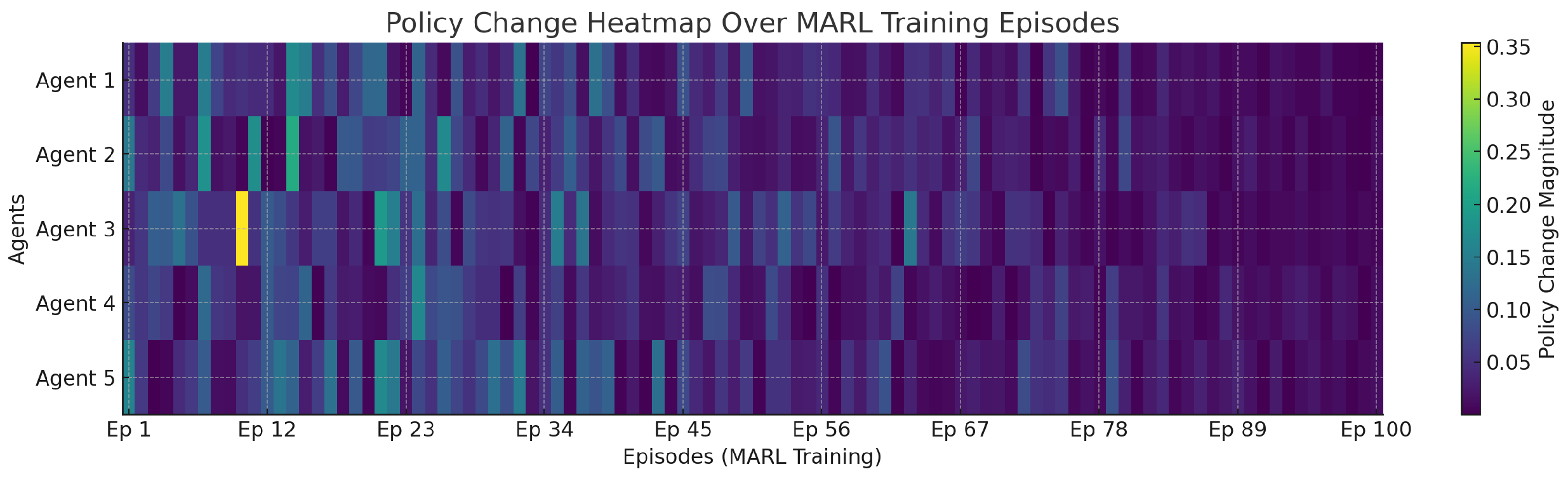
In section, the key concept of the proposed smart-grid framework, MARL, is presented as the decentralised part of decisions. MARL can be thought of as an extension of conventional reinforcement learning (RL) to a task with multiple autonomous agents acting and learning simultaneously in the same environment: through MARL, each agent can interact with its peers and with the system dynamics at large, in order to maximise the long-term reward. Contrary to the centralised or single-agent RL, MARL promotes localised scalable and adaptive local real-time policies where the centralised policy with the RL lacks scale habits and poor resolution of the highly coupled interdependencies existing dynamic within the players of the smart-grid context. These benefits are especially clear in the smart-grid context in which consumers, producers, electric-vehicle owners and grid operators can be independent of each other but where coordination is of paramount importance to maintain stability, efficiency and sustainability. They also include a number of different forms of agents, including prosumer agent (to represent households or buildings capable of consumption, generation and storage), an EV agent (administrate EV charging and discharging procedures including vehicle-to-grid (V2G) processes), grid-operator agent (that monitor system stability units like frequency and voltages) and renewable generator agents (that optimise renewable resources like solar and wind) within the framework. Vehicle-to-Grid (V2G) refers to bidirectional energy exchange between electric vehicles and the power grid. Within our MARL-based system, EV agents determine optimal charge/discharge schedules based on price signals and grid stress, enabling demand response and stabilizing renewable fluctuations.

Agents observe part of the situation, e.g., prices, or local load profiles or weather predictions, and make decisions involving buying or selling energy, load-shifting, or responding to demand response (DR) events. The Grid Operator Agent represents the supervisory control entity responsible for maintaining voltage and frequency stability, monitoring distributed resources, and enforcing network-level constraints during decentralized coordination. MARL allows load balancing by causing agents to learn consistent patterns so that load can be balanced in grids and distribution of consumption during peak hours can also be redirected by the mechanisms of prediction that are applied usually by the model TFT. In demand-response case, the agents modify behaviour to alleviate grid stress to a dynamic pricing incentive or smart-contract mechanism. In the case electric-vehicle and V2G involvement, EV agents decide when to charge or dump with regards to state-of-charge of batteries, anticipated energy prices and DR events, and therefore help in making the grid stable enough and maximise their personal profits. MARL mathematical construct takes the form of a Decentralised Partially Observable Markov Decision Process (Dec-POMDP) where the policy of each agent takes local observations as inputs and act as learners of the actor-critic methodology.

The critic approximates values of action across the global state-action pairs and the actor improves its policy by gradients based on this evaluation. Rewards are used to reinforce local MARL agent behavior to reflect global goals carbon reduction and integration of renewable electrical energy by molding them into the sustainability indicators. This combination of decentralised learning, local autonomy and globally-mediated optimisation makes MARL powerful and flexible enough to proceed the management of the dynamic, distributed nature of smart-grid operations. In our decentralized smart grid framework, multiple autonomous agents interact in a shared environment and learn to optimize energy-related objectives such as load balancing, peak shaving, and V2G coordination. This is formalized using the framework of MARL. Algorithm 2 presents the proposed MARL approach for decentralized grid decision-making with sustainability shaping.

Algorithm 2 Enhanced Multi-Agent Reinforcement Learning (MARL) Framework

Require:  Environment $\mathcal{E}$, agents $\mathcal{A}=\{a_1,a_2,\dots ,a_n\}$, initial policies ${\pi }_i$, sustainability metrics $\mathcal{M}$, learning rate $\eta$, equilibrium threshold $\epsilon$ Ensure:  Optimized agent policies ${\pi }_i^{\ast }$ aligned with sustainability goals   1: Initialize centralized critic $Q_{\varphi }(s,a)$ and global reward model R   2: Initialize trust scores $T_i\leftarrow 1.0$ for all agents   3: for each episode $k=1,2,\dots ,K$ do   4:       for each time step t do   5:             for each agent $a_i\in \mathcal{A}$ do   6:                   Observe local state $o_i$   7:                   Select action $a_i\sim {\pi }_i(a_i|o_i)$   8:                   Execute $a_i$ in environment $\mathcal{E}$   9:                   Receive local reward $r_i$ and next observation $o_i^{\prime }$ 10:                   Update trust score: $$T_i=1-{\displaystyle \frac{|R_i-\overline{R}|}{{\sigma }_R+ϵ}}$$ where $R_i$ is agent i’s mean episodic return, and $\overline{R},{\sigma }_R$ are the global mean and standard deviation. 11:             end for 12:             Compute global reward $r_t=R({\mathbf{a}}_t,{\mathbf{s}}_t,\mathcal{M})$ 13:             Update critic $Q_{\varphi }(s,a)$ via temporal-difference (TD) learning 14:             for each agent $a_i$ do 15:                   Update actor using policy gradient (MAPPO framework): $${\theta }_i\leftarrow {\theta }_i+\eta {\nabla }_{{\theta }_i}\log {\pi }_i(a_i|o_i)Q_{\varphi }(s,a)$$ 16:                   Apply sustainability shaping to rewards: $$r_i\leftarrow r_i+{\alpha }_{1}RUR-{\alpha }_{2}CI-{\alpha }_{3}PAR+{\alpha }_{4}NPV$$ 17:             end for 18:             if meta-learning enabled then 19:                   Aggregate high-trust agents’ gradients using MAML: $${\pi }_{\mathrm{meta}}\leftarrow \mathrm{Adapt}(\{{\pi }_i\mid T_i>{\tau }_T\})$$ 20:                   Update low-performing agents: ${\pi }_i\leftarrow \mathrm{FineTune}({\pi }_{\mathrm{meta}},o_i)$ 21:             end if 22:       end for 23:       Evaluate coordination stability: $$\mathrm{MeanRegret}={\displaystyle \frac{1}{n}}\sum _{i=1}^n\left(R_i^{\ast }-R_i\right)$$ 24:       if $\mathrm{MeanRegret}<\epsilon$ then 25:             break                                                                            ▷ Approximate Nash equilibrium achieved 26:       end if 27: end for 28: return Final policies ${\pi }_i^{\ast }$ with sustainability alignment

6. Optimization Layer: Hybrid GA-PSO Approach

Optimization Layer combines GA and PSO to add the flexibility and effectiveness to the decision mechanism present in the smart grid. The layer works in addition to MARL system and forecasting modules and enhances control actions and strategic parameters. Genetic Algorithms are used to model genetic Algorithms have been used to learn to maximise agent reward functions, determine dynamic pricing strategy and schedule EV charging. In reward shaping, the weightage of these sustainability metrics, such as carbon intensity, peak loads reduction, and use of renewable energy forms, which is calibrated by GA, sees to it that the behavioral limits of the agent are in line with grid level goals. GA can be used in tariff development in the context of the evolution of pricing strategies that can influence an attractive consumption structure, e.g., during off-peak activity, or use of solar energy. It also optimises charger schedules of EVs by creating variations of time and power levels that suit the minimum cost and stabilize the grid. Particle Swarm Optimization, on the contrary, uses social behavior in nature (particularly bird flocking) to provide real time continuous optimization. PSO is especially applicable to load optimization on dispatch generation, as in the continuous adjustment of power flows to obtain optimal holding of supply-demand equilibrium with minimum losses, and to optimal use of solar generation, again shifting variables dynamically to optimize generation so as to support load pattern and condition of storage. Also, PSO is a decentralized control approach where grid terminals are controlled by adjusting the control parameters for correcting the frequency and voltages. The GA-PSO hybrid benefits from both the PSO and GA approaches. On one hand, the global exploration and discrete optimization power of GA is added into the mix with the rapid convergence and precise fiddling that PSO can do on the continuous spaces. Such synergy helps the optimization layer to deal with problems that are complicated, non-convex and dynamic in nature when it comes to discrete and continuous variables.

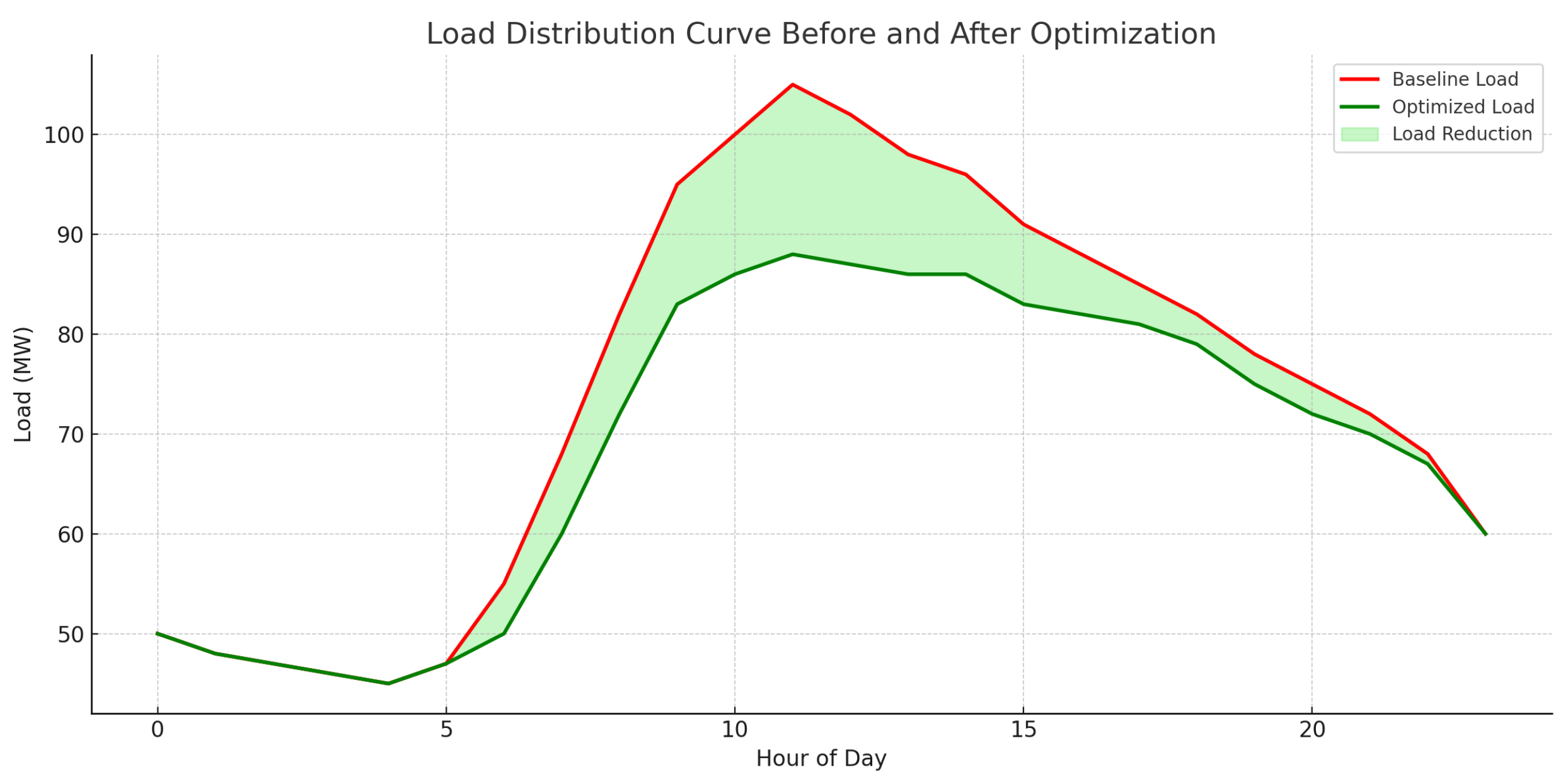
EV charging plans are important in improving grid stability, lowering costs of operations, and also increasing the use of renewable energy. The implementation of EV charging and discharging by strategically rearranging the process of EV charging and discharging with the proposed hybrid GA-PSO optimization allow shifting the energy demand outside of the peak hours, reducing the load pressure on the utility grid and decreasing the ratio of peak loads to average ones. Also, controlled V2G operations can allow EVs to feed stored energy back to the grid when using significant amounts of energy, essentially serving as distributed energy storage units. Such a two-way communication not only contributes to the control of voltage and frequency but also utilizes the maximum amount of renewable energy produced during off-peak. The optimization of charging rates hence saves money on energy consumption of the consumers, increases grid stability, and helps promote sustainable energy management by balancing EV activity with dynamic pricing indicators and renewable supply predictions based on the forecasting layer.

Unlike the conventional optimization technique, which may be either static or centrally synchronized and coordinated, the hybrid technique of the GA - PSO technique is dynamic adjusting to varying grid conditions, agent behaviors and external interactions such as weather forecasts and pricing forecasts. What makes it particularly stand out is that it is able to co-evolve multiple objectives with constraints and adaptively tune its MARL hyperparameters, contract thresholds and energy scheduling rules. As a result, the hybrid solution will be able to encourage the flexibility, performance and sustainability of the decentralized grid control framework and is more suitable for tackling the complexity of advanced smart energy systems compared to the individual optimization approaches. To improve the learning and decision-making process of agents we use GA and PSO across our architecture. These evolutionary optimization techniques are applied to reward shaping, parameter tuning for MARL agents, and energy dispatch and storage control optimization as well as demand response incentives optimization.

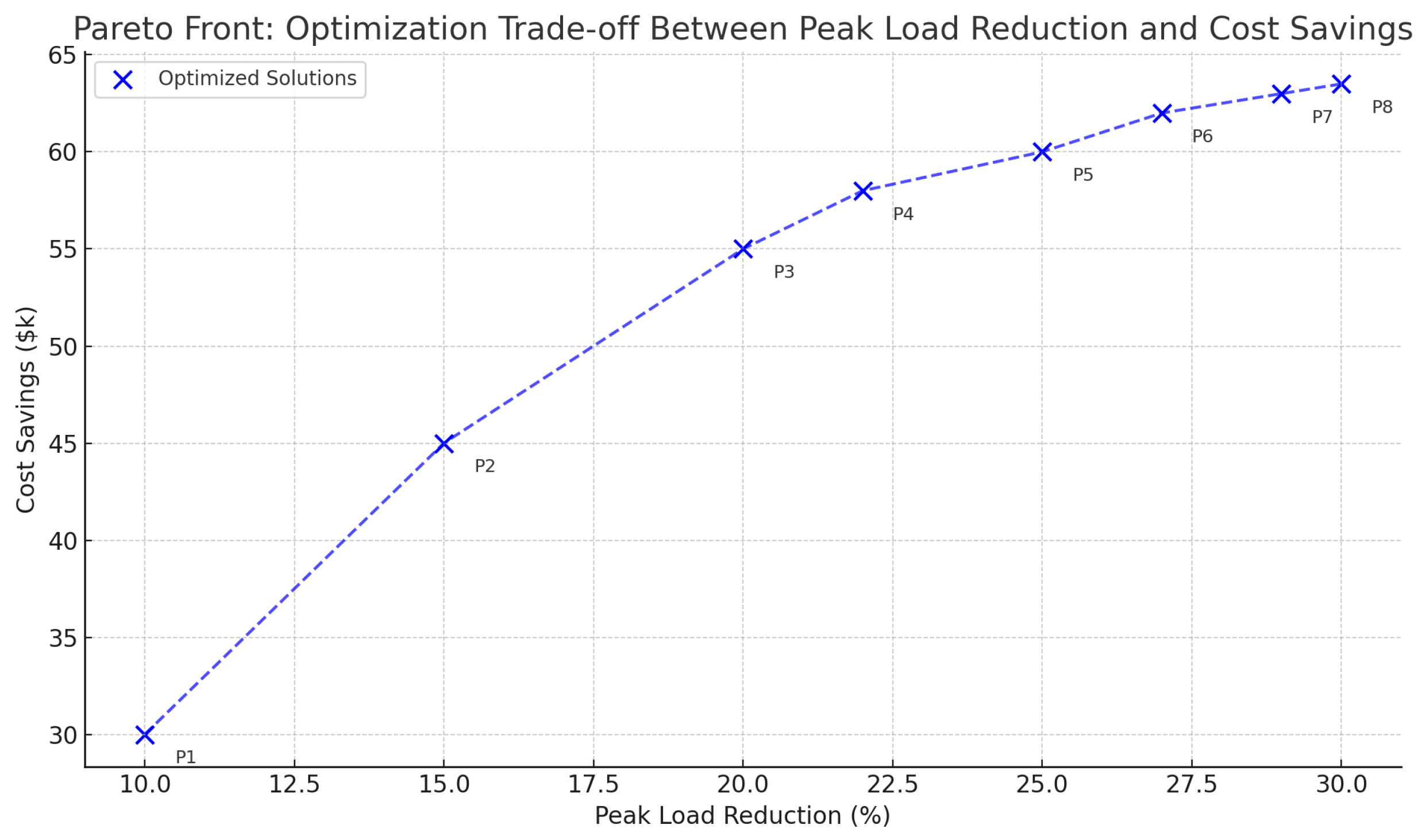
Numerous investigations have been conducted on using GA in combination with PSO to harness the capabilities of Genetic Algorithms in exploration and Particle swarm optimization in exploitation. Nevertheless, there are three key differences in our integration, which are also reflected in the comparative and sensitivity analysis. To begin with, instead of a fixed combination, our GA-PSO uses dynamic switching with respect to population diversity. These convergence graphs show that GA-PSO is not only able to attain the final objective lowest but also attains within 1 percent of its optimum in less time compared with the baselines. This tendency demonstrates its flexibility to change: once diversity reaches a certain limit, GA-inspired operators begin anew to bring variability to the process, avoiding stasis. Second, we combine surrogate modeling of fitness assessments with less computational cost per iteration. This is substantiated by the runtime comparison, when GA-PSO is competitive though more expensive per-iteration when compared to PSO, due to lower overall convergence of the algorithm. Lastly, our framework promotes real-time adaption to grid variation, which was confirmed in IEEE microgrid benchmarks.

In contrast to the static hybrids, the GA-PSO optimizer adjusts the value of crossover, mutation, and inertia weights dynamically in reaction to demand and renewable variations, as shown by the sensitivity plots. All these innovations combined render our GA-PSO not just a hybrid, but an adaptive and context-sensitive optimizer suited to the changing energy systems. Algorithm 3 details the main controller design for hybrid GA–PSO optimization of smart grid operations. Algorithm 4 describes the surrogate-model-based fitness evaluation used to reduce computational overhead during optimization. Algorithm 5 specifies the adaptive genetic operators applied for discrete parameter refinement in the GA–PSO framework. Algorithm 6 explains the PSO-based particle update procedure for continuous optimization of load and dispatch variables. Algorithm 7 implements reactive power control using the hybrid GA–PSO optimizer to minimize voltage deviations and reactive losses. Algorithm 8 introduces TFT-informed EV scheduling with GA–PSO, optimizing charging and discharging under grid and renewable constraints.

Algorithm 3 Main Controller: Hybrid GA–PSO Optimization

Require:  Initial population $P_0$, particle set $S_0$, grid data $D_t$, objectives $\mathcal{F}$, max generations $G_{max}$ Ensure:  Optimized non-dominated set $P^{\ast }$   1: Initialize Gaussian Process surrogate $\widehat{f}$ (SE/RBF kernel) using historical data   2: $g\leftarrow 0$   3: while not converged and $g<G_{max}$ do   4:       EvaluateFitness$(P_g,\widehat{f},\mathcal{F})$   5:       Compute normalized fitness proportions ${\{p_i\}}_{i=1}^N$; diversity (Shannon entropy): $$D=-\sum _{i=1}^N{p}_i\log (p_i)$$   6:       if $D<0.4$ then   7:             PSOUpdate$(S_g)$                                       ▷ Diversity restoration/exploitation   8:       else   9:             GeneticOperators$(P_g)$                                                     ▷ Exploration via GA 10:       end if 11:       Apply Pareto dominance and constraint repair (CI, RUR, PAR, NPV) 12:       if grid conditions shift in $D_t$ then 13:             Adapt objective weights dynamically 14:       end if 15:       Log interpretability metrics for top solutions 16:       $g\leftarrow g+1$ 17: end while 18: return Best non-dominated solutions $P^{\ast }$

Algorithm 4 EvaluateFitness with Gaussian Process Surrogate and Confidence Check

Require:  Population P, GP surrogate $\widehat{f}$ (SE kernel), objectives $\mathcal{F}$ Ensure:  Updated surrogate $\widehat{f}$ and fitness values   1: for each candidate $x\in P$ do   2:       Predict $\mu (x),{\sigma }^2(x)\leftarrow \widehat{f}(x)$   3:       if ${\sigma }^2(x)<0.01$ then   4:             Use surrogate fitness $\widehat{f}(x)\leftarrow \mu (x)$   5:       else   6:             Evaluate true objectives $f(x)$ via $\mathcal{F}$   7:             Update surrogate with $(x,f(x))$ (e.g., GP regression update)   8:       end if   9: end for

Algorithm 5 GeneticOperators

1: procedure GeneticOperators(P)   2:       Select parents using tournament or roulette selection   3:       Apply crossover to generate offspring   4:       Apply mutation with adaptive rate   5:       Replace least fit individuals to form new population   6: end procedure

Algorithm 6 PSOUpdate

1: procedure PSOUpdate(S)   2:       for each particle i do   3:             Update velocity: $$v_i\leftarrow \omega v_i+c_1{r}_1(p_i-x_i)+c_2{r}_2(g-x_i)$$   4:             Update position: $$x_i\leftarrow x_i+v_i$$   5:             Update personal best $p_i$ and global best g   6:       end for   7: end procedure

Algorithm 7 Reactive Power Control using Hybrid GA-PSO Optimization

Require:  Load flow model, bus voltage limits $V_{min}$, $V_{max}$, initial population size N, max iterations $G_{max}$ Ensure:  Optimal reactive power dispatch $Q^{\ast }$   1: Initialize population of N candidate solutions ${\{Q_i\}}_{i=1}^N$ for reactive power generation at PV and generator buses   2: Initialize PSO velocities ${\{v_i\}}_{i=1}^N$ and personal bests $p_i\leftarrow Q_i$   3: Set global best $g\leftarrow \arg \min f(Q_i)$ based on fitness function   4: for generation $g=1$ to $G_{max}$ do   5:       for each individual $Q_i$ in population do   6:             Evaluate power flow using $Q_i$   7:             Compute fitness $f(Q_i)$:       Minimize total voltage deviation $\sum |V_i-V_{ref}|$       Minimize total reactive losses $Q_{loss}$       Satisfy: $V_{min}\le V_i\le V_{max}$, $Q_{min}\le Q_i\le Q_{max}$   8:             if $f(Q_i)$ better than $f(p_i)$ then   9:                   Update personal best $p_i\leftarrow Q_i$ 10:             end if 11:       end for 12:        Update global best $g\leftarrow \arg \min f(p_i)$ 13:       for each particle $Q_i$ do 14:             Update velocity: 15: $v_i\leftarrow \omega v_i+c_1{r}_1(p_i-Q_i)+c_2{r}_2(g-Q_i)$ 16:             Update position: $Q_i\leftarrow Q_i+v_i$ 17:             Apply mutation or crossover (GA operator) with probability $P_{GA}$ 18:             Enforce constraints on $Q_i$ 19:       end for 20: end for         return Optimal reactive power settings $Q^{\ast }\leftarrow g$

Algorithm 8 TFT-Informed EV Scheduling with Hybrid GA–PSO

Require:  EV set $\mathcal{E}$, time horizon $\mathcal{T}$, historical data ${\mathcal{D}}_{\mathrm{hist}}$, charger and feeder limits, GA–PSO parameters $(N,G_{max},\omega ,c_1,c_2,P_{GA})$ Ensure:  Rolling optimal charging/discharging schedule $P^{★}$   1: Train or load a Temporal Fusion Transformer (TFT) using ${\mathcal{D}}_{\mathrm{hist}}$   2: At each control step $t_0$, use TFT to forecast:   • Electricity prices ${\widehat{\pi }}_t$   • Net load ${\widehat{d}}_t$   • Renewable availability ${\widehat{r}}_t$   • EV arrivals/departures ${\widehat{a}}_{e,t},{\widehat{d}}_{e,t}$   3: Encode a candidate solution X as a charging matrix $P_{e,t}$ for $e\in \mathcal{E},t\in [t_0,t_0+H]$   4: Initialize a population of N feasible schedules ${\{X_i\}}_{i=1}^N$ (guided by TFT forecasts)   5: Initialize PSO velocities ${\{V_i\}}_{i=1}^N$ and set personal bests $P_i\leftarrow X_i$   6: Set global best $G\leftarrow \arg \min f(X_i)$   7: for generation $g=1$ to $G_{max}$ do   8:       for each individual $X_i$ do   9:             Simulate EV SoC trajectory under $X_i$ 10:             Evaluate objective $f(X_i)$ including:   • Energy cost using ${\widehat{\pi }}_t$   • Peak demand ${max}_t{\sum }_e{P}_{e,t}$   • Battery degradation proxy   • Penalties for SoC violation, feeder limits, renewable mismatch 11:             if $f(X_i)<f(P_i)$ then 12:                   Update personal best $P_i\leftarrow X_i$ 13:             end if 14:       end for 15:       Update global best $G\leftarrow \arg \min f(P_i)$ 16:       for each particle $X_i$ do 17:             Update velocity $V_i$ and position $X_i$ using PSO rules 18:             With probability $P_{GA}$ apply GA operators:   • Crossover between two individuals   • Mutation on random charging slots 19:             Repair constraints: enforce bounds, feeder limits, and SoC feasibility 20:       end for 21: end for 22: Execute the first-slot charging decisions from G 23: Update ${\mathcal{D}}_{\mathrm{hist}}$ with new data and fine-tune TFT 24: Advance horizon and repeat until all EVs are scheduled         return Final rolling schedule $P^{★}$

7. Sustainability Modeling and Economic Feedback

The section indicates how environmental, social and financial factors are incorporated systematically into the optimization and control framework of the suggested framework. The elements of sustainability like the use of renewable sources of energy, carbon intensity, and fairness indices are not considered as post-analysis measures but embedded in the optimization goals and reward systems of the hybrid GA-PSO and multi-agent reinforcement learning layers. The proposed system guarantees that every scheduling cycle is pursuing operational efficiency, fair access, and reduction of emissions at the same time. The Renewable Utilization Ratio quantifies the efficiency with which renewable resources, like solar and wind, are taken into consideration, which directly promotes SDG 7 by making renewable energy more accessible and affordable and cleaner. MARL equity indices integrated into the MARL process would ensure that small or underprivileged prosumers receive their share of the cake, which would resolve distributional justice aspect of energy transitions. Smart contracts enhance this equality by automating peer-to-peer trading policies, stopping market distortions, and making the market transparent. Carbon intensity is one of the key optimization instruments of the prosed framework, as it aligns the framework with SDG 13, and prioritizes solutions that reduce greenhouse gas emissions as the system grows. The convergence and scalability studies verify the existence of a decreasing carbon intensity with increasing agent count, which shows that decentralized intelligence can improve climate performance without undermining efficiency.

The blockchain layer goes further, allowing tokenized sustainability payments such as renewable energy certificates and carbon credit schemes, so that emission cuts and clean energy donations are verifiable and tradeable. The use of tokens allows ecological performance to become directly linked with economic value and help in creating a positive feedback loop in which any sustainability success is turned into a concrete financial incentive. The economic response creates greater behavioural convergence, and encourages prosumers and operators to become greener. Bringing technical metrics in balance with financial incentives, and tying each to SDG 7 and SDG 13, the framework shows a holistic strategy in which the optimization, sustainability, and market mechanisms are mutually supporting and thus converting the functioning of microgrids into a means of both affordable energy access and climate action.

7.1. Sustainability Metrics and Feedback Loop

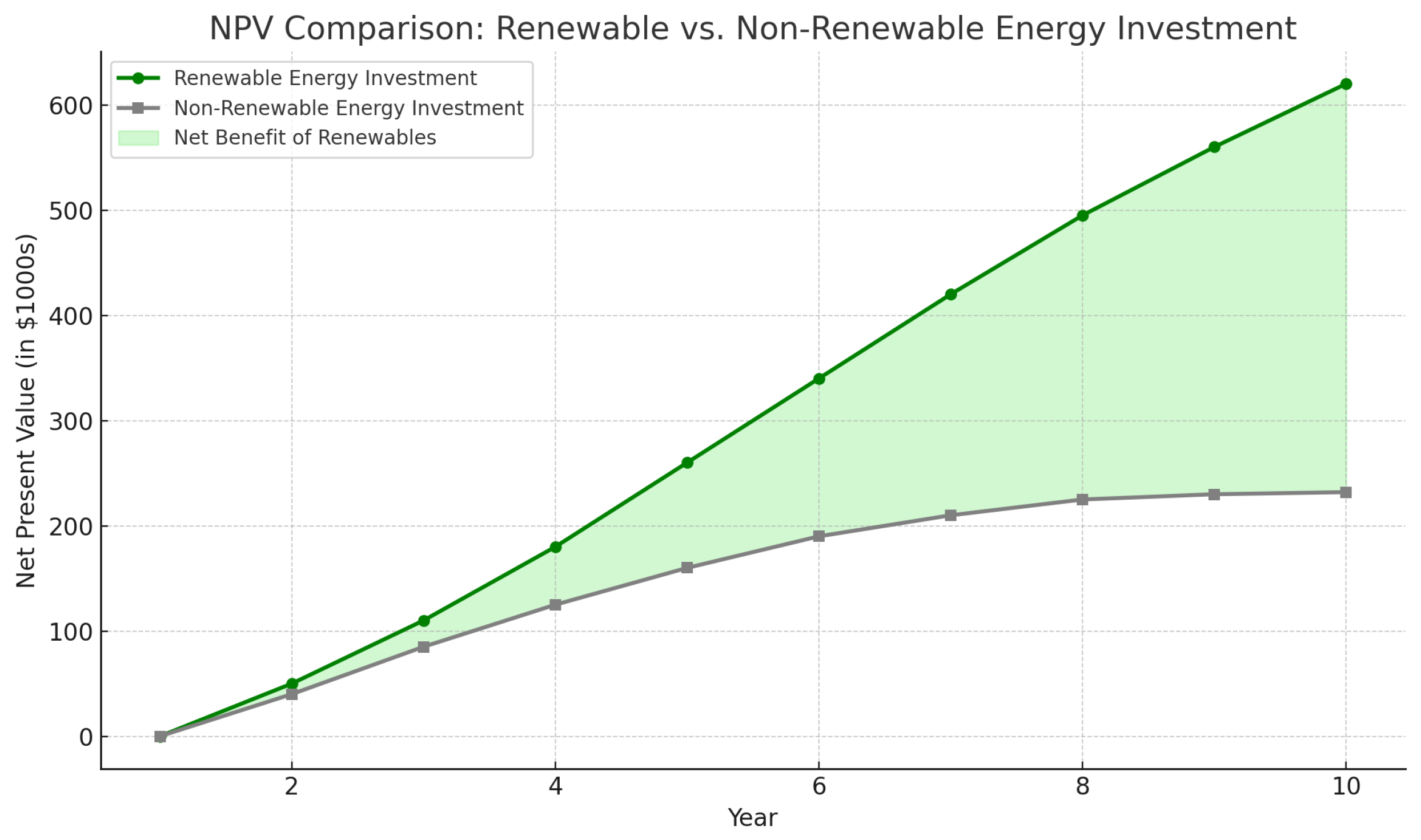
The section reviews the sustainability metrics and feedback loop as a central mechanism that makes sure that not only the smart grid operates effectively but also contributes to reaching long-term environmental and economic goals. In modern energy systems, merely optimization of operational regime costs or throughput is not satisfactory. It is suggested that, sustainability should be clearly measured and put in the decision-making framework. The four metrics, namely: Carbon Intensity, Peak-to-Average Load Ratio, Renewable Integration Percentage and financial measures such as Levelized Cost of Energy (LCOE) and Net Present Value (NPV) altogether describe the environmental impact that the grid has, the smooth functioning of the grid, the reliance on renewable sources, and cost-effectiveness of the grid, respectively. Carbon intensity measures the volume of CO2 released per unit of the consumed electricity, coupling the climate consequences and energy choices. The Peak-to-Average Load Ratio presents the smoothness of the load profile with an indicator of the ratio of the peak demand against average demand, and a smaller number results in a flatter and more steady demand curve that eases the infrastructure burden. Renewable Integration Percentage is the ratio of the amount of total energy consumption that comes as renewable to clean energy targets. LCOE gives an average long-term cost of electricity produced in kilowatts, and allows comparing the costs of conventional energy sources and renewable sources, but NPV measures the financial payback of energy projects, which are accumulating benefits and costs years into the future. Notably, none of these metrics works in isolation, and they are incorporated into MARL reward functions. As an example, agents that minimize the peak load or optimize the utilization of sun (solar energy) will be rewarded with even higher accumulated rewards, which encourages to be green. At the end of any given episode all the agents efforts towards these global measures are screened and policy gradients or reward weights changed accordingly.

The adaptive mechanism holds the stance that the agents always update their strategies to the changing sustainability fostering goals in spite of dynamic changes in the grid condition, weather, or user behavior. The feedback loop also determines contract incentives, rewards being provided in tokens to activities that reduce carbon intensity or increase the use of renewables. In completing this loop between the agents of measurement and the agents of decision-making, they are able to come to dynamic and data-driven harmony between the action of the local agent and the global goals of sustainability. Finally, the framework encourages efficiency in operations, an environmental conscience and economic stability, transforming sustainability as an outcome of computation to be one of the fundamental computation objectives. To ensure alignment between agent behavior and long-term grid sustainability, we define a set of measurable sustainability metrics. These metrics influence reward shaping in MARL, optimization constraints in GA/PSO, and execution conditions in smart contracts. Algorithm 9 defines the sustainability-driven economic feedback loop for MARL agents, integrating environmental and financial metrics into rewards.

Algorithm 9 Sustainability-Driven Economic Feedback Loop for MARL Agents (with Equity and Fairness Boost)

Require:  Agents $\mathcal{A}=\{a_1,\dots ,a_n\}$; metrics $\mathcal{M}=\{\mathrm{CI},\mathrm{RUR},\mathrm{PAR},\mathrm{NPV}\}$; learning rates $\{{\eta }_i\}$; contracts $\mathcal{C}=\{c_1,\dots ,c_J\}$; discount rate r; benefits ${\{B_t\}}_{t=0}^T$; monetary costs ${\{{\mathrm{Cost}}_t\}}_{t=0}^T$; fairness sensitivity $\lambda >0$; boost cap $b_{max}\ge 1$; tolerance $\epsilon$; small $ϵ>0$ Ensure:  Updated policies $\{{\pi }_i\}$, updated $\mathcal{C}$, sustainability-aligned behavior   1: for episode $k=1,2,\dots$ do   2:       Step 1: Agent Interaction and Learning Data   3:       for $t=0,\dots ,T$ do   4:             for each $a_i\in \mathcal{A}$ do   5:                   Observe $o_{i,t}$, take $a_{i,t}\sim {\pi }_i(·|o_{i,t})$, get $r_{i,t}$, $o_{i,t+1}$; store in buffer ${\mathcal{B}}_i$   6:             end for   7:       end for   8:       Step 2: Compute Episode-Level Sustainability Metrics   9:       Define totals: energy $E_k$, renewables $R_k$, peak load $L_k^{max}={max}_t{L}_t$, avg load ${\overline{L}}_k=\frac{1}{T+1}{\sum }_{t=0}^T{L}_t$, greenhouse gas ${\mathrm{C}\mathrm{O}2}_k$ 10:       ${\mathrm{CI}}_k\leftarrow {\displaystyle \frac{{\mathrm{C}\mathrm{O}2}_k}{E_k}}$;    ${\mathrm{RUR}}_k\leftarrow {\displaystyle \frac{R_k}{E_k}}$;    ${\mathrm{PAR}}_k\leftarrow {\displaystyle \frac{L_k^{max}}{{\overline{L}}_k}}$ 11:       ${\mathrm{NPV}}_k\leftarrow {\sum }_{t=0}^T{\displaystyle \frac{B_t-{\mathrm{Cost}}_t}{{(1+r)}^t}}$ 12:       Step 3: Reward Shaping and MAPPO Update 13:       For each transition $(o_{i,t},a_{i,t},r_{i,t},o_{i,t+1})$, define shaped reward $${\tilde{r}}_{i,t}^{(k)}=r_{i,t}+{\alpha }_1{\mathrm{RUR}}_k-{\alpha }_2{\mathrm{CI}}_k-{\alpha }_3{\mathrm{PAR}}_k+{\alpha }_4{\mathrm{NPV}}_k.$$ 14:       Estimate advantages ${\widehat{A}}_{i,t}$ (GAE) from ${\tilde{r}}_{i,t}^{(k)}$ and update MAPPO surrogate; apply clipping and entropy regularization. 15:       Step 4: Equity Scores and Fairness Boost (for next episode) 16:       Let $E_i^{\mathrm{access}}\in [0,1]$ be normalized energy access for i, and ${\overline{E}}^{\mathrm{access}}$ the mean. 17:       for each $a_i$ do $${\mathrm{Equity}}_i=1-{\displaystyle \frac{\left|E_i^{\mathrm{access}}-{\overline{E}}^{\mathrm{access}}\right|}{max({\overline{E}}^{\mathrm{access}},ϵ)}}\in [0,1]$$ $${\mathrm{boost}}_i=\min \left(b_{max},1+\lambda (1-{\mathrm{Equity}}_i)\right)$$ 18:             Apply to next episode: ${\alpha }_{j,i}^{\mathrm{next}}\leftarrow {\mathrm{boost}}_i·{\alpha }_j$ or ${\eta }_i^{\mathrm{next}}\leftarrow {\mathrm{boost}}_i·{\eta }_i$ 19:       end for 20:       Step 5: Smart Contract Adjustment (Token Incentives) 21:       for each $c_j\in \mathcal{C}$ with scope ${\mathcal{S}}_j\subseteq \mathcal{A}$ do $${\mathrm{EquityScore}}_j={\displaystyle \frac{1}{|{\mathcal{S}}_j|}}\sum _{i\in {\mathcal{S}}_j}{\mathrm{Equity}}_i,c_j^{\mathrm{reward}}={\gamma }_1{\mathrm{RUR}}_k-{\gamma }_2{\mathrm{CI}}_k+{\gamma }_3{\mathrm{EquityScore}}_j$$ 22:             Commit $c_j^{\mathrm{reward}}$ on-chain (subject to a rate limiter/governance policy) 23:       end for 24:       Step 6: System-Level Fairness Check (Optional) 25:       $F_k\leftarrow {\displaystyle \frac{1}{n}}{\sum }_i{\mathrm{Equity}}_i$ (or Jain’s index/min) 26:       if $F_k<F_{\mathrm{thr}}$ then 27:             Increase redistribution next episode: $\lambda \leftarrow \lambda (1+\delta )$ or raise ${\gamma }_3$ 28:       end if 29:       Step 7: Convergence to Sustainability 30:       ${\mathbf{M}}_k\leftarrow [{\mathrm{RUR}}_k,{\mathrm{CI}}_k,{\mathrm{PAR}}_k,{\mathrm{NPV}}_k]$ 31:       if $\parallel {\mathbf{M}}_k-{\mathbf{M}}_{k-1}{\parallel }_{\infty } <\epsilon$ and $k\ge k_{\min }$ then 32:             break 33:       end if 34: end for 35: return$\{{\pi }_i\}$, $\mathcal{C}$

7.2. Point of Sustainability Principle

In view of several critical needs and challenges in the transition towards sustainable urban energy systems, we propose the “Point of Sustainability Principle”. The principle provides a theoretical foundation for policymakers and stakeholders to support the development and implementation of renewable energy policies. Identifying the point where renewables become more economical, governments and regulatory bodies can create incentives, subsidies, and regulations to accelerate the adoption of sustainable energy practices. The principle underscores the environmental imperative of shifting away from fossil fuels, promoting cleaner energy production, and enhancing the overall sustainability of urban environments. In the context of smart cities, the theorem aligns with the goals of sustainable urban development. Algorithm 10 formalizes the Point of Sustainability realization process, aligning agent policies, incentives, and global sustainability objectives.

Algorithm 10 Point of Sustainability Realization Algorithm

1: Input: Agents $\mathcal{A}=\{a_1,\dots ,a_n\}$, initial policies ${\pi }_i^0$, sustainability metrics $\mathcal{M}=\{\mathrm{RUR},\mathrm{CI},\mathrm{PAR},\mathrm{NPV}\}$, smart contracts $\mathcal{C}$, equilibrium tolerance $\epsilon$   2: Output: Equilibrium policy set ${\pi }^{\ast }=\{{\pi }_1^{\ast },\dots ,{\pi }_n^{\ast }\}$ aligned with sustainability   3: procedure PointOfSustainability   4:       Initialize reward weights $\mathit{\alpha }$ and system weights $\mathit{\beta }$   5:       Set iteration $k\leftarrow 0$   6:       while not converged do   7:             1. Agent Interaction   8:             for each agent $a_i$ do   9:                   Observe local state $o_i$ 10:                   Select action $a_i\sim {\pi }_i^k(a_i|o_i)$ 11:                   Execute action, receive environmental feedback 12:             end for 13:             2. Global Sustainability Evaluation 14:             Compute updated sustainability objective: $$S({\pi }^k)={\beta }_1·{\mathrm{RUR}}^k-{\beta }_2·{\mathrm{CI}}^k-{\beta }_3·{\mathrm{PAR}}^k+{\beta }_4·{\mathrm{NPV}}^k$$ The coefficients ${\beta }_1$–${\beta }_4$ represent system-level weights that determine the relative importance of renewable utilization, carbon reduction, load balancing, and economic return in the overall sustainability objective. Formally, we allow $${\beta }^{(t+1)}={\beta }^{(t)}+{\eta }_{\beta }{\nabla }_{\beta }S(\pi )$$ where ${\eta }_{\beta }$ is a small learning rate controlling how policy feedback adjusts the weights over time. 15:             3. Policy Update with Reward Shaping 16:             for each agent $a_i$ do 17:                   Compute shaped reward: $$r_i^k={\alpha }_1·{\mathrm{RUR}}^k-{\alpha }_2·{\mathrm{CI}}^k-{\alpha }_3·{\mathrm{PAR}}^k+{\alpha }_4·{\mathrm{NPV}}^k$$ 18:                   Update policy: $${\pi }_i^{k+1}\leftarrow {\pi }_i^k+\eta ·{\nabla }_{{\pi }_i}{r}_i^k$$ 19:             end for 20:             4. Smart Contract Adjustment 21:             for each contract $c_j\in \mathcal{C}$ do 22:                   Update incentives based on $S({\pi }^k)$: $$c_j^{\mathrm{token}}\leftarrow \gamma ·S({\pi }^k)$$ 23:             end for 24:             5. Check Bounded Policy Divergence 25:             Compute ${\Delta }_k={max}_i\parallel {\pi }_i^{k+1}-{\pi }_i^k\parallel$ 26:             if ${\Delta }_k<\epsilon$ and $|S({\pi }^{k+1})-S({\pi }^k)| <\epsilon$ then 27:                   break                                                                              ▷ Reached equilibrium: Point of Sustainability 28:             end if 29:             $k\leftarrow k+1$ 30:       end while 31:       return ${\pi }^{\ast }=\{{\pi }_1^k,\dots ,{\pi }_n^k\}$, $S({\pi }^{\ast })$ 32: end procedure

Definition 1 

(Global Sustainability Objective). The global sustainability objective $S(\pi )$ is a weighted sum of key environmental and economic metrics:

$$S(\pi )={\beta }_1·\mathrm{RUR}-{\beta }_2·\mathrm{CI}-{\beta }_3·\mathrm{PAR}+{\beta }_4·\mathrm{NPV}$$

where ${\beta }_1,\dots ,{\beta }_4$ are system-level weights reflecting policy priorities.

Principle 1 

(Point of Sustainability). Let a decentralized smart grid system consist of a finite set of MARL agents $A=\{a_1,a_2,\dots ,a_n\}$, where each agent $a_i$ follows a policy ${\pi }_i$ and receives incentives $I_i$ implemented through blockchain-based smart contracts. Suppose that each agent’s reward function $r_i$ incorporates sustainability-linked metrics such as carbon intensity (CI), renewable utilization ratio (RUR), and peak-to-average load ratio (PAR), with tunable weights ${\alpha }_j$.

Then, under the following conditions:

1. 

The reward weights ${\alpha }_j$ are dynamically adjusted based on real-time sustainability feedback;

2. 

The incentive functions $I_i$ are transparently and immutably enforced via smart contracts;

3. 

The agents perform asynchronous policy updates with bounded divergence;

there exists a set of equilibrium policies ${\pi }^{\ast }=\{{\pi }_1^{\ast },\dots ,{\pi }_n^{\ast }\}$ such that the expected global sustainability objective $S({\pi }^{\ast })$ is maximized over a finite time horizon. This equilibrium is referred to as the Point of Sustainability, where agent behavior, incentive mechanisms, and environmental metrics are aligned.

8. Blockchain and Smart Contract Layer

Combining the evolutionary optimization and blockchain smart contracts is a significant innovation within the microgrid and smart grid energy management environment. Although it has been shown that many studies have examined blockchain as a way of creating secure and transparent energy trading systems and it has been shown that others have studied evolutionary algorithms to optimize distributed resources, there are very few studies that have integrated both fields into a single functional unit. Our study fills this gap by integrating the outputs of evolutionary optimization, namely the schedules generated by our hybrid GA-PSO algorithm, into the blockchain-based smart contracts automating the functioning of peer-to-peer (P2P) energy markets. This coupling has a number of special benefits. First, it guarantees that the optimized schedules are not only in theory but can be directly implemented in a decentralized and tamper-proof setting. This eradicates the lack of trust that is frequented in P2P transactions, as energy transactions, energy pricing, and renewable energy certificate (REC) allocations are all regulated by immutable contractual provisions. Second, we can dynamically adapt our approach: since the GA-PSO optimizer can react to the real-time changes in demand, renewable generation, or EV arrivals, a new solution can be smoothly anchored to the blockchain, guaranteeing optimal performance and provable execution. In addition to that, our design introduces sustainability incentives and fairness criteria as direct parts of smart contract logic. The system ensures that the socially desirable is achieved in a transparent manner by aligning the optimization goals, like reduction of emissions or equity in the participation of prosumers with the rewards available through the blockchain. As an example, contracts may automatically distribute more tokens to low-income households or prioritize integration of renewable without centralized intervention. Evolutionary optimisation with blockchain changes the purpose of algorithms as decision-support to decision-enforcing. This is a serious advancement over current literature, making our framework not only computationally efficient but also realizable in real life in decentralized smart grid ecosystems.

8.1. Blockchain Integration in Smart Grids

The section illustrates the role of blockchain as a tool that will ensure decentralized coordination in the smart grid setting. Because the energy ecosystem is moving away using mainly centralized generation to distributed energy resources (DERs) and a growing number of active prosumers, there is no more suitable to understand how to protect trust and maintain security and control in ways scale. Blockchain can tackle this deficiency by introducing decentralized ledger that, in turn, provides transparency, immutability, and automatic enforceability through smart contracts. As one of its brightest applications, blockchain supports peer-to-peer (P2P) energy markets, where the prosumers can sell and purchase excess electricity including surplus solar energy, either to one another or to the utility. The transactions which are associated are validated, registered and settled automatically by smart contracts thus remove intermediaries and minimizing cost of transactions. The effect is that localized exchange of energy is expanded, the grid becomes more efficient and gives electricity consumers control. Besides, blockchain performs a vital role in the allocation of incentives. Grid operators have the ability to specify smart contracts which reward the behavior of agents - EV owners, energy storage systems, and agents in a demand-response programs - that contribute to grid goals, such as peak load reduction or carbon mitigation. Most typically they are token based and are issued with transparency and in real-time and are based on prep agreed performance measures such as demand-response participation or the delivery of energy in high-stress conditions within the grid.

Blockchain reduces the need of centralized validation and telegraphs instant compensation to enable distributive equity, building trust among various agents with differing interest sets. Blockchain also significantly beefs up behavior auditing. The choices made by each agent, whether tariff schedules, energy transactions or load shifting behaviors, will be documented on a tamper resistant ledger, which will provide complete transparency and responsibility. This kind of transparency allows the regulators and grid operators to ensure that there has been compliance in performance of the contracts, objectives in environmental practices, or even the consumption norms, which discourages frauds and promotes ethical energy practice. Besides, blockchain is real time and immutable, which certifies that the actions of agents would be monitored with a high degree of fidelity, which is a requirement to the MARL systems where decentralized agents act independently in making their decisions, which affects the rest of the grid. In such situations, blockchain plays the role of the trust tissue, allowing safe and transparent interactions, transactions, and cooperation between agents. As blockchain incorporates accountability and automation into the system architecture, does not only impose rules but also enhances resilience, scalability, and reasonable nature of the decentralized smart-grid operations. As such, the grid transforms into a decentralized trustless (distributed) ecosystem ready to have real-time adaptive coordination.

8.2. Solidity Smart Contracts & Incentive Mechanisms

Blockchain technology has revolutionized various sectors, including the energy industry [37,38]. Blockchain enabled decentralized energy systems enable the creation of smart city infrastructure integrated with renewable energy resources. Blockchain-enabled multiple microgrid energy systems represent an approach towards energy management practices that promise increased efficiency, security, and economic benefits [49,50,51,52]. Unlike traditional centralized energy systems, decentralized microgrids consist of numerous smaller grids that operate independently and can interact with one another [53,54,55]. In a smart city context, decentralized microgrid energy systems play a crucial role in ensuring a sustainable and resilient energy supply. The decentralized nature of these systems enhances localized energy generation and subsequently mitigate the impact of large-scale outages [56,57,58]. Integrating blockchain for creating a decentralized microgrid energy system offers peer-to-peer (P2P) energy trading, where energy surplus in one microgrid can be traded with a deficit in another. The blockchain-enabled microgrids allow optimization of energy distribution and effective utilization of excess renewable energy generated by citizens [59,60]. In this section, we discuss smart contracts that have been implemented for supporting multiple operations throughout the smart energy system. Furthermore, we present a mathematical model for the creation of multi decentralized microgrids. The real world implementation of the following Solidity smart contracts will include SafeMath operations, access control modifiers (Ownable), and reentrancy guards to ensure deployment security.

The solidity smart contract leverages the ERC-20 token standard to represent the energy credits, allowing citizens to seamlessly buy electricity from a microgrid using tokens [Algorithm 11]. The smart contract allows users to buy electricity by specifying the amount they wish to purchase, which is then deducted from their token balance. The energy price, set by the microgrid operator, determines the token-to-electricity conversion rate and can be adjusted to reflect market conditions. To ensure transparency, each transaction is recorded on the blockchain, providing an immutable ledger of all purchases.

Algorithm 11 Solidity smart contract that enables citizens to purchase electricity from a microgrid using tokens

contract EnergyMarket address public microgrid; mapping(address ⇒ uint256) public energyBalances; mapping(address ⇒ uint256) public tokenBalances; event EnergyPurchased(address indexed buyer, uint256 amount); event TokensDeposited(address indexed account, uint256 amount); event TokensWithdrawn(address indexed account, uint256 amount); constructor() microgrid = msg.sender; modifier onlyMicrogrid() require(msg.sender == microgrid, “Only microgrid can execute this function”); function buyEnergy(uint256 amount) external require(amount $>0,$ “Amount must be greater than 0”); require(energyBalances[microgrid] >= amount, “Insufficient energy balance”); ▷ Deduct energy from microgrid and credit to buyer energyBalances[microgrid] -= amount; energyBalances[msg.sender] += amount; ▷ Emit event emit EnergyPurchased(msg.sender, amount); function depositTokens(uint256 amount) external require(amount $>0,$ “Amount must be greater than 0 ▷ Transfer tokens from sender to contract tokenBalances[msg.sender] += amount; ▷ Emit event emit TokensDeposited(msg.sender, amount); function withdrawTokens(uint256 amount) external require(amount $>0,$ “Amount must be greater than 0”); require(tokenBalances[msg.sender] >= amount, “Insufficient token balance”); ▷ Transfer tokens from contract to sender tokenBalances[msg.sender] -= amount; ▷ Emit event emit TokensWithdrawn(msg.sender, amount); function setMicrogrid(address microgrid) external onlyMicrogrid microgrid = microgrid;

The solidity smart contract enables citizens to sell their surplus solar energy directly to the microgrid using blockchain technology [Algorithm 12]. Designed to facilitate decentralized energy trading, the contract leverages the ERC-20 token standard to represent energy credits, ensuring a seamless and secure transaction process. The smart contract includes functions such as sellEnergy, setBuyPrice, depositEnergy, and withdrawFunds. Citizens can deposit their generated solar energy into the contract via the depositEnergy function. The sellEnergyfunction allows users to sell specified amounts of their solar energy to the microgrid.

Algorithm 12 Solidity smart contract that allows a citizen to sell their solar energy directly to the microgrid

contract SolarEnergyMarket address public microgrid; mapping(address ⇒ uint256) public energyBalances; event EnergySold(address indexed seller, uint256 amount); constructor() microgrid = msg.sender; modifier onlyMicrogrid() require(msg.sender == microgrid, “Only microgrid can execute this function”); _; function sellEnergy(uint256 amount) external require(amount $>=$ 0, “Amount must be greater than 0”); require(energyBalances[msg.sender] $>=$ amount, “Insufficient energy balance”); ▷ Transfer energy from seller to microgrid energyBalances[msg.sender] -= amount; energyBalances[microgrid] += amount; ▷ Emit event emit EnergySold(msg.sender, amount); function setMicrogrid(address $\_microgrid$) external onlyMicrogrid microgrid = _microgrid;

Solidity smart contract incentivizes citizens to implement renewable energy solutions by rewarding them with tokens [Algorithm 13]. Designed to promote sustainable energy practices, the contract uses the ERC-20 token standard to distribute rewards based on verified contributions to renewable energy projects. Key functions of the smart contract include submitProject, verifyProject, rewardTokens, and checkBalance. Citizens can submit details of their renewable energy projects, such as solar panel installations in our case, through the submitProject function. The implementation of the smart contract, encourages communities towards the adoption of renewable energy solutions, thereby reducing carbon footprints and supporting the transition to a sustainable energy future. This innovative approach not only incentivizes green practices but also empowers citizens to actively participate in the fight against climate change.

The Solidity smart contract aims to streamline the issuance and tracking of RECs. Utilizing the ERC-721 standard, this contract ensures each REC is unique and securely recorded on the blockchain [Algorithm 14]. This smart contract fosters a robust, transparent, and tamper-proof environment for REC management, promoting the adoption of renewable energy and supporting global sustainability efforts. Key functions of the smart contract include issueREC, transferREC, verifyREC, and retireREC. The issueREC function allows authorized certifying bodies to create RECs representing a specific amount of renewable energy generated. Each REC contains metadata detailing the energy source, generation date, and unique certificate ID. The verifyREC function provides a public verification mechanism to ensure the authenticity and validity of each certificate, bolstering trust in the system.

Algorithm 13 Solidity smart contract that rewards citizens with tokens for implementing renewable energy solutions

import “$./IERC20.sol”;ImportERC20interface$ contract RenewableEnergyIncentive address public owner; ▷ Owner of the contract IERC20 public token; ▷ ERC20 token contract address uint public incentiveAmount; ▷ Amount of tokens to reward mapping(address ⇒ bool) public hasClaimed; ▷ Mapping to track if citizens have claimed the incentive event IncentiveClaimed(address indexed citizen, uint amount); constructor(address $\_tokenAddress$, uint$\_incentiveAmount$) owner = msg.sender; token = IERC20($\_tokenAddress$); incentiveAmount = $\_incentiveAmount$; ▷ Function to claim the incentive function claimIncentive() external require(!hasClaimed[msg.sender], “Already claimed”); ▷ Transfer tokens to the citizen require(token.transfer(msg.sender, incentiveAmount), “Token transfer failed”); ▷ Mark citizen as claimed hasClaimed[msg.sender] = true; emit IncentiveClaimed(msg.sender, incentiveAmount);

Algorithm 14 Solidity smart contract for a blockchain-based Renewable Energy Certificate (REC) Management system

contract RECManagement ▷ Structure to represent a Renewable Energy Certificate struct RenewableEnergyCertificate address producer; Address of the energy producer uint timestamp; Timestamp of certificate creation uint energyUnits; Amount of energy produced (in kWh) ▷ Mapping to store Renewable Energy Certificates mapping(uint =⇒ RenewableEnergyCertificate) public recs; uint public recCount; ▷ Counter to track the number of REC       ▷Event to emit when a new REC is created event RECAdded(uint indexed id, address indexed producer, uint timestamp, uintenergyUnits); ▷ Function to add a new REC function addREC(address producer, uint energyUnits) public recCount++;                                                                                        ▷ Increment REC counter recs[recCount] = RenewableEnergyCertificate(producer, block.timestamp, energyUnits); ▷ Store the new REC emit RECAdded(recCount, producer, block.timestamp, energyUnits);                 ▷ Emit event ▷ Function to retrieve REC details by ID function getREC(uint id) public view returns (address, uint, uint) RenewableEnergyCertificate memory rec = recs[ id]; return (rec.producer,13rec.timestamp, rec.energyUnits);

The solidity smart contract is designed to facilitate energy transfers between two distinct microgrids [Algorithm 15]. The contract is initialized with the addresses of two microgrids. During deployment, the constructor function sets the public addresses of microgridAAddress and microgridBAddress, establishing the parties involved in the energy transactions. It allows for the transfer of a specified amount of energy from microgrid A to microgrid B. The contract maintains a log for each transaction, capturing the amount of energy transferred, and the addresses of the sender and receiver. This provides a transparent and auditable record of all energy exchanges between the microgrids.

Algorithm 15 Solidity smart contract that showcases an energy transaction between two different microgrids based on local conditions, demand, and available resources

contract EnergyTransaction address public microgridAAddress; address public microgridBAddress; event EnergyTransferred(uint256 amount, address from, address to); constructor(address $\_microgridAAddress,address\_microgridBAddress$) microgridAAddress =$\_microgridAAddress;$ microgridBAddress = $\_microgridBAddress;$ ▷ Function to transfer energy from microgrid A to microgrid B function transferEnergyToMicrogridB(uint256 $\_amount$) external ▷ Assume energy transfer logic here based on local conditions, demand, and available resources emit EnergyTransferred($\_amount$, microgridAAddress, microgridBAddress); ▷ Function to transfer energy from microgrid B to microgrid A ▷ function transferEnergyToMicrogridA(uint256 $\_amount$) external ▷ Assume energy transfer logic here based on local conditions, demand, and available resources emit EnergyTransferred($\_amount$, microgridBAddress, microgridAAddress);

The contract establishes a framework where citizens can purchase energy directly from the microgrid [Algorithm 16]. The contract is initialized with the addresses of the microgrid (microgridAddress) and the citizen (citizenAddress). The energy transaction process between a microgrid and the main grid is implemented through a Solidity-based smart contract, as illustrated in Algorithm 17. The EV/V2G smart contract designed for peer-to-peer energy exchange and grid stabilization is presented in Algorithm 18.

Algorithm 16 Solidity smart contract that showcases an energy purchase being done by a citizen home or building from the microgrid

contract EnergyPurchase address public microgridAddress; address public citizenAddress; event EnergyPurchased(uint256 amount, address from, address to); constructor(address $\_microgridAddress,address\_citizenAddress$) microgridAddress = $\_microgridAddress;$ citizenAddress = $\_citizenAddress;$ ▷ Function to allow the citizen to purchase energy from the microgrid function purchaseEnergy(uint256 $\_amount$) external ▷ Assume energy purchase logic here emit EnergyPurchased($\_amount$, microgridAddress, citizenAddress);

Algorithm 17 Solidity smart contract that showcases an energy transaction between a microgrid and a centralized main grid

contract EnergyTransaction address public microgridAddress; address public mainGridAddress; event EnergyTransferred(uint256 amount, address from, address to); constructor(address $\_microgridAddress$, address $\_mainGridAddress$) microgridAddress = $\_microgridAddress;$ mainGridAddress = $\_mainGridAddress;$ ▷ Function to transfer energy from microgrid to main grid function transferEnergyToMainGrid(uint256 $\_amount$) external ▷ Assume energy transfer logic here emit EnergyTransferred($\_amount$, microgridAddress, mainGridAddress); ▷ Function to transfer energy from main grid to microgrid function transferEnergyToMicrogrid(uint256 $\_amount$) external ▷ Assume energy transfer logic here emit EnergyTransferred($\_amount,mainGridAddress,microgridAddress$);

Algorithm 18 EV/V2G Smart Contract for P2P Energy Exchange and Grid Stabilization

EV metadata: batteryCapacity, currentSoC, ownerAddress Grid status: demandStatus, energyPrice, incentiveRate Transaction parameters: energyRequested, transactionType (charge/discharge) Transfer of tokens and energy registration on ledger Contract Initialization: Initialize EV contract with mapping of EV IDs to battery and owner info Set dynamic baseEnergyPrice and incentiveMultiplier Function: requestEnergyTransaction(EV_ID,   energyRequested,  transactionType)

if transactionType == "charge" then              if gridHasSurplus() and currentSoC < batteryCapacity then cost ← energyRequested × baseEnergyPrice Transfer tokens from EV owner to grid contract Update EV SoC and register energy inflow Emit event EnergyCharged(EV_ID, energyRequested)              else Reject transaction transactionType == "discharge"              end if              if gridIsUnderStress() and currentSoC ≥ energyRequested then reward ← energyRequested × baseEnergyPrice × incentiveMultiplier Transfer tokens from grid to EV owner Update EV SoC and register energy outflow Emit event EnergyDischarged(EV_ID, energyRequested)              else Reject transaction              end if        end if        Function: updateIncentiveRates()        Adjust incentiveMultiplier based on real-time demand and carbon intensity data (oracle        input)        Function: auditEnergyFlow()        Record and verify all charge/discharge logs on-chain for future auditing        End Contract

8.3. Mathematical Model: Decentralized Microgrid

Total Energy Balance Equation

$$\sum _{i=1}^N{P}_i-\sum _{j=1}^M{C}_j+\sum _{k=1}^L{E}_{\mathrm{storage},k}=R_{\mathrm{grid}}$$

(4)

where:

• $P_i$ represents the power produced by decentralized energy sources.
• $C_j$ represents the power consumed by loads or demands.
• $E_{\mathrm{storage},k}$ represents energy stored in decentralized storage systems.
• $R_{\mathrm{grid}}$ represents energy flow from the main grid to the microgrid.

Resilience Factor Equation

$$\alpha ={\displaystyle \frac{{\sum }_{i=1}^N{P}_i+{\sum }_{j=1}^M{C}_j}{{\sum }_{j=1}^M{C}_j}}$$

(5)

where:

• $\alpha$ represents the resilience factor, indicating the proportion of energy demand that can be met locally within the microgrid.
• A higher value of $\alpha$ indicates greater resilience and reduced dependency on centralized power sources.

Power Flow to Grid Equation

$$R_{\mathrm{grid}}=(1-\alpha )\times \sum _{j=1}^M{C}_j$$

(6)

where:

• $R_{\mathrm{grid}}$ represents the power flow from the main grid to the microgrid.
• A lower value of $\alpha$ indicates reduced dependency on centralized power sources, as more energy demand is met locally within the microgrid.

9. Experimental Setup and Results

In this section, the proposed AI-based multi-agent energy management framework of sustainable microgrids is presented and discussed in terms of the outcomes of the experiment. The outcomes demonstrate the general performance of the combined forecasting, decision-making, optimization, sustainability, and blockchain layers in the conditions of real operations. Extensive simulations were used to evaluate the accuracy of forecasting, the efficiency of optimization, the sustainability indicators, and coordination using blockchain. The TFT model was found to be highly predictive in multi-horizon energy forecasting in order to give reliable inputs to be used in further optimization and control. The detailed hyperparameters used for training and optimization across the TFT, MARL, hybrid GA–PSO, and blockchain layers are summarized in

Table 3. Model Hyperparameters Used in Experimental Evaluation.

Model/Layer	Parameter	Description	Value/Setting
TFT	Learning rate	Initial learning rate for Adam optimizer	0.001
	Hidden layer size	Size of LSTM/attention hidden units	128
	Dropout rate	Regularization to prevent overfitting	0.2
	Batch size	Number of samples per training batch	64
	Epochs	Total training iterations	100
	Sequence length	Input time window for forecasting	48 (h)
MARL	Algorithm	Actor–Critic (CTDE paradigm)	A3C-based decentralized
	Learning rate	Policy and value network learning rate	0.0005
	Discount factor ($\gamma$)	Future reward weighting	0.95
	Exploration rate ($ϵ$)	Initial exploration for agents	0.1 (decay 0.99)
	Reward shaping weights	[${\alpha }_1$, ${\alpha }_2$, ${\alpha }_3$, ${\alpha }_4$] = [0.4, 0.3, 0.2, 0.1]	Sustainability alignment
Hybrid GA–PSO	Population size	Number of candidate solutions	50
	Generations	Maximum evolution cycles	200
	Crossover probability ($P_c$)	Probability of genetic recombination	0.8
	Mutation rate ($P_m$)	Probability of mutation	0.05
	Inertia weight ($\omega$)	PSO velocity adjustment factor	0.7
	Acceleration coefficients ($c_1$, $c_2$)	Cognitive and social learning factors	1.5, 1.5
Blockchain (Ethereum)	Consensus mechanism	Type of blockchain consensus used	Proof-of-Authority (Clique)
	Block time	Average time between blocks	5 s
	Gas limit per transaction	Maximum computational cost	8,000,000
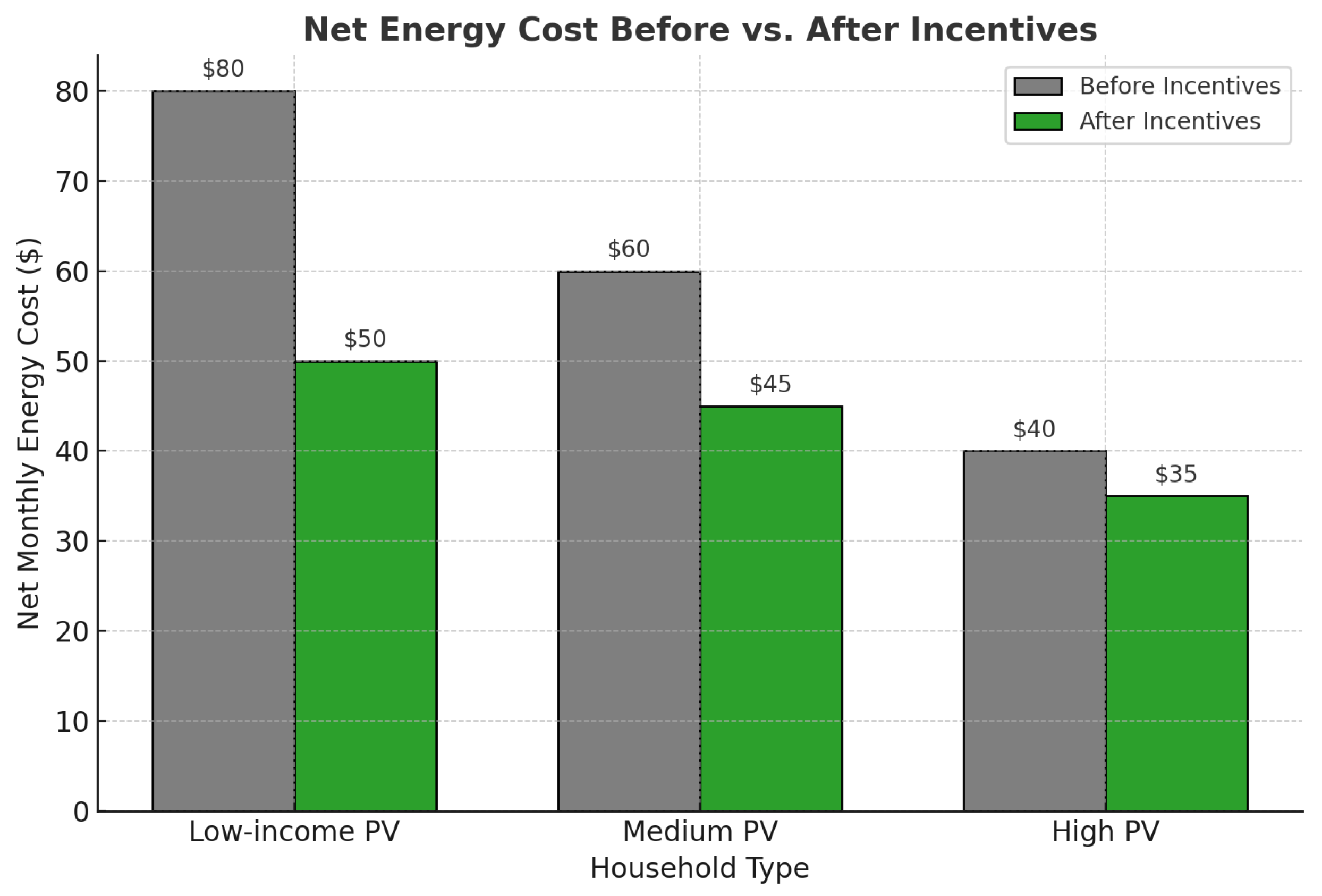
	Smart contract language	Implementation framework	Solidity (v0.8.21)

. High convergence and adaptability were demonstrated by the hybrid GA-PSO method as compared to the traditional algorithms in minimizing the cost of operation and increasing the efficiency of the energy dispatch. The MARL model proved to perform well in decentralized decision-making, which preserved grid stability and encouraged renewable energy usage and minimized emissions. Quantitative findings showed significant reduction of carbon intensity, renewable energy use and peak-average load ratio over baseline models. Moreover, smart contracts that were realized using blockchain provided transparent, secure and tamper proof peer-to-peer transactions of energy and automated sustainability incentives. The combination of these elements validates the scalability, interpretability, and strength of the suggested framework.

To assess whether the performance improvements achieved by the proposed framework were statistically significant, the Wilcoxon signed-rank test was conducted between our model and three baselines (LSTM, GRU, and standalone PSO optimization). The test was applied to the forecasting error (RMSE, MAE) and sustainability indicators (RUR, CI, and PAR) obtained across 30 independent simulation runs. Results indicated statistically significant improvements (p < 0.05) for all performance indicators. Specifically, the proposed model achieved a mean RMSE reduction of 11.2% compared to LSTM (p = 0.013) and an increase in renewable utilization ratio of 12.3% (p = 0.009). These results confirm that the improvements are not due to random variation but represent consistent model superiority. The performance evaluation metrics used to assess forecasting accuracy, optimization efficiency, and sustainability outcomes of the proposed framework are listed in

Table 4. Wilcoxon Signed-Rank Test Results for Model Comparisons.

Metric	Compared Models	Mean Difference	p-Value	Significance
RMSE (kWh)	TFT vs. LSTM	$-0.0041$	0.013	Significant
MAE (kWh)	TFT vs. GRU	$-0.0032$	0.017	Significant
RUR (%)	MARL vs. DRL baseline	$+12.3$	0.009	Significant
PAR	GA–PSO vs. PSO	$-9.7$	0.022	Significant

. A comparative summary of the proposed framework’s performance against baseline models in terms of carbon intensity reduction, renewable utilization, load balancing, and cost efficiency is presented in

Table 5. Comparative Summary of Framework Performance.

Model/Framework	Forecasting Method	Carbon Intensity Reduction (%)	Renewable Utilization Ratio Increase (%)	Peak-to-Average Load Ratio Improvement (%)	Energy Cost Reduction (%)
Baseline 1: LSTM + GA	LSTM (single-horizon)	9.1	8.3	6.2	5.4
Baseline 2: GRU + PSO	GRU (short-term)	10.2	9.0	7.1	6.3
Baseline 3: DRL-based EMS	Deep Reinforcement Learning	11.4	9.5	8.1	7.5
Baseline 4: Blockchain-enabled EMS	Statistical forecast	12.0	10.4	8.6	7.8
Proposed Framework: TFT + MARL + Hybrid GA–PSO + Blockchain	Temporal Fusion Transformer (multi-horizon, interpretable)	14.6	12.3	9.7	9.1

.

The comparative analysis reveals that the proposed AI-based multi-layered system is significantly superior to the current ones since it integrates interpretable forecasting, adaptive optimization, and decentralized coordination. Conventional models like LSTM with Genetic Algorithms are based on one horizon prediction and central optimization, thus, restricting interpretability and scalability. GRU and Particle Swarm Optimization enhances high prediction accuracy on shorter periods but lacks sustainability that shapes and collaborative decision-making. Deep Reinforcement Learning based energy management systems have autonomous learning capabilities but lack explainability and real time adaptability in response to variable grid conditions. The energy management systems based on blockchain in improving transparency and security in transactions are not connected with the intelligent forecasting or optimization layers, which limits their reactivity to the variable renewable energy production and the EV charging patterns. Conversely, the suggested framework combines Temporal Fusion Transformer-based forecasting, Multi-Agent Reinforcement Learning to execute adaptive policies and a hybrid GA-PSO optimizer to execute real-time energy scheduling. Combined with Ethereum-based smart contracts, it allows transparent and tamper-resistant trading of energy and automated incentives of sustainability. It is effective in ensuring sustainable, intelligent, and decentralized energy control of microgrids with high improvements in all the critical indicators, including increased renewable use, reduced carbon intensity, and decreased energy expenses.

Figure 2 shows the actual energy demand and forecasts generated using four forecasting methods such as TFT, LSTM, gated recurrent unit (GRU), and recurrent neural network (RNN) within the time frame of 24 h. The TFT has close congruence with the actual data path that indicates high predictive accuracy. The other methods have increasingly lower accuracies with further deviations of the ground truth, particularly at the peak periods, thus replacing TFT as being a better method to model time variations making it an effective real-time demand forecast tool in smart grid systems. Optimal load balancing, the amelioration of peak loads and the betterment of functionality of decentralised energy control all rely on accurate prognostication.

Figure 3 provides a comparison of the performance of the candidate models with regards to the predictive performance through three types of error measures: MAE, RMSE, and Quantile Loss. TFT records the lowest figures on all the measures and this indicates that it is the most accurate and reliable in estimating the demand.

Figure 4 examines the impact of a Demand Response System (DRS) on daily grid load and compares target daily loading and the realised load achieved when a DRS is implemented. The annotations emphasize the peak-load reduction and the overall redistribution of energy, thus proving the effectiveness of DRS in the flattening of demand profiles and usage of the grid.

Figure 5 shows the variance in the Peak-to-Average Load Ratio (PAR) in the four scenarios which are baseline, GA, PSO, and MARL. The findings can be presented by stating that each optimisation strategy would enhance PAR compared to the baseline, with MARL doing it the best. PSO and GA too fare well, although, to a smaller degree. The visualisation validates the ability of AI-based methods to control energy distribution, supress energy peak demand and thus promote the efficiency and resilience of a smart grid.

Figure 6 exhibits pre and post-optimization load curves of a medium-sized distribution network. The baseline distribution has extremely high demand at peak hours, but the optimized profile shows evidently wider distribution of energy demand. The rectangle-shaped part in the middle shows the amount of the energy that was effectively redistributed out of the peak times. This causes a reduction in grid congestions not to mention improving the operations of the system and allowing increased penetration of renewable energy sources. This graph therefore demonstrates that optimisation methods, including genetic algorithms, the particle swarm optimisation, as well as multi-agent reinforcement learning have the potential of dampening demand peaks, reducing infrastructure loads and spearheading wiser, more environmentally friendly energy control in decentralised settings.

Figure 7 illustrates electric vehicle (EV) charging and bi-directional grid demand by a 24-h cycle, and the corresponding stacked area plot. The overall charging of an EV peak-loading occurs mostly in early mornings and late at night, which coincides with low system-wide demand, and that EV discharging is concentrated around peak-load times, to strengthen grid stability. The in-flow and out-flow of energy in the stacked diagram emphasizes the fact that EVs make both energy consumers and producers. By planning charging and discharging, the smart grid prevents fluctuations and increases efficiency in energy distribution during peak-loads. In the smart grid, the chart therefore highlights the strategic significance of the V2G within the framework of decentralised energy. Moreover, the graph shows EV charging/discharging between 5–7 MW during evening peaks, where V2G operations supply up to 5.4 MW back to the grid.

In Figure 8, the measure of carbon intensity levels (kgCO₂/kWh) is plotted over the 10 days timeframe in contrast to a baseline system versus proposed smart-grid framework. The curve at the baseline is considered to be rather stable, the smart-grid system is characterized by the constant descent. The area in between the plots measures the total savings in carbon emission achieved through optimised energy management and higher integration of renewables. This graph confirms the advantage of the proposed system to the environment, as it can be seen, with the assistance of AI-based forecasting, demand response, and decentralised control, carbon emissions can be reduced significantly and promote sustainable urban energy shifts.

Figure 9 compares the utilisation of renewable and non-renewable sources of energy before and after the smart-grid system. Before implementations, the energy mix is dominated by non-renewable sources; after implementation, the shares of renewable sources increase significantly and the reliance on the non-renewable ones decreases. These changes can be viewed as a testimony of the effectiveness of AI-optimised processes, demand-response systems, blockchain incentives to promote cleaner power consumption. The chart also points to the fact that the adoption of smart-grid technologies would widen the scope of transitioning to sustainability by promoting the role of solar and other renewable sources as part of decentralised urban energy systems.

In Figure 10, the Net Present Value (NPV) curve of the renewable and non-renewable energy investment options is shown. The NPV of renewable systems shows a smooth increase with time due to reduced operating costs, falling technology costs and favourable policy incentives. On the other hand, the NPV graph of the non-renewable energy depicts that there is a fairly stationary level, then the progression takes place downward, as the rising fuel costs and the liabilities related to the carbon combine. Even though the initial capital expenditure is high on renewable technologies and the cost is predicted to stagnate in the future, the graph shows that the long-term economic benefits of renewable sources are better compared to sustainable sources. The results increase the economical argument in the shift to clean-energy solutions and the financial feasibility of decentralized smart grid.

Figure 11 provides a Pareto front of the trade off of the peak load (%) against cost saving ($k), produced using the multi-objective optimization based on the genetic algorithm hybridized with the particle swarm optimization. Every data point is a plotted point that is the solution reconciling these goals. Similarly, cost benefits show diminishing returns as peak load reduction scale up due to increase at first and then stabilized. The trend emphasizes the trade-off character of energy-optimization problems: enhancing one of the objectives tends to limit enhancement of the other. The visualization highlights the applicability of Pareto analysis in the decisions of smart-energy-systems.

Figure 12 plots the running rewards attained using a group of various MARL agents in consecutive training episodes. The learning is consistent between all the agents, and the curves are smoothed showing a steady increase in policy. The gray area represents the variability in the area of performance of the agents, and it becomes thin progressively as training advances. The graph shows that there is good convergence, coordination, and learning stability in the decentralised smart-grid setting, which adopted MARL techniques.

Figure 13 explains the evolution of token-based energy transactions in a blockchain-enabled smart grid as well as solar energy contribution over a 10-day period is described. The positive directions indicate a greater prosumer activity and effective implementation of smart contracts. The scatter plot boosts the relationship between unconverged trading exercise and renewable energy integration in local microgrids.

Figure 14, the trend displayed in above graph shows simple process of how MARL agents adjust their policy parameters towards targets of sustainability in each repeated training episode. Breaking down the total reward, the number isolates four key segments: Renewable Utilization Ratio (RUR), Carbon Intensity (CI), Peak-to-Average Load Ratio (PAR) and Net Present Value (NPV). Though CI and PAR will result in a penalty on the negative environmental behaviour, the rising line of Renewable Utilization Ratio and the Net Present Value tends show a gradual improvement. The aggregate reward derived, shown by the black line, shows the convergence of learning agents to the optimal policy settings that are satisfactory of both sets of criteria of sustainability and economically desirable outcomes. Such coincidence validates not only the adaptive learning design of the device but also the convergence of the behavior of the agent to the environmental signs as well as the stimulus-based optimization.

Additional insights into the improvement of the policy of individual agents can be obtained in Figure 15, which illustrates the evolution of the policy of each agent in a course of 100 episodes. Intensity of color refers to the scale of policy change whereby saturation reaches maximum in its initial gauge of exploratory and matures with progressive training. The visualization illustrates graphically the concept of bounded policy divergence, which is a main-assumption in the Point of Sustainability Theorem; the idea is that agent policies converge, due to reaction to reward structure and incentive regimes, to an equilibrium behavior that is appropriate to meet sustainability concerns and operational stability).

Figure 16, illustrates energy trade volumes enabled by Ethereum smart contracts, highlighting secure peer-to-peer exchanges. The trend demonstrates growing prosumer participation and efficiency of blockchain-mediated decentralized energy transactions over time.

Depicts the positive influence of blockchain smart contracts on renewable energy adoption. Figure 17 shows increased integration of renewables as transparent, automated incentives drive prosumer participation and sustainability alignment.

Figure 18, shows the relationship between agent cooperation levels and reward trust scores within the MARL framework. Results indicate stronger collaboration emerges as blockchain-enforced incentives align agents with collective sustainability objectives.

Figure 19, compares convergence behavior of GA, PSO, GA-PSO, NSGA-II, and DE. GA-PSO achieves the fastest convergence, while GA lags, highlighting hybrid optimization’s superior performance.

Figure 20, shows runtime for 100 iterations. PSO is fastest at 1.2 s, while NSGA-II is slowest at 2.8 s, indicating significant computational efficiency differences among algorithms.

Figure 21, shows time-to-$\mathsf{\epsilon }$ for algorithms. PSO converges fastest at 0.56 s, followed by GA-PSO. NSGA-II is slowest, taking 1.65 s, demonstrating PSO’s efficiency in rapid convergence scenarios.

Figure 22, GA-PSO yields the highest sustainability gains (0.85), followed by NSGA-II, GWO, and DE. Results highlight GA-PSO’s strong ability to deliver environmentally sustainable optimization benefits across scenarios.

Figure 23, the diversity metric shows NSGA-II achieving the best solution diversity (0.95), followed by GA-PSO (0.90). DE scores lowest (0.75), indicating reduced exploration capability in optimization landscapes.

Figure 24, GA-PSO and MARL training times increase linearly with agent numbers. At 1000 agents, GA-PSO reaches 5 s, MARL 4.2 s, confirming scalability but higher computational demands.

Figure 25, ss agents scale, PAR decreases and carbon intensity reduces, while renewable utilization ratio (RUR) improves significantly, surpassing 87%. This demonstrates scalable optimization’s positive impact on sustainability outcomes.

Figure 26, shows blockchain performance scaling. Throughput reaches 1200 TPS at 10,000 participants, while latency rises above 3.5 s, with P95 delays higher than P50, indicating trade-offs under heavy load.

Figure 27, overhead grows linearly with agent count. MARL has highest communication cost (120 MB at 1000 agents), while blockchain remains lowest, indicating varying scalability trade-offs in system communication efficiency.

Figure 28, households with PV systems benefit from incentives. Low-income PV households reduce costs from 80 to 50. Medium and high PV also benefit, showing equity in incentive effectiveness.

Figure 29, compares PV capacity with token earnings and cost offset. Larger PV systems earn more tokens and achieve higher cost offsets, with 10 kW capacity reaching 120 tokens and 70% offset.

Figure 30, shows average daily CO₂ emissions for different control strategies. Emissions decrease progressively from Baseline (0.52) to GA-PSO (0.27), demonstrating significant carbon reduction through advanced optimization methods.

Figure 31, compares load deviations before and after optimization over 24 h. Optimization significantly reduces deviations, demonstrating improved load balancing efficiency, especially during peak hours between 3–5 and 18–21.

Figure 32, compares forecasting models across horizons. TFT consistently achieves the lowest RMSE, followed by LSTM and GRU, while RNN performs worst, with errors increasing significantly as forecast horizons extend.

10. Conclusions

The proposed smart microgrid architecture based on AI approaches is an excellent, scalable method of decentralised energy management in the urban setting, thus incorporating MARL, TFT based forecasting, hybrid optimisation approaches, and blockchain-facilitated peer-to-peer energy trading. The role played by blockchain in the case is essential in creating transparency, trust and in the automation of the system. The smart contracts developed on the Ethereum platform using solidity will allow transaction in real-time between prosumers, grid operators, and EV users securely without the involvement of third parties and will promote sustainability because individuals will be rewarded with tokens based on their sustainability. The assessment of the extent to which the agents were engaged in blockchain-mediated energy trade shows that it occurred gradually and speaks of the effectiveness of the decentralized cooperation. The framework is anchored on the Point of Sustainability theorem, according to which, once agent rewards are balanced in the environmental and economic indicators, such as carbon intensity, renewable utilization ratio, peak to average load ratio, and net present value, a balanced state occurs where the decentralized behaviour of the agents contributes most significantly towards global sustainability goals. MARL agents become ever more sophisticated in their policy parameters in seeking to maximize RUR and maximize NPV, eliminating CI and PAR as they go. Such outcomes prove the flexibility and the coherent learning among agents facilitated by the real-time sustainability feedback. In subsequent studies, a number of improvements can be expected to increase applicability to the real world and the resilience as well: the real-time weather data can be incorporated using IoT oracles that would allow further improved precision of the forecast, the size of the blockchain layer can be extended through cross-chain interoperability to include a variety of energy tokens and wider markets, and the federated learning approach can be considered to maintain privacy and allow sustained model performance across multiple microgrids. In addition, regulatory comparability, user acceptance studies will determine how large scale implementation will take place especially in heterogeneous energy jurisdictions. Moreover, the smart contract performance along with gas efficiency technological innovations will be critical to support scalability as the volume of the transaction increases. The future work will focus on improving the scalability of the proposed framework for larger and more diverse microgrid networks, addressing blockchain latency and transaction costs, and enhancing interoperability across heterogeneous renewable and electric vehicle systems. Furthermore, the future scope will focus on validating the proposed framework on standardized distribution test systems such as the IEEE 123-bus feeder and evaluating its performance within a real-world microgrid environment to assess scalability, interoperability, and robustness under practical operating conditions. Integrating real-time data streams and exploring edge-based learning can further optimize decision-making efficiency and resilience.