Abstract
Orthogonal polynomials and their moments serve as pivotal elements across various fields. Discrete Krawtchouk polynomials (DKraPs) are considered a versatile family of orthogonal polynomials and are widely used in different fields such as probability theory, signal processing, digital communications, and image processing. Various recurrence algorithms have been proposed so far to address the challenge of numerical instability for large values of orders and signal sizes. The computation of DKraP coefficients was typically computed using sequential algorithms, which are computationally extensive for large order values and polynomial sizes. To this end, this paper introduces a computationally efficient solution that utilizes the parallel processing capabilities of modern central processing units (CPUs), namely the availability of multiple cores and multithreading. The proposed multi-threaded implementations for computing DKraP coefficients divide the computations into multiple independent tasks, which are executed concurrently by different threads distributed among the independent cores. This multi-threaded approach has been evaluated across a range of DKraP sizes and various values of polynomial parameters. The results show that the proposed method achieves a significant reduction in computation time. In addition, the proposed method has the added benefit of applying to larger polynomial sizes and a wider range of Krawtchouk polynomial parameters. Furthermore, an accurate and appropriate selection scheme of the recurrence algorithm is introduced. The proposed approach introduced in this paper makes the DKraP coefficient computation an attractive solution for a variety of applications.
1. Introduction
Recently, with advancements in sensors, Internet of Things (IoT) devices, and wearable devices, VLSI circuits have emerged as essential key solutions to meet the demands of expanding and modernizing various fields and mathematical disciplines such as distributed systems, computer vision, image analysis, automated systems, and automatic identification technology [1,2]. One critical component in this area is the design of efficient image descriptors and signal compression techniques. To this end, moment generation functions have been introduced and widely utilized, proving effective in extracting image features for 1D and 2D signal compression across various applications such as edge detection, object recognition, watermarking, face recognition, and robot vision [3,4].
Typically, the moment generation functions work by projecting an image onto a polynomial basis, which is considered a superior option to other types of bases. However, as moment functions have been widely used to describe images with complicated scenes, recently, researchers have been extensively working on finding effective ways to reduce computation times without compromising the outcome accuracy [5].
In general, two common types of orthogonal polynomials (OPs) have been widely used, namely, orthogonal on a disc and orthogonal on a rectangle [6,7]. Fourier–Mellin and Zernike polynomials [8,9] are examples of polynomials that are orthogonal on a disc. On the other hand, Krawtchouk, Legendre, and Tchebichef polynomials [10,11,12] are polynomials that are orthogonal on a rectangle.
In the theory of orthogonal polynomials, dimensionality refers to the underlying vector space in which the polynomials reside. Traditionally developed for a one-dimensional space (often denoted by a single variable), these polynomials exhibit orthogonality, meaning their inner product is zero when of different degrees [13]. The power of this framework lies in its extensibility. By generalizing the concept of the inner product and vector space to higher dimensions (e.g., multiple variables representing a plane or 3D space), mathematicians can construct sets of orthogonal polynomials that function effectively in these multi-dimensional domains. This allows for the application of these powerful tools to analyze and approximate functions in complex, high-dimensional settings [14]. One approach to achieving this extension involves constructing orthogonal polynomials in higher dimensions by multiplying the corresponding one-dimensional polynomials, leading to discrete orthogonality on a hypercube. This technique proves particularly valuable for analyzing digital images and other high-dimensional data as it avoids the need for coordinate transformations or discretization steps in moment computation [15].
The use of an orthogonal polynomial (OP) to extract distinctive features from signals is pivotal in determining its overall performance [12,16,17]. This capability is dependent on the polynomial properties, such as localization and energy compaction properties. The energy compaction term refers to the property of a signal transform, which allows it to preserve the energy of the original signal while reducing the number of coefficients used to represent it. The energy compaction represents the amount of energy that is concentrated in a small number of coefficients. Transformations with good energy compaction properties can represent the original signals with high accuracy using a small number of coefficients, making them useful for achieving various essential tasks such as data compression and signal processing.
On the other hand, the localization property refers to the ability of a signal transform to represent the structure of the original signal in a localized manner. This means that the coefficients of the transformed signal are closely associated with specific locations in the original signal. This property is particularly useful in tasks such as image processing, where accurately representing the local features of an image is important. Transforms with good localization properties can effectively capture the local variations of the original signal, making them useful for tasks such as edge detection, image denoising, and feature extraction. The energy compaction property can be achieved with Tchebyshev polynomials, while the localization property can be realized by utilizing Krawtchouk polynomials.
Reference [10] proposed using DKraP as an image descriptor, namely, the discrete Krawtchouk moment (DKraM). Due to the orthogonality of DKraM, the results showed that DKraM has a lower reconstruction error when compared to other types of moments [5]. Reference [10] used an indirect method to derive DKraM invariants. However, using the indirect method for DKraM invariants means that the moment invariants are computed using invariants of geometrical moments. Since these invariants were derived without the use of Krawtchouk polynomials, perfect invariance for digital images cannot be achieved. Venkataramana and Raj [18] used the direct method to obtain scale and translation invariance for Krawtchouk moments. They achieved scale invariance by eliminating the scale factor contained in the scaled Krawtchouk moments using algebraic techniques. The proposed method involves modifying Krawtchouk moments to maintain the property of translation invariance. This is accomplished by treating discrete weighted Krawtchouk polynomials as periodic, with each period equal to the number of data points, and then shifting these polynomials to be centered.
In general, orthogonal geometric moments become particularly apparent when numerical properties and implementation issues are considered. Therefore, it is not generally recommended to evaluate orthogonal geometric moments by expanding them into standard powers because this will lead to possible overflow and/or underflow and cause a loss of precision [5]. Moreover, most orthogonal polynomials concern hypergeometric functions; therefore, the polynomial computation and the corresponding moments are considered time-consuming [19]. Specifically, directly computing the Krawtchouk moment using factorial and gamma functions leads to two main issues: high numerical instability and significant computation time, especially when higher-order moments are required for an improved description of image contents. Various methods have been presented to accelerate the calculation of moment kernels and the summation of these kernels for different signal dimensions. These methods are based on recursive relationships and symmetry properties, which make the computation easy, fast, and effective [19,20,21]. For example, two original methods are proposed using the outputs of cascaded digital filters in deriving the Krawtchouk moment in [5]. These methods are faster for processing a real image of size pixels.
Moreover, recent developments in algorithms for computing Krawtchouk polynomial coefficients have been proposed to address instability issues associated with the computation of high-order polynomials [19,22,23]. One such approach involves the use of the three-term recurrence relation, which expresses each coefficient of the Krawtchouk polynomial in terms of the previous two coefficients. This method has been extensively adopted due to its simplicity and straightforward implementation. Yap et al. [10] developed a recurrence algorithm to calculate Krawtchouk polynomial coefficients in the n direction. In [24], a revised recurrence relation was introduced along the x direction. Both of the algorithms described above were developed by partitioning the DKraP plane into two rectangular regions. The coefficients in the first part were calculated using the recurrence algorithm, and the coefficients in the second half were obtained using a symmetry property. Therefore, only half of the KPCs were calculated recursively, i.e., 50% of the coefficients were computed only. The DKraP array can be split into four parts as described in [25], and the DKraP coefficients can be split into two parts, which are only calculated. Then, a symmetric property can be used to compute the remaining coefficients. The results show that this algorithm performs better than the algorithms presented in [10,24] for different values of parameter p, specifically when the polynomial size is limited. Abdulhussain et al. [4] proposed a new algorithm for computing Krawtchouk polynomial coefficients using the symmetry property of DKraP. The algorithm divides the DKraP array into four triangles and computes the DKraP coefficients for only one triangle. Then, the symmetry properties are used to compute the coefficients for the other three triangles. The algorithm outperforms previous literature in terms of computational costs and has been applied in a face recognition system, achieving promising results. Recently, Al-Utaibi et al. [26] introduced a more intricate yet more efficient algorithm, surpassing existing ones. In this algorithm, a new recurrence relation is proposed for computing the coefficients of DKraP that address the problem of numerical errors, particularly when the DKraP parameter values deviate from 0.5 to 0 and 1. The proposed algorithm used a diagonal recurrence relation and symmetry relations to compute DKraP coefficients for multiple partitions. The proposed algorithm can generate polynomials for high orders.
The aforementioned techniques are developed to mitigate the effects of propagation error, including the use of higher precision arithmetic and the implementation of error-correcting techniques. However, these techniques can also introduce additional overhead and may not always be practical, particularly for large values of the orthogonal polynomial order (n), the size of the orthogonal polynomial (N). The orthogonal polynomial order refers to the degree of the highest polynomial term in an orthogonal polynomial within a sequence. The polynomial order signifies the fine details of the signal represented by the polynomial. On the other hand, the size of the orthogonal polynomials indicates the total number of polynomials in a given set of orthogonal polynomials [27,28]. Note that the higher the order, the more accurate the representation of the signal in the transform domain [29]. Therefore, a scalable and more efficient solution for DKraP coefficient computation is required to make it a compelling choice for diverse applications reliant on discrete orthogonal polynomials and to enable practical applications of DKraP in real-world scenarios. Based on the issues mentioned, this paper proposes a computationally efficient solution using a novel multi-threaded method to enhance the efficiency of DKraP coefficient computation in terms of computation cost. The proposed multi-threaded implementation method offers the benefit of scalability to larger polynomial sizes and a broader range of Krawtchouk polynomial parameters. This makes it an attractive solution for a variety of applications that require the efficient computation of Krawtchouk polynomial coefficients.
Our contributions are listed as follows:
- A novel multi-threaded implementation method is proposed to improve the efficiency of the DKraP coefficient computation.
- A computationally efficient solution using a multi-threaded method to reduce computation time is proposed.
- The proposed algorithm for DKraP preserves the orthogonality condition for large signal sizes as well as higher polynomial sizes and improves performance across different parameter values.
The rest of the manuscript is organized as follows: Section 2 presents the mathematical definition of the DKraP and DKraM to clarify the mathematical calculations that may be parallelized. Section 3 describes three different recurrence algorithms and shows the proposed multi-threaded version for each algorithm, clarifying the parts of the algorithms that can be parallelized. The performance evaluations of the proposed algorithms are discussed in Section 4, where the different algorithms are compared, considering different order sizes at different thread numbers to identify the optimal cases. Finally, we conclude this paper in Section 5.
2. Mathematical Definitions of DKraP and DKraM
DKraPs are defined as a set of scalar quantities that are efficient and superior data descriptors, and they are utilized for signal information representation without redundancy. In addition, DKraMs are employed to reveal small variations in the signal intensity [30] and they can extract local features from any region of interest in the signal. These polynomials can be used for different applications such as pattern recognition, face recognition, speech enhancement, watermarking, edge detection, and template matching [31].
This section provides the mathematical definition of the DKraP in addition to the definitions of DKraM for 1D, 2D, and 3D signals.
The discrete Krawtchouk polynomials (DKraPs) are a family of orthogonal polynomials defined on a discrete set of points. The DKraP is parameterized by the order of the polynomial n, the parameter of DKraP p, and the size (a non-negative integer N). The DKraP satisfies the orthogonality relation [32]:
where is the Kronecker delta, which is defined by the following:
The DKraP satisfies the following three-term recurrence relation [33]:
Note that the range of the DKraP parameters is as follows:
- n is a non-negative integer .
- x is an integer such that .
- p is a real number in the range .
The xth DKraP of order n is denoted by and can be written as follows:
where () is the hypergeometric function [34], N represents the size of the polynomial, p represents the DKraP parameter that controls the shape of the polynomial, and x refers to the variable index.
The weight of the Krawtchouk polynomials is given by the binomial distribution with parameters n and p. The weight function is a non-negative function () defined over a specific interval . In addition, the weight function is essential in determining the inner product and orthogonality [35,36]. Specifically, the weight of the Krawtchouk polynomials can be defined as follows:
where is the weight of the DKraP. Note that p is a real number between 0 and 1. The norm of the Krawtchouk polynomials can be written as [37]:
where is the norm of the DKraP and is the Pochhammer symbol [38,39,40], also known as shifted factorials [41]. The weighted and normalized DKraP, , is computed as follows:
The moments can be computed using DKraP for different signals, which are given in Table 1.

Table 1.
The computation of moments for different types of signals.
3. Multi-Threaded Algorithm
To improve the efficiency of computing Krawtchouk polynomial coefficients, a multi-threaded process is employed in this paper for three recurrence algorithms, namely, DKTv1 [24], DKTv2 [4], and DKTv3 [26]. Parallel processing is effective in data-intensive tasks. As a result, the main objective is to identify the available parallelism in each algorithm and restructure the calculations by distributing independent processes among different threads. These threads will be processed by different processing resources in parallel, which are governed by the processor design, which increases resource utilization and reduces computation time.
3.1. Multi-Threaded Algorithm for DKTv1
The process of computing DKraP using hypergeometric series and the gamma function is time-consuming; thus, the utilization of the three-term recurrence algorithms can be more appropriate. For convenience, let be indicated by .
The recurrence algorithm in the x direction of DKraP is implemented, which was developed in [24] (DKTv1) (see Figure 1), given as follows:
where .
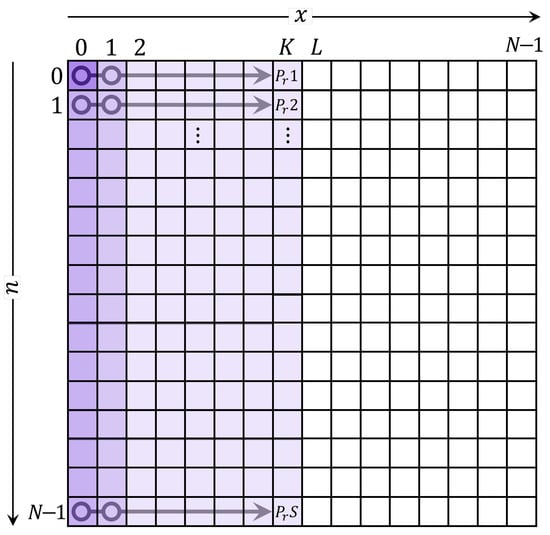
Figure 1.
Sequential DKTv1.
The definitions of variables A, B, and C are given in Table 2. To calculate the recurrence algorithm, it is necessary to predetermine the initial values. The initial sets are given in Table 2.

Table 2.
Variables and initial sets for DKTv1.
From (9), it is clear that the recurrence algorithm is carried out times. When a sequential process is applied, each process computes coefficients, where the total number of processes is equal to N.
To speed up the computation time of the DKraP coefficients, a multi-threaded implementation is proposed here. The speed-up process can be achieved because the coefficients at the nth order and in the range of are computed using the two previous coefficients, i.e., the coefficient at is computed using the coefficients at and . Therefore, the coefficients do not depend on the order n. Figure 2 shows the MDKTv1, which is a multi-threaded version of DKTv1. MDKTv1 utilizes parallel execution to speed up the computation of the DKTv1 coefficients, resulting in improved performance and efficiency.
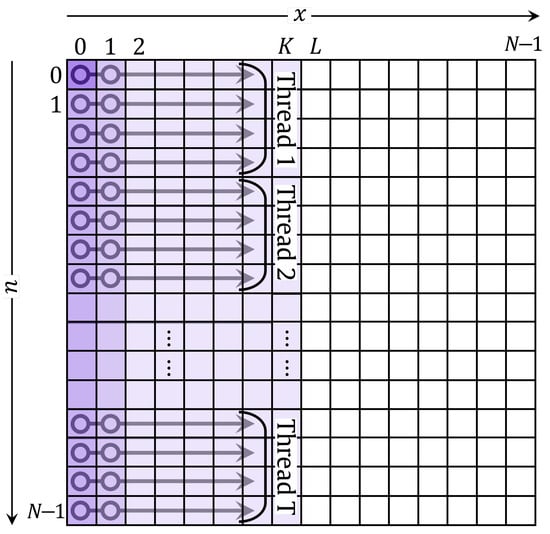
Figure 2.
Multi-threaded DKTv1.
The steps of the proposed algorithm can be summarized as follows:
- Compute initial sets and .
- Set number of threads (T).
- Start the loop for a thread to run the bunch such that bunch = N/T.
- Call the function (Krawtchouk_Rec) for multi-threaded.
- Function (Krawtchouk_Rec).
- Check for the total threads.
The design of the proposed multi-threaded method is illustrated in Algorithm 1 as a pseudocode. In Algorithm 1, the Compute_DKraP_Coefficients function takes the size of the Krawtchouk matrix N, the parameter p, and the number of threads T as inputs, and returns the resulting Krawtchouk matrix as an array. The function initializes an empty result array of size , creates a thread pool with T threads, and splits the Krawtchouk orders into T tasks. For each task, the function enqueues a process_krawtchouk_coefficients function to the thread pool with the task as an argument.
The process_krawtchouk_coefficients function takes a task as an input, which is a tuple of orders, size N, and parameter p. The function iterates through the Krawtchouk orders and computes the corresponding coefficients using the recurrence relation in the x-direction in the range of . The coefficients for x values in the range of are computed using the similarity relation.
| Algorithm 1 Compute DKraP coefficients using MDKTv1. |
| Input: N, p, T |
| N Size of DKraP (integer), |
| p parameter of DKraP (float), |
| T Number of threads (integer). |
| Output: |
| represents DKraP. |
|
|
|
|
|
|
|
|
|
|
3.2. Multi-threaded Algorithm for DKTv2
In ref. [4], the DKraP plane is partitioned into 4 parts to compute the coefficients based on a symmetry property of DKraP along the primary and secondary diagonals of the polynomial array. The proposed algorithm computes DKraP coefficients for only one part of the plane, while the coefficients of the other partitions are computed using the derived symmetry properties of the KP. Therefore, the proposed algorithm requires only recursion times, i.e., DKTv2 computes 50% less coefficients when compared to DKTv1. For more clarification, the DKraP plane and the sequential processes are shown in Figure 3. The recurrence algorithm used in DKTv2 is the same as DKTv1 (9). However, the recurrence algorithm is applied in the range , and . Then, the following recurrence relations are applied:
where (16) is used to find the coefficients in the upper triangle (Part 2), and (17) is used to find the coefficients in the left and lower triangles (Parts 3 and 4).
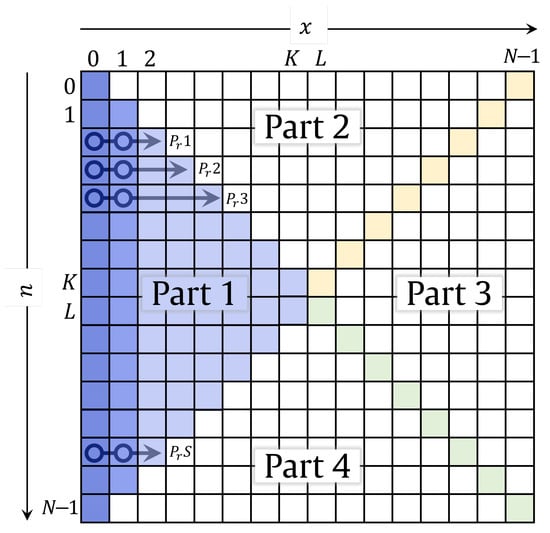
Figure 3.
Sequential DKTv2.
MDKTv2 represents the multi-threaded version of DKTv2. It should be noticed that when the threads are distributed over the DKraP orders, each thread will have a different number of coefficients to be computed. For example, if and threads are equal to 7, then each thread will process two orders. Thread_1 will process the coefficients at , which will run the recurrence relation three times. Thread_2 will process the coefficients at , which carries out the recurrence relation seven times. This multi-threaded version is called unbalanced multithreading and is shown in Figure 4a. Also, the pseudo code is given in pseudo code is given in Algorithm 2. On the other hand, we also presented a balanced multi-threaded version (see pseudo code in Algorithm 3), which ensures that each thread handles the same number of recurrence times, as shown in Figure 4b. For example, in the balanced multi-threaded version of DKTv2, if and threads are equal to 7, then each thread will process two orders. Thread_1 will process the coefficients at which will run the recurrence relation seven times. While Thread_2 processes the coefficients at , which also involves carrying out the recurrence relation seven times, all threads will handle the same processes of recurrence relations. It should be noted that the coefficients in other parts are computed using the similarity relation. However, when the similarity relation is used within the same thread, the coefficients in Part 3 will not be computed. Thus, to overcome this issue, the following similarity relation is also used:
| Algorithm 2 Compute DKraP coefficients using MDKTv2 with unbalanced threads. |
| Input: N, p, T |
| N Size of DKraP (integer), |
| p parameter of DKraP (integer), |
| T Number of threads (integer). |
| Output: |
| represents DKraP. |
|
|
|
|
|
|
|
|
|
|
|
|
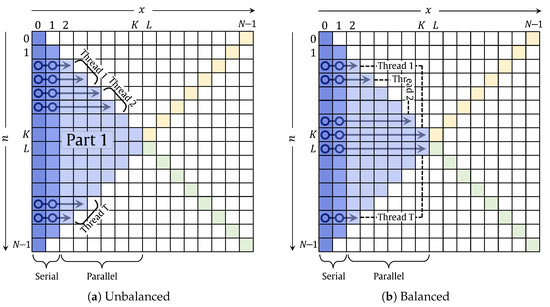
Figure 4.
Multi-threaded versions of MDKTv2.
| Algorithm 3 Compute DKraP coefficients using MDKTv2 with balanced threads. |
| Input: N, p, T |
| N Size of DKraP (integer), |
| p parameter of DKraP (float), |
| T Number of threads (integer). |
| Output: |
| represents DKraP. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3.3. Multi-Threaded Algorithm for DKTv3
The DKTv3 algorithm, which was developed by Al-Utaibi et al. [26], proposes a recurrence algorithm based on the symmetry property of DKraP similar to DKTv2 in order to reduce the recursion times required for the computation of DKraP coefficients. Most importantly, DKTv3 proposes a new approach for computing the initial value of DKraP, which prevents the initial value from dropping to zero. The approach of DKTv3 identifies the suitable non-zero values in the DKraP plane that need to be used as an initial value.
DKTv3 sets the initial value at to be commutable. This is achieved by reducing the values obtained from the polynomial coefficients’ formula, especially the Gamma function. To obtain the first initial value , the following formula is used:
where , and . The second initial value is computed at as follows:
After computing and , the coefficients and are computed using two terms recurrence relation, as follows:
After computing the four initials, the initial sets in the ranges of and are computed using the three-term recurrence relation in the n-direction, which can be written as follows:
The variables D and E are given in Table 3. In DKTv3, a developed recurrence relation is proposed to compute DKraP coefficients diagonally, as the recurrence relation in the n direction cannot be used. The recurrence relations compute the coefficients colored in yellow, as shown in Figure 5. The diagonal recurrence relation computes the coefficients along the main diagonal and . The KP coefficients along are computed as using the recurrence relation in (9). Then, the diagonal recurrence relation approach is used to compute values at the main diagonal by combining both n and x direction recurrence relations as follows:

Table 3.
Variables and initial sets for DKTv3.
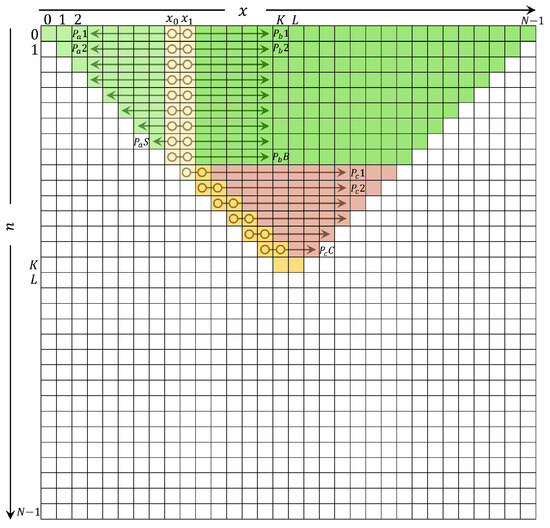
Figure 5.
Sequential DKTv3.
The variables F, G, and H are given in Table 3. It should be noted that after computing the coefficient using (23) at , Equation (24) can be applied directly to compute coefficients at .
In Figure 5, the total number of processes is given as S, where S = .
After computing the initial sets, the coefficients for the following regions are computed as follows:
The multi-threaded implementation method of the DKTv3 is shown in Figure 6. The reasons why the multithreading implementation method performs well for Regions 1, 2, and 3 are as follows:
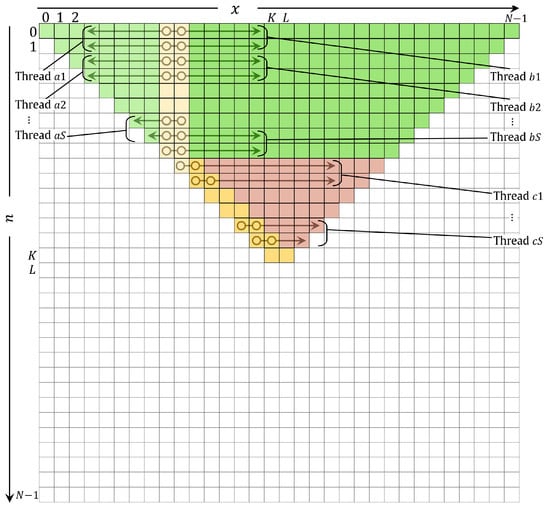
Figure 6.
Multi-threaded DKTv3.
- Region 1: This region covers the range and , with the recurrence relation given by Equation (30). The recurrence relation for each n depends only on the values of and , which are independent of each other for different values of n. This region can be parallelized across multiple threads by assigning each thread a subset of the values of n.
- Region 2: This region covers the range and , with the recurrence relation given by Equation (9). The recurrence relation for each n depends only on the values of and , which are independent of each other for different values of n. Thus, this region can be parallelized across multiple threads by assigning each thread a subset of the values of n.
- Region 3: This region covers the range and , with the recurrence relation given by Equation (9). Since the recurrence relation for each n depends only on the values of and , which are independent of each other for different values of n, this region can be parallelized across multiple threads by assigning each thread a subset of the values of n.
In Figure 6, the total number of threads is given as T, i.e., T = .
The applications of Krawtchouk polynomials in various fields such as signal processing, coding theory, and computer vision have been constrained by the computational complexity associated with their calculations. This limitation has hindered the ability to handle large datasets or perform real-time analysis. In this work, we present a multi-threaded implementation of Krawtchouk polynomials that achieved significant improvements in computational efficiency. This enhancement allows for broader applications in the aforementioned fields. For example, in image compression, faster computations facilitate the processing of high-resolution images, resulting in quicker image encoding/decoding.
4. Experimental Results
The different original recursive algorithms are compared with the proposed multi-threaded algorithms for different order sizes. The experiments were conducted on an 8-core computer using 16 GB RAM and Microsoft Windows runtime library threading. The proposed multi-threaded algorithms are analyzed at different thread numbers in order to study the effect of increasing the number of threads on performance. For the first algorithm, the improvement of the threaded version with respect to the unthreaded case is shown in Figure 7 at sizes ranging from 1024 to 8192. In general, it can be noticed that the improvement increases as the number of threads increases. This improvement is achieved by making use of the parallel processing resources enabled by distributing the workload among independent threads. More threads lead to more parallelism, which results in more improvement, reaching up to 8.6 times improvement in performance. This is limited by the amount of parallel workload available, which clearly limits the improvement in the 1024-order case when the number of threads exceeds 32. The improvement falls gradually as the number of threads increases, falling to less than 6 at 256 threads in the 1024-order case. This is because the workload associated with each thread is relatively small, as the order is small and the number of threads is large; this leads to thread overheads affecting the improvement achieved. However, this overhead diminishes with larger orders ranging from 2048 to 6144, as more workload is assigned to each thread. The optimal number of threads for managing these workloads is found to be between 32 and 64 threads in the different order sizes considered.
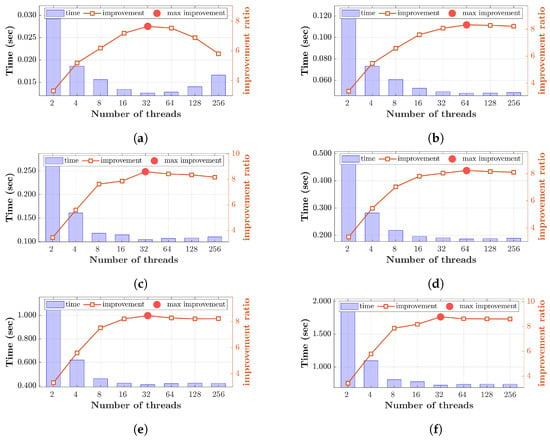
Figure 7.
Improvement of the threaded version of DKTv1 with respect to the unthreaded case for different polynomial sizes (N): (a) 1024, (b) 2048, (c) 3072, (d) 4096, (e) 6144, and (f) 8192.
For the second proposed multi-threaded algorithm, two versions were considered: the equal distribution (ED) and non-equal distribution (NED) versions. As in the previous analysis, order sizes ranged from 1024 to 8192, and different thread numbers, ranging from 2 to 256, were tested in each case. It was observed that the balanced threaded algorithm (ED) consistently outperformed the unbalanced threaded version (NED) in all considered cases. This comes from the fact that the balanced version evenly distributes the workload among the threads, leading to higher utilization of the processing resources as opposed to the unbalanced version (NED), which often results in some threads finishing early due to lighter workloads, leaving processing resources underutilized. These unused resources could be utilized by other threads, thus reducing idle time, leading to greater efficiency, and narrowing the performance gap between the two versions as the number of threads increases. As the number of threads increases, the delay decreases, consequently enhancing the performance of both the balanced (ED) and unbalanced (NED) versions. This improvement is achieved through the parallelism facilitated by the independent threads. The improvement reaches its peak when using 16 to 128 threads but begins to decline afterward, especially at smaller order sizes (1024). This drop in performance is caused by the overhead associated with the increased number of thread creations and context switching (see Figure 8).
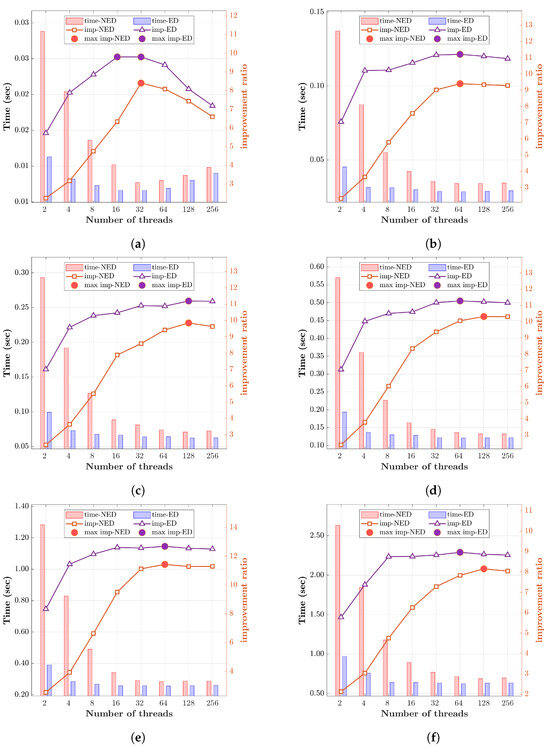
Figure 8.
Improvement of the threaded version (for both the balanced ED and unbalanced NED versions) of DKTv2 with respect to the unthreaded case for different polynomial sizes (N): (a) 1024, (b) 2048, (c) 3072, (d) 4096, (e) 6144, and (f) 8192.
The third proposed multi-threaded algorithm behaves differently according to the initialization parameter (p) of DKraP; thus, three cases are considered, namely p = 0.1, 0.25, and 0.5. For each considered parameter value, the order size varies from 1024 to 8192 at different thread numbers. For the p = 0.1 case, it can be seen from Figure 9 that the lowest delays are achieved at 32 and 64 threads with a clear drop in improvement at a higher and lower number of threads. It can be observed that at an order size of 1024, the delays experienced with 128 and 256 threads are higher than those with 2 threads, reaching up to a 50% increase in delay. Nevertheless, all threaded cases across different thread counts show a reduction in delay compared to the unthreaded case, as indicated by an improvement factor greater than 1. The highest improvement is 2.93, achieved at an order size of 8192 with 32 threads, while the lowest improvement is 1.21 at an order size of 1024 with 256 threads.
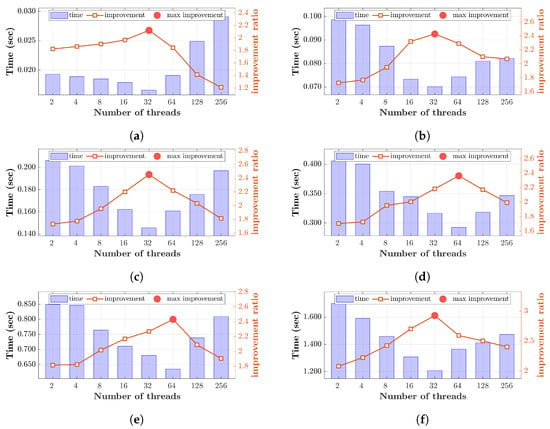
Figure 9.
Improvement of the threaded version of DKTv3 at DKraP parameter p = 0.1 with respect to the unthreaded case for different polynomial sizes (N): (a) 1024, (b) 2048, (c) 3072, (d) 4096, (e) 6144, and (f) 8192.
For the case of p = 0.25, it can be seen from Figure 10 that the highest improvement is achieved at 32 and 64 threads with a clear drop in improvement at a lower number of threads. At an order size of 1024, the delay at 256 threads is higher than the delay with 2 threads, reaching up to a 25% higher delay, and resulting in a clear drop in improvement. This point represents the lowest improvement among all sizes and thread numbers, namely 1.44. On the other hand, the highest improvement is achieved at 64 threads in the 6144 order size, reaching a value of 2.59.
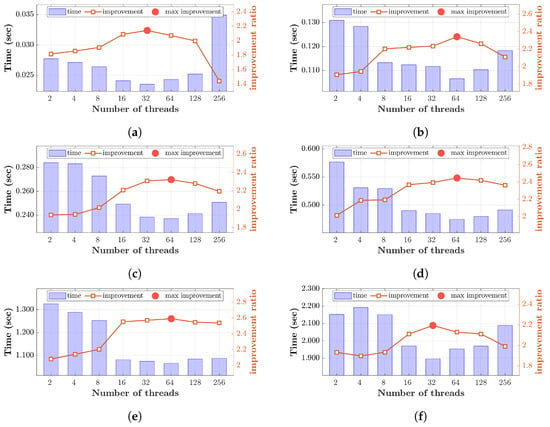
Figure 10.
Improvement of the threaded version of DKTv3 at DKraP parameter p = 0.25 with respect to the unthreaded case for different polynomial sizes (N): (a) 1024, (b) 2048, (c) 3072, (d) 4096, (e) 6144, and (f) 8192.
At p = 0.5, Figure 11 shows the delay and improvements achieved by the threaded algorithm compared to the unthreaded case for the same parameter value. Across all order sizes, the delay decreases as the number of threads increases, reaching the maximum improvement with 64 and 128 threads. Afterward, as the number of threads continues to increase, the delay begins to rise, leading to a drop in improvement. The order size of 1024 exhibits the most significant drop of 28.5 28.5% at 256 threads as compared to the highest improvement at 64 threads. The highest improvement observed was 4.33, achieved at an order size of 2048 with 64 threads, while the lowest improvement was 1.76 at an order size of 4096 with only 2 threads.
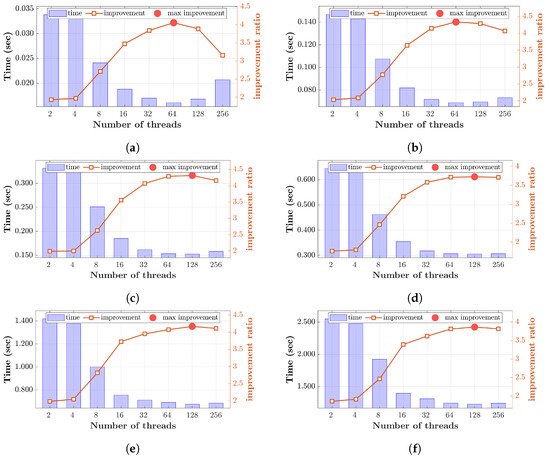
Figure 11.
Improvement of the threaded version of DKTv3 at DKraP parameter p = 0.5 with respect to the unthreaded case for different polynomial sizes (N): (a) 1024, (b) 2048, (c) 3072, (d) 4096, (e) 6144, and (f) 8192.
Figure 12 shows all the delays of the three unthreaded algorithms and their optimal timings in the threaded versions. Among the unthreaded algorithms, the third algorithm, namely DKTv3 with p = 0.1, has the lowest timing. Despite this, when threading is applied to the algorithms, the equally distributed version of the second algorithm, MDKTv2 ED, achieves the lowest timing in all the considered order sizes. The latter achieves a timing reduction of 13% to 48% with respect to the threaded version of the first algorithm, MDKTv1. Similarly, it reduces the processing time as compared to the threaded version of the third algorithm, from a minimum of 48% to a maximum of 60%, from 67% to 76%, and from 49% to 62%, at p = 0.1, 0.25, and 0.5, respectively.
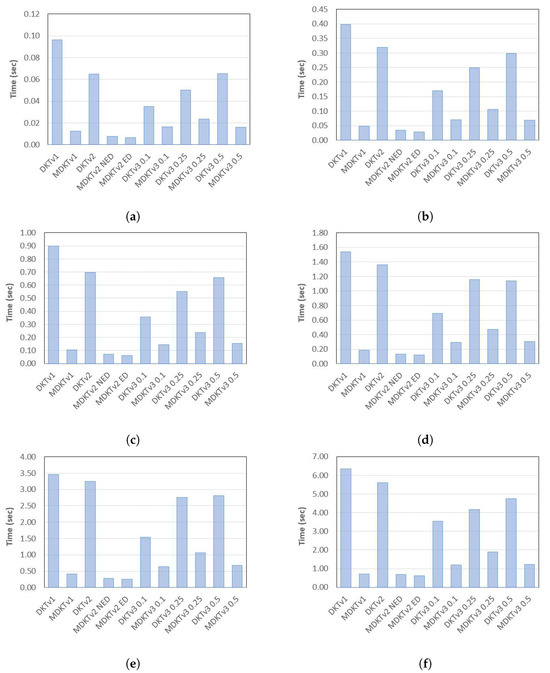
Figure 12.
Delays of the unthreaded algorithms and their optimal values in the threaded cases for different polynomial sizes (N): (a) 1024, (b) 2048, (c) 3072, (d) 4096, (e) 6144, and (f) 8192.
In summary, the proposed threaded implementations resulted in improved computational efficiency, achieving up to 8.6 times, 12.69 times, and 4.33 times faster computations for the DKTv1, DKTv2, and DKTv3 algorithms, respectively. The third algorithm, DKTv3, experienced the least improvement, which can be linked to the structure of the algorithm. The algorithm is divided into three regions, and each region is threaded separately. The threads of each region start after the previous region is completely computed. This serial sequence reduces the effective improvement. This effect is clear as the two cases, p = 0.1 (Figure 9) and p = 0.25 (Figure 10) in MDTv3, show lower improvement compared to p = 0.5 (Figure 11). This is attributed to the fact that the latter has two regions only, since x0 and x1 are exactly in the middle columns of the matrix. Thus, there is no region 3 when p = 0.5, leading to higher improvement when multithreading is applied.
Theoretically, the maximum improvement that can be achieved depends on the number of available parallel processing resources (cores), which is 8 in the testbed. This may be restricted by the serial part in the algorithm, where a stream of calculations is executed serially, thus reducing the achieved improvement according to Amdahl’s law. It can be seen that the improvement exceeds 8 in some cases. This is due to the effect of similarity, where in the unthreaded case, the similarity is applied after all coefficients are calculated, giving more possible cache misses. In contrast, in the threaded case, each calculated coefficient is directly stored in its symmetric location within each thread, increasing the likelihood of a cache hit. Additionally, the algorithm is executed in a system where other processes exist. Consequently, the unthreaded case does not fully utilize the single core processing resources, whereas when multiple threads are created and each core is given a set of threads, the core resources’ utilization by the algorithm’s threads will be higher than with a single thread. The serial calculations have minimal impact on performance as they represent a small percentage of the total coefficient calculations. For example, in MDKTv1 (Figure 2) with , the number of serially calculated coefficients is 2048 (first two columns), whereas the total number of coefficients to be calculated is (522240). Thus, the serial part represents less than 0.4% of the total computations. This percentage falls at higher values of N.
In general, the improvement that can be achieved depends on the structure of the algorithm, finding serial and potential parallel computations, restructuring the algorithm to exploit parallelism, and distributing the parallel computations among available resources to maximize utilization and performance.
5. Conclusions
This paper introduces a computationally efficient solution for the computation of DKraP coefficients. Utilizing a multi-threaded implementation method, the proposed algorithm significantly reduces computation time by concurrently executing independent tasks across different threads. The evaluation across various DKraP sizes and polynomial parameters demonstrates its effectiveness, particularly in leveraging the parallel processing capabilities of modern CPUs. Beyond the fast execution time, the proposed method extends its applicability to larger polynomial sizes and a broader range of Krawtchouk polynomial parameters. Additionally, this paper introduces an accurate recurrence algorithm selection scheme, which enhances the robustness of the proposed method. Overall, this paper offers a practical and efficient solution for DKraP coefficient computation, making it a compelling choice for diverse applications reliant on discrete orthogonal polynomials. The work can be further extended to explore graphical processing unit (GPU)-based parallel processing techniques, in addition to possibly realizing the algorithms on FPGA or ASIC-based accelerators.
Author Contributions
Methodology, S.H.A. and W.N.F.; software, W.N.F., A.H.A.-s. and B.M.M.; validation, M.A., B.M.M. and S.H.A.; formal analysis, W.N.F. and A.H.A.-s.; investigation, A.H.A.-s., B.M.M. and M.A.; writing—original draft preparation, S.H.A., B.M.M. and W.N.F.; writing—review and editing, A.H.A.-s. and M.A.; visualization, S.H.A. and M.A.; supervision, S.H.A.; project administration, W.N.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| DKraPs | discrete Krawtchouk polynomials |
| CPU | central processing unit |
| IoT | Internet of Things |
| OP | orthogonal polynomial |
| DKraM | discrete Krawtchouk moment |
| ED | equal distribution |
| NED | non-equal distribution |
| KPCs | Krawtchouk polynomial coefficients |
References
- Mahmood, B.M.; Younis, M.I.; Ali, H.M. Construction of a general-purpose infrastructure for RFID–based applications. J. Eng. 2013, 19, 1425–1442. [Google Scholar] [CrossRef]
- Ahmed, H.M. Recurrence relation approach for expansion and connection coefficients in series of classical discrete orthogonal polynomials. Integral Transform. Spec. Funct. 2009, 20, 23–34. [Google Scholar] [CrossRef]
- Yang, B.; Suk, T.; Flusser, J.; Shi, Z.; Chen, X. Rotation invariants from Gaussian-Hermite moments of color images. Signal Process. 2018, 143, 282–291. [Google Scholar] [CrossRef]
- Abdulhussain, S.H.; Ramli, A.R.; Al-Haddad, S.A.R.; Mahmmod, B.M.; Jassim, W.A. Fast Recursive Computation of Krawtchouk Polynomials. J. Math. Imaging Vis. 2018, 60, 285–303. [Google Scholar] [CrossRef]
- Asli, B.H.S.; Flusser, J. Fast computation of Krawtchouk Moments. Inf. Sci. 2014, 288, 73–86. [Google Scholar] [CrossRef]
- Shakibaei Asli, B.H.; Paramesr, R. Digital Filter Implementation of Orthogonal Moments. In Digital Filters and Signal Processing; InTech: Houston, TX, USA, 2013. [Google Scholar] [CrossRef][Green Version]
- Chang, K.H.; Paramesran, R.; Asli, B.H.S.; Lim, C.L. Efficient Hardware Accelerators for the Computation of Tchebichef Moments. IEEE Trans. Circuits Syst. Video Technol. 2012, 22, 414–425. [Google Scholar] [CrossRef]
- Mennesson, J.; Saint-Jean, C.; Mascarilla, L. Color Fourier–Mellin descriptors for image recognition. Pattern Recognit. Lett. 2014, 40, 27–35. [Google Scholar] [CrossRef]
- Genberg, V.L.; Michels, G.J.; Doyle, K.B. Orthogonality of Zernike polynomials. In Proceedings of the Optomechanical Design and Engineering, Seattle, WA, USA, 7–11 July 2002; SPIE: Bellingham, WA, USA, 2002; Volume 4771, pp. 276–286. [Google Scholar]
- Yap, P.-T.; Paramesran, R.; Ong, S.-H. Image analysis by krawtchouk moments. IEEE Trans. Image Process. 2003, 12, 1367–1377. [Google Scholar] [CrossRef] [PubMed]
- Chong, C.W.; Raveendran, P.; Mukundan, R. Translation and scale invariants of Legendre moments. Pattern Recognit. 2004, 37, 119–129. [Google Scholar] [CrossRef]
- Abdulhussain, S.H.; Mahmmod, B.M.; Baker, T.; Al-Jumeily, D. Fast and accurate computation of high-order Tchebichef polynomials. Concurr. Comput. Pract. Exp. 2022, 34, e7311. [Google Scholar] [CrossRef]
- Junkins, J.L.; Younes, A.B.; Bai, X. Orthogonal polynomial approximation in higher dimensions: Applications in astrodynamics. Adv. Astronaut. Sci 2013, 147, 531–594. [Google Scholar]
- Chihara, T.S. An Introduction to Orthogonal Polynomials; Dover Publications: Mineola, NY, USA, 2011. [Google Scholar]
- Pee, C.Y.; Ong, S.; Raveendran, P. Numerically efficient algorithms for anisotropic scale and translation Tchebichef moment invariants. Pattern Recognit. Lett. 2017, 92, 68–74. [Google Scholar] [CrossRef]
- Di Ruberto, C.; Loddo, A.; Putzu, L. On The Potential of Image Moments for Medical Diagnosis. J. Imaging 2023, 9, 70. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Meng, M.Q.H.; Liu, L. Direct Visual Servoing Based on Discrete Orthogonal Moments. IEEE Trans. Robot. 2024, 40, 1795–1812. [Google Scholar] [CrossRef]
- Venkataramana, A.; Ananth Raj, P. Combined Scale and Translation Invariants of Krawtchouk Moments. In Proceedings of the National Conference on Computer Vision, Pattern Recognition, Image Processing and Graphics, Gandhinagar, India, 11–13 January 2008. [Google Scholar]
- Honarvar Shakibaei Asli, B.; Rezaei, M.H. Four-Term Recurrence for Fast Krawtchouk Moments Using Clenshaw Algorithm. Electronics 2023, 12, 1834. [Google Scholar] [CrossRef]
- Koehl, P. Fast recursive computation of 3d geometric moments from surface meshes. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 2158–2163. [Google Scholar] [CrossRef] [PubMed]
- Asli, B.H.S.; Paramesran, R.; Lim, C.L. The fast recursive computation of Tchebichef moment and its inverse transform based on Z-transform. Digital Signal Process. 2013, 23, 1738–1746. [Google Scholar] [CrossRef]
- Rivera-Lopez, J.S.; Camacho-Bello, C.; Gutiérrez-Lazcano, L. Computation of 2D and 3D High-order Discrete Orthogonal Moments. In Recent Progress in Image Moments and Moment Invariants; Papakostas, G.A., Ed.; Gate to Computer Science and Research: Democritus, Greece, 2021; Volume 7, Chapter 3; pp. 53–74. [Google Scholar] [CrossRef]
- Mahmmod, B.M.; Flayyih, W.N.; Fakhri, Z.H.; Abdulhussain, S.H.; Khan, W.; Hussain, A. Performance enhancement of high order Hahn polynomials using multithreading. PLoS ONE 2023, 18, e0286878. [Google Scholar] [CrossRef] [PubMed]
- Jassim, W.A.; Raveendran, P.; Mukundan, R. New orthogonal polynomials for speech signal and image processing. IET Signal Process. 2012, 6, 713–723. [Google Scholar] [CrossRef]
- Zhang, G.; Luo, Z.; Fu, B.; Li, B.; Liao, J.; Fan, X.; Xi, Z. A symmetry and bi-recursive algorithm of accurately computing Krawtchouk moments. Pattern Recognit. Lett. 2010, 31, 548–554. [Google Scholar] [CrossRef]
- AL-Utaibi, K.A.; Abdulhussain, S.H.; Mahmmod, B.M.; Naser, M.A.; Alsabah, M.; Sait, S.M. Reliable Recurrence Algorithm for High-Order Krawtchouk Polynomials. Entropy 2021, 23, 1162. [Google Scholar] [CrossRef] [PubMed]
- He, W.; Li, G.; Nie, Z. An adaptive sparse polynomial dimensional decomposition based on Bayesian compressive sensing and cross-entropy. Struct. Multidiscip. Optim. 2022, 65, 26. [Google Scholar] [CrossRef]
- He, W.; Li, G.; Nie, Z. A novel polynomial dimension decomposition method based on sparse Bayesian learning and Bayesian model averaging. Mech. Syst. Signal Process. 2022, 169, 108613. [Google Scholar] [CrossRef]
- Vittaldev, V.; Russell, R.P.; Linares, R. Spacecraft uncertainty propagation using gaussian mixture models and polynomial chaos expansions. J. Guid. Control Dyn. 2016, 39, 2615–2626. [Google Scholar] [CrossRef]
- Xiao, B.; Zhang, Y.; Li, L.; Li, W.; Wang, G. Explicit Krawtchouk moment invariants for invariant image recognition. J. Electron. Imaging 2016, 25, 023002. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Y. A Piecewise and Bi-recursive Algorithm for Computing High-order Krawtchouk Moments. In Proceedings of the 2015 4th International Conference on Computer Science and Network Technology (ICCSNT), Harbin, China, 19–20 December 2015; pp. 1414–1418. [Google Scholar]
- Yap, P.T.; Raveendran, P.; Ong, S.H. Krawtchouk moments as a new set of discrete orthogonal moments for image reconstruction. In Proceedings of the 2002 International Joint Conference on Neural Networks, IJCNN ’02, Honolulu, HI, USA, 12–17 May 2002; pp. 908–912. [Google Scholar] [CrossRef]
- Koekoek, R.; Swarttouw, R.F. The Askey-scheme of hypergeometric orthogonal polynomials and its q-analogue. arXiv 1996, arXiv:math/9602214. [Google Scholar]
- Nikiforov, A.F.; Uvarov, V.B.; Suslov, S.K.; Nikiforov, A.F.; Uvarov, V.B.; Suslov, S.K. Classical Orthogonal Polynomials of a Discrete Variable; Springer: Berlin/Heidelberg, Germany, 1991. [Google Scholar]
- Milovanović, G.V.; Stanić, M.P.; Mladenović, T.V.T. Gaussian type quadrature rules related to the oscillatory modification of the generalized Laguerre weight functions. J. Comput. Appl. Math. 2024, 437, 115476. [Google Scholar] [CrossRef]
- Griffel, D. An introduction to orthogonal polynomials, by Theodore S. Chihara. Pp xii, 249.£ 26· 30. 1978. SBN 0 677 04150 0 (Gordon and Breach). Math. Gaz. 1979, 63, 222. [Google Scholar] [CrossRef]
- Rivero-Castillo, D.; Pijeira, H.; Assunçao, P. Edge detection based on Krawtchouk polynomials. J. Comput. Appl. Math. 2015, 284, 244–250. [Google Scholar] [CrossRef]
- Abd-Elhameed, W.M.; Ahmed, H.M.; Napoli, A.; Kowalenko, V. New formulas involving Fibonacci and certain orthogonal polynomials. Symmetry 2023, 15, 736. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; US Government Printing Office: Washington, DC, USA, 1948; Volume 55. [Google Scholar]
- Şahin, R.; Yağcı, O. A new generalization of pochhammer symbol and its applications. Appl. Math. Nonlinear Sci. 2020, 5, 255–266. [Google Scholar] [CrossRef]
- Koepf, W.; Schmersau, D. Representations of orthogonal polynomials. J. Comput. Appl. Math. 1998, 90, 57–94. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).