Topology Optimization and Efficiency Evaluation of Short-Fiber-Reinforced Composite Structures Considering Anisotropy
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials and Material Models
2.2. Methods
2.2.1. Topology Optimization
| minimize | f(x) = 0.5uTK(ρ(x), A(x))u, |
| by varying | ρ(x) ∈ (0, 1], x ∈ Ω, |
| subject to | h(x) = K(ρ(x), A(x))u − F = 0, |
| g1(x) = ∫ ρ(x)dΩ − Vret ≤ 0, | |
| g2(x) = ∫|∇ρ(x)|dΩ − δ ≤ 0, | |
| g3(x) = ρi − ρk ≤ 0 ∀ xi = xk, yi = yk, |zi| ≥ |zk|, |
Unidisciplinary Topology Optimization Considering Constant Molding
Multidisciplinary Topology Optimization: Considering Variable Molding
| Algorithm 1. Multidisciplinary topology optimization. |
| Input: BCstruct, BCinjMold, MPinjMold, MPmatrix+fiber, OPtopoOpt, th, δmap, Vdef, εobj, geo.stp (Optional) Output: topoOptStruct.stl write materialProperties.txt ← MPfiber+matrix write topoParameters.txt ← OPtopoOpt meshstruct, designelements, frozenelements = AnsysWorkbench_Mesh(BCstruct, geo.stp); write designRegionMesh.ans ← meshstruct, design.txt ← designelements, frozen.txt ← frozenelements; g = 1; counter_epsilon = 0; while (counter_epsilon < Kε) do if g == 1 then reducedMesh.ans = designRegionMesh.ans; else domain_mesh_reduced = delete_elements(designRegionMesh.ans, th, (density.txt)g-1); write reducedMesh.ans ← domain_mesh_reduced end if meshinjMold, A = AutodeskMoldFlow(reducedMesh.ans, BCinjMold, MPinjMold); write meshMoldFlow.pat ← meshinjMold, fiberOrientMoldFlow.xml ← A; A’ = DigimatMAP(fiberOrientMoldFlow.xml, meshMoldFlow.pat, designRegionMesh.ans, δ); write fiberOrientAnsys.xml ← A’; KEL = AnisoTopo(materialProperties.txt, fiberOrientAnsys.xml, topoPararmeters.txt, designRegionMesh.ans, design.txt, frozen.txt); write apdl_pre.txt ← KEL; if g == 1 then Wg = AnsysWorkbench_StructuralAnalysis(designRegionMesh.ans, apdl_pre.txt, BCstruct); else Wg = AnsysWorkbench_StructuralAnalysis(designRegionMesh.ans, apdl_pre.txt, BCstruct, ρ); εg = |(Wg − Wg-1)/Wg-1| if εg <= εobj then counter_epsilon ++ else counter_epsilon = 0 end if end if ρ = AnsysWorkbench_TopologyOptimization_Iteration(designRegionMesh.ans, design.txt, frozen.txt, Vdef, topoPara, apdl_pre.txt, Wg) write density.topo ← ρ; Convert density.topo to (density.txt)g with HDFView(); g++ end while topoOptStruct = delete_elements(designRegionMesh.ans, th, (density.txt)g-1); write topoOptStruct.stl ← topoOptStruct |
2.2.2. Metrics for Evaluating the Structure Design Quality of Composite Materials
2.2.3. Bracket Manufacturing and Load Testing Technique
3. Results
3.1. Topology of Optimal Constant Molding Structures
3.1.1. Topology Optimization and Structural Arrangement Quality Assessment
3.1.2. Influence of the Relationship between Elastic Moduli E1 and E2 of Composite Material on the Resulting Topology
3.1.3. Experimental Verification
3.2. Topology-Optimal Variable Molding Structures
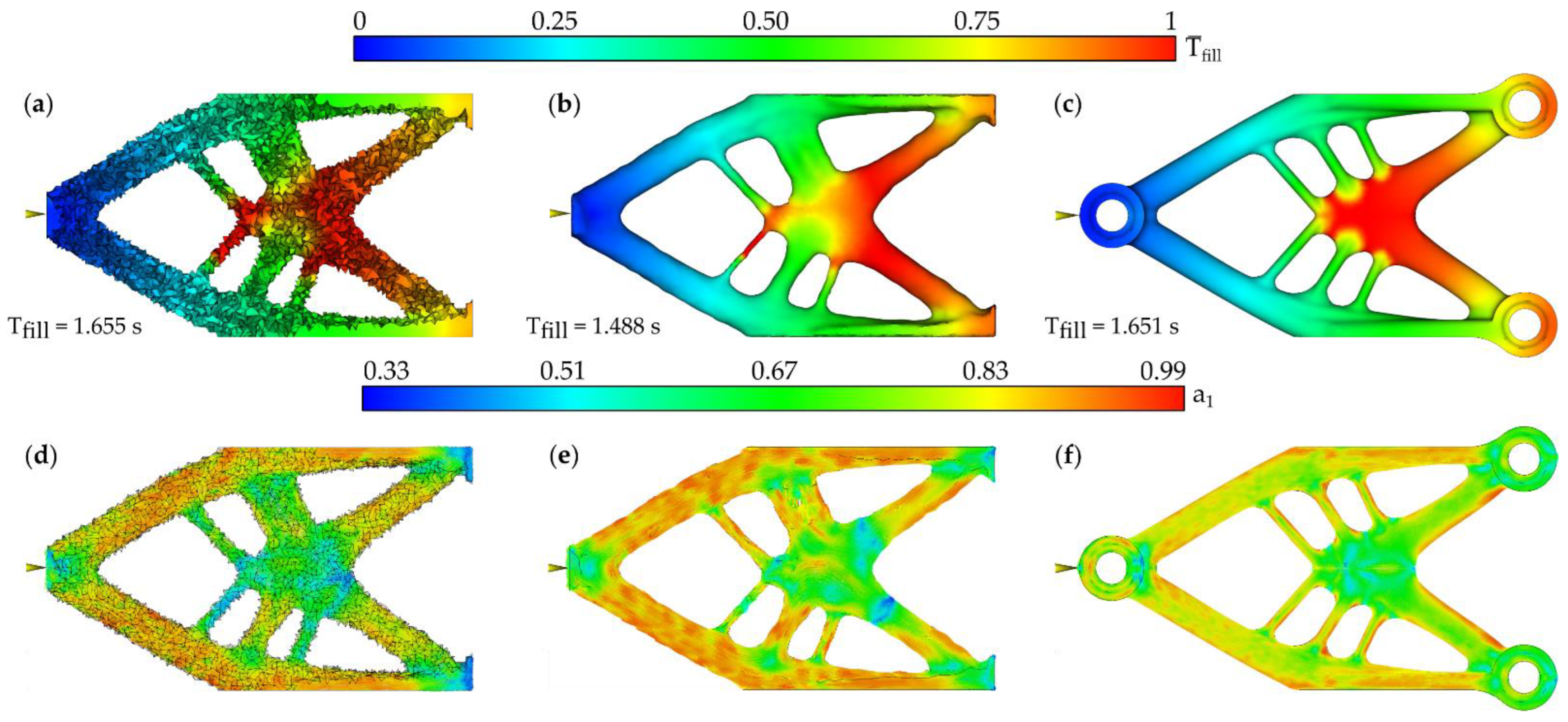
3.2.1. Topology Optimization and Topology Assessment
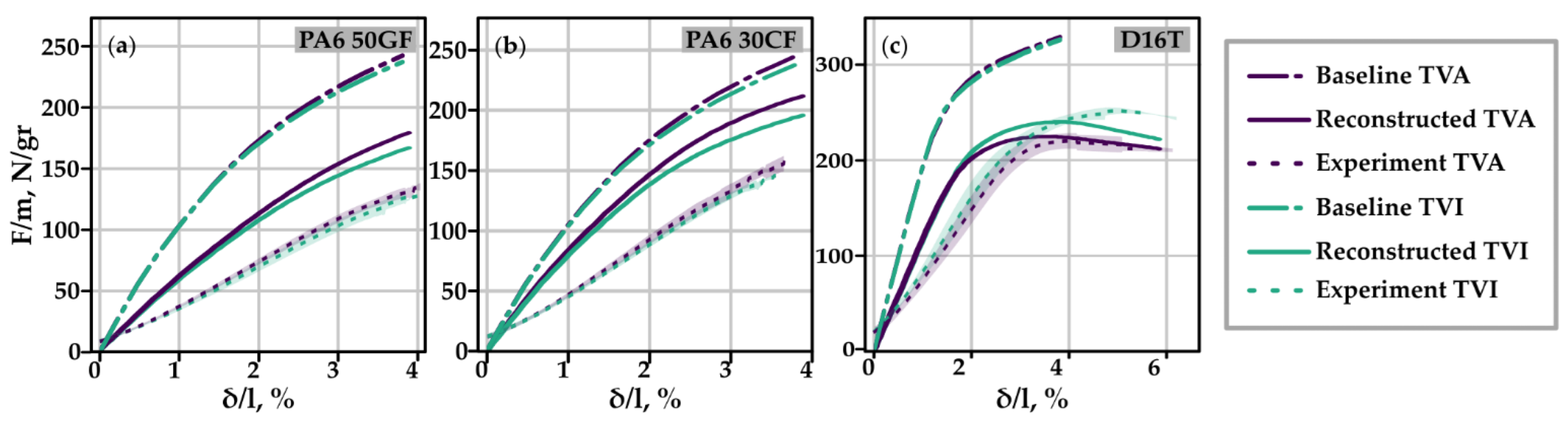
3.2.2. Topology Reconstruction
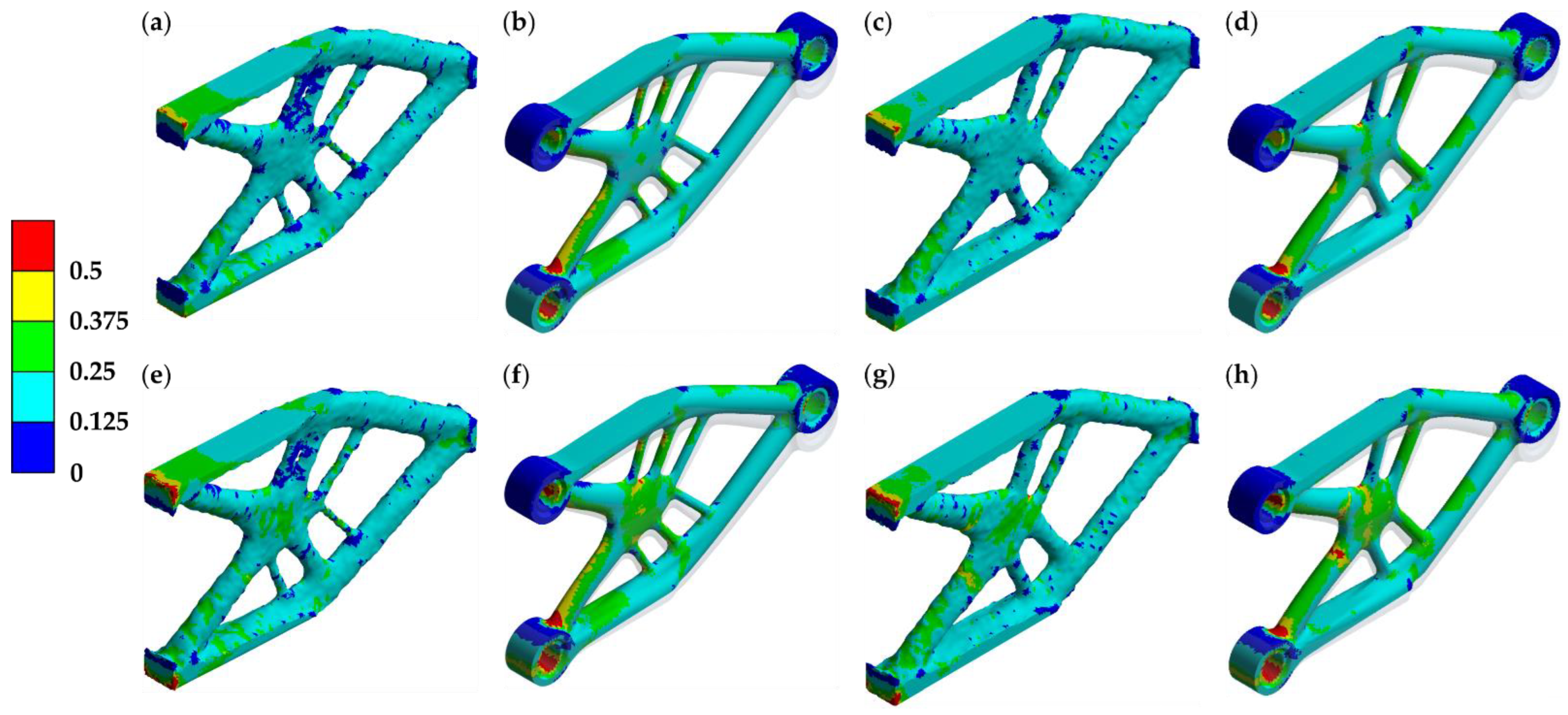
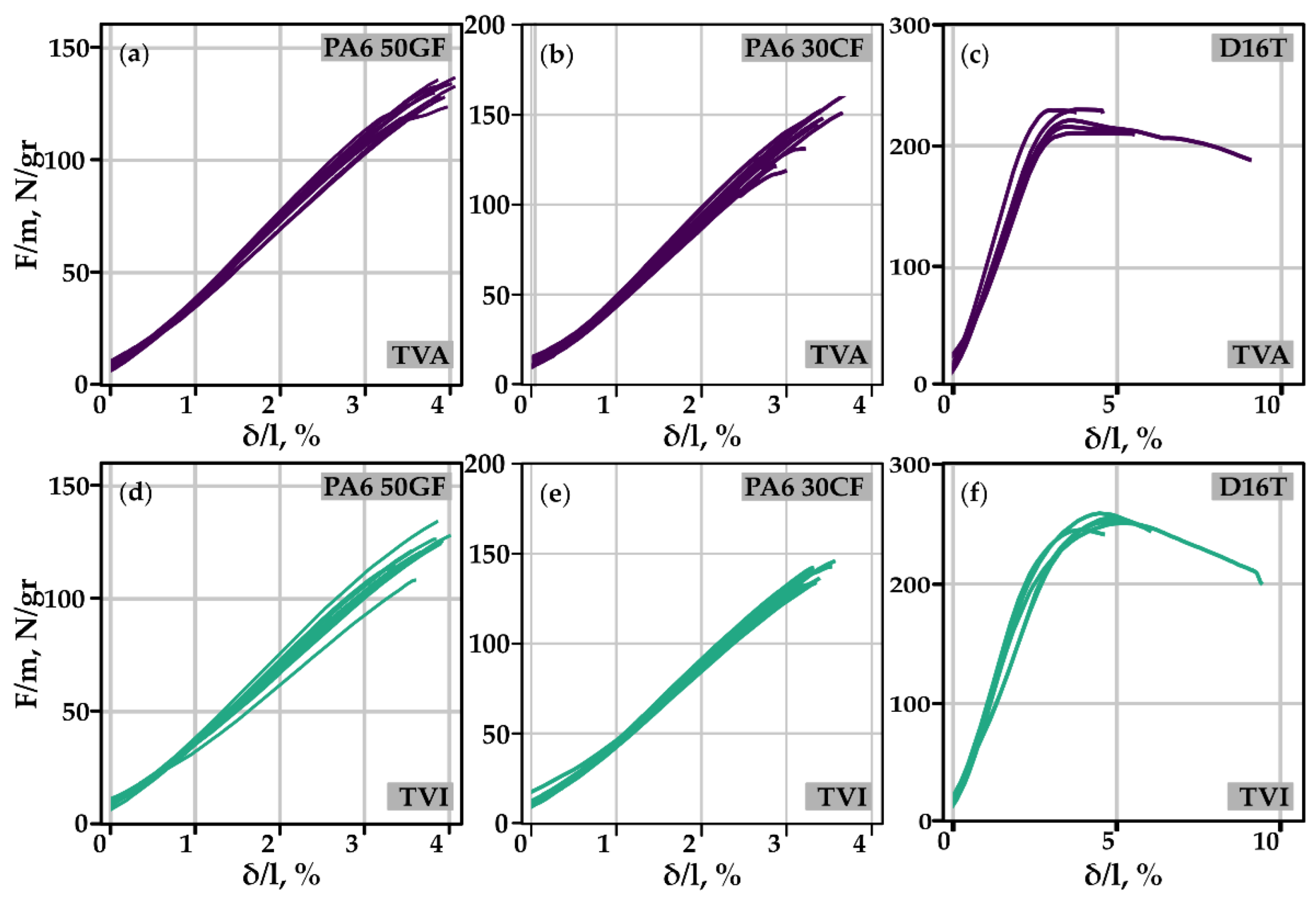
3.2.3. Experimental Validation
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhitomirskiy, G. Konstruktsiya Samoletov: Uchebnoye Posobiye [Aircraft Structure: Textbook], 4th ed.; Mashinostroyeniye: Moscow, Russia, 2018; ISBN 978-5-9500364-8-4. [Google Scholar]
- Yendogur, A. Proyektirovaniye Aviatsionnykh Konstruktsiy: Proyektirovaniye Konstruktsiy Detaley i Uzlov [Aircraft Structural Design: Structural Design of Parts and Assemblies]; MAI-Print: Moscow, Russia, 2009; ISBN 9785703521038. [Google Scholar]
- Kobelev, V. Design and Analysis of Composite Structures for Automotive Applications: Chassis and Drivetrain; WorldCat: Tarboro, NC, USA, 2019; ISBN 9781119513841. [Google Scholar]
- Wijker, J.J. Spacecraft Structures; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-75552-4. [Google Scholar]
- Alejandro Ortiz Morales, F.; Bejarano, W.; Zorto, F.; Mejuto, J.; Ortiz, F.; Bejarano Diana Rosales, W. Chassis Optimization of a 1U Cubesat Made in a Developing Country. In Proceedings of the 73rd International Astronautical Conference, Paris, France, 18–22 September 2022. [Google Scholar]
- Feng, Y.; Wu, X.; Chen, W.; Xie, Y.; Yu, T.; Hao, Y. Optimal Design of Space Assembly Microsatellite Structure Based on Sequential Quadratic Programming. Aircr. Eng. Aerosp. Technol. 2022, 95, 145–154. [Google Scholar] [CrossRef]
- Kawachi, T.; Kimoto, N.; Tsunemi, Y. Stiffness Increase and Weight Reduction Based on Stiffness Evaluation Techniques. Nippon Steel Tech. Rep. 2019, 122, 93–98. [Google Scholar]
- Formula_1_-_Technical_Regulations_-_2022_-_iss_9_-_2022-02-18. Available online: https://www.fia.com/sites/default/files/formula_1_-_technical_regulations_-_2022_-_iss_9_-_2022-02-18.pdf (accessed on 5 February 2024).
- Huh, J.; Kwon, S. A Practical Design Approach for a Single-Stage Sounding Rocket to Reach a Target Altitude. Aeronaut. J. 2022, 126, 1084–1100. [Google Scholar] [CrossRef]
- Gudmundsson, S. Aircraft Cost Analysis. In General Aviation Aircraft Design; Elsevier: Amsterdam, The Netherlands, 2014; pp. 33–53. [Google Scholar]
- Vasigh, B.; Azadian, F. Aircraft Financial and Operational Efficiencies. In Aircraft Valuation in Volatile Market Conditions: Guiding Toward Profitability and Prosperity; Springer International Publishing: Cham, Switzerland, 2022; pp. 113–163. ISBN 978-3-030-82450-1. [Google Scholar]
- Shukla, S.; Singh, H.V.; Mishra, L. Improvement in Design of Engines to Reduce Emissions in Aircarft and Increase Fuel Efficiency. In Outcomes of Best Practices in Classroom Research; L Ordine Nuovo Publication: New Delhi, India, 2021; ISBN 978-93-92995-10-1. [Google Scholar]
- Peters, M.; Kumpfert, J.; Ward, C.H.; Leyens, C. Titanium Alloys for Aerospace Applications. Adv. Eng. Mater. 2003, 5, 419–427. [Google Scholar] [CrossRef]
- Tseng, H.-C.; Chang, R.-Y.; Hsu, C.-H. Numerical Investigations of Fiber Orientation Models for Injection Molded Long Fiber Composites. Int. Polym. Process. 2018, 33, 543–552. [Google Scholar] [CrossRef]
- Buhl, H. (Ed.) Advanced Aerospace Materials; Springer: Berlin/Heidelberg, Germany, 1992; ISBN 978-3-642-50161-6. [Google Scholar]
- Garvey, R.E.; Andriulli, J.B.; Mckeever, J.W. Minimum-Gage, Maximum-Stiffness Graphite/Thermoplastic Spacecraft Structures. Polym. Compos. 1991, 12, 108–118. [Google Scholar] [CrossRef]
- Maleki, H.; Durães, L.; Portugal, A. An Overview on Silica Aerogels Synthesis and Different Mechanical Reinforcing Strategies. J. Non-Cryst. Solids 2014, 385, 55–74. [Google Scholar] [CrossRef]
- Tiwary, A.; Kumar, R.; Chohan, J.S. A Review on Characteristics of Composite and Advanced Materials Used for Aerospace Applications. In Materials Today: Proceedings; Elsevier: Amsterdam, The Netherlands, 2021; Volume 51, pp. 865–870. [Google Scholar]
- Tang, S.; Hu, C. Design, Preparation and Properties of Carbon Fiber Reinforced Ultra-High Temperature Ceramic Composites for Aerospace Applications: A Review. J. Mater. Sci. Technol. 2017, 33, 117–130. [Google Scholar] [CrossRef]
- Mangalgiri, P.D. Composite Materials for Aerospace Applications. Bull. Mater. Sci. 1999, 22, 657–664. [Google Scholar] [CrossRef]
- Bhat, A.; Budholiya, S.; Raj, S.A.; Sultan, M.T.H.; Hui, D.; Shah, A.U.M.; Safri, S.N.A. Review on Nanocomposites Based on Aerospace Applications. Nanotechnol. Rev. 2021, 10, 237–253. [Google Scholar] [CrossRef]
- Romero-Fierro, D.; Bustamante-Torres, M.; Bravo-Plascencia, F.; Esquivel-Lozano, A.; Ruiz, J.-C.; Bucio, E. Recent Trends in Magnetic Polymer Nanocomposites for Aerospace Applications: A Review. Polymers 2022, 14, 4084. [Google Scholar] [CrossRef] [PubMed]
- Rajput, A.; Upma; Shukla, S.K.; Thakur, N.; Debnath, A.; Mangla, B. Advanced Polymeric Materials for Aerospace Applications. In Aerospace Polymeric Materials; Wiley: Hoboken, NJ, USA, 2022; pp. 117–136. [Google Scholar]
- Sokolowski, W.M.; Tan, S.C. Advanced Self-Deployable Structures for Space Applications. J. Spacecr. Rockets 2007, 44, 750–754. [Google Scholar] [CrossRef]
- Liu, Y.; Du, H.; Liu, L.; Leng, J. Shape Memory Polymers and Their Composites in Aerospace Applications: A Review. Smart Mater. Struct. 2014, 23, 023001. [Google Scholar] [CrossRef]
- Soutis, C. Fibre Reinforced Composites in Aircraft Construction. Prog. Aerosp. Sci. 2005, 41, 143–151. [Google Scholar] [CrossRef]
- García, J.A. Study On 3d Printing with Fiber Reinforcement and Its Aerospace Applications. Bachelor’s Thesis, University of Cádiz, Cádiz, Spain, 2021. [Google Scholar]
- Öztoprak, N. Novel AA7075/AA2124-SiC-17p Laminated Structures for Aerospace Applications: A Comparative Study into the Mechanical Performance of PA6 and PA66 Composite Interlayers. J. Compos. Mater. 2022, 56, 4547–4559. [Google Scholar] [CrossRef]
- Neveu, F.; Cornu, C.; Olivier, P.; Castanié, B. Manufacturing and Impact Behaviour of Aeronautic Overmolded Grid-Stiffened Thermoplastic Carbon Plates. Compos. Struct. 2022, 284, 115228. [Google Scholar] [CrossRef]
- Arevo Applications. Available online: https://arevo.com/applications?lang=en (accessed on 9 November 2022).
- Aircraft Seat Support|Anisoprint. Available online: https://anisoprint.com/cases/aircraft-seat-support/ (accessed on 9 November 2022).
- Composite Tool for Turbine Blade Production|Anisoprint. Available online: https://anisoprint.com/cases/composite-tool-for-wind-blade-production/ (accessed on 9 November 2022).
- Kassapoglou, C. Design and Analysis of Composite Structures; Wiley: Hoboken, NJ, USA, 2013; ISBN 9781118401606. [Google Scholar]
- Lake, M.S. NASA Technical Paper 3210 Stiffness and Strength Tailoring in Uniform Space-Filling Truss Structures; Langley Research Center: Hampton, VA, USA, 1992. [Google Scholar]
- Campo, G.A.; Vettorello, A.; Giacalone, M. Optimization Methodology for Continuous Heterogeneous Structures: A Preliminary Design of an Engine Mounting Bracket. Key Eng. Mater. 2020, 827, 116–121. [Google Scholar] [CrossRef]
- Vasiliev, V.V.; Barynin, V.A.; Razin, A.F. Anisogrid Composite Lattice Structures—Development and Aerospace Applications. Compos. Struct. 2012, 94, 1117–1127. [Google Scholar] [CrossRef]
- Ermolaeva, N.S.; Castro, M.B.G.; Kandachar, P.V. Materials Selection for an Automotive Structure by Integrating Structural Optimization with Environmental Impact Assessment. Mater. Des. 2004, 25, 689–698. [Google Scholar] [CrossRef]
- Sienz, J.; Luege, M.; Fuerle, F. Continuous Optimization in Aerospace Structures. In Encyclopedia of Aerospace Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
- Pettit, C.L.; Grandhi, R.V. Multidisciplinary Optimization of Aerospace Structures with High Reliability. In Proceedings of the 8th ASCE Specialty Conference on Probabilistic Mechanics and Structural Reliabilit, Albuquerque, NM, USA, 26–28 July 2004. [Google Scholar]
- Komarov, V.A.; Kishov, E.A.; Kurkin, E.I.; Charkviani, R.V. Aircraft Composite Spoiler Fitting Design Using the Variable Density Model. Procedia Comput. Sci. 2015, 65, 99–106. [Google Scholar] [CrossRef]
- Komarov, V.; Kurkin, E.; Spirina, M.; Kishov, E. Estimation of Weight Efficiency of Topologically Optimal Aerospace Structures. In Proceedings of the 9th International Conference on Recent Advances in Space Technologies, RAST 2019, Istanbul, Turkey, 1 June 2019; Institute of Electrical and Electronics Engineers Inc.: New York, NY, USA, 2019; pp. 95–101. [Google Scholar]
- Rahmani, M.; Behdinan, K. Design Optimization of Multifunctional Aerospace Structures. In Advanced Multifunctional Lightweight Aerostructures; Design, Development, and Implementation; Wiley: Hoboken, NJ, USA, 2021; pp. 93–108. [Google Scholar]
- Zhu, J.H.; Zhang, W.H.; Xia, L. Topology Optimization in Aircraft and Aerospace Structures Design. Arch. Comput. Methods Eng. 2016, 23, 595–622. [Google Scholar] [CrossRef]
- Li, B.; Liu, H.; Zheng, S. Multidisciplinary Topology Optimization for Reduction of Sloshing in Aircraft Fuel Tanks Based on SPH Simulation. Struct. Multidiscip. Optim. 2018, 58, 1719–1736. [Google Scholar] [CrossRef]
- Maute, K.; Reich, G.W. Integrated Multidisciplinary Topology Optimization Approach to Adaptive Wing Design. J. Aircr. 2006, 43, 253–263. [Google Scholar] [CrossRef]
- Komarov, A. Osnovy Proyektirovaniya Silovykh Konstruktsiy [Fundamentals of Load-Carrying Structure Design]; Kuybyshev Book Publ.: Kuybyshev, Russia, 1965. [Google Scholar]
- Komarov, V. Ratsional’noye Proyektirovaniye Silovykh Aviatsionnykh Konstruktsiy [Rational Design of Load-Carrying Aircraft Structures]. Doctor of Technical Sciences Thesis, Kuibyshev Aviation Institute, Kuibyshev, Russia, 1975. [Google Scholar]
- Komarov, V. Proyektirovaniye Silovykh Skhem Aviatsionnykh Konstruktsiy [Design of Load-Carrying Diagrams of Aircraft Structures]. In Aktual’nyye Problemy Aviatsionnoy nauki i Tekhniki [Actual Problems of Aviation Science and Technology]; Lavrentyev, M., Ed.; Mashinostroyeniye: Moscow, Russia, 1984; p. 278. [Google Scholar]
- Komarov, V. Design of Aircraft Structures on the Basis of Discrete Models. In Optimal Design: Theory and Applications to Materials and Structures; Vasiliev, V., Gurdal, Z., Eds.; Technomic Publishing Company: Lancaster, Pennsylvania, 1999; p. 330. ISBN 9781566766869. [Google Scholar]
- Bendsøe, M.P.; Kikuchi, N. Generating Optimal Topologies in Structural Design Using a Homogenization Method. Comput. Methods Appl. Mech. Eng. 1988, 71, 197–224. [Google Scholar] [CrossRef]
- Bendsøe, M.P. Optimization of Structural Topology, Shape, and Material; Springer: Berlin/Heidelberg, Germany, 1995; ISBN 978-3-662-03117-9. [Google Scholar]
- de Luca, A.; Caputo, F. A Review on Analytical Failure Criteria for Composite Materials. AIMS Mater. Sci. 2017, 4, 1165–1185. [Google Scholar] [CrossRef]
- Paris, F.; Washington, G. A Study of Failure Criteria of Fibrous Composite Materials; NASA: Washington, DC, USA, 2001. [Google Scholar]
- HD-R138 091; A Survey Of Macroscopic Failure Criteria For Composite. Defense Technical Information Center: Fort Belvoir, VA, USA, 1984.
- Komarov, V.A.; Weisshaar, T.A. New Approach to Improving the Aircraft Structural Design Process. J. Aircr. 2002, 39, 227–233. [Google Scholar] [CrossRef]
- Komarov, V.A. Dimensionless Criterion of Power Perfection of a Structure. Mech. Solids 2018, 53, 385–396. [Google Scholar] [CrossRef]
- Komarov, V.A. Design and material. Ontol. Des. 2023, 13, 175–191. [Google Scholar] [CrossRef]
- Nomura, T.; Kawamoto, A.; Kondoh, T.; Dede, E.M.; Lee, J.; Song, Y.; Kikuchi, N. Inverse Design of Structure and Fiber Orientation by Means of Topology Optimization with Tensor Field Variables. Compos. B Eng. 2019, 176, 107187. [Google Scholar] [CrossRef]
- Papapetrou, V.S.; Patel, C.; Tamijani, A.Y. Stiffness-Based Optimization Framework for the Topology and Fiber Paths of Continuous Fiber Composites. Compos. B Eng. 2020, 183, 107681. [Google Scholar] [CrossRef]
- Hu, Z. A Review on the Topology Optimization of the Fiber-Reinforced Composite Structures. Aerosp. Tech. Technol. 2021, 171, 54–72. [Google Scholar] [CrossRef]
- Caivano, R.; Tridello, A.; Paolino, D.; Chiandussi, G. Topology and Fibre Orientation Simultaneous Optimisation: A Design Methodology for Fibre-Reinforced Composite Components. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2020, 234, 1267–1279. [Google Scholar] [CrossRef]
- Da Silva, A.L.F.; Salas, R.A.; Nelli Silva, E.C.; Reddy, J.N. Topology Optimization of Fibers Orientation in Hyperelastic Composite Material. Compos. Struct. 2020, 231, 111488. [Google Scholar] [CrossRef]
- Park, S.W.; Choi, J.H.; Lee, B.C. Multi-Objective Optimization of an Automotive Body Component with Fiber-Reinforced Composites. Struct. Multidiscip. Optim. 2018, 58, 2203–2217. [Google Scholar] [CrossRef]
- Ospald, F.; Herzog, R. SIMP Based Topology Optimization for Injection Molding of SFRPs. In Proceedings of the SIMP based Topology Optimization for Injection Molding of SFRPs, Braunschweig, Germany, 5–9 June 2017; p. 8. [Google Scholar]
- Folgar, F.; Tucker III, C.L. Orientation Behavior of Fibers in Concentrated Suspensions. J. Reinf. Plast. Compos. 1984, 3, 98–119. [Google Scholar] [CrossRef]
- Advani, S.G.; Tucker, C.L. The Use of Tensors to Describe and Predict Fiber Orientation in Short Fiber Composites. J. Rheol. 1987, 31, 751–784. [Google Scholar] [CrossRef]
- Kurkin, E.; Kishov, E. Programma AnisoTopo Postroyeniya Anizotropnykh Matrits Zhestkosti Elementov v Zadachakh Topologicheskoy Optimizatsii Konstruktsiy Iz Korotkoarmirovannykh Kompozitsionnykh Materialov [AnisoTopo Program for Constructing Anisotropic Stiffness Matrices of Elements in Problems of Topological Optimization of Structures from Short-Reinforced Composite Materials]; RU 2021613548; FIPS: Moscow, Russia, 2021; Available online: https://new.fips.ru/registers-doc-view/fips_servlet?DB=EVM&DocNumber=2021613548&TypeFile=html (accessed on 5 February 2024).
- Armamid PA6 GF 50-1 TDS TDS. Available online: https://polyplastic-compounds.ru/images/pdf/Armamid/Armamid_PA6_GF_50-1.pdf (accessed on 19 October 2023).
- Kurkin, E.; Spirina, M. Accuracy of the Short Fibers Reinforced Composite Material Plasticity Models. J. Phys. Conf. Ser. 2021, 1925, 12040. [Google Scholar] [CrossRef]
- Gamma Plast UPA 6 30 M TDS. Available online: https://gamma-plast.ru/poliamid/uglenapolnenniy/poliamid-upa-6-30-m/ (accessed on 19 October 2023).
- Kurkin, E.; Spirina, M.; Espinosa Barcenas, O.U.; Kurkina, E. Calibration of the PA6 Short-Fiber Reinforced Material Model for 10% to 30% Carbon Mass Fraction Mechanical Characteristic Prediction. Polymers 2022, 14, 1781. [Google Scholar] [CrossRef] [PubMed]
- GOST 4784-97; Aluminium and Wrought Aluminium Alloys. Grades, Standartinform: Moscow, Russia, 2009.
- Aluminum 2024-T4; 2024-T351. Available online: https://www.matweb.com/search/datasheet_print.aspx?matguid=67d8cd7c00a04ba29b618484f7ff7524 (accessed on 5 February 2024).
- Plastics—Determination of Tensile Properties—Part 2: Test Conditions for Moulding and Extrusion Plastics; International Organization for Standardization: Geneva, Switzerland, 2012; Volume 2012.
- Komarov, V.; Kurkin, E.; Spirina, M.; Chertykovtseva, V. Multi-Level Computational-Experimental System For The Analysis Of Strength And Stiffness Of Elements Of Structures From Composites Reinforced By Short Fibers. Izv. Samara Sci. Cent. Russ. Acad. Sci. 2017, 6, 36–45. [Google Scholar]
- Kurkin, E.I.; Kishov, E.A.; Lukyanov, O.E.; Espinosa Barcenas, O.U. Technique of Considering the Material Anisotropy in Topology Optimization of Short Fibers Composite Structures. Phys. Conf. Ser. 2021, 1925, 12036. [Google Scholar] [CrossRef]
- Tandon, G.P.; Weng, G.J. The Effect of Aspect Ratio of Inclusions on the Elastic Properties of Unidirectionally Aligned Composites. Polym. Compos. 1984, 5, 327–333. [Google Scholar] [CrossRef]
- Li, H.; Zare, Y.; Rhee, K.Y. Mathematical Simplification of the Tandon–Weng Approach to the Mori–Tanaka Model for Estimating the Young’s Modulus of Clay/Polymer Nanocomposites. JOM 2017, 69, 2819–2824. [Google Scholar] [CrossRef]
- Gusev, A.A. Finite Element Estimates of Viscoelastic Stiffness of Short Glass Fiber Reinforced Composites. Compos. Struc. 2017, 171, 53–62. [Google Scholar] [CrossRef]
- Ghoreishi, S.N.; Clausen, A.; Joergensen, B.N. Termination Criteria in Evolutionary Algorithms: A Survey. In Proceedings of the IJCCI 2017—the 9th International Joint Conference on Computational Intelligence, Funchal, Portugal, 1–3 November 2017; SciTePress: Setúbal, Portugal, 2017; pp. 373–384. [Google Scholar]
- Kurkin, E.I.; Lukyanov, O.E.; Kishov, E.A. Calculation of short fibers orientation on a finite element model reduced by algorithms for topological optimization of structures. Izv. Samara Sci. Cent. Russ. Acad. Sci. 2019, 21, 90–95. [Google Scholar]
- Komarov, V.; Spirina, M.; Kurkin, E.; Kishov, E. Estimation of Weight Efficiency of Topologically Optimal Aerospace Structures. In Proceedings of the 2019 9th International Conference on Recent Advances in Space Technologies (RAST), Istanbul, Turkey, 11–14 June 2019. [Google Scholar] [CrossRef]
- Guest, J.K.; Lotfi, R.; Gaynor, A.T.; Jalalpour, M. Structural Topology Optimization:Moving beyond Linear Elastic Design Objectives. In Proceedings of the 20th Analysis and Computation Specialty Conference, Chicago, IL, USA, 29–31 March 2012; pp. 245–256. [Google Scholar] [CrossRef]
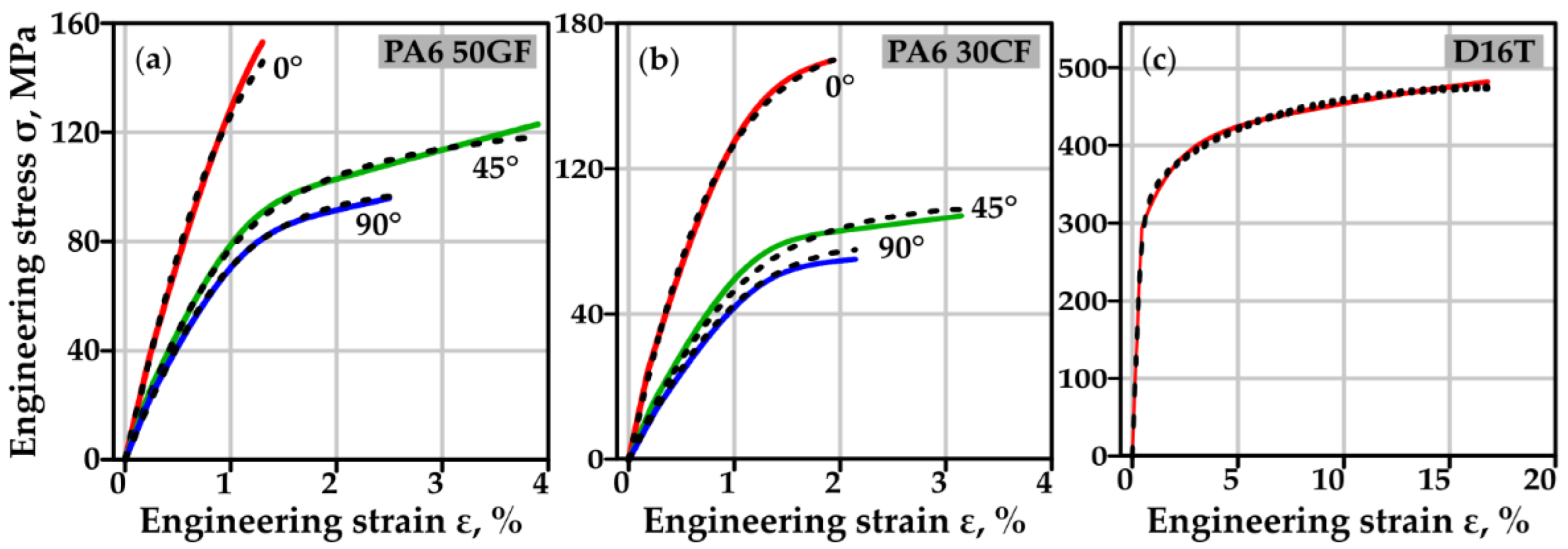


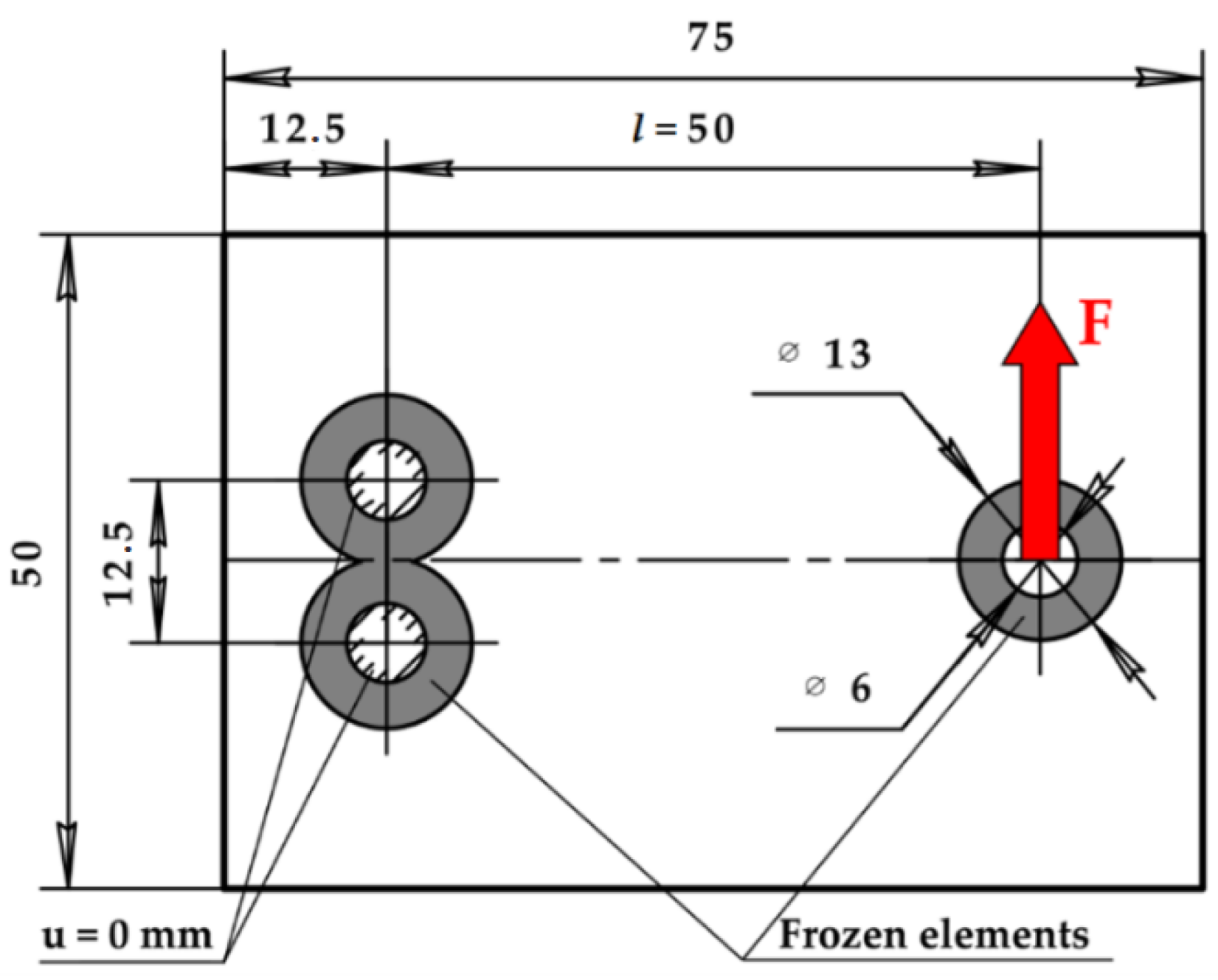

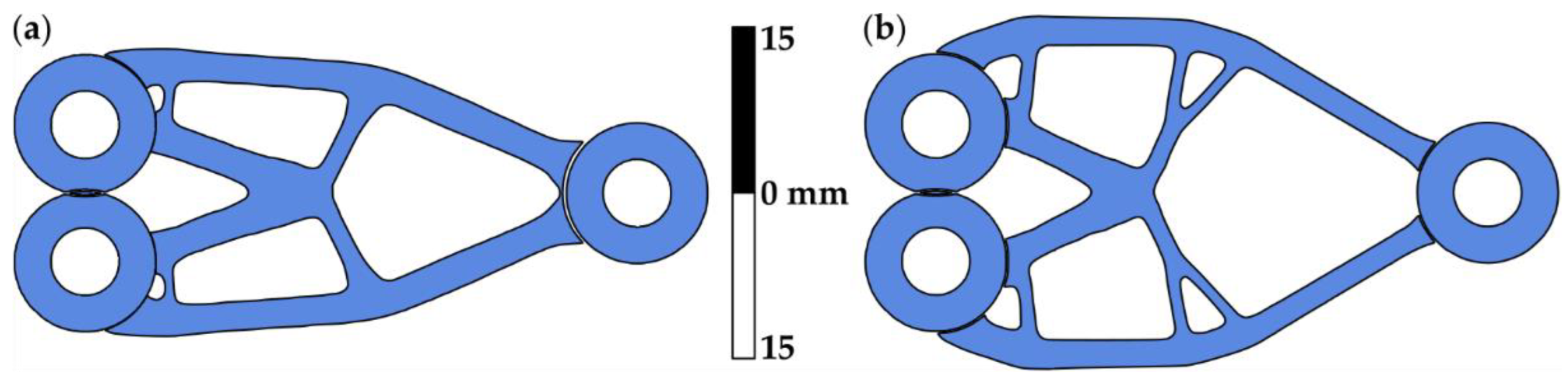
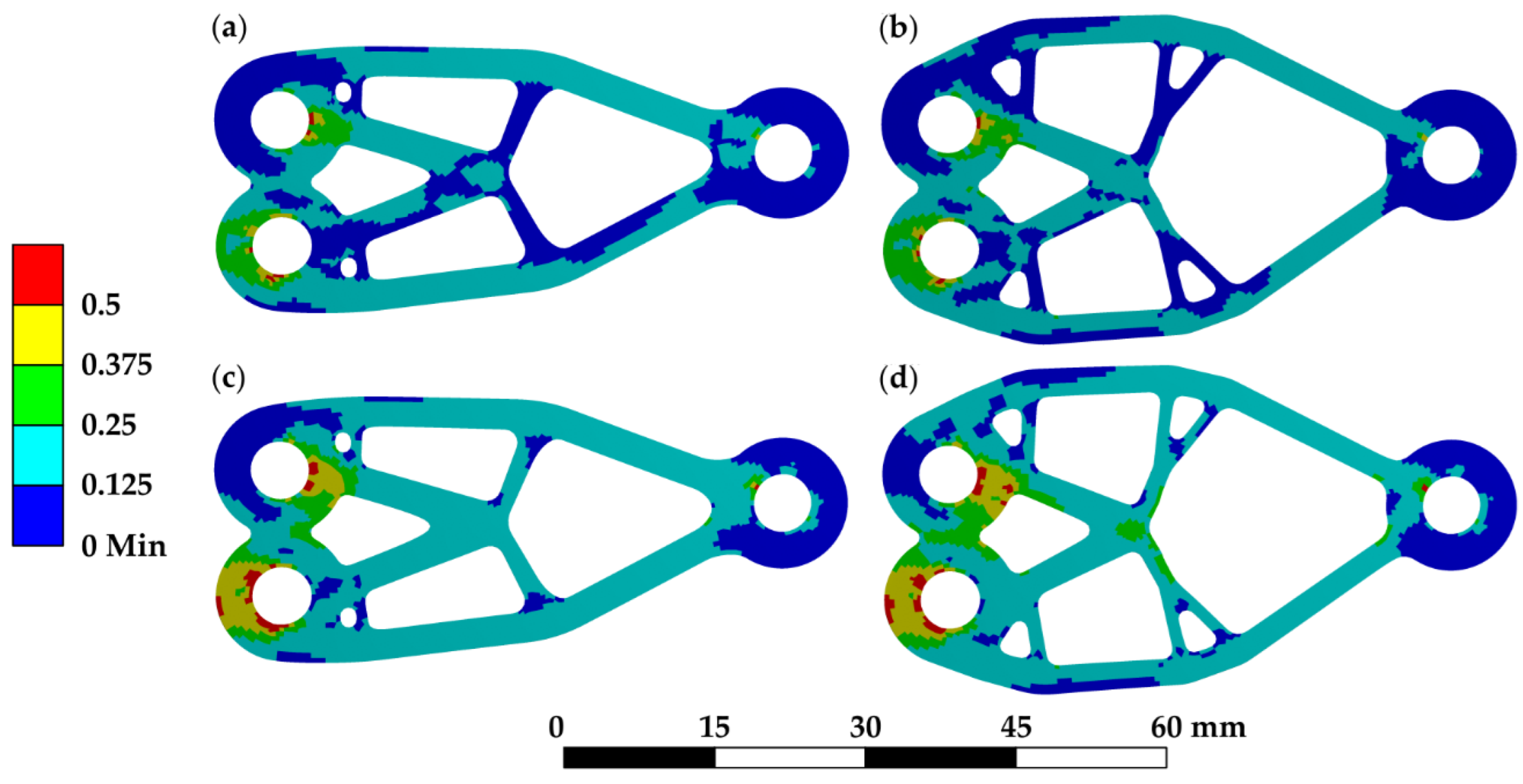
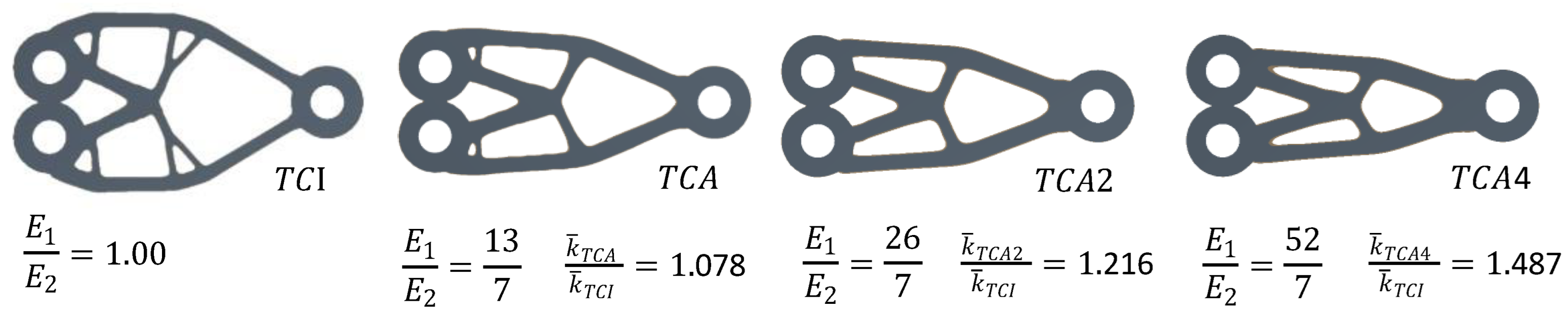


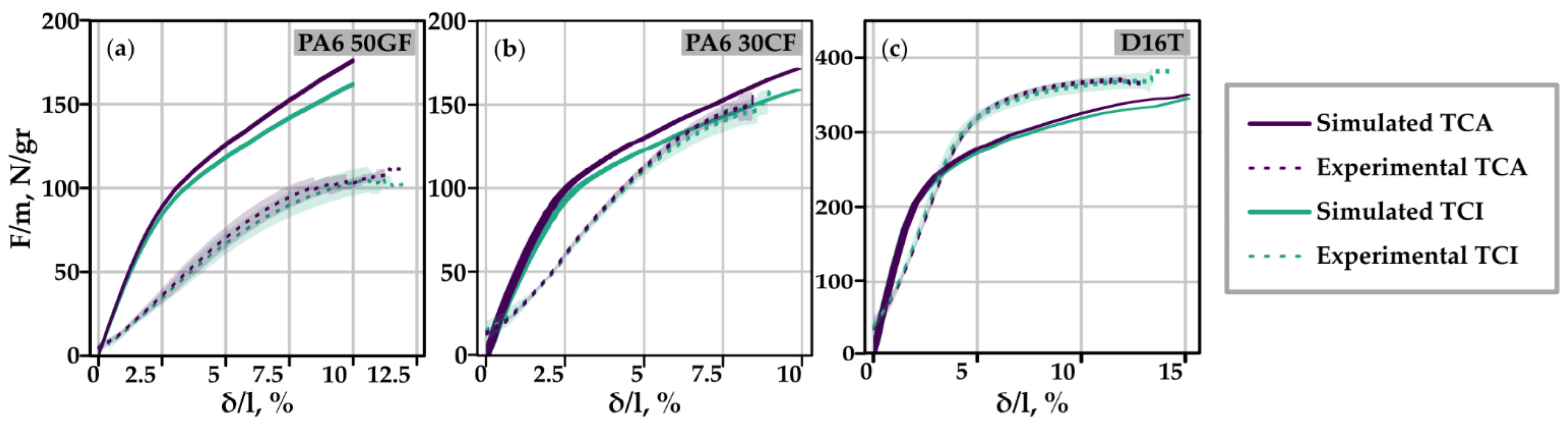

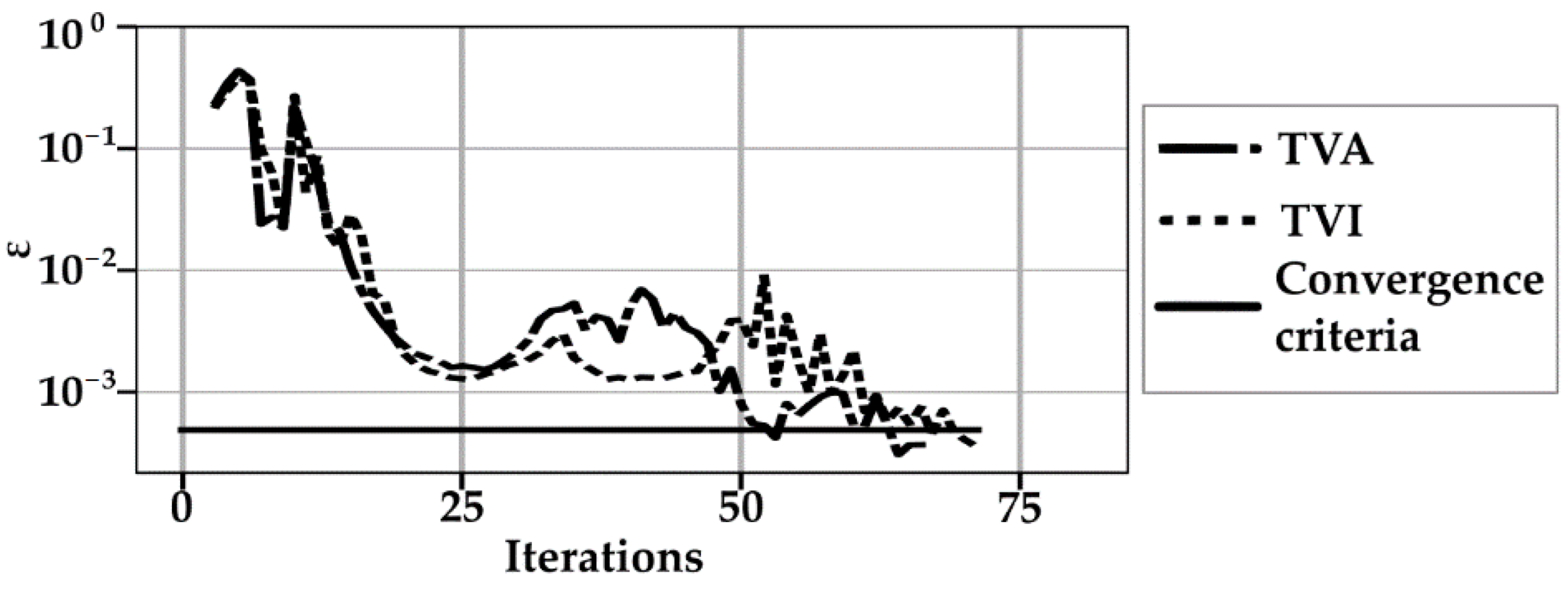

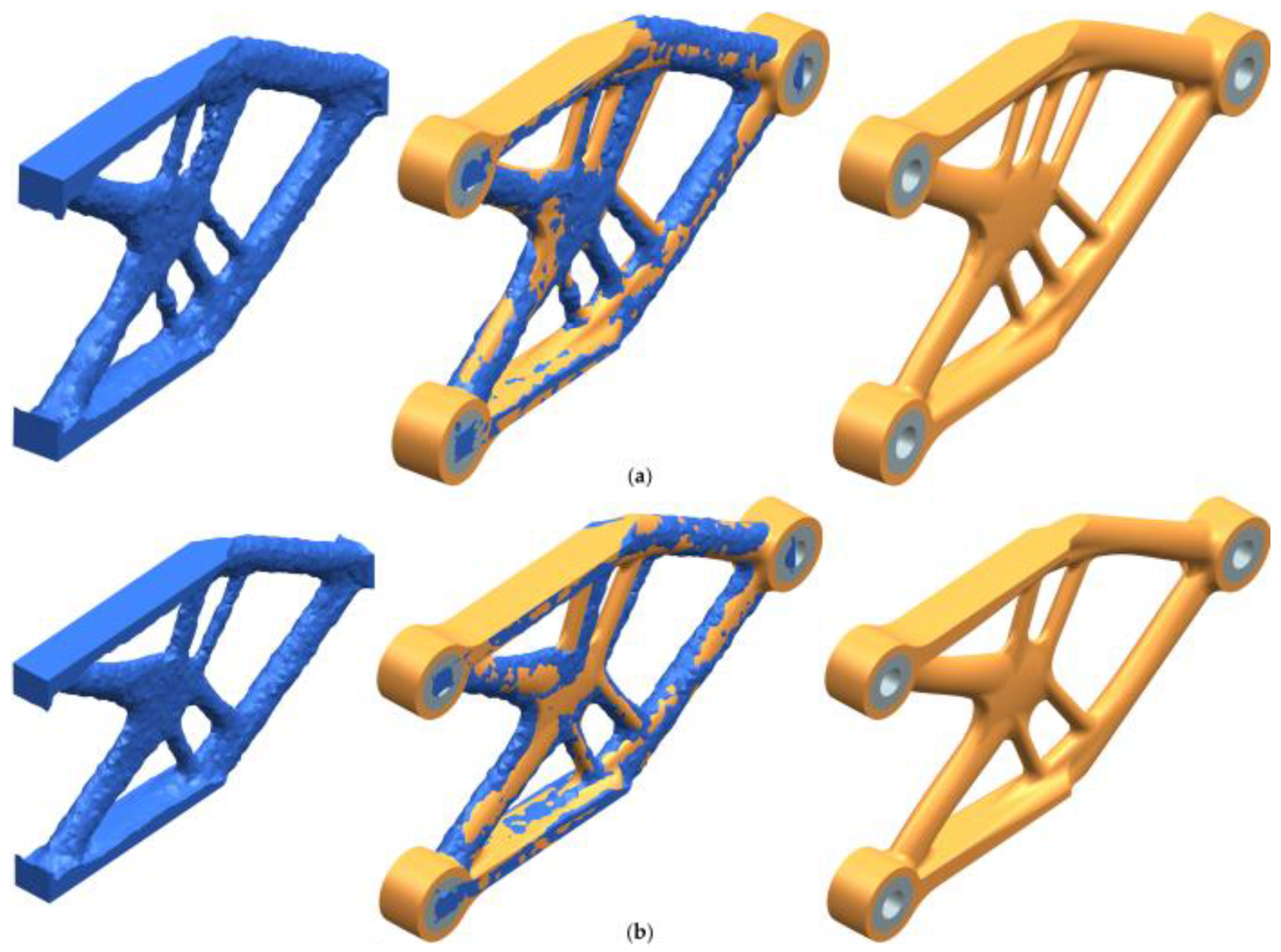




| Characteristics | Material | ||
|---|---|---|---|
| PA 50GF | PA 30CF | D16T | |
| Matrix phase | |||
| Matrix density, kg/m3 | 1148 | 2770 | |
| Young’s modulus, Em (MPa) | 4911 | 3994 | 66,059 |
| Poisson’s coefficient, υm | 0.372 | 0.372 | 0.330 |
| Yield stress, σy (MPa) | 17.21 | 14.5 | 294.48 |
| Hardening modulus, R∞ (MPa) | 37.1 | 37.00 | 109.51 |
| Hardening exponent, m | 371.21 | 458.30 | 75.72 |
| Linear hardening modulus, k (MPa) | 313.02 | 188.40 | 1107.60 |
| Reinforcement phase | |||
| Fiber density, kg/m3 | 2550 | 1780 | - |
| Young’s modulus, Ef (MPa) | 72,000 | 230,000 | - |
| Poisson’s coefficient, υf | 0.22 | 0.20 | - |
| Fibers’, AR | 13.58 | 16.54 | - |
| Wt. % | 30 | 50 | - |
| Material’s ultimate tensile strength | |||
| Longitudinal, X (MPa) | 153.31 | 169.35 | 476 |
| Transverse, Y (MPa) | 97.82 | 85.07 | - |
| Transverse shear strength, S (MPa) | 83.90 | 66.33 | - |
| Topology | m, g | f, N | CK | CKTH |
|---|---|---|---|---|
| PA6 50GF | ||||
| TCA | 4.655 | 326.8 | 5.2928 | 5.6994 |
| TCI | 4.658 | 326.1 | 5.2482 | 5.8285 |
| PA6 30CF | ||||
| TCA | 3.779 | 264.5 | 5.3407 | 6.7438 |
| TCI | 3.781 | 264.7 | 5.2874 | 7.1127 |
| D16T | ||||
| TCA | 8.146 | 570.3 | 5.1964 | - |
| TCI | 8.152 | 570.6 | 5.2287 | - |
| Topology | Normalized Specific Stiffness, N/gr | Percentage Change from TCA to TCI, % | |
|---|---|---|---|
| TCA | TCI | ||
| PA6 50GF | 3883 | 3661 | 6.06 |
| PA6 30CF | 4621 | 4194 | 10.18 |
| D16T | 11,474 | 11,654 | −1.54 |
| Material | Average, N/gr | Standard Deviation, N/gr | Coefficient of Variation, % | Percentage Change from TCA to TCI, % | |||
|---|---|---|---|---|---|---|---|
| TVA | TVI | TVA | TVI | TVA | TVI | ||
| PA6 50GF | 1551 | 1479 | 140 | 167 | 9.03 | 11.26 | 4.87 |
| PA6 30CF | 1833 | 1737 | 52 | 96 | 2.84 | 5.54 | 5.53 |
| D16T | 7192 | 7584 | 76 | 406 | 1.06 | 5.36 | −5.17 |
| Topology | Baseline | Reconstructed | Percentage Difference between Baseline and Reconstructed | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| m, g | f, N | CKeq | CKTH | m, g | f, N | CKeq | CKTH | CKeq | CKTH | |
| PA6 50GF | ||||||||||
| TVA | 22.94 | 1606 | 3.3183 | 3.4341 | 25.59 | 1791 | 3.5230 | 3.6541 | 5.98% | 6.21% |
| TVI | 23.24 | 1627 | 3.3214 | 3.4437 | 26.17 | 1832 | 3.5481 | 3.6926 | 6.60% | 6.98% |
| PA6 30CF | ||||||||||
| TVA | 18.62 | 1304 | 3.3225 | 3.6881 | 20.76 | 1448 | 3.5273 | 3.9025 | 5.98% | 5.65% |
| TVI | 18.86 | 1320 | 3.3238 | 3.7103 | 21.24 | 1481 | 3.5539 | 3.9799 | 6.69% | 7.01% |
| D16T | ||||||||||
| TVA | 40.15 | 2810 | 3.3122 | - | 47.34 | 3314 | 3.5707 | - | 7.51% | - |
| TVI | 40.66 | 2846 | 3.3176 | - | 48.36 | 3386 | 3.5892 | - | 7.86% | - |
| Material | Topology | Normalized Specific Stiffness, N/gr | Percentage Change from TVA to TVI, % | |
|---|---|---|---|---|
| TVA | TVI | |||
| PA6 50GF | Baseline | 7250 | 7187 | 0.88 |
| Reconstructed | 5500 | 5260 | 4.56 | |
| PA6 30CF | Baseline | 8993 | 8924 | 0.77 |
| Reconstructed | 7209 | 6893 | 4.58 | |
| D16T | Baseline | 19,737 | 19,869 | −0.66 |
| Reconstructed | 11,838 | 11,613 | 1.92 | |
| Material | Average, N/gr | Standard Deviation, N/gr | Coefficient of Variation, % | Percentage Change from TVA to TVI, % | |||
|---|---|---|---|---|---|---|---|
| TVA | TVI | TVA | TVI | TVA | TVI | ||
| PA6 50GF | 3529 | 3289 | 179 | 267 | 5.09 | 8.13 | 7.30 |
| PA6 30CF | 4533 | 4290 | 216 | 187 | 4.77 | 4.36 | 5.66 |
| D16T | 7293 | 7875 | 775 | 1150 | 10.63 | 14.60 | −7.39 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kurkin, E.; Espinosa Barcenas, O.U.; Kishov, E.; Lukyanov, O. Topology Optimization and Efficiency Evaluation of Short-Fiber-Reinforced Composite Structures Considering Anisotropy. Computation 2024, 12, 35. https://doi.org/10.3390/computation12020035
Kurkin E, Espinosa Barcenas OU, Kishov E, Lukyanov O. Topology Optimization and Efficiency Evaluation of Short-Fiber-Reinforced Composite Structures Considering Anisotropy. Computation. 2024; 12(2):35. https://doi.org/10.3390/computation12020035
Chicago/Turabian StyleKurkin, Evgenii, Oscar Ulises Espinosa Barcenas, Evgenii Kishov, and Oleg Lukyanov. 2024. "Topology Optimization and Efficiency Evaluation of Short-Fiber-Reinforced Composite Structures Considering Anisotropy" Computation 12, no. 2: 35. https://doi.org/10.3390/computation12020035
APA StyleKurkin, E., Espinosa Barcenas, O. U., Kishov, E., & Lukyanov, O. (2024). Topology Optimization and Efficiency Evaluation of Short-Fiber-Reinforced Composite Structures Considering Anisotropy. Computation, 12(2), 35. https://doi.org/10.3390/computation12020035






