Exploring Controlled Passive Particle Motion Driven by Point Vortices on a Sphere

Abstract

This work focuses on optimizing the displacement of a passive particle interacting with vortices located on the surface of a sphere. The goal is to minimize the energy expended during the displacement within a fixed time. The modeling of particle dynamics, whether in Cartesian or spherical coordinates, gives rise to alternative formulations of the identical problem. Thanks to these two versions of the same problem, we can assert that the algorithm, employed to transform the optimal control problem into an optimization problem, is effective, as evidenced by the obtained controls. The numerical resolution of these formulations through a direct approach consistently produces optimal solutions, regardless of the selected coordinate system.

1. Introduction

This study focuses on analyzing the movement of a passive particle within a flow generated by a specific configuration of point vortices on the surface of a sphere. Point vortices, which provide finite-dimensional approximations to the vortex dynamics of two-dimensional, incompressible ideal fluids, can be traced back to Helmholtz [1] and subsequent contributions by Kelvin [2] and Kirchhoff [3]. More recently, Hassan Aref was one of the world’s leading researchers in the dynamics of point vortices (see, for instance, [4,5,6]).

Ongoing research in this domain integrates various disciplines, such as theories of dynamical systems, differential geometry, numerical analysis, optimal control, and more. Notably, the exploration of point vortices extends beyond conventional planes to encompass diverse surfaces, including the sphere [7,8,9], plane [10], and hyperbolic sphere [11,12,13].

Point vortices on the sphere are relevant as they provide a simplified representation of the behavior observed in specific geophysical flows where the curvature of the Earth plays a crucial role, and these flows persist over extended periods [9]. In fact, vortex point models play a pivotal role in addressing numerous fundamental dynamics questions related to atmospheric flows [7]. Conceptual models of point vortices are also used to identify and evaluate physical phenomena affecting the structure and interaction of atmospheric and oceanic vortices [14].

This work focuses on optimizing the displacement of a passive particle interacting with vortices located on the surface of a sphere. More specifically, our focus lies in the optimal control of the passive particle’s displacement between two fixed points. The objective is to minimize the energy expended during the displacement while considering a fixed time for its completion. This problem can be conceptualized as a simplified model of an autonomous vehicle moving between two points, utilizing atmospheric circulation or oceanic currents, to achieve displacement with minimal energy consumption.

To tackle this problem, the displacement of the passive particle is reformulated as a control problem, and a direct numerical approach is employed for its solution. This approach, previously utilized in addressing a vortex problem in an infinite plane [15], involves the discretization of the available time (T) for displacement into n sub-intervals, each characterized by constant controls. The resulting nonlinear programming problem (NLP) is numerically solved using the fmincon solver from the MATLAB Optimization Toolbox [16].

Observe that the proposed approach for solving the control problem is opposed to Pontryagin’s Maximum Principle methodology [17] that first optimizes and then discretizes the problem (see, for instance, [18]).

A similar approach was implemented on the sphere in which the equations that govern the dynamics of the system composed of several vortices and a single passive particle were deduced using spherical coordinates [19]. It was observed that, in scenarios involving one, two, and three vortices, it is possible to show the existence of near or quasi-optimal trajectories for the passive particle.

In a separate study, the problem was addressed using Cartesian coordinates, with controls introduced in the form of tangent vectors to the sphere [20]. In this context as well, it was found that it is possible to obtain near or quasi-optimal trajectories for the passive particle, which is advected by one, two, three, or four vortices.

The possibility of modeling the problem through two different coordinate systems raises the question of whether the solution depends on the chosen coordinate system or if, on the contrary, it is unique regardless of the system. This study focuses on the answer to this question. The formulation of the problem is deduced in spherical and Cartesian coordinates. It is then shown how it is possible to convert the problem formulation from one coordinate system to another.

This document is structured as follows: In Section 2, we undertake the derivation of equations governing the dynamics of the passive particle in Cartesian coordinates. Section 3 explores the modeling of dynamics in spherical coordinates. The formulation of optimization problems, depending on the type of coordinates, and the presentation of the numerical strategy employed for their resolution are detailed in Section 4. Results obtained from the solution of discretized optimization problems are outlined in Section 5. The study concludes with final considerations presented in Section 6.

2. Modelling the Control Problem in Cartesian Coordinates

The problem under consideration involves the movement of a passive particle between two specified points on the surface of a non-rotating sphere within a fixed time. The particle’s autonomy in terms of displacement is governed by control, allowing it to move freely in any direction on the surface of the sphere.

In this section, we introduce the equations that govern the motion of controlled passive particles induced by a vortex on the sphere. The sphere is centered at the origin with a radius of $R.$

Let ${\mathbf{v}}_j=\left(x_j\left(t\right),y_j\left(t\right),z_j\left(t\right)\right)\equiv \left(x_j,y_j,z_j\right)$ denote the position of vortex j ($j=1,2,\cdots ,N$) on the sphere, where $\left|\right|{\mathbf{v}}_j\left|\right|=R.$ In Cartesian coordinates, the dynamics of this set of vortices is governed by the system of ordinary differential equations [21]:

$${\dot{\mathbf{v}}}_i=\frac{1}{2\pi R}\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^N{k}_j\frac{{\mathbf{v}}_j\times {\mathbf{v}}_i}{\parallel {\mathbf{v}}_i-{\mathbf{v}}_j{\parallel }^2},i=1,2,\dots ,N,$$

(1)

with the corresponding initial conditions. Here, $k_j$ represents the circulation of vortex $j,$ and N is the total number of vortices on the sphere. The distance along the chord between vortex i and j can be expressed as:

$$\parallel {\mathbf{v}}_i-{\mathbf{v}}_j{\parallel }^2=2\left(R^2-{\mathbf{v}}_i·{\mathbf{v}}_j\right).$$

(2)

The derivation of Equation (1) is outlined in Appendix A.

A passive particle, defined as a point vortex with circulation $k=0$, contributes to the dynamics of a system, where P such particles are advected by N point vortices. This behavior is governed by Equation (1), supplemented by equations specifying the motion of the passive particles:

$$\begin{array}{c}\hfill {\dot{\mathbf{x}}}_p=\frac{1}{2\pi R}\sum _{j=1}^N{k}_j\frac{{\mathbf{v}}_j\times {\mathbf{x}}_p}{\parallel {\mathbf{x}}_p-{\mathbf{v}}_j{\parallel }^2},p=1,2,\dots ,P,\end{array}$$

(3)

with the respective initial conditions.

Considering a single controlled passive particle ($P=1$) moving in a spherical fluid induced by N vortices, the corresponding equation is

$$\begin{array}{c}\hfill \dot{\mathbf{x}}=\frac{1}{2\pi R}\sum _{j=1}^N{k}_j\frac{{\mathbf{v}}_j\times \mathbf{x}}{\parallel \mathbf{x}-{\mathbf{v}}_j{\parallel }^2}+{\mathbf{U}}^c\left(t\right),\end{array}$$

(4)

with the respective initial conditions. In the right-hand side of Equation (4),

$${\mathbf{U}}^c\left(t\right)=\left(u_x\left(t\right),u_y\left(t\right),u_z\left(t\right)\right)\equiv \left(u_x,u_y,u_z\right)$$

(5)

is the control vector function. The interdependence among the entries of this control vector is evident. In the ensuing discussion, it will become clear that these entries must be configured in a manner to guarantee the particle’s trajectory on the spherical surface.

Considering the single vortex located at the North Pole of the sphere, i.e., its position vector is

$$\mathbf{v}=\left(0,0,R\right),$$

(6)

then

$$\mathbf{v}\times \mathbf{x}=\left(0,0,R\right)\times \left(x,y,z\right)=\left(-Ry,Rx,0\right),$$

(7)

and

$$∥\mathbf{v}-\mathbf{x}∥=x^2+y^2+{(R-z)}^2,$$

(8)

which enables us to write row-wise the Equation (4) for a single passive particle:

$$\left\{\begin{array}{c}\dot{x}=-\frac{k}{2\pi }\frac{y}{x^2+y^2+{(R-z)}^2}+u_x\hfill \\ \dot{y}=\frac{k}{2\pi }\frac{x}{x^2+y^2+{(R-z)}^2}+u_y\hfill \\ \dot{z}=u_z\hfill \end{array}\right.$$

(9)

The system (9), with the initial conditions ($∥\mathbf{x}\left(0\right)∥=∥\left(x\left(0\right),y\left(0\right),z\left(0\right)\right)∥=R$):

$$\left\{\begin{array}{c}x\left(0\right)=x_0\hfill \\ y\left(0\right)=y_0\hfill \\ z\left(0\right)=z_0\hfill \end{array}\right.$$

(10)

describes the dynamic of a controlled passive particle on a sphere advected by a point vortex located at the North Pole.

The problem addressed here is the displacement of the passive particle between two given points of the sphere. Starting from the point $P_0$, the passive particle has to reach a final destination point $P_f$ in a fixed time T. The autonomy of the particle in terms of displacement is given by the control ${\mathbf{U}}^c$. This control allows the particle to move in any direction on the surface of the sphere. Indeed, the particle should fully exploit the surface flow motion generated by the vortex, aiming to minimize the necessity for control input ${\mathbf{U}}^c$, since the application of control involves the expenditure of energy.

Since the particle $\mathbf{x}$ is constrained to move on the surface of the sphere with a radius of $R,$ then

$$\begin{array}{cc}\hfill & {∥\mathbf{x}∥}^2=R^2\iff \hfill \\ \hfill & {∥\left(x,y,z\right)∥}^2=R^2\iff \hfill \\ \hfill & x^2+y^2+z^2=R^2\iff \hfill \\ \hfill & \frac{d}{dt}\left(x^2+y^2+z^2\right)=0\iff \hfill \\ \hfill & 2\left(x\dot{x}+y\dot{y}+z\dot{z}\right)=0\iff \hfill \\ \hfill & x\dot{x}+y\dot{y}+z\dot{z}=0\hfill \end{array}$$

and, from (9), one obtains

$$\begin{array}{c}\hfill \left(u_x,u_y,u_z\right)·\left(x,y,z\right)=0.\end{array}$$

(11)

In other words, the control and position vectors are perpendicular to each other:

$$\left(u_x,u_y,u_z\right)\perp \left(x,y,z\right).$$

(12)

This indicates that the control vector $\left(u_x,u_y,u_z\right)$ lies within the tangent plane of the sphere at the point $\left(x,y,z\right)$. In simpler terms, for the particle to move on the sphere, the exerted control must be orthogonal to the particle’s position vector, i.e.,

$${\mathbf{U}}^c\left(t\right)\perp \mathbf{x}\left(t\right),\forall t\ge 0.$$

(13)

The control vector can be defined as a linear combination of two vectors ${\mathbf{w}}_1$ and ${\mathbf{w}}_2$ belonging to this plane, i.e.,

$${\mathbf{U}}^c=\alpha {\mathbf{w}}_1+\beta {\mathbf{w}}_2,$$

(14)

with $\alpha \equiv \alpha \left(t\right)$ and $\beta \equiv \beta \left(t\right)$ two real (controls) scalars functions. Given two vectors in the tangent plane, ${\mathbf{w}}_1=\left(y,-x,0\right)$ and ${\mathbf{w}}_2=\left(0,z,-y\right)$, where ${\mathbf{w}}_1·\mathbf{x}=0$ and ${\mathbf{w}}_2·\mathbf{x}=0,$ the control vector indeed assumes the form

$$\left(u_x,u_y,u_z\right)=\alpha \left(y,-x,0\right)+\beta \left(0,z,-y\right)=\left(\alpha y,-\alpha x+\beta z,-\beta y\right);$$

(15)

the dynamic of the passive particle is then given by

$$\left\{\begin{array}{c}\dot{x}=-\frac{k}{2\pi }\frac{y}{x^2+y^2+{(R-z)}^2}+\alpha y\hfill \\ \dot{y}=\frac{k}{2\pi }\frac{x}{x^2+y^2+{(R-z)}^2}-\alpha x+\beta z\hfill \\ \dot{z}=-\beta y\hfill \end{array}\right.$$

(16)

with initial conditions (10) and control

$$\mathbf{U}=\left(\alpha \left(t\right),\beta \left(t\right)\right).$$

(17)

The energy spent on the displacement aimed at minimization is represented by the integral over the time interval $[0,T]$ of the sum of the squares of the components of $\mathbf{U}$. Therefore, the objective function of the control problem is given by

$${\int }_0^T{∥\mathbf{U}∥}^{2}dt={\int }_0^T\left({\alpha }^2\left(t\right)+{\beta }^2\left(t\right)\right)dt.$$

(18)

3. Modeling the Control Problem in Spherical Coordinates

In spherical coordinates, the dynamics of the passive particle under control in identical conditions, as detailed in the preceding section, is determined by (see [19]):

$$\left\{\begin{array}{c}\dot{\theta }=u_{\theta }\hfill \\ \dot{\varphi }=\frac{k}{4\pi R^2}\frac{1}{1-cos\left(\theta \right)}+u_{\varphi }\hfill \end{array}\right.$$

(19)

with the given initial condition

$$\left\{\begin{array}{c}\theta \left(0\right)={\theta }_0\hfill \\ \varphi \left(0\right)={\varphi }_0\hfill \end{array}\right.$$

(20)

where $\theta \in [0,\pi ]$ is the colatitude (or polar) angle of the particle position, i.e., the angle between the radius passing through the North Pole, $(0,0,R),$ and the radius passing through the particle, and $\varphi \in [0,2\pi ]$ is the longitude (or azimuthal) angle, i.e., the angle that the meridian passing through $(R,0,0)$ makes with the meridian passing by the particle position. The variables $u_{\theta }$ and $u_{\varphi }$ represent the angular controls applied on the passive particle, i.e.,

$${\mathbf{U}}^s=(u_{\theta },u_{\varphi }),$$

(21)

and, as before, the circulation of the vortex located at the North Pole is given by k.

In a previous work [19], Equation (19) was employed to solve the control problem of displacing the passive particle between two specified points of the superficial sphere within a fixed time. However, a direct comparison of results with those obtained using Cartesian coordinates is not feasible due to inherent differences in controls, given that the controls are independent of each other.

To understand the transformation of controls between Cartesian and spherical coordinates, we will derive the particle dynamics equations in spherical coordinates from their counterparts in Cartesian coordinates. This approach allows us to observe the changes in controls that occur during this transformation.

The correspondence between the position vectors of the passive particle in Cartesian coordinates $\left(x,y,z\right)$ and spherical coordinates $\left(\theta ,\varphi \right)$ is given by

$$\left\{\begin{array}{c}x=Rcos\varphi sin\theta \hfill \\ y=Rsin\varphi sin\theta \hfill \\ z=Rcos\theta \hfill \end{array}\right.$$

(22)

The time derivatives of these coordinates are:

$$\left\{\begin{array}{c}\dot{x}=-R\dot{\varphi }sin\varphi sin\theta +R\dot{\theta }cos\varphi cos\theta \hfill \\ \dot{y}=R\dot{\varphi }cos\varphi sin\theta +R\dot{\theta }sin\varphi cos\theta \hfill \\ \dot{z}=-R\dot{\theta }sin\theta \hfill \end{array}\right.$$

(23)

The expression for the chord distance in spherical coordinates, as given by (8), can be written as

$$\begin{array}{cc}\hfill ∥\mathbf{v}-\mathbf{x}∥& =x^2+y^2+{(R-z)}^2\hfill \\ \hfill & =x^2+y^2+z^2+R^2-2zR\hfill \\ \hfill & =2R^2-2R\left(Rcos\theta \right)\hfill \\ \hfill & =2R^2\left(1-cos\theta \right)\hfill \end{array}$$

(24)

and the cross product (7) is modified to yield

$$\mathbf{v}\times \mathbf{x}=\left(-Ry,Rx,0\right)=\left(-R^{2}cos\varphi sin\theta ,R^{2}cos\varphi sin\theta ,0\right).$$

(25)

Substituting (24) and (25) into Equation (16) gives rise to

$$\left\{\begin{array}{c}\dot{x}=-\frac{k}{4\pi R}\frac{sin\varphi sin\theta }{1-cos\theta }+u_x\hfill \\ \dot{y}=\frac{k}{4\pi R}\frac{cos\varphi sin\theta }{1-cos\theta }+u_y\hfill \\ \dot{z}=u_z\hfill \end{array}\right.$$

(26)

Reciprocally, the controls specified in (15) can be transformed into Cartesian coordinates:

$$\left\{\begin{array}{c}{u}_x=\alpha y\hfill \\ u_y=-\alpha x+\beta z\hfill \\ u_z=-\beta y\hfill \end{array}\right.\iff \left\{\begin{array}{c}{u}_x=R\alpha sin\varphi sin\theta \hfill \\ u_y=-R\alpha cos\varphi sin\theta +R\beta cos\theta \hfill \\ u_z=-R\beta sin\varphi sin\theta \hfill \end{array}\right.$$

(27)

Replacing these controls in Equation (26) leads to

$$\left\{\begin{array}{c}\dot{x}=-\frac{k}{4\pi R}\frac{sin\varphi sin\theta }{1-cos\theta }+R\alpha sin\varphi sin\theta \hfill \\ \dot{y}=\frac{k}{4\pi R}\frac{cos\varphi sin\theta }{1-cos\theta }-R\alpha cos\varphi sin\theta +R\beta cos\theta \hfill \\ \dot{z}=-R\beta sin\varphi sin\theta \hfill \end{array}\right.$$

(28)

The Equations (23) and (28) produce a system of equations that provides the basis for deriving the equations for $\dot{\theta }$ and $\dot{\varphi }$. More precisely, the third equation of

$$\left\{\begin{array}{c}-R\dot{\varphi }sin\varphi sin\theta +R\dot{\theta }cos\varphi cos\theta =-\frac{k}{4\pi R}\frac{sin\varphi sin\theta }{1-cos\theta }+R\alpha sin\varphi sin\theta \hfill \\ R\dot{\varphi }cos\varphi sin\theta +R\dot{\theta }sin\varphi cos\theta =\frac{k}{4\pi R}\frac{cos\varphi sin\theta }{1-cos\theta }-R\alpha cos\varphi sin\theta +R\beta cos\theta \hfill \\ -R\dot{\theta }sin\theta =-R\beta sin\varphi sin\theta \hfill \end{array}\right.$$

(29)

yields

$$\dot{\theta }=\beta sin\varphi ,$$

(30)

while the first two equations of (29) provide us with

$$\left\{\begin{array}{c}\dot{\theta }=\beta sin\varphi \hfill \\ \dot{\varphi }=\frac{k}{4\pi R^2}\frac{1}{1-cos\theta }-\alpha +\beta cos\varphi cot\theta \hfill \end{array}\right.$$

(31)

for which, when compared to Equation (19), the result is

$${\mathbf{U}}^s=\left(u_{\theta },u_{\varphi }\right)=\left(\beta sin\varphi ,-\alpha +\beta cos\varphi cot\theta \right).$$

(32)

This expression allows for the computation of spherical controls $u_{\theta }\left(t\right)$ and $u_{\varphi }\left(t\right)$ as functions of the same parameters $\alpha \left(t\right)$ and $\beta \left(t\right)$ utilized in Cartesian control.

4. Numerical Control for Particle Displacement

The control problem arising from controlling the particle’s displacement on the surface of the sphere is numerically solved using a direct approach, akin to the one previously employed in the infinite plane [15]. Effectively, this control problem transforms into an optimization problem involving the minimization of the objective function, as defined by Equation (18), while taking into account the constraint arising from the passive particle’s displacement from an initial point $P_0$ to a target point $P_f$ within precisely T units of time.

4.1. Optimization Problems

As explained in the preceding section, the dynamics of the passive particle can be modeled in various ways, contingent on the choice of coordinates and the type of control. In the scenario of Cartesian coordinates, the optimization problem is formulated as follows:

P1: Cartesian Optimization Problem
$\mathrm{Minimize}:$
	${\int }_0^T{∥\mathbf{U}\left(t\right)∥}^{2}dt$
$\mathrm{subject}\mathrm{to}:$
	$\dot{\mathbf{x}}=\frac{k}{2\pi R}\frac{\mathbf{v}\times \mathbf{x}}{\left|\right|\mathbf{x}-{\mathbf{v}\left|\right|}^2}+{\mathbf{U}}^c$
	$\mathbf{x}\left(0\right)=P_0$
	$\mathbf{x}\left(T\right)=P_f$
	$∥\mathbf{U}∥\le u_{max}$

where $\mathbf{U}=\left(\alpha ,\beta \right)$, $P_0=x_0$, and $P_f=x_f\in \mathrm{I}{\mathrm{R}}^3$ represent the initial and final points, $T>0$ denotes the time available for the displacement, k is the circulation of the vortex $\mathbf{v}\in \mathrm{I}{\mathrm{R}}^3$, and $u_{max}>0$ is the upper limit value of the control.

In the generic optimization problem P1, the objective function to be minimized corresponds to the energy utilized for the displacement of the passive particle during the time interval $\left[0,T\right]$. The constraints are linked to the application of the equation governing particle dynamics, the specified initial and final positions, and the constraint on the maximum control norm. This last condition stems from the finite energy available for executing the displacement.

For spherical coordinates, the optimization problem can be formulated in the function of the controls ${\mathbf{U}}^s=\left(u_{\theta },u_{\varphi }\right),$ or $\mathbf{U}=\left(\alpha ,\beta \right).$ The version corresponding to the first case is:

P2: Spherical Optimization Problem—Version 1
$\mathrm{Minimize}:$
	${\int }_0^T{∥{\mathbf{U}}^s\left(t\right)∥}^{2}dt$
$\mathrm{subject}\mathrm{to}:$
	$\dot{\mathbf{y}}=\left(u_{\theta },\frac{k}{4\pi R^2}\frac{1}{1-cos\theta }+u_{\varphi }\right)$
	$\mathbf{y}\left(0\right)=p_0$
	$\mathbf{y}\left(T\right)=P_f$
	$∥{\mathbf{U}}_s∥\le u_{max}$

Here, $\mathbf{y}=\left(\theta ,\varphi \right)$ is the position of the passive particle described by Equation (19), ${\mathbf{U}}^s=\left(u_{\theta },u_{\varphi }\right)$ is the control, and $P_0=\left({\theta }_0,{\varphi }_0\right)$ and $P_f=\left({\theta }_T,{\varphi }_T\right)$ are the initial and final point, respectively. The meaning of the objective function and constraints in the generic optimization problem P2 is identical to that in P1.

The version of the optimization problem in spherical coordinates formulated in the function of the control $\mathbf{U}=\left(\alpha ,\beta \right)$ is:

P3: Spherical Optimization Problem—Version 2
$\mathrm{Minimize}:$
	${\int }_0^T{∥\mathbf{U}\left(t\right)∥}^{2}dt$
$\mathrm{subject}\mathrm{to}:$
	$\dot{\mathbf{z}}=\left(\beta sin\varphi ,\frac{k}{4\pi R^2}\frac{1}{1-cos\theta }-\alpha +\beta cos\varphi cot\theta \right)$
	$\mathbf{z}\left(0\right)=P_0$
	$\mathbf{z}\left(T\right)=P_f$
	$∥\mathbf{U}∥\le u_{max}$

Here, $\mathbf{z}=\left(\theta ,\varphi \right)$ is the position of the passive particle described by Equation (31), $\mathbf{U}=\left(\alpha ,\beta \right)$ is the control, and $P_0=\left({\theta }_0,{\varphi }_0\right)$ and $P_f=\left({\theta }_T,{\varphi }_T\right)$ are the initial and final point, respectively. The objective function and constraints of the generic optimization problem P3 have the same meaning as those in both P1 and P2.

4.2. Numerical Solutions

To address the optimization problems, the generic control function $\mathbf{U}(·)$ is discretized in n constant vector variables defined as

$$\begin{array}{ccc}\mathbf{U}\left(t\right)={\mathbf{u}}_0\hfill & \mathrm{if}& t_0\le t<t_1,\hfill \\ \mathbf{U}\left(t\right)={\mathbf{u}}_1\hfill & \mathrm{if}& t_1\le t<t_2,\hfill \\ \mathbf{U}\left(t\right)={\mathbf{u}}_2\hfill & \mathrm{if}& t_2\le t<t_3,\hfill \\ \hfill & ⋮\\ \mathbf{U}\left(t\right)={\mathbf{u}}_{n-1}\hfill & \mathrm{if}& t_{n-1}\le t\le t_n,\hfill \end{array}$$

(33)

with $t_0=0,$$t_n=T$. Each vector variable ${\mathbf{u}}_i$, $i=1,2,\cdots ,n$, corresponds to a constant value of the control function exercised in the sub-interval $\left[t_{i-1},t_i\right)$ with constant length $\Delta t=\left(t_n-t_0\right)/n.$

Therefore, the discretization of the objective function (18) in n time intervals lead to the approximation

$$\Delta t\left({∥{\mathbf{u}}_0∥}^2+{∥{\mathbf{u}}_1∥}^2+\dots +{∥{\mathbf{u}}_{n-1}∥}^2\right),$$

(34)

which represents the discretization of the energies function (18) using the rule of rectangles.

The Cartesian optimization problem is then replaced by its discretized version:

DP1: Discretized Cartesian Optimization Problem
$\mathbf{Minimize}:$
$f_n=\Delta t{\sum }_{i=0}^{n-1}{∥{\mathbf{u}}_i∥}^2$
$\mathbf{Subject}\mathbf{to}:$
$\dot{\mathbf{x}}=\frac{k}{2\pi R}\frac{\mathbf{v}\times \mathbf{x}}{\left|\right|\mathbf{x}-{\mathbf{v}\left|\right|}^2}+{\mathbf{u}}_0^c,\mathbf{x}\left(t_0\right)=x_0,∥{\mathbf{u}}_0∥\le u_{max},t_0\le t<t_1$
$\dot{\mathbf{x}}=\frac{k}{2\pi R}\frac{\mathbf{v}\times \mathbf{x}}{\left|\right|\mathbf{x}-{\mathbf{v}\left|\right|}^2}+{\mathbf{u}}_1^c,\mathbf{x}\left(t_1\right)=x_1,∥{\mathbf{u}}_1∥\le u_{max},t_1\le t<t_2$
⋮
$\dot{\mathbf{x}}=\frac{k}{2\pi R}\frac{\mathbf{v}\times \mathbf{x}}{\left|\right|\mathbf{x}-{\mathbf{v}\left|\right|}^2}+{\mathbf{u}}_{n-1}^c,\mathbf{x}\left(t_{n-1}\right)=x_{n-1},∥{\mathbf{u}}_{n-1}∥\le u_{max},t_{n-1}\le t<t_n$
$\mathbf{x}\left(t_n\right)=x_f$

Here, ${\mathbf{u}}_i^c=\left({\alpha }_{i}y,-{\alpha }_{i}x+{\beta }_{i}z,-{\beta }_{i}y\right)$, ${\mathbf{u}}_i=\left({\alpha }_i,{\beta }_i\right)$, $i=0,1,\dots ,n-1$ are the control variables, $x_0=P_0$, $x_f=P_f$ are the initial and final point, respectively, and $t_n=T$.

The discretization approach for the spherical optimization problem is analogous. The only difference is that the dynamics of the passive particle in each sub-interval are governed by Equation (19) in the case of Version 1, and by Equation (31) in the case of Version 2.

The discretized form of Version 1 of the spherical optimization problem is:

DP2: Discretized Spherical Optimization Problem—Version 1
$\mathbf{Minimize}:$
$f_n=\Delta t{\sum }_{i=0}^{n-1}{∥{\mathbf{u}}_i^s∥}^2$
$\mathbf{Subject}\mathbf{to}:$
$\dot{\mathbf{y}}=\left(0,\frac{k}{4\pi R^2}\frac{1}{1-cos\theta }\right)+{\mathbf{u}}_0^s,\mathbf{y}\left(t_0\right)=y_0,∥{\mathbf{u}}_0^s∥\le u_{max},t_0\le t<t_1$
$\dot{\mathbf{y}}=\left(0,\frac{k}{4\pi R^2}\frac{1}{1-cos\theta }\right)+{\mathbf{u}}_1^s,\mathbf{y}\left(t_1\right)=y_1,∥{\mathbf{u}}_1^s∥\le u_{max},t_1\le t<t_2$
⋮
$\dot{\mathbf{y}}=\left(0,\frac{k}{4\pi R^2}\frac{1}{1-cos\theta }\right)+{\mathbf{u}}_{n-1}^s,\mathbf{y}\left(t_{n-1}\right)=y_{n-1},∥{\mathbf{u}}_{n-1}^s∥\le u_{max},t_{n-1}\le t<t_n$
$\mathbf{y}\left(t_n\right)=y_f$

Here, ${\mathbf{u}}_i^s=\left(u_{{\theta }_i},u_{{\varphi }_i}\right)$ are the control variables, $i=0,1,\dots ,n-1$, $y_0=P_0$ and $y_f=P_f$ are the initial and final point, respectively, and $t_n=T$.

For Version 2 of the spherical optimization problem, the discretized optimization problem is:

DP3: Discretized Spherical Optimization Problem—Version 2
Minimize:
$f_n=\Delta t{\sum }_{i=0}^{n-1}{∥{\mathbf{u}}_i∥}^2$
Subject to:
$\dot{\mathbf{z}}=\left({\beta }_{0}sin\varphi ,\frac{k}{4\pi R^2}\frac{1}{1-cos\theta }-{\alpha }_0+{\beta }_{0}cos\varphi cot\theta \right),\mathbf{z}\left(t_0\right)=z_0,∥{\mathbf{u}}_0∥\le u_{max},t_0\le t<t_1$
$\dot{\mathbf{z}}=\left({\beta }_{1}sin\varphi ,\frac{k}{4\pi R^2}\frac{1}{1-cos\theta }-{\alpha }_1+{\beta }_{1}cos\varphi cot\theta \right),\mathbf{z}\left(t_1\right)=z_1,∥{\mathbf{u}}_1∥\le u_{max},t_1\le t<t_2$
⋮
$\dot{\mathbf{z}}=\left({\beta }_{n-1}sin\varphi ,\frac{k}{4\pi R^2}\frac{1}{1-cos\theta }-{\alpha }_{n-1}+{\beta }_{n-1}cos\varphi cot\theta \right),\mathbf{z}\left(t_{n-1}\right)=z_{n-1},$
$∥{\mathbf{u}}_{n-1}∥\le u_{max},t_{n-1}\le t<t_n$
$\mathbf{z}\left(t_n\right)=z_f$

Here, ${\mathbf{u}}_i=\left({\alpha }_i,{\beta }_i\right)$ are the control variables, $i=0,1,\dots ,n-1$, $z_0=P_0$ and $z_f=P_f$ are the initial and final point, respectively, and $t_n=T$.

To obtain the final position $\mathbf{x}\left(T\right)$ of the passive particle, the ordinary differential equation that models the dynamic of the passive particle is solved numerically in cascade by the fourth-order Runge–Kutta method. The initial position of the passive particle in each sub-interval is given by the final position in the previous one. The main restriction of the discretized optimization problem consists of reaching the targeted destination $P_f$ in a given time T, imposed in the last sub-interval by the condition $\mathbf{x}\left(t_n\right)=P_f$. Because achieving an exact value is challenging in finite precision computation, the condition $\mathbf{x}\left(t_n\right)=P_f$ is replaced by

$$\parallel \mathbf{x}\left(T\right)-P_f\parallel <\epsilon ,$$

(35)

where $\epsilon$ denotes a predefined small tolerance. In spherical optimization problems, the equivalent condition is applied by substituting $\mathbf{x}\left(T\right)$ with $\mathbf{y}\left(T\right)$ in the case of Version 1, or with $\mathbf{z}\left(T\right)$ in the case of Version 2, in (35).

The discretized optimization problems are solved numerically by mean of the MATLAB nonlinear optimization solver fmincon [16] that provides the constrained optimization algorithms Interior Point and Active-Set (see, for instance, [22,23]).

5. Results

The results presented in this section are related to the trajectory of a passive particle. The particle is required to move from an initial point $P_0=\left(\frac{\pi }{6},\pi \right)$ to a designated target point $P_f=\left(\frac{3\pi }{4},0\right)$ on the surface of a sphere. The passive particle can be conceptualized as a representation of autonomous technology. For the sake of simplicity, the radius of the sphere is fixed at $R=1$.

It is considered that the passive particle has reached the destination when its position $\mathbf{x}\left(T\right)$ is within a distance of $\epsilon ={10}^{-3}$ from $P_f$, as indicated in (35). The passive particles move in a flow that is induced by $N=1,2,3$ point vortex with circulations $k_i=1$, with $i=1,\dots ,N$.

The discrete optimization problems (DP1, DP2, and DP3), outlined earlier, have been computationally implemented using the MATLAB Optimization Toolbox [16]. The optimization tool fmincon, employed for nonlinear optimization, is utilized to identify optimal controls. Given that the solution is sensitive to the initial condition, which is randomly generated, multiple executions of this built-in function may yield diverse results. To mitigate the impact of the initial guess, the function is executed multiple times, and the solution leading to a lower value of the objective function (34) is chosen. For this purpose, the built-in function multistart is applied with twenty repetitions.

The nonlinear restrictions corresponding to the displacement of the passive particle in each sub-interval involve solving ordinary differential equations that govern both its dynamics and the dynamics of the vortices. These equations are numerically integrated using the ode45 built-in function, which implements the fourth and fifth-order Runge–Kutta methods.

The computational runs were conducted on a KVM virtual machine equipped with 16 vCores of an Intel Xeon W-2195 CPU, 64 GB of RAM, and an SSD-based virtual disk, operating on Linux Ubuntu 20.04 LTS. It is important to note that the computing times provided in the tables below are indicative, as they are significantly influenced by the virtual machine’s usage by other users.

Problems DP1, DP2, and DP3 are solved for the cases $N=1,2$, and 3 vortices. For the case of $N=1$, the equations that govern the dynamics are those introduced in the previous section. For the case of $N=2$ and $N=3$, the equations that govern the dynamics of the passive particle and the vortices are given below.

5.1. Flow Created by a Single Vortex ($N=1$)

Table 1. Solution of the discrete optimization problems with $n=3$ controls.

Problem	Controls	${\mathit{f}}_3$	CPU Time
	${\mathbf{u}}_0=\left(-0.189,-0.443\right)$
	${\mathbf{u}}_1=\left(-0.225,-0.529\right)$
DP1	${\mathbf{u}}_2=\left(-0.344,-0.468\right)$	1.50	41.0
	${\mathbf{u}}_0^s=\left(0.695,-0.096\right)$
	${\mathbf{u}}_1^s=\left(0.674,-0.096\right)$
DP2	${\mathbf{u}}_2^s=\left(0.673,-0.096\right)$	2.36	208.2
	${\mathbf{u}}_0=\left(-0.189,-0.443\right)$
	${\mathbf{u}}_1=\left(-0.225,-0.529\right)$
DP3	${\mathbf{u}}_2=\left(-0.344,-0.468\right)$	1.50	60.3

displays the results from solving the discrete optimization problems DP1, DP2, and DP3 with $n=3$ controls. It is noteworthy that the solutions for DP1 and DP3 produce identical values for both the controls and the objective function. This confirms the validity of the algorithm (33), which is employed for both problems DP1 and DP3. Due to their equivalence, given that one is derived from the other through a coordinate transformation, the algorithm is anticipated to yield consistent results for both cases.

The computational time is shorter when solving the DP1 problem. The DP2 problem takes about four times as long to resolve compared to the other two cases.

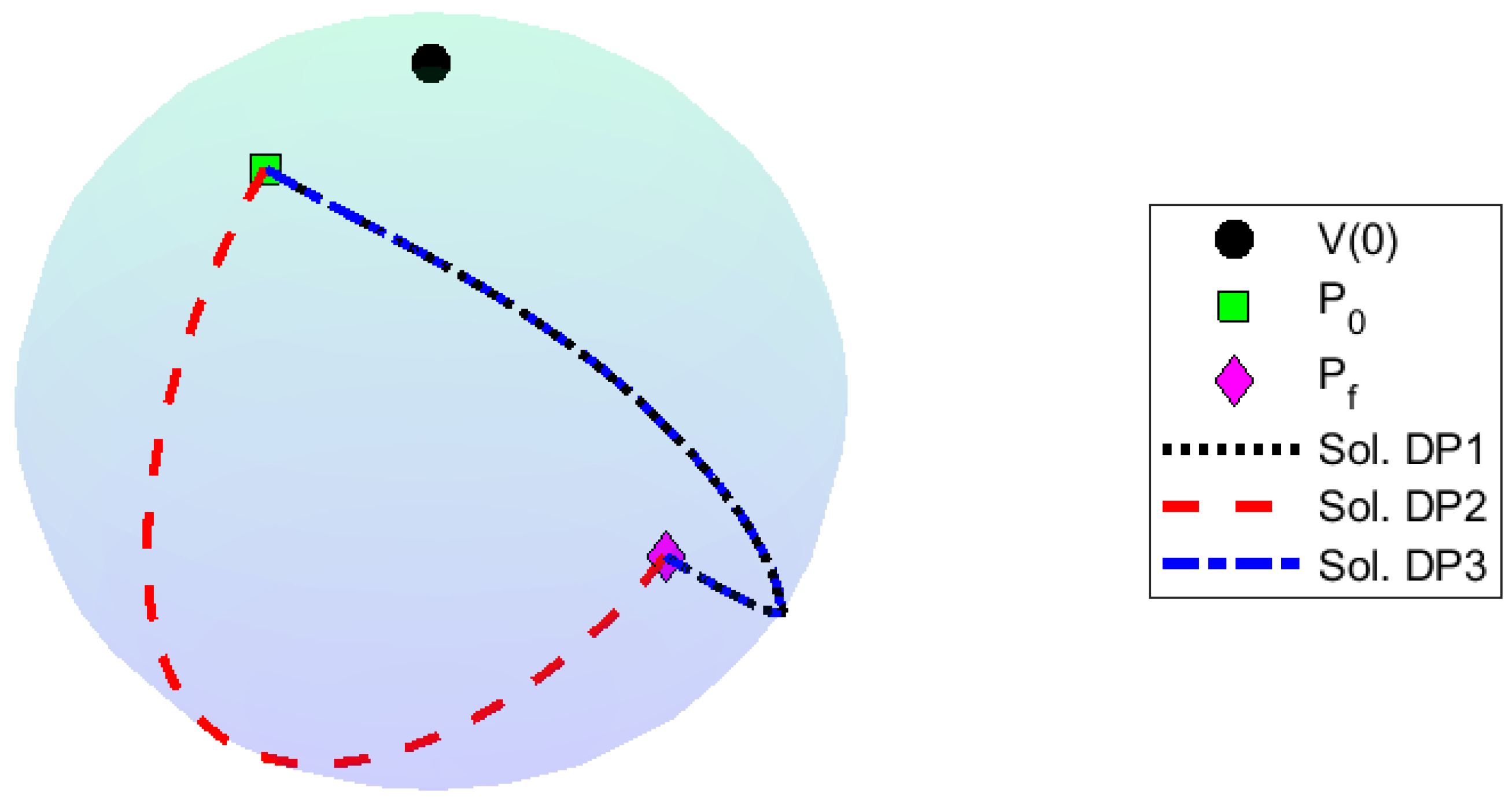
The trajectories corresponding to the solutions presented in Table 1 are illustrated in Figure 1. Trajectories resulting from the resolution of problems DP1 and DP3 are equal, as they both reach the final point by moving on the sphere through the same path. The trajectory resulting from DP2 leads to a longer path, leading to a larger value of the objective function. However, this value cannot be directly comparable with the objective function values resulting from the two other problems because the control parameters are different.

It can be seen that DP1 and DP3 present the same solution because they minimize the same objective function given by Equation (34). The optimization algorithm found the same minimum for the two problems.

Table 2. Discrete problem solutions in a flow generated by a single vortex.

	DP1		DP2		DP3
$\mathit{n}$	${\mathit{f}}_{\mathit{n}}$	CPUt [s]	${\mathit{f}}_{\mathit{n}}$	CPUt [s]	${\mathit{f}}_{\mathit{n}}$	CPUt [s]
1	1.53	21.2	1.84	265.5	1.53	25.9
2	1.51	25.8	1.65	371.9	1.51	43.3
4	1.50	24.7	1.30	385.8	1.50	87.0
6	1.49	16.3	1.30	188.3	1.49	127.4
8	1.49	17.7	1.29	575.1	1.49	181.3
10	1.49	25.5	1.25	185.5	1.49	181.5
12	1.49	55.9	1.23	728.1	1.49	181.5

displays the results obtained as a function of the number of controls n. As the number of control variables increases, the objective function shows a decreasing trend. The solution of DP1 and DP3 reaches a plateau after $n=6$. This indicates that the incremental gains in the objective function become marginal, remaining below a few hundred units. Notably, DP1 and DP3 consistently yield the same values for the objective function. Regarding computing time, there is a prevailing trend of an increase with the number, $n,$ of control variables, but with many irregularities. The computation times for solving DP1 are typically shorter compared to the other cases. Moreover, the times required for DP3 are lower than those observed for DP2.

5.2. Flow Created by Two Vortices ($N=2$)

In this section, the flow on the surface of the sphere is generated by two vortices. Considering Cartesian coordinates, the position of the two vortices, ${\mathbf{v}}_1$ and ${\mathbf{v}}_2,$ are described by

$$\left\{\begin{array}{c}{\dot{\mathbf{v}}}_1=\frac{k_2}{2\pi R}\frac{{\mathbf{v}}_2\times {\mathbf{v}}_1}{\parallel {\mathbf{v}}_1-{\mathbf{v}}_2{\parallel }^2}\hfill \\ \\ {\dot{\mathbf{v}}}_2=\frac{k_1}{2\pi R}\frac{{\mathbf{v}}_1\times {\mathbf{v}}_2}{\parallel {\mathbf{v}}_2-{\mathbf{v}}_1{\parallel }^2}\hfill \end{array}\right.$$

(36)

with the respective initial conditions where the initial position of the vortices are ${\mathbf{v}}_1\left(0\right)=\left(-0.3090,0,0.9511\right)$ and ${\mathbf{v}}_2\left(0\right)=\left(0.8660,0,-0.5000\right)$, and the passive particle, initially at $\mathbf{x}\left(0\right)=P_0,$ is modeled by the equation

$$\dot{\mathbf{x}}=\frac{1}{2\pi R}\left(k_1\frac{{\mathbf{v}}_1\times \mathbf{x}}{\parallel \mathbf{x}-{\mathbf{v}}_1{\parallel }^2}+k_2\frac{{\mathbf{v}}_2\times \mathbf{x}}{\parallel \mathbf{x}-{\mathbf{v}}_2{\parallel }^2}\right)+\alpha (y,-x,0)+\beta (0,z,-y),$$

(37)

for $i=0,1,\dots ,n-1$, where $\alpha$ and $\beta$ are the controllers, as presented in Section 2.

The determination of the optimal trajectory of the passive particle is obtained by solving a discrete optimization problem similar to DP1, where Equation (16) is replaced by Equations (36) and (37).

In spherical coordinates, the dynamics of the two vortices ${\mathbf{v}}_1=\left({\theta }_1,{\varphi }_1\right)$ and ${\mathbf{v}}_2=\left({\theta }_2,{\varphi }_2\right)$ are given by

$$\left\{\begin{array}{c}{\dot{\theta }}_1=-\frac{k_2}{4\pi R^2}\frac{sin\left({\theta }_2\right)sin({\varphi }_1-{\varphi }_2)}{1-cos\left({\gamma }_{12}\right)}\hfill \\ \\ {\dot{\varphi }}_1=-\frac{k_2}{4\pi R^2}\frac{cos\left({\theta }_2\right)-cot\left({\theta }_1\right)sin\left({\theta }_2\right)cos({\varphi }_1-{\varphi }_2)}{sin\left({\theta }_1\right)\left(1-cos\left({\gamma }_{12}\right)\right)}\hfill \\ \\ {\dot{\theta }}_2=-\frac{k_1}{4\pi R^2}\frac{sin\left({\theta }_1\right)sin({\varphi }_2-{\varphi }_1)}{1-cos\left({\gamma }_{21}\right)}\hfill \\ \\ {\dot{\varphi }}_2=-\frac{k_1}{4\pi R^2}\frac{cos\left({\theta }_1\right)-cot\left({\theta }_2\right)sin\left({\theta }_1\right)cos({\varphi }_2-{\varphi }_2)}{sin\left({\theta }_2\right)\left(1-cos\left({\gamma }_{21}\right)\right)}\hfill \end{array}\right.$$

(38)

with the given initial conditions ${\mathbf{v}}_1\left(0\right)=(\pi /10,\pi )$ and ${\mathbf{v}}_2\left(0\right)=(2\pi /3,0)$. In Equation (38), the value of $cos\left({\gamma }_{12}\right)$ and $cos\left({\gamma }_{21}\right)$ are computed in agreement with

$$cos\left({\gamma }_{ij}\right)=cos\left({\theta }_i\right)cos\left({\theta }_j\right)+sin\left({\theta }_i\right)sin\left({\theta }_j\right)cos({\varphi }_i-{\varphi }_j).$$

(39)

The motion of the passive particle is significantly influenced by the interaction between the two vortices and by the controls,

$$\left\{\begin{array}{c}{\dot{\theta }}_p=-\frac{1}{4\pi R^2}\left(k_1\frac{sin\left({\theta }_1\right)sin({\varphi }_p-{\varphi }_1)}{1-cos\left({\gamma }_{p1}\right)}+k_2\frac{sin\left({\theta }_2\right)sin({\varphi }_p-{\varphi }_2)}{1-cos\left({\gamma }_{p2}\right)}\right)+u_{\theta }\hfill \\ \\ {\dot{\varphi }}_p=\frac{1}{4\pi R^2}\left(k_1\frac{cos\left({\theta }_1\right)-cot\left({\theta }_p\right)sin\left({\theta }_1\right)cos({\varphi }_p-{\varphi }_1)}{1-cos\left({\gamma }_{p1}\right)}+k_2\frac{cos\left({\theta }_2\right)-cot\left({\theta }_p\right)sin\left({\theta }_2\right)cos({\varphi }_p-{\varphi }_2)}{1-cos\left({\gamma }_{p2}\right)}\right)+u_{\varphi }\hfill \end{array}\right.$$

(40)

with the initial conditions $P_0=({\theta }_{p0},{\varphi }_{p0}).$ As in the case of a single vortex, the control applied to the passive particle is represented by the vector ${\mathbf{U}}^s=\left(u_{\theta }{u}_{\varphi }\right)$. The determination of the optimal trajectory of the passive particle using spherical coordinates (Version 1) is obtained by solving a discrete optimization problem similar to DP2, where Equation (19) is replaced by Equation (38) together with Equation (40).

The spherical controls ${\mathbf{U}}^s=\left(u_{\theta },u_{\varphi }\right)$ can be expressed in terms of the Cartesian controls $\alpha$ and $\beta$. Using a methodology similar to that used in Section 2, an analogous relationship between these two types of controls is obtained:

$$\left\{\begin{array}{c}{u}_{\theta }=\beta sin\varphi \hfill \\ u_{\varphi }=-\alpha +\beta cos\varphi cot\theta \hfill \end{array}\right.$$

(41)

By employing (41) in Equation (40), the model of the passive particle’s dynamics in a flow induced by two vortices with spherical coordinates is obtained through the use of Cartesian control (Version 2). The solution of this equation together with Equation (38) enables us to determine the optimal trajectory of the passive particle.

Table 3. Discrete problem solutions in a flow generated by two vortices.

	DP1		DP2		DP3
$\mathit{n}$	${\mathit{f}}_{\mathit{n}}$	CPUt [s]	${\mathit{f}}_{\mathit{n}}$	CPUt [s]	${\mathit{f}}_{\mathit{n}}$	CPUt [s]
1	1.35	181.5	1.37	106.2	1.35	41.8
2	1.27	181.8	1.33	225.4	1.27	101.6
4	1.27	181.7	1.25	112.4	1.27	101.2
6	1.26	181.8	1.23	101.7	1.26	101.2
8	1.26	183.3	1.36	101.8	1.26	101.4
10	1.25	182.8	1.66	101.0	1.25	101.8
12	1.25	182.4	1.58	207.2	1.25	101.5

presents the results obtained from solving the discretized optimization problems DP1, DP2, and DP3 in the case of a flow induced by two vortices.

As in the case of a single vortex, DP1 and DP3 achieve the same values of the objective function of all number n of controls. In all three problems, the objective function values decrease as the number of controls increases. The computation times exhibit considerable constancy with the variation of n. Generally, the computation times for DP3 are lower than those for DP2 and lower than those for DP1.

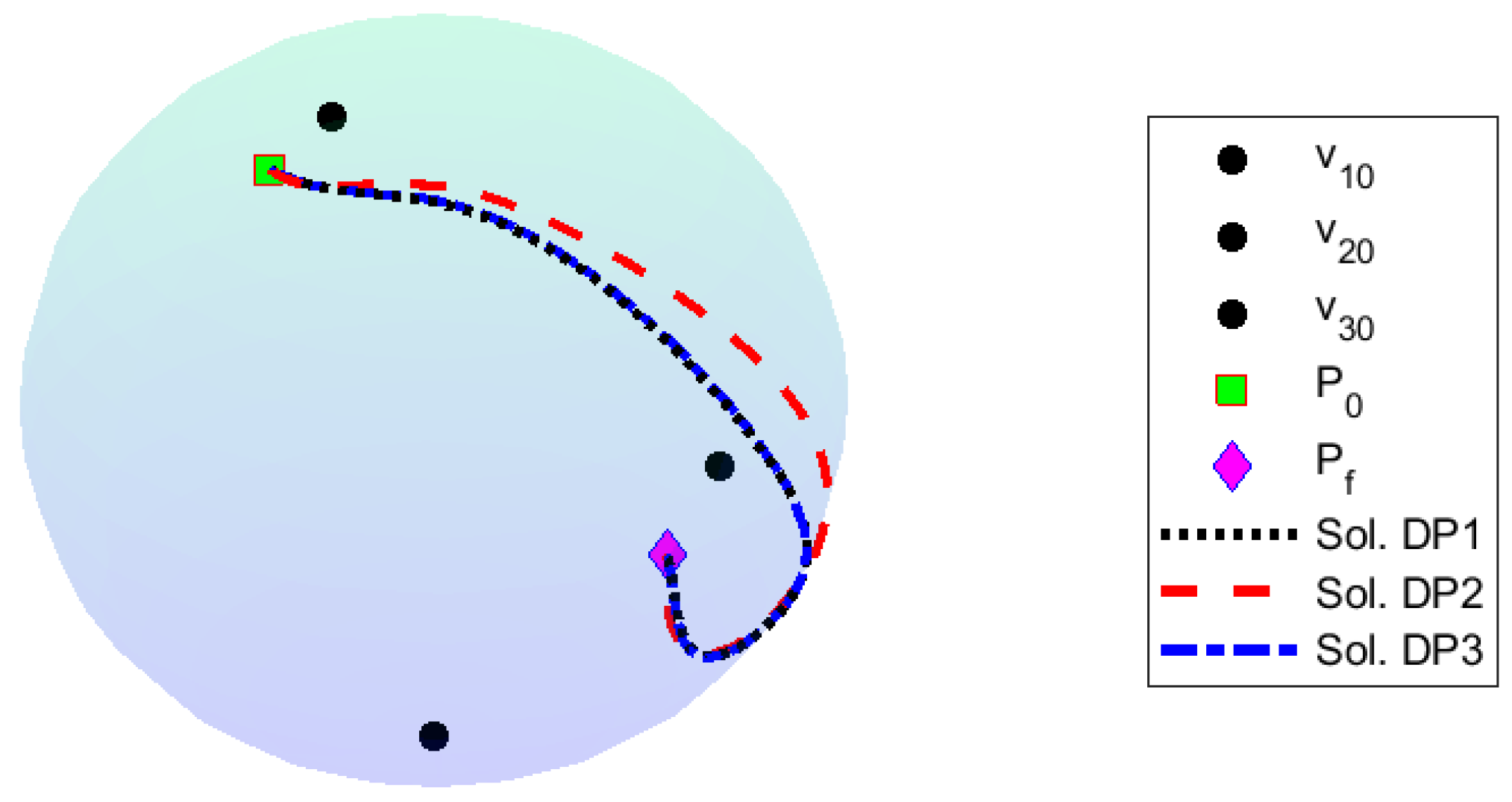
Figure 2 illustrates the trajectories corresponding to the minimum values of the objective function obtained in the resolution of DP1, DP2, and DP3 (see Table 3) in the case of a flow induced by two vortices. Notably, the trajectory resulting from DP1 is the same as the one resulting from DP3. The trajectory resulting from DP2 differs from the other two, being more extensive.

5.3. Flow Created by Three Vortices ($N=3$)

This section focuses on a flow generated by three vortices. Initially, we present the equations governing the displacement of a passive particle, introducing them in both Cartesian and spherical coordinates.

In Cartesian coordinates, the positions of the three vortices, ${\mathbf{v}}_1\left(t\right)$, ${\mathbf{v}}_2\left(t\right)$, and ${\mathbf{v}}_3\left(t\right)$, are governed by the following system of equations:

$$\left\{\begin{array}{c}{\dot{\mathbf{v}}}_1=\frac{1}{2\pi R}\left(k_2\frac{{\mathbf{v}}_2\times {\mathbf{v}}_1}{\left|\right|{\mathbf{v}}_1-{\mathbf{v}}_2{\left|\right|}^2}+k_3\frac{{\mathbf{v}}_3\times {\mathbf{v}}_1}{\left|\right|{\mathbf{v}}_1-{\mathbf{v}}_3{\left|\right|}^2}\right)\hfill \\ \\ {\dot{\mathbf{v}}}_2=\frac{1}{2\pi R}\left(k_1\frac{{\mathbf{v}}_1\times {\mathbf{v}}_2}{\left|\right|{\mathbf{v}}_2-{\mathbf{v}}_1{\left|\right|}^2}+k_3\frac{{\mathbf{v}}_3\times {\mathbf{v}}_2}{\left|\right|{\mathbf{v}}_2-{\mathbf{v}}_3{\left|\right|}^2}\right)\hfill \\ \\ {\dot{\mathbf{v}}}_3=\frac{1}{2\pi R}\left(k_1\frac{{\mathbf{v}}_1\times {\mathbf{v}}_3}{\left|\right|{\mathbf{v}}_3-{\mathbf{v}}_1{\left|\right|}^2}+k_2\frac{{\mathbf{v}}_2\times {\mathbf{v}}_3}{\left|\right|{\mathbf{v}}_3-{\mathbf{v}}_2{\left|\right|}^2}\right)\hfill \end{array}\right.$$

(42)

with the respective initial conditions for the vortices ${\mathbf{v}}_1\left(0\right)=\left(-0.3090,0,0.9511\right)$, ${\mathbf{v}}_2\left(0\right)=\left(0.8660,0,-0.5000\right)$, and ${\mathbf{v}}_3\left(0\right)=\left(0,0,-1\right)$. The constants $k_1$, $k_2$, and $k_3$ represent the circulation of each vortex.

The dynamics of the passive particle is governed by the equation

$$\dot{\mathbf{x}}=\frac{1}{2\pi R}\sum _{i=1}^3{k}_i\frac{{\mathbf{v}}_i\times \mathbf{x}}{\parallel \mathbf{x}-{\mathbf{v}}_i{\parallel }^2}+\alpha (y,-x,0)+\beta (0,z,-y),$$

(43)

with the given initial condition $\mathbf{x}\left(0\right)=P_0$.

In spherical coordinates, the dynamics of the vortices positions ${\mathbf{v}}_1\left(t\right)=\left({\theta }_1,{\varphi }_1\right),$ ${\mathbf{v}}_2\left(t\right)=\left({\theta }_2,{\varphi }_2\right)$, and ${\mathbf{v}}_3\left(t\right)=\left({\theta }_3,{\varphi }_3\right)$ are given by

$$\left\{\begin{array}{c}{\dot{\theta }}_1=-\frac{1}{4\pi R^2}\left(k_2\frac{{\rho }_{12}}{1-cos\left({\gamma }_{12}\right)}+k_3\frac{{\rho }_{13}}{1-cos\left({\gamma }_{13}\right)}\right)\hfill \\ \\ {\dot{\varphi }}_1=\frac{1}{4\pi R^2}\left(k_2\frac{{\sigma }_{12}}{sin\left({\theta }_1\right)(1-cos\left({\gamma }_{12}\right))}+k_3\frac{{\sigma }_{13}}{sin\left({\theta }_1\right)(1-cos\left({\gamma }_{13}\right))}\right)\hfill \\ \\ {\dot{\theta }}_2=-\frac{1}{4\pi R^2}\left(k_1\frac{{\rho }_{21}}{1-cos\left({\gamma }_{21}\right)}+k_3\frac{{\rho }_{23}}{1-cos\left({\gamma }_{23}\right)}\right)\hfill \\ \\ {\dot{\varphi }}_2=\frac{1}{4\pi R^2}\left(k_1\frac{{\sigma }_{21}}{sin\left({\theta }_2\right)(1-cos\left({\gamma }_{21}\right))}+k_3\frac{{\sigma }_{23}}{sin\left({\theta }_2\right)(1-cos\left({\gamma }_{23}\right))}\right)\hfill \\ \\ {\dot{\theta }}_3=-\frac{1}{4\pi R^2}\left(k_1\frac{{\rho }_{31}}{1-cos\left({\gamma }_{31}\right)}+k_2\frac{{\rho }_{32}}{1-cos\left({\gamma }_{32}\right)}\right)\hfill \\ \\ {\dot{\varphi }}_3=\frac{1}{4\pi R^2}\left(k_1\frac{{\sigma }_{31}}{sin\left({\theta }_3\right)(1-cos\left({\gamma }_{31}\right))}+k_2\frac{{\sigma }_{32}}{sin\left({\theta }_3\right)(1-cos\left({\gamma }_{32}\right))}\right)\hfill \end{array}\right.$$

(44)

with the initial conditions ${\mathbf{v}}_1\left(0\right)=(\pi /10,\pi )$, ${\mathbf{v}}_2\left(0\right)=(2\pi /3,0)$, and ${\mathbf{v}}_3\left(0\right)=(\pi ,\pi ).$ In Equation (44), the values of ${\gamma }_{ij}$ are given, as before, by (39), and ${\rho }_{ij}$ and ${\sigma }_{ij}$ are given by the Bogomolov notation [24,25]:

$${\rho }_{ij}=sin\left({\theta }_j\right)sin({\varphi }_i-{\varphi }_j),$$

(45)

and

$${\sigma }_{ij}=sin\left({\theta }_i\right)cos\left({\theta }_j\right)-cos\left({\theta }_i\right)sin\left({\theta }_j\right)cos({\varphi }_i-{\varphi }_j).$$

(46)

Hence, the dynamics of the controlled passive particle in a flow created by the three vortices is expressed as:

$$\left\{\begin{array}{c}{\dot{\theta }}_p=-\frac{1}{4\pi R^2}\left(k_1\frac{{\rho }_{p1}}{1-cos\left({\gamma }_{p1}\right)}+k_2\frac{{\rho }_{p2}}{1-cos\left({\gamma }_{p2}\right)}+k_3\frac{{\rho }_{p3}}{1-cos\left({\gamma }_{p3}\right)}\right)+u_{\theta }\hfill \\ \\ {\dot{\varphi }}_p=\frac{1}{4\pi R^2}\left(k_1\frac{{\sigma }_{p1}}{sin\left({\theta }_p\right)(1-cos\left({\gamma }_{p1}\right))}+k_2\frac{{\sigma }_{p2}}{sin\left({\theta }_p\right)(1-cos\left({\gamma }_{p2}\right))}+k_3\frac{{\sigma }_{p3}}{sin\left({\theta }_p\right)(1-cos\left({\gamma }_{p3}\right))}\right)+u_{\varphi }\hfill \end{array}\right.$$

(47)

with the given initial conditions $P_0=({\theta }_{p0},{\varphi }_{p0})$. As in the previous cases, the variables $u_{\theta }$ and $u_{\varphi }$ represent the angular controls applied on the passive particle.

Table 4. Discrete problem solutions in a flow generated three vortices.

	DP1		DP2		DP3
$\mathit{n}$	${\mathit{f}}_{\mathit{n}}$	CPUt [s]	${\mathit{f}}_{\mathit{n}}$	CPUt [s]	${\mathit{f}}_{\mathit{n}}$	CPUt [s]
1	1.46	181.3	2.13	105.9	1.46	101.3
2	1.37	181.3	1.90	101.1	1.37	101.8
4	1.35	181.4	1.68	101.6	1.35	101.4
6	1.34	181.9	1.68	101.5	1.34	101.9
8	1.34	182.5	1.62	102.5	1.34	101.9
10	1.33	182.4	1.62	104.9	1.33	103.1
12	1.33	183.9	1.59	104.8	1.33	103.1

showcases the results obtained from solving the discrete optimization problems DP1, DP2, and DP3 for the spherical flow created by three vortices. In the resolution of DP1, the dynamics of the passive particle are determined by solving Equations (42) and (43). Similarly, for DP2, the dynamics of the passive particle are governed by resolving Equations (44) and (47). In DP3, analogous to the one and two vortex cases, the equations governing the displacement of passive particles are Equations (44) and (47). Here, the spherical controls $u_{\theta }$ and $u_{\varphi }$ are substituted with Cartesian controls $\alpha$ and $\beta$, as indicated in Equation (32).

In this scenario, a consistent pattern is observed in the gradual decrease of objective function values as the number of controls increases for all three problems. As before, DP1 and DP3 exhibit the same values of the objective function that attains the lowest value (1.33) for $n\ge 10$. DP2 attains the smallest value (1.59) for $n=12$. Generally, computation times slightly increase with the number n of controls, with DP2 and DP3 achieving lower times than DP1.

Figure 3 depicts the trajectories corresponding to the minimum values of the objective function achieved in the solutions of DP1, DP2, and DP3 (refer to Table 4) for a flow induced by three vortices. As expected, the trajectories from DP1 and DP3 are the same. It is also observed that the trajectory resulting from DP2 is close to the other two.

6. Conclusions

The results discussed in this research originate from an exploration into the modeling of surface displacement for a controlled passive particle. This displacement takes place in a flow generated by a set of vortex points, ranging from one to three, on the surface of a sphere.

The equations governing the dynamics of the passive particle are presented in both Cartesian and spherical coordinates. For each coordinate system, the task of determining the particle’s trajectory between two points is translated into an optimization problem aimed at minimizing overall control. In the case of spherical coordinates, two forms of controls were applied. Initially, the problem was conceptualized with angular controls, and subsequently, the control parameters from the Cartesian formulation were employed in a second approach.

The three optimization problems arising from this study were solved using a direct method. This method involves dividing the available time for displacement into a predetermined number of sub-intervals. Throughout each sub-interval, the controls are constant.

The results obtained from resolving the three discretized problems suggest that each formulation produces a feasible solution. In simpler terms, each approach allows the passive particle to attain the desired displacement within the allocated time. These two versions of the same problem affirm the effectiveness of the algorithm used to convert the optimal control problem into an optimization problem, as demonstrated by the obtained controls. The numerical resolution of these formulations through a direct approach consistently yields optimal solutions, irrespective of the chosen coordinate system.

Generally, as the number of controls increases, the objective function’s value decreases. However, beyond a certain threshold, the objective function ceases to decrease and remains constant.

Computation times generally rise, when addressing the problem using spherical coordinates and angular controls. In general, the most efficient computational times are achieved through either the Cartesian formulation or the spherical formulation with Cartesian controls.

In the context of this work, it is worth noting that several interesting problems come to light. For instance, real-world applications involving point vortices on a sphere often utilize the rotating sphere to simulate Earth’s rotation. How the sphere’s rotation impacts the control of passive particles will be the focus of an upcoming investigation.