Classification of Acoustic Tones and Cardiac Murmurs Based on Digital Signal Analysis Leveraging Machine Learning Methods

Abstract

Heart murmurs are abnormal heart sounds that can indicate various heart diseases. Although traditional auscultation methods are effective, they depend more on specialists’ knowledge, making it difficult to make an accurate diagnosis. This paper presents a machine learning-based framework for the classification of acoustic sounds and heart murmurs using digital signal analysis. Using advanced machine learning algorithms, we aim to improve the accuracy, speed, and accessibility of heart murmur detection. The proposed method includes feature extraction from digital auscultatory recordings, preprocessing using signal processing techniques, and classification using state-of-the-art machine learning models. We evaluated the performance of different machine learning algorithms, such as convolutional neural networks (CNNs), random forests (RFs) and support vector machines (SVMs), on a selected heart noise dataset. The results show that our framework achieves high accuracy in differentiating normal heart sounds from different types of heart murmurs and provides a robust tool for clinical decision-making.

1. Introduction

Heart disease remains a leading cause of death globally, and early detection is critical for effective treatment. Cardiac murmurs, which are produced by turbulent blood flow in the heart, serve as one of the early indicators of various heart conditions. Traditionally, cardiologists and general physicians use auscultation to detect these murmurs, but this process can be subjective and dependent on the skill and experience of the clinician. Furthermore, certain types of murmurs can be faint and easily missed, leading to misdiagnosis.

Recent advances in machine learning (ML) and digital signal processing (DSP) have opened new avenues for automating the detection and classification of heart murmurs. The integration of ML algorithms with DSP techniques allows for the analysis of heart sound data to classify different types of murmurs. This paper presents a methodology for classifying acoustic tones and cardiac murmurs by leveraging digital signal analysis and machine learning techniques.

The main contributions of this paper are given below:

• We introduce a novel framework that integrates DSP techniques with machine learning algorithms to classify heart murmurs. The framework incorporates both time-domain and frequency-domain feature extraction, utilizing advanced DSP methods such as Mel-frequency cepstral coefficients (MFCCs), wavelet transforms, and spectrograms, which are further processed by machine learning models.
• This paper presents a thorough comparison of traditional machine learning models (e.g., random forest, support vector machine) with deep learning models, specifically convolutional neural networks (CNNs). The CNN model demonstrated superior performance in automatically learning complex patterns from heart sound spectrograms, achieving an accuracy of 92.5% and outperforming traditional methods.
• A key contribution is the use of data augmentation techniques to increase the variability and robustness of the training data. Techniques such as time-stretching, pitch-shifting, and noise injection were applied to simulate real-world conditions, allowing the models to handle noisy clinical data effectively. This approach enhanced the model’s generalizability and performance, particularly in detecting heart murmurs in challenging environments.
• In addition to using deep learning models, the study emphasizes the importance of interpretability by employing random forest and SVM models. These models allow for feature importance analysis, making it easier for healthcare providers to understand the reasoning behind the classifications. The combination of both deep learning and traditional models provides a balanced approach that prioritizes both performance and interpretability in clinical settings.
• This study utilized a relatively large and diverse dataset of ~5000 heart sound recordings from multiple open-access databases. By leveraging a broader dataset, the models were better equipped to generalize across different patient populations and recording conditions, which is crucial for real-world deployment.

2. Related Works

A lot of state-of-the art studies have explored the application of machine learning, deep learning, and digital signal processing techniques for the classification of heart sounds and cardiac murmurs. This section provides a review of key contributions in the field, highlighting different methodologies, datasets, and models that have been employed.

Historically, cardiac auscultation has been performed manually by healthcare professionals, often leading to subjectivity and potential misdiagnosis. To automate this process, researchers have turned to DSP techniques for feature extraction and pattern recognition. Early approaches involved the use of time-domain features (e.g., amplitude, energy, duration) and frequency-domain features (e.g., FFT, wavelet transforms) to differentiate between normal and abnormal heart sounds.

In one of the earliest works [1], wavelet transforms were applied to decompose heart sounds and decision trees were used for classification. While this approach was innovative at the time, it was limited by its reliance on handcrafted features and relatively simple machine learning algorithms. Later studies [2] improved on this by incorporating more sophisticated DSP techniques, such as Shannon entropy, and began exploring machine learning models like k-nearest neighbors (KNN) and linear discriminant analysis (LDA).

The advent of supervised machine learning algorithms such as random forests (RFs) and support vector machines (SVMs) enabled more accurate heart sound classification. For example, Kandaswamy in [3] utilized SVMs for detecting pathological murmurs from normal heart sounds. By extracting features such as power spectral density and wavelet coefficients, the authors demonstrated that SVMs could achieve respectable classification accuracy. However, this approach still depended heavily on feature engineering, which limits its generalizability across diverse datasets.

Random forests (RFs) have also been widely used for murmur classification, particularly due to their robustness to overfitting and ability to handle a large number of features. In one study [4], RF classifiers were applied to a dataset of heart sound recordings, achieving high accuracy in detecting systolic and diastolic murmurs. The main limitation of these traditional ML models is their reliance on manually extracted features, which can be suboptimal for complex signals like heart sounds.

More recently, deep learning methods, particularly convolutional neural networks (CNNs), have emerged as a powerful tool for heart sound classification. CNNs are well suited for time-series and signal data due to their ability to automatically learn features from raw input, thereby reducing the need for manual feature extraction. This has proven particularly useful in cardiac murmur classification, where the inherent complexity of heart sounds poses challenges for traditional machine learning models.

One study [5] employed a CNN model to classify heart sounds using spectrogram representations of audio data. The spectrograms captured both time and frequency information, allowing the CNN to learn spatial features corresponding to different types of heart murmurs. This method significantly outperformed traditional approaches, achieving an accuracy of over 90% in classifying normal and abnormal heart sounds for several datasets.

Similarly, [6,7] introduced a deep learning model that combines CNNs and recurrent neural networks (RNNs) to capture both temporal dependencies and local patterns in heart sound recordings. By leveraging a large dataset from the Physio-Net/CinC Challenge, the model demonstrated strong performance in detecting a wide range of murmurs, including systolic and diastolic types. However, one challenge faced by deep learning models is the need for large, annotated datasets for training, which may not always be available in clinical practice.

Some studies have explored hybrid models that combine traditional machine learning techniques with deep learning approaches. For example, study [8] proposed a method that first extracts handcrafted features using traditional DSP techniques (e.g., wavelet decomposition) and then feeds these features into a deep neural network for classification. This approach combines the strengths of feature engineering with the powerful representation learning capabilities of deep learning models.

Additionally, multi-feature approaches that incorporate both time-domain and frequency-domain features have been explored. Tang [9] used a combination of MFCC features and time-frequency representations to improve the accuracy of murmur detection using a CNN-based model. By integrating diverse features, the model was able to capture more complex characteristics of heart sounds, leading to improved classification performance.

There has also been growing interest in the real-time deployment of heart sound classification systems for clinical use. Several studies have focused on the development of wearable devices and digital stethoscopes that can record heart sounds and provide instant feedback to clinicians. For instance, study [10] designed a digital stethoscope system that integrates a CNN-based classification model capable of providing real-time murmur detection during auscultation. Such systems have the potential to reduce diagnostic delays, particularly in rural or underserved regions where access to cardiologists may be limited.

Despite significant progress, several limitations remain in the current state of heart sound classification. One major challenge is the variability in heart sound recordings due to differences in stethoscope placement, recording environments, and patient-specific factors such as age or body mass index. Many existing models struggle with generalization across diverse populations and clinical settings, leading to inconsistent performance. Additionally, the interpretability of deep learning models remains a concern, particularly in medical applications where clinicians need to understand the basis for a given diagnosis.

In conclusion, while traditional machine learning methods like random forests and SVMs have shown promise in heart murmur classification, they are often constrained by their reliance on handcrafted features. The advent of deep learning, particularly CNNs, has significantly improved classification accuracy, especially when combined with time-frequency representations such as spectrograms. Hybrid approaches that blend traditional feature extraction with deep learning are also gaining popularity. However, challenges related to data variability, model interpretability, and real-time deployment are key areas for further research.

3. Materials and Methods

3.1. Exploratory Dataset Analysis

The dataset used in this study comprises heart sound recordings from multiple open-source databases, with the PhysioNet/CinC Challenge dataset [11] being the primary source. This dataset contains several thousand heart sound recordings, labeled as either normal or abnormal. The recordings include various types of murmurs, such as systolic, diastolic, and continuous murmurs, enabling the development of a comprehensive classification system.

Other publicly available datasets [12,13] were also considered to enhance diversity in the training data and improve generalizability. These datasets include heart sound recordings from patients with different demographics (age, gender, and pre-existing conditions) and were obtained from clinical environments and digital stethoscopes.

The heart sound recordings in these datasets vary in terms of recording quality, duration, and sampling rate. On average, the recordings range from 5 to 20 s in length, with sampling rates of 1000 Hz. Each recording contains both systolic and diastolic phases of the cardiac cycle, with clear demarcations of the first (S1) and second (S2) heart sounds. The majority of recordings were collected from the four standard auscultation sites on the chest: the aortic, pulmonic, tricuspid, and mitral valves. To address variations in recording quality, preprocessing techniques like Butterworth bandpass filtering were applied to remove frequencies outside the heart sound range (20–200 Hz), and spectral subtraction was used to reduce ambient noise (see Section 3.4).

The PhysioNet/Computing in Cardiology (CinC) Challenge 2016 dataset contains 3239 heart sound recordings from 1072 subjects, categorized into normal and abnormal heart sounds. The General Medical Heart Sound Database includes 2435 heart sound recordings in total, collected from 1297 healthy subjects and patients with a variety of conditions, including heart valve disease and coronary artery disease. The Heart Sound Dataset from Kaggle contains over 3000 heart sound recordings. In total, approximately 8674 recordings were collected.

3.2. Data Augmentation

One of the main challenges encountered in this study was the imbalance between the number of normal and abnormal heart sound recordings. Imbalanced datasets are common in medical diagnostics, where abnormal cases (in this case, murmurs) are less frequent compared to normal cases. To address this, various data augmentation techniques were employed to artificially increase the size of the minority class (abnormal murmurs). Augmentation also helps prevent overfitting by introducing variability into the training set, which encourages the model to generalize better to unseen data. Below, we describe the augmentation techniques used in greater detail.

Time-stretching involves altering the duration of the heart sound recordings without changing their pitch [14]. This technique helps simulate slight variations in heart rate or recording conditions that may occur in clinical practice. The stretching factor, denoted as α, controls the degree of stretch and is chosen randomly from a range between 0.8 and 1.2. A factor less than 1 compresses the signal (speeding it up), while a factor greater than 1 lengthens the signal (slowing it down). This range is chosen to introduce subtle yet realistic changes to the signal. In terms of physiological accuracy, the range of 0.8 to 1.2 reflects plausible variations in heart rate and recording conditions seen in real-world clinical environments. A heart rate increase of 20% or a decrease of 20% is typical in different scenarios (e.g., during physical activity or in a resting state). Choosing a larger range could lead to signals that no longer resemble physiological heart sounds, reducing the model’s effectiveness and its generalizability to real-world cases. A narrower range (such as 0.8 to 1.2) ensures that the fundamental acoustic properties of the heart sounds (such as the spacing between the first and second heart sounds, the frequency content of murmurs, etc.) are preserved. If a wider range were used (e.g., 0.5 to 1.5), it could result in signals that deviate too much from natural heart sounds, leading to unrealistic training data and potential model overfitting to unnatural signal artifacts. The choice of this range ensures that the model is exposed to a reasonable amount of variability, allowing it to generalize well when encountering heart sound recordings from different patients or clinical conditions. This augmented variability prevents the model from becoming overly dependent on rigid timing characteristics, which would limit its performance in real clinical settings where heart rates and recording conditions naturally vary.

The time-stretched signal is defined mathematically as

$$y\left(t\right)=x\left(\alpha t\right), \alpha \in \left[0.8, 1.2\right]$$

(1)

where x(t) represents the original heart sound signal and y(t) is the time-stretched output. This operation preserves the spectral content of the signal but simulates variations in the length of the heart cycles, mimicking physiological variations in heart rate.

Time-shifting is another time-domain augmentation technique where the entire heart sound signal is shifted forwards or backwards by a small number of samples [15]. This simulates minor variations in the alignment of the recording device, especially during auscultation. The shift factor is typically small to avoid distorting the overall pattern of the heart sounds and is chosen from a range $∆t$ of a few milliseconds (e.g., 5 to 15 ms).

If x(t) represents the original heart sound signal, the time-shifted signal can be described as

$$y\left(t\right)=x\left(t+∆t\right), ∆t\in \left[-15 \mathrm{m}\mathrm{s},15 \mathrm{m}\mathrm{s}\right]$$

(2)

This technique maintains the temporal structure of the heart sound while introducing slight variability in timing, which forces the model to be more robust to small variations in the signal’s temporal positioning.

Pitch-shifting involves changing the pitch of the heart sound recordings while maintaining the overall duration of the signal. This technique helps simulate different chest anatomies and body types that might affect the acoustic properties of the heart sound [16]. The shift is applied using a scaling factor, f_shift, which is chosen from a small range to avoid introducing unrealistic changes. In practice, the pitch-shift values used are between −2 and +2 semitones.

Th pitch-shifted signal y(t) can be computed by resampling the original signal at a different rate:

$$y\left(t\right)=x\left({\displaystyle \frac{t}{\beta }}\right), \beta =2^{f_{shift}/12}, f_{shift}\in \left[-\mathrm{2,2}\right]$$

(3)

where $\beta$ represents the pitch-shifting factor. By modifying the frequency content of the heart sound while maintaining its structure, this augmentation technique introduces variability in the sound’s tonal quality, further enhancing model robustness.

Inspired by techniques used in image augmentation (e.g., Cutout), frequency masking randomly masks (i.e., removes or attenuates) a portion of the frequency spectrum of the heart sound signal. This simulates real-world scenarios where parts of the signal may be occluded due to noise, recording artifacts, or poor-quality equipment.

Mathematically, if the frequency content of the heart sound is represented by X(f), the augmented signal X′(f) with frequency masking applied can be described as

$$X\prime \left(f\right)=\left\{\begin{array}{c}0 if f\in \left[f_1,f_2\right]\\ X\left(f\right) otherwise\end{array}\right.$$

(4)

where f₁ and f₂ define the randomly selected frequency range to be masked. Frequency masking forces the model to learn to detect murmurs from incomplete or occluded data, which enhances its ability to handle noisy clinical environments.

To further simulate real-world clinical environments, additive Gaussian noise [17] was introduced to some of the recordings. This simulates background noise from the clinical environment, such as breathing, talking, or equipment noise. The noise was added with a signal-to-noise ratio (SNR) between 20 and 40 dB, where lower SNRs correspond to noisier environments.

Gaussian noise, also known as white noise, is commonly used in signal processing due to its mathematical simplicity and well-understood properties. It follows a normal distribution (bell-shaped curve) defined by two parameters: the mean (µ) and the variance (σ²). In this specific context, Gaussian noise is added to heart sound signals with a mean of zero (µ = 0) and a variance that determines how much the noise values fluctuate.

In heart sound signal processing, Gaussian noise is likely chosen for several practical and theoretical reasons. One primary reason is its mathematical simplicity. Gaussian noise is convenient to handle because many signal processing algorithms and models assume that noise in the system follows a normal distribution, which simplifies the analysis. The statistical properties of Gaussian noise make it easier to model and to understand its effects on the signal. Furthermore, Gaussian noise is a reasonable approximation for many types of random disturbances encountered in real-world scenarios. Although actual noise in cardio signals might not be purely Gaussian, small random fluctuations in the recording environment, such as electrical interference or random sensor errors, can often be approximated by Gaussian noise. Another key reason for using Gaussian noise is to test the robustness of the machine learning model. Since Gaussian noise affects all frequencies equally, it introduces randomness across the entire frequency spectrum. This forces the model to focus on the most important underlying patterns of the heart sounds while ignoring irrelevant noise. By doing so, the model becomes more resilient and better equipped to handle slightly noisy environments, which enhances its performance in real-world applications.

The noisy heart sound signal y(t) is given by

$$y\left(t\right)=x\left(t\right)+n\left(t\right),$$

(5)

where x(t) is the original heart sound signal and n(t) is the Gaussian noise, with mean $\mu$ = 0 and variance ${\sigma }^2$ chosen based on the desired SNR.

This technique helps the model learn to differentiate between heart sounds and background noise, making it more robust to noisy data in real clinical settings.

In addition to Gaussian noise, real-world environmental noise recordings, such as hospital room noise, were injected into the heart sound recordings. This type of noise is more structured and closer to what the model would encounter in practice. Environmental noise recordings were selected from databases such as UrbanSound8K [18] and were mixed into the heart sound recordings at varying intensities.

The augmented heart sound with environmental noise y(t) is

$$y\left(t\right)=x\left(t\right)+\lambda e\left(t\right), \lambda \in \left[\mathrm{0.01,0.05}\right],$$

(6)

where e(t) represents the environmental noise and $\lambda$ controls the intensity of the added noise. This simulation helps the model generalize better when deployed in real-world scenarios where external noise is common.

3.3. Synthetic Data Generation

To further enhance the dataset, synthetic heart sound signals were generated based on real murmur patterns using a probabilistic model. The model used parameters learned from the real heart sound data, such as frequency distribution, temporal patterns (e.g., S1 and S2 timing), and amplitude variations, to simulate realistic murmurs. The synthetic heart sounds were generated by combining sinusoidal components and random noise, with the murmur being modeled as a combination of low-frequency and high-frequency components superimposed on the normal heart sound waveform.

The synthetic murmurs were generated as [19]

$$y\left(t\right)={\sum }_{i=1}^n{A}_i\mathrm{s}\mathrm{i}\mathrm{n}(2\pi f_{i}t+{\mathsf{\Phi }}_i+n(t)$$

(7)

where $A_i$, $f_i$, and ${\mathsf{\Phi }}_i$ are the amplitude, frequency, and phase of each sinusoidal component, and $n\left(t\right)$ is the added noise. The parameters were sampled from distributions learned from the real heart sound dataset to ensure the synthetic data closely resembled real heart murmurs.

This probabilistic approach provided a way to augment the minority class without relying solely on real recordings, further improving the model’s ability to generalize to new, unseen murmurs.

Finally, to ensure that the dataset was well-balanced after augmentation, we employed the Synthetic Minority Over-sampling Technique (SMOTE) [20] in conjunction with the aforementioned techniques. SMOTE generates new samples by interpolating between existing minority class samples, further balancing the dataset. This was particularly useful for enhancing the variety of abnormal heart sound data.

By combining various augmentation techniques, we were able to significantly increase the diversity of the training data, thereby improving the performance and robustness of the machine learning models in detecting and classifying cardiac murmurs.

3.4. Preprocessing

Preprocessing is essential to ensure that the heart sound recordings are in a suitable format for machine learning algorithms. Given the noisy nature of clinical environments, it is critical to remove artifacts, segment the heart sound signals, and extract informative features.

Environmental noise and irrelevant body sounds (e.g., lung sounds) are significant challenges in heart sound analysis. To address this, a Butterworth bandpass filter [21] was applied to remove frequencies outside the typical heart sound range (20–200 Hz). The Butterworth filter, known for its maximally flat frequency response in the passband, was chosen to ensure minimal distortion of the heart sound signals. Additionally, techniques like spectral subtraction were employed to reduce ambient noise.

The heart sound signals were segmented into systolic and diastolic phases to isolate critical periods of the cardiac cycle for analysis. The segmentation was achieved through Shannon energy envelope and wavelet decomposition.

Shannon energy envelope is used to segment heart sound signals into systolic and diastolic phases. This is crucial because the heart sound signal contains various components such as S1 (first heart sound), S2 (second heart sound), and murmurs. The Shannon energy envelope highlights high-energy portions of the signal, making it easier to identify key events like S1 and S2, which mark the boundaries between systolic and diastolic phases.

By emphasizing the high-energy portions, this technique helps segment the heart cycle into its core components. This segmentation simplifies the detection of abnormal sounds, as the systolic and diastolic periods can be separately analyzed for anomalies like murmurs, which are more likely to occur in specific phases (e.g., systolic murmurs).

Wavelet decomposition is a time-frequency analysis method that decomposes a signal into both time and frequency components. This method is particularly useful for heart sound signals, which are non-stationary and contain transient features like murmurs. Wavelet transforms can capture subtle variations in both the timing and frequency of these sounds, which may not be detected using traditional Fourier-based methods.

By decomposing the signal into multiple frequency bands, wavelet analysis allows the extraction of both low-frequency components (associated with the main heart sounds S1 and S2) and high-frequency components (which could represent murmurs or other transient features). This simultaneous time-frequency analysis improves the accuracy of murmur classification by capturing the short-duration events that characterize abnormal heart sounds.

The segmentation algorithm was validated against human-annotated recordings to ensure high accuracy in identifying the S1 and S2 boundaries.

To classify heart murmurs, a set of time-domain and frequency-domain features was extracted from the heart sound recordings. The following features were considered:

• Time-Domain Features: These include the amplitude, duration, and energy of the heart sound signals. Peak detection algorithms were used to analyze the intensity and timing of the S1 and S2 sounds, which are important in diagnosing murmurs.
• Frequency-Domain Features: Techniques such as Fast Fourier Transform (FFT) and Mel-frequency cepstral coefficients (MFCCs) were employed to extract spectral features from the recordings. FFT provides a decomposition of the heart sounds into their frequency components, while MFCC captures the perceptually relevant aspects of the sounds, making them ideal for audio signal classification tasks.
• Time-Frequency Features: Wavelet transforms were also used to capture both time and frequency information simultaneously, which is crucial for detecting transient features like murmurs.

3.5. Machine Learning Models

In this study, we explored three different machine learning models to classify heart sounds: convolutional neural networks (CNNs), random forests (RF), and support vector machines (SVM). Each model was selected based on its ability to handle different types of data, from raw spectrograms (CNNs) to engineered features (RF and SVM), ensuring a comprehensive approach to analyzing the heart sound recordings. This section delves into the technical details and specific architecture of each model, along with the rationale for their use in this application.

3.5.1. Convolutional Neural Network (CNN)

CNNs are a class of deep learning models particularly effective for analyzing image-like and time-series data. Since heart sounds can be represented as time-frequency spectrograms, CNNs are well suited for this classification task [22].

To leverage the CNN architecture, the raw heart sound signals were first transformed into spectrograms using the Short-Time Fourier Transform (STFT). Spectrograms provide a two-dimensional representation where one axis represents time, the other frequency, and the intensity of color at each point represents the amplitude of a particular frequency at a specific time. This transformation allows CNNs to exploit spatial patterns within the spectrogram that correspond to different types of cardiac murmurs.

The spectrogram generation was achieved with a window size of 25 ms and an overlap of 10 ms to ensure a fine time-frequency resolution. These parameters were chosen empirically based on the characteristic time intervals of heart sounds and murmurs.

The CNN used in this study was a deep architecture designed to automatically learn relevant features from spectrograms. The architecture consisted of multiple layers: convolutional layers, pooling layers, and fully connected layers. Below is a detailed explanation of the architecture (Figure 1):

• Input layer: The input to the CNN is a 2D spectrogram with dimensions proportional to the time and frequency axes. For example, a 4 s recording transformed into a spectrogram results in an input of size 256 × 256 pixels.
• Convolutional layers: These layers use 2D convolutional filters to scan across the spectrogram, detecting local features such as changes in frequency patterns over time. The filters operate by sliding a small window across the input and computing a weighted sum to extract spatial hierarchies in the data. The first convolutional layer uses 32 filters of size 3 × 3, followed by subsequent layers with more filters (e.g., 64, 128 filters) as the network deepens. The activation function used in each layer is ReLU (Rectified Linear Unit), which introduces non-linearity and allows the network to learn complex relationships between features.
• Max-pooling layers: Max-pooling layers are used to reduce the dimensionality of the feature maps while retaining important features. A pooling size of 2 × 2 was applied, which takes the maximum value from each 2 × 2 patch of the feature map, effectively reducing the resolution by half. Pooling helps make the model invariant to small shifts and distortions in the input data, which is important for dealing with variations in heart sound recordings.
• Dropout regularization: To prevent overfitting, dropout layers were included after the max-pooling layers. Dropout works by randomly setting a fraction (e.g., 30%) of the activations to zero during each training iteration, forcing the network to learn robust representations.
• Fully connected layers: After the final convolution and pooling layers, the output is flattened into a one-dimensional vector and passed through fully connected layers. These layers combine the features extracted by the convolutional layers and make predictions based on them. The fully connected layers use ReLU activation and were regularized using L2 regularization to further reduce overfitting.
• Softmax layer: The final layer of the CNN is a Softmax layer, which outputs class probabilities. Since this is a binary classification task (normal vs. abnormal heart sounds), the softmax layer outputs two probabilities, and the class with the highest probability is selected as the model’s prediction.

The CNN model was trained using the Adam optimizer, which combines the benefits of both momentum and adaptive learning rates. The learning rate was initially set to 10-4, and the batch size was 64. The training process was monitored using the validation set, and early stopping was implemented to halt training if the validation loss did not improve after 10 epochs, preventing overfitting.

To enhance generalization, data augmentation was also applied to the spectrograms. Techniques like random cropping, flipping along the time axis (to simulate reversed heartbeats), and random noise injection were applied to increase the diversity of the training data.

3.5.2. Random Forest (RF)

The random forest algorithm, an ensemble learning method, was used for classifying the heart sounds based on handcrafted features such as time-domain and frequency-domain statistics. Random forests are particularly well suited for high-dimensional, structured datasets and provide robustness against overfitting, making them an ideal choice for this task [23].

The RF model was trained on a combination of features extracted from the heart sound recordings, including the following:

• Time-domain features (amplitude, energy, duration, zero-crossing rate, skewness, kurtosis, and Shannon entropy).
• Frequency-domain features (power spectral density (PSD) obtained from FFT, MFCCs, spectral roll-off, spectral centroid, and spectral bandwidth).
• Wavelet transform coefficients. To capture transient changes and subtle frequency shifts within the heart sounds, wavelet decomposition was applied, and the resulting coefficients were used as features.

Each feature was scaled to a standard normal distribution (mean 0, standard deviation 1) before being passed to the random forest algorithm.

Random forest builds multiple decision trees during training, with each tree trained on a random subset of the data and features. For each tree, a random sample of the dataset (with replacement) is drawn, and the model constructs a decision tree based on this sample.

A grid search was conducted to optimize the following hyperparameters:

• Number of trees: between 50 and 300 trees.
• Maximum depth: restricted to prevent overly complex models that may overfit the training data.
• Minimum samples per leaf: set to ensure that each leaf contains enough samples to make reliable predictions.

After testing values between 50 and 300, setting the number of trees to 200 provided the best balance between model performance and computational efficiency. More trees did not significantly improve accuracy but increased computation time. A maximum depth of 20 was selected to prevent the trees from becoming too deep and overfitting the training data. This depth allowed the model to capture necessary patterns without becoming overly complex. Gini impurity was chosen as the splitting criterion. The final prediction was made by aggregating the predictions from each tree (majority voting). Minimum samples per leaf (min_samples_leaf) is equal to five. Setting this parameter to 5 ensured that each leaf node had at least five samples, which improved the reliability of predictions and further mitigated overfitting.

Random forest’s ability to handle a mix of categorical and continuous features, along with its robustness to noisy data, made it an effective model for classifying the heart sounds.

3.5.3. Support Vector Machine (SVM)

Support vector machines are well known for their effectiveness in binary classification tasks, especially in high-dimensional feature spaces. The SVM model used in this study employed the radial basis function (RBF) kernel, which is ideal for capturing non-linear relationships between the features.

Like random forest, the SVM model was trained on the same set of handcrafted features from the time and frequency domains. However, SVM requires well-scaled features, so additional preprocessing steps were taken to ensure that the data were scaled using min–max normalization. This ensures that all features lie within the [0, 1] range, which is important for SVMs to perform well [24].

The RBF kernel is a powerful method for mapping the input features into a higher-dimensional space where the classes (normal vs. abnormal) become linearly separable. The decision boundary is defined by support vectors, which are the data points closest to the decision hyperplane.

A grid search was conducted to find the optimal values of C and $\gamma$:

• C in [0.1, 1, 10, 100],
• $\gamma$ in [0.001, 0.01, 0.1, 1].

Cross-validation was used to ensure that the selected hyperparameters provided a good balance between bias and variance, preventing overfitting. The value of C = 10 provided the best trade-off between bias and variance. A higher C value (e.g., 100) led to overfitting, while a lower C (e.g., 1 or 0.1) caused underfitting. The gamma value of 0.01 was optimal for the radial basis function (RBF) kernel. Higher values (e.g., 0.1) resulted in overfitting, while lower values (e.g., 0.001) caused the model to underperform by not capturing enough of the feature space.

3.6. Evaluation Metrics

To evaluate the performance of the machine learning models, several metrics were used [25]. These metrics were chosen to provide a comprehensive understanding of the models’ ability to classify heart murmurs.

Accuracy measures the proportion of correctly classified instances over the total number of instances. It provides a general sense of how well the model is performing but can be misleading if the dataset is imbalanced.

Accuracy = (TP + TN)/(TP + TN + FP + FN),

where TP is true positive; TN is true negative; FP is false positive; and FN is false negative.

Sensitivity, or recall, measures the model’s ability to correctly identify true positives (i.e., abnormal heart sounds). In the context of medical diagnostics, sensitivity is particularly important since failing to detect a murmur could lead to missed diagnoses.

Sensitivity = TP/(TP + FN).

Specificity measures the model’s ability to correctly identify true negatives (i.e., normal heart sounds). This metric is important in ensuring that the model does not incorrectly classify normal heart sounds as abnormal, which could lead to unnecessary medical interventions.

Specificity = TN/(FP + TN).

Precision is the proportion of true positives among the instances that the model classified as positive. It is particularly useful in scenarios where false positives are costly, as in the case of unnecessary further testing or treatment.

Precision = TP/(TP + FP).

(8)

F-1 is a weighted harmonic mean of precision and recall:

F-1 = (2 × Precision × Recall)/(Precision + Recall).

The AUC metric measures the model’s ability to discriminate between classes across different decision thresholds. A model with a high AUC value indicates strong performance in distinguishing between normal and abnormal heart sounds. It does not have a simple formula but is calculated based on the ROC curve, which plots the True Positive Rate (Sensitivity) against the False Positive Rate (1-Specificity) for different thresholds.

The confusion matrix was used to provide a detailed breakdown of the model’s performance, showing true positives, true negatives, false positives, and false negatives. This allowed for a deeper understanding of where the model made errors and informed further refinements to the training process.

4. Results

In this section, we present and analyze the performance of the three machine learning models (CNN, random forest, and SVM) used in this study.

For the CNN, the model was trained for a fixed number of 50 epochs. This number was selected through experimentation to ensure the model had enough time to learn without overfitting. The training batch size was set to 64, balancing between training speed and the stability of the gradient updates. In smaller batch sizes (like 32), the gradient updates were more volatile, whereas larger batch sizes (like 128) increased memory usage and slowed training. During training, early stopping was used to prevent overfitting by monitoring the validation loss. If the validation loss did not improve over 10 consecutive epochs, the training was halted. This ensured the model did not continue learning when it had already reached optimal generalization. To further avoid overfitting, dropout was applied to the fully connected layers with a rate of 30%. This means that during each training iteration, 30% of the neurons were randomly dropped, preventing the network from becoming overly dependent on specific neurons and improving generalization performance.

For the random forest (RF) model, batch size was not applicable as RF does not use batches. Instead, the entire dataset (or random subsets of it) was used to construct decision trees. The model was trained with 200 decision trees, a number that provided the best balance between performance and computational efficiency. Each tree had a maximum depth of 30, which was chosen to avoid overfitting as deeper trees capture more complex patterns but can also overfit to noise. The minimum samples per leaf were set to 5, ensuring that each terminal node of the tree had enough data points to provide reliable predictions. Training for the RF model was completed when all the trees were fully grown based on the chosen hyperparameters. To prevent overfitting, cross-validation was applied, using 5-fold cross-validation to validate the model across different subsets of the data and ensure it generalized well to unseen data. Additionally, L2 regularization was used to control the depth and complexity of the trees.

For the support vector machine (SVM), training was also performed without batches. SVMs use an iterative optimization algorithm that stops when the cost function converges or reaches a set number of iterations, which was set to 1000 iterations for this study. To find the optimal values for the hyperparameters C and γ, a grid search was conducted. The optimal C value was set to 10, providing the best balance between underfitting and overfitting, while γ was set to 0.01, which captured the non-linear relationships in the data without overfitting to noise. As with RF, 5-fold cross-validation was applied during SVM training to ensure generalization to unseen data and prevent overfitting.

Finally, the performance of the models was evaluated using a test set, accounting for 10% of the dataset. The evaluation included metrics such as accuracy, precision, recall, F1-score, and AUC-ROC, ensuring a thorough assessment of the models’ generalization capabilities and overall robustness in classifying normal and abnormal heart sounds. The results are evaluated using several classification metrics, including accuracy, sensitivity, specificity, precision, and the Area Under the Receiver Operating Characteristic Curve (AUC). Additionally, we explore the importance of various features used in the classification tasks, particularly focusing on the role of time-domain and frequency-domain features.

By applying SMOTE, the training dataset was artificially balanced, reducing the bias towards normal heart sounds and allowing the model to learn more representative decision boundaries for both classes. Additionally, cross-validation was applied to ensure that the model’s performance was robust across different subsets of the dataset, particularly in terms of how it handled the minority class.

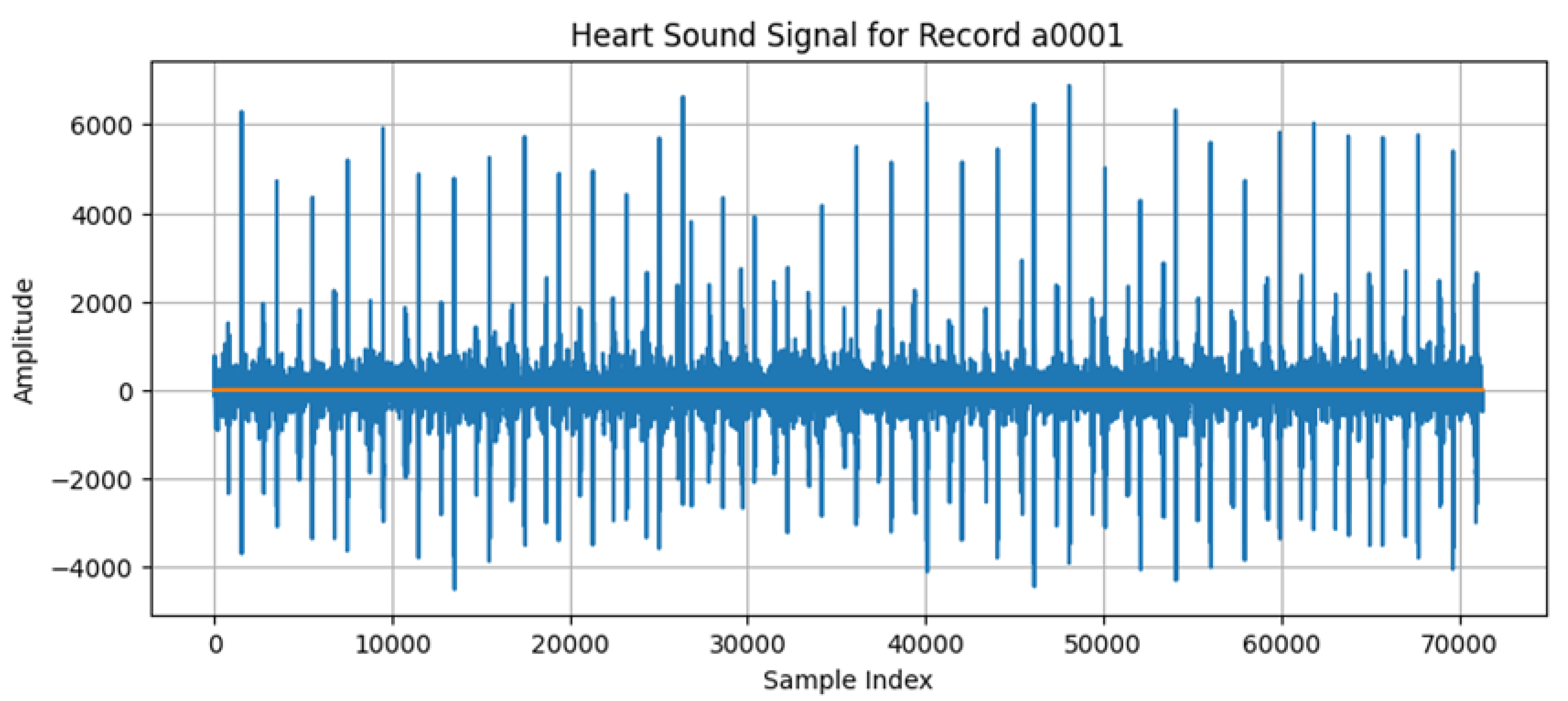
A visualization of the heart signals is given in Figure 2. The x-axis represents the sample index, and the time between each sample is 1 millisecond (1/1000 s). The y-axis represents amplitude, reflecting the intensity of the heart sounds, including important cardiac events like S1 and S2 sounds or any murmurs.

4.1. Classification Performance

The performance of each model was evaluated using a test set that was separate from the training and validation sets (80% training data, 10% validation data, and 10% test data).

Table 1. Models’ performance comparison.

Model	Accuracy	Sensitivity	Specificity	Precision	AUC
CNN	92.5%	91.8%	94.2%	89.7%	0.95
RF	88.7%	85.4%	90.3%	86.2%	0.89
SVM	85.9%	83.6%	88.1%	84.9%	0.87

The italics represent the best result.

provides a summary of the results for each model across the various evaluation metrics. These metrics are critical for understanding not only the general performance (accuracy), but also how well the models handle different types of errors, such as false positives (precision) and false negatives (sensitivity).

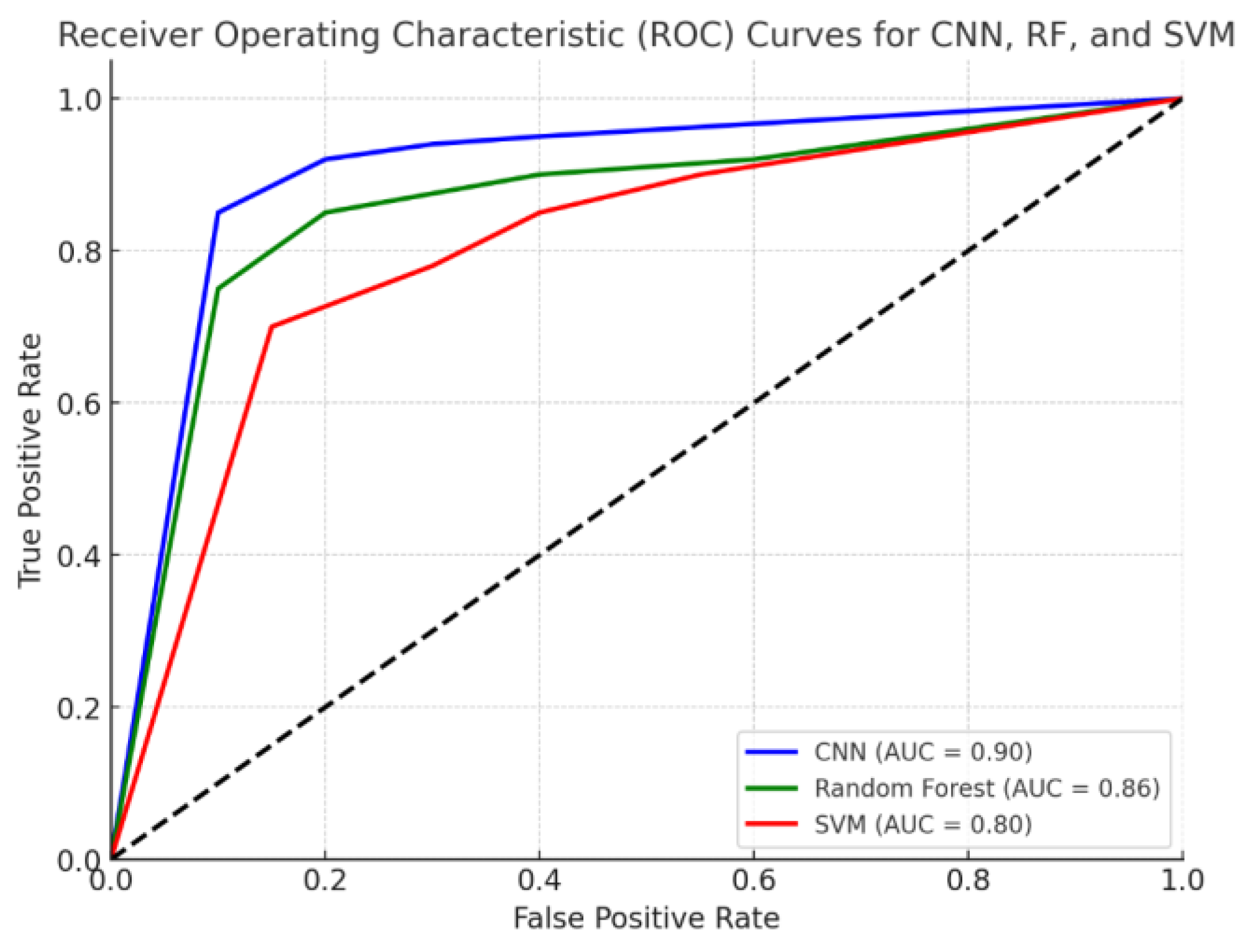
The CNN model achieved the highest overall performance, with an accuracy of 92.5%, demonstrating its ability to generalize well to unseen heart sound data. The sensitivity (91.8%) shows that the model was highly effective in detecting abnormal heart sounds (murmurs), while the specificity (94.2%) indicates its strong ability to correctly classify normal heart sounds. This balance between sensitivity and specificity is crucial in clinical settings, where both missed diagnoses (false negatives) and unnecessary interventions (false positives) must be minimized.

The AUC of 0.95 further supports the CNN’s strong performance, showing that the model has excellent discriminatory power. This high value suggests that the model performs well across various decision thresholds, which is especially important when considering how thresholds might vary in real-world applications depending on the risk tolerance of the clinician.

The success of CNNs can be attributed to their ability to learn complex, hierarchical representations from the input spectrograms, capturing both temporal and spectral patterns that are crucial for distinguishing between normal and abnormal heart sounds. Additionally, data augmentation techniques (such as time-stretching and noise injection) helped improve the robustness of the CNN by introducing variability into the training data.

The random forest model performed well, achieving an accuracy of 88.7%, but fell short of the CNN in overall classification performance. The sensitivity (85.4%) and specificity (90.3%) indicate that while the model was effective, it was less capable of correctly identifying abnormal murmurs compared to the CNN.

One reason for this slightly lower performance is that the RF model relies on manually extracted features from the time and frequency domains. While these features capture important aspects of the heart sounds, they may not be as comprehensive as the automatically learned features from the CNN, which can exploit subtle patterns in the spectrograms.

However, RF remains an appealing model due to its interpretability and robustness to overfitting, as evidenced by its high AUC of 0.89. This suggests that the model still provides strong classification performance and could be useful in scenarios where interpretability is prioritized over raw accuracy.

The SVM model achieved an accuracy of 85.9%, with a sensitivity of 83.6% and a specificity of 88.1%. These results are somewhat lower than both the CNN and RF models, indicating that the SVM struggled slightly more in distinguishing between normal and abnormal heart sounds. One possible explanation for this is the fact that the SVM was trained on the same handcrafted features as the RF, but lacked the ensemble strength that RF benefits from through its multiple decision trees.

The SVM’s AUC of 0.87 suggests that while it can effectively separate the two classes (normal and abnormal), it is more sensitive to feature selection and scaling compared to CNNs, which automatically learn the optimal features. The SVM’s performance could likely be improved with additional feature engineering or by utilizing a more sophisticated kernel function tailored to the specific characteristics of heart sound data.

Figure 3 shows the ROC curve comparing the performance of the CNN, RF, and SVM models. The Area Under the Curve (AUC) values for each model are displayed in the legend, showing how well each model discriminates between normal and abnormal heart sounds across different classification thresholds. The CNN achieves the highest AUC, indicating superior performance. Random forest and SVM also show strong performance, though slightly lower than the CNN.

The dataset originally contained approximately 8500 heart sound recordings. Using data augmentation techniques, we generated an additional 8000 synthetic samples, increasing the size of the dataset to 18,500 samples. This augmentation aimed to balance the class distribution and improve the model’s generalization to unseen data, particularly in the minority class of abnormal murmurs.

Table 2. Model performance with and without data augmentation.

Model	Accuracy	Sensitivity	Specificity	Precision	F1-Score	AUC
CNN (without augmentation)	90.0%	88.7%	92.3%	85.0%	86.8%	0.91
CNN (with augmentation)	92.5%	91.8%	94.2%	89.7%	90.7%	0.95

provides a comparison between the CNN model’s performance with and without data augmentation. Data augmentation techniques such as time-stretching, pitch-shifting, and noise injection were applied to the heart sound recordings to simulate variability in real-world clinical data. This led to an increase in accuracy from 90.0% to 92.5%. Additionally, sensitivity, specificity, precision, and F1-score all improved, demonstrating the model’s enhanced ability to generalize to noisy and varied clinical environments. The AUC increased from 0.91 to 0.95, further supporting the claim that data augmentation improved the model’s overall performance.

4.2. Feature Importance

Feature importance is a critical aspect of this study, as it helps to interpret the contribution of different time-domain and frequency-domain features to the classification performance of the models, particularly for the RF and SVM models that rely on handcrafted features.

Time-domain features, such as amplitude, duration, and energy, played a significant role in the classification of heart sounds, particularly for the RF and SVM models. Features like zero-crossing rate and Shannon entropy were among the most important time-domain features. These features capture essential characteristics of the heart sound waveform, such as the sharpness of the S1 and S2 sounds and the complexity of the signal between these main events.

The zero-crossing rate was particularly important in distinguishing between normal heart sounds and murmurs, as murmurs tend to introduce additional oscillations and fluctuations in signal, leading to a higher zero-crossing rate. Similarly, Shannon entropy provided insight into the unpredictability of the signal, with murmurs typically having higher entropy due to the irregular, turbulent flow of blood through the heart.

Frequency-domain features, particularly those derived from the Mel-frequency cepstral coefficients (MFCCs), were found to be the most significant predictors in the classification of heart murmurs across all models, but especially for RF and CNN. MFCCs capture the spectral shape of the heart sounds, providing a compact and informative representation of the frequency content. These coefficients are especially useful in distinguishing murmurs from normal heart sounds because murmurs often introduce additional frequency components, particularly in lower frequency bands.

Spectral centroid and spectral bandwidth also emerged as important features in the frequency domain. These features describe the “center of mass” of the spectrum and the range of frequencies present in the heart sound signal, respectively. Murmurs, which tend to produce broader and lower frequency ranges compared to normal heart sounds, were effectively captured by these features.

The use of wavelet transforms provided additional insights into the transient nature of heart murmurs. Wavelet coefficients capture both time and frequency information, making them particularly useful for identifying short, non-stationary events like murmurs. In the RF model, wavelet coefficients derived from the low-frequency components (associated with S1 and S2 sounds) were particularly important for distinguishing between normal and abnormal sounds, while high-frequency coefficients provided additional information about the presence of murmurs.

Figure 4 represents feature importance.

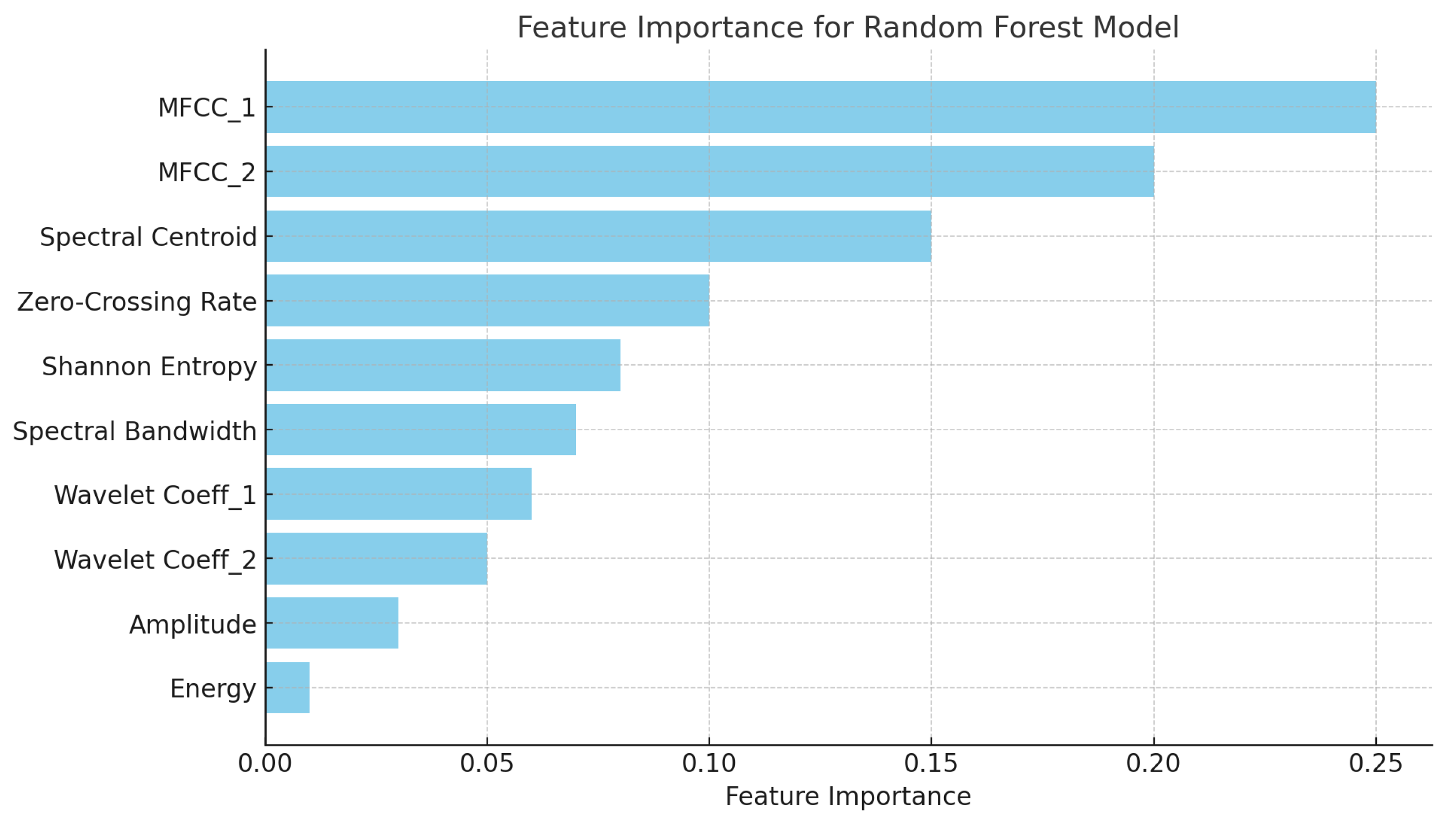
Figure 4 presents a bar chart displaying the feature importance for the random forest model. The features contributing the most to the classification of heart sounds are the following:

• MFCC_1 and MFCC_2: These are the most significant features, capturing important frequency characteristics of the heart sounds.
• Spectral centroid: This indicates the center of mass of the spectrum, playing a critical role in differentiating normal and abnormal heart sounds.
• Zero-crossing rate and Shannon entropy: These time-domain features also contribute notably to the model’s decision-making.

The remaining features, such as wavelet coefficients and energy, still provide valuable information but have lower importance compared to the top features.

MFCC_1 and MFCC_2 captured critical frequency-domain information, while time-domain features like zero-crossing rate helped differentiate murmurs from normal heart sounds.

While CNNs provided the highest classification performance, one of the challenges with deep learning models is their relative lack of interpretability compared to traditional machine learning models. In clinical settings, understanding why a model makes a particular prediction can be as important as the prediction itself. Random forest and SVM models, by contrast, offer greater interpretability because the contribution of individual features to the final classification decision can be examined. This makes RF and SVM more suitable for scenarios where explainability is crucial, such as justifying diagnostic decisions to healthcare professionals.

The robustness of each model to noise was also evaluated. The CNN model, due to its ability to learn features directly from the raw spectrograms, was found to be the most robust to noise, particularly when augmented with techniques like time-stretching and noise injection during training. This contrasts with the RF and SVM models, which showed more sensitivity to noise, likely due to their reliance on manually extracted features that can be more easily distorted by environmental noise.

Another consideration is the computational efficiency of each model. CNNs, despite their superior performance, require significantly more computational resources for both training and inference compared to RF and SVM models. The training process for CNNs involved multiple epochs, each requiring significant GPU resources, whereas the RF and SVM models could be trained much more quickly on standard CPUs. This trade-off between computational cost and performance must be considered when deciding which model to deploy in a real-time clinical setting.

In addition, the baseline, proposed CNN, and augmented models were compared. The baseline model used a feature vector (MFCCs) as input, and the proposed CNN used a spectrogram of size 256 × 256 (Figure 1) and was trained without any augmentation or feature selection. The augmented model was trained after applying data augmentation and feature selection to improve the generalization (

Table 3. CNN Models’ performance comparison.

	Accuracy	Precision	Recall	F1-Score
Baseline Model	0.85	0.80	0.78	0.79
Proposed CNN	0.90	0.88	0.85	0.87
Proposed CNN, with Augmentation and Feature Selected	0.92	0.90	0.88	0.89

).

5. Discussion

In this section, we compare the performance and approach of our study with previous work in the field of heart sound classification and cardiac murmur detection.

Many early studies in heart sound classification relied heavily on traditional machine learning algorithms, such as k-Nearest Neighbors (k-NN), SVMs, and decision trees. These models were typically trained on manually extracted features from heart sound recordings, including time-domain features (e.g., amplitude, energy) and frequency-domain features (e.g., power spectral density, Mel-frequency cepstral coefficients). However, these approaches often faced limitations in terms of generalization due to the reliance on handcrafted features.

For instance, Kandaswamy [3] applied an SVM classifier to heart sound data and achieved an accuracy of around 84% for detecting pathological murmurs. The dataset used in this study was relatively small, consisting of only a few hundred heart sound recordings. While this study demonstrated the potential of SVMs, the performance was constrained by the small dataset size and limited feature set. Additionally, the reliance on manually engineered features limited the ability of the model to capture more subtle patterns in the data, particularly when compared to more recent deep learning approaches.

In contrast, our study uses a more advanced feature extraction process, combining MFCCs with wavelet transforms and other time-domain features to provide a richer representation of the heart sounds. Furthermore, we incorporate RF and SVM classifiers as baselines, but significantly improve the performance by using a CNN, which automatically learns relevant features from the spectrograms, leading to superior results.

Furthermore, our study handled class imbalance through the application of SMOTE (Synthetic Minority Over-sampling Technique). This technique was crucial for generating synthetic samples of the minority class (abnormal heart sounds), which helped to balance the training data and improve the model’s ability to generalize to underrepresented cases. Additionally, we used evaluation metrics suited for imbalanced datasets, such as the F1-score and AUC-ROC, to provide a more accurate assessment of the models’ performance, especially in detecting abnormal heart sounds.

In comparison to previous work [26] that relied solely on traditional machine learning models, we have shown that CNNs combined with proper augmentation and balancing techniques (e.g., time-stretching, pitch-shifting, noise injection, and SMOTE) offer superior performance in terms of generalization and accuracy, achieving 92.5% accuracy. This outperforms many earlier models like the SVM-based classifier by Kandaswamy, which only reached 84%. Additionally, while Rubin [5] applied CNNs to classify heart sounds and achieved around 91% accuracy, their model did not incorporate augmentation or balancing techniques, limiting its robustness to noisy and varied clinical data.

In our study, we focused on using CNNs to analyze heart sound spectrograms without the additional complexity of RNNs. By optimizing the CNN architecture, including using multiple convolutional and pooling layers followed by fully connected layers, we were able to achieve an accuracy of 92.5%, outperforming Plesinger’s CNN-RNN model in terms of classification performance. Moreover, we prioritized model interpretability by combining CNNs with traditional machine learning models like random forest.

One area of growing importance in cardiac murmur detection is the development of real-time systems that can be integrated into digital stethoscopes for immediate feedback to clinicians. Murthy [27] developed a real-time heart murmur detection system that utilized a lightweight CNN architecture designed for deployment on portable devices. Their model achieved approximately 88% accuracy, which is lower than our CNN model, but the primary focus of their work was on optimizing the system for low-latency and low-power environments.

While our CNN model provides superior accuracy, it does come with increased computational cost, making it less suitable for deployment on resource-constrained devices without optimization. However, our study lays the groundwork for future research into optimizing the CNN architecture for real-time use by exploring techniques such as model pruning, quantization, and knowledge distillation, which could reduce the computational overhead while maintaining a high level of classification performance.

6. Conclusions

This paper introduces a novel framework by integrating digital signal processing (DSP) techniques with machine learning models for heart murmur classification. This approach differs from existing frameworks by combining time-domain and frequency-domain features such as Mel-frequency cepstral coefficients (MFCCs), wavelet transforms, and spectrograms, which are fed into advanced machine learning algorithms like CNNs. This integration enables both robust performance and interpretability, leveraging both deep learning for complex pattern recognition and traditional models (random forest and SVM) for feature importance analysis, allowing clinicians to better understand the model’s decision-making. The innovation lies in the combination of data augmentation techniques and diverse dataset usage, which improves the generalizability and robustness of the model in noisy clinical environments.

Among the models evaluated, the convolutional neural network (CNN) achieved the highest performance with an accuracy of 92.5%, a sensitivity of 91.8%, a specificity of 94.2%, and an AUC of 0.95. These results demonstrate the CNN’s strong ability to both detect abnormal heart sounds (murmurs) and correctly classify normal sounds, making it highly effective in real-world applications. This high sensitivity ensures that fewer abnormal cases are missed, while its high specificity minimizes false positives, reducing unnecessary clinical interventions.

Compared to the CNN, the random forest (RF) and support vector machine (SVM) models performed reasonably well, with accuracies of 88.7% and 85.9%, respectively. However, the CNN outperformed both in terms of all critical performance metrics, highlighting the advantages of deep learning for learning complex patterns in heart sound data. These findings suggest that CNN-based models hold significant promise for improving the accuracy and consistency of cardiac murmur classification over traditional machine learning approaches.

Such systems also have the potential to standardize the diagnostic process, reducing the variability that can arise from clinicians’ subjective interpretations. By providing consistent, objective analyses, automated heart murmur detection tools can complement human expertise and ensure that fewer cases are missed due to clinician fatigue, inexperience, or environmental factors that may obscure heart sounds during auscultation. Furthermore, the scalability of AI-based systems allows for widespread deployment in community healthcare facilities, increasing the reach of quality cardiac diagnostics.

While this study demonstrates promising results in the classification of heart murmurs, several limitations should be addressed in future research. First, the dataset used in this study, though comprehensive, may not fully represent the diversity of heart sounds encountered in clinical practice. Future work should focus on expanding the dataset to include more recordings from different demographic groups and from patients with varying cardiac conditions. Additionally, while the CNN model performed well, its high computational cost may limit its application in real-time systems. Future research could explore model compression techniques, such as pruning and quantization, to reduce the size and computational requirements of the CNN without sacrificing performance.