Abstract
Currently, the tasks of intelligent data analysis in medicine are becoming increasingly common. Existing artificial intelligence tools provide high effectiveness in solving these tasks when analyzing sufficiently large datasets. However, when there is very little training data available, current machine learning methods do not ensure adequate classification accuracy or may even produce inadequate results. This paper presents an enhanced input-doubling method for classification tasks in the case of limited data analysis, achieved via expanding the number of independent attributes in the augmented dataset with probabilities of belonging to each class of the task. The authors have developed an algorithmic implementation of the improved method using two Naïve Bayes classifiers. The method was modeled on a small dataset for cardiovascular risk assessment. The authors explored two options for the combined use of Naïve Bayes classifiers at both stages of the method. It was found that using different methods at both stages potentially enhances the accuracy of the classification task. The results of the improved method were compared with a range of existing methods used for solving the task. It was demonstrated that the improved input-doubling method achieved the highest classification accuracy based on various performance indicators.
1. Introduction
Modern lifestyle, ecology, nutrition, harmful habits, stress, and many other factors significantly affect people’s health and lives [1]. In particular, cardiovascular diseases, which arise due to the aforementioned problems, remain one of the leading causes of mortality worldwide, with heart attacks being one of the most threatening and common forms [2]. Since early diagnosis and prevention of heart attacks significantly increase the chances of survival, the scientific community is actively researching new technologies for predicting the risks of such events. One of the most promising directions is the use of machine learning (ML), which allows for the analysis of large volumes of data and the identification of patterns that are imperceptible to the human eye [3]. However, despite the great potential, the task of determining the risk of a heart attack using ML is accompanied by several problems and challenges [4,5,6].
One of the most significant problems is incomplete or unrepresentative data [7]. Since medical data often tends to be incomplete or noisy, this can affect the accuracy of the chosen machine learning model [8]. Additionally, such data may have a very small volume. This results in an inability to apply existing machine learning tools, a very small validation sample size for tuning the hyperparameters of the selected method, overfitting, and many other issues that arise when analyzing small datasets [9,10].
Another equally serious problem is the class imbalance in the data [11], where the number of positive cases of heart attacks is significantly smaller than the number of negative ones. This issue arises quite often, as heart attacks are rare events. In such cases, applying machine learning models to analyze the data may lead to inadequate model performance, particularly favoring negative predictions (i.e., the absence of an attack), as this may seem more ‘correct’ due to the quantitative predominance of negative examples [12]. This leads to a high rate of false-negative results, where the model fails to detect a real threat to the patient in time.
The simultaneous occurrence of both problems, particularly a small dataset and class imbalance, significantly reduces the number of existing machine learning methods that can be effectively applied to solve binary classification problems. Specifically, in [13], the authors addressed the task of classifying medical data. The main focus of this study was to investigate the effectiveness of machine learning classifiers when using data samples of various sizes. Modeling was performed using two large datasets, the sizes of which were reduced for experimentation. The authors found that both simple models, such as the naive Bayes classifier, and more complex models, like the adaptive boosting algorithm, provided the highest classification accuracy. Reducing the dataset size in this study did not significantly affect the classifiers’ accuracy, provided that the representativeness of the data sample was maintained while decreasing the number of instances. Despite these findings, many real medical tasks only have a limited amount of data for training procedures, which diminishes the effectiveness of machine learning classifiers when processing such data. In [14], the authors focused on improving the accuracy of machine learning methods during the analysis of short medical datasets through quality preprocessing of the data. They performed searches for and removal of anomalies, addressed missing data, and carried out feature selection, normalization, etc., which ultimately ensured the correct operation of the machine learning method. However, this approach does not solve the classification problem, particularly in cases of analyzing extremely short datasets. The authors of [15] took a different approach to enhance the analysis of short, imbalanced medical datasets. Their work was dedicated to exploring undersampling methods, which aim to generate representatives of the smaller class. This approach, on one hand, addresses the issue of imbalance in medical datasets, frequently encountered during medical data analysis. On the other hand, it allows for an increase in the data sample size, positively affecting the performance of machine learning classifiers. The results of this research demonstrated an improvement in the effectiveness of the task at hand. However, the issue of analyzing extremely short datasets remains unresolved. In [16], the authors investigated the effectiveness of state-of-the-art methods to address this problem. This study evaluated the effectiveness of generative adversarial networks (GANs) and autoencoders for artificial data generation. Such an approach can significantly increase the sample size for training classifiers, which in theory should enhance their accuracy. Experimental results showed that several machine learning methods could benefit from these artificial data generation techniques. However, the authors demonstrated several challenges associated with using such methods. One of these challenges involves selecting the appropriate machine learning method that will enhance accuracy when solving the task on an augmented dataset. Some of the methods studied even demonstrated a decrease in accuracy when working with the augmented dataset. Another equally important issue is finding the optimal complexity model when using artificial data generation methods. This task involves determining the right amount of artificially generated data that will improve the accuracy of the machine learning method without requiring excessive time and resources to resolve the problem. As shown via the research results in [16], this is a lengthy process. However, the most significant issue when working with artificial data generation methods is that they can produce data that do not accurately reflect the natural state of affairs in the given dataset. On one hand, this can lead to worse generalization properties of the chosen machine learning method; on the other, it significantly undermines the trust of medical professionals in AI-based solutions. Therefore, this approach is not the best option for solving the task at hand. To address the aforementioned issues, in [17,18,19], the authors developed and studied the effectiveness of a new methodology for processing small data samples. As demonstrated in these papers, the developed methods do not create entirely new artificial instances for the dataset under study, while still increasing the size of the specified dataset, ensuring the adequacy of the machine learning model for small data analysis and demonstrating high generalization properties. However, the accuracy of such methods is not always satisfactory.
Therefore, this paper aims to improve the methodology for processing small datasets, particularly to enhance the accuracy of solving the heart attack risk assessment problem when analyzing small, imbalanced datasets.
The primary contributions of this paper can be outlined as follows:
- We improved the input-doubling method for classification tasks in the case of limited data analysis, utilizing the principle of linearizing the response surface via expanding the number of independent attributes in the augmented dataset with probabilities of belonging to each task class.
- We developed an algorithmic implementation of the improved input-doubling method using two Naïve Bayes classifiers with different inference procedures and provided flowcharts of its training and application algorithms.
- We investigated the effectiveness of the improved input-doubling method using both different Naïve Bayes algorithms and their various combinations. By comparing it with machine learning methods from different classes, we demonstrated its highest performance in solving the heart attack risk assessment task under conditions of processing a small dataset.
The article is organized as follows. In the second section, various Naïve Bayes classifiers are analyzed, the basic input-doubling method and its improvements are described, and its flowchart is presented. The algorithmic implementation of the improved method using two Naïve Bayes classifiers is also provided. In the third section, a series of experimental results is presented concerning the selection of optimal Naïve Bayes classifiers for each of the two steps of the improved input-doubling method. The results of its performance are shown based on various effectiveness indicators during the analysis of a small-volume heart attack dataset. The fourth section contains results comparing the improved input-doubling method with the basic method, simple machine learning methods, and their ensembles. The final section includes conclusions based on the results of the conducted research.
2. Materials and Methods
This section describes the operation of the classical input-doubling classifier [17], analyzes various implementation options [18], and discusses the advantages and disadvantages of Naïve Bayes classifiers [20], which form the basis of the enhanced input-doubling classifier. The algorithms for augmentation and application of the enhanced input-doubling classifier are described, and flowcharts of its operation are provided.
2.1. Classical Input-Doubling Method
The input-doubling method for solving regression or classification tasks with limited training data was first introduced in [19]. More comprehensive studies on its implementation using both machine learning methods and artificial neural networks, including unsupervised learning, are presented in [18]. The method is based on the combined use of two ideas—data augmentation and ensemble learning elements—through a single nonlinear machine learning method or artificial neural network. A distinguishing feature of this method is that it involves data augmentation only within the available dataset, without synthesizing entirely new samples. This approach preserves the natural order of the available data in extremely small (up to 100 observations) or small datasets. The idea behind the augmentation procedure, according to the method, is to quadratically increase the number of vectors by concatenating all possible pairs of vectors, including concatenating a vector with itself [18]. The output value (z) that should be learned for prediction or classification via the chosen machine learning method or artificial neural network is the difference between the dependent attributes of the corresponding concatenated vector pairs (y). Due to this fact, such an approach to augmentation is not a standalone method for increasing the dataset size and works only in conjunction with the input-doubling method application procedure. This procedure is based on ensemble learning principles, specifically averaging the results. Notably, ensemble learning is implemented using only a single artificial intelligence tool.
Let us consider the augmentation and application procedures in more detail [19]. For ease of understanding, Figure 1 presents a visualization of all the processes involved in the data augmentation procedure described above.
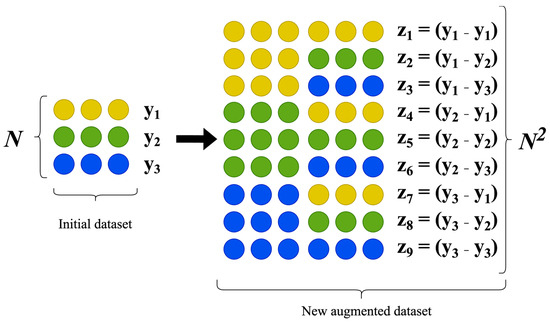
Figure 1.
Data augmentation procedure according to the classical input-doubling method.
As illustrated in Figure 1, concatenating all possible pairs of vectors from the initial dataset produces a new dataset that is quadratically expanded compared with the original set, with twice the number of independent features resulting from the concatenation. This expanded dataset serves as the sample for training the selected artificial intelligence model.
The procedure for applying the classic input-doubling method involves concatenating a vector with an unknown output (for which the predicted or classified value needs to be determined) with each vector in the training dataset. This results in a temporary dataset that is then fed into a pre-trained regressor or classifier to obtain the predicted difference between vectors (). This predicted difference, along with the corresponding values of the dependent attributes from the original training dataset, is averaged to derive the desired value of the dependent attribute [19]. Mathematically, this procedure is depicted in Figure 2.
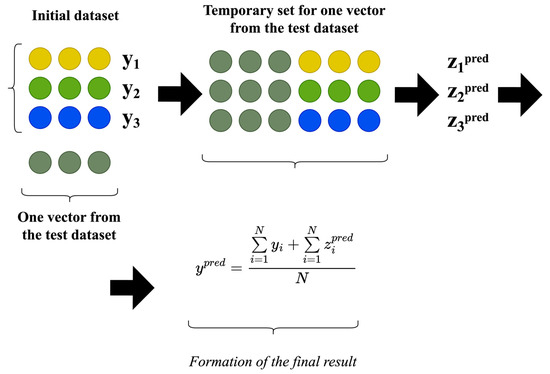
Figure 2.
Application procedure of the classical input-doubling method.
As demonstrated in research [18], the classic input-doubling method does not consistently achieve high accuracy in prediction or classification, highlighting the need for its refinement.
2.2. Enhanced Input-Doubling Classifier
This paper introduces the enhanced input-doubling classifier, which is based on the principle of linearizing the response surface. In this approach, the principle is implemented using the probabilities of an observation belonging to each of the defined classes in the task [21]. To realize this principle, this paper proposes the use of two machine learning algorithms. The first algorithm is designed to obtain these probabilities and use them as additional features in the augmented dataset. The second machine learning method serves as the base for generating the final classification. This approach provides the classifier with additional information, potentially leading to significantly improved accuracy in solving the given task.
The enhanced input-doubling classifier described in this paper, which employs two machine learning algorithms, includes augmentation, training, and application procedures that differ significantly from those of the basic method outlined in [18]. In this study, variations of the Naive Bayes classifier are chosen as the machine learning methods. We will now examine these procedures in more detail.
2.2.1. Augmentation Procedure
As previously mentioned, the data augmentation algorithm based on the input-doubling method is not an independent augmentation technique and cannot function on its own. It is part of a method for processing small datasets. The data augmentation algorithm according to the enhanced input-doubling classifier presented in this paper differs somewhat from the basic method [19]. The flowchart for this algorithm is provided in Figure 3.
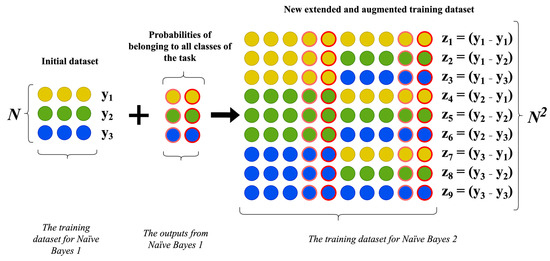
Figure 3.
Visualization of the data augmentation algorithm for the enhanced input-doubling classifier.
Let us examine the main steps of its implementation in more detail:
- Compute the probabilities of each vector in the training dataset belonging to each class using the first Naive Bayes classifier.
- Increase the number of independent features for each vector in the original training dataset by adding the probabilities obtained in the previous step.
- Create an augmented dataset by concatenating all possible pairs of vectors using the expanded features from the previous step.
- Form the dependent attributes for each expanded vector in the augmented dataset by finding the differences in the corresponding dependent variables for each concatenated vector pair.
As a result of performing all the aforementioned steps, we obtain a quadratically expanded dataset. However, unlike the basic method in [18], the dimensionality of each vector in the augmented dataset will be doubled, plus an additional four independent attributes corresponding to the set of probabilities for belonging to each of the two classes. In this way, we implement the principle of linearizing the response surface and provide additional information for the classifier.
2.2.2. Naïve Bayes Classifiers
To implement training algorithms on the augmented dataset and for application, this work uses various variations of the Naive Bayes classifier [22]. This choice is based on several reasons, including [23,24,25] the following:
- Simple Mathematical Model.
- The clear and interpretable workings of the method.
- Fast processing capabilities.
- Low Memory and Computational Requirement.
- Effective results with relatively small datasets.
- Ability to provide results both as a set of probabilities for each class (required for the first classifier in the enhanced method) and as class labels (needed for the second classifier in the enhanced input-doubling method).
Naïve Bayes classifiers are popular tools for classification in machine learning, leveraging Bayes’ theorem to compute the probability of an object belonging to a certain class [26]. These classifiers use statistics from the training dataset to estimate the conditional probabilities of features for each class. Probabilities of individual features are assessed for each class and then combined to determine the most likely class for a new sample [27]. Overall, they are very simple to implement and are well-suited for analyzing both small and large datasets.
In this paper, the effectiveness of using four different Naïve Bayes algorithms as weak classifiers in the enhanced input-doubling method was investigated. Key information about these algorithms, including their operational principles, advantages, and disadvantages, is summarized in Table 1 [23,24,25].

Table 1.
Principles of operation, advantages, and disadvantages of the investigated variations of Naïve Bayes classifiers.
These classifiers were used in various combinations during the implementation of the training procedure for the enhanced input-doubling classifier.
2.2.3. Application Procedure
The application algorithm of the enhanced input-doubling classifier involves the sequential use of both Naïve Bayes classifiers. The flowchart for this algorithm is provided in Figure 4.
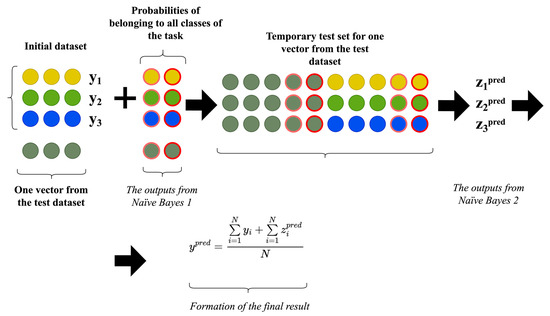
Figure 4.
Visualization of the application algorithm for the enhanced input-doubling classifier.
The main steps of the algorithmic implementation of this procedure are outlined below as follows:
- Compute the probabilities of the current vector with an unknown dependent attribute belonging to each class of the task based on the first pre-trained Naïve Bayes classifier. It should be noted that this search is performed using the initial dataset.
- Expand the number of independent attributes of the current vector with an unknown dependent attribute by adding the two probabilities found in the previous step (since it is a binary classification task). If there are more classes, there will be additional attributes.
- Concatenate the already expanded current vector with an unknown dependent attribute with all expanded probability vectors from the training dataset to form a temporary dataset.
- Apply the second Naïve Bayes classifier, pre-trained on the augmented dataset from Figure 3, to find the output signals of the temporary dataset from the previous step.
- Average the sums of the output signals from the previous step and their corresponding known values of dependent attributes from the initial training dataset to form the desired result.
These steps are repeated for all input data vectors for which the class label needs to be determined.
3. Modeling and Results
The method was modeled using a publicly available dataset. The authors developed their own software in Python 1.2. To ensure the reliability of the results, the authors employed ten-fold cross-validation, and the averaged result was used for analysis.
3.1. Dataset Description
The tabular dataset used for modeling was collected to address the problem of rapid risk assessment for heart attacks. It is available in a public repository [28]. The dataset includes 13 independent attributes and one dependent attribute. The dependent attribute takes two values—0 and 1. Therefore, from a machine learning perspective, it is a binary classification problem, and given the available data size, it is a binary classification problem in the context of small data analysis.
The dataset contains no missing values or anomalies. Therefore, among the preprocessing procedures, only input normalization was performed using MaxAbsScaler() [29].
3.2. Performance Indicators
To assess the performance of both the enhanced method and the various machine learning methods compared in this study, several standard metrics were employed, including [30] the following:
- Precision.
- Recall.
- F1-score.
- Cohen’s kappa.
- Matthews correlation coefficient (MCC).
Mathematical expressions for calculating each of the metrics are provided in [31,32,33]. The choice of these metrics is due to the dataset being somewhat imbalanced. Therefore, the study employs three of the most commonly used metrics for evaluating the results of solving imbalanced classification problems in the context of machine learning. Considering all three metrics together during the analysis of the results will provide a comprehensive and holistic assessment of the problem-solving effectiveness [32].
3.3. Optimal Parameters Selection
The enhanced input-doubling classifier discussed in this paper is based on the sequential use of two Gaussian Naïve Bayes algorithms. Like any machine learning method, the enhanced method described here is characterized by a number of hyperparameters, the optimal selection of which will affect the overall effectiveness of the method.
Since the method involves the use of two Naïve Bayes algorithms, of which there are several variations, this paper explores two options for their combination. The first option involves using the same Naïve Bayes algorithms at both steps of the method. The second option involves using different Naïve Bayes algorithms at each step of the enhanced input-doubling classifier described in this paper.
3.3.1. Investigation of the Effectiveness of Using Identical Naïve Bayes Classifiers at Both Stages of the Enhanced Method
This paper utilizes four different Naïve Bayes algorithms. Accordingly, the first experiment involves selecting a pair of identical Naïve Bayes algorithms to be used at both stages of the method, with the goal of achieving the highest classification accuracy. Table 2 summarizes the results of the first experiment based on all the investigated metrics, both in the training and application phases.

Table 2.
Results of the enhanced method when using identical Naïve Bayes classifiers at both the first and second steps of the method.
For clarity and ease of analysis, Figure 5 presents a summary of the accuracy results for all examined variants of the enhanced input-doubling classifier, using the F1-score in both operational modes.
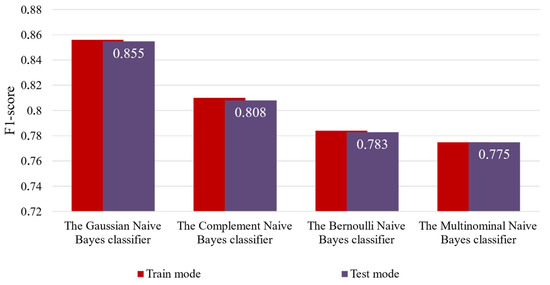
Figure 5.
Visual representation of the results of the first experiment.
As illustrated in Table 2, the Bernoulli Naive Bayes and Multinomial Naive Bayes classifiers achieved the lowest accuracy in both modes. In contrast, the Gaussian Naive Bayes classifier delivered the highest accuracy across both steps of the enhanced input-doubling classifier. Furthermore, the experimental results indicate that the improved method exhibits excellent generalization capabilities with all tested algorithms. This is a notable advantage of the enhanced method, especially given the limited dataset available for training.
3.3.2. Investigation of the Effectiveness of Using Different Naïve Bayes Classifiers at Both Stages of the Enhanced Method
The second experiment involves investigating the use of different pairs of Naive Bayes classifiers to achieve the highest accuracy for the given task. The unique aspect of this experiment is that the Gaussian Naive Bayes algorithm is always used in the first step of the enhanced input-doubling classifier, while the second step involves applying one of the four studied Naive Bayes classifiers (including the Gaussian Naive Bayes algorithm). This experimental setup is driven by the specifics of the improvement procedure for the input-doubling classifier proposed in this study.
Specifically, the results from the Naive Bayes classifier in the form of a set of probabilities for each observation (for both training and test datasets) belonging to each class used in the first step should ensure the highest possible classification accuracy. This is because these results are used to expand the input space with two new features in the augmented dataset, which the second-level classifier uses to assign the final class label. Therefore, to optimally leverage the benefits of response surface linearization, the predictions from the first step need to be as accurate as possible.
Table 3 presents the results of this experiment based on all studied metrics, both in training and application modes. For ease of analysis, Figure 6 summarizes the accuracy results of all examined variants of the enhanced input-doubling classifier based on the F1-score in both operational modes.

Table 3.
Results of the enhanced method when using different Naïve Bayes classifiers at the first and second steps of the method.
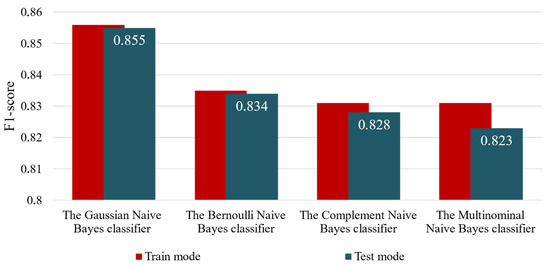
Figure 6.
Visual representation of the results of the second experiment.
The first conclusion to be drawn from Table 3 and Figure 6 is that using the Gaussian Naive Bayes classifier at both steps of the enhanced input-doubling classifier results in a significant accuracy improvement compared with all other examined variants of the method. Additionally, this combination exhibits the highest generalization capabilities among all studied variants. In contrast, using the Gaussian Naive Bayes classifier in the first step and the Multinomial Naive Bayes classifier in the second step results in both the lowest accuracy (more than 3% lower) and significantly poorer generalization.
The most important takeaway from this experiment is that employing different Naive Bayes classifiers at both steps of the enhanced input-doubling classifier significantly improves accuracy compared with the first experiment. This suggests that further investigation into other nonlinear machine learning methods or artificial neural networks for the second step of the method is warranted. The choice of such methods will be less restricted and should be based on their performance in handling large datasets. This is because the second step of the method involves analyzing a quadratically expanded dataset, which will not limit the data available for training procedures, even when starting with a very small dataset (100 observations or fewer), as it expands to 10,000 observations (from 100 input observations).
3.4. Results
Table 4 summarizes the evaluation of the performance of the enhanced input-doubling classifier using Gaussian Naïve Bayes algorithms based on various metrics, both in the training and application modes.

Table 4.
Results of the enhanced input-doubling classifier when using Gaussian Naïve Bayes algorithms at both steps of the method.
Table 4 clearly shows that overfitting, which is typical when using various machine learning methods for analyzing such small datasets, is not observed. Moreover, if you review Table 3, which contains values of all investigated metrics up to the third decimal place, it is evident that the enhanced input-doubling classifier demonstrates very high generalization properties. This serves as another important advantage of using this method for analyzing small datasets, for which classical methods, in most cases, cannot provide an adequate level of generalization. This is because existing models tend to memorize observations from very limited training data and do not generalize well to new data. Consequently, the accuracy of the new data is very low, and thus, the use of such methods for analyzing small datasets yields unsatisfactory results, which undermines their practical applicability.
4. Discussion
The comparison of the performance of the enhanced input-doubling classifier using Gaussian Naïve Bayes algorithms at both steps of the method was conducted against the basic input-doubling classifier [17] as well as several well-known machine learning methods from [34] that were used to solve this task, including the following:
- AdaBoost;
- Gradient Boosting;
- Decision Tree;
- Bagged Decision Tree;
- Random Forest;
- Gaussian Naive Bayes;
- Bagged K-Nearest Neighbors;
- K-Nearest Neighbors;
- XGBoost;
- Support Vector Machine (with rbf kernel).
Modeling of all the aforementioned methods was performed using ten-fold cross-validation, and the results from these ten steps were averaged. Figure 7 presents a comparison of the accuracy of all investigated methods in terms of the F1-score.
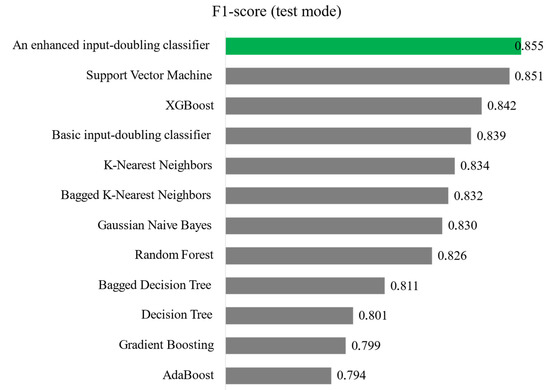
Figure 7.
Comparison of the accuracy of all investigated methods for solving the heart attack risk assessment task in the case of small data analysis.
As shown in Figure 7, two ensemble methods from the boosting class demonstrate accuracy below 80%. All other investigated methods exhibit satisfactory accuracy in solving the task. The basic input-doubling classifier [17] ranks 4th in accuracy among the methods considered. Slightly better results are shown by XGBoost and SVR with the RBF kernel. Nevertheless, the enhanced input-doubling classifier using two Gaussian Naïve Bayes algorithms demonstrates the highest accuracy among the methods reviewed. It is worth noting that Naïve Bayes is not one of the most accurate methods, and ensemble machine learning methods usually show significant accuracy advantages compared with single models. However, the enhanced input-doubling classifier also operates on the principle of ensemble learning through plurality voting when forming the final prediction result. Additionally, the principle of linearizing the response surface is employed, which provides a significant increase in accuracy compared with the basic input-doubling classifier [17]. Furthermore, this principle is implemented through adding a set of probabilities of belonging to each class of the task. This approach not only expands the input data space of the task but also provides much more useful information to the classifier at the second level of the method, which is reflected in its accuracy.
If we consider the limitations of the proposed method, the main one is the necessity for a quadratic increase in the sample size for training. On one hand, this leads to an increase in the duration of the training procedure even when analyzing extremely short datasets (up to 100 observations). On the other hand, analyzing medium-sized datasets using this method will only be appropriate if there is a need for high accuracy without constraints on time or computational resources. Another limitation of the modification proposed in this work is the use of the naive Bayes classifier in the second step of the method. It does not always demonstrate high accuracy. Therefore, among the prospects for further research, it is important to investigate the effectiveness of using different nonlinear classifiers, particularly artificial neural networks [35,36,37], at the second step of the enhanced input-doubling classifier, while utilizing the Gaussian Naïve Bayes algorithm at its first level. Such an approach could further improve classification accuracy, positively impacting the practical applicability of the method in various fields of medicine.
5. Conclusions
Modern tasks in intelligent data analysis in medicine increasingly require effective tools for working with large volumes of information. Existing artificial intelligence technologies demonstrate high performance in analyzing large datasets. However, with a limited amount of training data, traditional machine learning methods often do not provide sufficient classification accuracy or may even produce inadequate results.
In this paper, the authors present the enhanced input-doubling classifier using two machine learning algorithms for analyzing limited information. The method is based on the principle of linearizing the response surface. This is achieved via expanding the number of independent attributes in the augmented dataset with probabilities of belonging to each class of the task. An algorithmic implementation of the augmentation and application procedures for this approach has been developed using two Naïve Bayes classifiers.
The method was tested on a limited dataset for heart attack risk assessment. Various combinations of Naïve Bayes classifiers at different stages of the method were explored. The results showed that using different classifiers at each stage can potentially enhance classification accuracy. The comparison of the improved method with existing approaches demonstrated its advantage: the input-doubling method provided high generalization and achieved nearly 3% higher classification accuracy based on the F1-score compared with the baseline method. It outperformed all investigated single machine learning algorithms and several modern ensemble methods used to solve the task.
One promising avenue for future research is to explore the effectiveness of various nonlinear classifiers, especially artificial neural networks, in the second step of the enhanced input-doubling classifier. This would be coupled with the Gaussian Naïve Bayes algorithm at the first level. Implementing this approach could significantly enhance classification accuracy, ultimately increasing the method’s practical relevance across different areas of medicine.
Author Contributions
Conceptualization, I.I. and R.T.; methodology, I.I.; software, P.Y.; validation, I.P., Y.B., and M.G.; formal analysis, M.G.; investigation, I.I.; resources, I.I.; data curation, P.Y.; writing—original draft preparation, I.I.; writing—review and editing, I.I., R.T., I.P., and Y.B.; visualization, I.P.; supervision, R.T.; project administration, M.G.; funding acquisition, M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the European Union (through the EURIZON H2020 project, grant agreement 871072).
Data Availability Statement
A small open-access dataset used in this paper is available here: [28].
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Overview of Lifestyle Medicine—StatPearls—NCBI Bookshelf. Available online: https://www.ncbi.nlm.nih.gov/books/NBK589672/ (accessed on 18 September 2024).
- Rubiś, P.P. Cardiac Disease: Diagnosis, Treatment, and Outcomes. JPM 2022, 12, 1212. [Google Scholar] [CrossRef] [PubMed]
- Subramani, S.; Varshney, N.; Anand, M.V.; Soudagar, M.E.M.; Al-keridis, L.A.; Upadhyay, T.K.; Alshammari, N.; Saeed, M.; Subramanian, K.; Anbarasu, K.; et al. Cardiovascular Diseases Prediction by Machine Learning Incorporation with Deep Learning. Front. Med. 2023, 10, 1150933. [Google Scholar] [CrossRef] [PubMed]
- Kovalchuk, O.; Barmak, O.; Radiuk, P.; Krak, I. ECG Arrhythmia Classification and Interpretation Using Convolutional Networks for Intelligent IoT Healthcare System. CEUR Workshop Proc. 2024, 3736, 47–62. [Google Scholar]
- Kovalchuk, O.; Radiuk, P.; Barmak, O.; Krak, I. Robust R-Peak Detection Using Deep Learning Based on Integrating Domain Knowledge. CEUR Workshop Proc. 2023, 3609, 1–14. [Google Scholar]
- Slobodzian, V.; Radiuk, P.; Zingailo, A.; Barmak, O.; Krak, I. Myocardium Segmentation Using Two-Step Deep Learning with Smoothed Masks by Gaussian Blur. CEUR Workshop Proc. 2023, 3609, 77–91. [Google Scholar]
- Ferrara, E. Fairness and Bias in Artificial Intelligence: A Brief Survey of Sources, Impacts, and Mitigation Strategies. Sci 2023, 6, 3. [Google Scholar] [CrossRef]
- Tolstyak, Y.; Zhuk, R.; Yakovlev, I.; Shakhovska, N.; Gregus Ml, M.; Chopyak, V.; Melnykova, N. The Ensembles of Machine Learning Methods for Survival Predicting after Kidney Transplantation. Appl. Sci. 2021, 11, 10380. [Google Scholar] [CrossRef]
- Hekler, E.B.; Klasnja, P.; Chevance, G.; Golaszewski, N.M.; Lewis, D.; Sim, I. Why We Need a Small Data Paradigm. BMC Med 2019, 17, 133. [Google Scholar] [CrossRef]
- Dolgikh, S. Modeling of Small Data with Unsupervised Generative Ensemble Learning. CEUR-WS.org 2022, 3302, 35–43. [Google Scholar]
- Zhang, Y.; Deng, L.; Wei, B. Imbalanced Data Classification Based on Improved Random-SMOTE and Feature Standard Deviation. Mathematics 2024, 12, 1709. [Google Scholar] [CrossRef]
- Gholampour, S. Impact of Nature of Medical Data on Machine and Deep Learning for Imbalanced Datasets: Clinical Validity of SMOTE Is Questionable. MAKE 2024, 6, 827–841. [Google Scholar] [CrossRef]
- Althnian, A.; AlSaeed, D.; Al-Baity, H.; Samha, A.; Dris, A.B.; Alzakari, N.; Abou Elwafa, A.; Kurdi, H. Impact of Dataset Size on Classification Performance: An Empirical Evaluation in the Medical Domain. Appl. Sci. 2021, 11, 796. [Google Scholar] [CrossRef]
- Szijártó, Á.; Fábián, A.; Lakatos, B.K.; Tolvaj, M.; Merkely, B.; Kovács, A.; Tokodi, M. A Machine Learning Framework for Performing Binary Classification on Tabular Biomedical Data. Imaging 2023, 15, 1–6. [Google Scholar] [CrossRef]
- Kumar, V.; Lalotra, G.S.; Sasikala, P.; Rajput, D.S.; Kaluri, R.; Lakshmanna, K.; Shorfuzzaman, M.; Alsufyani, A.; Uddin, M. Addressing Binary Classification over Class Imbalanced Clinical Datasets Using Computationally Intelligent Techniques. Healthcare 2022, 10, 1293. [Google Scholar] [CrossRef] [PubMed]
- Izonin, I.; Tkachenko, R.; Pidkostelnyi, R.; Pavliuk, O.; Khavalko, V.; Batyuk, A. Experimental Evaluation of the Effectiveness of ANN-Based Numerical Data Augmentation Methods for Diagnostics Tasks. In Proceedings of the 4th International Conference on Informatics&Data-Driven Medicine, Valencia, Spain, 19–21 November 2021; pp. 223–232. [Google Scholar]
- Izonin, I.; Tkachenko, R.; Havryliuk, M.; Gregus, M.; Yendyk, P.; Tolstyak, Y. An Adaptation of the Input Doubling Method for Solving Classification Tasks in Case of Small Data Processing. Procedia Comput. Sci. 2024, 241, 171–178. [Google Scholar] [CrossRef]
- Izonin, I.; Tkachenko, R. Universal Intraensemble Method Using Nonlinear AI Techniques for Regression Modeling of Small Medical Data Sets. In Cognitive and Soft Computing Techniques for the Analysis of Healthcare Data; Elsevier: Amsterdam, The Netherlands, 2022; pp. 123–150. ISBN 978-0-323-85751-2. [Google Scholar]
- Izonin, I.; Tkachenko, R.; Fedushko, S.; Koziy, D.; Zub, K.; Vovk, O. RBF-Based Input Doubling Method for Small Medical Data Processing. In Advances in Artificial Systems for Logistics Engineering; Hu, Z., Zhang, Q., Petoukhov, S., He, M., Eds.; Lecture Notes on Data Engineering and Communications Technologies; Springer International Publishing: Cham, Switzerland, 2021; Volume 82, pp. 23–31. ISBN 978-3-030-80474-9. [Google Scholar]
- Shahadat, N.; Pal, B. An Empirical Analysis of Attribute Skewness over Class Imbalance on Probabilistic Neural Network and Naïve Bayes Classifier. In Proceedings of the 2015 International Conference on Computer and Information Engineering (ICCIE), Rajshahi, Bangladesh, 26–27 November 2015; IEEE: Rajshahi, Bangladesh, 2015; pp. 150–153. [Google Scholar]
- Zub, K.; Zhezhnych, P.; Strauss, C. Two-Stage PNN–SVM Ensemble for Higher Education Admission Prediction. BDCC 2023, 7, 83. [Google Scholar] [CrossRef]
- Changpetch, P.; Pitpeng, A.; Hiriote, S.; Yuangyai, C. Integrating Data Mining Techniques for Naïve Bayes Classification: Applications to Medical Datasets. Computation 2021, 9, 99. [Google Scholar] [CrossRef]
- Sugahara, S.; Ueno, M. Exact Learning Augmented Naive Bayes Classifier. Entropy 2021, 23, 1703. [Google Scholar] [CrossRef]
- Kaushik, K.; Bhardwaj, A.; Dahiya, S.; Maashi, M.S.; Al Moteri, M.; Aljebreen, M.; Bharany, S. Multinomial Naive Bayesian Classifier Framework for Systematic Analysis of Smart IoT Devices. Sensors 2022, 22, 7318. [Google Scholar] [CrossRef]
- Alenazi, F.S.; El Hindi, K.; AsSadhan, B. Complement-Class Harmonized Naïve Bayes Classifier. Appl. Sci. 2023, 13, 4852. [Google Scholar] [CrossRef]
- Ou, G.; He, Y.; Fournier-Viger, P.; Huang, J.Z. A Novel Mixed-Attribute Fusion-Based Naive Bayesian Classifier. Appl. Sci. 2022, 12, 10443. [Google Scholar] [CrossRef]
- Yang, Z.; Ren, J.; Zhang, Z.; Sun, Y.; Zhang, C.; Wang, M.; Wang, L. A New Three-Way Incremental Naive Bayes Classifier. Electronics 2023, 12, 1730. [Google Scholar] [CrossRef]
- Heart Attack Analysis & Prediction Dataset (A Dataset for Heart Attack Classification). Available online: https://www.kaggle.com/datasets/rashikrahmanpritom/heart-attack-analysis-prediction-dataset (accessed on 7 September 2024).
- Sklearn.Preprocessing.MaxAbsScaler. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.MaxAbsScaler.html (accessed on 21 August 2023).
- Manna, S. Small Sample Estimation of Classification Metrics. In Proceedings of the 2022 Interdisciplinary Research in Technology and Management (IRTM), Kolkata, India, 24 February 2022; pp. 1–3. [Google Scholar]
- Orozco-Arias, S.; Piña, J.S.; Tabares-Soto, R.; Castillo-Ossa, L.F.; Guyot, R.; Isaza, G. Measuring Performance Metrics of Machine Learning Algorithms for Detecting and Classifying Transposable Elements. Processes 2020, 8, 638. [Google Scholar] [CrossRef]
- Kozak, J.; Probierz, B.; Kania, K.; Juszczuk, P. Preference-Driven Classification Measure. Entropy 2022, 24, 531. [Google Scholar] [CrossRef]
- Kenyeres, É.; Kummer, A.; Abonyi, J. Machine Learning Classifier-Based Metrics Can Evaluate the Efficiency of Separation Systems. Entropy 2024, 26, 571. [Google Scholar] [CrossRef]
- Heart Attack—From EDA to Prediction (Notebook). Available online: https://kaggle.com/code/dreygaen/heart-attack-from-eda-to-prediction (accessed on 7 September 2024).
- Subbotin, S. Radial-Basis Function Neural Network Synthesis on the Basis of Decision Tree. Opt. Mem. Neural Netw. 2020, 29, 7–18. [Google Scholar] [CrossRef]
- Chumachenko, D.; Butkevych, M.; Lode, D.; Frohme, M.; Schmailzl, K.J.G.; Nechyporenko, A. Machine Learning Methods in Predicting Patients with Suspected Myocardial Infarction Based on Short-Time HRV Data. Sensors 2022, 22, 7033. [Google Scholar] [CrossRef]
- Krak, I.; Barmak, O.; Manziuk, E.; Kulias, A. Data Classification Based on the Features Reduction and Piecewise Linear Separation. In Intelligent Computing and Optimization; Vasant, P., Zelinka, I., Weber, G.-W., Eds.; Advances in Intelligent Systems and Computing; Springer International Publishing: Cham, Switzerland, 2020; Volume 1072, pp. 282–289. ISBN 978-3-030-33584-7. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).