Explainable Boosting Machine Learning for Predicting Bond Strength of FRP Rebars in Ultra High-Performance Concrete
Abstract
1. Introduction
2. Previous Experimental Works on Bond Strength Assessment of Various FRP Bars in UHPFRC
| Research | Test Type | Fiber Type | Variables | Findings |
|---|---|---|---|---|
| Hu et al. (2024) [40] | Pullout, beam | GFRP | Embedment length Concrete cover Rebar type | Two distinct bond stress-slip relationships were identified based on the embedment length of GFRP rebars. The bond strength of GFRP rebars was higher in the beam test compared to the pullout test, with the modified pullout test showing only a slight difference. GFRP bars exhibited lower bond strength with UHPC than steel bars, regardless of the testing method. Increasing the embedment length and decreasing the cover led to a linear reduction in bond strength between GFRP bars and UHPC. It is recommended that the development length for sand-coated or deformed GFRP rebars with smaller diameters in UHPC should be at least 13 times the bar diameter, with a cover thickness not less than twice the bar diameter. |
| Yoo et al. (2023) [8] | Pullout | CFRP | Rebar profile Embedment length Rebar diameter | The critical concrete cover thickness for helically ribbed CFRP bars to prevent splitting failure is greater in high-strength concrete than in normal-strength concrete. Bond strength in UHPC increases consistently with greater concrete cover thickness. As the compressive strength of concrete increases, both the bond strength and bond stiffness of ribbed CFRP bars also improve. Helically, ribbed CFRP bars in UHPC with longer embedment lengths exhibit higher bond strength than shorter lengths. The bond strength of helically ribbed CFRP bars is more than double that of sand-coated CFRP bars. Helically, ribbed CFRP bars demonstrate greater initial and post-toughness than sand-coated bars, although the post-toughness difference narrows due to the friction in sand-coated bars. Existing bond design codes and proposed formulas inadequately predict the bond strength of CFRP bars in UHPC, particularly due to variations in CFRP bar profiles. Bond strength predictions using modified equations and an artificial neural network (ANN) method proved more accurate, with the ANN demonstrating superior predictive capability. A modified bond equation for helically ribbed and sand-coated CFRP bars enhanced prediction accuracy using the ANN approach. |
| Mahaini et al. (2023) [27] | Four-point loading | GFRP | Reinforcement ratio Number of rebars Surface texture bars | GFRP-UHPC beams exhibited a typical bilinear response in both deflections and strains. All GFRP beams showed similar stiffness during pre-cracking, independent of the reinforcement ratio. Post-cracking stiffness increased with higher GFRP reinforcement ratios. Higher reinforcement ratios improved the energy absorption capacity of the beams, reducing post-cracking strains in the GFRP bars. Increasing the reinforcement ratio also enhanced the flexural capacity of the GFRP-UHPC beams. When maintaining the same axial stiffness, the number of bars had minimal impact on the flexural behavior of UHPC beams. Shifting the failure mode from GFRP rupture to concrete crushing improved the ductility of the UHPC beams. GFRP-reinforced UHPC beams demonstrated significantly higher flexural capacity than steel-reinforced beams due to the higher tensile strength of GFRP. However, steel-reinforced beams had greater stiffness and lower midspan deflection. The ACI equation provided reasonable predictions for under-reinforced beams but was unconservative for over-reinforced beams, overestimating flexural capacity. The CSA code produced better deflection predictions than the ACI440 equations. However, at ultimate capacity, both ACI440 and CSA specifications were unconservative, particularly for over-reinforced beams, as they failed to account for the increased ductility. |
| Yoo et al. (2024) [39] | Pullout | CFRP Ribbed CFRP Sand coated CFRP Ribbed GFRP Steel rebar | Rebar type Embedment length Fibers (with and without fibers in UHPC) Presence of shear reinforcement | Initially, stiffness was highest for steel bars, followed by sand-coated CFRP, ribbed CFRP, and ribbed GFRP bars. However, after the steel bars yielded, the order shifted to sand-coated CFRP, ribbed CFRP, ribbed GFRP, and steel. Rupture occurred in ribbed CFRP, ribbed GFRP, and steel bars at certain bond lengths, while sand-coated CFRP bars did not rupture even at longer bond lengths. The bond strength of FRP bars decreased as the bonded length increased. The maximum bond strength followed the order: ribbed CFRP bars, ribbed GFRP bars, steel bars, and sand-coated CFRP bars. Combining fiber mixing with a reinforcement cage will significantly enhance bond strength and ductility. Due to different stress transfer mechanisms, bond strength measured in the hinged beam test was lower than in the direct pullout test. |
| Eltantawi et al. (2022) [42] | Four-point loading | BFRP | Rebar diameter Embedment length Rebar surface texture (sand coated (SC) and helically wrapped (HW)) | The load-carrying capacities of beams reinforced with SC-BFRP and HW-BFRP bars were nearly identical for the same embedment length. The surface texture of BFRP bars had a minimal effect on the bond with concrete. SC-BFRP bars exhibited slightly higher bond strength compared to HW-BFRP bars. The bond strength of spliced BFRP bars decreased as splice length increased, with longer splice lengths reducing bond strength. Larger diameter bars require longer splice lengths to reach maximum capacity, suggesting that smaller diameter bars enhance splice bond capacity. The ACI 440.1R-15 and CSA S806-12 equations are conservative in predicting splice lengths for BFRP bars, while the CSA-S6-14 equation is more accurate for larger diameters but less so for smaller diameters. |
| Qasem et al. (2020) [41] | Pullout | CFRP Steel rebars | Rebar type Rebar diameter | Steel rebars exhibit superior bond strength compared to CFRP rebars across various types of concrete. Control specimens without carbon nanotubes (CNTs) showed that steel rebars required higher bond stress for pullout than CFRP rebars due to stronger concrete-steel bonding. Due to their high reactivity, the inclusion of CNT nanoparticles enhances the bond strength between rebars and UHPC. Increasing CNT content in UHPC mix design raises the force needed to pull out steel rebars compared to control specimens. However, excessive CNT content leads to increased porosity due to agglomeration, reducing the bond strength of CFRP rebars in UHPC. |
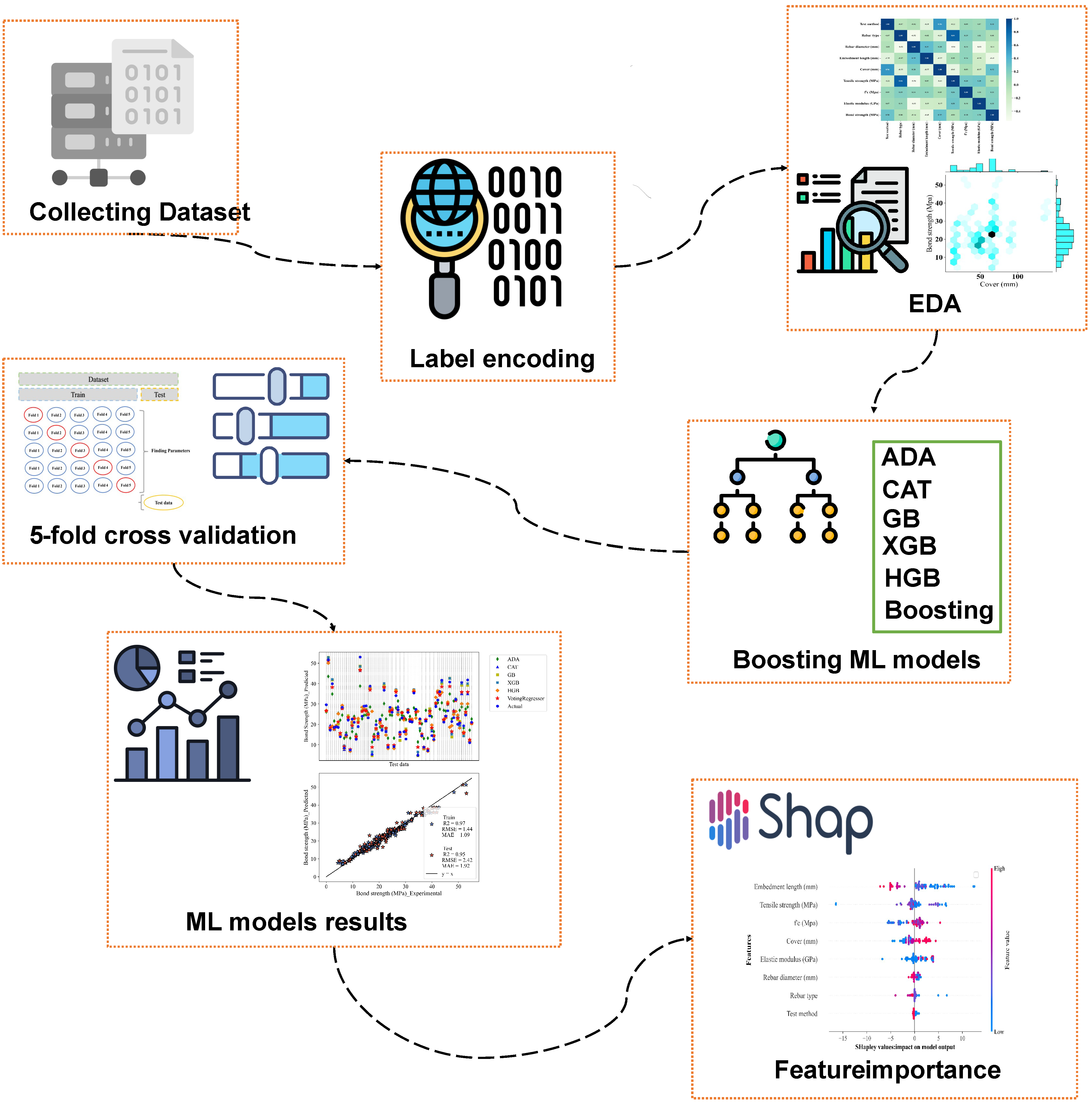
3. Dataset Collection
4. Dataset Construction
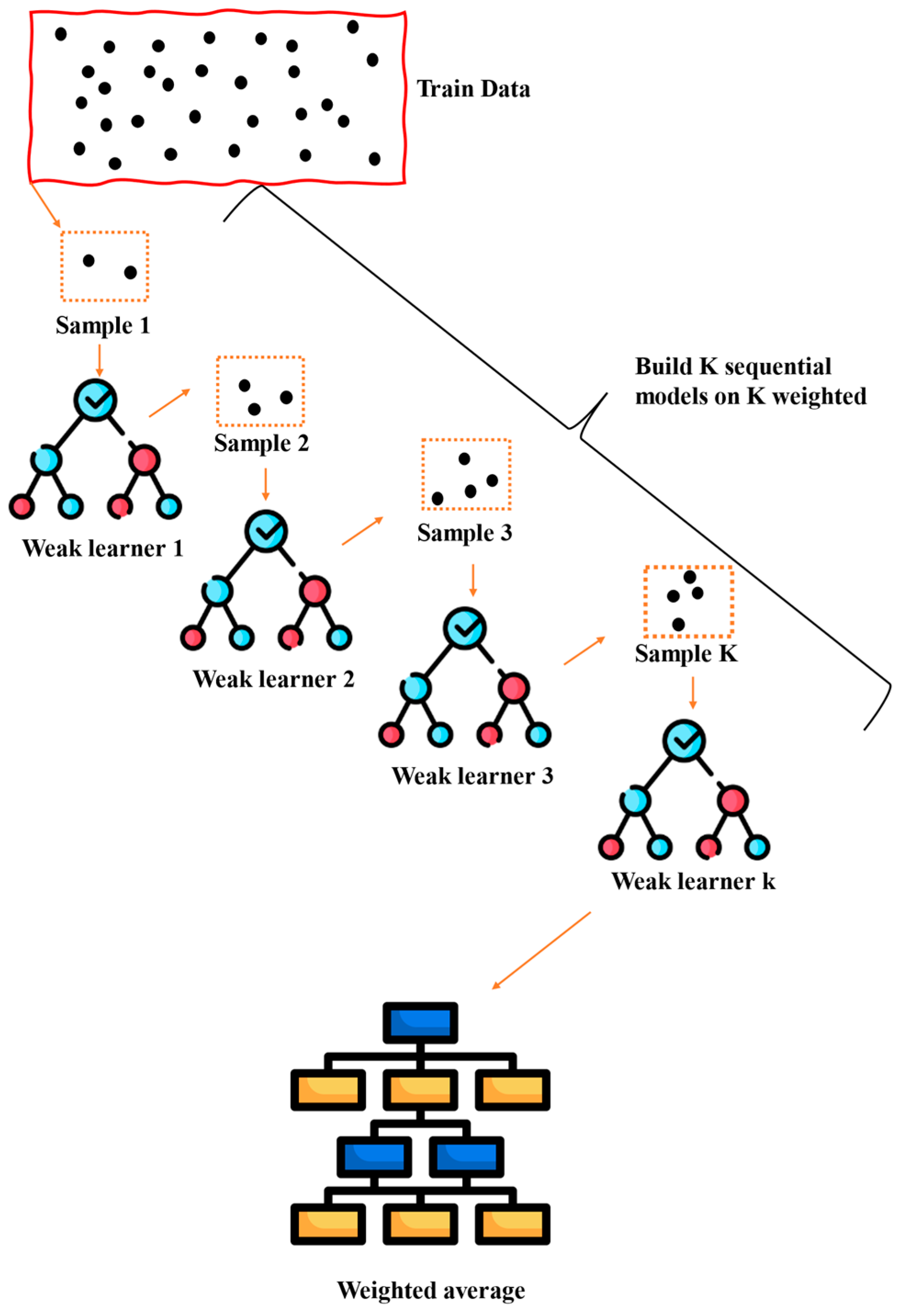
5. Boosting
| Algorithm 1. Algorithm of AdaBoost regressor |
| STEP 1: Initialize the weight distribution , where N is the number of training samples. |
| STEP 2: For each iteration m: |
| (A) Train a weak learner using the weighted data. |
| (B) Compute the error rate. as: |
| (C) Compute the model weight : |
| (D) Update the weights: |
| (E) Normalize the weights |
| STEP 3: The final prediction is a weighted majority vote of the weak learners. |
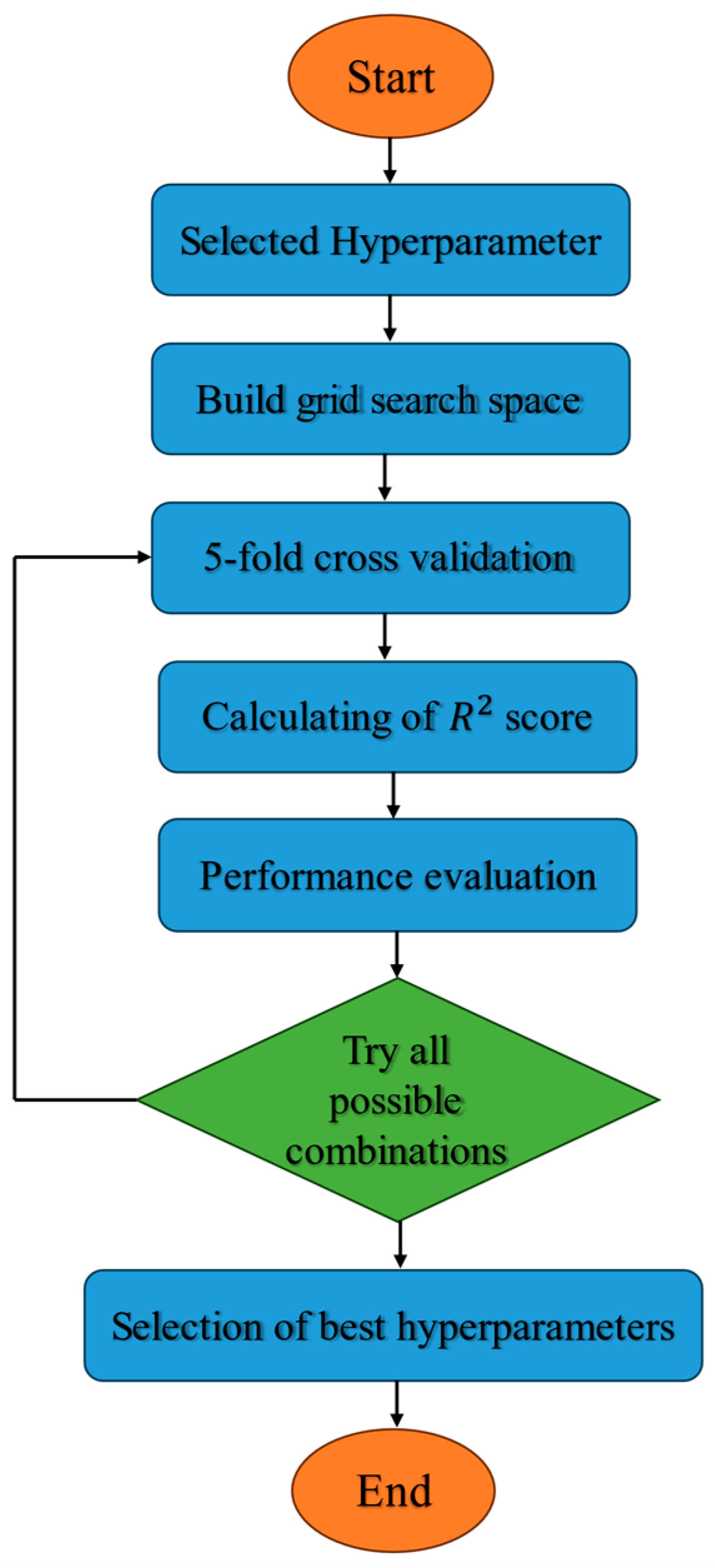
6. Hyperparameter Tuning
7. Results
7.1. Machine Learning Results
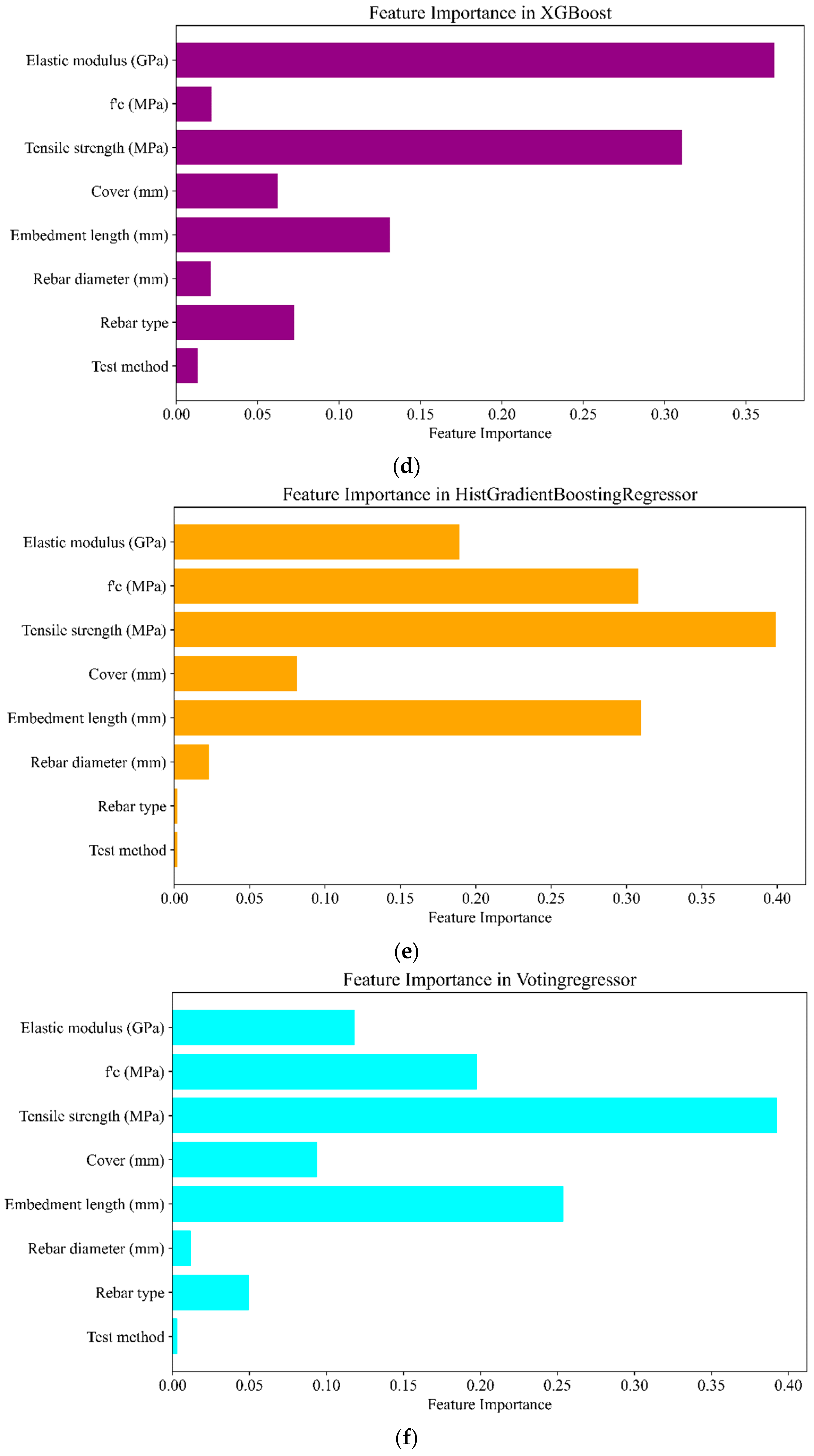
7.2. Shapley Values
7.3. Predictive Formulas for Bond Strength of FRP Rebars in UHPC
8. Conclusions
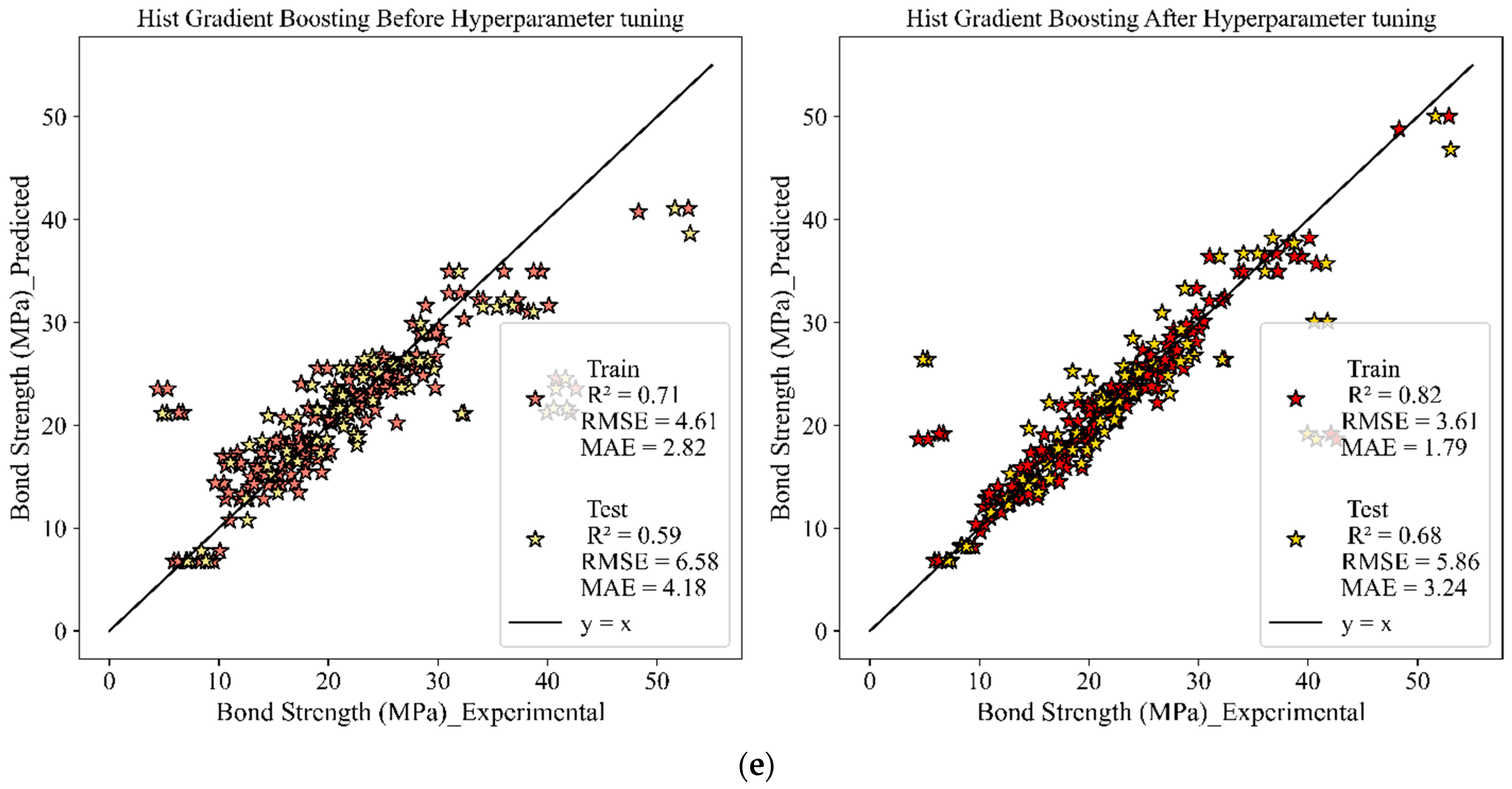
- The results indicated that hyperparameter tuning significantly improved the performance of all models, particularly those that initially exhibited lower accuracy, such as AdaBoost and Hist Gradient Boosting.
- The analysis revealed that CatBoost, Gradient Boosting, and XGBoost consistently outperformed the other models, with XGBoost achieving the highest predictive accuracy after tuning. This was further corroborated by the Taylor diagrams, which illustrated the robustness of these models across training, testing, and combined datasets.
- The study also explored using a Voting Regressor to combine the strengths of multiple models. The findings showed that a Voting Regressor combining only the best-performing models (CatBoost, Gradient Boosting, and XGBoost) slightly improved predictive accuracy, demonstrating the value of model voting in enhancing prediction reliability.
- In addition to traditional feature importance analysis, SHAP values were employed to gain deeper insights into the impact of individual features on the model’s predictions. The SHAP analysis highlighted that embedment length had a significant impact on predictions.
- The insights gained from this study underscore the importance of hyperparameter optimization and advanced interpretability techniques such as SHAP values in developing and evaluating machine learning models for structural engineering applications. The consistent identification of key features such as tensile strength, elastic modulus, and embedment length across different models and analyses reinforces their critical role in predicting bond strength, providing valuable guidance for future research and practical applications in this field.
- The findings demonstrate that while traditional predictive formulas can provide insights within specific experimental contexts, their limited generalizability highlights the need for more adaptable approaches, such as ML models, which have proven to deliver more accurate and reliable bond strength predictions across diverse scenarios.
- The user interface developed in this study enhances accessibility and practical application by allowing engineers to seamlessly implement and evaluate ML models for bond strength prediction in FRP-reinforced UHPC. By providing an interactive platform that supports customization of model parameters and real-time evaluation of model performance, the user interface bridges the gap between advanced ML techniques and their practical application in structural engineering. This tool empowers users to leverage state-of-the-art predictive models, thereby contributing to more accurate and efficient design and analysis processes in the field.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- El-Nemr, A.; Ahmed, E.A.; Barris, C.; Benmokrane, B. Bond-dependent coefficient of glass-and carbon-FRP bars in normal-and high-strength concretes. Constr. Build. Mater. 2016, 113, 77–89. [Google Scholar] [CrossRef]
- Ahmed, E.A.; El-Sayed, A.K.; El-Salakawy, E.; Benmokrane, B. Bend strength of FRP stirrups: Comparison and evaluation of testing methods. J. Compos. Constr. 2010, 14, 3–10. [Google Scholar] [CrossRef]
- ACI Committee 440. 440.1R-06: Guide for the Design and Construction of Concrete Reinforced with FRP Bars; ACI: Farmington Hills, MI, USA, 2006. [Google Scholar]
- Chin, W.J.; Park, Y.H.; Cho, J.-R.; Lee, J.-Y.; Yoon, Y.-S. Flexural behavior of a precast concrete deck connected with headed GFRP rebars and UHPC. Materials 2020, 13, 604. [Google Scholar] [CrossRef]
- Kim, B.; Doh, J.-H.; Yi, C.-K.; Lee, J.-Y. Effects of structural fibers on bonding mechanism changes in interface between GFRP bar and concrete. Compos. Part B Eng. 2013, 45, 768–779. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Banthia, N.; Yoon, Y.-S. Flexural behavior of ultra-high-performance fiber-reinforced concrete beams reinforced with GFRP and steel rebars. Eng. Struct. 2016, 111, 246–262. [Google Scholar] [CrossRef]
- Saleh, N.; Ashour, A.; Lam, D.; Sheehan, T. Experimental investigation of bond behaviour of two common GFRP bar types in high–Strength concrete. Constr. Build. Mater. 2019, 201, 610–622. [Google Scholar] [CrossRef]
- Yoo, S.-J.; Hong, S.-H.; Yoon, Y.-S. Bonding behavior and prediction of helically ribbed CFRP bar embedded in ultra high-performance concrete (UHPC). Case Stud. Constr. Mater. 2023, 19, e02253. [Google Scholar] [CrossRef]
- Taha, A.; Alnahhal, W. Bond durability and service life prediction of BFRP bars to steel FRC under aggressive environmental conditions. Compos. Struct. 2021, 269, 114034. [Google Scholar] [CrossRef]
- Hassan, M.; Benmokrane, B.; ElSafty, A.; Fam, A. Bond durability of basalt-fiber-reinforced-polymer (BFRP) bars embedded in concrete in aggressive environments. Compos. Part B Eng. 2016, 106, 262–272. [Google Scholar] [CrossRef]
- Michaud, D.; Fam, A. Development length of small-diameter basalt FRP bars in normal-and high-strength concrete. J. Compos. Constr. 2021, 25, 04020086. [Google Scholar] [CrossRef]
- Jeddian, S.; Ghazi, M.; Sarafraz, M.E. Experimental study on the seismic performance of GFRP reinforced concrete columns actively confined by AFRP strips. Structures. 2024, 62, 106248. [Google Scholar] [CrossRef]
- Liang, K.; Chen, L.; Shan, Z.; Su, R. Experimental and theoretical study on bond behavior of helically wound FRP bars with different rib geometry embedded in ultra-high-performance concrete. Eng. Struct. 2023, 281, 115769. [Google Scholar] [CrossRef]
- Yang, K.; Wu, Z.; Zheng, K.; Shi, J. Design and flexural behavior of steel fiber-reinforced concrete beams with regular oriented fibers and GFRP bars. Eng. Struct. 2024, 309, 118073. [Google Scholar] [CrossRef]
- Ding, Y.; Ning, X.; Zhang, Y.; Pacheco-Torgal, F.; Aguiar, J. Fibres for enhancing of the bond capacity between GFRP rebar and concrete. Constr. Build. Mater. 2014, 51, 303–312. [Google Scholar] [CrossRef]
- Jamshaid, H.; Mishra, R. A green material from rock: Basalt fiber–a review. J. Text. Inst. 2016, 107, 923–937. [Google Scholar] [CrossRef]
- Yoshitake, I.; Hasegawa, H.; Shimose, K. Monotonic and cyclic loading tests of reinforced concrete beam strengthened with bond-improved carbon fiber reinforced polymer (CFRP) rods of ultra-high modulus. Eng. Struct. 2020, 206, 110175. [Google Scholar] [CrossRef]
- Jia, L.; Fang, Z.; Hu, R.; Pilakoutas, K.; Huang, Z. Fatigue behavior of UHPC beams prestressed with external CFRP tendons. J. Compos. Constr. 2022, 26, 04022066. [Google Scholar] [CrossRef]
- Fang, Y.; Fang, Z.; Feng, L.; Xiang, Y.; Zhou, X. Bond behavior of an ultra-high performance concrete-filled anchorage for carbon fiber-reinforced polymer tendons under static and impact loads. Eng. Struct. 2023, 274, 115128. [Google Scholar] [CrossRef]
- Pan, R.; Zou, J.; Liao, P.; Dong, S.; Deng, J. Effects of fiber content and concrete cover on the local bond behavior of helically ribbed GFRP bar and UHPC. J. Build. Eng. 2023, 80, 107939. [Google Scholar] [CrossRef]
- Shaikh, F.U.A.; Luhar, S.; Arel, H.Ş.; Luhar, I. Performance evaluation of Ultrahigh performance fibre reinforced concrete–A review. Constr. Build. Mater. 2019, 232, 117152. [Google Scholar] [CrossRef]
- Tan, H.; Hou, Z.; Li, Y.; Xu, X. A flexural ductility model for UHPC beams reinforced with FRP bars. Structures. 2022, 45, 773–786. [Google Scholar] [CrossRef]
- Ke, L.; Liang, L.; Feng, Z.; Li, C.; Zhou, J.; Li, Y. Bond performance of CFRP bars embedded in UHPFRC incorporating orientation and content of steel fibers. J. Build. Eng. 2023, 73, 106827. [Google Scholar] [CrossRef]
- Zhu, H.; He, Y.; Cai, G.; Cheng, S.; Zhang, Y.; Larbi, A.S. Bond performance of carbon fiber reinforced polymer rebars in ultra-high-performance concrete. Constr. Build. Mater. 2023, 387, 131646. [Google Scholar] [CrossRef]
- Wu, C.; Ma, G.; Hwang, H.-J. Bond performance of spliced GFRP bars in pre-damaged concrete beams retrofitted with CFRP and UHPC. Eng. Struct. 2023, 292, 116523. [Google Scholar] [CrossRef]
- CSA S806-2012; Design and Construction of Building Structures with Fibre Reinforced Polymers. Canadian Standard Association: Mississauga, ON, Canada, 2012.
- Mahaini, Z.; Abed, F.; Alhoubi, Y.; Elnassar, Z. Experimental and numerical study of the flexural response of Ultra High Performance Concrete (UHPC) beams reinforced with GFRP. Compos. Struct. 2023, 315, 117017. [Google Scholar] [CrossRef]
- Mahmoudian, A.; Bypour, M.; Kontoni, D.-P.N. Tree-based machine learning models for predicting the bond strength in reinforced recycled aggregate concrete. Asian J. Civ. Eng. 2024, 1–26. [Google Scholar] [CrossRef]
- Bypour, M.; Mahmoudian, A.; Tajik, N.; Taleshi, M.M.; Mirghaderi, S.R.; Yekrangnia, M. Shear capacity assessment of perforated steel plate shear wall based on the combination of verified finite element analysis, machine learning, and gene expression programming. Asian J. Civ. Eng. 2024, 25, 5317–5333. [Google Scholar] [CrossRef]
- Feng, D.-C.; Liu, Z.-T.; Wang, X.-D.; Chen, Y.; Chang, J.-Q.; Wei, D.-F.; Jiang, Z.-M. Machine learning-based compressive strength prediction for concrete: An adaptive boosting approach. Constr. Build. Mater. 2020, 230, 117000. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Kumar, D.; Samui, P.; Hu, J.W.; Kim, D. Compressive strength prediction of high-performance concrete using gradient tree boosting machine. Constr. Build. Mater. 2020, 264, 120198. [Google Scholar] [CrossRef]
- Zhu, F.; Wu, X.; Lu, Y.; Huang, J. Strength estimation and feature interaction of carbon nanotubes-modified concrete using artificial intelligence-based boosting ensembles. Buildings 2024, 14, 134. [Google Scholar] [CrossRef]
- Hossain, K.; Ametrano, D.; Lachemi, M. Bond strength of GFRP bars in ultra-high strength concrete using RILEM beam tests. J. Build. Eng. 2017, 10, 69–79. [Google Scholar] [CrossRef]
- Ahmad, F.S.; Foret, G.; Le Roy, R. Bond between carbon fibre-reinforced polymer (CFRP) bars and ultra high performance fibre reinforced concrete (UHPFRC): Experimental study. Constr. Build. Mater. 2011, 25, 479–485. [Google Scholar] [CrossRef]
- Sayed-Ahmed, M.; Sennah, K. Str-894: Bond strength of ribbed-surface high-modulus glass FRP bars embedded into unconfined UHPFRC. In Proceedings of the Canadian Society for Civil Engineering Annual Conference 2016, Resilient Infrastructure, London, UK, 1–4 June 2016. [Google Scholar]
- Michaud, D.; Fam, A.; Dagenais, M.-A. Development length of sand-coated GFRP bars embedded in Ultra-High performance concrete with very small cover. Constr. Build. Mater. 2021, 270, 121384. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Yoon, Y.-S. Bond behavior of GFRP and steel bars in ultra-high-performance fiber-reinforced concrete. Adv. Compos. Mater. 2017, 26, 493–510. [Google Scholar] [CrossRef]
- Yoo, D.-Y.; Kwon, K.-Y.; Park, J.-J.; Yoon, Y.-S. Local bond-slip response of GFRP rebar in ultra-high-performance fiber-reinforced concrete. Compos. Struct. 2015, 120, 53–64. [Google Scholar] [CrossRef]
- Yoo, S.-J.; Hong, S.-H.; Yoo, D.-Y.; Yoon, Y.-S. Flexural bond behavior and development length of ribbed CFRP bars in UHPFRC. Cem. Concr. Compos. 2024, 146, 105403. [Google Scholar] [CrossRef]
- Hu, X.; Xue, W.; Xue, W. Bond properties of GFRP rebars in UHPC under different types of test. Eng. Struct. 2024, 314, 118319. [Google Scholar] [CrossRef]
- Qasem, A.; Sallam, Y.S.; Eldien, H.H.; Ahangarn, B.H. Bond-slip behavior between ultra-high-performance concrete and carbon fiber reinforced polymer bars using a pull-out test and numerical modelling. Constr. Build. Mater. 2020, 260, 119857. [Google Scholar] [CrossRef]
- Eltantawi, I.; Alnahhal, W.; El Refai, A.; Younis, A.; Alnuaimi, N.; Kahraman, R. Bond performance of tensile lap-spliced basalt-FRP reinforcement in high-strength concrete beams. Compos. Struct. 2022, 281, 114987. [Google Scholar] [CrossRef]
- ACI Committee 440. Guide Test Methods for FiberReinforced Polymer (FRP) Composites for Reinforcing or Strengthening Concrete and Masonry Structures; ACI: Farmington Hills, MI, USA, 2012. [Google Scholar]
- Tong, D.; Chi, Y.; Huang, L.; Zeng, Y.; Yu, M.; Xu, L. Bond performance and physically explicable mathematical model of helically wound GFRP bar embedded in UHPC. J. Build. Eng. 2023, 69, 106322. [Google Scholar] [CrossRef]
- Ahmed, M.S.; Sennah, K. Pullout strength of sand-coated GFRP bars embedded in ultra-high performance fiber reinforced concrete. In Proceedings of the CSCE 2014 4th International Structural Speciality, Halifax, NS, Canada, 28–31 May 2014. [Google Scholar]
- Esteghamati, M.Z.; Gernay, T.; Banerji, S. Evaluating fire resistance of timber columns using explainable machine learning models. Eng. Struct. 2023, 296, 116910. [Google Scholar] [CrossRef]
- Mahmoudian, A.; Tajik, N.; Taleshi, M.M.; Shakiba, M.; Yekrangnia, M. Ensemble machine learning-based approach with genetic algorithm optimization for predicting bond strength and failure mode in concrete-GFRP mat anchorage interface. Structures 2023, 57, 105173. [Google Scholar] [CrossRef]
- Tajik, N.; Mahmoudian, A.; Taleshi, M.M.; Yekrangnia, M. Explainable XGBoost machine learning model for prediction of ultimate load and free end slip of GFRP rod glued-in timber joints through a pull-out test under various harsh environmental conditions. Asian J. Civ. Eng. 2024, 25, 141–157. [Google Scholar] [CrossRef]
- Shams, M.Y.; Tarek, Z.; Elshewey, A.M.; Hany, M.; Darwish, A.; Hassanien, A.E. A machine learning-based model for predicting temperature under the effects of climate change. In The Power of Data: Driving Climate Change with Data Science and Artificial Intelligence Innovations; Studies in Big Data; Springer: Berlin/Heidelberg, Germany, 2023; pp. 61–81. [Google Scholar]
- Alhakeem, Z.M.; Jebur, Y.M.; Henedy, S.N.; Imran, H.; Bernardo, L.F.A.; Hussein, H.M. Prediction of ecofriendly concrete compressive strength using gradient boosting regression tree combined with GridSearchCV hyperparameter-optimization techniques. Materials 2022, 15, 7432. [Google Scholar] [CrossRef]
- Lee, J.-Y.; Kim, T.-Y.; Kim, T.-J.; Yi, C.-K.; Park, J.-S.; You, Y.-C.; Park, Y.-H. Interfacial bond strength of glass fiber reinforced polymer bars in high-strength concrete. Compos. Part B Eng. 2008, 39, 258–270. [Google Scholar] [CrossRef]





















| Research | Test Method | Rebar Type | Rebar Diameter (mm) | Embedment Length (mm) | Tensile Strength (MPa) | (MPa) | Elastic Modulus (GPa) | Number of Specimens |
|---|---|---|---|---|---|---|---|---|
| Hu et al. (2024) [40] | Pullout and Beam | GFRP and Steel | 16 | 40–160 | 609 and 894 | 133.2 | 54 and 198 | 16 |
| Zhu et al. (2023) [24] | Beam | CFRP | 8, 10, and 12 | 25–120 | 2030 and 2702 | 131–143 | - | 11 |
| Liang et al. (2023) [13] | Pullout | GFRP, BFRP, and Steel | 12 | 42 | 355–1321 | 93–122 | 48–200.4 | 48 |
| Tong et al. (2023) [44] | Pullout | GFRP | 12, 16, and 20 | 60–100 | 702–782 | 90–132 | 54–58 | 54 |
| Decebal et al. (2021) [36] | Beam | GFRP | 17.2 | 69–276 | 1100 | 87–132 | 60 | 28 |
| Hossain et al. (2017) [33] | Beam | GFRP | 15.9 and 19.1 | 47–133 | 751–1439 | 71–174 | 47–64 | 48 |
| Ahmed and Sennah (2014) [45] | Pullout | GFRP | 20 | 80–160 | 1105 | 166–181 | 64.7 | 35 |
| Ahmad et al. (2011) [34] | Pullout | CFRP | 7.5, 8, 10, and 12 | 40–160 | 2300 and 2400 | 170 | 130 and 158 | 9 |
| N_Estimators | Learning_Rate | Loss |
|---|---|---|
| 50 | 0.01 | Linear |
| 100 | 0.1 | Square |
| 200 | 0.2 | Exponential |
| 300 | 0.3 | - |
| 400 | 0.5 | - |
| Iterations | Learning_Rate | Depth | L2_Leaf_Reg | Bagging_Temperature |
|---|---|---|---|---|
| 100 | 0.01 | 4 | 3 | 0.8 |
| 150 | 0.05 | 6 | 5 | 1 |
| 200 | 0.1 | 8 | 7 | - |
| 300 | 0.2 | - | 9 | - |
| 400 | - | - | - | - |
| N_Estimators | Learning_Rate | Max_Depth | Max_Features |
|---|---|---|---|
| 50 | 0.01 | None | sqrt |
| 100 | 0.1 | 4 | log2 |
| 200 | 0.2 | 5 | - |
| 300 | 0.3 | 8 | - |
| 400 | 0.5 | 10 | - |
| L2_Regularization | Learning_Rate | Max_Depth | Max_Iter |
|---|---|---|---|
| 0 | 0.01 | None | 100 |
| 0.1 | 0.1 | 4 | 200 |
| 0.5 | 0.2 | 5 | 300 |
| 1 | 0.3 | 8 | - |
| - | 0.5 | 10 | - |
| Model | R2 (Default) | RMSE (Default) | MAE (Default) | R2 (Tuned) | RMSE (Tuned) | MAE (Tuned) |
|---|---|---|---|---|---|---|
| ADAboost | 0.61 | 6.46 | 5.03 | 0.7 | 5.63 | 2.67 |
| Catboost | 0.94 | 2.56 | 1.9 | 0.95 | 2.34 | 1.74 |
| Gradient Boosting | 0.94 | 2.58 | 1.95 | 0.95 | 2.26 | 1.73 |
| XGBoost | 0.94 | 2.33 | 1.78 | 0.95 | 2.21 | 1.68 |
| Hist Gradient Boosting | 0.59 | 6.58 | 4.18 | 0.68 | 5.86 | 3.24 |
| Model | N_Estimators | Max_Depth | Max_Features | Learning_Rate | Loss |
|---|---|---|---|---|---|
| AdaBoost | 100 | - | - | 0.5 | exponential |
| Gradient Boosting | 200 | 4 | sqrt | 0.1 | - |
| XGBoost | 150 | 10 | - | 0.1 | - |
| Research | Formula | Note |
|---|---|---|
| Yoo et al. 2023 [8] | (a): for sand-coated CFRP (b): for helically ribbed CFRP | Separate equation according to CFRP type. |
| Lee et al. 2008 [51] | for GFRP bars (a) for steel bars (b) | Only considers . |
| Zhu et al. [24] | CFRP rebars in UHPC based on both pullout test data and beam test | Does not consider rebar type. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahmoudian, A.; Bypour, M.; Kioumarsi, M. Explainable Boosting Machine Learning for Predicting Bond Strength of FRP Rebars in Ultra High-Performance Concrete. Computation 2024, 12, 202. https://doi.org/10.3390/computation12100202
Mahmoudian A, Bypour M, Kioumarsi M. Explainable Boosting Machine Learning for Predicting Bond Strength of FRP Rebars in Ultra High-Performance Concrete. Computation. 2024; 12(10):202. https://doi.org/10.3390/computation12100202
Chicago/Turabian StyleMahmoudian, Alireza, Maryam Bypour, and Mahdi Kioumarsi. 2024. "Explainable Boosting Machine Learning for Predicting Bond Strength of FRP Rebars in Ultra High-Performance Concrete" Computation 12, no. 10: 202. https://doi.org/10.3390/computation12100202
APA StyleMahmoudian, A., Bypour, M., & Kioumarsi, M. (2024). Explainable Boosting Machine Learning for Predicting Bond Strength of FRP Rebars in Ultra High-Performance Concrete. Computation, 12(10), 202. https://doi.org/10.3390/computation12100202







