Numerical Homogenization Method Applied to Evaluate Effective Converse Flexoelectric Coefficients

Abstract

This paper presents a numerical homogenization method for estimating the effective converse flexoelectric coefficients. A 2D model made of two-phase composite is developed at the microscale in consideration of a representative volume element that includes a continuous flexoelectric fiber embedded in a pure elastic matrix. In the implementation, the constitutive equations are derived from the electromechanical enthalpy accounting for higher-order coupling terms. Electric boundary conditions associated with an inhomogeneous electric field are imposed, allowing the approximation of the generated mechanical strains and stresses. Accordingly, the numerical simulations yield the overall equivalent converse flexoelectricity tensor for the longitudinal, transversal, and shear couplings. The results showed that the composite undergoes an obvious straining, which creates actuation due to the converse effect. The components of the homogenized longitudinal and transverse coefficients were found to be dependent on the volume fraction and elastic properties of the constituents.

1. Introduction

Flexoelectricity is a physical property related to the break of the symmetry inversion in dielectrics. In this case, the electromechanical coupling is defined by the relationship between the displacement of ions (i.e., polarization) and the mechanical deformation. The energy conversion mechanism is, at best, notable at small length scales. With recent developments in nanotechnology, increasing interest has been shown in studying the modification in the electromechanical behavior of flexoelectric nanocomposites that provides the possibility to produce considerably larger flexoelectric outcomes [1,2]. The concept of direct flexoelectricity was introduced by Kogan in the 1960s, who quantified the effect in solid crystals by a coefficient that couples the strain gradient and the induced electric polarization [3]. In this direct form, an electrical polarization is induced in the presence of an inhomogeneous strain. Later, Tagantsev [4] extended the phenomenological flexoelectricity theory of Kogan by accounting for surface and bulk contributions [4]. Further experimental investigations have confirmed the theory of Tagantsev for the role of electric susceptibility in improving the flexoelectric effect [5]. In addition, several theoretically based studies have been devoted to better understand the fundamentals of electromechanical coupling [2,6,7].

In contrast, the converse effect of flexoelectricity causes a deformation when applying an electric field. The direct and converse coefficients are widely used to measure flexoelectric performance. Still, their sign and relative magnitude are contradictory in the relevant literature. Flexoelectric effects have been experimentally reported in the range of ${10}^{-9}–{10}^{-6}\mathrm{C}/\mathrm{m}$ for certain ferroelectrics and perovskite oxides [8]. To calculate the converse coefficients, the common setup includes measuring the bending in a capacitor after applying a voltage or applying a voltage across a truncated pyramid; see [9,10,11] among others. Analogously, a large effective piezoelectric response has been produced in nonpiezoelectric materials, and the converse flexoelectricity showed non-negligible effects in thin films [12]. The equivalent piezoelectric effect has been shown to increase with the converse flexoelectricity in permittivity gradient composites [13]. The mechanism has been investigated in an asymmetric structure around $90°$ domain walls at which large polarization and strain gradients are clearly concentrated [14]. An analysis of atomic-scale electron microscopy imaging data has been integrated with phenomenological phase field modeling to study the influence of flexocoupling on the global vortex structure [15]. Moreover, flexoelectric coefficients were extracted for a homogeneous domain from simulations based on ab initio lattice dynamics [16] and first-principles calculations [17]. An explicit solution was presented relying on a micro-hole model. The formulations were based on higher-order governing equations that take into account the strain gradient elasticity, the direct flexoelectricity, and the converse flexoelectricity [18]. Approaches along these lines were implemented to exact solutions for the flexoelectric response in [19].

In two- (or multiple-)phase composites, an active material which has the flexoelectric properties can increase the efficiency of energy conversion in the zones of high strain gradients. A significant enhancement of polarization could be attributed to the flexoelectric effect [20]. Nevertheless, it has been shown that it is possible to produce piezoelectric nanocomposites without the use of piezoelectric materials [21]. In this regard, elastic heterogeneity impacts the effective piezo- and flexoelectric responses as well. Analytical and computational homogenization have provided insight into the coupling at the microscale to determine the average macroscopic properties where a heterogeneous domain is transformed into a small body of a homogeneous one. Worth mentioning here are the documented works for piezoelectric, electrets, and electrostrictive composites in [22,23,24,25]. The homogenized flexoelectric, dielectric, and elastic response was theoretically studied by [26]. In the mean time, an analytical micromechanic approach was exploited to calculate the effective flexoelectric coefficients in a multifunctional fiber composite [27]. Asymptotic homogenization was applied to flexoelectric rods [28] and flexoelectric composite plates with a periodically varying thickness [29]. Considering the flexoelectric effect, the effective elastic piezoelectric constants were examined via analytical-based micromechanical models and finite element models [30,31,32].

The numerical implementation of computational homogenization commonly used a representative volume element (RVE) to approximate the kinematic and constitutive equations in equilibrium. In [33], an apparent flexoelectricity response was concluded in heterogeneous piezoelectricity by applying a computational approach on the finite element method. As the flexoelectricity of the constituent materials was not considered, the effective flexoelectric tensor was approximated in different geometries. Similarly, an inclusion-based piezoelectric planar composite was examined, and the effective properties were predicted using a variational formulation [34]. The effective material properties and flexoelectric coefficients were evaluated using a 3D RVE with periodic boundary conditions in [35]. The numerical simulation was implemented on a microstructure composed of an elastic matrix and cylindrical flexoelectric filler. Ref. [36] has solved the higher-order electromechanical coupling using a high-order approximation space constrained to periodicity conditions. Special attention was given to the homogenization of architected metamaterials with apparent piezoelectricity. It is worth noting that the above-mentioned works have focused on the direct effects of flexoelectricity. With regard to the converse effect, a numerical study was provided in [37] which revealed an enhanced overall flexoelectric response in periodic piezoelectric composites. The apparent converse coefficients were found to be in the same order as the direct coefficients in the local constituents. Indeed, to the author’s best knowledge, the contributions in this direction are scarce. A thorough and robust numerical technique is at high demand, as it can provide a deeper understanding of the direct and converse flexoelectricity.

The main objective of this study is to evaluate the effect of converse flexoelectricity in two-phase composites, namely elastic and flexoelectric. In particular, a numerical homogenization method is presented, offering significant advantages in predicting the effective converse flexoelectric coefficients. The electromechanical coupling terms associated with the strain, the electric field gradient, and the strain gradient elasticity are derived from the electrical enthalpy. Non-Uniform Rational B-spline (NURBS)-based isogeometric analysis (IGA) is used to address the problem leveraging its higher-order continuity. The study relies on numerical simulations conducted on a two-dimensional model subjected to inhomogeneous electric field. The solution involves computing the distribution of the electrical field, as well as the generated stress and strain fields. Then, the overall performance of the heterogeneous system is obtained by calculating the equivalent coefficients. The converse flexoelectricity tensor is evaluated at varying volume fractions including comparison with respect to the ratio of the elasticity between the two constituents. The paper is organized as follows. Section 2 introduces the mathematical formulation of the continuum flexoelectric boundary value problem, and presents how NURBS-based isogeometric analysis (IGA) is used to approximate the solution of the electromechanically coupled system. Section 3 describes the setup of the problem, including an in-depth discussion of the results of computational experiments. Afterwards, the summary and conclusions are shown in Section 4.

2. Flexoelectricity Modeling Formulation

Direct and converse flexoelectricity are characterized by fourth-order tensors that couple polarization and strain gradient in the former, and strain and polarization gradient in the latter. Considering flexoelectricity theory, the internal energy includes additional terms related to the electromechanical coupling. The Gibbs-free (electromechanical enthalpy) bulk energy for a linear flexoelectric solid can be written as

$$\begin{array}{cc}\hfill \mathcal{H}\left({\epsilon }_{ij},E_i,{\epsilon }_{jk,l},E_{k,l}\right)=& {\displaystyle \frac{1}{2}}{\mathbb{C}}_{ijkl}{\epsilon }_{ij}{\epsilon }_{kl}-{\displaystyle \frac{1}{2}}{\kappa }_{ij}{E}_i{E}_j-e_{ikl}{E}_i{\epsilon }_{kl}\hfill \\ \hfill & +d_{ijkl}{E}_i{\epsilon }_{jk,l}+f_{ijkl}{E}_{i,j}{\epsilon }_{kl}+{\displaystyle \frac{1}{2}}{\mathrm{g}}_{\mathrm{ijklmn}}{\epsilon }_{ij,k}{\epsilon }_{lm,n}\hfill \end{array}$$

(1)

where ${\epsilon }_{ij}$ is the strain tensor and $E_i=-{\varphi }_{,i}$ is the vector of the electric field, with $\varphi$ being the electric potential. The comma notation $(,)$ in the subscript denotes the first derivative with respect to one spatial variable. The first two terms represent elastic and electrostatic potentials, respectively, where ${\mathbb{C}}_{ijkl}$ is the fourth-order tensor of elastic moduli and ${\kappa }_{ij}$ indicates the second-order tensor of dielectric permittivity. The contribution of piezoelectricity is represented by the third-order piezoelectric tensor, $e_{ikl}$, which couples the strain and the electric field. Likewise, the flexoelectric effect is accounted for by fourth-order flexocoupling tensors in the fourth and fifth terms in the above expression. Here, $d_{ijkl}$ and $f_{ijkl}$ represent the direct and converse tensors, respectively. For cubic symmetry materials, each tensor has only three nonzero independent components: longitudinal, transverse, and shear coefficients [38]. The particular focus hereinafter is on the converse constants, which correspond to the ratio of the polarization gradient to the produced strain. In addition, this study considers the nonlocal elastic energy associated with the strain gradient elasticity. To ensure positive strain energy, a relatively small value is assumed for a length scale parameter $\left(l\right)$ according to the simplified model of strain gradient elasticity theory, such that the sixth-order elastic tensor ${\mathrm{g}}_{\mathrm{ijklmn}}=l^2{\mathbb{C}}_{\mathrm{jkmn}}$ [39]. Further higher-order coupling terms are neglected for the sake of simplicity.

From the above-mentioned enthalpy, the constitutive relations for the electric displacement $\left(\mathbf{D}\right)$, the stress tensor $\left(\mathbf{\sigma }\right)$, and the higher-order tensors (hyper) of stress $\left(\mathbf{S}\right)$ and electric displacement ($\mathbf{P}$, known as the electric quadrupole) are obtained as follows:

$$\begin{array}{cc}\hfill & D_i=e_{ikl}{\epsilon }_{kl}+{\kappa }_{ij}{E}_j-d_{ijkl}{\epsilon }_{jk,l}\hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill & {\sigma }_{ij}={\mathbb{C}}_{ijkl}{\epsilon }_{kl}-e_{ikl}{E}_i+f_{ijkl}{E}_{i,j}\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill & S_{ijk}=d_{lijk}{E}_l+{\mathrm{g}}_{\mathrm{ijklmn}}{\epsilon }_{lm,n}\hfill \end{array}$$

(2c)

$$\begin{array}{cc}\hfill & P_{ij}=f_{iklj}{\epsilon }_{kl}\hfill \end{array}$$

(2d)

When solving the weak form, it is required to solve fourth-order partial differential equations (PDEs), which necessitates $C^1$ continuity. This study employs the isogeometric analysis (IGA) approach for the discretization, because it includes higher-order smooth basis functions. For this purpose, the formulation presented in [40,41] is adopted based on Non-Uniform Rational B-spline (NURBS) basis functions, $N_{(i,p)}\left(\xi \right)$. The geometry is discretized by control points. In doing so, mechanical and electrical degrees of freedom are assigned for each control point. To approximate the solution of field variables, the nodal values are multiplied with their corresponding basis functions. The mechanical displacement ($\mathbf{u}$) and electric potential ($\varphi$) fields with the corresponding variations are approximated by

$$\begin{array}{cc}\hfill & \mathbf{u}={{\mathbf{N}}_{\mathrm{u}}}^{\mathrm{T}}{\mathbf{u}}^{\mathrm{e}}\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill & \varphi ={{\mathbf{N}}_{\varphi }}^{\mathrm{T}}{\mathit{\varphi }}^{\mathrm{e}}\hfill \end{array}$$

(3b)

$$\begin{array}{cc}\hfill & {\partial }_{j}u={\partial }_j{\left({\mathbf{N}}_{\mathrm{u}}\right)}^{\mathrm{T}}{\mathbf{u}}^{\mathrm{e}}={\left({\mathbf{B}}_{\mathrm{u}}\right)}^{\mathrm{T}}{\mathbf{u}}^{\mathrm{e}}=\mathit{\epsilon }\hfill \end{array}$$

(3c)

$$\begin{array}{cc}\hfill & {\partial }_j\theta ={\partial }_j{\left({\mathbf{N}}_{\varphi }\right)}^{\mathrm{T}}{\mathit{\varphi }}^{\mathrm{e}}={\left({\mathbf{B}}_{\varphi }\right)}^{\mathrm{T}}{\mathit{\varphi }}^{\mathrm{e}}=-\mathbf{E}\hfill \end{array}$$

(3d)

$$\begin{array}{cc}\hfill & {\partial }_j{\partial }_{k}u={\partial }_j{\partial }_k{\left({\mathbf{N}}_{\mathrm{u}}\right)}^{\mathrm{T}}{\mathbf{u}}^{\mathrm{e}}={\left({\mathbf{H}}_{\mathrm{u}}\right)}^{\mathrm{T}}{\mathbf{u}}^{\mathrm{e}}=\nabla \mathit{\epsilon }\hfill \end{array}$$

(3e)

$$\begin{array}{cc}\hfill & {\partial }_j{\partial }_k\varphi ={\partial }_j{\partial }_k{\left({\mathbf{N}}_{\varphi }\right)}^{\mathrm{T}}{\mathit{\varphi }}^{\mathrm{e}}={\left({\mathbf{H}}_{\mathrm{s}}\right)}^{\mathrm{T}}{\mathit{\varphi }}^{\mathrm{e}}=-\nabla \mathbf{E}\hfill \end{array}$$

(3f)

where the superscript $\mathrm{e}$ denotes nodal parameters at the control points. The gradient operators ${\mathbf{B}}_{\mathrm{u}}$ and ${\mathbf{B}}_{\varphi }$ are the spatial derivatives of the basis functions ${\mathbf{N}}_{\mathrm{u}}$ and ${\mathbf{N}}_{\varphi }$, respectively, while ${\mathbf{H}}_{\mathrm{u}}$ and ${\mathbf{H}}_{\mathrm{s}}$ are their second-order (Hessian) derivatives. Note that the NURBS basis functions are continuously differentiable up to $p-1$ a polynomial order of p [42].

The boundary conditions can be imposed as mechanical tractions, $\overline{\mathbf{t}}$, or surface charge density, $\mathit{\varpi }$, at the boundaries ${\Gamma }_t$ and ${\Gamma }_D$. By integration over the domain $\Omega$, the discrete representation of Equation (1), after some algebra, reads [41]

$$\begin{array}{c}\hfill H={\displaystyle \frac{1}{2}}\sum _{\mathrm{e}}{\mathbf{u}}^{\mathrm{T}}\left({\int }_{{\Omega }_{\mathrm{e}}}{\mathbf{B}}_{\mathrm{u}}\mathbb{C}{\left({\mathbf{B}}_{\mathrm{u}}\right)}^{\mathrm{T}}d{\Omega }_{\mathrm{e}}\right)\mathbf{u}-{\displaystyle \frac{1}{2}}\sum _{\mathrm{e}}\left({\int }_{{\Omega }_{\mathrm{e}}}{\mathbf{B}}_{\varphi }\mathbf{\kappa }{\left({\mathbf{B}}_{\varphi }\right)}^{\mathrm{T}}d{\Omega }_{\mathrm{e}}\right)\varphi \varphi +\sum _{\mathrm{e}}{\mathbf{u}}^{\mathrm{T}}\left({\int }_{{\Omega }_{\mathrm{e}}}{\mathbf{B}}_{\mathrm{u}}\mathbf{e}{\left({\mathbf{B}}_{\varphi }\right)}^{\mathrm{T}}d{\Omega }_{\mathrm{e}}\right)\varphi \\ \hfill +\sum _{\mathrm{e}}{\mathbf{u}}^{\mathrm{T}}\left({\int }_{{\Omega }_{\mathrm{e}}}{\mathbf{H}}_{\mathrm{u}}{\mathbf{d}}^{\mathrm{T}}{\left({\mathbf{B}}_{\varphi }\right)}^{\mathrm{T}}d{\Omega }_{\mathrm{e}}\right)\varphi +\sum _{\mathrm{e}}{\mathbf{u}}^{\mathrm{T}}\left({\int }_{{\Omega }_{\mathrm{e}}}{\left({\mathbf{B}}_{\mathrm{u}}\right)}^{\mathrm{T}}\mathit{f}{\left({\mathbf{H}}_{\varphi }\right)}^{\mathrm{T}}d{\Omega }_{\mathrm{e}}\right)\varphi +{\displaystyle \frac{1}{2}}\sum _{\mathrm{e}}{\mathbf{u}}^{\mathrm{T}}\left({\int }_{{\Omega }_{\mathrm{e}}}{\mathbf{H}}_{\mathrm{s}}\mathrm{g}{\left({\mathbf{H}}_{\mathrm{s}}\right)}^{\mathrm{T}}d{\Omega }_{\mathrm{e}}\right)\mathbf{u}\\ \hfill -\sum _{\mathrm{e}}\left({\int }_{{\Gamma }_{t_{\mathrm{e}}}}{\mathbf{N}}_{\mathrm{u}}^{\mathrm{T}}{\mathbf{t}}_{\Gamma }ds\right)\mathbf{u}+\sum _{\mathrm{e}}\left({\int }_{{\Gamma }_{D_{\mathrm{e}}}}{\mathbf{N}}_{\varphi }^{\mathrm{T}}\mathit{\varpi }ds\right)\varphi \end{array}$$

(4)

The corresponding mechanical and electrostatic equilibrium are obtained for $\mathbf{u}$ and $\varphi$, respectively. Hence, the global stiffness coupled matrix is assembled from the mechanical, electromechanical, and electrical elemental stiffness matrices [43].

3. Numerical Implementation and Results

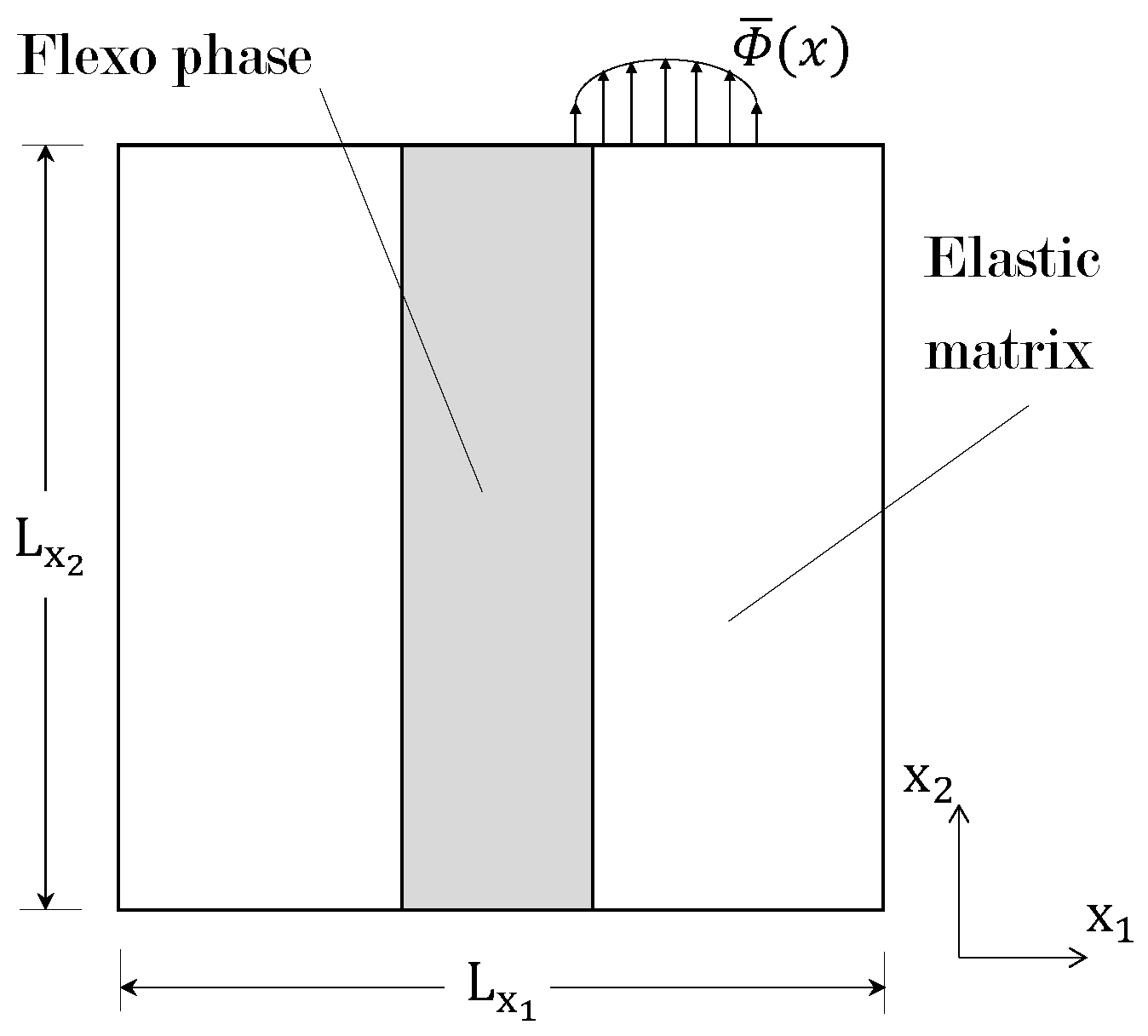
This study investigates a two-phase composite constituted by flexo (active phase) and elastic (passive phase) materials under the assumption of plane strain conditions. The former experiences pure flexoelectricity (i.e, non-piezoelectric with $e_{ij}=0$, ${\kappa }_{ij}=12.48\times {10}^{-9}\mathrm{C}/\mathrm{Vm}\mathrm{and}$ $f_{ijkl}=1.0\times {10}^{-6}\mathrm{C}/\mathrm{m})$, whereas the latter is a plain elastic material. This can provide a clear distinction between their individual physics. The geometry of the reference problem is sketched in Figure 1, which takes the shape of a square RVE with dimensions ${\mathrm{L}}_{{\mathrm{x}}_1}={\mathrm{L}}_{{\mathrm{x}}_2}=100\times {10}^{-6}$ m. A two-dimensional configuration with longitudinally oriented active fibers is being considered. This configuration enables the study of the converse effect in both the longitudinal and transverse directions.

In the analysis, a transversely isotropic elasticity is assumed, incorporating softer passive material that can yield enhanced deflection. The elastic properties for the matrix are taken as ${\mathbb{C}}_{11}$ = 60 $\mathrm{GPa}$, ${\mathbb{C}}_{12}$ = 32.3 $\mathrm{GPa}$, and ${\mathbb{C}}_{44}$ = 13.8 $\mathrm{GPa}$; while for the flexo phase, they are ${\mathbb{C}}_{11}$ = 120 $\mathrm{GPa}$, ${\mathbb{C}}_{12}$ = 40 $\mathrm{GPa}$, and ${\mathbb{C}}_{44}$ = 40 $\mathrm{GPa}$. However, we will change these properties and examine their effects on the effective coefficients at a varied volume fraction. A no-slippage condition is accounted for, ensuring continuity in displacement, traction, and electrical potential along the interfaces.

While the effective dielectric properties can be estimated using a uniform electric field, the homogenized piezoelastic (piezoelectric and elastic) constants can be obtained under boundary conditions of uniform strain. Differently, the direct flexoelectric constants can be determined by imposing a strain gradient. However, the scope of this study is to evaluate the converse flexoelectricity. Boundary conditions that create a polarization gradient are considered for this purpose. An electric field gradient is generated independently, ensuring that all other kinematic conditions remain at zero, except for the component under investigation. Note in this case that $\overline{\mathbf{F}}=\overline{\mathbf{P}}:{\left[\overline{\mathit{\epsilon }}\right]}^{-1}$. In doing so, the RVE is subjected to a periodically fluctuating electric potential, $\varphi$, which will result in non-homogeneous electric fields. Quadratic electric boundary conditions for the system are applied at the surfaces/boundaries as follows:

$${\left.\varphi \right|}_{\mathrm{x}=0,\mathrm{L}}=\varphi \left(\mathrm{x}\right)=V_0-V_0{\left({\displaystyle \frac{2\mathrm{x}}{\mathrm{L}}}-1\right)}^2$$

(5)

where $V_0$ is the amplitudes of the electric potential.

For the numerical implementation, the model with the established geometry is meshed by quadratic B-spline elements. The control points are utilized to discretize the geometry and encompass the degrees of freedom (DoF). Two DoF pertaining to mechanical displacement and one for the electric potential are assigned. Mesh sensitivity is evaluated using different sizes associated with a quadratic shape function in all simulations. It has been determined that discretization of 40 × 40 elements is sufficient to achieve accurate results, revealing only a negligible impact on the numerical approximation. Macroscopic quantities are obtained via the volume averaging operator $\overline{\left(·\right)}=〈·〉:=1/V{\int }_{\Omega }\left(·\right)dV$.

Throughout all simulations, we consider the converse flexoelectricity effect under predefined electrical loading. An electric field gradient with respect to ${\mathrm{x}}_2$, $(\nabla E_{22}=E_{2,2})$, can be obtained by applying a non-uniform electric potential on the left and right edges of the RVE in accordance to Equation (5). In similar way, $\nabla E_{11}$ is generated from a non-uniform voltage on the top and bottom surfaces. 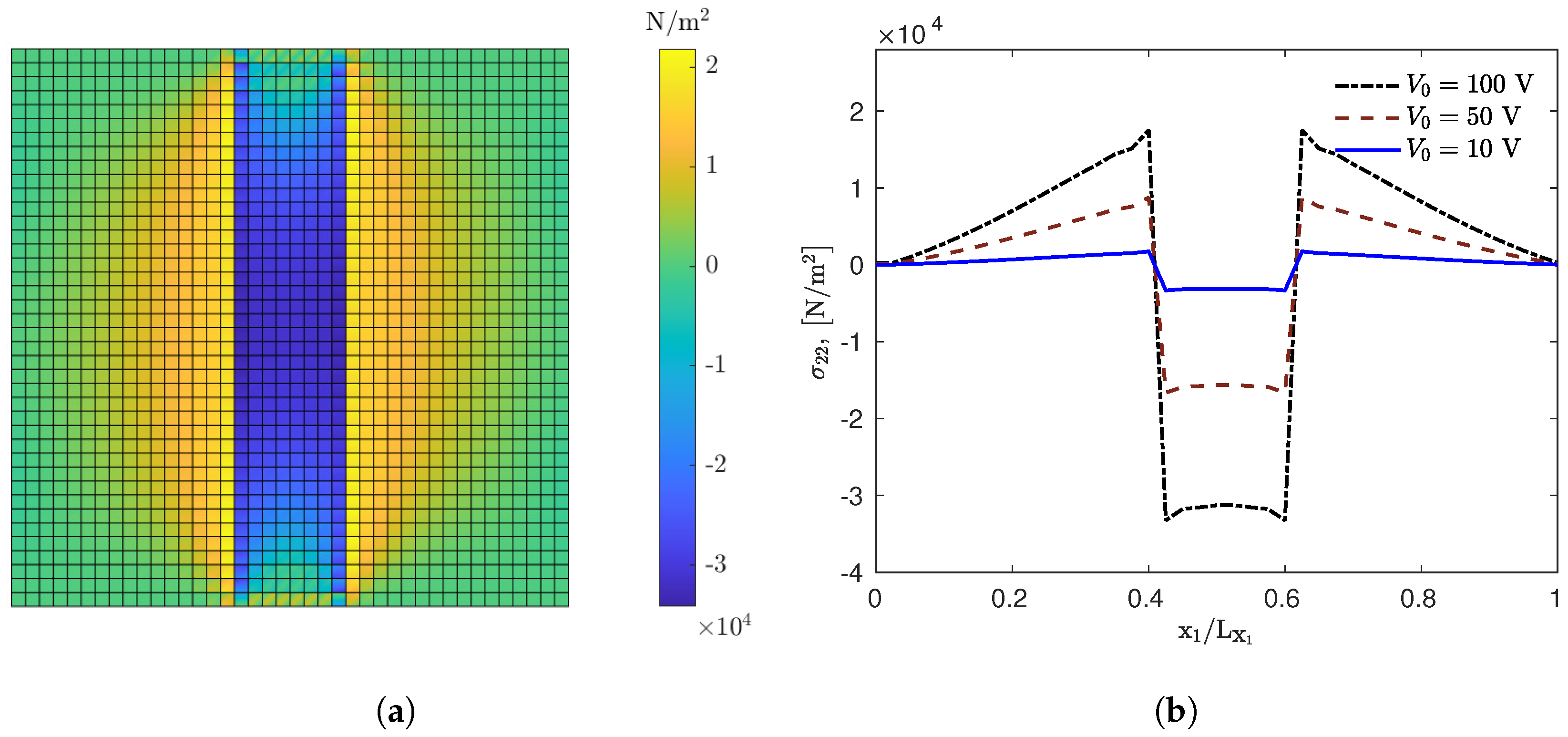Figure 2 illustrates the distribution of the axial stresses ${\sigma }_{22}$ within an RVE subjected to an electric gradient $\nabla E_{22}$. The micro-structure is loaded with flexo material ratio of 20% by volume and the amplitude $V_0$ is 100 V. Negative and positive concentrations of electric quadrupoles are induced in the ${\mathrm{x}}_1$ and ${\mathrm{x}}_2$ directions, respectively, within the flexo phase due to the electric gradient. The contours of stress fields in Figure 2a exhibit an axis of symmetry along ${\mathrm{x}}_2$-axis attributed to the symmetrical microstructure along this axis. Furthermore, the applied electrical loading primarily induces negative stresses within the inclusion and positive stresses in its surrounding matrix, because of perfect bonding of the two materials and the absence of boundary constraints. Consequently, the flexo phase contracted while the matrix expanded due to stresses. The direction of the electric potential determines the sign of the straining. It can be revealed that the generated stresses are a clear indication of actuation as a result of the converse flexoelectric effect. The stress profiles across the mid height calculated at different loadings are depicted in Figure 2b. The plots confirm that the axial stress developed through the flexo phase is considerably stronger. This is attributed to the flexoelectric coupling. It is also observed that with an increase in the magnitude of the applied voltage, a proportionate increase in the actuation is produced.

Table 1. Effective converse flexoelectric coefficients and their ratios to the flexo phase of $f_{ijkl}=1.0\times {10}^{-6}\mathrm{C}/\mathrm{m}$.

	${\overline{\mathit{f}}}_{\mathit{ijkl}}$$[\times {10}^{-6}\mathbf{C}/\mathbf{m}]$
	${\overline{\mathit{f}}}_{\mathbf{2222}}$	${\overline{\mathit{f}}}_{\mathbf{2211}}$	${\overline{\mathit{f}}}_{\mathbf{1212}}$
Coefficient	0.49	0.51	0.94
Relative percentage	49%	51%	94%

presents the homogenized converse coefficients of the longitudinal, transversal and shear couplings in a system including flexo phase comprising a volume fraction of 20%. The second row of the table includes the percentages of the equivalent coefficients relative to the flexo phase of $f_{ijkl}=1.0\times {10}^{-6}\mathrm{C}/\mathrm{m}$. The effective converse shear coefficient ${\overline{f}}_{1212}$ exhibits the largest value of 0.94 $\times {10}^{-6}\mathrm{C}/\mathrm{m}$, leading to a remarkable contribution to the shear strain. The components ${\overline{f}}_{2222}$ and ${\overline{f}}_{2211}$ are 0.49 $\times {10}^{-6}\mathrm{C}/\mathrm{m}$ and 0.51 $\times {10}^{-6}\mathrm{C}/\mathrm{m}$, respectively. Interestingly, ${\overline{f}}_{2222}$ and ${\overline{f}}_{2211}$ are proportional to in-plane actuation, while ${\overline{f}}_{1212}$ is proportional to out-of-plane actuation. When reinforcing an elastic matrix with only 20% by volume, the overall coefficients can be improved by up to 50% of the flexo material. This clearly demonstrates the significant impact of converse flexoelectricity on electromechanical coupling.

Additionally, the evolution of the components of the converse flexoelectric coefficients with respect to the volume fraction is studied and plotted in Figure 3. It also demonstrates the impact of material elasticity by considering different ratios of the elasticity modulus of the matrix relative to the inclusion, $\rho ={{\mathbb{C}}_{11}}_{elastic}/{{\mathbb{C}}_{11}}_{flexo}$. From the figure, it can be observed that the components ${\overline{f}}_{2222}$ and ${\overline{f}}_{2211}$, which couple the polarization gradient and strain in the axial and transverse directions, are characterized by an obvious increasing trend. The reason for these improvements is that the inclusion is considered with electromechanical properties while the matrix is purely elastic material. An upward shift of can be noticed as the ratio $\rho$ increases from 0.5 to 2.0 implying a stronger converse effect. The change in ${\overline{f}}_{1212}$, is almost marginal over the entire range resulting in a relatively modest improvement, particularly at microstructure filled with ⩾10% volume fractions.

4. Summary

Flexoelectricity is a complex electromechanical coupling phenomenon that is challenging to fully comprehend and precisely quantify. The system is characterized by fourth-order partial differential equations, requiring $C^1$ continuity. The energy conversion relies on higher-order coupling terms that relate the electric polarization and mechanical strain, along with their corresponding gradients. The mechanism can stand for direct or converse effects concerning to the induced energy terms. The impact of strain and electric field gradients is evident in two-phase materials, because the high gradients can contribute more to the total energy.

In this study, numerical homogenization was employed to evaluate the overall effective converse coefficients in composites. The continuum flexoelectric boundary value problem was formulated and solved numerically accounting for the electrical enthalpy. The constitutive relationships are defined as the work conjugates of strain, electric field, and their gradients. Isogeometric analysis with Non-Uniform Rational B-spline (NURBS) was considered in solving the governing equations and approximating the solution. Particular attention was given to a heterogeneous composite system formed by unidirectional continuous fibers aligned in an elastic matrix. The fibers are non-piezoelectric and are assumed to feature purely flexoelectric behavior with a fully bonded interface with the surrounding matrix, involving continuity in both displacement and electric potential. For this purpose, a standard continuum model was adopted employing a 2D representative volume element at microstructure. The geometry was meshed with 40 × 40 B-Spline elements. Each control point was defined with two types of DoFs, namely conventional displacement and electric potential. The study examined a pre-designed electrical loading as the RVE was subjected to fluctuated electric potential, resulting in non-homogeneous electric fields. Subsequently, the homogenized values were obtained by integrating over the volume.

The simulations revealed a significant contribution of the converse flexoelectricity to the electromechanical coupling. Apparent mechanical stresses were created in the inclusion and its surrounding matrix. The disparity between the compression and tension stresses increased with the amplitude of the applied electric potential. The components of the effective coefficients that couple a polarization gradient and strain in the longitudinal and transverse directions (${\overline{f}}_{2222}$ and ${\overline{f}}_{2211}$) demonstrated an approximately similar tendency for the addressed geometry. The equivalent coefficients of a composite with a 20% volume fraction reached up to 50% the flexo phase. These coefficients steadily increased with the increasing volume fraction, which fits with the rule of mixture. However, the change in the shear constant, ${\overline{f}}_{1212}$, was found to be marginal. Therefore, further study is essential to evaluate its performance. Additionally, the study examined the impact of material elasticity. A stronger effect was observed when using softer inclusion.