Comprehensive Evaluation of the Massively Parallel Direct Simulation Monte Carlo Kernel “Stochastic Parallel Rarefied-Gas Time-Accurate Analyzer” in Rarefied Hypersonic Flows—Part B: Hypersonic Vehicles
Abstract
1. Introduction
- Exo-atmospheric ballistic systems: These rockets operate at hypersonic speeds, partially traversing the Earth’s atmosphere. They follow predictable flight paths and are well-established in military engagements.
- Hyper-glide vehicles (HGVs) or wave-riders: These unpowered vehicles are launched to high altitudes (around 100 km) using rockets and subsequently glide at hypersonic speeds (exceeding Mach 8) for significant distances, leveraging the wave-riding effect. HGVs exhibit maneuverability during flight, rendering their trajectory unpredictable compared to exo-atmospheric ballistic systems. They are designed to operate at high altitudes where rarefied gas conditions prevail.
- Hypersonic cruise vehicles: This type of hypersonic vehicle is propelled by scramjet engines, specifically supersonic combustion ramjets (SCRJ). In scramjet engines, the airflow remains supersonic throughout the engine, devoid of any rotating parts, and combustion transpires under supersonic conditions. These vehicles achieve speeds of approximately Mach 5, with the scramjet engine operating at peak efficiency. They fly at lower altitudes, as their air-breathing engines necessitate high-density air for combustion.
2. Hypersonic Technology Projects—An Overview
3. Hypersonic Simulations with SPARTA Kernel
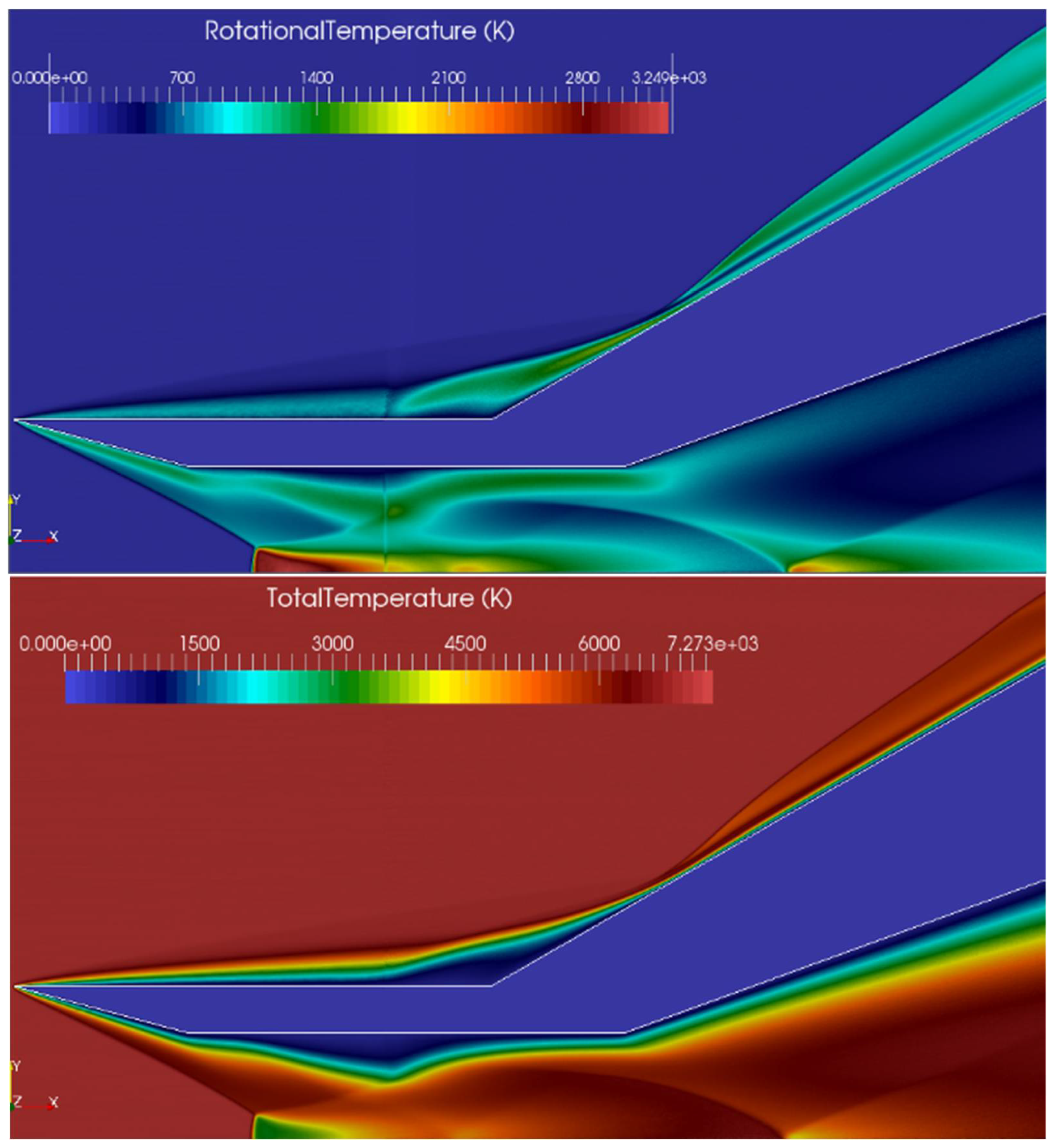
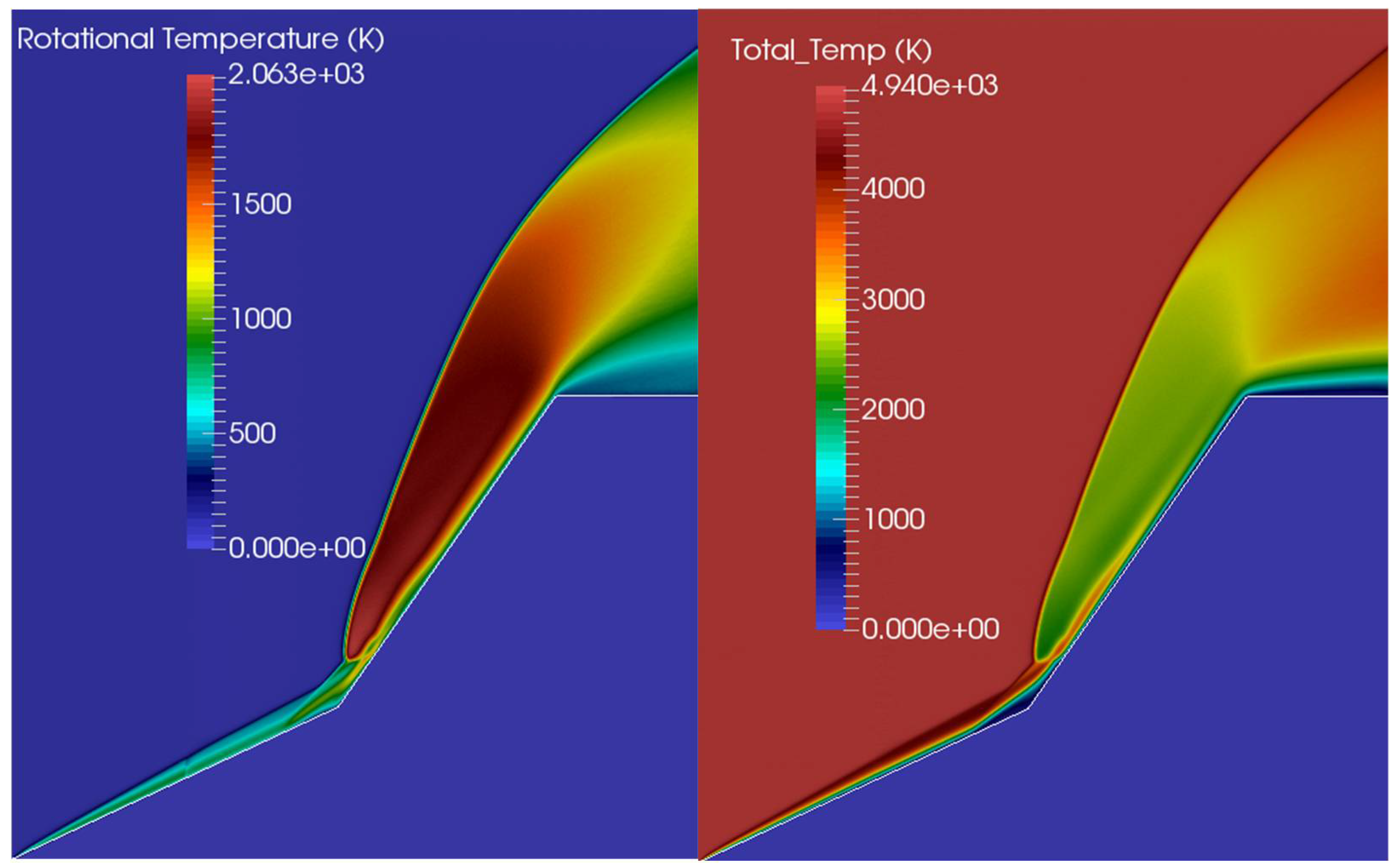
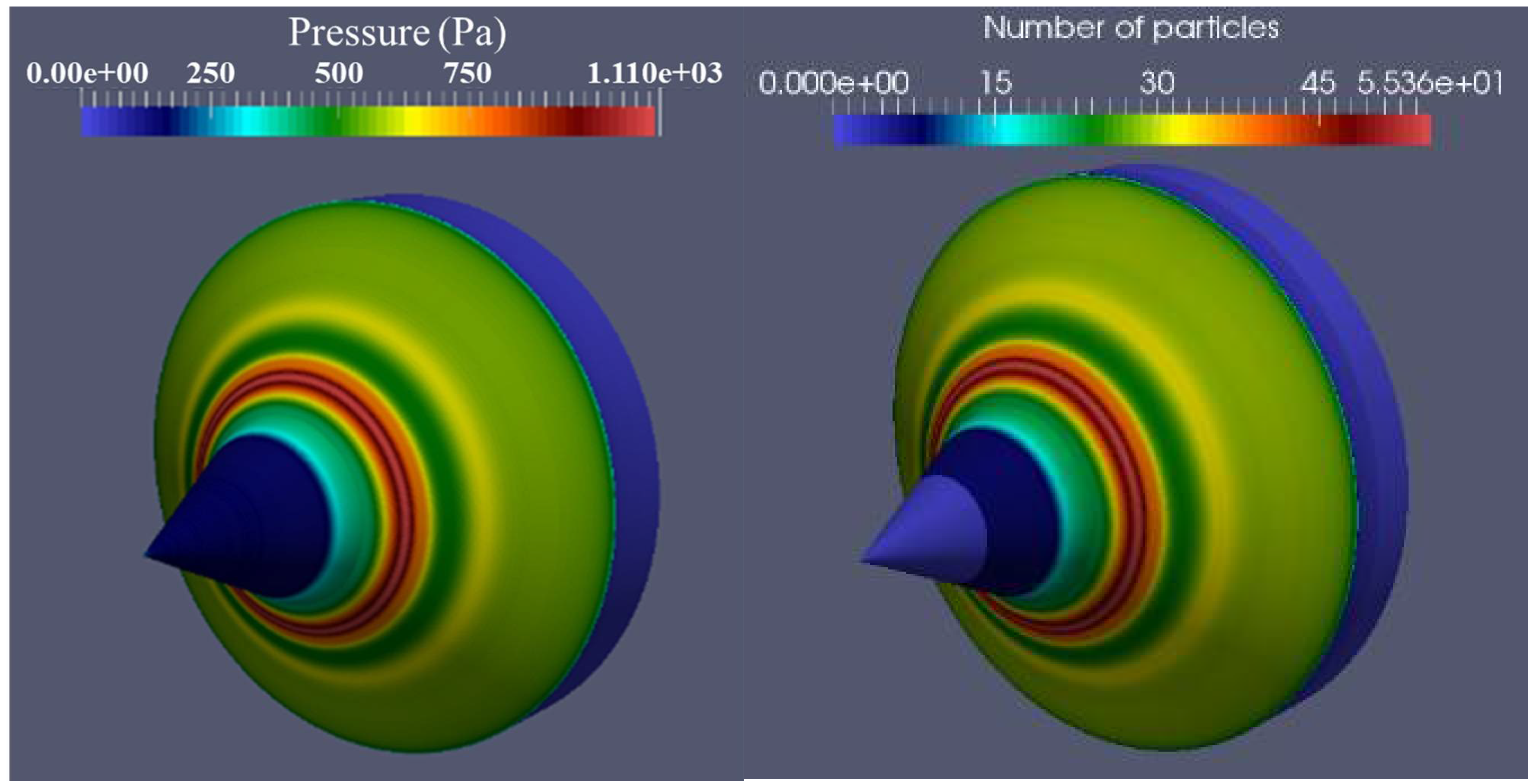
3.1. A Mach 12.4 Flow over a Flared Cylinder
3.2. A Mach 15.6 Flow over a 25/55-Degree Biconic
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Acton, J.M. Silver Bullet? Asking the Right Questions; Carnegie Endowment for International Peace: Washington, DC, USA, 2013. [Google Scholar]
- Speier, R.H.; Nacouzi, G.; Lee, C.A.; Moore, R.M. Hypersonic Missile Nonproliferation: Hindering the Spread of a New Class of Weapons; RAND Corporation: Santa Monica, CA, USA, 2017; Available online: https://www.rand.org/content/dam/rand/pubs/research_reports/RR2100/RR2137/RAND_RR2137.pdf (accessed on 30 July 2024).
- Besser, H.L.; Goege, D.; Huggins, A.; Shaffer, D.; Zimper, D. Hypersonic vehicles-game changers for future warfare. Transform. Jt. Air Power J. JAPCC 2017, 17, 11–27. [Google Scholar]
- Kh-47M2 Kinzhal. Missile Threat, 19 March 2022. Available online: https://missilethreat.csis.org/missile/kinzhal/ (accessed on 30 July 2024).
- Judd, D.J. Biden Confirms Russia’s Use of Hypersonic Missiles in Ukraine. CNN, 22 March 2022. Available online: https://edition.cnn.com/europe/live-news/ukraine-russia-putin-news-03-21-22/h_38fe9317803ffd4f7cafe92e6bb53c1c (accessed on 30 July 2024).
- Novichkov, N. Russia Announces Successful Flight Test of Avangard Hypersonic Glide Vehicle. Janes, 3 January 2019. Available online: https://www.janes.com/osint-insights/defence-news/russia-announces-successful-flight-test-of-avangard-hypersonic-glide-vehicle (accessed on 30 July 2024).
- Panda, A. Introducing the DF-17: China’s Newly Tested Ballistic Missile Armed with a Hypersonic Glide Vehicle. The Diplomat, 28 December 2017. Available online: https://thediplomat.com/2017/12/introducing-the-df-17-chinas-newly-tested-ballistic-missile-armed-with-a-hypersonic-glide-vehicle/ (accessed on 30 July 2024).
- Lockheed Martin. Lockheed Martin’s Hypersonic OpFires Missile Has Medium Range Covered. 2020. Available online: https://www.lockheedmartin.com/en-us/news/features/2020/lockheed-martins-hypersonic-opfires-missile-has-medium-range-covered.html (accessed on 30 July 2024).
- DARPA. Operational Fires Program Successfully Completes First Flight Test. 2022. Available online: https://www.darpa.mil/news-events/2022-07-13a#:~:text=The%20OpFires%20system%20achieved%20all,to%20initiate%20the%20test%20mission (accessed on 30 July 2024).
- U.S. Air Force. Propulsion Directorate Monthly Accomplishment Report; September 2005. Available online: http://www.pr.afrl.af.mil/mar/2005/sep2005.pdf (accessed on 1 October 2024).
- Flightglobal. August Failure of Boeing X-51 Likely Due to fin Resonance. 2016. Available online: https://web.archive.org/web/20161014135102/http://www.flightglobal.com/news/articles/august-failure-of-boeing-x-51-likely-due-to-fin-resonance-378080/ (accessed on 30 July 2024).
- Boeing. Boeing X-51A WaveRider Sets Record with Successful 4th Flight. 3 May 2013. Available online: https://boeing.mediaroom.com/2013-05-03-Boeing-X-51A-WaveRider-Sets-Record-with-Successful-4th-Flight (accessed on 30 July 2024).
- Kay, L. Boeing, Lockheed Win SCIFiRE Hypersonic Weapons Preliminary Design Contracts. Defence World. 2021. Available online: https://www.defenseworld.net/2021/09/02/boeing-lockheed-win-scifire-hypersonic-weapons-preliminary-design-contracts.html (accessed on 30 July 2024).
- Freedberg, S.J., Jr. Hypersonics: Army, Navy Test Common Glide Body. Defence Magazine, 20 March 2020. Available online: https://breakingdefense.com/2020/03/hypersonics-army-navy-test-common-glide-body/ (accessed on 30 July 2024).
- Army Technology. Advanced Hypersonic Weapon (AHW). 18 July 2022. Available online: https://www.army-technology.com/projects/advanced-hypersonic-weapon-ahw/ (accessed on 30 July 2024).
- DARPA. Third Test Flight for DARPA’s HAWC Yields New Performance Data. 18 July 2022. Available online: https://www.darpa.mil/news-events/2022-07-18 (accessed on 30 July 2024).
- Little, G. Mach 20 or Bust, Weapons Research May Yet Produce a true Spaceplane. Air & Space Magazine, 1 January 2013. Available online: https://www.smithsonianmag.com/air-space-magazine/mach-20-or-bust-20679807/ (accessed on 30 July 2024).
- Airforce Technology. SR-72 Hypersonic Demonstrator Aircraft. Airforce Technology, 30 January 2014. Available online: https://www.airforce-technology.com/projects/sr-72-hypersonic-demonstrator-aircraft/ (accessed on 30 July 2024).
- Air & Space Forces. AGM-183 ARRW. Air & Space Forces, 17 May 2022. Available online: https://www.airandspaceforces.com/weapons-platfoms/agm-183-arrw/ (accessed on 30 July 2024).
- Defencetalk. DARPA Hypersonic Vehicle Advances Technical Knowledge. Defence Talk, 11 August 2011. Available online: https://www.defencetalk.com/darpa-hypersonic-vehicle-advances-technical-knowledge-36347/ (accessed on 30 July 2024).
- Hindustan Times. India successfully tests nuclear-capable Shaurya missile. Hindustan Times, 3 October 2020. Available online: https://www.hindustantimes.com/india-news/india-successfully-tests-nuclear-capable-shaurya-missile/story-fkYlozVJ5oq1MWO26GOwNN.html (accessed on 30 July 2024).
- Fry, R.S. A Century of Ramjet Propulsion Technology Evolution. J. Propuls. Power 2004, 20, 27–58. [Google Scholar] [CrossRef] [PubMed]
- Amati, V.; Bruno, C.; Simone, D.; Schiubba, E. Exergy analysis of hypersonic propulsion systems: Performance comparison of two different scramjet configurations at cruise conditions. Energy 2008, 33, 116–129. [Google Scholar] [CrossRef]
- Bird, G.A. Molecular Gas Dynamics and the Direct Simulation of Gas Flows; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Bird, G.A. The DSMC Method; Version 1.2; CreateSpace Independent Publishing Platform: North Charleston, SC, USA, 2013; ISBN 9781492112907. [Google Scholar]
- Gallis, M.A.; Boyles, K.A.; LeBeau, G.J. DSMC simulations in support of the STS-107 accident investigation. AIP Conf. Proc. 2005, 762, 1211–1216. [Google Scholar]
- Gallis, M.A.; Torczynski, J.; Rader, D.; Bird, G. Convergence behavior of a new DSMC algorithm. J. Comput. Phys. 2009, 228, 4532–4548. [Google Scholar] [CrossRef]
- Gallis, M.A.; Torczynski, J.R.; Plimpton, S.J.; Rader, D.J.; Koehler, T. Direct Simulation Monte Carlo: The Quest for Speed. In Proceedings of the 29th Rarefied Gas Dynamic (RGD) Symposium, Xi’an, China, 13–18 July 2014. [Google Scholar]
- Moss, J.N.; Bird, G.A. Direct Simulation Monte Carlo Simulations of Hypersonic Flows with shock interactions. AIAA J. 2005, 43, 2565–2573. [Google Scholar] [CrossRef]
- Knight, D. RTO WG 10—Test cases for CFD validation of hypersonic flight. In Proceedings of the 40th AIAA Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. AIAA Paper 2002-0433 (RTO-TR-AVT-007-V3). [Google Scholar]
- Walker, S.; Schmisseur, J.D. CFD Validation of Shock-Shock Interaction Flow Fields; RTO-TR-AVT-007-V3; NATO Research and Technology Organisation: Brussels, Belgium, 2006. [Google Scholar]
- Candler, G.V.; Nompelis, I.; Druguet, M.-C.; Holden, M.S.; Wadhams, T.P.; Boyd, I.D.; Wang, W.-L. CFD Validation for Hypersonic Flight: Hypersonic Double-Cone Flow Simulations; RTO-TR-AVT-007-V3; NATO Research and Technology Organisation: Brussels, Belgium, 2006. [Google Scholar]
- Moss, J.N.; Bird, G.A.; Markelov, G.N. DSMC simulations of hypersonic flows and comparison with experiments. AIP Conf. Proc. 2005, 762, 547–552. [Google Scholar]
- Wang, W.-L.; Boyd, I.D. Hybrid DSMC-CFD simulations of hypersonic flow over sharp and blunted bodies. In Proceedings of the 36th AIAA Thermophysics Conference, Orlando, FL, USA, 23–26 June 2003. AIAA Paper AIAA 2003-3644. [Google Scholar]
- Gimelshein, S.F.; Levin, D.A.; Markelov, G.N.; Kudryavtsev, A.N.; Ivanov, M.S. Statistical Simulation of Laminar Separation in Hypersonic Flows: Numerical Challenges. In Proceedings of the 40th Aerospace Sciences Meeting & Exhibit, Reno, NV, USA, 14–17 January 2002. AIAA paper 2002-0736. [Google Scholar]
- Moss, J.N. Hypersonic Flows about a 25° Sharp Cone, NASA/TM-2001-211253; National Aeronautics and Space Administration: Washington, DC, USA, 2001.
- Ahmad, A.O. Capturing Shock Waves Using an Open-Source, Direct Simulation Monte Carlo (DSMC) Code. In Proceedings of the 4th European Conference for Aero-Space Sciences (EUCASS), St. Petersburg, Russia, 4–8 July 2011. [Google Scholar]
- Goshayeshi, B.; Roohi, E.; Stefanov, S. A novel simplified Bernoulli trials collision scheme in the direct simulation Monte Carlo with intelligence over particle distances. Phys. Fluids 2015, 27, 107104. [Google Scholar] [CrossRef]
- Tumuklu, O.; Theofilis, V.; Levin, D.A. On the unsteadiness of shock–laminar boundary layer interactions of hypersonic flows over a double cone. Phys. Fluids 2018, 30, 106111. [Google Scholar] [CrossRef]










| Project Name | Organization | Type | Mach | Expected Date of Service | Status |
|---|---|---|---|---|---|
| OPERATIONAL FIRES (OpFIRES) | DARPA | Hypersonic glide missile | 5 | - | Under development |
| BOEING X-51 WAVERIDER | DARPA | Unmanned research experimental aircraft | 5 | - | Under development |
| Southern Cross Intergrated Flight Research Experiment (SCIFIRE) | USA/Australia | Hypersonic cruise missile | 5 | Before 2030 | Under development |
| Long Range Hypersonic Weapon (LRHW) | US Army | ICBM | 5 | Before 2023 | Under development |
| Advanced Hypersonic Weapon (AHW) | DARPA | HGV | 5+ | Before 2025 | Under development |
| Hypersonic Air-Breathing Weapon Concept (HAWC) | USASMDC/ARSTRAT | Hypersonic cruise missile | 5+ | Before 2025 | Under development |
| Hypersonic Technology Vehicle HTV-3X | DARPA | HGV | 5–10 | - | Cancelled |
| SR-72 Blackbird | Lockheed Martin | Hypersonic reconnaissance UAV | 6 | Before 2030 | Under development |
| AGM-183 Rapid Response Weapon (ARRW) | Lockheed Martin | Hypersonic air-to-ground missile - glide vehicle | 5+ | Before 2025 | Under development |
| Hypersonic Technology Vehicle HTV-2 | DARPA | HGV | 20+ | - | Cancelled |
| Run | Gas | |||||||
|---|---|---|---|---|---|---|---|---|
| 48-inch Run 7 | N2 | |||||||
| LENS Run 11 | N2 |
| Fnum | |||||
|---|---|---|---|---|---|
| Flow Condition | Gas | Number Density (m−3) | Flow Temperature (K) | Surface Temperature (K) | |
|---|---|---|---|---|---|
| CUBRC Run 7 | 2072.6 | 42.61 | 297.2 |
| Flow Condition | Gas | Transient Period (Timesteps) | Sampling Period (Timesteps) | Interval Sample Data | |
|---|---|---|---|---|---|
| CUBRC Run 7 | 250,000 | 27,000 | 2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klothakis, A.; Nikolos, I.K. Comprehensive Evaluation of the Massively Parallel Direct Simulation Monte Carlo Kernel “Stochastic Parallel Rarefied-Gas Time-Accurate Analyzer” in Rarefied Hypersonic Flows—Part B: Hypersonic Vehicles. Computation 2024, 12, 200. https://doi.org/10.3390/computation12100200
Klothakis A, Nikolos IK. Comprehensive Evaluation of the Massively Parallel Direct Simulation Monte Carlo Kernel “Stochastic Parallel Rarefied-Gas Time-Accurate Analyzer” in Rarefied Hypersonic Flows—Part B: Hypersonic Vehicles. Computation. 2024; 12(10):200. https://doi.org/10.3390/computation12100200
Chicago/Turabian StyleKlothakis, Angelos, and Ioannis K. Nikolos. 2024. "Comprehensive Evaluation of the Massively Parallel Direct Simulation Monte Carlo Kernel “Stochastic Parallel Rarefied-Gas Time-Accurate Analyzer” in Rarefied Hypersonic Flows—Part B: Hypersonic Vehicles" Computation 12, no. 10: 200. https://doi.org/10.3390/computation12100200
APA StyleKlothakis, A., & Nikolos, I. K. (2024). Comprehensive Evaluation of the Massively Parallel Direct Simulation Monte Carlo Kernel “Stochastic Parallel Rarefied-Gas Time-Accurate Analyzer” in Rarefied Hypersonic Flows—Part B: Hypersonic Vehicles. Computation, 12(10), 200. https://doi.org/10.3390/computation12100200






