A Lightweight Model Enhancing Facial Expression Recognition with Spatial Bias and Cosine-Harmony Loss
Abstract
1. Introduction
- This paper introduces a lightweight and efficient Lightweight Facial Network with Spatial Bias(LFNSB) model that utilizes a deep convolutional neural network to capture both detailed and global features of facial images while maintaining high computational efficiency.
- This paper introduces a new loss function called Cosine-Harmony Loss. It utilizes adjusted cosine distance to optimize the computation of class centers, balancing intra-class compactness and inter-class separation.
- Experimental results show that the proposed LFNSB method achieves an accuracy of 63.12% on AffectNet-8, 66.57% on AffectNet-7, and 91.07% on RAF-DB.
2. Methods
2.1. Related Work
2.1.1. FER
2.1.2. Attention Mechanism
2.1.3. Loss Function
2.2. Method
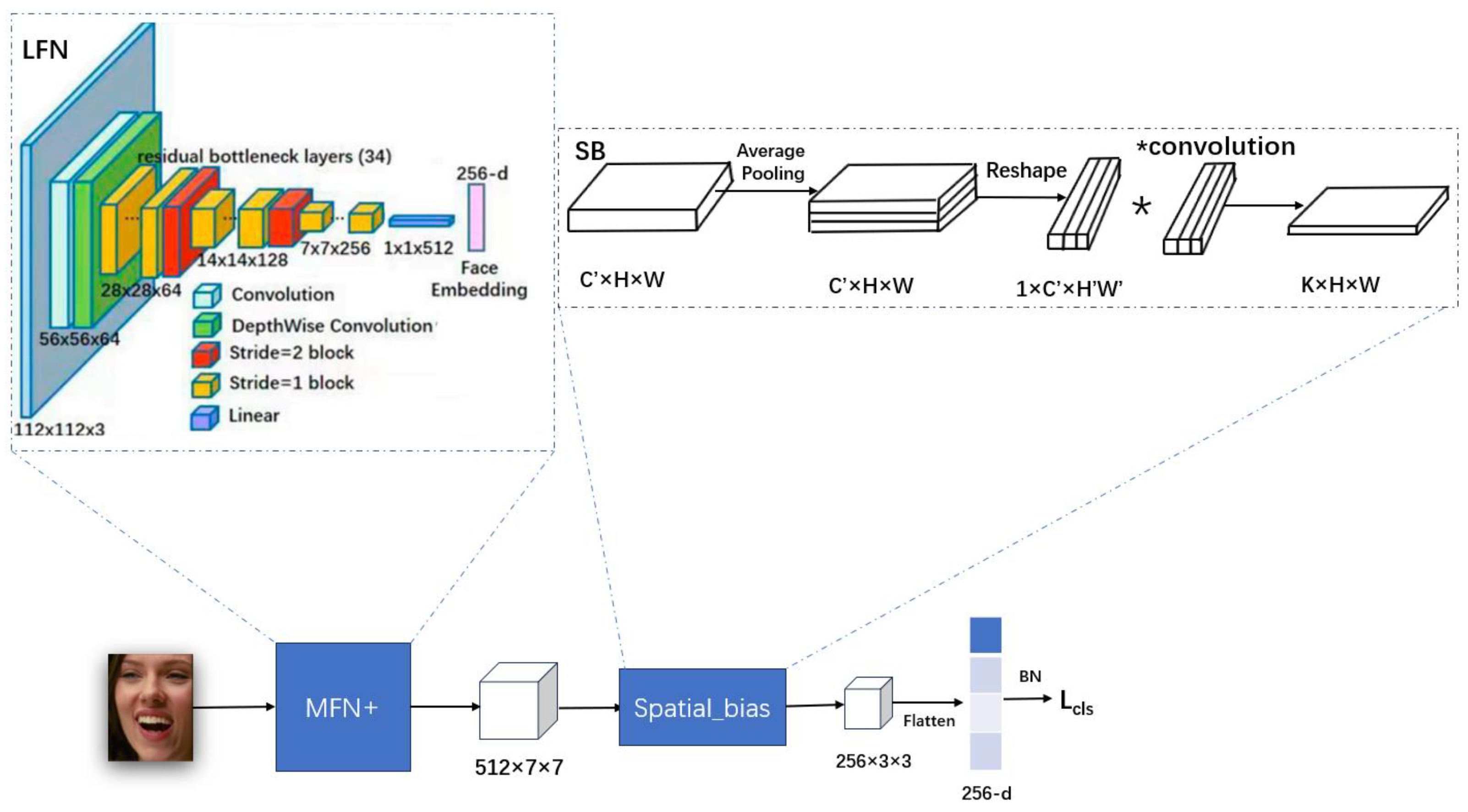
2.2.1. LFN
Improved Face Expression Recognition Network LFN Based on MFN
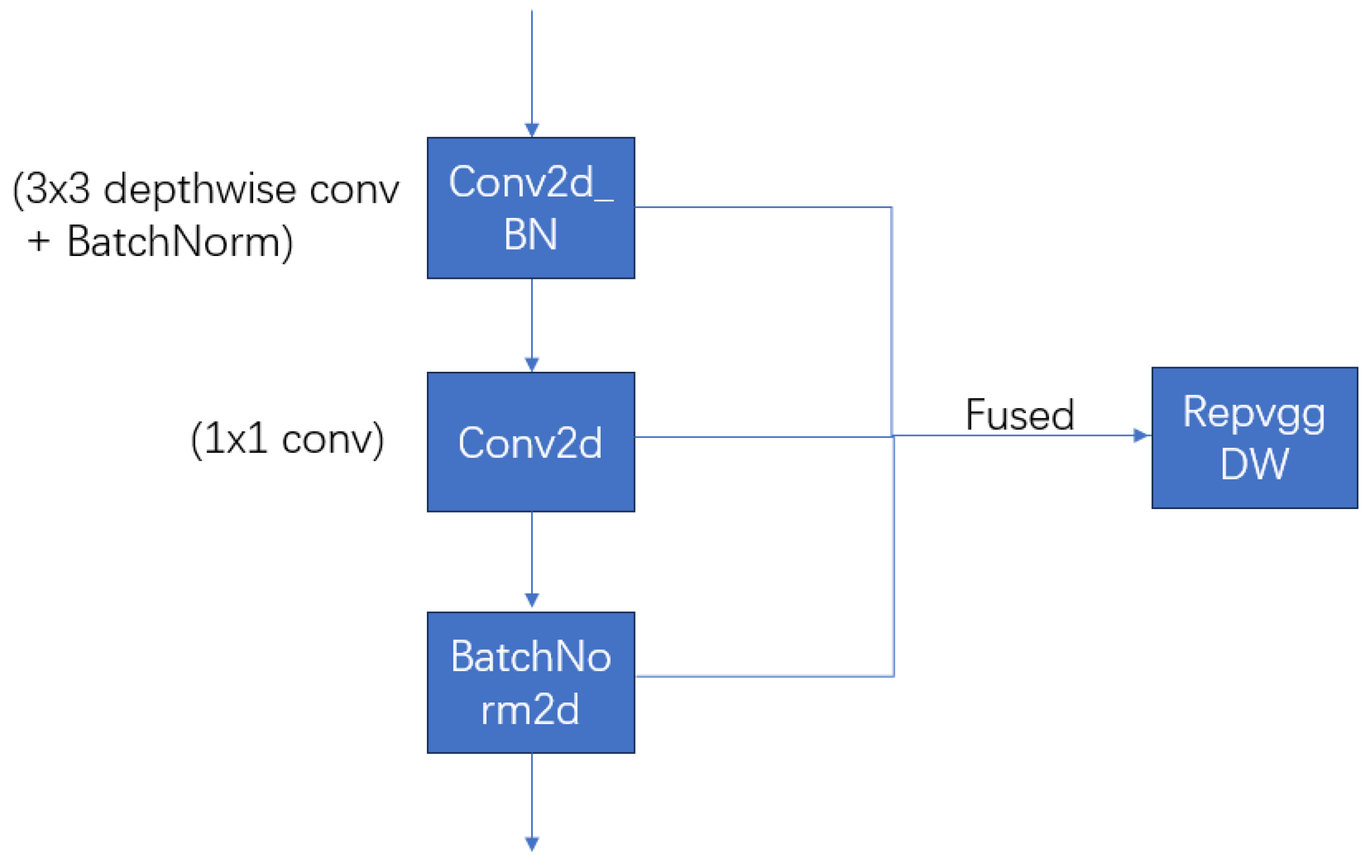
Conv2d_BN
RepVGGDW
2.2.2. Spatial Bias
- Input Feature Map Compression: The input feature map is first compressed through a 1 × 1 convolution, resulting in a feature map with fewer channels. Then, an adaptive average pooling layer is used to spatially compress the feature map, producing a smaller feature map.
- Feature Map Flattening: The feature map for each channel is flattened into a one-dimensional vector, resulting in a transformed feature map.
- Global Knowledge Aggregation: A 1D convolution is applied to the flattened feature map to encode global knowledge, capturing global dependencies and generating the spatial bias map.
- Upsampling and Concatenation: The spatial bias map is upsampled to the same size as the original convolutional feature map using bilinear interpolation, and then concatenated with the convolutional feature map along the channel dimension.
2.2.3. Cosine-Harmony Loss
3. Results
3.1. Datasets
3.2. Implementation Details
3.3. Ablation Studies
3.3.1. Effectiveness of the LFN
3.3.2. Effectiveness of the Cosine-Harmony Loss
3.3.3. Effectiveness of the LFNSB
3.4. Quantitative Performance Comparisons
3.5. K-Fold Cross-Validation
3.6. Confusion Matrix
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Application of the LFNSB Model in a Real-Time Music Recommendation System

References
- Banerjee, R.; De, S.; Dey, S. A survey on various deep learning algorithms for an efficient facial expression recognition system. Int. J. Image Graph. 2023, 23, 2240005. [Google Scholar] [CrossRef]
- Sajjad, M.; Ullah, F.U.M.; Ullah, M.; Christodoulou, G.; Cheikh, F.A.; Hijji, M.; Muhammad, K.; Rodrigues, J.J. A comprehensive survey on deep facial expression recognition: Challenges, applications, and future guidelines. Alex. Eng. J. 2023, 68, 817–840. [Google Scholar] [CrossRef]
- Adyapady, R.R.; Annappa, B. A comprehensive review of facial expression recognition techniques. Multimed. Syst. 2023, 29, 73–103. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, Y.; Zhang, Y.; Wang, Y.; Song, Z. A dual-direction attention mixed feature network for facial expression recognition. Electronics 2023, 12, 3595. [Google Scholar] [CrossRef]
- Tan, M.; Le, Q.V. Mixconv: Mixed depthwise convolutional kernels. In Proceedings of the 30th British Machine Vision Conference 2019, Cardiff, UK, 9–12 September 2019. [Google Scholar]
- Go, J.; Ryu, J. Spatial bias for attention-free non-local neural networks. Expert Syst. Appl. 2024, 238, 122053. [Google Scholar] [CrossRef]
- Li, S.; Deng, W. Deep Facial Expression Recognition: A Survey. IEEE Trans. Affect. Comput. 2020, 13, 1195–1215. [Google Scholar] [CrossRef]
- Deng, J.; Guo, J.; Xue, N.; Zafeiriou, S. Arcface: Additive angular margin loss for deep face recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2019, Long Beach, CA, USA, 16–17 June 2019; pp. 4690–4699. [Google Scholar]
- Wang, H.; Wang, Y.; Zhou, Z.; Ji, X.; Gong, D.; Zhou, J.; Li, Z.; Liu, W. Cosface: Large margin cosine loss for deep face recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 5265–5274. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. In Proceedings of the International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015; pp. 1–14. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Altaher, A.; Salekshahrezaee, Z.; Abdollah Zadeh, A.; Rafieipour, H.; Altaher, A. Using multi-inception CNN for face emotion recognition. J. Bioeng. Res. 2020, 3, 1–12. [Google Scholar]
- Xue, F.; Wang, Q.; Tan, Z.; Ma, Z.; Guo, G. Vision transformer with attentive pooling for robust facial expression recognition. IEEE Trans. Affect. Comput. 2022, 14, 3244–3256. [Google Scholar] [CrossRef]
- Wang, A.; Chen, H.; Lin, Z.; Han, J.; Ding, G. Repvit: Revisiting mobile cnn from vit perspective. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2024, Seattle, WA, USA, 16–22 June 2024; pp. 15909–15920. [Google Scholar]
- Sandler, M.; Howard, A.; Zhu, M.; Zhmoginov, A.; Chen, L.C. Mobilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 4510–4520. [Google Scholar]
- Zhang, X.; Zhou, X.; Lin, M.; Sun, J. Shufflenet: An extremely efficient convolutional neural network for mobile devices. In Proceedings of the IEEE conference on computer vision and pattern recognition 2018, Salt Lake City, UT, USA, 18–22 June 2018; pp. 6848–6856. [Google Scholar]
- Chen, S.; Liu, Y.; Gao, X.; Han, Z. Mobilefacenets: Efficient cnns for accurate real-time face verification on mobile devices. In Biometric Recognition: 13th Chinese Conference, CCBR 2018, Urumqi, China, August 11–12, 2018, Proceedings 13; Springer International Publishing: Berlin/Heidelberg, Germany, 2018; pp. 428–438. [Google Scholar]
- Hou, Q.; Zhou, D.; Feng, J. Coordinate Attention for Efficient Mobile Network Design. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 13713–13722. [Google Scholar]
- You, Q.; Jin, H.; Luo, J. Visual sentiment analysis by attending on local image regions. In Proceedings of the AAAI Conference on Artificial Intelligence 2017, San Francisco, CA, USA, 4–9 February 2017; pp. 231–237. [Google Scholar]
- Zhao, S.; Jia, Z.; Chen, H.; Li, L.; Ding, G.; Keutzer, K. PDANet: Polarity-consistent deep attention network for fine-grained visual emotion regression. In Proceedings of the 27th ACM International Conference on Multimedia, Nice, France, 21–25 October 2019; pp. 192–201. [Google Scholar]
- Farzaneh, A.H.; Qi, X. Facial expression recognition in the wild via deep attentive center loss. In Proceedings of the IEEE/CVF Winter Conference on Applications of Computer Vision 2021, Virtual, 5–9 January 2021; pp. 2402–2411. [Google Scholar]
- Li, Y.; Lu, Y.; Li, J.; Lu, G. Separate loss for basic and compound facial expression recognition in the wild. In Proceedings of the Asian Conference on Machine Learning 2019, Nagoya, Japan, 17–19 November 2019; pp. 897–911. [Google Scholar]
- Wen, Y.; Zhang, K.; Li, Z.; Qiao, Y. A discriminative feature learning approach for deep face recognition. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; Springer: Berlin/Heidelberg, Germany, 2016; pp. 499–515. [Google Scholar]
- Wen, Z.; Lin, W.; Wang, T.; Xu, G. Distract your attention: Multi-head cross attention network for facial expression recognition. Biomimetics 2023, 8, 199. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.V.; Bai, L. Cosine similarity metric learning for face verification. In Proceedings of the Asian Conference on Computer Vision 2010, Queenstown, New Zealand, 8–12 November 2010; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Liu, W.; Wen, Y.; Yu, Z.; Li, M.; Raj, B.; Song, L. Sphereface: Deep hypersphere embedding for face recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition 2017, Honolulu, HI, USA, 21–26 July 2017; pp. 212–220. [Google Scholar]
- Liu, Y.; Li, H.; Wang, X. Learning deep features via congenerous cosine loss for person recognition. arXiv 2017, arXiv:1702.06890. [Google Scholar]
- Dhall, A.; Goecke, R.; Lucey, S.; Gedeon, T. Collecting large, richly annotated facial expression databases from movies. IEEE Multimed. 2012, 19, 34–41. [Google Scholar] [CrossRef]
- Li, S.; Deng, W. Reliable crowdsourcing and deep locality-preserving learning for unconstrained facial expression recognition. IEEE Trans. Image Process. 2018, 28, 356–370. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Zhang, L.; Hu, Y.; He, X.; Gao, J. Ms-celeb-1m: A dataset and benchmark for large-scale face recognition. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 11–14 October 2016; pp. 87–102. [Google Scholar]
- Wang, K.; Peng, X.; Yang, J.; Meng, D.; Qiao, Y. Region attention networks for pose and occlusion robust facial expression recognition. IEEE Trans. Image Process. 2020, 29, 4057–4069. [Google Scholar] [CrossRef] [PubMed]
- Wang, K.; Peng, X.; Yang, J.; Lu, S.; Qiao, Y. Suppressing uncertainties for large-scale facial expression recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2020, Seattle, WA, USA, 13–19 June 2020; pp. 6897–6906. [Google Scholar]
- Vo, T.-H.; Lee, G.-S.; Yang, H.-J.; Kim, S.-H. Pyramid with super resolution for in-the-wild facial expression recognition. IEEE Access 2020, 8, 131988–132001. [Google Scholar] [CrossRef]
- Savchenko, A.V.; Savchenko, L.V.; Makarov, I. Classifying emotions and engagement in online learning based on a single facial expression recognition neural network. IEEE Trans. Affect. Comput. 2022, 13, 2132–2143. [Google Scholar] [CrossRef]
- Wagner, N.; Mätzler, F.; Vossberg, S.R.; Schneider, H.; Pavlitska, S.; Zöllner, J.M. CAGE: Circumplex Affect Guided Expression Inference. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition 2024, Seattle, WA, USA, 16–22 June 2024; pp. 4683–4692. [Google Scholar]
- Li, H.; Sui, M.; Zhao, F.; Zha, Z.; Wu, F. Mvt: Mask vision transformer for facial expression recognition in the wild. arXiv 2021, arXiv:2106.04520. [Google Scholar]
- Zhao, Z.; Liu, Q.; Wang, S. Learning deep global multi-scale and local attention features for facial expression recognition in the wild. IEEE Trans. Image Process. 2021, 30, 6544–6556. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Wang, J.; Chen, S.; Shi, Z.; Cai, J. Facial motion prior networks for facial expression recognition. In Proceedings of the 2019 IEEE Visual Communications and Image Processing (VCIP), Suzhou, China, 13–16 December 2019; pp. 1–4. [Google Scholar]
- Farzaneh, X.Q.; Hossein, A. Discriminant distribution-agnostic loss for facial expression recognition in the wild. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops 2020, Seattle, WA, USA, 14–19 June 2020; pp. 406–407. [Google Scholar]
- Zhang, W.; Ji, X.; Chen, K.; Ding, Y.; Fan, C. Learning a Facial Expression Embedding Disentangled from Identity. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 19–25 June 2021; pp. 6755–6764. [Google Scholar]
- Shaila, S.G.; Gurudas, V.R.; Rakshita, R.; Shangloo, A. Music therapy for mood transformation based on deep learning framework. In Computer Vision and Robotics: Proceedings of CVR 2021; Springer: Singapore, 2022; pp. 35–47. [Google Scholar]
- Shaila, S.G.; Rajesh, T.M.; Lavanya, S.; Abhishek, K.G.; Suma, V. Music therapy for transforming human negative emotions: Deep learning approach. In Proceedings of the International Conference on Recent Trends in Computing: ICRTC 2021, Delhi, India, 4–5 June 2021; Springer: Singapore, 2022; pp. 99–109. [Google Scholar]





| Input | Operator | t | c | n | s |
|---|---|---|---|---|---|
| 112 × 112 ×3 | Conv2d_BN | - | 64 | 1 | 2 |
| 56 × 56 × 64 | depthwiseConv2d_BN | - | 64 | 1 | 1 |
| 56 × 56 × 64 | bottleneck (MixConv 3 × 3, 5 × 5) | 2 | 64 | 1 | 2 |
| 28 × 28 × 64 | bottleneck (MixConv 3 × 3) | 2 | 128 | 9 | 1 |
| 28 × 28 × 128 | bottleneck (MixConv 3 × 3, 5 × 5) | 4 | 128 | 1 | 2 |
| 14 × 14 × 128 | bottleneck (MixConv 3 × 3) | 2 | 128 | 16 | 1 |
| 14 × 14 × 128 | bottleneck (MixConv 3 × 3, 5 × 5, 7 × 7) | 8 | 256 | 1 | 2 |
| 7 × 7 × 256 | bottleneck (MixConv 3 × 3, 5 × 5) | 2 | 256 | 6 | 1 |
| 7 × 7 × 256 | RepvggDW | - | 256 | 1 | 1 |
| 7 × 7 × 256 | linear GDConv 7 × 7 | - | 256 | 1 | 1 |
| 1 × 1 × 256 | Linear | - | 256 | 1 | 1 |
| Methods | Accuracy (%) | Params | Flops |
|---|---|---|---|
| MobileFaceNet | 87.52 | 1.148 M | 230.34 M |
| MFN | 90.32 | 3.973 M | 550.74 M |
| LFN (ours) | 90.22 | 2.749 M | 401.48 M |
| Methods | RAF-DB | AffectNet-7 |
|---|---|---|
| CrossEntropyLoss | 89.57 | 64.26 |
| CrossEntropyLoss + Cosine-Harmony Loss | 90.22 | 65.45 |
| Accuracy | Loss | |
|---|---|---|
| 0.1 | 90.22% | 0.066 |
| 0.2 | 90.12% | 0.083 |
| 0.3 | 89.96% | 0.137 |
| 0.4 | 90.03% | 0.096 |
| 0.5 | 89.86% | 0.161 |
| Model | RAF-DB | AffectNet-7 |
|---|---|---|
| LFN | 90.22 | 65.45 |
| LFNSB | 91.07 | 66.57 |
| Methods | Accuracy (%) |
|---|---|
| Separate-Loss [22] | 86.38 |
| RAN [31] | 86.90 |
| SCN [32] | 87.03 |
| DACL [21] | 87.78 |
| APViT [13] | 91.98 |
| DDAMFN [4] | 91.34 |
| DAN [24] | 89.70 |
| LFNSB (ours) | 91.07 |
| Methods | Accuracy (%) |
|---|---|
| PSR [33] | 60.68 |
| Multi-task EfficientNet-B0 [34] | 61.32 |
| DAN [24] | 62.09 |
| CAGE [35] | 62.3 |
| MViT [36] | 61.40 |
| MA-Net [37] | 60.29 |
| DDAMFN [4] | 64.25 |
| LFNSB (ours) | 63.12 |
| Methods | Accuracy (%) |
|---|---|
| Separate-Loss [22] | 58.89 |
| FMPN [38] | 61.25 |
| DDA-Loss [39] | 62.34 |
| DLN [40] | 63.7 |
| CAGE [35] | 67.62 |
| DAN [24] | 65.69 |
| DDAMFN [4] | 67.03 |
| LFNSB (ours) | 66.57 |
| Fold | Fold 1 | Fold 2 | Fold 3 | Fold 4 | Fold 5 | Fold 6 | Fold 7 | Fold 8 | Fold 9 | Fold 10 | Average |
|---|---|---|---|---|---|---|---|---|---|---|---|
| RAF-DB | 90.48 | 90.22 | 90.61 | 90.35 | 90.48 | 90.12 | 91.07 | 90.65 | 90.32 | 90.16 | 90.34 |
| Afectnet-7 | 65.71 | 66.57 | 66.11 | 64.69 | 65.65 | 65.45 | 65.61 | 65.25 | 65.12 | 66.03 | 65.72 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Huang, L. A Lightweight Model Enhancing Facial Expression Recognition with Spatial Bias and Cosine-Harmony Loss. Computation 2024, 12, 201. https://doi.org/10.3390/computation12100201
Chen X, Huang L. A Lightweight Model Enhancing Facial Expression Recognition with Spatial Bias and Cosine-Harmony Loss. Computation. 2024; 12(10):201. https://doi.org/10.3390/computation12100201
Chicago/Turabian StyleChen, Xuefeng, and Liangyu Huang. 2024. "A Lightweight Model Enhancing Facial Expression Recognition with Spatial Bias and Cosine-Harmony Loss" Computation 12, no. 10: 201. https://doi.org/10.3390/computation12100201
APA StyleChen, X., & Huang, L. (2024). A Lightweight Model Enhancing Facial Expression Recognition with Spatial Bias and Cosine-Harmony Loss. Computation, 12(10), 201. https://doi.org/10.3390/computation12100201






