A New Investigation on Dynamics of the Fractional Lengyel-Epstein Model: Finite Time Stability and Finite Time Synchronization

Abstract

In this paper, we present an investigation into the stability of equilibrium points and synchronization within a finite time frame for fractional-order Lengyel–Epstein reaction-diffusion systems. Initially, we utilize Lyapunov theory and multiple criteria to examine the finite-time stability of equilibrium points. Following this analysis, we design efficient, interdependent linear controllers. By applying a Lyapunov function, we define new adequate conditions to ensure finite-time synchronization within a specified time interval. Finally, we provide two illustrative examples to demonstrate the effectiveness and practicality of our proposed method and validate the theoretical outcomes.

1. Introduction

The chlorite-iodide-malonic acid (CIMA) chemical reaction serves as a pivotal model for the fractional variant of the Lengyel-Epstein reaction-diffusion system, capturing the attention of numerous neuroscientists [1,2,3,4]. This interest stems from its historical significance as one of the earliest experimental validations of Alan Turing’s 1952 theoretical propositions, particularly regarding the chemical mechanisms underlying morphogenesis and pattern formation [5]. The CIMA reaction encompasses three chemical reaction schemes:

$$\begin{array}{c}\hfill MA+I_2\to IMA+I^{-}+H^{+},\end{array}$$

(1)

$$\begin{array}{c}\hfill Cl{O}_2+I^{-}\to Cl{O}_2^{-}+{\displaystyle \frac{1}{2}}{I}_2,\end{array}$$

(2)

$$\begin{array}{c}\hfill Cl{O}_2^{-}+4I^{-}+4H^{+}\to C{l}^{-}+2I_2+2H_{2}O.\end{array}$$

(3)

The simplified representation of this reaction into the traditional Lengyel-Epstein model incorporates the empirical rate laws while neglecting constant factors. This model features two dependent variables, ${\mathcal{E}}_1$ and ${\mathcal{E}}_2$, which represent the temporal variations in the concentrations of $\left[I^{-}\right]$ and $\left[Cl{O}_2^{-}\right]$, respectively. Various studies have examined the overall behavior of the Lengyel-Epstein system, detailing sufficient criteria for both its local and global asymptotic stability [6,7,8,9]. Furthermore, ref. [10] provides sufficient criteria for either Turing or diffusion-driven instability of the system.

Finite-time stability in a dynamical system implies that trajectories converge to an equilibrium point within a finite time span, maintaining proximity to this equilibrium throughout. In contrast, finite-time synchronization involves achieving coordination among the states of multiple dynamical systems within a finite duration, aligning their states irrespective of initial conditions. This concept is critical in applications requiring rapid coordination within specific time constraints [11,12,13,14,15,16,17,18].

This research introduces a novel approach to exploring finite-time stability and synchronization within a subset of fractional-order spatiotemporal partial differential systems. The primary goal is to investigate both finite-time stability and finite-time synchronization in interconnected fractional reaction-diffusion systems. Utilizing a fractional Lyapunov method, we propose a linear control technique to achieve finite-time synchronization for general fractional reaction-diffusion systems. The effectiveness and practicality of these control methods are demonstrated through the synchronization behaviors of interconnected fractional-order Lengyel-Epstein systems.

The paper is structured as follows: Section 2 establishes the foundational concepts necessary for understanding the fractional-order nonlinear system described by the Caputo fractional-order derivative. Section 3 describes the model for the Lengyel-Epstein reaction-diffusion system, which simulates the chlorite-iodide-malonic acid (CIMA) reaction in an open, unstirred gel reactor. The model is presented with equations that define the dynamics of the activator and inhibitor concentrations over time and space. Section 4 focuses on establishing the prerequisites for ensuring the finite-time stability of the equilibrium point in a fractional-order nonlinear system. Section 5 examines finite-time synchronization in reaction-diffusion systems, particularly focusing on the Lengyel-Epstein subsystem. The aim is to achieve rapid synchronization of spatially distributed components within a specified time frame, ensuring efficient coherence across the system’s spatial elements. Section 6 presents two practical scenarios to validate the proposed approach and verify the theoretical findings.

2. Preliminaries

Consider the following fractional-order nonlinear system described by the Caputo fractional-order derivative:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}_0{}^{C}D_t^{\aleph }z\left(t\right)=\Psi (t,z\left(t\right)),t>0,\hfill \\ z\left(0\right)=z_0,\hfill \end{array}\right.\end{array}$$

(4)

where $z\in {\mathbb{R}}^n$ and $z\left(t\right)\in C^1[0,+\infty )$. The order $\aleph \in (0,1)$ and $\Psi (t,z\left(t\right)):[0,+\infty )\times \Omega \to {\mathbb{R}}^n$. The origin $z=0$ is within the domain $\Omega \subset {\mathbb{R}}^n$, and $\Psi (t,z(t\left)\right)$ is piecewise continuous in t on $[0,+\infty )$ [19].

Definition 1 

([20]). The Riemann–Liouville fractional-order integral operator of an arbitrary integrable function $\mathcal{E}$ is defined as:

$$\begin{array}{c}\hfill I_t^{\aleph }\mathcal{E}\left(t\right)={\displaystyle \frac{1}{\Gamma \left(\aleph \right)}}{\int }_0^t{\left(t-\varsigma \right)}^{\aleph -1}\mathcal{E}\left(\varsigma \right)d\varsigma ,\end{array}$$

(5)

where $t\ge 0$, $0<\aleph <1$, and $\Gamma \left(.\right)$ is the gamma function.

Definition 2 

([21]). The Caputo fractional derivative of order $\aleph >0$ is defined as

$$\begin{array}{c}\hfill {}_0{}^{C}D_t^{\aleph }\mathcal{E}\left(t\right)=\left\{\begin{array}{cc}{\displaystyle \frac{1}{\Gamma \left(m-\aleph \right)}}{\int }_0^t{\left(t-\varsigma \right)}^{m-\aleph -1}{\mathcal{E}}^{\left(m\right)}\left(\varsigma \right)d\varsigma ,\hfill & m-1<\aleph <m,\hfill \\ {}_{0}D_t^m\mathcal{E}\left(t\right),\hfill & \aleph =m,\hfill \end{array}\right.\end{array}$$

(6)

where m is the smallest integer greater than ℵ and $t>0$.

Definition 3 

([22]). The Mittag-Leffler function with $\aleph >0$, denoted by ${\mathsf{E}}_{\aleph }$, is defined as:

$$\begin{array}{c}\hfill {\mathsf{E}}_{\aleph }\left(t\right)=\sum _{\mathsf{j}=0}^{+\infty }{\displaystyle \frac{t^{\mathsf{j}}}{\Gamma \left(\aleph \mathsf{j}+1\right)}}.\end{array}$$

(7)

Lemma 1 

([12,19]). For all $z\in {\mathbb{R}}^n$ and $\aleph \in (0,1)$, the following inequality holds:

$$\begin{array}{c}\hfill {}_0{}^{C}D_t^{\aleph }\left(z^{\mathsf{T}}\left(t\right)z\left(t\right)\right)\le 2z^{\mathsf{T}}\left(t\right){}_0{}^{C}D_t^{\aleph }z\left(t\right),t\ge 0.\end{array}$$

(8)

Definition 4 

([23]). Suppose $D\subseteq \Omega$ is an open neighborhood of $0,$ if there is a function $t^{*}:D\backslash \left\{0\right\}\to {\mathbb{R}}_{+}^{*}$ called the setting-time satisfying (1) and (2), then, $z^{*}$ is called a finite-time stable equilibrium point of the system (4).

1. 

$\forall z_0\in D\backslash \left\{0\right\},z\left(t\right)=z\left(t,z_0\right)\in D\backslash \left\{0\right\},\forall t\in \left[0,t^{*}\left(z_0\right)\right),{lim}_{t\to t^{*}\left(z_0\right)}z\left(t\right)=0,$ and $z\left(t\right)\equiv 0$ for $t\in \left[t^{*}\left(z_0\right),+\infty \right).$

2. 

For every open neighborhood $U_{ϵ}$ of 0, there is an open subset $U_{\delta }$ containing 0 in $D,$ satisfying for $\forall z_0\in U_{\delta }\backslash \left\{0\right\}$ and $\forall t\in \left[0,t^{*}\left(z_0\right)\right),z\left(t\right)=z\left(t,z_0\right)\in U_{ϵ}.$

Theorem 1 

([23]). $z^{*}$ is an finite-time stability equilibrium point of the fractional-order nonlinear systems (4) if there exists a differentiable Lyapunov function $\mathcal{L}:\left[0,+\infty \right)\times \Omega \to {\mathbb{R}}_{+},$ three class $\mathcal{M}$ functions ${\beta }_1,{\beta }_2,{\beta }_3,$ and a $\delta >0$ such that

1. 

${\beta }_1∥z\left(t\right)∥\le \mathcal{L}\left(t,z\left(t\right)\right)\le {\beta }_2∥z\left(t\right)∥,$

2. 

${}_{0}D_t\mathcal{L}\left(t,z\left(t\right)\right)<-{\beta }_3\mathcal{L}\left(t,z\left(t\right)\right),$

3. 

${\int }_0^{ϵ}{\displaystyle \frac{1}{{\beta }_3\left(z\right)}}dz<+\infty ,(\forall ϵ:0<ϵ\le \delta )$.

3. Problem Description

The Lengyel-Epstein reaction-diffusion system effectively captures the fundamental characteristics of the chlorite-iodide-malonic acid (CIMA) reaction observed in an open, unstirred gel reactor. This system initially provided experimental evidence for the existence of Turing patterns in 1990. The model proposed by Lengyel and Epstein is formulated as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}_0{}^{C}D_t^{\aleph }{\mathcal{E}}_1(x,t)=\Delta {\mathcal{E}}_1+\mathfrak{a}-{\mathcal{E}}_1-{\displaystyle \frac{4{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}},x\in \Omega ,t>0,\hfill \\ {}_0{}^{C}D_t^{\aleph }{\mathcal{E}}_2(x,t)=\sigma \left({\mathfrak{d}}_1\Delta {\mathcal{E}}_2+\mathfrak{b}\left({\mathcal{E}}_1-{\displaystyle \frac{{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}\right)\right),x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial {\mathcal{E}}_1}{\partial \eta }}={\displaystyle \frac{\partial {\mathcal{E}}_2}{\partial \eta }}=0,x\in \partial \Omega ,t>0,\hfill \\ {\mathcal{E}}_1(x,0)={\mathcal{E}}_{1,0}\left(x\right)>0,{\mathcal{E}}_2(x,0)={\mathcal{E}}_{2,0}\left(x\right)>0,x\in \Omega .\hfill \end{array}\right.\end{array}$$

(9)

Here, $\Omega$ denotes a bounded domain in ${\mathbb{R}}^n$ with a sufficiently smooth boundary $\partial \Omega$. The operator ${}_0{}^{C}D_t^{\aleph }$ represents the Caputo fractional derivative of order ℵ. In this context, ${\mathcal{E}}_1$ signifies the concentration of the activator (iodide), while ${\mathcal{E}}_2$ denotes the inhibitor (chlorite) within the domain $\Omega$. The parameters $\mathfrak{a}$ and $\mathfrak{b}$ correspond to the supply concentration, ${\mathfrak{d}}_1$ represents the diffusion coefficient ratio, and $\sigma >0$ is an adjusting parameter influenced by the starch concentration.

Lemma 2 

([6]). The system (9) admits a unique solution $\left({\mathcal{E}}_1,{\mathcal{E}}_2\right)$, defined for all x and $t>0$. Morover, there exist two positive constants ${\mathsf{C}}_1$ and ${\mathsf{C}}_2$ such that

$$\begin{array}{c}\hfill {\mathsf{C}}_1<{\mathcal{E}}_1\left(x,t\right),{\mathcal{E}}_2\left(x,t\right)<{\mathsf{C}}_2,x\in \Omega ,t>0.\end{array}$$

(10)

The critical equilibrium point is denoted as ${\mathcal{E}}^{*}=\left({\displaystyle \frac{\mathfrak{a}}{5}},1+{\displaystyle \frac{{\mathfrak{a}}^2}{25}}\right)$ within the Caputo fractional Lengyel-Epstein dynamic system. This equilibrium is determined by solving the following system of Equations (11):

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\Delta {\mathcal{E}}_1^{*}+\mathfrak{a}-{\mathcal{E}}_1^{*}-{\displaystyle \frac{4{\mathcal{E}}_1^{*}{\mathcal{E}}_2^{*}}{1+{\mathcal{E}}_1^{*2}}}=0,\hfill \\ \sigma \left({\mathfrak{d}}_1\Delta {\mathcal{E}}_2^{*}+\mathfrak{b}\left({\mathcal{E}}_1^{*}-{\displaystyle \frac{{\mathcal{E}}_1^{*}{\mathcal{E}}_2^{*}}{1+{\mathcal{E}}_1^{*2}}}\right)\right)=0,\hfill \end{array}\right.\end{array}$$

(11)

From [2], according to Ouannes et al. it is clear that

$$\begin{array}{cc}\hfill \left|{\displaystyle \frac{4{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}-{\displaystyle \frac{4{\mathcal{E}}_1^{*}{\mathcal{E}}_2^{*}}{1+{\mathcal{E}}_1^{*2}}}\right|& \le \left|{\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right|+4\left|{\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right|,\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill \left|{\displaystyle \frac{\sigma \mathfrak{b}{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}-{\displaystyle \frac{\sigma \mathfrak{b}{\mathcal{E}}_1^{*}{\mathcal{E}}_2^{*}}{1+{\mathcal{E}}_1^{*2}}}\right|& \le \left|{\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right|+\sigma \mathfrak{b}\left|{\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right|.\hfill \end{array}$$

(13)

4. Finite-Time Stability Result

In this section, we establish the necessary prerequisites for ensuring the finite-time stability of the equilibrium point ${\mathcal{E}}^{*}=\left({\displaystyle \frac{\mathfrak{a}}{5}},1+{\displaystyle \frac{{\mathfrak{a}}^2}{25}}\right)$. We begin by introducing various stability criteria:

Lemma 3 

([24]). (Poincaré Integral Inequality) $\Omega \subset {\mathbb{R}}^n$ is a bounded domain with its smooth boundary $\partial \Omega$ that is of ${\mathcal{C}}^2$. $\vartheta \left(x\right)\in H_0^1\left(\Omega \right)$ is a real-valued function and ${\displaystyle \frac{\partial \vartheta \left(x\right)}{\partial \eta }}{|}_{\partial \Omega }=0$. Then,

$$\begin{array}{c}\hfill {\int }_{\Omega }{\left|\nabla \vartheta \left(x\right)\right|}^{2}dx\ge {\zeta }_1{\int }_{\Omega }{\left|\vartheta \left(x\right)\right|}^{2}dx,\end{array}$$

(14)

where ${\zeta }_1$ is a positive eigenvalue of the problem:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}\Delta \vartheta \left(x\right)=-\zeta \vartheta \left(x\right),x\in \Omega ,\hfill \\ {\displaystyle \frac{\partial \vartheta \left(x\right)}{\partial \eta }}=0,x\in \partial \Omega .\hfill \end{array}\right.\end{array}$$

(15)

Here, η is the unit normal vector to $\partial \Omega$.

Theorem 2. 

The point ${\mathcal{E}}^{*}=\left({\displaystyle \frac{\mathfrak{a}}{5}},1+{\displaystyle \frac{{\mathfrak{a}}^2}{25}}\right)$ constitutes a finite-time stable equilibrium for the fractional-order nonlinear systems (9) if the following conditions are satisfied:

$$\begin{array}{c}\hfill min\left\{{\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}},{\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}\right\}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}>0,\end{array}$$

(16)

$$\begin{array}{c}\hfill 0<\underset{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{min}{\mathcal{E}}_1\le {\mathcal{E}}_1\le {\displaystyle \frac{\mathfrak{a}}{5}},\end{array}$$

(17)

$$\begin{array}{c}\hfill 0<\underset{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{min}{\mathcal{E}}_2\le {\mathcal{E}}_2\le 1+{\displaystyle \frac{{\mathfrak{a}}^2}{25}}.\end{array}$$

(18)

The finite-time stability of this equilibrium point is characterized by the settling time:

$$\begin{array}{c}\hfill t_1^{*}={\displaystyle \frac{{\mathcal{L}}_1\left(0\right)}{\left(min\left\{\frac{{\zeta }_1}{{\mathcal{E}}_1^{*}},\frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}\right\}-\frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}-\frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}\right){\mathcal{L}}_1\left(t_{max}\right)}}.\end{array}$$

(19)

Proof. 

We define a positive Lyapunov function as follows:

$$\begin{array}{c}\hfill {\mathcal{L}}_1\left(t\right)={\int }_{\Omega }\left[{\mathcal{E}}_1-{\mathcal{E}}_1^{*}\left(1+ln\left({\displaystyle \frac{{\mathcal{E}}_1}{{\mathcal{E}}_1^{*}}}\right)\right)\right]dx+{\int }_{\Omega }\left[{\mathcal{E}}_2-{\mathcal{E}}_2^{*}\left(1+ln\left({\displaystyle \frac{{\mathcal{E}}_2}{{\mathcal{E}}_2^{*}}}\right)\right)\right]dx,\end{array}$$

(20)

Thus, we obtain

$$\begin{array}{cc}\hfill {}_{0}D_t{\mathcal{L}}_1\left(t\right)& ={\int }_{\Omega }{}_{0}D_t\left[{\mathcal{E}}_1-{\mathcal{E}}_1^{*}\left(1+ln\left({\displaystyle \frac{{\mathcal{E}}_1}{{\mathcal{E}}_1^{*}}}\right)\right)\right]dx+{\int }_{\Omega }{}_{0}D_t\left[{\mathcal{E}}_2-{\mathcal{E}}_2^{*}\left(1+ln\left({\displaystyle \frac{{\mathcal{E}}_2}{{\mathcal{E}}_2^{*}}}\right)\right)\right]dx\hfill \\ \hfill & ={\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_1^{*}}{{\mathcal{E}}_1}}\right)\left({}_{0}D_t{\mathcal{E}}_1-{}_{0}D_t{\mathcal{E}}_1^{*}\right)dx+{\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_2^{*}}{{\mathcal{E}}_2}}\right)\left({}_{0}D_t{\mathcal{E}}_2-{}_{0}D_t{\mathcal{E}}_2^{*}\right)dx\hfill \\ \hfill & ={\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_1^{*}}{{\mathcal{E}}_1}}\right)\left[\Delta \left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)-\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)-\left({\displaystyle \frac{4{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}-{\displaystyle \frac{4{\mathcal{E}}_1^{*}{\mathcal{E}}_2^{*}}{1+{\mathcal{E}}_1^{*2}}}\right)\right]dx\hfill \\ \hfill & +{\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_2^{*}}{{\mathcal{E}}_2}}\right)\left[\sigma \left({\mathfrak{d}}_1\Delta \left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)+\mathfrak{b}\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)-\mathfrak{b}\left({\displaystyle \frac{{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}-{\displaystyle \frac{{\mathcal{E}}_1^{*}{\mathcal{E}}_2^{*}}{1+{\mathcal{E}}_1^{*2}}}\right)\right)\right]dx\hfill \\ \hfill & \le {\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_1^{*}}{{\mathcal{E}}_1}}\right)\Delta \left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)dx+\sigma {\mathfrak{d}}_1{\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_2^{*}}{{\mathcal{E}}_2}}\right)\Delta \left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)dx\hfill \\ \hfill & -{\int }_{\Omega }{\displaystyle \frac{{\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2}{{\mathcal{E}}_1}}dx+\sigma \mathfrak{b}{\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_2^{*}}{{\mathcal{E}}_2}}\right)\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)dx\hfill \\ \hfill & -{\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_1^{*}}{{\mathcal{E}}_1}}\right)\left({\displaystyle \frac{4{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}-{\displaystyle \frac{4{\mathcal{E}}_1^{*}{\mathcal{E}}_2^{*}}{1+{\mathcal{E}}_1^{*2}}}\right)dx-{\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_2^{*}}{{\mathcal{E}}_2}}\right)\left({\displaystyle \frac{\sigma \mathfrak{b}{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}-{\displaystyle \frac{\sigma \mathfrak{b}{\mathcal{E}}_1^{*}{\mathcal{E}}_2^{*}}{1+{\mathcal{E}}_1^{*2}}}\right)dx\hfill \\ \hfill & \le {\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_1^{*}}{{\mathcal{E}}_1}}\right)\Delta \left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)dx+\sigma {\mathfrak{d}}_1{\int }_{\Omega }\left(1-{\displaystyle \frac{{\mathcal{E}}_2^{*}}{{\mathcal{E}}_2}}\right)\Delta \left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)dx\hfill \\ \hfill & -{\int }_{\Omega }{\displaystyle \frac{{\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2}{{\mathcal{E}}_1}}dx+{\displaystyle \frac{\sigma \mathfrak{b}}{2}}{\int }_{\Omega }{\displaystyle \frac{{\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2+{\left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)}^2}{{\mathcal{E}}_2}}dx\hfill \\ \hfill & +{\int }_{\Omega }\left|1-{\displaystyle \frac{{\mathcal{E}}_1^{*}}{{\mathcal{E}}_1}}\right|\left|{\displaystyle \frac{4{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}-{\displaystyle \frac{4{\mathcal{E}}_1^{*}{\mathcal{E}}_2^{*}}{1+{\mathcal{E}}_1^{*2}}}\right|dx+{\int }_{\Omega }\left|1-{\displaystyle \frac{{\mathcal{E}}_2^{*}}{{\mathcal{E}}_2}}\right|\left|{\displaystyle \frac{\sigma \mathfrak{b}{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}-{\displaystyle \frac{\sigma \mathfrak{b}{\mathcal{E}}_1^{*}{\mathcal{E}}_2^{*}}{1+{\mathcal{E}}_1^{*2}}}\right|dx.\hfill \end{array}$$

(21)

where ${}_{0}D_t$ is the normal derivative. Using Green’s formula in conjunction with the inequalities (12) and (13), we derive

$$\begin{array}{cc}\hfill {}_{0}D_t{\mathcal{L}}_1\left(t\right)& \le -{\mathcal{E}}_1^{*}{\int }_{\Omega }{\displaystyle \frac{{\left|\nabla \left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)\right|}^2}{{\mathcal{E}}_1^2}}dx-\sigma {\mathfrak{d}}_1{\mathcal{E}}_2^{*}{\int }_{\Omega }{\displaystyle \frac{{\left|\nabla \left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)\right|}^2}{{\mathcal{E}}_2^2}}dx-{\int }_{\Omega }{\displaystyle \frac{{\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2}{{\mathcal{E}}_1}}dx\hfill \\ \hfill & +{\displaystyle \frac{\sigma \mathfrak{b}}{2}}{\int }_{\Omega }{\displaystyle \frac{{\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2+{\left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)}^2}{{\mathcal{E}}_2}}dx+{\int }_{\Omega }\left|1-{\displaystyle \frac{{\mathcal{E}}_1^{*}}{{\mathcal{E}}_1}}\right|\left(\left|{\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right|+4\left|{\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right|\right)dx\hfill \\ \hfill & +{\int }_{\Omega }\left|1-{\displaystyle \frac{{\mathcal{E}}_2^{*}}{{\mathcal{E}}_2}}\right|\left(\left|{\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right|+\sigma \mathfrak{b}\left|{\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right|\right)dx\hfill \\ \hfill & \le -{\mathcal{E}}_1^{*}{\int }_{\Omega }{\displaystyle \frac{{\left|\nabla \left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)\right|}^2}{{\mathcal{E}}_1^2}}dx-\sigma {\mathfrak{d}}_1{\mathcal{E}}_2^{*}{\int }_{\Omega }{\displaystyle \frac{{\left|\nabla \left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)\right|}^2}{{\mathcal{E}}_2^2}}dx\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\int }_{\Omega }{\displaystyle \frac{\left(1+\sigma \mathfrak{b}\right){\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2+\left(1+3\sigma \mathfrak{b}\right){\left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)}^2}{{\mathcal{E}}_2}}dx\hfill \\ \hfill & +2{\int }_{\Omega }{\displaystyle \frac{{\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2+{\left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)}^2}{{\mathcal{E}}_1}}dx.\hfill \end{array}$$

(22)

According to Lemma 3, we can conclude

$$\begin{array}{cc}\hfill {}_{0}D_t{\mathcal{L}}_1\left(t\right)& \le -{\zeta }_1{\mathcal{E}}_1^{*}{\int }_{\Omega }{\displaystyle \frac{{\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2}{{\mathcal{E}}_1^2}}dx-{\zeta }_2\sigma {\mathfrak{d}}_1{\mathcal{E}}_2^{*}{\int }_{\Omega }{\displaystyle \frac{{\left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)}^2}{{\mathcal{E}}_2^2}}dx\hfill \\ \hfill & +{\displaystyle \frac{1}{2}}{\int }_{\Omega }{\displaystyle \frac{\left(1+\sigma \mathfrak{b}\right){\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2+\left(1+3\sigma \mathfrak{b}\right){\left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)}^2}{{\mathcal{E}}_2}}dx\hfill \\ \hfill & +2{\int }_{\Omega }{\displaystyle \frac{{\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2+{\left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)}^2}{{\mathcal{E}}_1}}dx\hfill \\ \hfill & =-{\int }_{\Omega }\left({\displaystyle \frac{{\zeta }_1{\mathcal{E}}_1^{*}}{{\mathcal{E}}_1^2}}-{\displaystyle \frac{1+\sigma \mathfrak{b}}{2{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{\mathcal{E}}_1}}\right){\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^{2}dx\hfill \\ \hfill & -{\int }_{\Omega }\left({\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1{\mathcal{E}}_2^{*}}{{\mathcal{E}}_2^2}}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{\mathcal{E}}_1}}\right){\left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)}^{2}dx.\hfill \end{array}$$

(23)

Given $0<{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1\le {\mathcal{E}}_1\le {\mathcal{E}}_1^{*}$ and $0<{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2\le {\mathcal{E}}_2\le {\mathcal{E}}_2^{*},$ we have:

$$\begin{array}{cc}\hfill {}_{0}D_t{\mathcal{L}}_1\left(t\right)& \le -{\int }_{\Omega }\left({\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}}-{\displaystyle \frac{1+\sigma \mathfrak{b}}{2{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{\mathcal{E}}_1}}\right){\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^{2}dx\hfill \\ \hfill & -{\int }_{\Omega }\left({\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{\mathcal{E}}_1}}\right){\left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)}^{2}dx\hfill \\ \hfill & \le -\left(min\left\{{\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}},{\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}\right\}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}\right)\times \hfill \\ \hfill & {\int }_{\Omega }\left({\left({\mathcal{E}}_1-{\mathcal{E}}_1^{*}\right)}^2+{\left({\mathcal{E}}_2-{\mathcal{E}}_2^{*}\right)}^2\right)dx.\hfill \end{array}$$

(24)

Assuming ${\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}}+{\displaystyle \frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}\le min\left\{{\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}},{\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}\right\},$ we find

$$\begin{array}{cc}\hfill {}_{0}D_t{\mathcal{L}}_1\left(t\right)& \le -\left(min\left\{{\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}},{\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}\right\}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}\right){\mathcal{L}}_1\left(t\right).\hfill \end{array}$$

(25)

Let ${\beta }_{3,0}=min\left\{{\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}},{\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}\right\}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}>0$. Then,

$$\begin{array}{c}\hfill {\int }_0^{ϵ}{\displaystyle \frac{1}{{\beta }_{3,0}}}d\varsigma ={\displaystyle \frac{ϵ}{min\left\{\frac{{\zeta }_1}{{\mathcal{E}}_1^{*}},\frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}\right\}-\frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}-\frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}}<+\infty ,\end{array}$$

(26)

The function ${\mathcal{L}}_1$ is monotonically decreasing. For $0\le t<t_1^{*}\le t_{max}$, it follows that ${\mathcal{L}}_1\left(t\right)>{\mathcal{L}}_1\left(t_1^{*}\right)>{\mathcal{L}}_1\left(t_{max}\right)$. Moreover,

$$\begin{array}{cc}\hfill {\mathcal{L}}_1\left(t\right)& \le {\mathcal{L}}_1\left(0\right)-\left(min\left\{{\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}},{\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}\right\}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}\right){\int }_0^t{\mathcal{L}}_1\left(\varsigma \right)d\varsigma \hfill \\ & \le {\mathcal{L}}_1\left(0\right)-\left(min\left\{{\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}},{\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}\right\}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}\right){\int }_0^t{\mathcal{L}}_1\left(t_{max}\right)d\varsigma \hfill \\ & ={\mathcal{L}}_1\left(0\right)-\left(min\left\{{\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}},{\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}\right\}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}\right){\mathcal{L}}_1\left(t_{max}\right)t.\hfill \end{array}$$

(27)

Here, ${\mathcal{E}}^{*}$ termed as the finite-time equilibrium point if there exists $t_1^{*}>0,$ such that

$$\begin{array}{cc}\hfill \underset{t\to t_1^{*}}{lim}{\mathcal{L}}_1\left(t\right)& \le {\mathcal{L}}_1\left(0\right)-\left(min\left\{{\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}},{\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}\right\}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}\right){\mathcal{L}}_1\left(t_{max}\right)t_1^{*}=0.\hfill \end{array}$$

(28)

The settling time $t_1^{*}$ is estimated as follows:

$$\begin{array}{c}\hfill t_1^{*}={\displaystyle \frac{{\mathcal{L}}_1\left(0\right)}{\left(min\left\{\frac{{\zeta }_1}{{\mathcal{E}}_1^{*}},\frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}\right\}-\frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}-\frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}\right){\mathcal{L}}_1\left(t_{max}\right)}}.\end{array}$$

Therefore, the equilibrium point ${\mathcal{E}}^{*}=\left({\displaystyle \frac{\mathfrak{a}}{5}},1+{\displaystyle \frac{{\mathfrak{a}}^2}{25}}\right)$ for the nonlinear systems described by system (9) is stable over a finite period, as stated in Theorem 1. This stability implies that the system remains near the equilibrium point for a finite duration, demonstrating predictability and stability in its behavior. □

5. Finite-Time Synchronization Scheme

The concept of finite-time synchronization in reaction-diffusion systems focuses on achieving rapid synchronization among spatially dispersed elements within a specified time frame. The primary goal is to ensure efficient coherence across the spatial components of the system.

Consider the subsystem of the Lengyel-Epstein reaction-diffusion system described by the following equations:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}_0{}^{C}D_t^{\aleph }{\overline{\mathcal{E}}}_1\left(x,t\right)=\Delta {\overline{\mathcal{E}}}_1+\mathfrak{a}-{\overline{\mathcal{E}}}_1-{\displaystyle \frac{4{\overline{\mathcal{E}}}_1{\overline{\mathcal{E}}}_2}{1+{\overline{\mathcal{E}}}_1^2}}+{\mathcal{C}}_1,x\in \Omega ,t>0,\hfill \\ {}_0{}^{C}D_t^{\aleph }{\overline{\mathcal{E}}}_2\left(x,t\right)=\sigma \left({\mathfrak{d}}_1\Delta {\overline{\mathcal{E}}}_2+\mathfrak{b}\left({\overline{\mathcal{E}}}_1-{\displaystyle \frac{{\overline{\mathcal{E}}}_1{\overline{\mathcal{E}}}_2}{1+{\overline{\mathcal{E}}}_1^2}}\right)\right)+{\mathcal{C}}_2,x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial {\overline{\mathcal{E}}}_1}{\partial \eta }}={\displaystyle \frac{\partial {\overline{\mathcal{E}}}_2}{\partial \eta }}=0,x\in \partial \Omega ,t>0,\hfill \\ {\overline{\mathcal{E}}}_1\left(x,0\right)={\overline{\mathcal{E}}}_{1,0}\left(x\right)>0,{\overline{\mathcal{E}}}_2\left(x,0\right)={\overline{\mathcal{E}}}_{2,0}\left(x\right)>0,x\in \Omega .\hfill \end{array}\right.\end{array}$$

(29)

We examine the discrepancies in synchronization between Equations (9) and (29) through the error vector:

$$\begin{array}{c}\hfill \mathfrak{e}\left(x,t\right)=\left(\begin{array}{c}{\mathfrak{e}}_1\\ {\mathfrak{e}}_2\end{array}\right)=\left(\begin{array}{c}{\overline{\mathcal{E}}}_1-{\mathcal{E}}_1\\ {\overline{\mathcal{E}}}_2-{\mathcal{E}}_2\end{array}\right).\end{array}$$

(30)

In the following discussion, we will identify the linear controllers ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$, which are designed to drive the error system solution towards zero as t approaches the settling time $t^{*}$.

Theorem 3 

([25]). Let $\mathcal{L}\left(t\right)$ be a continuous and positive definite function satisfying:

$$\begin{array}{c}\hfill {}_0{}^{C}D_t^{\aleph }\mathcal{L}\left(t\right)\le -Q\mathcal{L}\left(t\right),\forall t\ge 0,\end{array}$$

(31)

where $0<\aleph <1$ and =Q is a non-negative constant. Then,

$$\begin{array}{c}\hfill \mathcal{L}\left(t\right)\le \mathcal{L}\left(0\right){\mathsf{E}}_{\aleph }\left(-Q{t}^{\aleph }\right),\forall t\in \left[0,t^{*}\right),\end{array}$$

(32)

where ${\mathsf{E}}_{\aleph }$ is the Mittag-Leffler function and the settling time is given by:

$$\begin{array}{c}\hfill t^{*}={\left({\displaystyle \frac{\Gamma \left(\aleph +1\right)}{Q}}\right)}^{{\aleph }^{-1}}.\end{array}$$

(33)

Moreover, $\mathcal{L}\left(0\right)$ is positive, and $\mathcal{L}\left(t\right)\equiv 0$ for $t\ge t^{*}$.

Definition 5 

([26,27]). If there exists a specific time parameter $t^{*}>0$ such that:

$$\begin{array}{c}\hfill \underset{t\to t^{*}}{lim}∥{\mathfrak{e}}_1\left(t\right)∥+∥{\mathfrak{e}}_2\left(t\right)∥=0,\end{array}$$

(34)

and

$$\begin{array}{c}\hfill ∥{\mathfrak{e}}_1\left(t\right)∥+∥{\mathfrak{e}}_2\left(t\right)∥\equiv 0,\forall t\ge t^{*},\end{array}$$

(35)

then, the master-slave systems (9) and (29) are synchronized in finite time.

Theorem 4. 

The master-slave systems represented by (9) and (29) achieve stable and synchronized states within a finite time frame when the following conditions are satisfied:

$$\begin{array}{c}\hfill min\left\{{\zeta }_1+3\sigma \mathfrak{b}-{\displaystyle \frac{5}{2}},5\sigma \mathfrak{b}\left(1+{\displaystyle \frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}}-{\displaystyle \frac{1}{2\sigma \mathfrak{b}}}\right)\right\}>0,\end{array}$$

(36)

where ${\zeta }_1$ and ${\zeta }_2$ are positive eigenvalues. This can be accomplished by employing a 2-dimensional linear control law:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{C}}_1=-3\sigma \mathfrak{b}{\mathfrak{e}}_1,\hfill \\ {\mathcal{C}}_2=-\sigma \mathfrak{b}\left({\mathfrak{e}}_1+6{\mathfrak{e}}_2\right),\hfill \end{array}\right.\end{array}$$

(37)

with the settling time defined as:

$$\begin{array}{c}\hfill t_2^{*}={\left({\displaystyle \frac{\Gamma \left(\aleph +1\right)}{2min\left\{{\zeta }_1+3\sigma \mathfrak{b}-\frac{5}{2},5\sigma \mathfrak{b}\left(1+\frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}-\frac{1}{2\sigma \mathfrak{b}}\right)\right\}}}\right)}^{{\aleph }^{-1}}.\end{array}$$

(38)

Proof. 

By incorporating the control described in the theorem into the error system, we derive the following dynamics:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{}_0{}^{C}D_t^{\aleph }{\mathfrak{e}}_1\left(x,t\right)=\Delta {\mathfrak{e}}_1-\left(1+3\sigma \mathfrak{b}\right){\mathfrak{e}}_1-\left({\displaystyle \frac{4{\overline{\mathcal{E}}}_1{\overline{\mathcal{E}}}_2}{1+{\overline{\mathcal{E}}}_1^2}}-{\displaystyle \frac{4{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}\right),x\in \Omega ,t>0,\hfill \\ {}_0{}^{C}D_t^{\aleph }{\mathfrak{e}}_2\left(x,t\right)=\sigma \left[{\mathfrak{d}}_1\Delta {\mathfrak{e}}_2-6\mathfrak{b}{\mathfrak{e}}_2-\mathfrak{b}\left({\displaystyle \frac{{\overline{\mathcal{E}}}_1{\overline{\mathcal{E}}}_2}{1+{\overline{\mathcal{E}}}_1^2}}-{\displaystyle \frac{{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}\right)\right],x\in \Omega ,t>0,\hfill \\ {\displaystyle \frac{\partial {\mathfrak{e}}_1}{\partial \eta }}={\displaystyle \frac{\partial {\mathfrak{e}}_2}{\partial \eta }}=0,x\in \partial \Omega ,t>0,\hfill \\ {\mathfrak{e}}_1\left(x,0\right)={\overline{\mathcal{E}}}_{1,0}\left(x\right)-{\mathcal{E}}_{1,0}\left(x\right),{\mathfrak{e}}_2\left(x,0\right)={\overline{\mathcal{E}}}_{2,0}\left(x\right)-{\mathcal{E}}_{2,0}\left(x\right),x\in \Omega .\hfill \end{array}\right.\end{array}$$

(39)

Then, we define a function ${\mathcal{L}}_3\left(t\right)$ as follows:

$$\begin{array}{c}\hfill {\mathcal{L}}_3\left(t\right)={\displaystyle \frac{1}{2}}{\int }_{\Omega }\left({\mathfrak{e}}_1^2+{\mathfrak{e}}_2^2\right)dx,\end{array}$$

(40)

To compute ${}_0{}^{C}D_t^{\aleph }{\mathcal{L}}_3\left(t\right)$ using Lemmas 1 and 3 and inequalities (12) and (13), we find

$$\begin{array}{cc}\hfill {}_0{}^{C}D_t^{\aleph }{\mathcal{L}}_3\left(t\right)& \le {\int }_{\Omega }{\mathfrak{e}}_1{}_0{}^{C}D_t^{\aleph }{\mathfrak{e}}_{1}dx+{\int }_{\Omega }{\mathfrak{e}}_2{}_0{}^{C}D_t^{\aleph }{\mathfrak{e}}_{2}dx\hfill \\ & ={\int }_{\Omega }{\mathfrak{e}}_1\left[\Delta {\mathfrak{e}}_1-\left(1+3\sigma \mathfrak{b}\right){\mathfrak{e}}_1-\left({\displaystyle \frac{4{\overline{\mathcal{E}}}_1{\overline{\mathcal{E}}}_2}{1+{\overline{\mathcal{E}}}_1^2}}-{\displaystyle \frac{4{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}\right)\right]dx\hfill \\ & +{\int }_{\Omega }{\mathfrak{e}}_2\left[\sigma {\mathfrak{d}}_1\Delta {\mathfrak{e}}_2-6\sigma \mathfrak{b}{\mathfrak{e}}_2-\left({\displaystyle \frac{\sigma \mathfrak{b}{\overline{\mathcal{E}}}_1{\overline{\mathcal{E}}}_2}{1+{\overline{\mathcal{E}}}_1^2}}-{\displaystyle \frac{\sigma \mathfrak{b}{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}\right)\right]dx\hfill \\ & \le {\int }_{\Omega }{\mathfrak{e}}_1\Delta {\mathfrak{e}}_{1}dx-\left(1+3\sigma \mathfrak{b}\right){\int }_{\Omega }{\mathfrak{e}}_1^{2}dx+{\int }_{\Omega }\left|{\mathfrak{e}}_1\right|\left|{\displaystyle \frac{4{\overline{\mathcal{E}}}_1{\overline{\mathcal{E}}}_2}{1+{\overline{\mathcal{E}}}_1^2}}-{\displaystyle \frac{4{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}\right|dx\hfill \\ & +\sigma {\mathfrak{d}}_1{\int }_{\Omega }{\mathfrak{e}}_2\Delta {\mathfrak{e}}_{2}dx-6\sigma \mathfrak{b}{\int }_{\Omega }{\mathfrak{e}}_2^{2}dx+{\int }_{\Omega }\left|{\mathfrak{e}}_2\right|\left|{\displaystyle \frac{\sigma \mathfrak{b}{\overline{\mathcal{E}}}_1{\overline{\mathcal{E}}}_2}{1+{\overline{\mathcal{E}}}_1^2}}-{\displaystyle \frac{\sigma \mathfrak{b}{\mathcal{E}}_1{\mathcal{E}}_2}{1+{\mathcal{E}}_1^2}}\right|dx\hfill \\ & \le {\int }_{\Omega }{\mathfrak{e}}_1\Delta {\mathfrak{e}}_{1}dx-\left(1+3\sigma \mathfrak{b}\right){\int }_{\Omega }{\mathfrak{e}}_1^{2}dx+{\int }_{\Omega }\left|{\mathfrak{e}}_1\right|\left(\left|{\overline{\mathcal{E}}}_1-{\mathcal{E}}_1\right|+4\left|{\overline{\mathcal{E}}}_2-{\mathcal{E}}_2\right|\right)dx\hfill \\ & +\sigma {\mathfrak{d}}_1{\int }_{\Omega }{\mathfrak{e}}_2\Delta {\mathfrak{e}}_{2}dx-6\sigma \mathfrak{b}{\int }_{\Omega }{\mathfrak{e}}_2^{2}dx+{\int }_{\Omega }\left|{\mathfrak{e}}_2\right|\left(\left|{\overline{\mathcal{E}}}_1-{\mathcal{E}}_1\right|+\sigma \mathfrak{b}\left|{\overline{\mathcal{E}}}_2-{\mathcal{E}}_2\right|\right)dx\hfill \\ & \le -{\int }_{\Omega }{\left|\nabla {\mathfrak{e}}_1\right|}^{2}dx-\sigma {\mathfrak{d}}_1{\int }_{\Omega }{\left|\nabla {\mathfrak{e}}_2\right|}^{2}dx-3\sigma \mathfrak{b}{\int }_{\Omega }{\mathfrak{e}}_1^{2}dx-5\sigma \mathfrak{b}{\int }_{\Omega }{\mathfrak{e}}_2^{2}dx+5{\int }_{\Omega }\left|{\mathfrak{e}}_1\right|\left|{\mathfrak{e}}_2\right|dx\hfill \\ & \le -\left({\zeta }_1+3\sigma \mathfrak{b}-{\displaystyle \frac{5}{2}}\right){\int }_{\Omega }{\mathfrak{e}}_1^{2}dx-5\sigma \mathfrak{b}\left(1+{\displaystyle \frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}}-{\displaystyle \frac{1}{2\sigma \mathfrak{b}}}\right){\int }_{\Omega }{\mathfrak{e}}_2^{2}dx\hfill \\ & \le -2min\left\{{\zeta }_1+3\sigma \mathfrak{b}-{\displaystyle \frac{5}{2}},5\sigma \mathfrak{b}\left(1+{\displaystyle \frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}}-{\displaystyle \frac{1}{2\sigma \mathfrak{b}}}\right)\right\}{\mathcal{L}}_3\left(t\right).\hfill \end{array}$$

(41)

From [28], as the parameter ℵ gradually approaches 1 from the left side, the fractional derivative operator ${}_0{}^{C}D_t^{\aleph }{\mathcal{L}}_3\left(t\right)$ tends to converge towards the standard derivative operator ${}_{0}D_t{\mathcal{L}}_3\left(t\right)$. This convergence suggests or implies something further, likely related to simplification or a change in behavior as the fractional order approaches a whole number.

$$\begin{array}{c}\hfill \underset{\aleph \to 1}{lim}{}_0{}^{C}D_t^{\aleph }{\mathcal{L}}_3\left(t\right)={}_{0}D_t{\mathcal{L}}_3\left(t\right).\end{array}$$

(42)

That is,

$$\begin{array}{c}\hfill {}_{0}D_t{\mathcal{L}}_3\left(t\right)\le -2min\left\{{\zeta }_1+3\sigma \mathfrak{b}-{\displaystyle \frac{5}{2}},5\sigma \mathfrak{b}\left(1+{\displaystyle \frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}}-{\displaystyle \frac{1}{2\sigma \mathfrak{b}}}\right)\right\}{\mathcal{L}}_3\left(t\right),\end{array}$$

(43)

Denote ${\beta }_{3,2}=2min\left\{{\zeta }_1+3\sigma \mathfrak{b}-{\displaystyle \frac{5}{2}},5\sigma \mathfrak{b}\left(1+{\displaystyle \frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}}-{\displaystyle \frac{1}{2\sigma \mathfrak{b}}}\right)\right\}>0,$ we can obtain:

$$\begin{array}{c}\hfill {\int }_0^{ϵ}{\displaystyle \frac{1}{{\beta }_{3,2}}}d\varsigma ={\displaystyle \frac{ϵ}{2min\left\{{\zeta }_1+3\sigma \mathfrak{b}-\frac{5}{2},5\sigma \mathfrak{b}\left(1+\frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}-\frac{1}{2\sigma \mathfrak{b}}\right)\right\}}}<+\infty ,\end{array}$$

(44)

Using Theorem 1, we establish that if the error system (39) attains a zero solution, it indicates the finite-time stability of the equilibrium point $\left({\mathfrak{e}}_1,{\mathfrak{e}}_2\right)=\left(0,0\right)$. Furthermore, by employing Theorem 3, we draw further conclusions:

$$\begin{array}{cc}\hfill {\mathcal{L}}_3\left(t\right)& \le {\mathcal{L}}_3\left(0\right){\mathsf{E}}_{\aleph }\left(-2min\left\{{\zeta }_1+3\sigma \mathfrak{b}-{\displaystyle \frac{5}{2}},5\sigma \mathfrak{b}\left(1+{\displaystyle \frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}}-{\displaystyle \frac{1}{2\sigma \mathfrak{b}}}\right)\right\}{t}^{\aleph }\right),\forall t\in \left[0,t_2^{*}\right),\hfill \end{array}$$

(45)

with the settling-time

$$\begin{array}{c}\hfill t_2^{*}={\left({\displaystyle \frac{\Gamma \left(\aleph +1\right)}{2min\left\{{\zeta }_1+3\sigma \mathfrak{b}-\frac{5}{2},5\sigma \mathfrak{b}\left(1+\frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}-\frac{1}{2\sigma \mathfrak{b}}\right)\right\}}}\right)}^{{\aleph }^{-1}},\end{array}$$

Moreover, ${\mathcal{L}}_3\left(0\right)$ is positive and ${\mathcal{L}}_3\left(t\right)\equiv 0$ for $t\ge t_2^{*}.$ In conclusion, the master-slave systems described by Equations (9) and (29) have the capability to achieve synchronization within a finite period of time when subjected to a specific linear control law. Definition 5 outlines the conditions under which synchronization can be achieved within these systems, implying that such synchronization occurs within a finite time frame using the prescribed linear control law. □

6. Numerical Simulations

In this section, two practical scenarios are presented to demonstrate the effectiveness and practicality of the proposed approach, as well as to verify the theoretical findings. The theoretical conclusions are tested through numerical simulations conducted using MATLAB software.

Example 1. 

We define the domains as follows: $\Omega =[0,4]$ and $t\in [0,16]$. The parameters are set as:

Variable	Value
$\sigma$	6
${\mathfrak{d}}_1$	2
$\mathfrak{a}$	5
$\mathfrak{b}$	5
${\zeta }_1$	106
${\zeta }_2$	106
$\aleph$	0.995
$\mathbb{N}$	100

The boundary conditions are given by:

$$\begin{array}{c}\hfill {\displaystyle \frac{\partial {\mathcal{E}}_1(0,t)}{\partial t}}={\displaystyle \frac{\partial {\mathcal{E}}_2(4,t)}{\partial t}}=0,t\in [0,16].\end{array}$$

(46)

The initial conditions are:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{E}}_{1,0}\left(x\right)=0.25+0.0625cos\left(3x\right),\hfill \\ {\mathcal{E}}_{2,0}\left(x\right)=1.25+0.3125sin\left(4x\right).\hfill \end{array}\right.\end{array}$$

(47)

The point ${\mathcal{E}}^{*}=(1,2)$ constitutes a finite-time stable equilibrium for the fractional-order nonlinear systems if the conditions of Theorem 2 are satisfied:

$$\begin{array}{c}\hfill 0.1876\le {\mathcal{E}}_1\le 1,\end{array}$$

(48)

$$\begin{array}{c}\hfill 0.9375\le {\mathcal{E}}_2\le 2.\end{array}$$

(49)

We find:

$$\begin{array}{c}\hfill min\left\{{\displaystyle \frac{{\zeta }_1}{{\mathcal{E}}_1^{*}}},{\displaystyle \frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}}\right\}-{\displaystyle \frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}}-{\displaystyle \frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}}=9.9994\times {10}^5,\end{array}$$

(50)

$$\begin{array}{c}\hfill {\mathcal{L}}_1\left(0\right)=85.6450,\end{array}$$

(51)

$$\begin{array}{c}\hfill {\mathcal{L}}_1\left(16\right)=5.3801\times {10}^{-6}.\end{array}$$

(52)

The finite-time stability of this equilibrium point is characterized by the settling time:

$$\begin{array}{c}\hfill t_1^{*}={\displaystyle \frac{{\mathcal{L}}_1\left(0\right)}{\left(min\left\{\frac{{\zeta }_1}{{\mathcal{E}}_1^{*}},\frac{{\zeta }_2\sigma {\mathfrak{d}}_1}{{\mathcal{E}}_2^{*}}\right\}-\frac{1+3\sigma \mathfrak{b}}{2{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_2}-\frac{2}{{min}_{\begin{array}{c}x\in \Omega \\ t\ge 0\end{array}}{\mathcal{E}}_1}\right){\mathcal{L}}_1\left(16\right)}}=15.9198\mathrm{s}.\end{array}$$

(53)

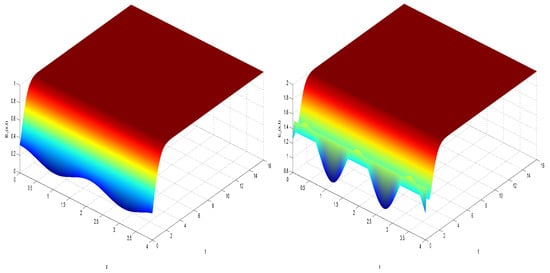
Figure 1 illustrate the spatiotemporal solutions of the system under consideration, observed across both spatial and temporal dimensions, while adhering to homogeneous Neumann boundary conditions. The equilibrium point of particular interest, denoted as ${\mathcal{E}}^{*}=(1,2)$, is identified based on the principles outlined in Theorem 2. This theorem suggests that the system maintains stability over a finite duration, an assertion we seek to validate through numerical analysis.

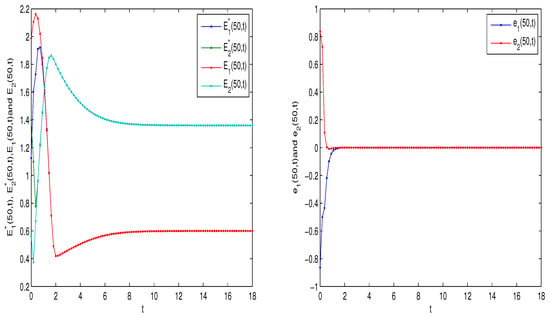
To substantiate this theoretical proposition, Figure 2 are presented, providing visual representations of the system’s solutions alongside the associated error profiles, focusing specifically on one-dimensional spatial scenarios. These figures offer numerical insights into how deviations between the actual system behavior and its equilibrium state evolve over time.

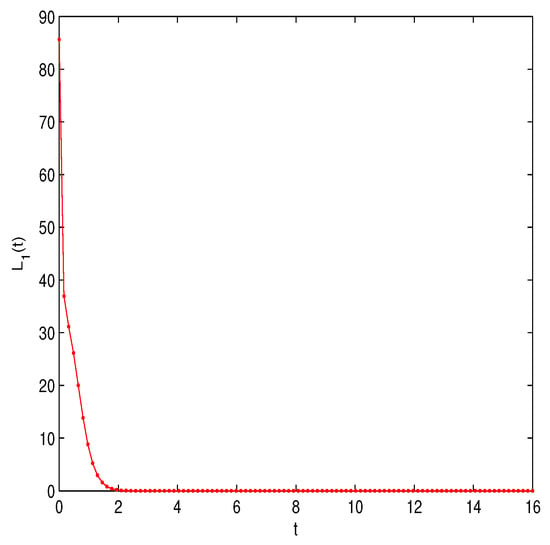
Furthermore, Figure 3 specifically examines the behavior of the Lyapunov function ${\mathcal{L}}_1\left(t\right)$. It demonstrates that as time t approaches the critical value $t_1^{*}=15.9200s$, ${\mathcal{L}}_1\left(t\right)$ asymptotically tends toward 0. This observation serves as empirical evidence supporting the finite-time stability of the system at the equilibrium point ${\mathcal{E}}^{*}$.

Example 2. 

We define the domain Ω as $[0,18]$ and t ranges within $[0,18]$. The parameters are specified as follows:

Variable	Value
$\sigma$	1
${\mathfrak{d}}_1$	1
$\mathfrak{a}$	3
$\mathfrak{b}$	0.8393
${\zeta }_1$	0.01
${\zeta }_2$	0.01
$\aleph$	0.9995
$\mathbb{N}$	100

The boundary conditions are given by:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\displaystyle \frac{\partial {\mathcal{E}}_1(0,t)}{\partial t}}={\displaystyle \frac{\partial {\mathcal{E}}_2(18,t)}{\partial t}}=0,t\in [0,18],\hfill \\ {\displaystyle \frac{\partial {\overline{\mathcal{E}}}_1(0,t)}{\partial t}}={\displaystyle \frac{\partial {\overline{\mathcal{E}}}_2(18,t)}{\partial t}}=0,t\in [0,18],\hfill \end{array}\right.\end{array}$$

(54)

Then, we specify the initial conditions for the master-slave systems (9) and (29) as follows:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{E}}_{1,0}\left(x\right)=2+0.5cos\left(3x\right),\hfill \\ {\mathcal{E}}_{2,0}\left(x\right)=1+0.5sin\left(4x\right).\hfill \end{array}\right.\end{array}$$

(55)

and

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\overline{\mathcal{E}}}_{1,0}\left(x\right)=2.25-1.125sin\left(3x\right),\hfill \\ {\overline{\mathcal{E}}}_{2,0}\left(x\right)=1.25-0.3125cos\left(4x\right),\hfill \end{array}\right.\end{array}$$

(56)

The master-slave systems (9) and (29) achieve stable and synchronized states within a finite time frame when the conditions of Theorem 4 are satisfied:

$$\begin{array}{c}\hfill min\left\{{\zeta }_1+3\sigma \mathfrak{b}-{\displaystyle \frac{5}{2}},5\sigma \mathfrak{b}\left(1+{\displaystyle \frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}}-{\displaystyle \frac{1}{2\sigma \mathfrak{b}}}\right)\right\}=0.0279,\end{array}$$

(57)

This is accomplished by employing a 2-dimensional linear control law:

$$\begin{array}{c}\hfill \left\{\begin{array}{c}{\mathcal{C}}_1=-2.5179\mathfrak{b}{\mathfrak{e}}_1,\hfill \\ {\mathcal{C}}_2=-0.8393\mathfrak{b}\left({\mathfrak{e}}_1+6{\mathfrak{e}}_2\right),\hfill \end{array}\right.\end{array}$$

(58)

where

$$\begin{array}{c}\hfill {\mathcal{L}}_3\left(t\right)\le G\left(t\right)=51.6067{\mathsf{E}}_{0.9995}\left(-0.0558t^{0.9995}\right),\forall t\in [0,t_2^{*}),\end{array}$$

(59)

with the settling-time

$$\begin{array}{c}\hfill t_2^{*}={\left({\displaystyle \frac{\Gamma (\aleph +1)}{2min\left\{{\zeta }_1+3\sigma \mathfrak{b}-\frac{5}{2},5\sigma \mathfrak{b}\left(1+\frac{{\zeta }_2{\mathfrak{d}}_1}{5\mathfrak{b}}-\frac{1}{2\sigma \mathfrak{b}}\right)\right\}}}\right)}^{{\aleph }^{-1}}=17.9432\mathrm{s}.\end{array}$$

(60)

We find:

$$\begin{array}{c}\hfill {\mathcal{L}}_3\left(17.9432\right)=8.7296\times {10}^{-10},\end{array}$$

(61)

where $17.9432\le t\le 18$. We can conclude that

$$\begin{array}{c}\hfill {\mathcal{L}}_3\left(t\right)\equiv 0.\end{array}$$

(62)

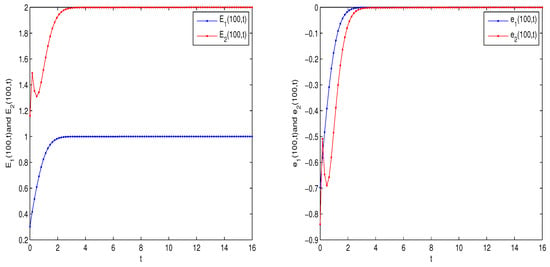
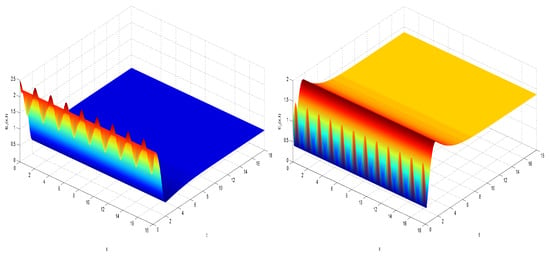
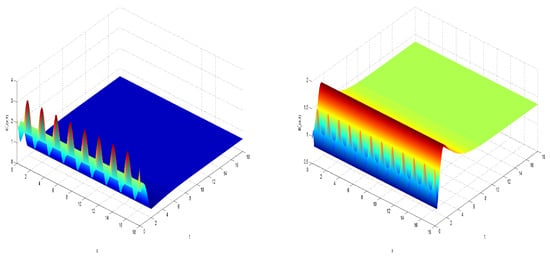
The analysis of spatiotemporal dynamics in two distinct systems, referenced as (9) and (29), is visually presented in Figure 4, Figure 5 and 7. These figures provide graphical depictions of how these systems behave both in two-dimensional and one-dimensional contexts. They illustrate how the variables evolve over time and space, showing the interaction and synchronization between different components within each system.

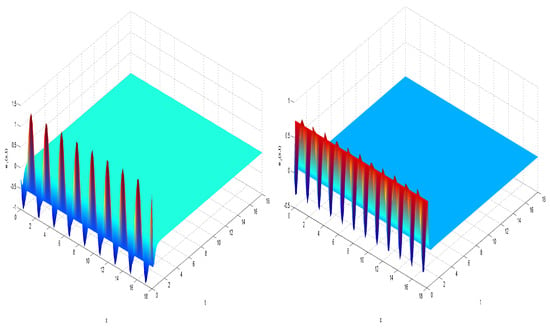
Furthermore, Figure 6 and Figure 7 offer numerical insights into the spatiotemporal solutions of the error synchronization system (39). These figures demonstrate how discrepancies between the master and slave systems, as represented by the error variables ${\mathfrak{e}}_1$ and ${\mathfrak{e}}_2$, diminish over time. Specifically, as time t approaches $t_2^{*}=17.9432s$, the errors converge to zero, indicating that the systems achieve synchronization within a finite time frame.

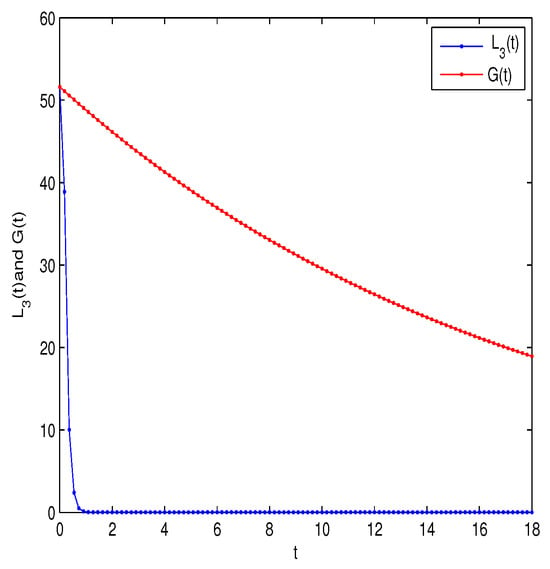
Figure 8 complements these findings by showcasing the behavior of the Lyapunov function ${\mathcal{L}}_3\left(t\right)$. It highlights that ${\mathcal{L}}_3\left(t\right)$ steadily approaches zero as t approaches $t_2^{*}=17.9432s$, reinforcing the finite-time stability observed in the synchronization process.

Together, these visual and numerical representations provide comprehensive evidence of the finite-time synchronization achieved in the studied systems (9), (29), and (39), offering valuable insights into their spatiotemporal dynamics and stability properties.

7. Conclusions

In this study, the Lengyel-Epstein reaction-diffusion system effectively models the chlorite-iodide-malonic acid (CIMA) reaction, demonstrating the emergence of Turing patterns within a bounded domain. We have established the existence of a unique solution for this system, constrained by positive constants. The equilibrium point ${\mathcal{E}}^{*}=\left({\displaystyle \frac{\mathfrak{a}}{5}},1+{\displaystyle \frac{{\mathfrak{a}}^2}{25}}\right)$ serves as a finite-time stable equilibrium under specific conditions regarding the concentrations of the activator and inhibitor. The settling time associated with this stability provides crucial insights into the dynamics of the system. This work lays the foundation for further investigation into finite-time stability and synchronization in reaction-diffusion systems, with potential implications in various fields such as biological pattern formation and chemical processes.

The strategy for achieving finite-time synchronization in reaction-diffusion systems aims to establish rapid coherence among spatially distributed components within a specified time frame. By implementing specific linear controllers and utilizing the Mittag-Leffler function to quantify settling times, we demonstrate that the master-slave systems described by Equations (9) and (29) can achieve stable synchronization within finite time intervals. This synchronization is ensured by the designed control laws ${\mathcal{C}}_1$ and ${\mathcal{C}}_2$, which drive the error dynamics to zero as time approaches the respective settling times $t^{*}$ and $t_2^{*}$. The analytical framework, supported by Theorems 3 and 4, provides a rigorous basis for understanding and achieving finite-time synchronization in complex reaction-diffusion systems.

To validate our theoretical findings and demonstrate the practical efficacy of the proposed approach, we conducted numerical simulations using MATLAB. Two distinct scenarios were examined: the first involving a fractional-order nonlinear system and the second focusing on a master-slave system with linear control. These simulations confirmed the finite-time stability and synchronization of both systems, as anticipated by our theoretical analyses. The graphical representations and numerical results presented in Figure 1, Figure 2, Figure 3, Figure 4, Figure 5, Figure 6, Figure 7 and Figure 8 provide compelling evidence of the systems’ behaviors over time and space, illustrating their convergence to stable states within defined time frames. These findings substantiate the applicability and robustness of the proposed methodologies in achieving finite-time synchronization in complex dynamical systems.