Interface Splitting Algorithm: A Parallel Solution to Diagonally Dominant Tridiagonal Systems

Abstract

We present an interface-splitting algorithm (ITS) for solving diagonally dominant tridiagonal systems in parallel. The construction of the ITS algorithm profits from bidirectional links in modern networks, and it only needs one synchronization step to solve the system. The algorithm trades some necessary accuracy for better parallel performance. The accuracy and the performance of the ITS algorithm are evaluated on four different parallel machines of up to 2048 processors. The proposed algorithm scales very well, and it is significantly faster than the algorithm used in ScaLAPACK. The applicability of the algorithm is demonstrated in the three-dimensional simulations of turbulent channel flow at Reynolds number 41,430.

1. Introduction

The numerical solution process for tridiagonal systems is a crucial task in scientific computing, such as in, for example, wavelets [1,2,3], spline interpolations [2], and numerical simulations of partial differential equations, such as heat transfer problems [4], convection–diffusion phenomena [5,6], and computational fluid dynamics [7,8], among others. Traditionally, the approximation schemes used in the finite difference method (FDM) and the finite volume method (FVM) are explicit schemes that are very easy to parallelize by using ghost cells that are padded to the actual computing domain. These ghost cells act as a surrogate for the true data, which are actually being solved on other processors. However, explicit schemes often exhibit relatively poor resolving power compared to implicit schemes. Lele [5] proposed to use compact schemes to approximate the first and second derivatives. He shows that, in a broad spectrum problem where the fundamental physics contains a vastly different range of length scale, a compact scheme is superior to the explicit scheme of the same order of accuracy. For example, instead of computing the second derivative through an explicit scheme, he suggests using compact higher-order schemes such as

$$l_i{T}_{i-1}^{″}+d_i{T}_i^{″}+r_i{T}_{i+1}^{″}={\kappa }_i{\varphi }_{i+1}+{\varsigma }_i{\varphi }_{i-1},$$

(1)

which is considerably more efficient than the explicit scheme of the same convergence rate. The parameters $l_i$, $d_i$, $r_i$, ${\kappa }_i$, and ${\varsigma }_i$ are the approximation coefficients. These compact schemes have far-reaching implications, serving as a foundation for diverse algorithms in various fields. This includes applications in Navier–Stokes equations [9,10,11], magnetohydrodynamics [12], acoustics [13,14], chemical reacting flow [15], as well as emerging discretization approaches like finite surface discretization [8,16,17] and the multi-moment method [6].

When numerical grids sufficiently capture the underlying phenomenon, employing high-order numerical methods can yield remarkable efficiency. Hokpunna et al. [7] demonstrate that a compact fourth-order scheme outperforms the classical second-order finite volume method (FVM) by a factor of 10. The efficiency improvement continues with the sixth-order compact finite surface method [8], which is 2.7 times more effective than the compact fourth-order FVM. Thus, the integration of a compact scheme in physical simulations significantly accelerates scientific research. However, the equation mentioned above needs an efficient solution method for solving diagonally dominant tridiagonal systems in parallel. The implicit nature that enhances the approximation’s resolving power introduces a directional dependency (in this case, i). The simplest problem configuration is illustrated in Figure 1. Efficient parallelization of the solution process in this context is not straightforward.

Applications in the previously mentioned areas often necessitate transient solutions with an extensive number of grid points. This scale is still challenging today even for massively parallel computer systems. For instance, isotropic turbulence simulations conducted on the Earth Simulator to explore turbulent flow physics involved up to 68 billion grid points [18,19,20]. Applying a compact scheme to this case involves solving tridiagonal systems with a system size of 4096 and a substantial number of right-hand sides (rhs), amounting to ${4096}^2$. Similarly, in wall-bounded flows, Lee and Moser [21] utilized 121 billion grid points for solving one problem. The computational power required for these problems far surpasses the capabilities of shared memory computers and requires distributed memory computers for the simulation. Despite the remarkable scale of these simulations, the Reynolds numbers in these cases are still far smaller than those seen in industrial applications. Therefore, efficient parallel algorithms for solving such systems are in demand.

Let us consider a cooling down process of a metal slab that was initially heated with the temperature distribution $T(x,y,z,0)=\Theta (x,y,z)$ i.e., $\forall (x,y,z)\in \Omega$, with the following governing equation:

$$\frac{\partial T}{\partial t}-\Gamma \Delta T=0,$$

(2)

where $\Gamma$ is the Péclet number, and the boundary condition is homogeneous. We can evolve the temperature in time by solving

$$T^{n+1}=T^n+\Gamma {\int }_{t_n}^{t_{n+1}}\left(\frac{{\partial }^{2}T}{\partial x^2}+\frac{{\partial }^{2}T}{\partial y^2}+\frac{{\partial }^{2}T}{\partial z^2}\right)dt.$$

(3)

The spatial approximation from the compact scheme (Equation (1)) can be used to obtain the three second derivatives in this equation. The implicitness of the compact scheme is only carried in one direction. Thus, for the above setting, we have three independent linear systems. If an explicit time integration is used for Equation (3), each second derivative of the Laplacian must be evaluated and then summed up to compute the time integral. The linear system of equation (LSE) at each time step is

$$\mathbf{AX}=\mathbf{B},$$

(4)

where $\mathbf{X}=\left[{\mathbf{x}}_1|\dots |{\mathbf{x}}_{Nx\times Ny}\right]$ and $\mathbf{B}=\left[{\mathbf{b}}_1|\dots |{\mathbf{b}}_{Nx\times Ny}\right]$, the augmentation of the unknown and the right-hand vectors, respectively. Each unknown vector ${\mathbf{x}}_i$ is the second derivative containing $Nz$ members.

Let us consider a simple setting depicted in Figure 1. Here, the domain is divided and distributed to two processors, $P_1$ and $P_2$. The two domains are separated at the midplane in the k direction. It is not straightforward to find the solution to the LSE of ${\partial }^{2}T/\partial z^2$ because the right-hand sides are located on different processors. In this setting, the linear system for ${\partial }^{2}T/\partial x^2$ and ${\partial }^{2}T/\partial y^2$ can be solved without any problem because the needed data are located within the processor. It should be clear that, in a large scaled simulation, there will be multiple cuts in all three directions. The missing dependency across the interfaces has to be fulfilled by some means.

It is clear that the approximation in each tuple $(i,j)$ normal to the $xy$-plane is independent of one another, and one can transfer half of the missing data to one processor, solve the systems, and then transfer the solution back to it. This approach is called the transpose algorithm [22]. This algorithm achieves the minimum number of floating point operations, but it has to relocate a lot of data. The minimum data transfer of this algorithm is $NxNyNz$. This approach is therefore not suitable for massively parallel computers in which the floating point operations are much faster than the intercommunication. Another approach that achieves the minimum number of floating point operations and also the minimum amount of data transfer is the pipelined algorithm [23]. In this approach, the tuples are solved successively after the dependency is satisfied. For example, the processor $p_1$ can start the forward elimination first on the $(1,1)$ tuple until the mth row and then send the result to $p_2$. Once $p_2$ obtains the data, it can start the forward elimination on that tuple, and $p_1$ can work on the forward elimination of the next tuple. The simplest pipelined algorithm will send a real number $2NxNy$ times per interface. The performance of this algorithm depends heavily on the latency and availability of the communication system.

When designing an algorithm, the designer should be aware of the disproportion between the data transfer and computing power. Take the AMD 7763 processor as an example: it has a memory bandwidth ($B{W}_{mem}$) of 205 GBytes/s, while its theoretical peak performance reaches 3580 giga floating point operations per second (GFLOPS). This performance is based on the fused–multiplied–add operation that needs four data for each calculation. For the processor to work at the peak rate, it would need to obtain the data at 114,560 GB/s (for the double precision data). Let us call this the transfer rate $B{W}_{peak}$. The ratio $B{W}_{peak}$/$B{W}_{mem}$ is about 560. This disparity requires algorithms to excel in terms of communication efficiency. In parallel computing, things become even more difficult regarding the interconnection between computing nodes. A dual-socket computing node with this setting linked to other nodes by a network bandwidth $B{W}_{net}$ = 80 GB/s would have the ratio $B{W}_{peak}$/$B{W}_{mem}$ = 2200. For a GPU cluster with a recent NVIDIA H100, the ratio of the $B{W}_{peak}$/$B{W}_{net}$ is even higher at 16,320. And this unbalance keeps growing. This disparity between the computational power and the ability to communicate between computing units renders fine-grain parallel algorithms unsuitable for the current massively parallel computer systems. Coarse-grained parallelism such as that in [24,25,26,27,28,29] is thus preferable. These coarse-grained algorithms send data less frequently but in a larger package. Lawrie and Sameh [30], Bondeli [26], and Sun [27] developed algorithms specialized for tridiagonal systems with the diagonal dominant property. The reduced parallel diagonal dominant algorithm (RPDD) in [27] can use p processors to solve a tridiagonal system of n equations with $\gamma$ right-hand sides using a complexity of $(5n/p+4J+1)\gamma$ operations (with some small number J described later). This algorithm is very efficient for this problem.

In this paper, we present a new interface-splitting algorithm (ITS) for solving diagonally dominant tridiagonal linear systems with the system size of n and $\gamma$ right-hand sides on p processor. The algorithm has a complexity of $(5n/p+4J-4)\gamma$. The idea is to reduce the communications, truncate the data dependency, and fully take advantage of bi-directional communication. The proposed method makes use of exponential decay in the inverse of diagonally dominant matrices explained in [31]. The proposed scheme is competitive and applicable for non-Toeplitz as well as periodic systems and non-uniform meshes. It has less complexity than the algorithm presented in [27], requires one synchronization step fewer, and the cost of the data transfer is potentially halved. Therefore, the proposed algorithm is less sensitive to load balancing and network congestion problems.

The presentation of this paper is organized as follows. First, we present the interface-splitting algorithm and then discuss its complexity and accuracy. The accuracy and the performance of the algorithm are evaluated on four specialized systems, starting with a single-node Intel Xeon 8168, and then SGI ALTIX 4700, IBM BladeCenter HS21XM, and NEC HPC 144Rb-1. The performance of the proposed algorithm is compared with the ScaLAPACK and the RPDD algorithms. After that, the application to Navier–Stokes equations is presented, followed by the conclusion and remarks.

2. Interface-Splitting Algorithm

2.1. Concept

The decomposition of the domain on different processors led to the problem mentioned earlier in Figure 1. The second processor cannot start the forward elimination because the interface value ($x_m$) is not known. However, if they have already computed the central row of $\mathbf{C}={\mathbf{A}}^{-\mathbf{1}}$, then they can both compute

$$x_m=\sum _{j=1}^{2m}{c}_{mj}{b}_j=\underset{\mathrm{from}\mathrm{processor}1}{\sum _{j=1}^m{c}_{mj}{b}_j}+\underset{\mathrm{from}\mathrm{processor}2}{\sum _{j=m+1}^{2m}{c}_{mj}{b}_j}$$

after exchanging a single real number. In this way, both processors can continue to solve their systems without further communication. It is well known that the inverse of the diagonally dominant tridiagonal matrix decays away from the diagonal, both row and column. The minimum decay rate of non-symmetric matrices has been developed in [32] and [31]. Thus, the interface value can be computed from the row inverse of a smaller matrix, e.g.,

$$\begin{array}{c}\mathcal{A}=\left[\begin{array}{cc}{d}_{m-1}& r_{m-1}\\ l_m& d_m\\ ine& l_{m+1}\\ & \end{array}\mid \begin{array}{cc}& \\ r_m& \\ d_{m+1}& r_{m+1}\\ l_{m+2}& d_{m+2}\end{array}\right],\end{array}$$

(5)

by computing

$$x_m\approx \sum _{j=m-1}^{m+2}{\left({\mathcal{A}}^{-1}\right)}_{mj}{b}_j=\underset{\mathrm{from}\mathrm{processor}1}{\sum _{j=m-1}^m{\left({\mathcal{A}}^{-1}\right)}_{mj}{b}_j}+\underset{\mathrm{from}\mathrm{processor}2}{\sum _{j=m+1}^{m+2}{\left({\mathcal{A}}^{-1}\right)}_{mj}{b}_j}.$$

This truncation introduces an error into the solution. However, in the system that originated from a simulation-based problem, there is a certain level of accuracy in how that particular system represents the true value. For example, the compact scheme in Equation (1) differs from the true second derivative by the size of the local truncation error (LTE). Any errors that are much smaller than LTE will not be observable. For example, in most approximations of the compact scheme above, the LTE should be larger than 1 $\times {10}^{-10}$. When such system is solved by a direct method under double precision, the error due to the solution process should be on the order of 1 $\times {10}^{-14}$. Using quadruple precision can reduce the solution error to about 1 $\times {10}^{-32}$, and the error of the differentiation would still be  1 $\times {10}^{-10}$.

In the next step, we explain the algorithm in detail, including the strategy for reducing the number of operations and controlling the truncation errors.

2.2. The Parallel Interface-Splitting Algorithm

For simplicity of notation, let us consider a tridiagonal system of size n with a single right-hand side,

$$\mathbf{A}\mathbf{x}=\mathbf{b},$$

(6)

where $\mathbf{A}$ is a strictly diagonal dominant matrix, $\mathbf{A}=[l_i,d_i,r_i]$, $|d_i| > |l_i| + |r_i|$, and $l_1=r_n$ = 0. In order to solve this system in parallel, one can decompose the matrix using $\mathbf{A}=\mathbf{TQ}$ and solve the original system in two steps:

$$\begin{array}{c}\mathbf{T}\mathbf{v} = \mathbf{b},\end{array}$$

(7)

$$\begin{array}{c}\mathbf{Q}\mathbf{x} = \mathbf{v}.\end{array}$$

(8)

The first equation computes the solution at the interface using the coefficients stored locally. This factorization can be considered as a preprocessing scheme where the right-hand side is modified such that the solution of the simpler block matrices delivers the desired result. The partitioning algorithm [24] and the parallel line solver [33] belong to this type.

Suppose that $\mathbf{A}$ is a tridiagonal matrix of size $n=pm$, where p is the number of processors and m is the size of our subsystems. The kth processor is holding the right-hand side ${\mathbf{b}}^k=b_j$, $(k-1)m+1\le j\le km$. Here, it is sufficient to consider one right-hand side. The application to multiple right-hand sides is straightforward.

Let ${\mathbf{D}}^k$ be the kth block subdiagonal matrix of $\mathbf{A}$, that is, ${\mathbf{D}}^k=\left\{a_{ij}\right|(k-1)m+1\le i,j\le km\}$ and ${\mathbf{N}}^k$ is the matrix ${\mathbf{D}}^k$, except the last row is replaced by that of the identity matrix:

$${\mathbf{N}}^k=\left[\begin{array}{cccc}{d}_{\nu +1}& r_{\nu +1}& & \\ l_{\nu +2}& d_{\nu +2}& r_{\nu +2}& \\ & \ddots & \ddots & \ddots \\ & & l_{\nu +m-1}& d_{\nu +m-1}\\ ine& & & \end{array}\mid \begin{array}{c}\\ \\ \\ r_{\nu +m-1}\\ 1\end{array}\right]$$

(9)

Instead of using the block diagonal matrix of ${\mathbf{D}}^k$ as an independent subsystem as in the alternative algorithms, the interface-splitting algorithm builds the matrix $\mathbf{Q}$ up form the special block matrix ${\mathbf{N}}^k$:

$$\mathbf{Q}=\left[\begin{array}{cccc}{\mathbf{N}}^1& & & \\ & {\mathbf{N}}^2& & \\ & & \ddots & \\ & & & {\mathbf{N}}^p\end{array}\right]$$

(10)

The neighboring subsystems (kth and $(k+1)$th) are separated by the kth interface, which is the last row of the kth subsystem. Note that if we use ${\mathbf{D}}^k$ as an independent subsystem, the algorithm will be the transposed version of the PDD algorithm.

The algorithm corresponding to the selected decomposition is given by

$$\begin{array}{c}{\mathbf{A}}^T{\mathbf{z}}_k = {\widehat{\mathbf{g}}}_{km},\end{array}$$

(11)

$$\begin{array}{c}{\mathbf{f}}^k = \left({\mathbf{z}}^k·\mathbf{b}\right){\widehat{\mathbf{g}}}_{km}+l_1^k\left({\mathbf{z}}^{k-1}·\mathbf{b}\right){\widehat{\mathbf{g}}}_{(k-1)m+1},\end{array}$$

(12)

$$\begin{array}{c}{\mathbf{v}}^k = {\mathbf{b}}^k-{\mathbf{f}}^k,\end{array}$$

(13)

$$\begin{array}{c}{\mathbf{N}}^k{\mathbf{x}}^k = {\mathbf{v}}^k,\end{array}$$

(14)

where ${\widehat{\mathbf{g}}}_{km}$ is the vector whose $km$th component is one and zero otherwise. The vector ${\mathbf{z}}^k$ is given by $z_j^k=c_{km,j}$, $1\le j\le n$, with $\mathbf{C}={\mathbf{A}}^{-1}$, which is the result of the decomposition. For the system in Figure 1, we solve Equation (7) by setting

$$\mathbf{v}={\mathbf{T}}^{-1}\mathbf{b}=\left(\begin{array}{ccccccc}1& 0& 0& & & & \\ \ddots & \ddots & \ddots & & & & \\ & 0& 1& 0& & & \\ c_{m,1}& \cdots & c_{m,m-1}& c_{m,m}& c_{m,m+1}& \cdots & c_{m,2m}\\ & & & 0& 1& 0& \\ & & & & \ddots & \ddots & \ddots \\ & & & & & 0& 1\end{array}\right)\left(\begin{array}{c}{b}_1\\ ⋮\\ b_{m-1}\\ b_m\\ ⋮\\ ⋮\\ b_{2m}\end{array}\right).$$

(15)

This means the vector ${\mathbf{v}}^k$ can be obtained by manipulating b only at the top and the bottom elements ($b_1^k$ and $b_m^k$).

If we think of the vector ${\left({\mathbf{z}}^k\right)}^T$ as the spikes similar to that in the SPIKE algorithm, our spike can be thought of as two spikes pointing away from $(km,km)$ horizontally, unlike the spikes of the RPDD and SPIKE algorithms, which are column spikes (vertical).

2.3. Cost Savings

The key to the efficiency of the proposed algorithm is based on the decay of the matrix $\mathbf{C}$. By exploiting this decay, we truncate scalar product ${\mathbf{z}}^k·\mathbf{b}$ to 2J terms. This truncation introduces an approximation to ${\tilde{x}}_m^k$, which is then transferred to ${\mathbf{f}}^k$ and propagates to the solutions in the inner domain. Letting ${\mathbf{e}}^k={\mathbf{f}}^k-{\tilde{\mathbf{f}}}^k$, the kth subsystem of $\mathbf{A}$ then takes the following form:

$${\mathbf{N}}^k{\mathbf{x}}^k={\mathbf{b}}^k-{\tilde{\mathbf{f}}}^k-{\mathbf{e}}^k.$$

(16)

The components of the vector ${\mathbf{f}}^k$ are zero except for the first and the last components, which are given by $f_1^k=l_m^{k-1}{\tilde{x}}_m^{k-1}$ and $f_m^k=-{\tilde{x}}_m^k+b_m^k$. The vector ${\mathbf{e}}^k$ represents the errors in the solution due to the approximation at the top. It should be kept in mind that the elements of ${\mathbf{e}}^k$ are non-zero only in the first and the last components. The interface-splitting algorithm neglects the error term ${\mathbf{e}}^k$ and solves the following system:

$${\mathbf{N}}^k{\tilde{\mathbf{x}}}^k={\tilde{\mathbf{v}}}^k={\mathbf{b}}^k-{\tilde{\mathbf{f}}}^k.$$

(17)

As mentioned earlier, it is not necessary to find the actual inverse of the matrix. It is sufficient to compute ${\mathbf{z}}^k$ from ${\mathbf{A}}^T{\mathbf{z}}^k={\widehat{\mathbf{g}}}_{km}^k$. This way, the inversion of the matrix $\mathbf{A}$ is avoided. A further savings can be achieved by reducing the matrix $\mathbf{A}$ to a submatrix $\mathcal{A}$, enclosing the interface.

To summarize, the ITS algorithm consists of seven steps described in the following algorithm.

• The Algorithm

Letting J and L be some small positive integers, then the interface splitting algorithm is defined as follows (Algorithm 1):

Algorithm 1 The interface splitting algorithm.

1: On $p_k$ ($1\le k\le p$), allocate ${\mathbf{N}}^k$, ${\mathbf{b}}^k$, ${\mathbf{x}}^k$ and $l_1^k$. 2: On $p_k$ ($k\le (p-1)$), 1. allocate submatrix $\mathcal{A}=a_{ij}$, $(km-J-2L+1)\le i, j\le (km+J+2L)$, where $a_{ij}=\mathbf{A}$; 2. allocate $\widehat{{\mathbf{g}}^{\prime }}={\widehat{g}}_{km,i}$, $(km-J-2L+1)\le i\le (km+J+2L)$, where ${\widehat{g}}_{km,i}$ is the ith element of ${\widehat{\mathbf{g}}}_{km}$; 3. solve $\mathcal{A}{\mathbf{z}}^{\prime k}=\widehat{{\mathbf{g}}^{\prime }}$       (Equation (11)); 4. allocate ${\mathbf{s}}^k=z_j^{\prime k}$, $(km-J+1)\le j\le km$; 5. allocate $\mathbf{u}=z_j^{\prime k}$, $(km+1)\le j\le (km+J)$ and send it to $p_{k+1}$. 3: On $p_k$ ($2\le k$), 1. receive $\mathbf{u}$ from $p_{k-1}$ and store it in ${\mathbf{t}}^k$. 4: Compute parts of the solution at the interface. 1. On $p_k$ ($k\le (p-1)$), $a_b^k={\mathbf{s}}^k·{\mathsf{b}}_b^k$; 2. On $p_k$ ($2\le k$), $a_t^k={\mathbf{t}}^k·{\mathsf{b}}_t^k$, where ${\mathsf{b}}_t^k$ and ${\mathsf{b}}_b^k$ are the first and the last J elements of ${\mathbf{b}}^k$, respectively. 5: Communicate the results. 1. On $p_k$ ($k\le (p-1)$), send $a_b^k$ to $p_{k+1}$ and receive $a_t^{k+1}$ from it. 2. On $p_k$ ($2\le k$), send $a_t^k$ to $p_{k-1}$ and receive $a_b^{k-1}$ from it. 6: Modify the rhs. 1. On $p_k$ ($k\le (p-1)$), ${\tilde{v}}_m^k=a_b^k+a_t^{k+1}$; 2. On $p_k$ ($2\le k$), ${\tilde{v}}_1^k=b_1^k-(a_t^k+a_b^{k-1})l_1^k$. Note: ${\tilde{\mathbf{v}}}_m$ is stored in place of ${\mathbf{b}}^k$. 7: On $p_k$$1\le k\le p$, solve ${\mathbf{N}}^k{\mathbf{x}}^k={\tilde{\mathbf{v}}}^k$      (Equation (14)).

In this algorithm, J is the number of terms that we chose to truncate the scalar product. The interface-splitting algorithm is equivalent to the direct method up to the machine’s accuracy (ϵ) if ${\mathbf{z}}^k$ decays below ϵ within this truncation length, i.e., $z_i^k<ϵ$ for $|i-km|>J$.

Supposing the J was chosen and the omitted terms in the scalar product are not larger than ${\epsilon }_c$, then we do not need to compute ${\mathbf{z}}^k$ to full precision. In order to maintain the accuracy of the smallest terms retained for the scalar product, we need to solve a larger system containing the $\left(km\right)$th row. In the second step, we chose $\mathcal{A}$, whose dimension is $2(J+L)$, with $L<J$. The choice of L and its effects on the accuracy of ${\mathbf{z}}^{\prime k}$ will be explained later.

One of the most important features of the ITS algorithm (Algorithm 1) lies in step 4. Instead of using one-way communication in two sequential steps as in the RPDD algorithm, the ITS algorithm communicates in only one step. The communications with the two nearest neighbors are allowed to overlap. Therefore, the cost of the communication can be reduced by up to $50\%$ with the ITS algorithm, depending on the actual capability of the interconnection link and the network topology.

The error of the interface-splitting algorithm consists of the approximation error of $x_m^k$ and the propagation of this error into the solutions in the inner domain. The factors determining the accuracy of this approximation are: (i) the row diagonal dominance factor ${\sigma }_i= |d_i|/(|l_i| + |r_i\left|\right)$ and (ii) the matrix bandwidth $2J$ used to compute ${\tilde{x}}_m^k$. The complexity and the effect of $\sigma$ on L and J are described in the next section.

2.4. Comparison to Other Approaches

Our approach exploits the decay of the LU decomposition of the system. This property has been exploited many times already in the literature. The low complexity of the RPDD algorithm is achieved by the same means, apart from RPDD [27] and the truncated SPIKE [32], in which the amount of data transfer is optimal. McNally, Garey, and Shaw [34] developed a communication-less algorithm. In this approach, each processor $p^k$ holding the subsystem ${\mathbf{x}}^k$ solves a larger system enveloping this subsystem. This new system has to be large enough such that the errors propagated into the desired solution ${\mathbf{x}}^k$ due to the truncation of the system can be neglected. It can be shown that, for the same level of accuracy, this approach requires J times more data transfer than the proposed algorithm. This high communication overhead and the increase in the subsystem size make this algorithm non-competitive for multiple-rhs problems. A similar concept has been applied to compact finite differences by Sengupta, Dipankar, and Rao in [35]. However, their algorithm requires a symmetrization that doubles the number of floating point operations. It should be noted that the current truncated SPIKE implementation utilizes bidirectional communication as well. However, this improvement is not made public. It will be shown later that such a simple interchange to the communication pattern can greatly improve the performance of parallel algorithms. There are a number of algorithms using biased stencils that mimic the spectral transfer of the inner domain [36,37,38]. In this approach, the user has no control over the error of the parallel algorithm. Even though the local truncation error of the approximation at the boundary is matched with that of the inner scheme, the discrepancies in spectral transfer can lead to a notable error at the interface in under-resolved simulations.

3. Complexity, Speedup, and Scalability

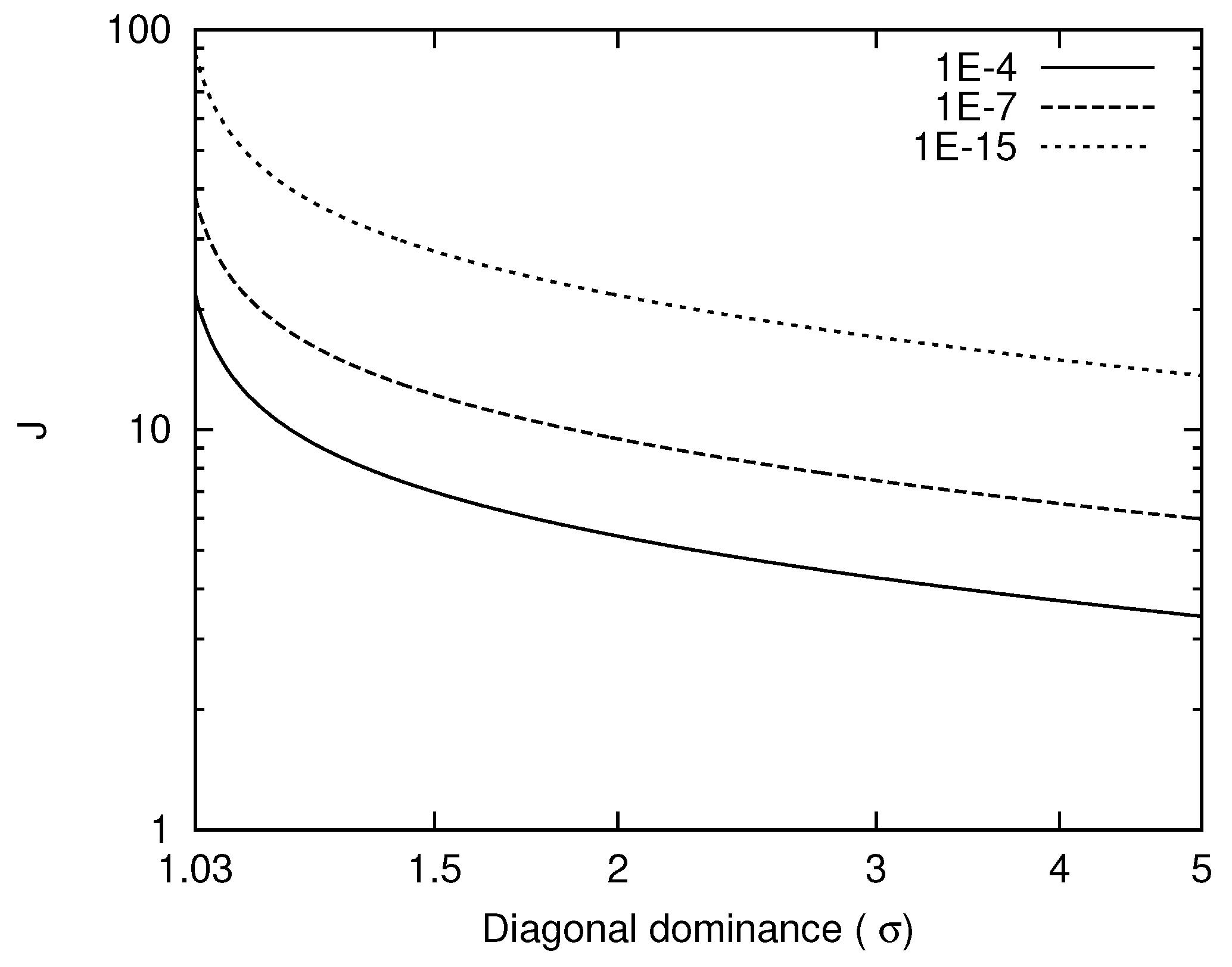
The complexity of the interface-splitting algorithm depends on two parameters, the one-digit decay length L and the half-matrix bandwidth J. These numbers are determined by the cut-off threshold ${\epsilon }_c$ and the degree of diagonal dominance of the system ($\sigma =min\left\{{\sigma }_i\right\}$). For Toeplitz systems $\mathbf{T}=[1,\lambda ,1]$, the entries of the matrices in the LU-decomposition of this system converge to certain values, and the half-matrix bandwidth J can be estimated from them. Bondeli [39] deduces this convergence and estimates J with respect to the cut-off threshold ${\epsilon }_c$ by

$$J=-\frac{ln{\epsilon }_c}{ln\left(\frac{1}{2}\left(\left|\lambda \right|+\sqrt{\left({\lambda }^2-4\right)}\right)\right)}.$$

(18)

For example, J equals 7 and 27 for ${\epsilon }_c={10}^{-4}$ and ${10}^{-15}$ when $\lambda =4$ ($\sigma =2$), which corresponds to the fourth-order compact differentiation [5] and the cubic spline interpolation. These two numbers are much smaller than the usual size of the subsystem used in scientific computing. Effects of diagonal dominance on J are shown in Figure 2. The proposed algorithm is thus not recommended for a very small $\sigma$. This includes the inversion of the Laplace operator. For solving such systems, we refer the reader to the work of Bondeli [26,39], in which he adapts his DAC algorithm for the Poisson equation. In the fourth-order compact schemes, the diagonal dominance of the first derivative and the second derivative are 2 and 5, respectively. In sixth-order compact schemes, the values are $1.5$ and $2.75$, respectively. Therefore, the proposed scheme is well-suited for these approximations. On the contrary, if the system is not diagonally dominant, J will decay linearly to zero at half the size of the global system e.g., $pm/2$. In such a system, the proposed algorithm will perform poorly. It will be beneficial to combine the ITS and RPDD algorithms in this situation. Using ITS as the pre-processor will reduce the amount of back-correction in the RPDD. This approach will have better cache coherence, in contrast to computing the full correction in any single method by going from one end of the system to the other.

3.1. Complexity

The interface-splitting algorithm is an approximate method, but it can be made equivalent to other direct methods by setting ${\epsilon }_c$ to machine accuracy. The minimum decay rate of non-symmetric matrices has been developed in [31,32] and can be used to approximate J. However, the matrix bandwidth obtained in this way is usually too pessimistic for the computation to be efficient because the minimum decay rate depends on $\sigma$, which may not be in the vicinity of the interfaces. In multiple-rhs problems, it is worth solving the subdiagonal matrix consisting of the two subsystems enclosing the kth interface and then choosing J according to the desired cut-off threshold. In single-rhs problems, backward elimination of ${\mathbf{D}}^{k-1}$ and forward elimination of ${\mathbf{D}}^k$ could be an effective way to determine the appropriate J.

In the second step of the algorithm, we have to solve a linear system for the $km$th row of the matrix $\mathbf{C}$. This system has to be larger than $2J$ such that the truncated ${\mathbf{z}}^k$ is sufficiently accurate. In this work, we solve a system of size $2J+2L$, which ensures that the smallest element of the truncated ${\mathbf{z}}^k$ is at least correct in the first digit. Since it is unlikely that one would be satisfied with errors larger than ${10}^{-4}$, we assume that $L=J/4$ and use this relation to report the operation count of the ITS algorithm in

Table 1. Computation and communication costs of the interface-splitting algorithm. The coefficients of the system are assumed to be known only to the owner processor. For multiple-rhs problems, the cost in the first to the third step is neglected. The symbol $\gamma$ stands for the number of rhs, $\alpha$ is the latency (seconds per communication) of the bandwidth, and $\beta$ is the data bandwidth (operands per second).

System	Matrix	Sequential	Interface-Splitting Algorithm
			Computation	Communication
Single-rhs	Non-periodic	$8n-7$	$8\frac{n}{p}+24J-11$	$2\alpha +19\beta J/4$
	Periodic	$14n-16$	$8\frac{n}{p}+24J-11$	$2\alpha +19\beta J/4$
Multiple-rhs	Non-periodic	$(5n-3)\gamma$	$\left(5\frac{n}{p}+4J-4\right)\gamma$	$\alpha +\beta \gamma$
	Periodic	$(7n-1)\gamma$	$\left(5\frac{n}{p}+4J-4\right)\gamma$	$\alpha +\beta \gamma$

. A cut-off threshold lower than this leads to lower complexity. Thus, we assume $L=J/4$ reflects the practical complexity in general applications. In this table, we also list the communication time, which can be expressed by a simple model: ${\tau }_{com}=\alpha +\beta \Delta$, where $\alpha$ is the fixed latency, $\beta$ is the transmission time per datum, and $\Delta$ is the number of data. Note that, for multiple-rhs problems, we neglect the cost of the first to the third step of the algorithm because the number of rhs is considered to be much larger than m.

In Table 1, the complexity of the proposed algorithm is presented, assuming that each processor only has knowledge of its subsystem and that they do not know the global system. The coefficients thus have to be sent among the neighbors, leading to a higher data transfer in single-rhs problems. Otherwise, the communication is reduced to that of the multiple-rhs problem.

3.2. Speedup and Scalability of the Algorithm

Using Table 1, we can estimate the absolute speedup of the ITS algorithm. The absolute speedup here means the solution time on a single processor from the fastest sequential algorithm divided by the time used by the ITS algorithm on p processors. In theoretical complexity analysis, one usually assumes a constant value of communication bandwidth. In practice, the interconnection network is not completely connected, and the computing nodes are usually linked by less expensive topologies such as tree, fat tree, hypercube, array, etc. The data bandwidth is thus a function of the number of processors as well as the amount of the data being transferred. Let the communication cost be a function of p and $\gamma$, that is $\beta =\chi (p,\gamma )$, and assume that n and $\gamma$ are sufficiently large such that the latency and $1/n$ can be neglected. Then, the absolute speedup of the ITS algorithm in multiple-rhs problems is given by Equation (19) below:

$$\begin{array}{cc}\hfill {\mathcal{S}}_{\gamma }\left(p\right)& =\frac{p}{1+0.8\frac{{\displaystyle J}}{{\displaystyle m}}+0.2\frac{{\displaystyle \rho \chi (p,\gamma )}}{{\displaystyle m}}},\hfill \end{array}$$

(19)

where $\rho$ is the peak performance of the machine. The key numbers determining the performance of the interface-splitting algorithm are thus the ratios $J/m$ and $\rho \chi (p,\gamma )/m$. The first one is the computation overhead, and the latter is the communication overhead. If the ratio $J/m$ is small and $\chi$ is negligible, an excellent speedup can be expected, otherwise the algorithm suffers a penalty. For example, the absolute efficiency will drop from $92\%$ to $56\%$ when J is increased from $0.1m$ to m on multiple right-hand side systems.

In general, one must size the subsystem appropriately such that the speedup from load distribution justifies the increased complexity, overhead, and communication costs. In the previous speedup equation (Equation (19)), the function $\chi (p,\gamma )$ is the inverse of the data transfer rate, and the product $\rho \chi (p,\gamma )$ is simply the ratio of the peak performance (operation/s) to the data transfer rate (operand/s), similar to the one mentioned in the introduction. Therefore, as long as J is smaller than $4\rho \chi (p,\gamma )$, the overhead of the ITS algorithm will be less than the cost of the communication. For example, let us consider a cluster consisting of older-generation hardware such as dual AMD EPYC 7302 nodes connected by a 100 G network. The value of $\rho \chi (p,\gamma )$ is 983. During the latency time alone, which is (1 $\mathsf{\mu }$s), the processor could have solved a compact differentiation on a ${67}^3$ Cartesian grid. We already discussed this number in modern computers, and it is much higher than this value. Thus, the $4J$ overhead of the ITS algorithm is very small.

According to Equation (19), our algorithm is perfectly scalable because the speedup does not explicitly contain the number of processors, except for the one hidden in $\chi$. The cost of communication per datum $\chi (p,\gamma )$ is determined by the latency, the data bandwidth, and the topology of the interconnection networks among the computing nodes and the pattern of communication. When p and $\gamma$ are large, $\chi$ can be the major cost of the computation. Even if the exact formula for $\chi$ is not known, we can predict when the algorithm will be scalable for the scaled problem size (fixed $\gamma$ and m). Using the costs from Table 1 and substituting $\chi (p,\gamma )$ for $\beta$, it is easy to see that the proposed algorithm is scalable, i.e., $(S_{\gamma }(p+1)>S_{\gamma }\left(p\right))$ when $\partial \chi /\partial p>0$. This means that, as long as the interconnection network is scalable, the ITS algorithm is scalable.

Note that the algorithm assumes $J\le m$; if this is not true, the program adopting this algorithm should issue a warning or an error to the user. The user then can decide whether to adjust the size of the subsystem or extend the scalar product by including more processors.

4. Accuracy Analysis

In the previous section, we discussed the complexity and established the half-matrix bandwidth J for the selected cut-off threshold ${\epsilon }_c$. In this section, we analyze how the cut-off threshold propagates into the solution in the inner variables.

Solving Equation (16) for ${\mathbf{x}}^k$ is equivalent to solving the $(m+1)\times (m+1)$ linear system

$${\mathbf{F}}^k{\mathbf{u}}^k={\omega }^k$$

(20)

for ${\mathbf{u}}^k={\left[x_m^{k-1}{\left({\mathbf{x}}^k\right)}^T\right]}^T$ with

$${\mathbf{F}}^k=\left(\begin{array}{cc}1& {\mathbf{0}}^T\\ ine{\mathbf{w}}^k& {\mathbf{N}}^k\end{array}\right),{\omega }^k={[x_m^{k-1}{b}_1^k{b}_2^k\cdots b_{m-1}^k{x}_m^k]}^T,\mathrm{and}{\mathbf{w}}^k={[l_1^{k}0\cdots 0]}^T.$$

Due to the structure of ${\mathbf{N}}^k$, it follows that

$$\begin{array}{cc}\hfill {\mathbf{F}}^k& =\left(\begin{array}{c}1\\ ine{\psi }^k\\ ine0\end{array}\mid \begin{array}{c}{\mathbf{0}}^T\\ {\Pi }^k\\ {\mathbf{0}}^T\end{array}\mid \begin{array}{c}0\\ \xi \\ 1\end{array}\right),\hfill \end{array}$$

where ${\psi }^k={[w_1^{k}0\cdots 0]}^T$ and ${\xi }^k={[0\cdots 0r_{m-1}^k]}^T$. The vector $\mathbf{0}$ is a column vector of zero. Its size should be clear from the context. The interface-splitting algorithm injects an approximation in place of $x_m^{k-1}$ and $x_m^k$, changes the rhs to ${\tilde{\omega }}^k={[{\tilde{x}}_m^{k-1}{b}_1^k\cdots b_{m-1}^k{\tilde{x}}_m^k]}^T$, and solves

$${\mathbf{F}}^k{\tilde{\mathbf{u}}}^k={\tilde{\omega }}^k,$$

(21)

instead of the original system. This process introduces the following error into the solution:

$$\begin{array}{c}{\mathbf{h}}^k = {\tilde{\mathbf{u}}}^k-{\mathbf{u}}^k.\end{array}$$

It follows that the error in the solution vector satisfies

$$\begin{array}{c}{\mathbf{F}}^k{\mathbf{h}}^k = {\left[{\tilde{x}}_m^{k-1}{\left({\tilde{\mathbf{x}}}^k\right)}^T\right]}^T-{\left[x_m^{k-1}{\left({\mathbf{x}}^k\right)}^T\right]}^T,\end{array}$$

(22)

$$\begin{array}{c}{\mathbf{F}}^k{\mathbf{h}}^k = \left(\begin{array}{c}{e}_m^{k-1}\\ \mathbf{0}\end{array}\right)+\left(\begin{array}{c}\mathbf{0}\\ e_m^k\end{array}\right).\end{array}$$

(23)

Equation (23) indicates that the error at the inner indices ($h_i^k$, $1<i<m+1$) is a sum of the error propagated from both interfaces. In order to establish the error bound of the ITS algorithm, we first identify the position of the maximum error.

Proposition 1.

Errors of the interface-splitting algorithm for diagonally dominant tridiagonal matrices are maximal at the interfaces.

Proof. 

Since the errors of the interface-splitting algorithm $h_i^k$ in the inner domain satisfy Equation (23), that is,

$$d_i{h}_i^k=-l_i{h}_{i-1}^k-r_{i+1}{h}_{i+1}^k,$$

the error of the inner indices, i.e., $h_{i-1}^k$, $1<i<m$, is not larger than the maximum error introduced at the interface because

$$\begin{array}{c}|d_i{h}_i^k| \le |l_i{h}_{i-1}^k|+|r_i{h}_{i+1}^k|\\ |h_i^k| \le \frac{\left(|l_i|+|r_i|\right)}{|d_i|}\max \left(\right|h_{i-1}^k|,|h_{i+1}^k\left|\right)\\ |h_i^k| \le |{\sigma }_i\left|\max \right(|h_{i-1}^k|,|h_{i+1}^k\left|\right)<\max \left(\right|e_m^{k-1}|,|e_m^k\left|\right).\end{array}$$

□

In the next step, we assume that a small number ${\epsilon }_c$ is set as the error threshold and was used to truncate the vector ${\mathbf{z}}^k$. A small number J is the minimum $j>0$ satisfying $z_{km\pm j}^k>{\epsilon }_c$. The maximum error of the proposed algorithm thus consists of two parts: (i) the truncated terms and (ii) the round-off error in the calculation of the dot product in Step 3. The following theorem states that the sum of these errors is bounded by a small factor of the cut-off threshold.

Theorem 1.

The maximum error of the interface-splitting algorithm $e_{max}=x_k^m-{\tilde{x}}_m^k$ is bounded by

$$e_{max}\le \left[(2+L)ϵ+L{\epsilon }_c)\right]{\left|\mathbf{b}\right|}_{\infty },$$

(24)

with the cut-off threshold ${\epsilon }_c$ of the coefficient vector ${\mathbf{z}}^k$, the machine accuracy ϵ, and the length L, in which the magnitude of the coefficients is reduced by at least one significant digit.

Proof. 

First, let us assume that the rhs stored by the machine is exact, and let ${\mu }^k$ be the error in the coefficient vector ${\mathbf{z}}^k$ when it is represented by machine numbers ${\widehat{\mathbf{z}}}^k$; that is, ${\mu }^k={\widehat{\mathbf{z}}}^k-{\mathbf{z}}^k$. The hat symbol denotes that the number is a machine-accurate numerical value of the respective real number. Let $fl\left(x\right)$ be the floating point operation on x. For instance, if $\varphi$ and $\phi$ are real numbers, then $fl\left(\varphi \right)=\widehat{\varphi }$. The addition obeys the following inequalities:

$$\begin{array}{c}\hfill |fl(\widehat{\varphi }+\widehat{\phi })|\le |\widehat{\varphi }+\widehat{\phi }|+ϵ\le |\widehat{\varphi }|+|\widehat{\phi }|+ϵ.\end{array}$$

(25)

The numerical value obtained for ${\widehat{x}}_m^k$ by computing ${\left({\widehat{\mathbf{z}}}^k\right)}^T\mathbf{b}$ is thus

$$\begin{array}{c}{\widehat{x}}_m^k = fl\left(\sum _{j=1}^n\left(z_j^k+{\mu }_j^k\right)b_j^k\right)\end{array}$$

(26)

$$\begin{array}{c}{\widehat{x}}_m^k = fl\left(\sum _{j=1}^{km}\left(z_j^k+{\mu }_j^k\right)b_j^k\right)+fl\left(\sum _{j=km+1}^n\left(z_j^k+{\mu }_j^k\right)b_j^k\right)+{\delta }_1.\end{array}$$

(27)

For general matrices whose inverse does not decay, the error ${\delta }_1$ is bounded by $ϵ{\left|\mathbf{b}\right|}_{\infty }$, and the error in Equation (27) is given by $|{\widehat{x}}_m^k-x_m^k|\le nϵ{\left|\mathbf{b}\right|}_{\infty }$. Thus, the result can be inaccurate for a very large n. However, this is not the case for the matrices considered here.

On computers, a floating point number is stored in a limited mantissa and exponent. Adding a small number b to a very large number a will not change a if their magnitude differs from the range of the mantissa. In other words, $fl(\widehat{a}+\widehat{b})=fl\left(\widehat{a}\right)$ if $|\widehat{b}/\widehat{a}| <ϵ$. Since ${\mathbf{z}}^k$ decays exponentially, there is a smallest number L such that $\left|z_{j-L}^k\right|<\left|\frac{1}{10}{z}_j^k\right|$ for $j\le km$ and $\left|z_{j+L}^k\right|<\left|\frac{1}{10}{z}_j^k\right|$ for $j\ge km$. Thus, let us assume that the machine accuracy $ϵ$ lies in $({10}^{-\eta },{10}^{-\eta +1})$; for some natural number $\eta$, we can rewrite (27) as

$$\begin{array}{c}{\widehat{x}}_m^k = fl\left(\sum _{j=km-\eta L+1}^{km}\left(z_j^k+{\mu }_j^k\right)b_j^k\right)+fl\left(\sum _{j=km+1}^{km+\eta L}\left(z_j^k+{\mu }_j^k\right)b_j^k\right)+{\delta }_2,\end{array}$$

(28)

with $|{\delta }_2| <ϵ{\left|\mathbf{b}\right|}_{\infty }$, provided that ${\left|{\mathbf{b}}_{(km-L):(km+L+1)}\right|}_{\infty }={\left|\mathbf{b}\right|}_{\infty }$.

Next, we consider the effects of the exponential decay of ${\mathbf{z}}^k$ on the behavior of the round-off error. Let ${\widehat{a}}_b^k$ and ${\widehat{a}}_t^{k+1}$ be the first and the second sum in Equation (28). Due to the decaying of ${\mathbf{z}}^k$, the round-off errors only affect the result coming from the first L largest terms; thus, the first sum is reduced to:

$$\begin{array}{c}{\widehat{a}}_t^k = fl\left(\sum _{j=km-\eta L+1}^{km-L}{z}_j^k{b}_j^k+\sum _{j=km-L+1}^{km}{\mu }_j^k{b}_j^k\right).\end{array}$$

(29)

Since the exponential decay is bounded by a linear decay, we can conservatively approximate the numerical error due to the second sum in Equation (29), bounded by $Lϵ/2$. Therefore, the error ${\widehat{h}}_{m+1}^k$ of the solution $x_m^k$ computed by the scalar product with ${\epsilon }_c<ϵ$ is given by

$$\begin{array}{c}{\left|{\widehat{h}}_m^k\right|}_{\infty } = {\left|{\widehat{x}}_m^k-\left({\widehat{a}}_t^k+{\widehat{a}}_b^k\right)\right|}_{\infty }\le (L+1)ϵ{\left|\mathbf{b}\right|}_{\infty }.\end{array}$$

(30)

We now have the error bound when the full scalar product ${\widehat{\mathbf{z}}}^k·\mathbf{b}$ was used to approximate $x_m^k$. It is thus straightforward to show that the error of the interface-splitting algorithm with the cut-off threshold ${\epsilon }_c$ is

$$\begin{array}{c}{\left|{\widehat{\tilde{h}}}_m^k\right|}_{\infty } = {\left|{\tilde{x}}_m^k-x_m^k\right|}_{\infty }\end{array}$$

(31)

$$\begin{array}{c}\le {\left|{\widehat{h}}_m^k-fl\left(\sum _{j=1}^{km-J}{z}_j^k{b}_j^k\right)-fl\left(\sum _{j=km+J+1}^n{z}_j^k{b}_j^k\right)\right|}_{\infty }\end{array}$$

(32)

$$\begin{array}{cc}& \le \left[(L+2)ϵ+L{\epsilon }_c)\right]{\left|\mathbf{b}\right|}_{\infty }.\end{array}$$

(33)

□

The application of the ITS algorithm to numerical simulations does not need to be extremely accurate. The cut-off threshold ${\epsilon }_c$ can be set several digits lower than the approximation errors. The numerical errors of the algorithm would then be dwarfed by the approximation error. Any effort to reduce the numerical error beyond this point would not improve the final solution. In most cases, the approximation errors are much greater than the machine’s accuracy. In such situations, the maximum error of the algorithm is bounded by ${\epsilon }_{c}L{\left|\mathbf{b}\right|}_{\infty }$.

It should be noted that, when one applies the ITS algorithm to approximation problems, the physical requirement of the underlying principle should be respected. For example, if the ITS algorithm is applied to an interpolation problem, the sum of the coefficients should be one to maintain consistency. Likewise, the sum of the differentiation coefficients should be zero. This correction is on the order of $\epsilon$ and can be applied to the two smallest (farthest) coefficients.

5. Results

In this section, we present the results of the proposed algorithm. First, the accuracy of the algorithm is investigated using a single-rhs problem. Then, the performance is evaluated using multiple-rhs problems on four different parallel computers. The scalability of the interface-splitting algorithm is compared with the ScaLAPACK package and the RPDD algorithm. Finally, the scalabilities of the algorithm are tested on massively parallel machines of up to 2048 processors. The algorithm is implemented in FORTRAN, and the processors communicate via the Message Passing Interface (MPI) library. In all of the tests, we solve the tridiagonal system by using the vectorized kernel modified from LAPACK’s DGTSV [40]. The LU-decomposition is computed once. Intel’s compiler and the MPI library are used with the -O3-xCORE-AVX512 optimization option.

5.1. Accuracy

5.1.1. Effects of Cut-Off Threshold

Table 2. Normalized error of the interface-splitting algorithm applied the fourth-order compact differentiation problem. The error from a different cut-off threshold (${\epsilon }_c$) is compared with the local truncation ($E_a$) of the differentiation at $12.5$ grid points per wave.

J	${\mathit{\epsilon }}_{\mathit{c}}$	$\frac{1}{{\left|\mathit{b}\right|}_{\mathit{\infty }}}{|{\tilde{\mathit{f}}}_{\mathit{seq}}^{\prime }-{\tilde{\mathit{f}}}_{\mathit{par}}^{\prime }|}_{\mathit{\infty }}$	${\mathit{E}}_{\mathit{a}}={\left|\frac{{\mathit{f}}_{\mathit{exact}}^{\prime }-{\tilde{\mathit{f}}}_{\mathit{seq}}^{\prime }}{{\mathit{f}}_{\mathit{exact}}^{\prime }}\right|}_{\mathit{\infty }}$
7	9.92 $\times {10}^{-5}$	7.13 $\times {10}^{-6}$	2.77 $\times {10}^{-5}$
15	2.64 $\times {10}^{-9}$	7.26 $\times {10}^{-11}$
27	3.61 $\times {10}^{-16}$	3.85 $\times {10}^{-17}$

shows the errors of the interface-splitting algorithm applied to a matrix $[l_i,d_i,r_i]$ = $[1,4,1]$ encountered in some approximation problems, such as spline interpolation, compact differentiation [5], and compact deconvolution [41]. In this table, we consider the case of differentiation of $f=$ sin$\left(20\pi x\right)$ on $x=[0,1]$. The unknowns are placed at $x_i=ih,0\le i\le 251$. This problem is solved using three partitions. Table 2 shows that the bound given in Equation (24) is close to the actual error. The smallest J in the table already produces an error smaller than the local truncation error of the differentiation. Note that, in this test, the number of grid points per wave is $12.5$, which is a very fine resolution. The smallest J here should be adequate for most simulation-based applications because, in practice, it is difficult to reach this resolution for all relevant scales.

If higher accuracy is needed, the bandwidth J can be extended as required. Figure 3 illustrates that the error is not sensitive to the number of unknowns or to the order of the matrix. The errors of the algorithm are well below the bound given in Equation (24). According to the figure, we can choose J to match the approximation errors in each problem we are solving. It should be noted that, if the J is set too small, the convergence will be saturated at the level close to Equation (24), as shown in Table 2, where the algorithm produces errors about twice that of the machine accuracy, with the two largest values of J.

We would like to emphasize that the bandwidth here depends only on the diagonal dominance of the matrix in the neighborhood of the interface and the chosen cut-off threshold ${\epsilon }_c$. The number of unknowns does not have a direct influence on this number because the condition number of diagonally dominant matrices converges very fast when the dimension of the matrix is increased.

5.1.2. Non-Constant Coefficient Problem

In this section, we investigate the accuracy of the ITS algorithm on a non-constant coefficient problem. In order to create a reproducible test, we set up the matrix using $\mathbf{A}=$ [ sin$\left(i\right)$, 2(| sin$\left(i\right)| + |$ cos$\left(i\right)\left|\right)$, cos$\left(i\right)]$ and solve a single system of order 1000 with $b_i=1$ on four processors. The off-diagonal coefficients of this matrix vary relatively fast. The signs change roughly once every three rows. The errors of the ITS algorithm with respect to to the sequential solution are displayed in

Table 3. Normalized error of the interface-splitting algorithm applied to a system with non-constant coefficients with different truncation bandwidth J.

J	7	15	18	20	27
$\frac{1}{{\left|b\right|}_{\infty }}{|x_{seq}-x_{par}|}_{\infty }$	1.4 $\times {10}^{-5}$	2.1 $\times {10}^{-11}$	4.7 $\times {10}^{-14}$	4.4 $\times {10}^{-16}$	4.4 $\times {10}^{-16}$

, showing that the non-constant coefficients of the matrix do not have negative effects on the accuracy of the algorithm.

5.2. Performance

In this subsection, we investigate the performance of the proposed algorithm on three different parallel machines. First, we investigate the scalability of a fixed-size problem by comparing the parallel runtime to the sequential runtime on a single processor. In the second test, we investigate the performance of a scaled problem size. In all tests, a tridiagonal system is solved, with the interface bandwidth J set to 9.

In the first test, we measure a fixed-size speedup on an eight-socket CPU system with Intel Xeon 8168 processors at the Thailand National e-Science Infrastructure Consortium. Each CPU is equipped with three Intel Ultra Path Interconnect (UPI) processors, with a transfer bandwidth of 20.8 GB/s per link per direction. It takes at most two hops for a package to reach the farthest CPU. The problem size in this test is set to 19,200 with ${64}^3$ right-hand sides. This fixed-size speedup measures how much faster a parallel algorithm helps shorten the solution time compared to one CPU. The result is plotted in Figure 4a. Surprisingly, we see a superlinear speedup for $n_p\le 64$. After $n_p=64$, the speedup drops below the linear line. This superlinear speedup does not mean the parallel algorithm is better than the sequential one. In a periodic problem, the complexity of our algorithm is indeed lower than the direct Gaussian elimination (see Table 1). However, in this case, our complexity is slightly higher than the sequential code. The superlinear speedup we see here comes from increased memory bandwidth aggregation and better caching. The Xeon processor possesses six memory channels that can transfer the data from the main memory independently in parallel. As the number of processors is increased, the data transfer increases. Our system is an eight-socket with six channels each. Thus, a superlinear speedup up to $n_p=64$ is reasonable.

In reality, massively parallel systems are not constructed to solve a problem that can be solved on a single CPU faster. Their actual purpose is to solve a very large system that is impossible to solve on a workstation or on a small cluster. Therefore, the scaled speedup is more relevant to high-performance computing. We conduct a test on the same machine with different problem sizes

We set the number of rhs to $\gamma =m^2$ and measure the scaled speedup, in which each processor solves a system of size m for $m^2$ right-hand sides. The result is plotted in Figure 4b. We still see a superlinear speedup for the smallest problem size. For other sizes, the scaled speedup is slightly lower than the linear speedup, and the efficiency at the largest number of CPUs is $92\%$ on average.

Comparison with ScaLAPACK

Next, we evaluate the performance of the algorithm on an ALTIX 4700 at the Leibniz-Rechenzentrum LRZ. The scaled speedup of the algorithm is studied for the single- and the multiple-rhs. In this test, the number of unknowns grows linearly with the number of processors, i.e., $n_{total}=p{N}_{sub}$. The size of the subsystem ($N_{sub}$) is set to ${10}^6$ in the single-rhs problem. For the multiple-rhs problem, the problem size is 100, and the number of rhs is ${10}^4$. This corresponds to a data block of ${100}^3$ grid points. To highlight the effects of the communications in the solution process, we only report the time used to solve the subsystems (Steps 3 and 4). Likewise, the parallel runtime of ScaLAPACK reported here is the time spent in the PDDTTRS subroutine. The results of the test are shown in Figure 5a. The CPU time of ScaLAPACK is approximately doubled when the number of processors is increased from one to two. This is in accordance with the increase in the complexity of the algorithm [29] used in the ScaLAPACK. Even though the numbers of unknowns in these two problems are equal (${10}^6$), the parallel runtimes of both algorithms are significantly different due to the communications. Interestingly enough, the differences in the CPU time of the multiple rhs problems grow sharply with the number of processors. This behavior indicates that ScaLAPACK is sensitive to the characteristics of the interconnection network and is not as scalable as our algorithm.

The efficiencies of the ITS algorithm and ScaLAPACK are presented in Figure 5b. In the single-rhs problem, the efficiency of the proposed algorithm falls to $50\%$ at $p=64$ because of the increase in communication overhead, which is half of the parallel runtime there. In the multiple-rhs problem, both algorithms exhibit better performances. At $p=64$, the ITS algorithm delivers $85\%$ efficiency, compared to $30\%$ of ScaLAPACK. In both problems, the ITS algorithm is at least four times faster than ScaLAPACK.

We implemented the RPDD described in [27] and compared the parallel runtime and the scalability in a scaled problem size on the BW-Grid cluster (IBM BladeCenter HS21XM) of the High-Performance Computing Center, Stuttgart (HLRS). In this version, we solve the tridiagonal systems by the same subroutine used in our algorithm. Therefore, the differences between RPDD and our algorithms lie only in the communication pattern. Figure 6a displays the parallel runtimes and the overhead of both algorithms applied to the compact interpolation problem on a 3D Cartesian grid where the size of the subsystem (m) equals 128, with ${128}^2$ right-hand sides. It is not possible to separate the communication time from other overhead in our algorithm because the calculations and the synchronizations are allowed to overlap. Therefore, the overhead of the ITS algorithm here is taken as the total time used in Steps 4–6 of the algorithm described in Section 2. Likewise, the overhead of the RPDD algorithm is the total time used to synchronize and calculate the correction term, including the correction of the computed solution. The parallel runtimes of both algorithms rise sharply from one to eight processors. This increase in the parallel runtime is due to the bandwidth saturation of the bus, which is a typical behavior of shared-memory architecture. The behavior of the parallel runtimes here differs from what is seen in Figure 5 for two reasons: first, because of the density of the node, and second, because of the size of the cache. The computing node on the ALTIX machine used earlier was based on two dual-core processors, but the BW-Grid is composed of two quad-core processors. Both are bus-based shared-memory computers. On the ALTIX 4700, the average cache size per core is 4 MB, which is large enough to accommodate all the right-hand sides. The cache size per core on the IBM machine is only 3 MB, and the right-hand sides do not fit into the cache. The parallel runtimes are thus limited by the data transfer of the memory, which is much slower than the processor speed. After eight processors, the overhead of the ITS algorithms increases slightly, but the overhead of the RPDD algorithm continues to rise very fast. This large overhead is coming from the additional synchronization step. Each processor in the RPDD algorithm must wait for the neighboring processors before the blocking synchronization can be initiated. Therefore, the idle time is potentially doubled, and it eventually leads to a longer overall runtime.

Because the exhaustion of the memory transfer on the computing node can affect the parallel runtime greatly, it is more realistic to measure the scalability relative to the parallel runtime on one computing node rather than the runtime on a single processor. Thus, we plot the relative efficiencies $\left(E_8\right)$ in Figure 6b, in which the runtime on the p processor is divided by that of a single node (eight processors). The RPDD algorithm shows good efficiency, but the proposed algorithm is significantly better. At $p=512$, the RPDD algorithm delivers a relative efficiency of $63\%$, while the ITS delivers $92\%$, which is approximately $50\%$ higher performance.

5.3. Advantage of Overlapping Bidirectional Communications

The main advantage we expect from our algorithm is a reduction in the communication time during the synchronization phases. The performance is therefore strongly dependent on the implementation of the MPI, which is usually optimized to the size of the data being transferred. In Figure 7a, we present the overall performance of the ITS algorithm on an NEC HPC 144Rb-1 at HLRS with a larger number of processors. The results are gathered from five different runs in which the multiple-rhs system is solved repeatedly 100 times. The same compiler optimization is kept unchanged, and the bandwidth J is set to 10. Each processor holds a set of $m^3$ data, and for the problem size of m, the number of the right-hand side is $m^2$.

A sharp rising of the CPU seconds due to memory access is observed in Figure 7a,b for the two largest cases. The parallel runtimes increase by $60\%$ when the number of processors is increased from two to eight processors. Note that this is much better than what was seen earlier in Figure 6a, where the parallel runtime was increased by a factor of six. For $n_p>8$, the parallel runtime of the ITS algorithm is relatively constant, except for the smallest problem size. The relative efficiencies ($E_8$) are $50\%,89\%,99\%$, and $97\%$ from the smallest to the largest problem size, respectively. The speedup in the smallest size suffers from the overhead, which is increased from 40 $\mathsf{\mu }$s to 400 $\mathsf{\mu }$s for $p=8$ to $p=2048$. When taking into account the minimum time used to solve the system, which is 300 $\mathsf{\mu }$s, this low efficiency is natural. On the other hand, the parallel runtimes of the RPDD algorithm continue to increase after $p=8$ as a linear function of p, as shown in Figure 7c,d.

We have examined the ITS algorithm when the non-blocking communications are replaced by the blocking communications (the results are not shown here). This version behaves similarly to the original RPDD algorithm presented above, and the parallel runtime is comparable. Likewise, we have implemented the improved RPDD, which achieves the same performance as our algorithm. In the original algorithm, Sun [27] tried to save computations by having one processor responsible for one interface. This led to the need for two synchronization phases with two blocking communications. See Steps 4 and 5 of the algorithm in Section 2.2 of [27]. However, it is more rewarding to double the computation of that small matrix and have every processor solve both interfaces (top and bottom). There is some redundant work in this approach, but the synchronization in Steps 4 and 5 can be overlapped. This simple change renders the RPDD algorithm as efficient as ours. This gain in the performance comes solely from the reduction in the synchronization step. This role reversal confirms that our version of RPDD is a fair implementation.

5.4. Application to Navier–Stokes Equations

In this subsection, we present the application of the ITS algorithm to the solution process of the Navier–Stokes equations:

$${\oint }_A^{}\mathbf{u}·\mathbf{n}dA=0,$$

(34)

$$\frac{\partial }{\partial t}{\int }_{\Omega }^{}\mathbf{u}d\Omega +{\oint }_A^{}(\mathbf{u}·\mathbf{n})\mathbf{u}dA=\nu {\oint }_A^{}\mathbf{T}dA-\frac{1}{\rho }{\oint }_A^{}p\mathbf{I}·\mathbf{n}dA.$$

(35)

In the following test, the finite volume discretization of the above equations is solved by using compact fourth-order finite volumes described in [7,17,41,42]. First, the two-dimensional inviscid flow is presented, followed a simulation of three-dimensional turbulent channel flow.

5.4.1. Inviscid Doubly-Periodic Shear Layer

This simple 2D flow contains Kelvin–Helmholtz instabilities in which the horizontal shear layer is perturbed by a vertical sinusoidal velocity, leading to a roll-up of the vortex sheet into a cone-like shape. The domain $\Omega ={[0,1]}^2$ is taken for this study, and the initial velocities are given by

$$u=\left\{\begin{array}{cc}\tan \mathrm{h}\left(\sigma \right(y-0.25\left)\right)\hfill & \mathrm{for}\mathrm{y}\le 0.5,\hfill \\ \tan \mathrm{h}\left(\sigma \right(0.75-y\left)\right)\hfill & \mathrm{for}\mathrm{y}>0.5.\hfill \end{array}\right.$$

(36)

$$v=\epsilon \sin \left(2\pi x\right).$$

(37)

This flow is governed by two parameters: the shear layer width parameter $\sigma$ and the perturbation magnitude $\epsilon$. The flow is set to be inviscid ($\nu =0$) to expose any instabilities the ITS algorithm may cause. In this test, the shear layer parameter and the perturbation magnitude are 30 and $0.05$, respectively. To ensure that the approximation error of the ITS algorithm is not affecting the flow, the approximation bandwidth J is set to 12. This will not obtain direct solver-like accuracy, but the parallelization error should be well below the truncation error.

Two grid resolutions are considered for this test case, ${512}^2$ and ${1024}^2$, and the computational domain is equally divided into $4\times 4$ and $8\times 8$, respectively. Figure 8a shows the roll-up of the shear layer, which further reduces the thickness of the layer. Even though the number 512 is illusorily large, it cannot resolve this inviscid flow, and the solution suffers from numerical wiggles. Once the grid resolution is sufficient, the numerical wiggles disappear (Figure 8b). In this fine grid, there are 112 interfaces, and we do not observe any artifacts from the ITS algorithm. Note that the subsystem size of these two simulations is ${128}^2$. At each evaluation of the derivatives in the convection term, the compact scheme costs 6.6 $\times {10}^5$ floating-point operations, while the ITS algorithm costs merely 5.9 $\times {10}^3$—two orders of magnitude smaller. It should be stressed that this case is an inviscid flow, and any numerical artifacts will be amplified. Thus, the approximate nature of the algorithm does not degrade the quality of the simulation nor introduce any numerical artifacts into the solution.

5.4.2. Turbulent Channel Flow

In this section, we present the result from applying the proposed scheme to a turbulent channel flow at the friction Reynolds number $R{e}_{\tau }=950$. The flow is driven by a constant pressure gradient, and the corresponding bulk flow Reynolds number is 41,430. The computational domain is $[L_x,L_y,L_z]=[2\pi H,\pi H,2H]$, where the x-axis is the stream-wise direction and z-axis is the wall-normal direction. The numbers of grid points in each direction are $[N_x,N_y,N_z]=[480,400,320]$. This problem is solved on $N_{px}\times N_{py}\times N_{pz}\times =8\times 8\times 2$ processors. In the z-direction, the grid is stretched towards the wall.

The mean stream-wise velocity profiles of the fourth-order scheme in Figure 9a collapse on that of the spectral scheme [43]. The r.m.s. of the cell-averaged fluctuations in the span-wise and wall-normal velocities is in excellent agreement (Figure 9b). The position of the peak of u- r.m.s. is correctly predicted. Away from the wall, the prediction of r.m.s. of the stream-wise velocity is slightly lower than what is predicted by the spectral scheme. This difference is due to the averaging procedure, which averages the staggered variables to the location of the pressure cells. This averaging filter removes some of the small scales from the statistics. This shortcoming can be improved by deconvolving the field to the pointwise value.

Finally, a snapshot of the vertical plan $z^{+}=5$ is shown in Figure 10. The plot shows fine detail structures of the wall flow. Small elongated stream-wise streaks are observed. The figure does not show any sign of numerical artifacts. Therefore, the proposed algorithm is accurate and can be used to study real physical phenomena.

6. Conclusions

We have presented the interface-splitting algorithm tailored for diagonal dominant tridiagonal systems. The accuracy and performance of the algorithm rest on the diagonal dominance of the matrix. This algorithm is an approximate method, but it is iteration-less. The user has full control over the accuracy, provided that the subsystem size is sufficiently large. It can be used equivalently to a direct method if desired. Unlike other direct methods, the complexity of this algorithm does not depend on the number of processors, and the leading complexity of the best sequential algorithm is maintained. The algorithm is four times faster than the direct algorithm used in ScaLAPACK. The proposed algorithm is highly efficient and scalable for multiple right-hand side problems.

In massive-scaled computing, the amount of synchronization and overlapping communication is very important. At the same amount of data transfer, the algorithm using overlapping communication can be much faster than the equivalent algorithm using unidirectional communication. The algorithm designer should always check if overlapping communication and a reduction in the synchronization phase are possible. Even though such changes can lead to higher computation costs, the gain from lower communication time can be surprisingly rewarding.