Tire–Pavement Interaction Simulation Based on Finite Element Model and Response Surface Methodology
Abstract
:1. Introduction
2. Calibration of the Parameter Inversion Model
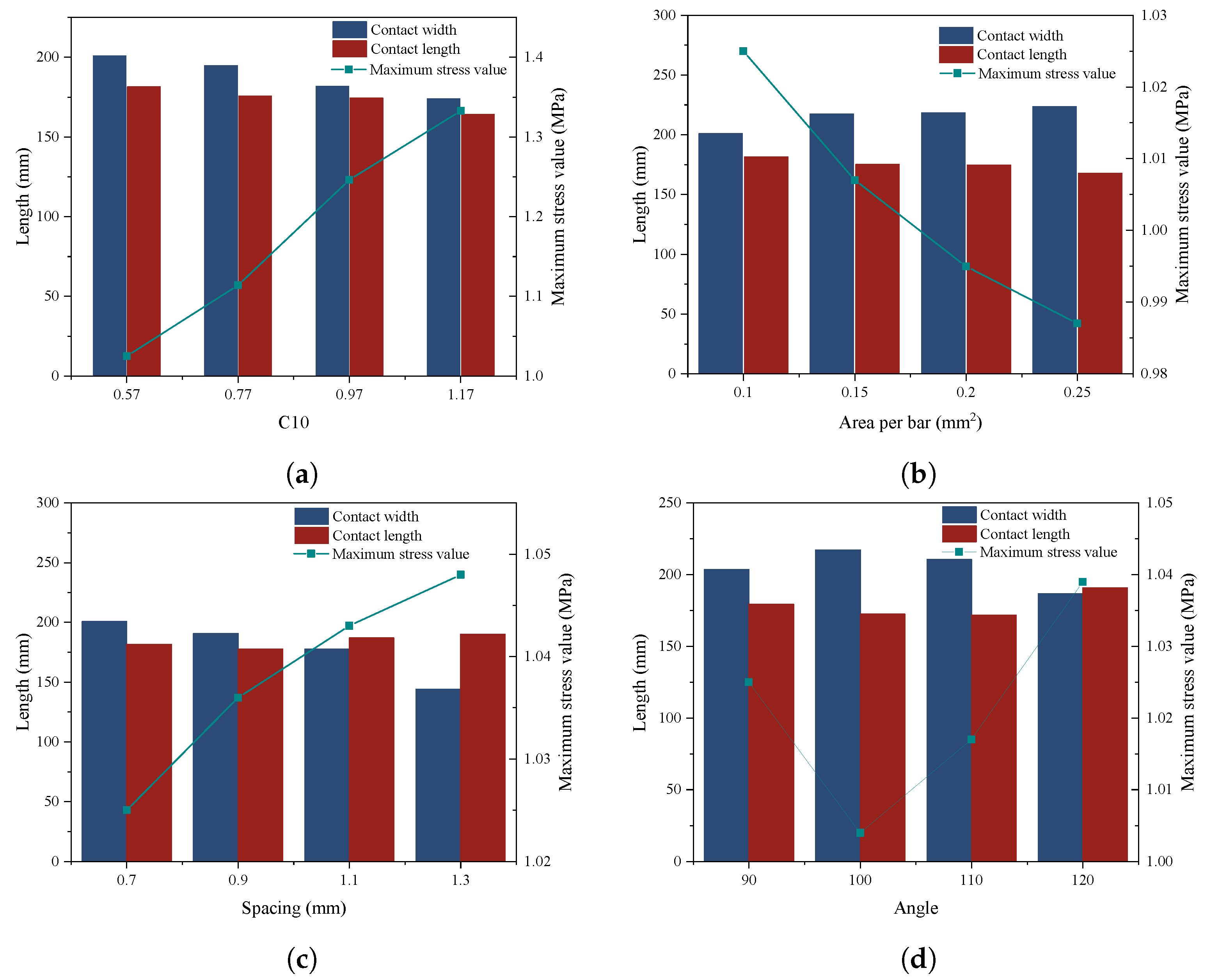
2.1. The Determination of Input Variables and Response
2.2. The Design of the Experiment
2.3. The Calibration of the Response Surface Model
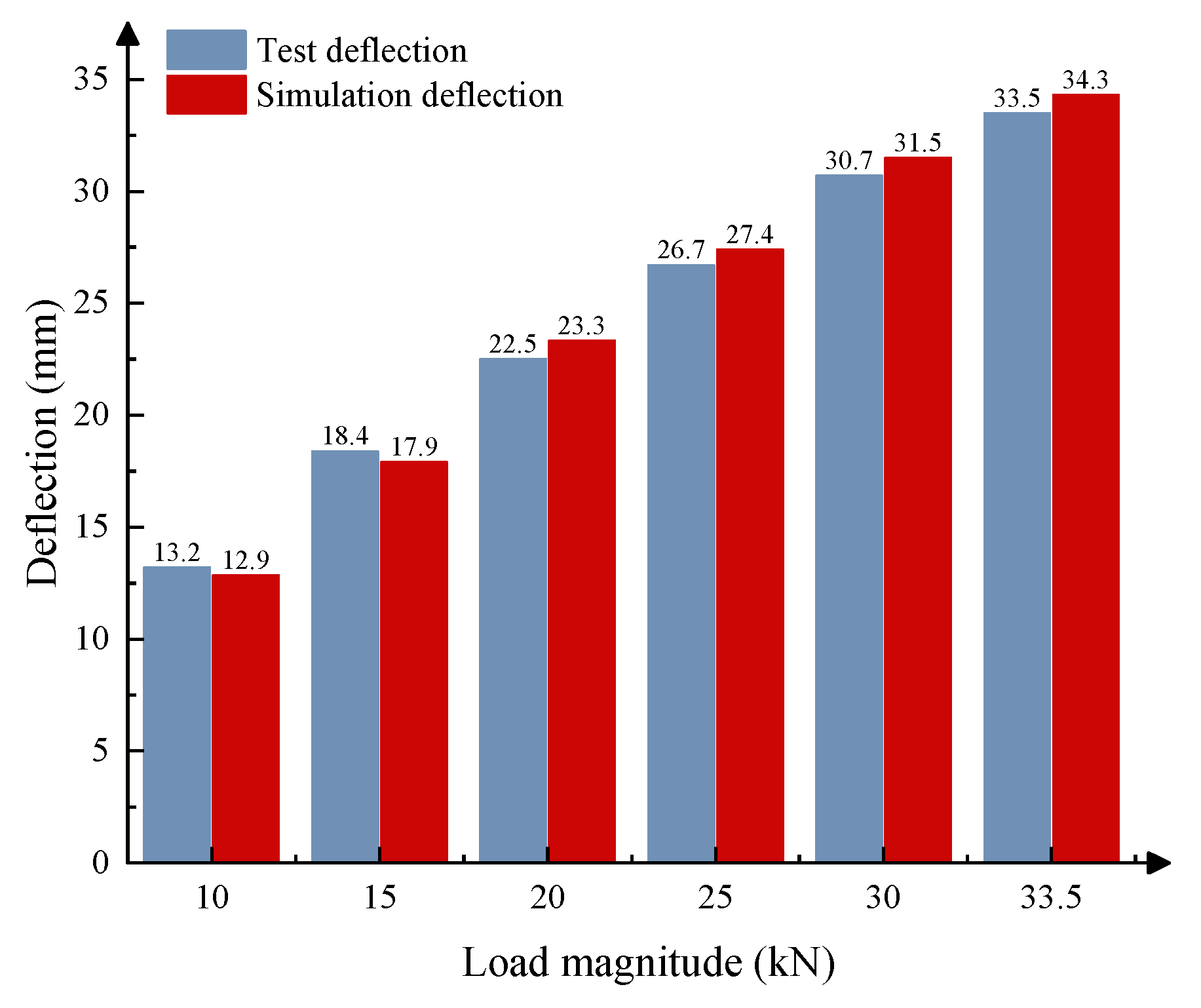
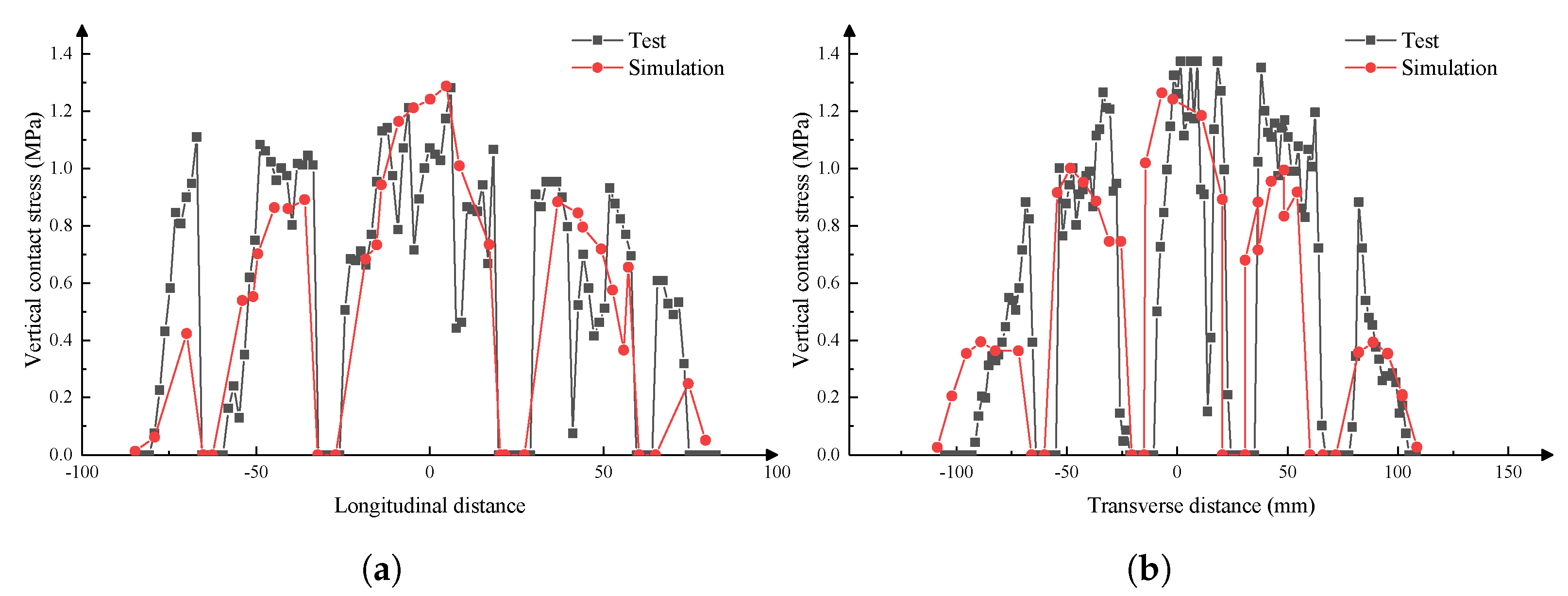
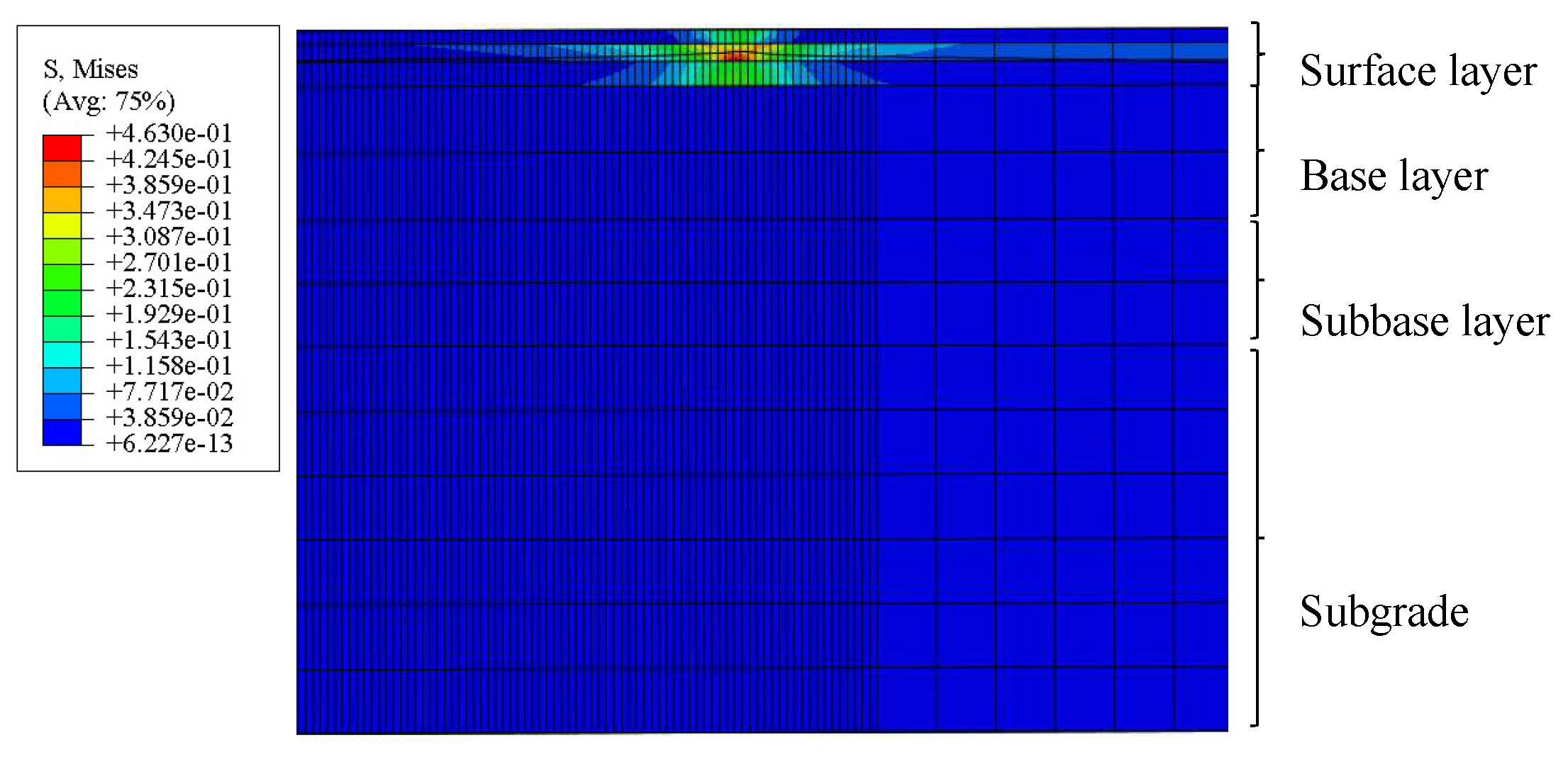
3. The Verification of the FEM with the Optimal Parameter Combination
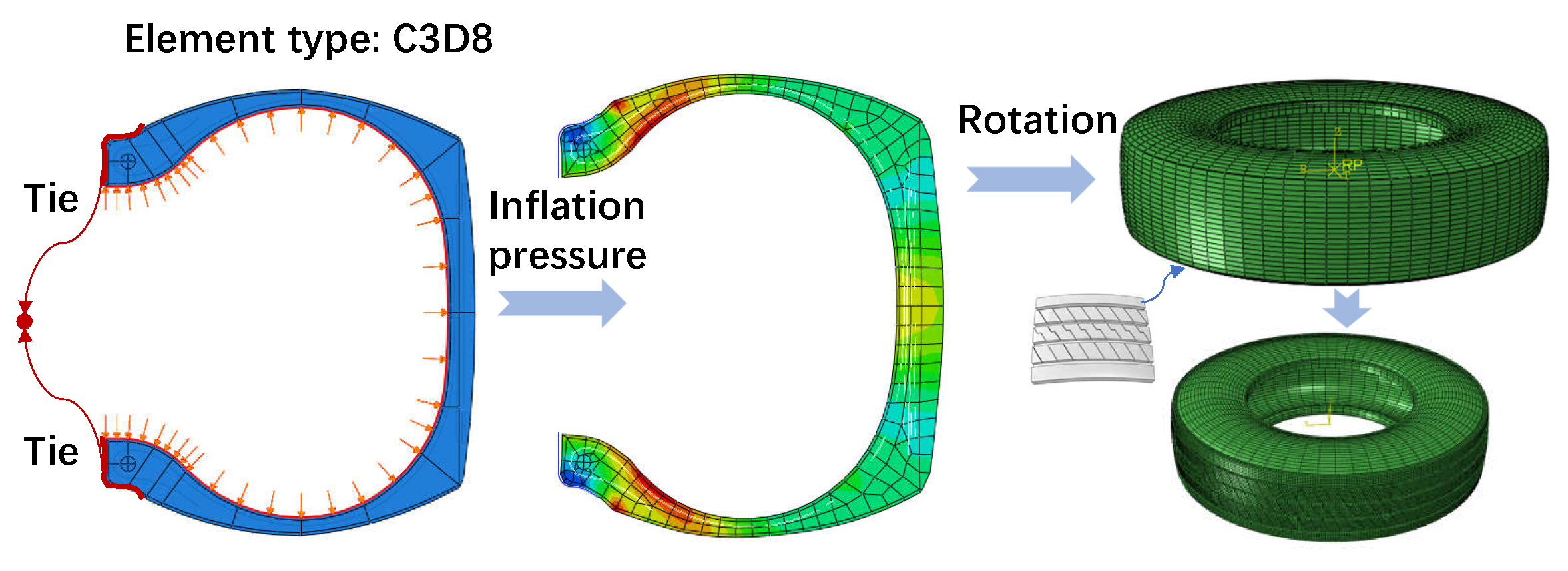
4. Tire–Pavement Interaction Simulation
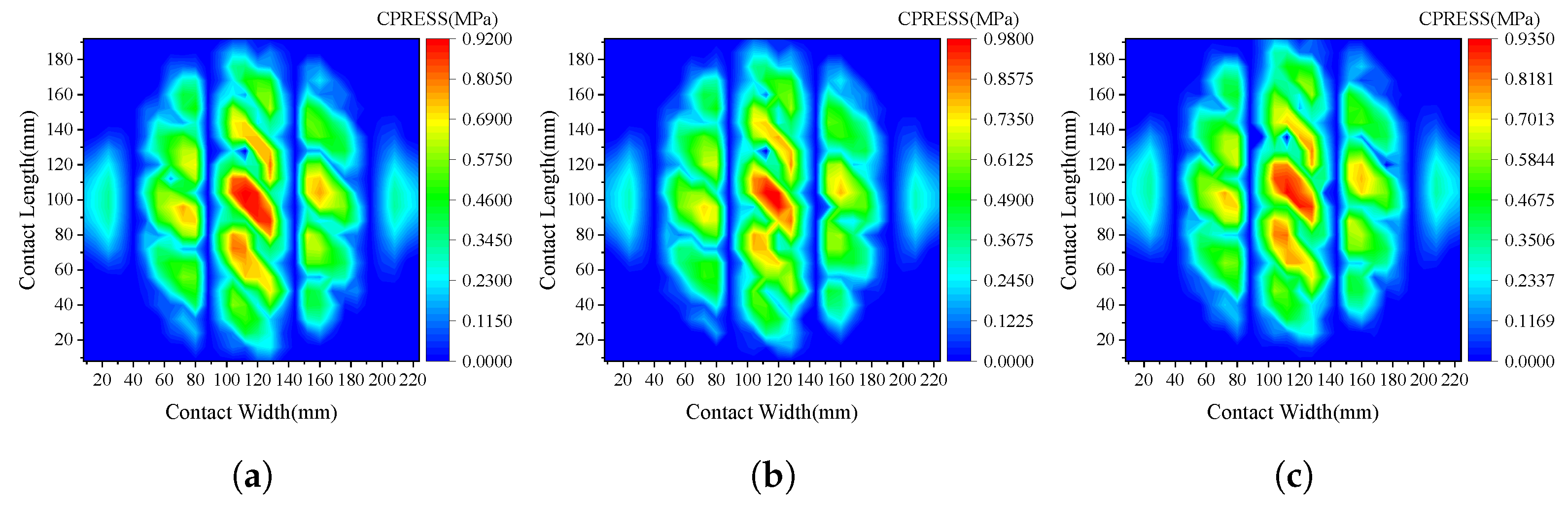
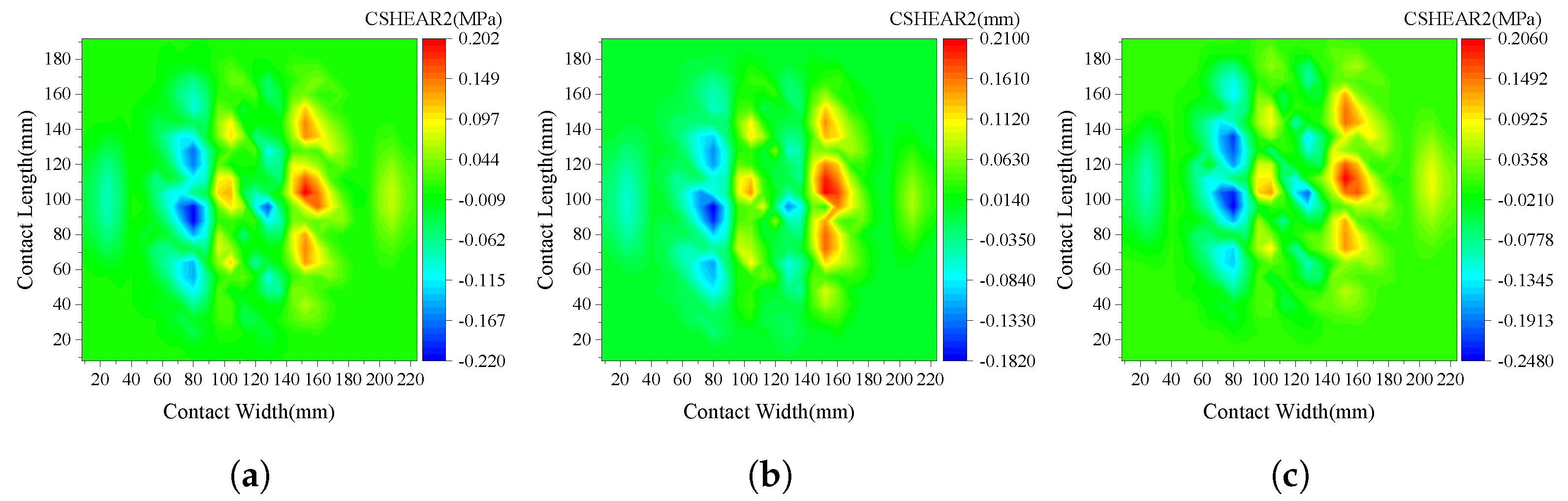
4.1. The Tire Rolling Simulation
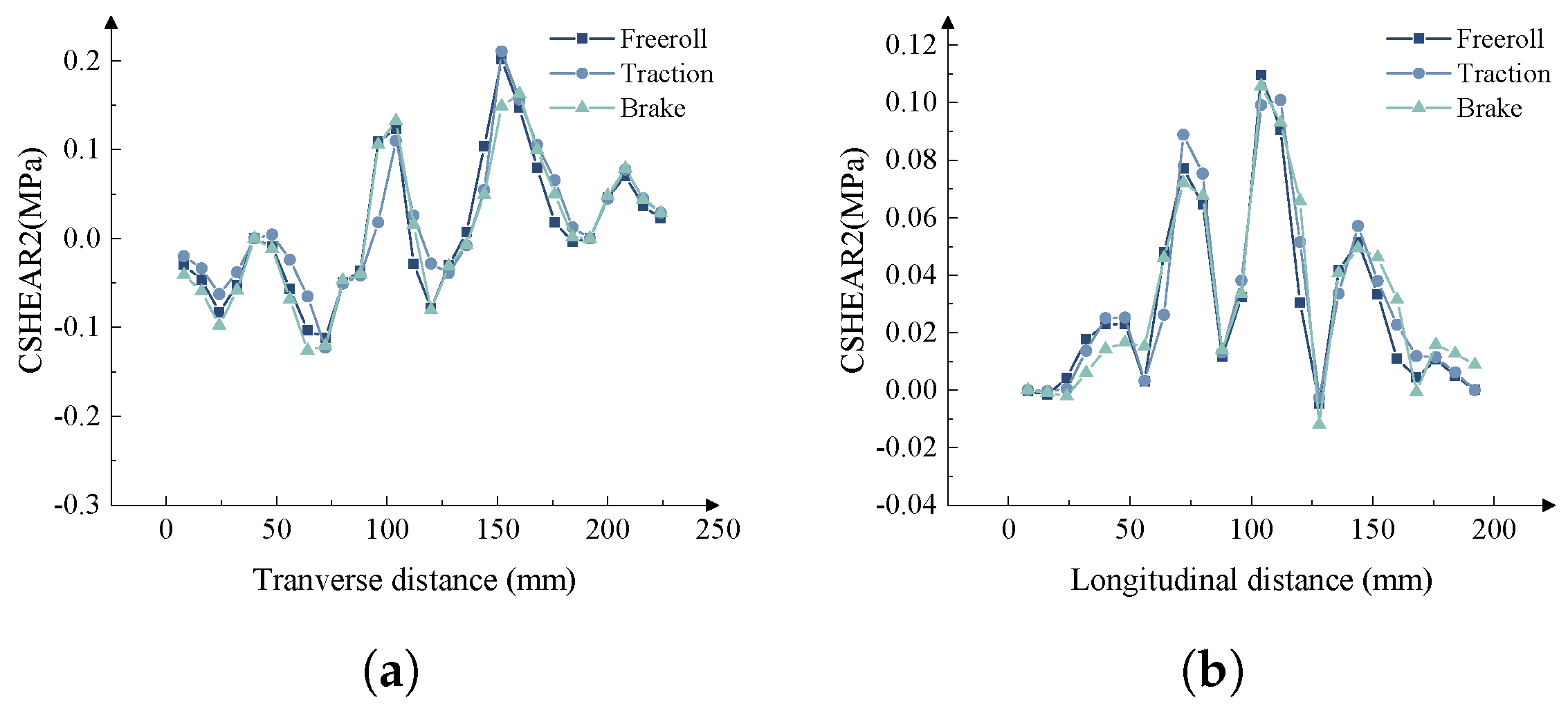
4.2. Pavement Mechanical Response Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guan, J.; Zhou, X.; Liu, L.; Ran, M. Measurement of Tire-Pavement Contact Tri-Axial Stress Distribution Based on Sensor Array. Coatings 2023, 13, 416. [Google Scholar] [CrossRef]
- Zhu, X.; Zhang, Q.; Chen, L.; Du, Z. Mechanical response of hydronic asphalt pavement under temperature–vehicle coupled load: A finite element simulation and accelerated pavement testing study. Constr. Build. Mater. 2021, 272, 121884. [Google Scholar] [CrossRef]
- Assogba, O.C.; Tan, Y.; Zhou, X.; Zhang, C.; Anato, J.N. Numerical investigation of the mechanical response of semi-rigid base asphalt pavement under traffic load and nonlinear temperature gradient effect. Constr. Build. Mater. 2020, 235, 117406. [Google Scholar] [CrossRef]
- Hu, X.; Sun, L. Stress response analysis of asphalt pavement under measured tire ground pressure of heavy vehicle. J.-Tongji Univ. 2006, 34, 64. [Google Scholar]
- Ge, H.; Quezada, J.C.; Le Houerou, V.; Chazallon, C. Multiscale analysis of tire and asphalt pavement interaction via coupling FEM–DEM simulation. Eng. Struct. 2022, 256, 113925. [Google Scholar] [CrossRef]
- Assogba, O.C.; Sun, Z.; Tan, Y.; Nonde, L.; Bin, Z. Finite-element simulation of instrumented asphalt pavement response under moving vehicular load. Int. J. Geomech. 2020, 20, 04020006. [Google Scholar] [CrossRef]
- Hu, X.; Faruk, A.N.; Zhang, J.; Souliman, M.I.; Walubita, L.F. Effects of tire inclination (turning traffic) and dynamic loading on the pavement stress–strain responses using 3-D finite element modeling. Int. J. Pavement Res. Technol. 2017, 10, 304–314. [Google Scholar] [CrossRef]
- Behnke, R.; Wollny, I.; Hartung, F.; Kaliske, M. Thermo-mechanical finite element prediction of the structural long-term response of asphalt pavements subjected to periodic traffic load: Tire-pavement interaction and rutting. Comput. Struct. 2019, 218, 9–31. [Google Scholar] [CrossRef]
- Yang, X.; Olatunbosun, O.; Bolarinwa, E. Materials testing for finite element tire model. Sae Int. J. Mater. Manuf. 2010, 3, 211–220. [Google Scholar] [CrossRef]
- Arachchi, N.; Abegunasekara, C.; Premarathna, W.; Jayasinghe, J.; Bandara, C.; Ranathunga, R. Finite Element Modeling and Simulation of Rubber Based Products: Application to Solid Resilient Tire. In Proceedings of the ICSECM 2019: Proceedings of the 10th International Conference on Structural Engineering and Construction Management; Springer: Berlin/Heidelberg, Germany, 2021; pp. 517–531. [Google Scholar]
- Boyce, M.C.; Arruda, E.M. Constitutive models of rubber elasticity: A review. Rubber Chem. Technol. 2000, 73, 504–523. [Google Scholar] [CrossRef]
- Yeoh, O.H. Some forms of the strain energy function for rubber. Rubber Chem. Technol. 1993, 66, 754–771. [Google Scholar] [CrossRef]
- Ogden, R. Nearly isochoric elastic deformations: Application to rubberlike solids. J. Mech. Phys. Solids 1978, 26, 37–57. [Google Scholar] [CrossRef]
- Meyer, K.H.; Ferri, C. The elasticity of rubber. Rubber Chem. Technol. 1935, 8, 319–334. [Google Scholar] [CrossRef]
- Giovanni, M. Response Surface Methodology and Product Optimization; Wiley: Hoboken, NJ, USA, 1983. [Google Scholar]
- Li, J.; Zuo, W.; Jiaqiang, E.; Zhang, Y.; Li, Q.; Sun, K.; Zhou, K.; Zhang, G. Multi-objective optimization of mini U-channel cold plate with SiO2 nanofluid by RSM and NSGA-II. Energy 2022, 242, 123039. [Google Scholar] [CrossRef]
- Pali, H.S.; Sharma, A.; Kumar, N.; Singh, Y. Biodiesel yield and properties optimization from Kusum oil by RSM. Fuel 2021, 291, 120218. [Google Scholar] [CrossRef]
- Benzannache, N.; Belaadi, A.; Boumaaza, M.; Bourchak, M. Improving the mechanical performance of biocomposite plaster/Washingtonian filifira fibres using the RSM method. J. Build. Eng. 2021, 33, 101840. [Google Scholar] [CrossRef]
- Yang, H.; Xu, X.; Neumann, I. Optimal finite element model with response surface methodology for concrete structures based on Terrestrial Laser Scanning technology. Compos. Struct. 2018, 183, 2–6. [Google Scholar] [CrossRef]
- Rajabi, M.; Aboutalebi, M.; Seyedein, S.; Ataie, S. Simulation of residual stress in thick thermal barrier coating (TTBC) during thermal shock: A response surface-finite element modeling. Ceram. Int. 2022, 48, 5299–5311. [Google Scholar] [CrossRef]
- Gent, A.N.; Walter, J.D. Pneumatic Tire 2006. Available online: https://ideaexchange.uakron.edu/mechanical_ideas/854 (accessed on 11 September 2023).
- Khuri, A.I.; Mukhopadhyay, S. Response surface methodology. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 128–149. [Google Scholar] [CrossRef]
- Wang, T.; Dong, Z.; Xu, K.; Ullah, S.; Wang, D.; Li, Y. Numerical simulation of mechanical response analysis of asphalt pavement under dynamic loads with non-uniform tire-pavement contact stresses. Constr. Build. Mater. 2022, 361, 129711. [Google Scholar] [CrossRef]
- Wang, H.; Al-Qadi, I.L.; Stanciulescu, I. Simulation of tyre–pavement interaction for predicting contact stresses at static and various rolling conditions. Int. J. Pavement Eng. 2012, 13, 310–321. [Google Scholar] [CrossRef]
- Liu, X.; Jayme, A.; Al-Qadi, I.L. ContactGAN development–prediction of tire-pavement contact stresses using a generative and transfer learning model. Int. J. Pavement Eng. 2022, 1–11. [Google Scholar] [CrossRef]







| Parameter | Level | ||
|---|---|---|---|
| −1 | 0 | 1 | |
| C10 (MPa) | 0.57 | 0.87 | 1.17 |
| Angle of cord (°) | 90 | 105 | 120 |
| Interval of cord (mm) | 0.7 | 1 | 1.3 |
| Area of cord cross-section (mm2) | 0.1 | 0.175 | 0.25 |
| Serial Number | C10 (MPa) | Area of Cord Cross-Section (mm2) | Interval of Cord (mm) | Angle of Cord (°) |
|---|---|---|---|---|
| 1 | 1.17 | 0.25 | 1 | 105 |
| 2 | 0.87 | 0.25 | 0.7 | 105 |
| 3 | 0.87 | 0.1 | 1.3 | 105 |
| 4 | 0.57 | 0.175 | 1 | 120 |
| 5 | 1.17 | 0.1 | 1 | 105 |
| 6 | 0.87 | 0.175 | 1.3 | 90 |
| 7 | 0.57 | 0.175 | 0.7 | 105 |
| 8 | 0.87 | 0.175 | 1 | 105 |
| 9 | 0.87 | 0.25 | 1 | 120 |
| 10 | 0.57 | 0.175 | 1.3 | 105 |
| 11 | 1.17 | 0.175 | 0.7 | 105 |
| 12 | 0.57 | 0.175 | 1 | 90 |
| 13 | 0.57 | 0.25 | 1 | 105 |
| 14 | 0.87 | 0.175 | 1 | 105 |
| 15 | 0.87 | 0.175 | 1 | 105 |
| 16 | 0.87 | 0.175 | 0.7 | 120 |
| 17 | 0.87 | 0.1 | 1 | 120 |
| 18 | 0.87 | 0.175 | 0.7 | 90 |
| 19 | 0.87 | 0.1 | 0.7 | 105 |
| 20 | 0.87 | 0.25 | 1.3 | 105 |
| 21 | 1.17 | 0.175 | 1.3 | 105 |
| 22 | 0.87 | 0.1 | 1 | 90 |
| 23 | 1.17 | 0.175 | 1 | 120 |
| 24 | 0.87 | 0.175 | 1 | 105 |
| 25 | 0.57 | 0.1 | 1 | 105 |
| 26 | 0.87 | 0.175 | 1 | 105 |
| 27 | 1.17 | 0.175 | 1 | 90 |
| 28 | 0.87 | 0.175 | 1.3 | 120 |
| 29 | 0.87 | 0.25 | 1 | 90 |
| Index | Std. Dev. | Adjusted | Mean | C.V. (%) | Adeq Precision | |
|---|---|---|---|---|---|---|
| Value | 0.14 | 0.91 | 0.83 | 0.75 | 19.42 | 11.85 |
| Item | C10 (MPa) | Angle of Cord (°) | Interval of Cord (mm) | Area of Cord Cross-Section (mm2) |
|---|---|---|---|---|
| Value | 1.166 | 0.25 | 1.3 | 100 |
| Loading Magnitude (kN) | 10 | 15 | 20 | 25 | 30 | 33.5 | |
|---|---|---|---|---|---|---|---|
| Error rate (%) | Footprint area | 2.07 | 1.45 | 0.18 | 0.23 | 0.69 | 0.82 |
| Contact area | 2.06 | 2.30 | 0.82 | 1.52 | 2.03 | 0.17 | |
| Ratio of pattern | 0.05 | 3.72 | 2.81 | 8.39 | 6.46 | 4.80 | |
| Contact length | 3.59 | 0.33 | 0.80 | 1.11 | 3.39 | 4.22 | |
| Contact width | 0.45 | 4.30 | 1.76 | 1.76 | 1.32 | 0.43 | |
| Direction | Vertical Contact Stress (MPa) | Longitudinal Contact Stress (MPa) | Transverse Contact Stress (MPa) | |
|---|---|---|---|---|
| Longitudinal | Free rolling | 0.920 | 0.052 | 0.115 |
| Full traction | 1.035 | 0.211 | 0.101 | |
| Full braking | 0.921 | 0.190 | 0.110 | |
| Transverse | Free rolling | 0.918 | 0.041 | 0.203 |
| Full traction | 1.031 | 0.214 | 0.202 | |
| Full braking | 0.929 | 0.191 | 0.202 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Q.; Shangguan, L.; Li, T.; Ma, X.; Yin, Y.; Dong, Z. Tire–Pavement Interaction Simulation Based on Finite Element Model and Response Surface Methodology. Computation 2023, 11, 186. https://doi.org/10.3390/computation11090186
Zhang Q, Shangguan L, Li T, Ma X, Yin Y, Dong Z. Tire–Pavement Interaction Simulation Based on Finite Element Model and Response Surface Methodology. Computation. 2023; 11(9):186. https://doi.org/10.3390/computation11090186
Chicago/Turabian StyleZhang, Qingtao, Lingxiao Shangguan, Tao Li, Xianyong Ma, Yunfei Yin, and Zejiao Dong. 2023. "Tire–Pavement Interaction Simulation Based on Finite Element Model and Response Surface Methodology" Computation 11, no. 9: 186. https://doi.org/10.3390/computation11090186
APA StyleZhang, Q., Shangguan, L., Li, T., Ma, X., Yin, Y., & Dong, Z. (2023). Tire–Pavement Interaction Simulation Based on Finite Element Model and Response Surface Methodology. Computation, 11(9), 186. https://doi.org/10.3390/computation11090186








