A Parametric Family of Triangular Norms and Conorms with an Additive Generator in the Form of an Arctangent of a Linear Fractional Function
Abstract
1. Introduction
2. Materials and Methods
3. Results
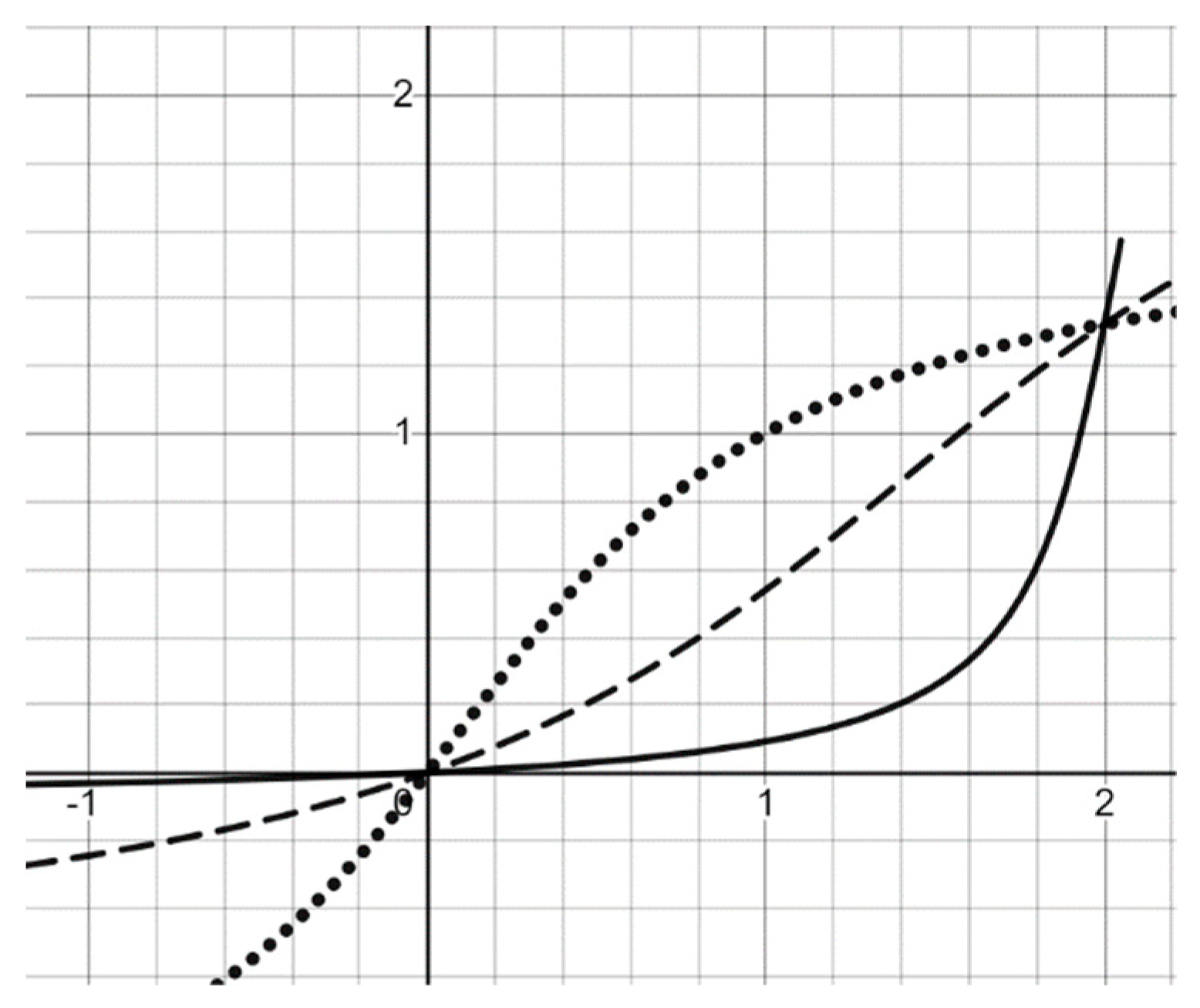
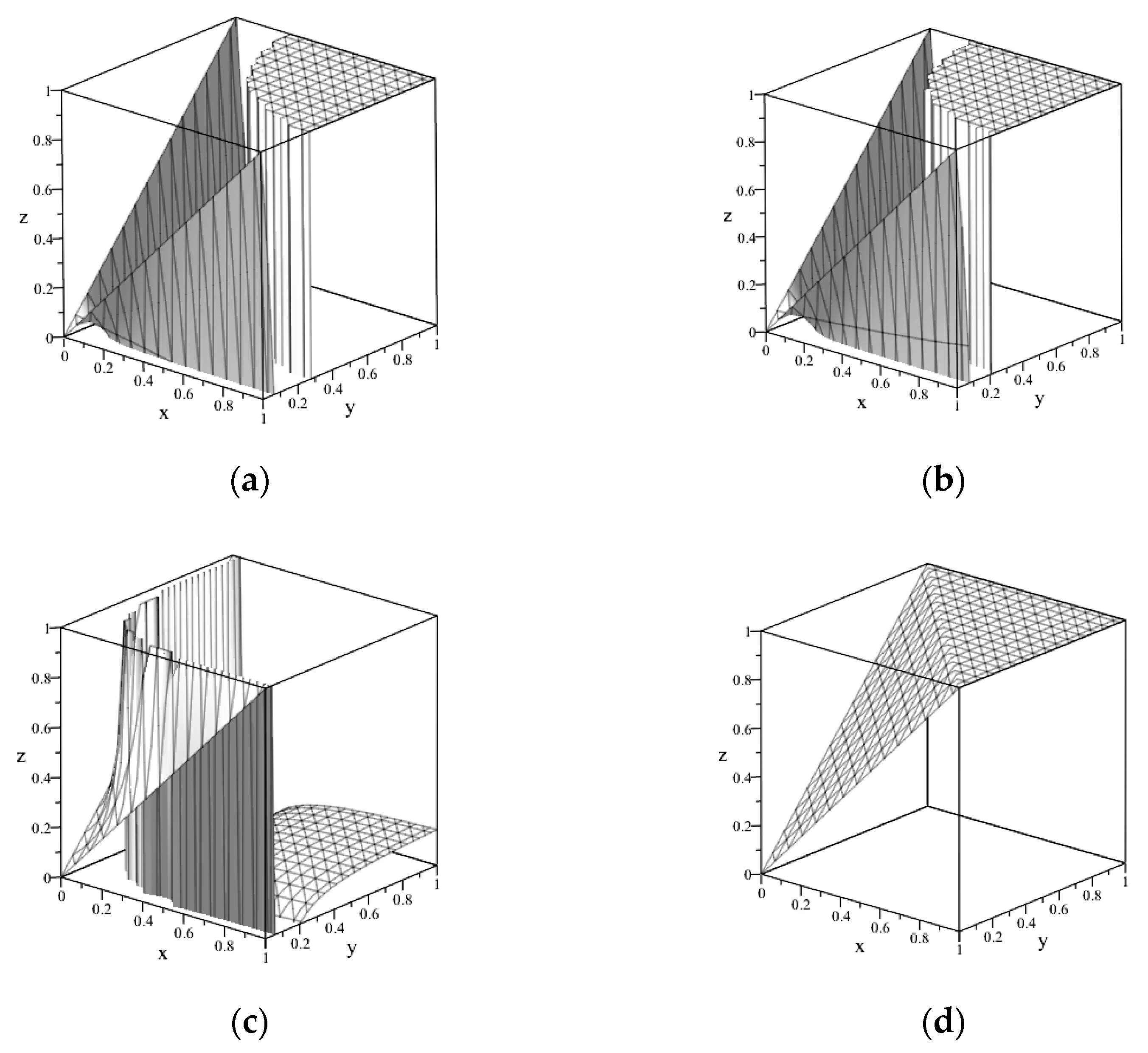
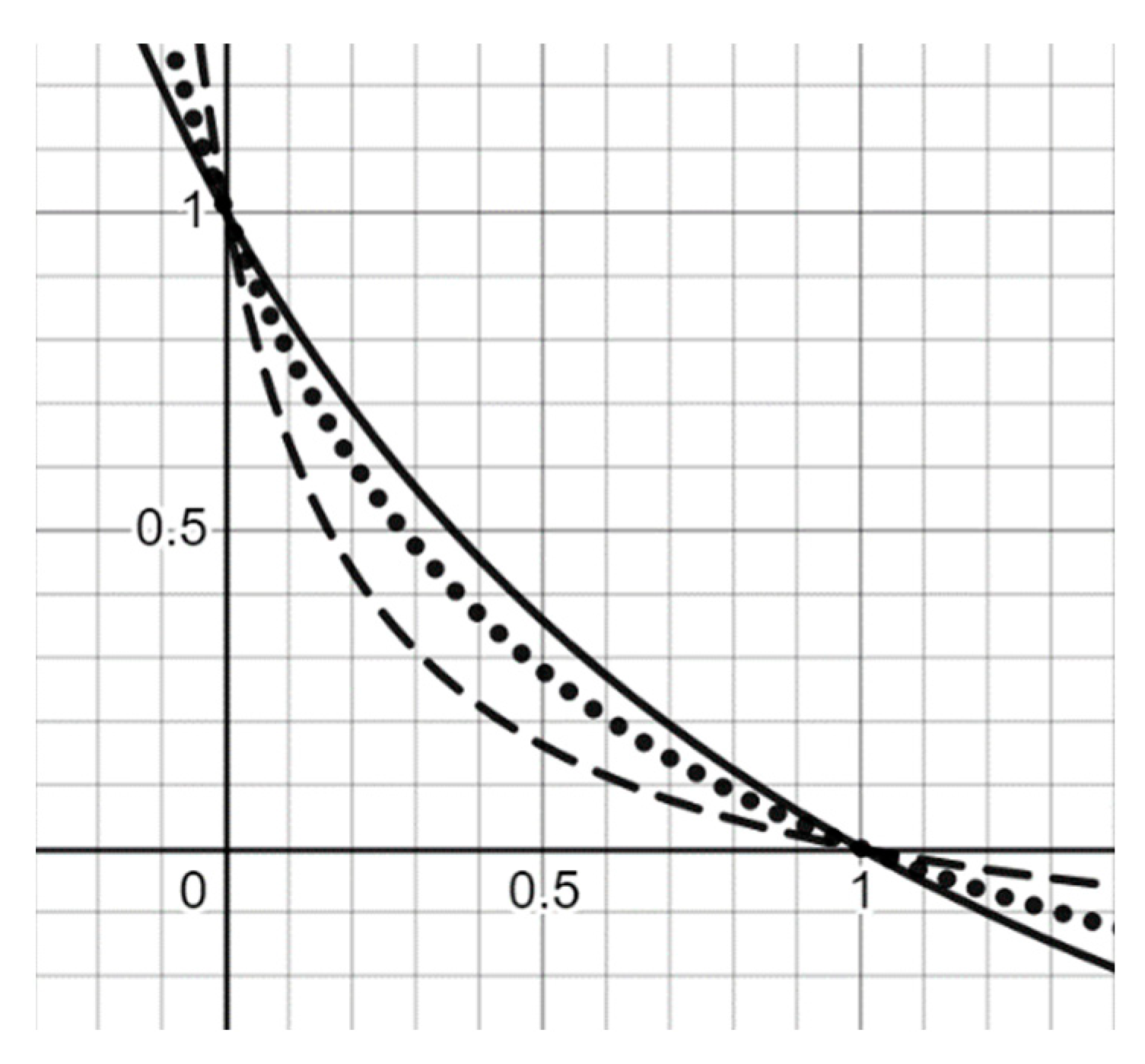
3.1. Increasing Generator in the Form of an Arctangent of a Linear Fractional Function and the Corresponding Triangular Conorm
- (a)
- If , then the asymptote is located to the right of ;
- (b)
- If , then the asymptote is located to the left of the given interval (left asymptote).
- (a)
- ;
- (b)
- ;
- (c)
- .
- (1)
- ,;
- (2)
- , ;
- (3)
- ;
- (4)
- , .
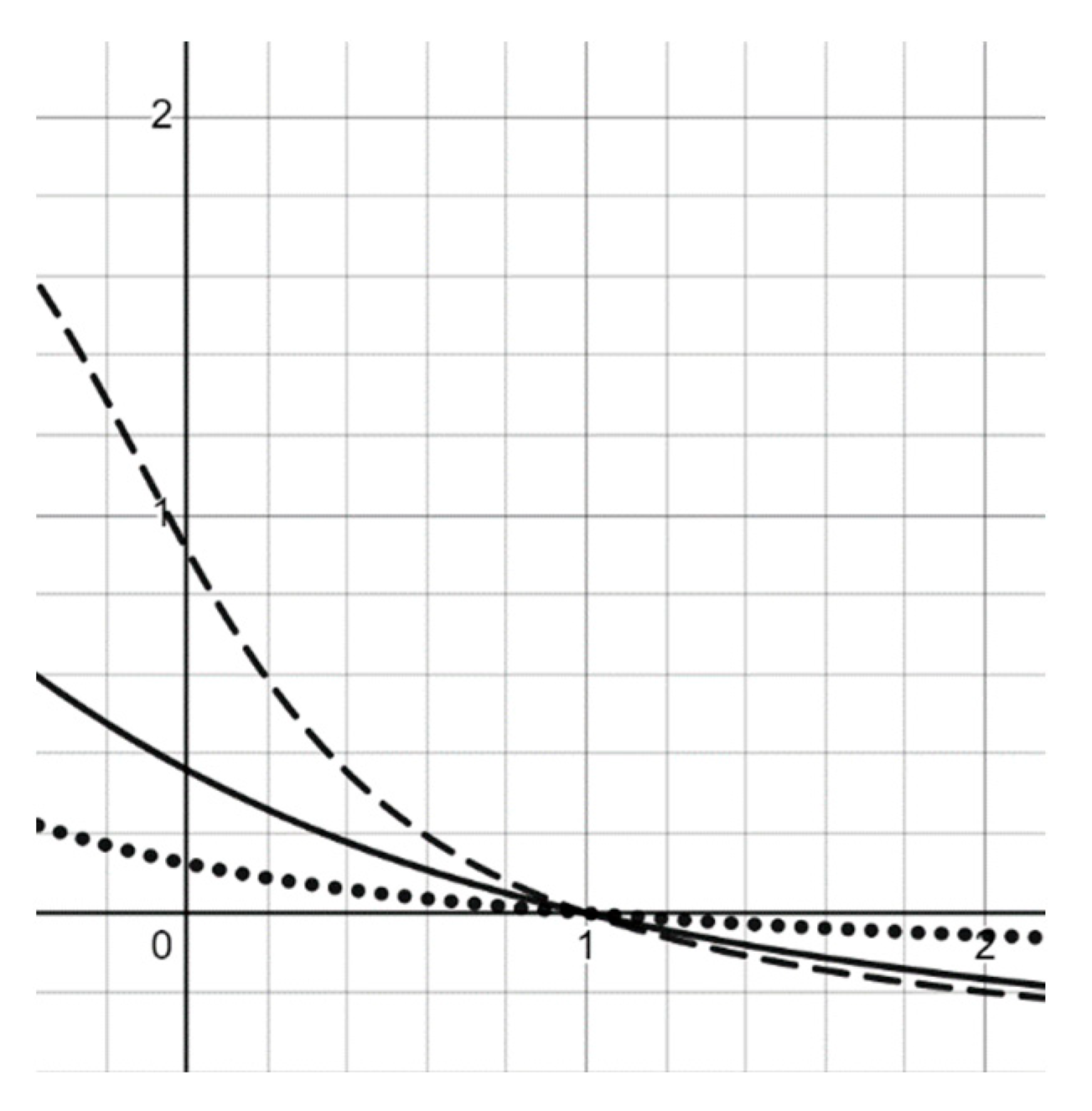
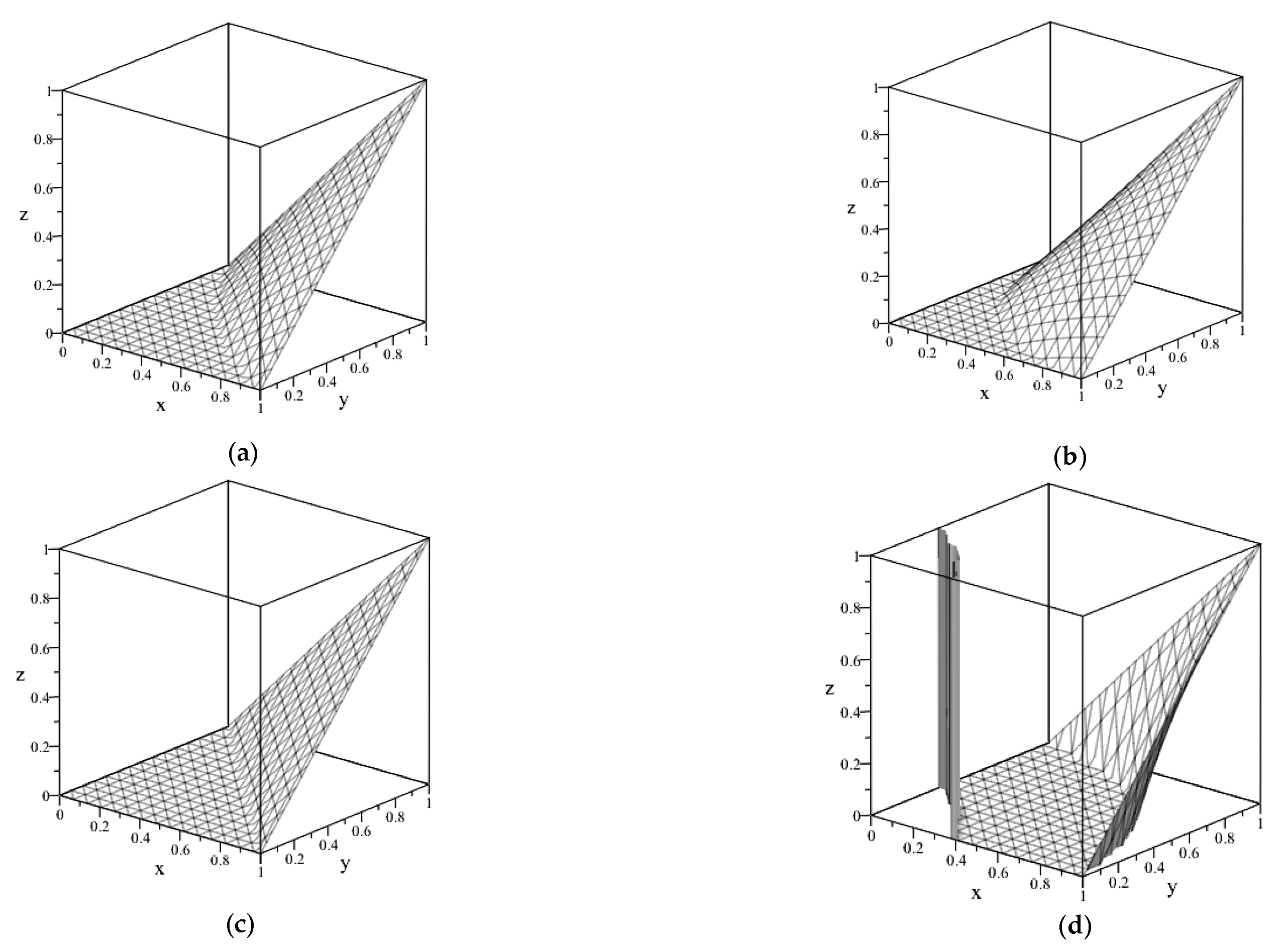
3.2. Decreasing Generator in the Form of an Arctangent of a Linear Fractional Function and the Corresponding Triangular Norm
- (1)
- The vertical asymptote is located to the left of if or ;
- (2)
- The vertical asymptote is located to the right of if .
- (1)
- ;
- (2)
- ;
- (3)
- .
4. Discussion
- For the function, , ensure the continuity, strict decrease (or increase), and fulfillment of condition (or condition ) by adjusting the parameters. If at least one of the requirements is not met, then the given function cannot be considered a generator.
- The construction of a t-norm or s-conorm from the class of rational functions is conducted on the basis of the commutative and associative function of form (7). Based on the constructed generator, , one can find the coefficients of the function, .
- Define restrictions on the parameters of the function, , that ensure the fulfillment of the boundary conditions from the definition of a triangular norm or conorm.
- Investigate the continuity of on the basis of the function . At this step, those parameter values for which the function, , has points of discontinuity on are excluded.
- Determine whether the design operation is needed: if , then . Otherwise, , and the design operation must be used. Similar reasoning takes place for the t-norm: if , then ; if , then .
5. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zimmermann, H.J. Fuzzy Sets Theory and Its Applications; Kluwer Academic Publishers: London, UK, 2001. [Google Scholar]
- Precup, R.; Hellendoorn, H. A survey on industrial applications of fuzzy control. Comput. Ind. 2011, 62, 213–226. [Google Scholar]
- De Silva, C.W. Intelligent Control: Fuzzy Logic Applications; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular norms. Position paper II: General constructions and parameterized families. Fuzzy Sets Syst. 2004, 145, 411–438. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular norms. Position paper III: Continuous t-norms. Fuzzy Sets Syst. 2004, 145, 439–454. [Google Scholar]
- Klement, E.P.; Mesiar, R.; Pap, E. Problems on triangular norms and related operators. Fuzzy Sets Syst. 2004, 145, 471–479. [Google Scholar]
- Ling, C.M. Representation of associative function. Publ. Math. Debrecen 1965, 12, 189–212. [Google Scholar]
- Dimuro, G.P.; Bedregal, B.; Bustince, H.; Asiain, M.J.; Mesiar, R. On additive generators of overlap functions. Fuzzy Sets Syst. 2016, 287, 76–96. [Google Scholar]
- Najjari, V. On Generators in Archimedean Copulas. Commun. Math. Analysis 2018, 12, 155–166. [Google Scholar]
- Sun, X.; Liu, H. The additive generators of t-norms and t-conorms on bounded lattices. Fuzzy Sets Syst. 2020, 408, 13–25. [Google Scholar] [CrossRef]
- Dimuro, G.P.; Bedregal, B.C.; Reiser, R.H.S.; Santiago, R.H.N. Interval additive generators of interval T-norms. In Logic, Language, Information and Computation. WoLLIC 2008. Lecture Notes in Computer Science; Hodges, W., de Queiroz, R., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Vol. 5110. [Google Scholar] [CrossRef]
- Calvo, T.; Mesiar, R. Weighted triangular norms-based aggregation operators. Fuzzy Sets Syst. 2003, 137, 3–10. [Google Scholar]
- Torra, V. The Weighted OWA Operator. Int. J. Intell. Syst. 1997, 12, 153–166. [Google Scholar] [CrossRef]
- Kolesárová, A. Triangular norm-addition of linear fuzzy numbers. Tatra Mt. Math. Publ. 1992, 6. [Google Scholar]
- Kolesárová, A.; Kerre, E.E. Compositional Rule of Inference Based on Triangular Norms. In Fuzzy If-Then Rules in Computational Intelligence; Ruan, D., Kerre, E.E., Eds.; The Springer International Series in Engineering and Computer Science: Boston, MA, USA, 2000; Volume 553, pp. 61–80. [Google Scholar] [CrossRef]
- Navara, M.; Petrik, M.; Sarkoci, P. Explicit formulas for generators of triangular norms. Publ. Math. Debrecen 2010, 77, 171–191. [Google Scholar]
- Ouyang, Y. On the construction of boundary weak triangular norms through additive generators. Nonlinear Anal. 2007, 66, 125–130. [Google Scholar] [CrossRef]
- Vicenik, P. Additive generators of associative functions. Fuzzy Set Syst. 2005, 153, 137–160. [Google Scholar] [CrossRef]
- Babu, M.S.; Ahmed, S. Function as the Generator of Parametric T-norms. Am. J. Appl. Math. 2017, 5, 114–118. [Google Scholar] [CrossRef]
- Ledeneva, T. Additive generators of fuzzy operations in the form of linear fractional functions. Fuzzy Sets Syst. 2019, 386, 1–24. [Google Scholar] [CrossRef]
- Ledeneva, T. New Family of Triangular Norms for Decreasing Generators in the Form of a Logarithm of a Linear Fractional Function. Fuzzy Sets Syst. 2022, 427, 37–54. [Google Scholar] [CrossRef]
- Klement, E.P.; Mesiar, R.; Pap, E. Triangular norms. Position paper I: Basic analytical and algebraic properties. Fuzzy Sets Syst. 2004, 143, 5–26. [Google Scholar]
- Klir, G.J.; Yuan, B. Fuzzy Sets and Fuzzy Logic: Theory and Applications; Prentice Hall: Hoboken, NJ, USA, 1995. [Google Scholar]
- Ledeneva, T. Some aspects of the representation of fuzzy operators by the relation of two polynomials. News Higher Educ. Inst. Math. 1997, 11, 33–40. [Google Scholar]
- Ledeneva, T. Analysis of additive generators of fuzzy operations represented by rational functions. J. Phys. Conf. Ser. 2018, 973, 012037. [Google Scholar] [CrossRef]
- Demirci, M. Topological properties of the class of generators of an indistinguishability operator. Fuzzy Sets Syst. 2004, 143, 413–426. [Google Scholar] [CrossRef]
- Grigorenko, O.; Miñana, J.-J.; Valero, O. Two new methods to construct fuzzy metrics from metrics. Fuzzy Sets Syst. 2023, 467, 108483. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ledeneva, T. A Parametric Family of Triangular Norms and Conorms with an Additive Generator in the Form of an Arctangent of a Linear Fractional Function. Computation 2023, 11, 155. https://doi.org/10.3390/computation11080155
Ledeneva T. A Parametric Family of Triangular Norms and Conorms with an Additive Generator in the Form of an Arctangent of a Linear Fractional Function. Computation. 2023; 11(8):155. https://doi.org/10.3390/computation11080155
Chicago/Turabian StyleLedeneva, Tatiana. 2023. "A Parametric Family of Triangular Norms and Conorms with an Additive Generator in the Form of an Arctangent of a Linear Fractional Function" Computation 11, no. 8: 155. https://doi.org/10.3390/computation11080155
APA StyleLedeneva, T. (2023). A Parametric Family of Triangular Norms and Conorms with an Additive Generator in the Form of an Arctangent of a Linear Fractional Function. Computation, 11(8), 155. https://doi.org/10.3390/computation11080155





