The Problem of Effective Evacuation of the Population from Floodplains under Threat of Flooding: Algorithmic and Software Support with Shortage of Resources
Abstract
1. Introduction
- (A)
- (B)
- (C)
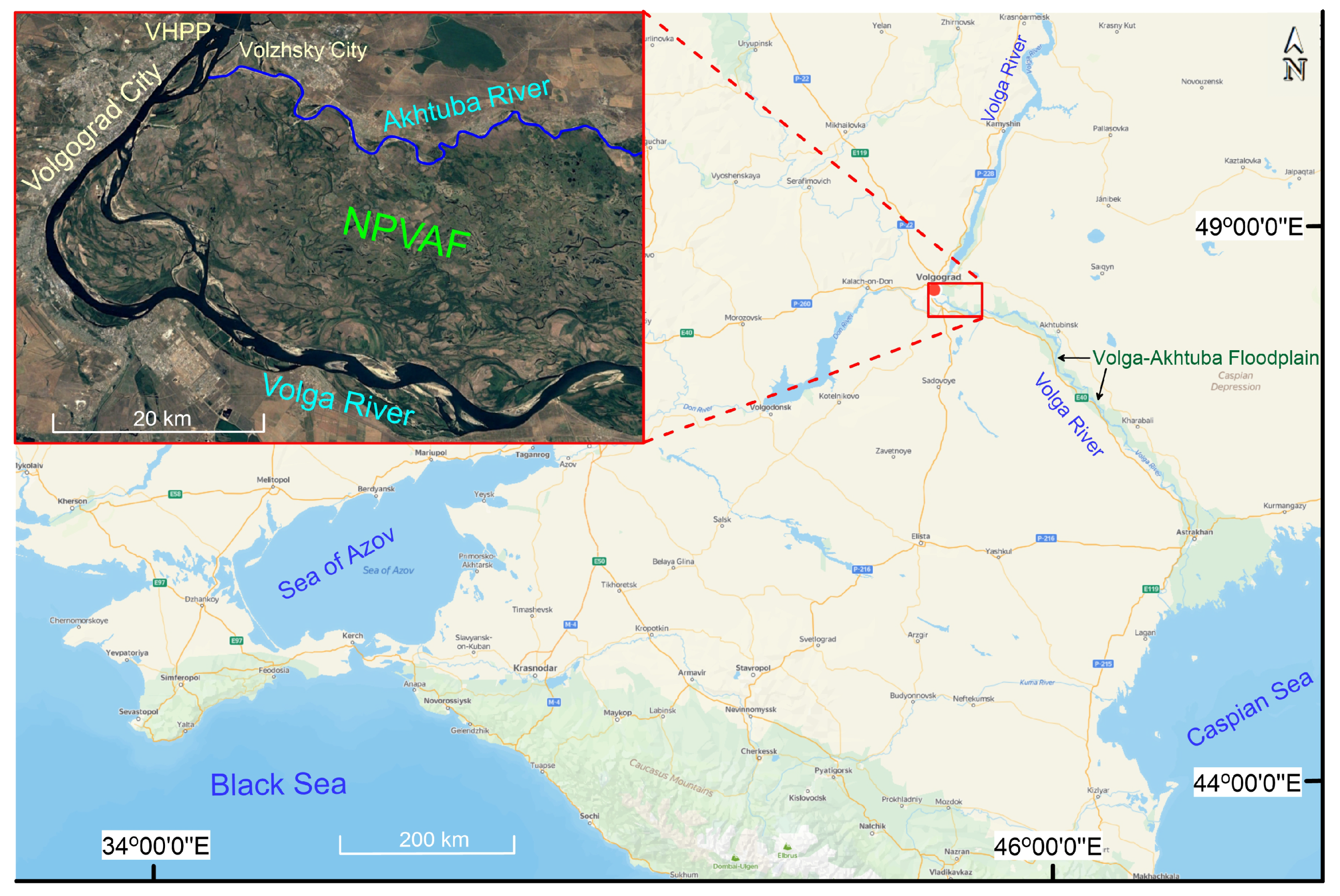
2. Formulation of the Problem
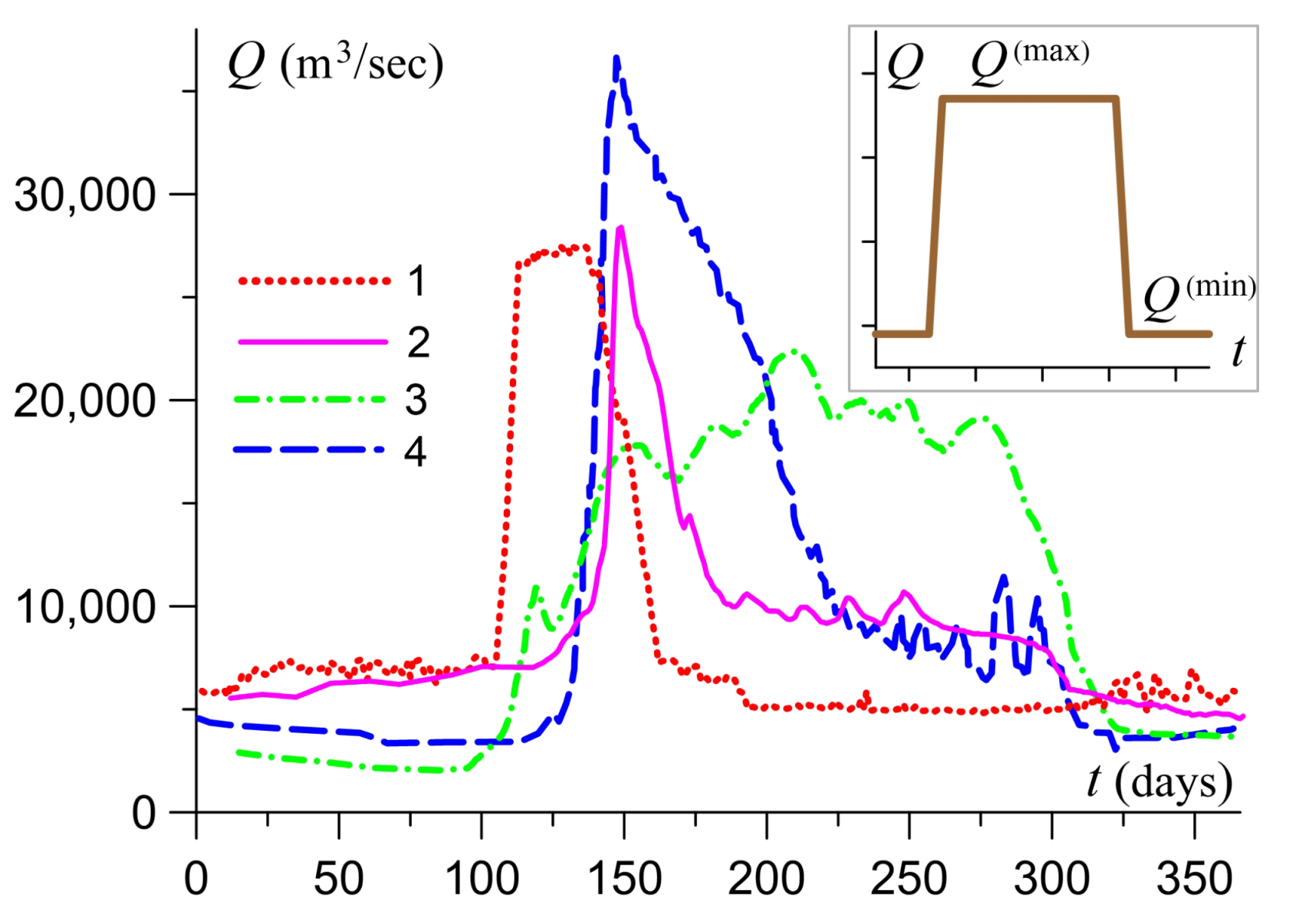
3. Materials and Methods
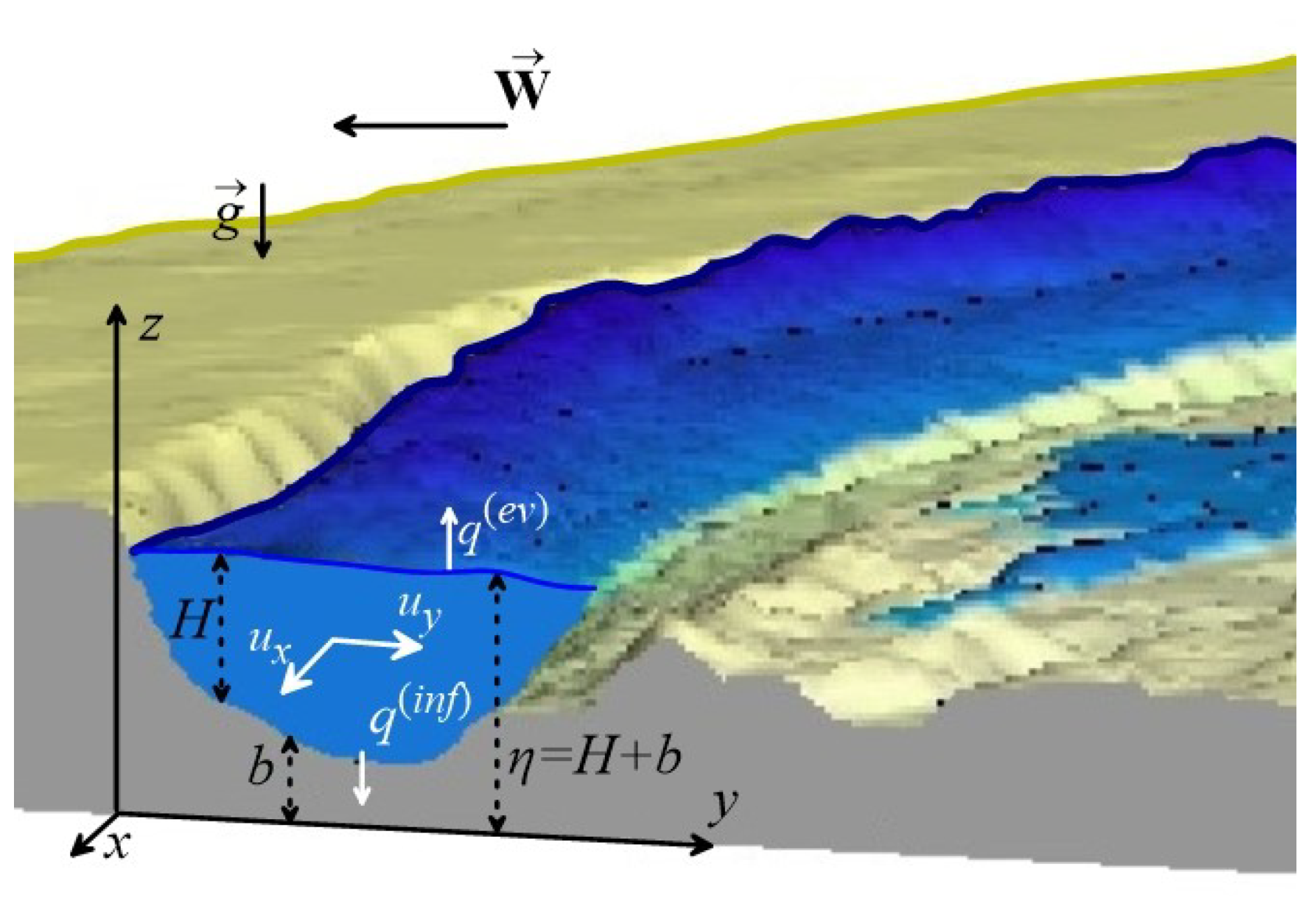
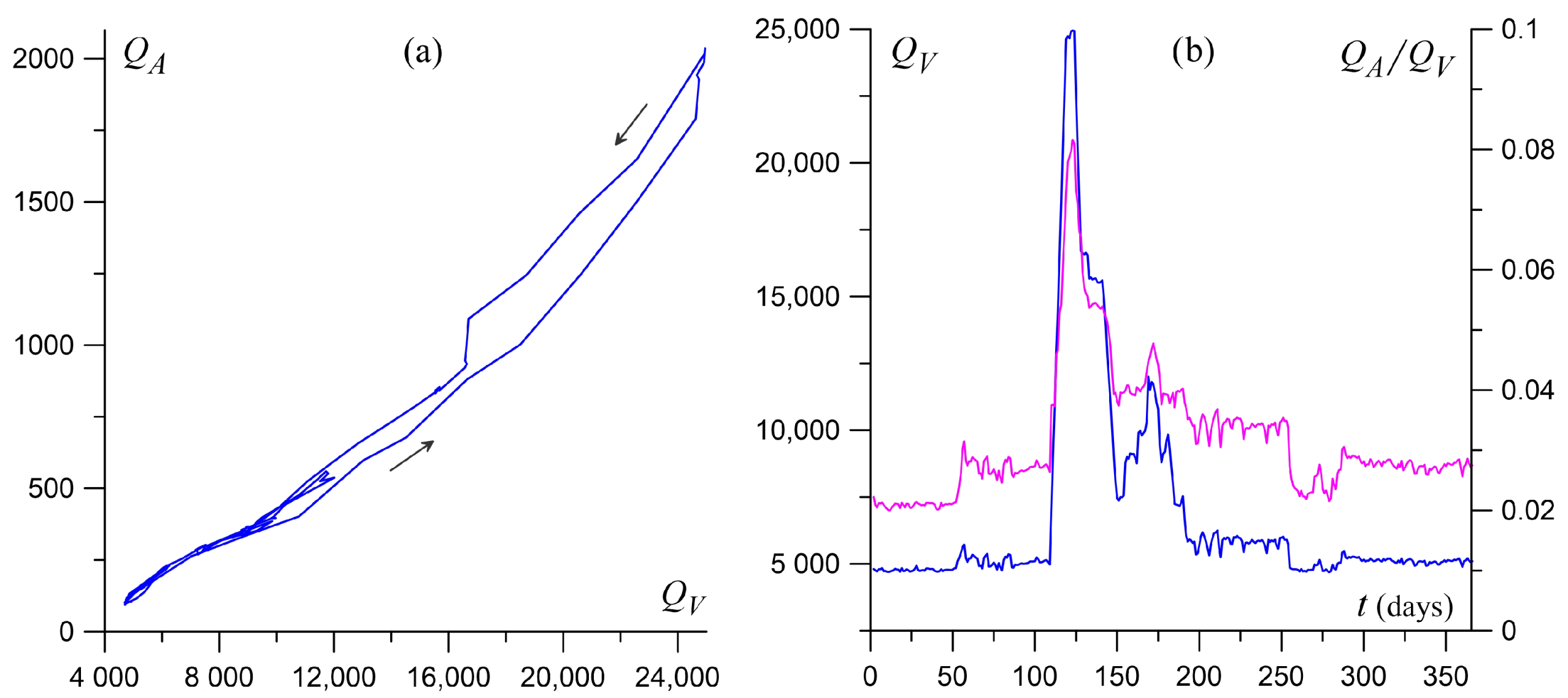
3.1. Hydrodynamic Model of Flooding
3.2. Digital Hydrological Landscape Model as the Basis for Flood Modeling
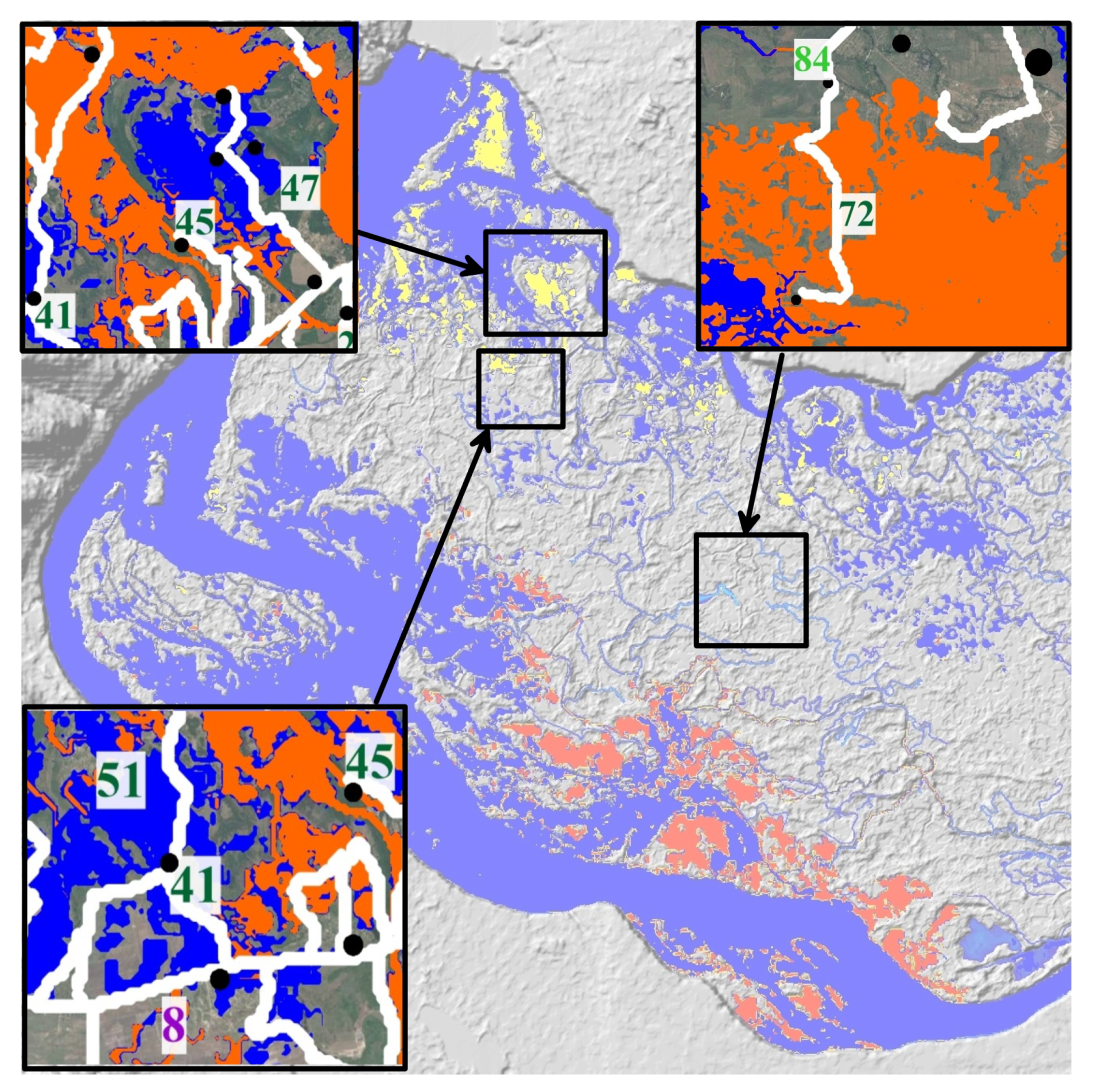
3.3. Algorithm for Calculating the Flooding Moments of Settlements and Evacuation Routes
3.4. Creation of Safe Schedule
3.5. Construction of the Function of Minimum Resource Support for Safe Evacuation and Selection of Evacuation Routes
4. Results
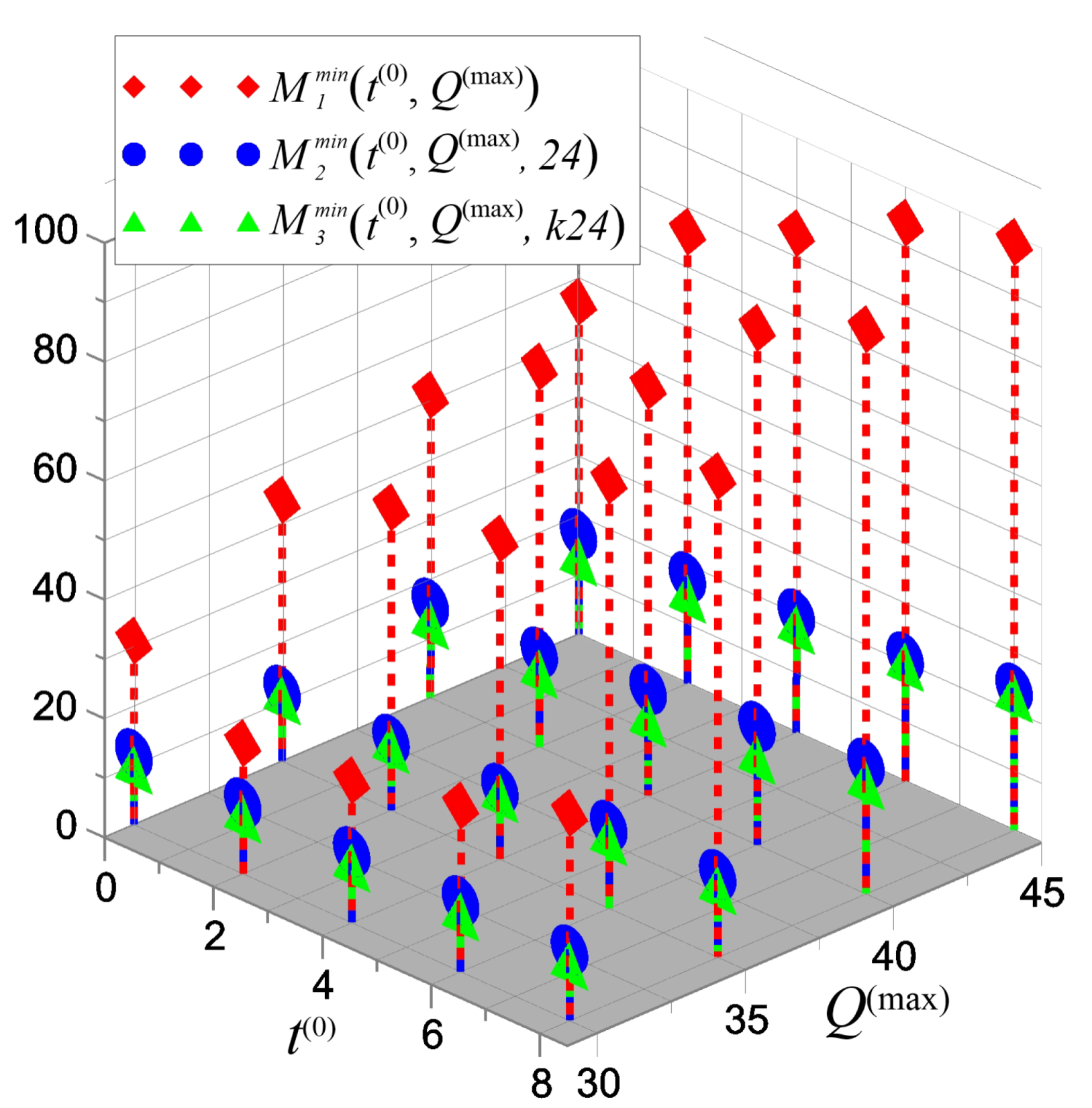
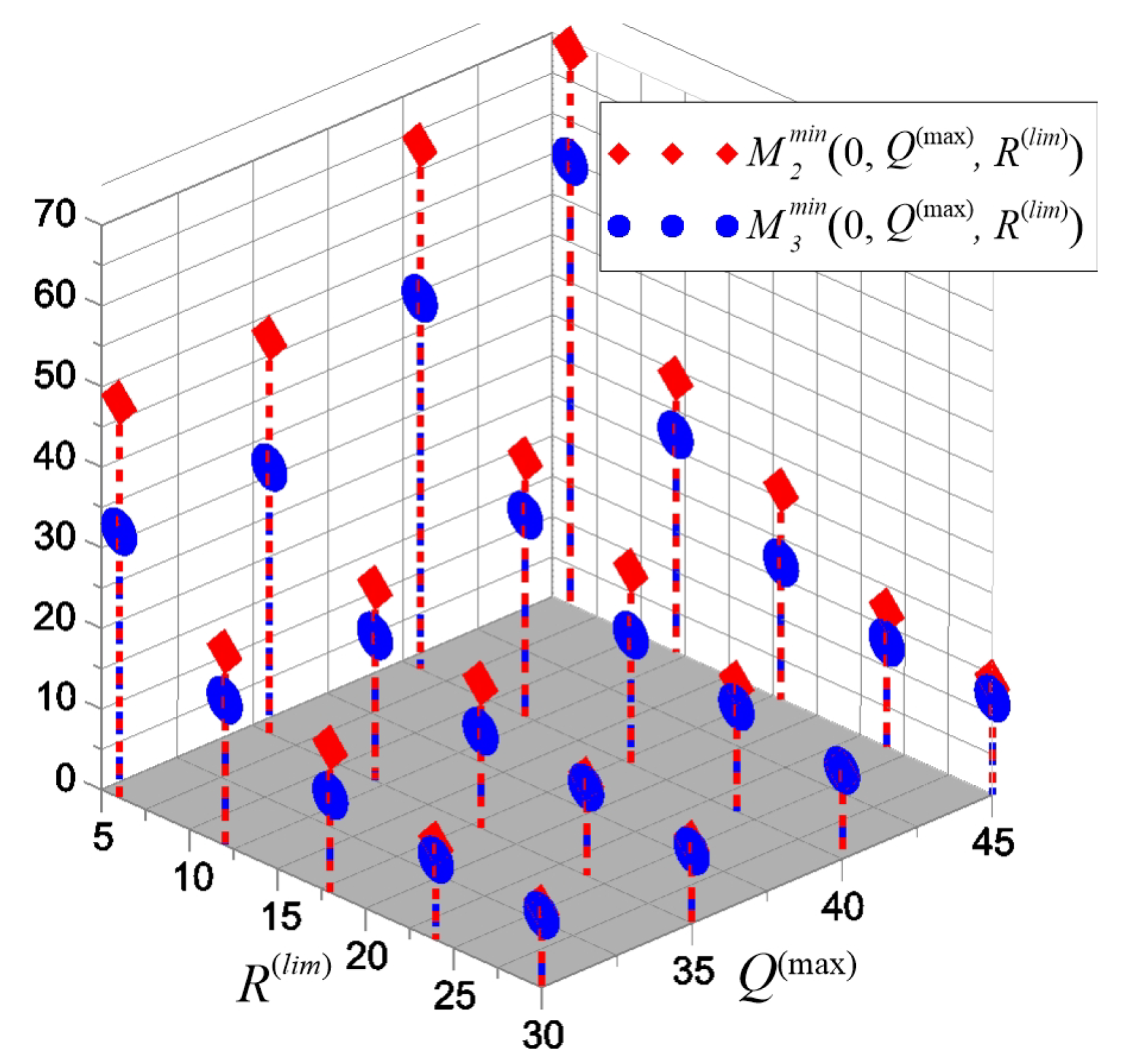
The Minimum Resource Support Function for the Safe Evacuation of the Northern Part of the Volga-Akhtuba Floodplain Population
- (1)
- for 1-stage safe vehicle-pedestrian evacuation in NPVAF;
- (2)
- for 2-stage safe pedestrian evacuation of the population in the NPVAF;
- (3)
- for 2-stage safe vehicle-pedestrian evacuation in NPVAF with accommodation of the temporary evacuation points in settlements, (see Figure 12).
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Arnell, N.W.; Lloyd-Hughes, B. The global-scale impacts of climate change on water resources and flooding under new climate and socio-economic scenarios. Clim. Chang. 2014, 122, 127–140. [Google Scholar] [CrossRef]
- Cea, L.; Costabile, P. Flood risk in urban areas: Modelling, management and adaptation to climate change. A review. Hydrology 2022, 9, 50. [Google Scholar] [CrossRef]
- Duan, L.; Liu, C.; Xu, H.; Pan, H.; Liu, H.; Yan, X.; Liu, T.; Yang, Z.; Liu, G.; Dai, X.; et al. Susceptibility Assessment of Flash Floods: A Bibliometrics Analysis and Review. Remote Sens. 2022, 14, 5432. [Google Scholar] [CrossRef]
- The Centre for Research on the Epidemiology of Disasters. Available online: https://www.cred.be/publications (accessed on 27 July 2023).
- Alizadeh, B.; Li, D.; Hillin, J.; Meyer, M.A.; Thompson, C.M.; Zhang, Z.; Behzadan, A.H. Human-centered flood mapping and intelligent routing through augmenting flood gauge data with crowdsourced street photos. Adv. Eng. Inform. 2022, 54, 101730. [Google Scholar] [CrossRef]
- Ivanova, O.; Ivanov, M.; Revetria, R. Estimation of the environmental damage of floods in Russia at the end of the 20th century. IOP Conf. Ser. Mater. Sci. Eng. 2019, 492, 012019. [Google Scholar] [CrossRef]
- Frolova, N.L.; Kireeva, M.B.; Magrickiy, D.V.; Bologov, M.B.; Kopylov, V.N.; Hall, J.; Semenov, V.A.; Kosolapov, A.E.; Dorozhkin, E.V.; Korobkina, E.A.; et al. Hydrological hazards in Russia: Origin, classification, changes and risk assessment. Nat. Hazards 2017, 88, 103–131. [Google Scholar] [CrossRef]
- Belikov, V.V.; Borisova, N.M.; Glotko, A.V. Numerical hydrodynamic 2D-simulation of the inundation of Tulun town on the Iya R. during Flood 2019. Water Resour. 2021, 48, 713–725. [Google Scholar] [CrossRef]
- Zemtsov, S.P.; Goryachko, M.D.; Baburin, V.L.; Krylenko, I.N.; Yumina, N.M. Integrated assessment of socio-economic risks of hazardous hydrological phenomena in Slavyansk municipal district. Nat. Hazards 2016, 82, 43–61. [Google Scholar] [CrossRef]
- Danilov-Danilyan, V.I.; Gelfan, A.N.; Motovilov, Y.G.; Kalugin, A.S. Disastrous flood of 2013 in the Amur basin: Genesis, recurrence assessment, simulation results. Water Resour. 2014, 41, 115–125. [Google Scholar] [CrossRef]
- Grigorev, V.Y.; Kharlamov, M.A.; Semenova, N.K.; Sazonov, A.A.; Chalov, S.R. Impact of precipitation and evaporation change on flood runoff over Lake Baikal catchment. Environ. Earth Sci. 2023, 82, 16. [Google Scholar] [CrossRef]
- Belikov, V.V.; Vasil’eva, E.S.; Prudovskii, A.M. Numerical modeling of a breach wave through the dam at the Krasnodar reservoir. Power Technol. Eng. 2010, 44, 269–278. [Google Scholar] [CrossRef]
- Veremenyuk, V.V.; Ivashechkin, V.V.; Nemerovets, O.V. Modeling of Process for Level Changes in Cascade of Two Channel Water Reservoirs in Case of Flooding. Sci. Tech. 2019, 18, 146–154. [Google Scholar] [CrossRef]
- Wang, W.; Chen, W.; Huang, G. Research on Flood Propagation for Different Dam Failure Modes: A Case Study in Shenzhen, China. Front. Earth Sci. 2020, 460, 527363. [Google Scholar] [CrossRef]
- Ferdous, M.R. Socio-Hydrological Dynamics in Bangladesh-Understanding the Interaction Between Hydrological and Social Processes along the Jamuna Floodplain; CRC Press: Leiden, The Netherlands, 2020; p. 205. [Google Scholar]
- Zakharchuk, E.A.; Tikhonova, N.A.; Sukhachev, V.N. Spatial structure and propagation of the Neva flood waves. Russ. Meteorol. Hydrol. 2020, 45, 245–253. [Google Scholar] [CrossRef]
- Sukhinov, A.I.; Chistyakov, A.E.; Nikitina, A.V.; Kuznetsova, I.Y.; Atayan, A.M.; Protsenko, E.A.; Litvinov, V.N. Supercomputer-Based Simulation of the Hydrodynamics of River Mouth Areas. Commun. Comput. Inf. Sci. 2021, 1437, 255–269. [Google Scholar] [CrossRef]
- Divinsky, B.V.; Fomin, V.V.; Kosyan, R.D.; Ratner, Y.D. Extreme wind waves in the Black Sea. Oceanologia 2020, 62, 23–30. [Google Scholar] [CrossRef]
- Kuprin, A.V.; Novakov, A.D.; Kantarzhi, I.G.; Gubina, N.A. Local and General Scours Caused by Tsunami Waves. Power Technol. Eng. Vol. 2021, 54, 836–840. [Google Scholar] [CrossRef]
- Zemtsov, V.A.; Vershinin, D.A.; Inishev, N.G. Imitation modeling of ice dams (case study of Tom’River, Western Siberia). ICE Snow 2015, 54, 59–68. [Google Scholar] [CrossRef]
- Alekseevskii, N.I.; Krylenko, I.N.; Belikov, V.V.; Kochetkov, V.V.; Norin, S.V. Numerical Hydrodynamic Modeling of Inundation in Krymsk on 6–7 July 2012. Power Technol. Eng. 2014, 48, 179–186. [Google Scholar] [CrossRef]
- De Caro, M.; Crosta, G.B.; Castellanza, R.; Agliardi, F.; Volpi, G.; Alberti, S. 2D Modelling of rockslide displacements by non-linear time dependent relationships. In Landslides and Engineered Slopes. Experience, Theory and Practice; CRC Press: London, UK, 2016; pp. 765–770. [Google Scholar] [CrossRef]
- Paronuzzi, P.; Bolla, A.; Pinto, D.; Lenaz, D.; Soccal, M. The clays involved in the 1963 Vajont landslide: Genesis and geomechanical implications. Eng. Geol. 2021, 294, 106376. [Google Scholar] [CrossRef]
- Klikunova, A.Y.; Dyakonova, T.A.; Agafonnikova, E.O.; Makoveev, I.S.; Kornaukhova, M.A.; Radchenko, V.P. Modeling of flooding of settlements during the spring flood. Math. Phys. Comput. Simul. 2021, 24, 63–72. [Google Scholar] [CrossRef]
- Isaeva, I.I.; Voronin, A.A.; Khoperskov, A.V.; Dubinko, K.E.; Klikunova, A.Y. Decision Support System for the Socio-Economic Development of the Northern Part of the Volga-Akhtuba Floodplain (Russia). Commun. Comput. Inf. Sci. 2019, 1083, 63–77. [Google Scholar] [CrossRef]
- Wyzga, B.; Kundzewicz, Z.W.; Konieczny, R.; Piniewski, M.; Zawiejska, J.; Radecki-Pawlik, A. Comprehensive approach to the reduction of river flood risk: Case study of the Upper Vistula Basin. Sci. Total. Environ. 2018, 631, 1251–1267. [Google Scholar] [CrossRef]
- Rizzo, C.; Maranzoni, A.; D’Oria, M. Probabilistic mapping and sensitivity assessment of dam-break flood hazard. Hydrol. Sci. J. 2023, 68, 700–718. [Google Scholar] [CrossRef]
- Chatzichristaki, C.; Stefanidis, S.; Stefanidis, P.; Stathis, D. Analysis of the flash flood in Rhodes Island (South Greece) on 22 November 2013. Silva Balc. 2015, 16, 76–86. [Google Scholar]
- Diakakis, M.; Deligiannakis, G. Vehicle-related flood fatalities in Greece. Environ. Hazards 2013, 12, 278–290. [Google Scholar] [CrossRef]
- Belyakova, A.Y.; Ivanyo, Y.M.; Petrova, S.A. Modeling of rare rain floods on the example of middle rivers of Angara basin. IOP Conf. Ser. Earth Environ. Sci. 2021, 677, 042103. [Google Scholar] [CrossRef]
- Alam, M.D.J.; Habib, M.A. Mass evacuation of Halifax, Canada: A dynamic traffic microsimulation modeling approach. Procedia Comput. Sci. 2019, 151, 535–542. [Google Scholar] [CrossRef]
- Yin, D.; Wang, S.; Ouyang, Y. ViCTS: A novel network partition algorithm for scalable agent-based modeling of mass evacuation. Comput. Environ. Urban Syst. 2020, 80, 101452. [Google Scholar] [CrossRef]
- Nguyen-Thi, L.Q.; Nguyen, V.D.; Pierens, X.; Coorevits, P. An experimental and numerical study of the influence of viscosity on the behavior of dam-break flow. Theor. Comput. Fluid Dyn. 2021, 35, 345–362. [Google Scholar] [CrossRef]
- Dyakonova, T.; Khoperskov, A.; Khrapov, S. Numerical Model of Shallow Water: The Use of NVIDIA CUDA Graphics Processors. Commun. Comput. Inf. Sci. 2016, 687, 132–145. [Google Scholar] [CrossRef]
- Khrapov, S.S.; Khoperskov, A.V. Application of Graphics Processing Units for Self-Consistent Modelling of Shallow Water Dynamics and Sediment Transport. Lobachevskii J. Math. 2020, 41, 1475–1484. [Google Scholar] [CrossRef]
- Klikunova, A.Y.; Khoperskov, A.V.; Agafonnikova, E.O.; Kuz’mich, A.S.; Dyakonova, T.A.; Khrapov, S.S.; Gusev, I.M. Creation of cadastral maps of flooding based on numerical modeling. J. Comput. Eng. Math. 2019, 6, 3–17. [Google Scholar] [CrossRef]
- Shaikh, A.A.; Pathan, A.I.; Waikhom, S.I.; Agnihotri, P.G.; Islam, M.; Singh, S.K. Application of latest HEC-RAS version 6 for 2D hydrodynamic modeling through GIS framework a case study from coastal urban foodplain in India. Model. Earth Syst. Environ. 2022, 9, 1369–1385. [Google Scholar] [CrossRef]
- Akiyanova, F.; Ongdas, N.; Zinabdin, N.; Karakulov, Y.; Nazhbiyev, A.; Mussagaliyeva, Z.; Atalikhova, A. Operation of Gate-Controlled Irrigation System Using HEC-RAS 2D for Spring Flood Hazard Reduction. Computation 2023, 11, 27. [Google Scholar] [CrossRef]
- Lamichhane, N.; Sharma, S. Development of flood warning system and flood inundation mapping using field survey and LiDAR data for the Grand River near the city of Painesville, Ohio. Hydrology 2017, 4, 24. [Google Scholar] [CrossRef]
- Yu, X.; Zhang, J. The Application and Applicability of HEC-HMS Model in Flood Simulation under the Condition of River Basin Urbanization. Water 2023, 15, 2249. [Google Scholar] [CrossRef]
- Alam, M.D.J.; Habib, M.A.; Pothier, E. Shelter locations in evacuation: A Multiple Criteria Evaluation combined with flood risk and traffic microsimulation modeling. Int. J. Disaster Risk Reduct. 2021, 53, 102016. [Google Scholar] [CrossRef]
- Hsiao, C.C.; Sun, M.C.; Chen, A.Y.; Hsu, Y.T. Location problems for shelter-in-place deployment: A case study of vertical evacuation upon dam-break floods. Int. J. Disaster Risk Reduct. 2021, 57, 102048. [Google Scholar] [CrossRef]
- Kim, K.; Pant, P.; Yamashita, E. Integrating travel demand modeling and flood hazard risk analysis for evacuation and sheltering. Int. J. Disaster Risk Reduct. 2018, 31, 1177–1186. [Google Scholar] [CrossRef]
- Kongsomsaksakul, S.; Yang, C.; Chen, A. Shelter location-allocation model for flood evacuation planning. J. East. Asia Soc. Transp. Stud. 2005, 6, 4237–4252. [Google Scholar] [CrossRef]
- Mollah, A.K.; Sadhukhan, S.; Das, P.; Anis, M.Z. A cost optimization model and solutions for shelter allocation and relief distribution in flood scenario. Int. J. Disaster Risk Reduct. 2018, 31, 1187–1198. [Google Scholar] [CrossRef]
- Na, L.; Xueyan, S.; Mingliang, Q. A bi-objective evacuation routing engineering model with secondary evacuation expected costs. Syst. Eng. Procedia 2012, 5, 1–7. [Google Scholar] [CrossRef]
- Oh, W.S.; Yu, D.J.; Muneepeerakul, R. Efficiency-fairness trade-offs in evacuation management of urban floods: The effects of the shelter capacity and zone prioritization. PLoS ONE 2021, 16, e0253395. [Google Scholar] [CrossRef]
- Rahman, M.; Chen, N.; Islam, M.M.; Dewan, A.; Pourghasemi, H.R.; Washakh, R.M.A.; Nepal, N.; Tian, S.; Faiz, H.; Alam, M.; et al. Location-allocation modeling for emergency evacuation planning with GIS and remote sensing: A case study of Northeast Bangladesh. Geosci. Front. 2021, 12, 101095. [Google Scholar] [CrossRef]
- Wen, Y.; Zhang, N. Evacuation and Settlement Model of Personnel in Major Flood Disasters and Its Application. IOP Conf. Ser. Earth Environ. Sci. 2019, 304, 042016. [Google Scholar] [CrossRef]
- Liu, X.; Lim, S. An agent-based evacuation model for the 2011 Brisbane City-scale riverine flood. Nat. Hazards 2018, 94, 53–70. [Google Scholar] [CrossRef]
- Chelariu, O.-E.; Iatu, C.; Ionuț, M. A GIS-Based Model for Flood Shelter Locations and Pedestrian Evacuation Scenarios in a Rural Mountain Catchment in Romania. Water 2022, 14, 3074. [Google Scholar] [CrossRef]
- Lee, Y.H.; Kim, H.I.; Han, K.Y.; Hong, W.H. Flood Evacuation Routes Based on Spatiotemporal Inundation Risk Assessment. Water 2020, 12, 2271. [Google Scholar] [CrossRef]
- Nakanishi, H.; Wise, S.; Suenaga, Y.; Manley, E. Simulating emergencies with transport outcomes Sim (SETOSim): Application of an agent-based decision support tool to community evacuation planning. Int. J. Disaster Risk Reduct. 2020, 49, 101657. [Google Scholar] [CrossRef]
- Davidson, R.A.; Nozick, L.K.; Wachtendorf, T.; Blanton, B.; Colle, B.; Kolar, R.L.; DeYoung, S.; Dresback, K.M.; Yi, W.; Yang, K.; et al. An integrated scenario ensemble-based framework for hurricane evacuation modeling: Part 1—Decision support system. Risk Anal. 2020, 40, 97–116. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Hu, B.; Zhang, D.; Gong, J.; Song, Y.; Sun, J. Flood evacuation simulations using cellular automata and multiagent systems—A human-environment relationship perspective. Int. J. Geogr. Inf. Sci. 2019, 33, 2241–2258. [Google Scholar] [CrossRef]
- Shirvani, M.; Kesserwani, G.; Richmond, P. Agent-based simulator of dynamic flood-people interactions. J. Flood Risk Manag. 2021, 14, e12695. [Google Scholar] [CrossRef]
- Yang, L.E.; Scheffran, J.; Süsser, D.; Dawson, R.; Chen, Y.D. Assessment of flood losses with household responses: Agent-based simulation in an urban catchment area. Environ. Model. Assess. 2018, 23, 369–388. [Google Scholar] [CrossRef]
- Manna, P.; Anis, M.Z.; Das, P.; Banerjee, S. Probabilistic modeling of flood hazard and its risk assessment for eastern region of India. Risk Anal. 2019, 39, 1615–1633. [Google Scholar] [CrossRef]
- Lu, C.; Zhou, J.; He, Z.; Yuan, S. Evaluating typical flood risks in Yangtze River Economic Belt: Application of a flood risk mapping framework. Nat. Hazards 2018, 94, 1187–1210. [Google Scholar] [CrossRef]
- Kidyaeva, V.; Chernomorets, S.; Krylenko, I.; Wei, F.; Petrakov, D.; Su, P.; Yang, H.; Xiong, J. Modeling potential scenarios of the Tangjiashan Lake outburst and risk assessment in the downstream valley. Front. Earth Sci. 2017, 11, 579–591. [Google Scholar] [CrossRef]
- Maranzoni, A.; D’Oria, M.; Rizzo, C. Quantitative flood hazard assessment methods: A review. J. Flood Risk Manag. 2022, 16, e12855. [Google Scholar] [CrossRef]
- Jamrussri, S.; Toda, Y. Available Flood Evacuation Time for High-Risk Areas in the Middle Reach of Chao Phraya River Basin. Water 2018, 10, 1871. [Google Scholar] [CrossRef]
- Hamdy, O.; Abdelhafez, M.H.H.; Touahmia, M.; Alshenaifi, M.; Noaime, E.; Elkhayat, K.; Alghaseb, M.; Ragab, A. Simulation of Urban Areas Exposed to Hazardous Flash Flooding Scenarios in Hail City. Land 2023, 12, 353. [Google Scholar] [CrossRef]
- Si, Y.; Li, J.; Si, Y. Urban Flood Loss Estimation and Evacuation Design Based on a 500-Year Extreme Flood Event in Syracuse City. Water 2023, 15, 3. [Google Scholar] [CrossRef]
- Karbasi, M.; Shokoohi, A.; Saghafian, B. Loss of life estimation due to flash floods in residential areas using a regional model. Water Resour. Manag. 2018, 32, 4575–4589. [Google Scholar] [CrossRef]
- Voronin, A.; Kharitonov, M.; Vasilchenko, A.; Isaeva, I. Control Model for Hydrologic Safety of Flooded Territories. In Proceedings of the 2021 3rd International Conference on Control Systems, Mathematical Modeling, Automation and Energy Efficiency, SUMMA 2021, Lipetsk, Russia, 10–12 November 2021; pp. 344–348. [Google Scholar] [CrossRef]
- Du, W.; FitzGerald, G.J.; Clark, M.; Hou, X.Y. Health impacts of floods. Prehospital Disaster Med. 2010, 25, 265–272. [Google Scholar] [CrossRef] [PubMed]
- Penning-Rowsell, E.; Tapsell, S.; Wilson, T. Key policy implications of the health effects of floods. In Extreme Weather Events and Public Health Responses; Springer: Berlin/Heidelberg, Germany, 2005; pp. 207–223. [Google Scholar] [CrossRef]
- Ruidas, D.; Saha, A.; Islam, A.R.M.T.; Costache, R.; Pal, S.C. Development of geo-environmental factors controlled flash flood hazard map for emergency relief operation in complex hydro-geomorphic environment of tropical river, India. Environ. Sci. Pollut. Res. 2022, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Borowski, E.; Stathopoulos, A. Protection or Peril of Following the Crowd in a Pandemic-Concurrent Flood Evacuation. Nat. Hazards Rev. 2023, 24, 04022045. [Google Scholar] [CrossRef]
- Atayan, A.M.; Nikitina, A.V.; Sukhinov, A.I.; Chistyakov, A.E. Mathematical modeling of hazardous natural phenomena in a shallow basin. Comput. Math. Math. Phys. 2022, 62, 269–286. [Google Scholar] [CrossRef]
- Khoperskov, A.; Khrapov, S. A Numerical Simulation of the Shallow Water Flow on a Complex Topography. In Numerical Simulations in Engineering and Science; Rao, S., Ed.; InTechOpen: London, UK, 2018; pp. 237–254. [Google Scholar] [CrossRef]
- Dyakonova, T.A.; Krivko, V.V.; Agafonnikova, E.O.; Klikunova, A.Y.; Sokolovskiy, E.V.; Savin, E.S. Determination of the boundaries of flooded zones based on hydrodynamic modeling. Math. Phys. Comput. Simul. 2020, 23, 12–22. [Google Scholar] [CrossRef]
- Khrapov, S.S.; Agafonnikova, E.O.; Klikunova, A.Y.; Radchenko, V.P.; Baskakov, E.V.; Savin, E.S.; Makoveev, I.S.; Khrapov, N.S. Numerical modeling of self-consistent dynamics of shallow waters, traction and suspended sediments: I. Influence of commercial sand mining on the safety of navigation in the channel of the Volga river. Math. Phys. Comput. Simul. 2022, 25, 31–57. [Google Scholar] [CrossRef]
- Khrapov, S.S. Numerical modeling of self-consistent dynamics of shallow and ground waters. Math. Phys. Comput. Simul. 2021, 24, 45–62. [Google Scholar] [CrossRef]
- Agafonnikova, E.O.; Klikunova, A.Y.; Khoperskov, A.V. A computer simulation of the Volga river hydrological regime: A problem of water-retaining dam optimal location. Bull. South Ural. State Univ. Ser. Math. Model. Program. Comput. Softw. 2017, 10, 148–155. [Google Scholar] [CrossRef]
- Isaeva, I.I.; Voronin, A.A.; Khoperskov, A.V.; Kharitonov, M.A. Modeling the Territorial Structure Dynamics of the Northern Part of the Volga-Akhtuba Floodplain. Computation 2022, 10, 62. [Google Scholar] [CrossRef]
- Khrapov, S.; Pisarev, A.; Kobelev, I.; Zhumaliev, A.; Agafonnikova, E.; Losev, A.; Khoperskov, A. The Numerical Simulation of Shallow Water: Estimation of the Roughness Coefficient on the Flood Stage. Adv. Mech. Eng. 2013, 5, 787016. [Google Scholar] [CrossRef]
- Voronin, A.; Vasilchenko, A.; Klikunova, A.; Vatyukova, O.; Khoperskov, A. The Problem of Safe Evacuation of Large Floodplains Population During Flooding. Adv. Syst. Sci. Appl. 2022, 22, 65–78. [Google Scholar] [CrossRef]
- Drexl, A.; Kimms, A. Optimization guided lower and upper bounds for the resource investment problem. J. Oper. Res. Soc. 2001, 52, 340–351. [Google Scholar] [CrossRef]
- Neumann, K.; Schwindt, C.; Zimmermann, J. Recent results on resource-constrained project scheduling with time windows: Models, solution methods, and applications. Cent. Eur. J. Oper. Res. 2002, 10, 113–148. [Google Scholar]
- Neumann, K.; Zimmermann, J. Procedures for resource leveling and net present value problems in project scheduling with general temporal and resource constraints. Eur. J. Oper. Res. 2000, 127, 425–443. [Google Scholar] [CrossRef]
- Ranjbar, M.; Kianfar, F.; Shadrokh, S. Solving the resource availability cost problem in project scheduling by path relinking and genetic algorithm. Appl. Math. Comput. 2008, 196, 879–888. [Google Scholar] [CrossRef]
- Yamashita, D.S.; Armentano, V.A.; Laguna, M. Robust optimization models for project scheduling with resource availability cost. J. Sched. 2007, 10, 67–76. [Google Scholar] [CrossRef]
- Fraccarollo, L.; Toro, E.F. Experimental and numerical assessment of the shallow water model for two-dimensional dam-break type problems. J. Hydraul. Res. 1995, 33, 843–864. [Google Scholar] [CrossRef]
- Wang, J.S.; Ni, H.G.; He, Y.S. Finite-difference TVD scheme for computation of dam-break problems. J. Hydraul. Eng. 2000, 126, 253–262. [Google Scholar] [CrossRef]
- D’yakonova, T.A.; Khrapov, S.S.; Khoperskov, A.V. The problem of boundary conditions for the shallow water equation. Vestn. Udmurt. Univ. Mat. Mekhanika Komp’Yuternye Nauk. 2016, 26, 401–417. (In Russian) [Google Scholar] [CrossRef]
- Winter, T.C. The concept of hydrologic landscapes 1. JAWRA J. Am. Water Resour. Assoc. 2001, 37, 335–349. [Google Scholar] [CrossRef]
- Mazzoleni, M.; Brandimarte, L. Modelling flood awareness in floodplain dynamics. Hydrol. Sci. 2023, 604–613. [Google Scholar] [CrossRef]
- Mondal, M.S.H. Factors of Influence on Evacuation Behaviour: Survey Results from the Riverine Floodplain Communities in Bangladesh. Quaest. Geogr. 2021, 40, 85–93. [Google Scholar] [CrossRef]
- Lim, M.B.; Lim, H.; Piantanakulchai, M. Factors Affecting Flood Evacuation Decision and Its Implication to Transportation Planning. J. East. Asia Soc. Transp. Stud. 2013, 10, 163–177. [Google Scholar]
- Dawson, R.J.; Peppe, R.; Wang, M. An agent-based model for risk-based flood incident management. Nat. Hazards 2011, 59, 167–189. [Google Scholar] [CrossRef]
- Siebeneck, L.K.; Cova, T.J. Spatial and temporal variation in evacuee risk perception throughout the evacuation and return-entry process. Risk Anal. 2022, 32, 1468–1480. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, J.; Wang, H.; Kang, J.; Cao, W. Analysis of Flood Evacuation Process in Vulnerable Community with Mutual Aid Mechanism: An Agent-Based Simulation Framework. Int. J. Environ. Res. Public Health 2020, 17, 560. [Google Scholar] [CrossRef]
- Munawar, H.S.; Mojtahedi, M.; Hammad, A.W.A.; Ostwald, M.J.; Waller, S.T. An AI/ML-Based Strategy for Disaster Response and Evacuation of Victims in Aged Care Facilities in the Hawkesbury-Nepean Valley: A Perspective. Buildings 2022, 12, 80. [Google Scholar] [CrossRef]
- Prasad, S. Assessing the need for evacuation assistance in the 100 year floodplain of South Florida. Appl. Geogr. 2016, 67, 67–76. [Google Scholar] [CrossRef]
- Li, X.; Maghelal, P.; Arlikatti, S.; Dorsett, C. Review of evacuee mobilization challenges causing time-lag: Conceptualizing a new framework. Emerg. Manag. Sci. Technol. 2022, 2, 1–9. [Google Scholar] [CrossRef]

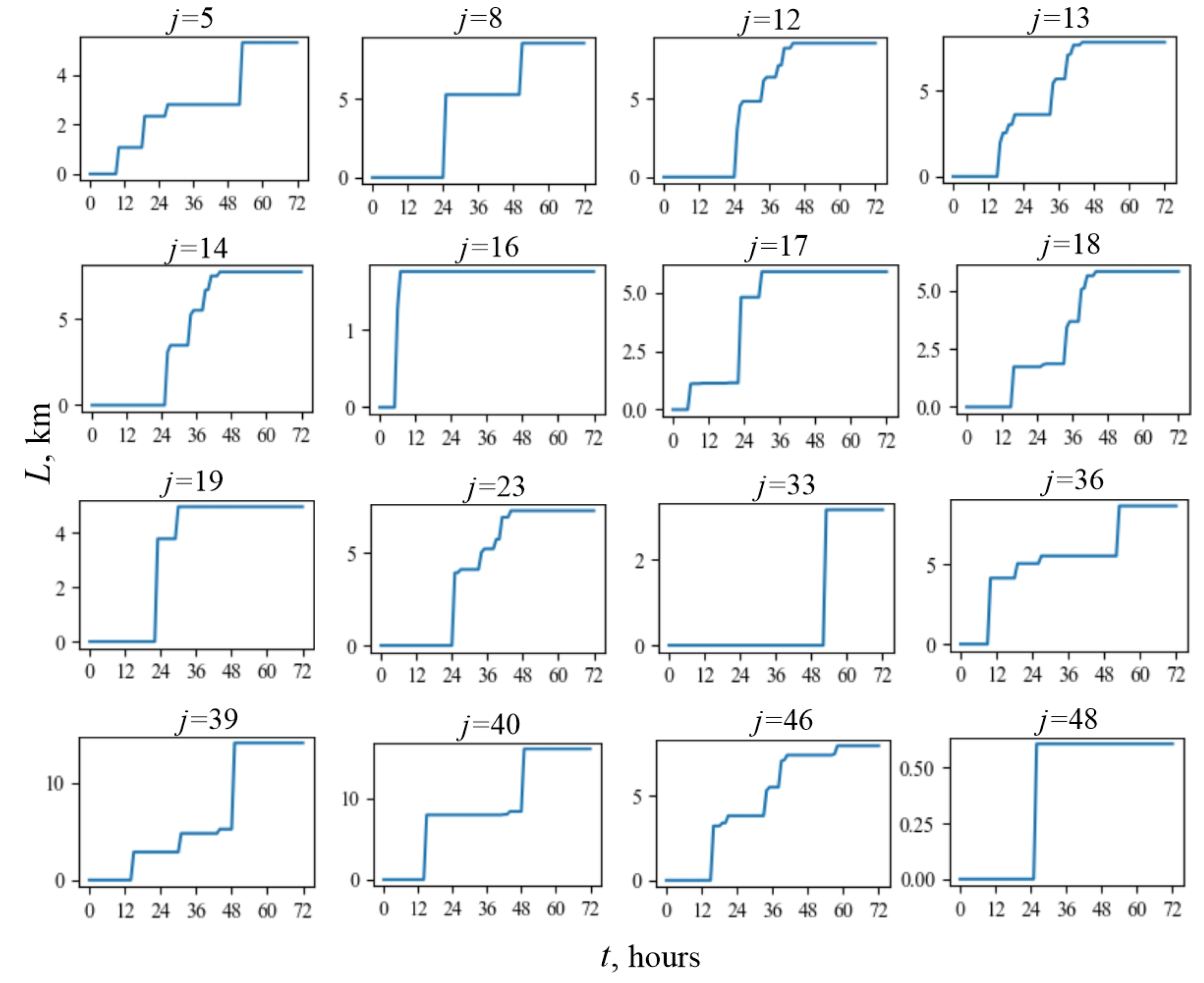
| № | = 35,000 ms | = 60,000 ms | L, km | ||||||
|---|---|---|---|---|---|---|---|---|---|
| = 0.045 | const | = 0.045 | const | = 0.045 | const | = 0.045 | const | ||
| 1 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 25 | 16.25 |
| 2 | 25 | 25 | 25 | 25 | 16 | 14 | 25 | 25 | 6.85 |
| 3 | 25 | 25 | 25 | 25 | 14 | 13 | 25 | 25 | 5.25 |
| 4 | 17 | 17 | 25 | 25 | 7 | 6 | 16 | 17 | 2.45 |
| 5 | 25 | 25 | 15 | 16 | 15 | 15 | 8 | 9 | 21.35 |
| 6 | 25 | 25 | 25 | 25 | 15 | 15 | 14 | 15 | 34.15 |
| 7 | 25 | 25 | 25 | 25 | 17 | 18 | 14 | 15 | 29.9 |
| 8 | 25 | 25 | 25 | 25 | 9 | 9 | 12 | 12 | 21.55 |
| 9 | 25 | 25 | 25 | 25 | 17 | 18 | 14 | 15 | 18.1 |
| 10 | 25 | 25 | 25 | 25 | 16 | 18 | 16 | 19 | 11.6 |
| 11 | 25 | 25 | 25 | 25 | 10 | 11 | 10 | 11 | 20 |
| 12 | 25 | 25 | 14 | 15 | 8 | 8 | 7 | 6 | 21.8 |
| 13 | 24 | 25 | 12 | 13 | 7 | 7 | 5 | 5 | 25.65 |
| 14 | 21 | 22 | 22 | 24 | 7 | 6 | 8 | 9 | 18.7 |
| 15 | 11 | 11 | 25 | 25 | 5 | 5 | 14 | 15 | 10.2 |
| 16 | 15 | 15 | 5 | 6 | 6 | 6 | 3 | 3 | 13.85 |
| 17 | 25 | 25 | 3 | 3 | 6 | 6 | 2 | 2 | 15.5 |
| 18 | 18 | 19 | 15 | 16 | 8 | 8 | 6 | 6 | 22.5 |
| 19 | 25 | 25 | 16 | 17 | 9 | 9 | 5 | 5 | 12.2 |
| 20 | 24 | 25 | 25 | 25 | 9 | 9 | 11 | 12 | 13.65 |
| 21 | 25 | 25 | 25 | 25 | 10 | 10 | 11 | 12 | 7.6 |
| 22 | 25 | 25 | 25 | 25 | 11 | 12 | 11 | 12 | 7.6 |
| 23 | 25 | 25 | 14 | 15 | 11 | 12 | 7 | 6 | 21.8 |
| 24 | 25 | 25 | 25 | 25 | 11 | 10 | 13 | 13 | 6.6 |
| 25 | 25 | 25 | 25 | 25 | 15 | 16 | 16 | 17 | 3.6 |
| 26 | 25 | 25 | 25 | 25 | 11 | 12 | 13 | 13 | 8.15 |
| 27 | 25 | 25 | 25 | 25 | 13 | 13 | 13 | 14 | 7.9 |
| 28 | 25 | 25 | 25 | 25 | 13 | 14 | 13 | 14 | 10.4 |
| 29 | 25 | 25 | 25 | 25 | 25 | 25 | 21 | 21 | 15.6 |
| 30 | 25 | 25 | 25 | 25 | 25 | 25 | 21 | 21 | 21.5 |
| 31 | 25 | 25 | 25 | 25 | 19 | 20 | 16 | 17 | 13.7 |
| 32 | 25 | 25 | 25 | 25 | 16 | 17 | 13 | 13 | 11.3 |
| 33 | 25 | 25 | 25 | 25 | 15 | 15 | 16 | 19 | 16.6 |
| 34 | 25 | 25 | 25 | 25 | 25 | 25 | 16 | 19 | 14.7 |
| 35 | 25 | 25 | 25 | 25 | 21 | 22 | 16 | 19 | 14.7 |
| 36 | 25 | 25 | 15 | 16 | 25 | 25 | 8 | 9 | 27.25 |
| 37 | 25 | 25 | 25 | 25 | 21 | 22 | 14 | 15 | 35.45 |
| 38 | 25 | 25 | 25 | 25 | 21 | 22 | 14 | 15 | 32.9 |
| 39 | 25 | 25 | 23 | 24 | 23 | 23 | 14 | 15 | 40.6 |
| 40 | 25 | 25 | 23 | 24 | 25 | 25 | 14 | 15 | 47.95 |
| 41 | 25 | 25 | 25 | 25 | 18 | 20 | 16 | 19 | 10.2 |
| 42 | 25 | 25 | 25 | 25 | 19 | 19 | 14 | 15 | 14.5 |
| 43 | 25 | 25 | 25 | 25 | 12 | 12 | 12 | 11 | 4.95 |
| 44 | 25 | 25 | 25 | 25 | 25 | 25 | 16 | 19 | 10.2 |
| 45 | 25 | 25 | 25 | 25 | 25 | 25 | 16 | 19 | 9.45 |
| 46 | 22 | 23 | 15 | 16 | 7 | 7 | 6 | 6 | 24.35 |
| 47 | 25 | 25 | 25 | 25 | 18 | 20 | 14 | 15 | 10.2 |
| 48 | 21 | 22 | 24 | 25 | 7 | 7 | 7 | 7 | 7.2 |
| 49 | 25 | 25 | 25 | 25 | 20 | 19 | 25 | 25 | 6.85 |
| 50 | 25 | 25 | 25 | 25 | 24 | 25 | 25 | 25 | 6.85 |
| 51 | 25 | 25 | 25 | 25 | 23 | 25 | 21 | 21 | 15.6 |
| 52 | 25 | 25 | 25 | 25 | 25 | 25 | 21 | 21 | 16.5 |
| 53 | 25 | 25 | 25 | 25 | 25 | 25 | 16 | 19 | 14 |
| 54 | 25 | 25 | 25 | 25 | 12 | 10 | 15 | 14 | 10.4 |
| 55 | 25 | 25 | 25 | 25 | 11 | 12 | 12 | 13 | 19.35 |
| 56 | 25 | 25 | 25 | 25 | 12 | 13 | 11 | 12 | 19.05 |
| Number of HS | Number of Permanent ER | List of Permanent ER Road Numbers | Number of HS | Number of Permanent ER | List of Permanent ER Road Numbers |
|---|---|---|---|---|---|
| 1 | 1 | 66, 75, 26 | 27 | 25 | 38, 8, 9, 10 |
| 2, 49, 50 | 2 | 75, 26 | 28 | 26 | 19, 8, 9, 10 |
| 3 | 3 | 26 | 29, 51 | 27 | 65, 75, 26 |
| 4 | 4 | 10 | 30 | 28 | 67, 78, 65, 75, 26 |
| 5 | 5 | 55, 74, 77, 54, 68, 1, 0 | 31 | 29 | 63, 20, 9, 10 |
| 6 | 6 | 59, 17, 76, 16, 4, 3, 2, 1, 0 | 32 | 30 | 18, 7, 8, 9, 10 |
| 7 | 7 | 17, 76, 16, 4, 3, 2, 1, 0 | 33 | 31 | 74, 77, 54, 68, 1, 0 |
| 8 | 8 | 58, 57, 14, 0 | 34, 35 | 32 | 77, 54, 68, 1, 0 |
| 9 | 9 | 76, 16, 4, 3, 2, 1, 0 | 36 | 33 | 61, 55, 74, 77, 54, 68, 1, 0 |
| 10 | 10 | 80, 2, 1, 0 | 37 | 34 | 70, 60, 17, 76, 16, 4, 3, 2, 1, 0 |
| 11 | 11 | 32, 5, 4, 3, 2, 1, 0 | 38 | 35 | 60, 17, 76, 16, 4, 3, 2, 1, 0 |
| 12, 23 | 12 | 51, 49, 47, 46, 36, 7, 8, 9, 10 | 39 | 36 | 62, 70, 60, 17, 76, 16, 4, 3, 2, 1, 0 |
| 13 | 13 | 50, 69, 48, 46, 36, 7, 8, 9, 10 | 40 | 37 | 72, 62, 70, 60, 17, 76, 16, 4, 3, 2, 1, 0 |
| 14 | 14 | 49, 47, 46, 36, 7, 8, 9, 10 | 41, 44 | 38 | 68, 1, 0 |
| 15, 47 | 15 | 14, 0 | 42 | 39 | 53, 14, 0 |
| 16 | 16 | 44, 73, 43, 0 | 43 | 40 | 23, 10 |
| 17 | 17 | 45, 27, 0 | 45 | 41 | 2, 1, 0 |
| 18 | 18 | 69, 48, 46, 36, 7, 8, 9, 10 | 46 | 42 | 52, 69, 48, 46, 36, 7, 8, 9, 10 |
| 19 | 19 | 27, 0 | 48 | 43 | 43, 0 |
| 20 | 20 | 46, 36, 7, 8, 9, 10 | 52 | 44 | 78, 65, 75, 26 |
| 21, 22 | 21 | 42, 10 | 53 | 45 | 29, 3, 2, 1, 0 |
| 24 | 22 | 41, 9, 10 | 54 | 46 | 25 |
| 25 | 23 | 22, 10 | 55 | 47 | 35, 6, 5, 4, 3, 2, 1, 0 |
| 26 | 24 | 40, 9, 10 | 56 | 48 | 33, 5, 4, 3, 2, 1, 0 |
| Class Definition | Class Dynamics | 35,000 m/s | 45,000 m/s | 60,000 m/s |
|---|---|---|---|---|
| : No evacuation | → (, ) | 31/10,015 | 19/4825 | 5/815 |
| : Pedestrian evacuation at the 1st stage at | →(, ) | STER2: 9/3690 STER3: 8/3490 | STER2: 6/3130 STER3: 5/2930 | STER2: 9/2415 STER3: 7/2015 |
| : Transport evacuation at the 1st stage at | → | STER2: 6/3375 STER3: 10/21,505 | STER2: 14/7070 STER3: 18/25,200 | STER2: 27/10,855 STER3: 30/28,885 |
| : Pedestrian evacuation at the 1st stage at | → | STER2: 8/21,170 STER3: 7/3040 | STER2: 12/21,660 STER3: 8/3530 | STER2: 12/24,270 STER3: 9/6240 |
| : Transport evacuation at the 1st stage at | STER2: 2/555 STER3: 3/755 | STER2: 5/2120 STER3: 6/2320 | STER2: 3/450 STER3: 5/850 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vatyukova, O.Y.; Klikunova, A.Y.; Vasilchenko, A.A.; Voronin, A.A.; Khoperskov, A.V.; Kharitonov, M.A. The Problem of Effective Evacuation of the Population from Floodplains under Threat of Flooding: Algorithmic and Software Support with Shortage of Resources. Computation 2023, 11, 150. https://doi.org/10.3390/computation11080150
Vatyukova OY, Klikunova AY, Vasilchenko AA, Voronin AA, Khoperskov AV, Kharitonov MA. The Problem of Effective Evacuation of the Population from Floodplains under Threat of Flooding: Algorithmic and Software Support with Shortage of Resources. Computation. 2023; 11(8):150. https://doi.org/10.3390/computation11080150
Chicago/Turabian StyleVatyukova, Oksana Yu., Anna Yu. Klikunova, Anna A. Vasilchenko, Alexander A. Voronin, Alexander V. Khoperskov, and Mikhail A. Kharitonov. 2023. "The Problem of Effective Evacuation of the Population from Floodplains under Threat of Flooding: Algorithmic and Software Support with Shortage of Resources" Computation 11, no. 8: 150. https://doi.org/10.3390/computation11080150
APA StyleVatyukova, O. Y., Klikunova, A. Y., Vasilchenko, A. A., Voronin, A. A., Khoperskov, A. V., & Kharitonov, M. A. (2023). The Problem of Effective Evacuation of the Population from Floodplains under Threat of Flooding: Algorithmic and Software Support with Shortage of Resources. Computation, 11(8), 150. https://doi.org/10.3390/computation11080150







