Abstract
We studied obtaining exact solutions to a set of equations related to the SEIR (Susceptible-Exposed-Infectious-Recovered) model of epidemic spread. These solutions may be used to model epidemic waves. We transformed the SEIR model into a differential equation that contained an exponential nonlinearity. This equation was then approximated by a set of differential equations which contained polynomial nonlinearities. We solved several equations from the set using the Simple Equations Method (SEsM). In doing so, we obtained many new exact solutions to the corresponding equations. Several of these solutions can describe the evolution of epidemic waves that affect a small percentage of individuals in the population. Such waves have frequently been observed in the COVID-19 pandemic in recent years. The discussion shows that SEsM is an effective methodology for computing exact solutions to nonlinear differential equations. The exact solutions obtained can help us to understand the evolution of various processes in the modeled systems. In the specific case of the SEIR model, some of the exact solutions can help us to better understand the evolution of the quantities connected to the epidemic waves.
1. Introduction
In this article, we discuss the classic version of the SEIR model of spread of epidemics in a population. The spread of an epidemic is an example of a nonlinear process in a complex system. Such processes are frequently observed in nature and in society [1,2,3,4,5,6,7,8]. They are usually studied by the methodology of nonlinear time series analysis or by numerical simulations of models containing nonlinear differential or difference equations [9,10,11,12]. The exact analytical solutions to the model equations are very informative. These solutions allow us to understand the relationships among the characteristic parameters of the investigated system. In addition, the solutions may be used to test the correctness of corresponding computer programs.
Below, we reduce the classic SEIR model to a single nonlinear differential equation, which can be connected to a set of differential equations containing polynomial nonlinearities. Exact solutions to several of these equations are described, and a number of these are used to study epidemic waves. We obtain the solutions using the SEsM (Simple Equations Method) methodology [13]. This methodology is an example of the large field of research on methods for obtaining exact analytical solutions of nonlinear differential equations, which has roots in the Hopf–Cole transformation [14,15] and the inverse scattering transform method [16]. The study of the truncated Painleve expansions [17,18,19,20,21] led Kudryashov [22] to propose of the Method of Simplest Equation (MSE) [23,24,25]. MSE is connected to the SEsM methodology [26,27,28,29,30]. Specific cases of SEsM are visible in our articles written many years ago [31,32]. In [33], we applied a specific case of SEsM called MMSE in order to obtain exact solutions of a model from the population dynamics [34]. The MMSE [35] applied the concept of balancing equations in order to fix the simplest equation. Then, the solution of the complicated equation was constructed as a power series of the solution to the used simplest equation [36,37]. MMSE led to results which were equivalent to the results of the MSE. The capacity of the MMSE was then extended in the direction of using more than one simple equation. Because of this, the name of the methodology was changed from MMSE to SEsM. SEsM based on two simple equations can be seen in [38]. Other specific cases of application of SEsM are presented in [26,30,39,40].
Below, we apply SEsM to the SEIR model of the spread of an epidemic in a population. One of the most basic such compartmental models [41,42,43,44,45,46,47,48,49,50,51,52,53] is the SIR model for the dynamics of an infectious disease in a population. This model considers individuals who are infected (I) and those who have recovered (R) with immunity. We previously studied the SIR model in [30]. With respect to the SIR model, the SEIR model has an additional group of individuals, namely, those who are exposed to the infection. Epidemic models can be applied to study other processes as well, such as the spread of ideas (for overviews, see [4,54]). An important recent application of epidemic models is in research on the spread of COVID-19 [55,56,57,58,59,60,61,62,63,64,65,66,67,68]. We proceed as follows: the methodology of SEsM is described briefly in Section 2; in Section 3, we derive a sequence of nonlinear differential equations connected to the SEIR model of epidemic spread and use SEsM to obtain exact solutions of these equations; and in Section 4, the applicability of the obtained solutions for describing the evolution of epidemic waves is discussed. Finally, we present our concluding remarks in Section 5.
2. Simple Equations Method (SEsM)
The full notation of SEsM is SEsM(n,m), where n denotes the number of solved equations and m denotes the number of simpler equations for which the solutions are used. The most commonly used version of SEsM to date is SEsM(1,1), in which a single complicated nonlinear differential equation is solved on the basis of known solutions to a single simpler differential equation. SEsM(1,1) is sometimes called the MMSE, and this specific case of SEsM has many applications [69,70,71].
The idea of SEsM is to transform the solved system of nonlinear differential equations
(here, depends on the functions , and a number of their derivatives and functions can depend on several spatial coordinates) into
The transformation is performed by the choice of as composite functions of known analytical solutions to simpler equations. Here, are functions of the time and the spatial variables, and the quantities are algebraic relationships among the parameters of Equation (1), the parameters of the solutions to the simpler equations, and the parameters of the solutions to (1); do not contain the time and the spatial coordinates, and is a characteristic parameter for the i-th equation from (1). If we succeed in transforming (1) to (2), then we can write
and we obtain a system of nonlinear algebraic equations. Each of the nontrivial solutions to (3) leads to a solution to system (1).
The idea of SEsM is realized in four steps.
- Step 1: Transformation of the nonlinearities of (1).In rare cases, this transformation leads to the removal of the nonlinearity. In this case, the solved nonlinear equation is transformed into a linear equation. In most cases, however, the nonlinearity of the equation remains after the transformation. For these cases:
- If the nonlinearities in (1) or in the transformed equations are polynomial, then there is no need for a transformation for these nonlinearities.
- If the nonlinearities in (1) are not polynomial, transformations can be used to turn them into polynomial nonlinearities or more treatable kinds of nonlinearities.
An example of an appropriate transformation is the transformation of Hopf and Cole, which transforms the (nonlinear) Burgers equation into the linear heat equation [14,15]. As we have already noted, such successful transformations are rare. Therefore, the goal is to convert the nonlinearity to polynomial nonlinearity. For the specific case of SEsM(1,1), two examples of such transformations are as follows: for the sine–Gordon equation –>; and for the Poisson–Boltzmann equation –> [31,32].The exact forms of the transformations may remain unfixed at this step of SEsM. In this case, the forms must be determined at some point during Steps 2 and 3. - Step 2: Construction of solutions to the transformed equations.The idea of SEsM is to use composite functions of known solutions to simpler differential equations in order to construct the sought-after solutions. The presence of derivatives in the solved differential equations requires the use of the Faa di Bruno formula for the derivatives of the composite functions. Using composite functions, we can transform the solved equations into equations which are constructed by functions which are solutions to more simple equations. There is no need to fix the form of the composite function and the form of the solutions of the simpler equations at this step. However, it can be done; one example of a fixation for the needs of SEsM(1,n) is
- Step 3: Determine the form of the simpler equations with solutions that can be used to construct the desired solutions of (1).The rule is as follows: choose the composite functions and the simple equations in such a way that we arrive at the relationships (2). In addition, we have to be sure that the relationships for contain more than one term. This requirement leads to more relationships among the parameters from the relationships for . These new relationships are denoted as balance equations.
- Step 4: Solution of (3).
For specific cases of applications of SEsM, see [26,27,28,29,30,33,34,35,36,37,38].
3. SEsM and Exact Analytical Solutions for a Sequence of Equations Connected to the SEIR Model of Epidemics
Below, we apply SEsM to obtain exact solutions to a sequence of nonlinear differential equations connected to a specific differential equation obtained from the SEIR model in epidemiology. Several of the discussed solutions are appropriate for describing epidemic waves caused by different diseases, including COVID-19. The rest of the obtained solutions are not appropriate for such a purpose.
The aforementioned nonlinear differential equation is obtained by realizing the idea of transforming the SEIR model with constant coefficients into a single differential equation. The idea was proposed by Kermack and McKendrick for the case of the SIR model [73]. This idea was further developed in [30], and a sequence of nonlinear differential equations was obtained. Then, SEsM(1,1) was used to obtain exact solutions of several of these equations. Below, we realize the same idea for the case of the SEIR model of epidemics.
The initial impetus for the SEIR model lay in the specific characteristics of certain diseases. Specifically, an additional class of individuals in addition to the three classes in the SIR model is necessary in modeling the evolution of the spread of these diseases. The individuals in this additional class are infected by the corresponding pathogen, but are not capable of passing infection to others during a latent period. For example, this kind of infection is connected to the spread of malaria. Malaria was extensively studied in the early 20th century [74]. In order to build an SIR-like model similar to [73], the new class of individuals, called exposed individuals, was introduced, leading to the SEIR model (for more mathematical models of malaria, see [75]).
The SEIR epidemic model has several versions [42,76,77,78,79,80,81,82,83]. Below, we consider the classic version of the SEIR model of epidemics in a population. The population is divided into four groups: susceptible individuals—S; exposed individuals—E; infected individuals—I; and recovered individuals—R. The model equations for the time change in the numbers of individuals from the above three groups are as follows:
In (5), is the incubation rate, is the transmission rate, and is the recovery rate. We assume constant values of these rates. From (5), we obtain the relationship
N is the total population. We assume that N is a constant. (5) is reduced to a single equation for R; the reduction is as follows. From the last equation of (5), we obtain
Here, and are the numbers of susceptible individuals and those recovered at time . The substitution of (6) and (8) in the last equation of (5) leads to the differential equation for R:
Below, we assume (no recovered individuals at ). Next, we reduce (9) to an equation for R. The reduction is as follows. We write (9) as
(10) is differentiated with respect to t. The result is
In (11), we substitute and by the corresponding relationships from the first two equations of (5). The result is a relationship which relates R and E. From this relationship, we obtain
We substitute (12) in (9) and obtain
Below, we assume . This happens, for example, when and . The last relationship indicates that there is an epidemic wave affecting a small percentage of the population. Here, can be written as a Taylor series
Although M has infinite value in the full Taylor series, we can truncate it at , ,…, if is small enough. From (13), we obtain
We set
Then, (15) becomes
The sequences of Equations (15) and (17) are the orders of approximation of (9) with respect to M.
The time t is the independent variable in (17). In general, the independent variable of a differential equation can be a combination of several spatial variables and time. Below, we use just such an independent variable, denoted as . In this way, we are able to apply SEsM(1,1) to the equation
As simple equations, we use the differential equations of Bernoulli and Riccati.
We begin with the equation of Bernoulli:
as a simple equation. The transformation reduces (19) to a linear equation. Using this, we can obtain the solution to the equation of Bernoulli:
In (20), C is a constant of integration.
We skip Step 1 of SEsM. No transformation is needed because the kind of nonlinearity in (18) is polynomial. In Step 2 of SEsM, we choose the composite function to be of the kind
where is the solution to (19) and is the solution to (18). In Step 3 of SEsM, we have to obtain the balance equation; (19) and (21) fix the balance equation of (18) to
Then, a specific solution to (18) is
Several of the the parameters , p, q, and C are fixed during the Step 4 of SEsM.
A specific case exists for which we can obtain an interesting and important solution to the simple equation, namely, the case of . Then, we can use the equation of Riccati as a simple equation:
where , and r are parameters. We know that a specific solution of (24) is
where and C is a constant of integration. The specific solution (25) of (24) allows us to write the general solution to (24) as , where D is a constant and is the solution to the linear differential equation
The solution to (26) is
where is a constant of integration. Thus, the general solution to (24) is
Next, we obtain several solutions of the kind in (18). We begin with . In this case, we have to solve the equation
The balance equation is . We start with . In this case, we can use the equation of Riccati as the simple equation. We have , and the solution of (29) is of the kind , where y is the specific solution (25) or the general solution (28). The substitution of the last relationships in (29) leads to the system of nonlinear algebraic equations in Equation (A1) (see Appendix A); (A1) has two solutions The first solution to (A1) is (A2); thus, the equation
where has the specific exact analytical solution
with , along with the more general solution
with .
The second solution of (A1) is (A3). For this solution, we obtain the following solutions of the corresponding differential equation:
where . The first solution is the specific analytical solution
The second solution is the more general solution
Next, we consider the case of , . Here, . We must use the equation of Bernoulli as a simple equation. The equation of Bernoulli for this case is , and the solution to (29) is . The substitution of the last relationships in (29) leads to the system of nonlinear algebraic equations in Equation (A4) One solution to (A4) is (A5) In this case, the corresponding equation
has the specific exact analytical solution
The system of algebraic equations (A4) has three additional solutions. The first of these solutions is (A6). Then, the corresponding equation
has the specific exact solution
The second of the additional solutions is (A7). Then, the corresponding equation
has the specific exact solution
The third of the additional solutions is (A8). Then, the corresponding equation
has the specific exact solution
Next, we consider the case of , . In this case, . We have to solve the equation
and the desired solution has the form , where is the solution of the Bernoulli equation , which is
The use of SEsM(1,1) leads to the system of algebraic equations (A9). This system has four solutions. These solutions lead to equations and solutions which are identical to the equations and solutions for the case of , , . As an an example, the solution (A10) of (A9) leads to the solution (37) of the Equation (36).
Because of the above, we continue with a discussion of the case of . Here, we have to solve the equation
For the case of a simple equation of the same kind as the Bernoulli equation, the balance equation for SEsM(1,1) is . Thus, the simple equation of Bernoulli is and its solution is . The solution to (46) is of the kind .
We start with , meaning that . As we know, in this case we can use the equation of Riccati as the simple equation for SEsM(1,1). In this case, we can use the specific solution (25) and the general solution (28). In this case, SEsM(1,1) leads to the system of nonlinear algebraic relationships (A11) One of the solutions to this system is (A12). Thus, the corresponding equation
has the specific solution
Here,
with (48) being based on the solution (25) to the equation of Riccati. Another specific solution is
with (50) being based on the general solution (28) to the equation of Riccati.
The second solution of system (A11) is (A13). Thus, the corresponding equation
has the specific solution
Here,
The solution (52) leads to profiles which are appropriate for description of epidemic waves. The epidemic waves are connected to bell-shaped profile forms. These waves represent the number of infected individuals, and this number is proportional to . Figure 1 shows several profiles of which are connected to (52). The characteristic bell-shaped form of the profile is evident.
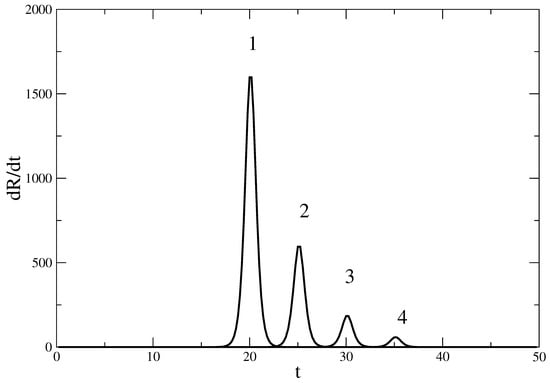
Figure 1.
Influence of the parameters of the solution (52) on the profile of . In this case, the coordinate is the time t. The parameters of the profiles are as follows. Profile 1: , , , , , , . Profile 2: , , , , , , . Profile 3: , , , , , , . Profile 4: , , , , , , .
Above, we have seen that (52) is based on the solution (25) of the equation of Riccati. Another specific solution of (51) is
with (54) being based on the general solution (28) to the equation of Riccati.
System (A11) has two additional solutions, which the interested reader can easily obtain. We proceed to a solution obtained by using the equation of Bernoulli as a simple equation.
Next, we consider the case . From the balance equation we have . The simple equation is the equation of Bernoulli . The solution to this equation is . The solution of (46) is of the kind . The application of SEsM(1,1) leads to the system of nonlinear algebraic equations in (A14). This system has four solutions. The first solution is (A15). The corresponding equation
has the specific solution
Figure 2 shows several profiles of R connected to the solution (58). These profiles are appropriate for modeling processes that have a level of saturation; for these profiles decreases.
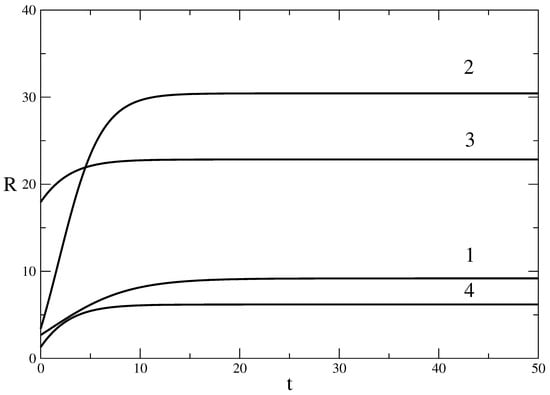
Figure 2.
Influence of the parameters of the solution (58) on the profile R. In this case, the coordinate is the time t. Profile1: , , , , , , . Profile2: , , , , , , . Profile3: , , , , , , . Profile4: , , , , , , .
The third solution of system (A14) is (A17). Thus, the corresponding equation
has the specific solution
The fourth solution of system (A15) is (A18). Thus, the corresponding equation
has the specific solution
Next, we consider the case of . In this case, we have to solve the equation
For the case of a simple equation of the same kind as the equation of Bernoulli, the balance equation for SEsM(1,1) is . Thus, the simple equation of Bernoulli is and its solution is . The solution of (46) is of the kind .
We next consider the case of , for which . SEsM(1,1) leads to the system of Equation (A19), which has the following two solutions. The first solution is (A20); thus, the corresponding equation
has the specific solution
We stop the description of the solutions here, as the list becomes long. Additional solutions are discussed elsewhere.
4. The Obtained Solutions to the Studied Set of Equations from the Point of View of Modeling Epidemic Waves
In the previous section, we obtained several exact solutions to equations that are connected to the SEIR model of epidemic spread. The solutions are of two classes: (i) solutions that can be used for modeling of epidemic spread, and (ii) solutions that are not appropriate for modeling epidemic spread. We begin by discussing the solutions that can be used for modeling the spread of epidemics.
Below, we consider the specific case when the general coordinate is the time t. We obtain solutions to the number of recovered people for the SEIR model. Then, we calculate the time evolution of infected people I by means of (7):
The number of exposed and susceptible people is
In addition, we have
Then, we can calculate the relative growth rate
which can be written as
In (69),
is the time-varying effective reproduction number. The notation is used for the effective reproduction number in order to distinguish it from the number of recovered people, which is denoted by R; (69) shows that there is an important value . For , we have , and the relative growth rate is negative. Then, is negative; the number of infected individuals decreases, and the epidemic shrinks. For , we have , and the relative growth rate is positive. Thus, is positive; the number of infected individuals increases, and the epidemic expands.
Note that our assumption for reducing the SEIR model to a sequence of equations is . This means that we can describe epidemic waves for which . In other words, such epidemic waves affect a small percentage of the entire population. If the last condition is not true, we have to solve the SEIR model numerically. For the rest of this section, we assume that the assumption holds.
The solutions obtained in the previous section can be classified as follows:
- I.
- Solutions that can be used to describe specific cases of the evolution of epidemic waves within the scope of the SEIR model.
- II.
- Solutions that can be used to describe specific cases of the part of the evolution of the epidemic wave or solutions that are not appropriate for the case of description of evolution of epidemic wave within the scope of the SEIR model.
The solutions in class I are the solutions generated by using the equation of Riccati as the simple equation in SEsM(1,1). Among these solutions are (31), (32), (34), (35), (48), (50), and (52). Below, we write the quantities corresponding to the SEIR model for one of these solutions, (31). This is the solution of Equation (30) which has a quadratic nonlinearity with respect to R. We note that , meaning that we have the requirement . We first consider the solution (31). The relationship for leads to a requirement for :
where (71) is a necessary condition for existence of the waves (31) and (32). This condition reduces the probability of the waves occurring. The positive point is that the analytical relationship for the waves allows us to calculate and study the corresponding quantities for epidemics. Thus, we can gain better understanding of the processes. For example, on the basis of solution (31) we obtain a relationship for the behaviour over time of the number of infected
Recall that C is an integration constant which is determined by the initial condition.
The corresponding number of exposed is
The number of susceptible persons is approximately
The corresponding relative growth rate is
The corresponding effective reproduction number is
The corresponding quantities for the SEIR model on the basis of the other solutions (32), (34), (35), (48), and (50) can be calculated in a similar manner as above.
We note that solution (32) contains (31) as specific case when the constant of integration . Thus, (32) can lead to the same profile as (31), meaning that (32) can be used for the description of epidemic waves within the scope of the SEIR model. In addition, solution (32) can produce more complicated profiles in comparison to solution (31), as D can be different from 0. One of these possible profiles is shown in Figure 3, along with the corresponding profile for its derivative. The profile from Figure 3a is different from the kink profile for the evolution of the number of recovered individuals, which is typical for an epidemic wave. The derivative of this profile shown in Figure 3b is different from the typical bell-shaped profile associated with the evolution of the number of infected individuals during an epidemic wave. Such profiles provided by (32) may not be suitable for the description of epidemic waves, though they may be useful for other applications of Equation (30).
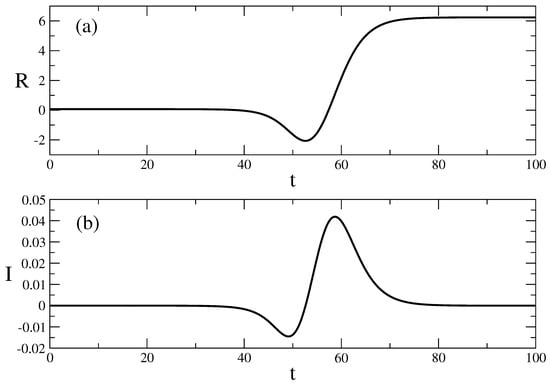
Other solutions that are suitable for the study of a specific case of the evolution of epidemic waves from the point of view of the SEIR model are some of the ones based on the use of a simple equation of the Bernoulli kind in SEsM(1,1). Candidates for such solutions include (37), (39), (43), (41), (56), (58), (60), (62), (65), and (67). From these solutions, the suitable solutions are these which do not contain more than one relationship connecting the parameters of the solved equations. Such solutions include (37), (39), (43), (41), (56), (58), (60), and (62). These solutions are constructed by functions with a shape that is similar to the shape of the logistic function in Figure 2. Because of this, they are suitable for modeling part of the epidemic wave. For instance, these solutions can model the declining part of the wave. As an example, we can consider the solution (58). For this solution, , , and N are free parameters. The solution is realized for
where
We have the condition
The last two solutions, (65) and (67), contain three relationships among the parameters of the solved equation. Because of this, it is necessary to fix more parameters of the SEIR model. This very much limits the area of application of these two solutions for the purpose of describing part of the epidemic wave within the scope of the SEIR model. Thus, (65) and (67) are practically unsuitable for the description of epidemic waves.
5. Concluding Remarks
The main goal of this article is the application of the Simple Equations Method (SEsM) for computing exact solutions of nonlinear differential equations from a sequence of differential equations connected to the SEIR model of epidemic spread. We compute two kinds of exact solutions. The first kind of solution is based on the use of the Riccati equation as a simple equation. These solutions can describe specific cases of epidemic waves given the condition that the wave does not affect a large part of the corresponding population. This kind of solution can lead to profiles which are not suitable for description of epidemic waves, as shown in Figure 3. Such profiles can be useful for other possible applications of the corresponding equation, however.
The second kind of computed solutions are based on the use of the equation of Bernoulli as a simple equation. These solutions have profiles that are similar to those of the logistic function. Several of these solutions can describe specific cases of the evolution of epidemic waves within the scope of the SEIR model. Other solutions are not appropriate for modeling the evolution of epidemics. Note that the last solutions are exact solutions of the corresponding nonlinear partial differential equations, and can find applications in the modeling of other phenomena.
The difference between the SIR and the SEIR models of epidemic spread is that an additional class of individuals is presented in the SEIR model, namely, the class of exposed individuals. Thus, the SEIR model accounts for the latent period during which the individuals in this additional class are infected by the pathogen but are not capable of passing infection to others. The presence of this additional class of individuals leads to changes in the equation for the evolution of the number of recovered persons. This equation is
for the SIR model of epidemic spread [30], while for the SEIR model of epidemic spread the equation changes to (13)
This change in the equation leads to different solutions and different behaviour of the evolution of the epidemic wave . Consequently, the evolution of the relative growth rate is different for the two models. The time behaviour of the effective reproduction number changes as well.
Finally, we note that this study has shown SEsM to be a very useful methodology for computing exact analytical solutions of nonlinear differential equations. We have demonstrated that this methodology leads to numerous exact solutions to various equations, and that these solutions can be useful for modeling phenomena in various complex systems.
Author Contributions
Conceptualization, N.K.V. and Z.I.D.; methodology, N.K.V.; software, N.K.V.; validation, Z.I.D.; formal analysis, N.K.V. and Z.I.D.; resources, N.K.V.; data curation, Z.I.D.; writing—original draft preparation, N.K.V. and Z.I.D.; writing—review and editing, N.K.V.; visualization, N.K.V.; supervision, N.K.V. and Z.I.D.; project administration, Z.I.D.; funding acquisition, N.K.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data sharing not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. Systems of Nonlinear Algebraic Equations and Their Solutions
The SEsM methodology leads to systems of nonlinear algebraic equations corresponding to solutions of the solved differential equations. Below, we list those systems and their solutions which have been used in the main text.
First, we consider the case of differential Equation (29). For the case of the values of the parameters , the system of nonlinear algebraic relations corresponding to (29) is
The second solution of (A1) is
Next, we consider the values of the parameters , , . In this case, the system of nonlinear algebraic equations corresponding to Equation (29) is
System (A4) has the following solutions. The first solution is
The second solution is
The third solution is
The fourth solution is
Next, we consider the case , . In this case, . We have to solve Equation (44). In this case, SEsM(1,1) leads to the system of nonlinear algebraic equations
A solution of this system is
Next, we consider the case of . We have to solve Equation (46). First of all, we consider the case , . SEsM(1,1) leads to the system of nonlinear algebraic equations
One of the solutions to this system is
where
The following case is , . The application of SEsM(1,1) leads to the system of nonlinear algebraic equations
The first solution of (A14) is
The second solution of (A14) is
The third solution of the system (A14) is
The fourth solution of (A14) is
Next, we consider the case , , . SEsM(1,1) leads to the system of equations
(A19) has the following solutions. The first solution is
The second solution is
References
- Treiber, M.; Kesting, A. Traffic Flow Dynamics: Data, Models, and Simulation; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-32460-4. [Google Scholar]
- Latora, V.; Nicosia, V.; Russo, G. Complex Networks. Principles, Methods, and Applications; Cambridge University Press: Cambridge, UK, 2017; ISBN 978-1-107-10318-4. [Google Scholar]
- Chian, A.C.-L. Complex Systems Approach to Economic Dynamics; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-540-39752-6. [Google Scholar]
- Vitanov, N.K. Science Dynamics and Research Production. Indicators, Indexes, Statistical Laws and Mathematical Models; Springer: Cham, Switzerland, 2016; ISBN 978-3-319-41629-8. [Google Scholar]
- Dimitrova, Z.I. Flows of Substances in Networks and Network Channels: Selected Results and Applications. Entropy 2022, 24, 1485. [Google Scholar] [CrossRef]
- Ganji, D.D.; Sabzehmeidani, Y.; Sedighiamiri, A. Nonlinear Systems in Heat Transfer; Elsevier: Amsterdam, The Netherlands, 2018; ISBN 978-0-12-812024-8. [Google Scholar]
- Dimitrova, Z. On Traveling Waves in Lattices: The Case of Riccati Lattices. J. Theor. Appl. Mech. 2012, 42, 3–22. [Google Scholar] [CrossRef]
- Drazin, P.G. Nonlinear Systems; Cambridge University Press: Cambridge, UK, 1992; ISBN 0-521-40489-4. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2004; ISBN 978-0511755798. [Google Scholar]
- Verhulst, F. Nonlinear Differential Equations and Dynamical Systems; Springer: Berlin/Heidelberg, Germany, 2006; ISBN 978-3-540-60934-6. [Google Scholar]
- Struble, R. Nonlinear Differential Equations; Dover: New York, NY, USA, 2018; ISBN 978-0486817545. [Google Scholar]
- Vitanov, N.K.; Sakai, K.; Jordanov, I.P.; Managi, S.; Demura, K. Analysis of a Japan Government Intervention on the Domestic Agriculture Market. Physica A 2007, 382, 330–335. [Google Scholar] [CrossRef]
- Vitanov, N.K. Simple Equations Method (SEsM): An Effective Algorithm for Obtaining Exact Solutions of Nonlinear Differential Equations. Entropy 2022, 24, 1653. [Google Scholar] [CrossRef]
- Hopf, E. The Partial Differential Equation: ut + uux = ϵuxx. Commun. Pure Appl. Math. 1950, 3, 201–230. [Google Scholar] [CrossRef]
- Cole, J.D. On a Quasi-Linear Parabolic Equation Occurring in Aerodynamics. Q. Appl. Math. 1951, 9, 225–236. [Google Scholar] [CrossRef]
- Ablowitz, M.J.; Clarkson, P.A. Solitons, Nonlinear Evolution Equations and Inverse Scattering; Cambridge University Press: Cambridge, UK, 1991; ISBN 978-0511623998. [Google Scholar]
- Tabor, M. Chaos and Integrability in Dynamical Systems; Wiley: New York, NY, USA, 1989; ISBN 978-0471827283. [Google Scholar]
- Carrielo, F.; Tabor, M. Similarity Reductions from Extended Painleve Expansions for Nonintegrable Evolution Equations. Physica D 1991, 53, 59–70. [Google Scholar] [CrossRef]
- Carrielo, F.; Tabor, M. Painleve Expansions for Nonintegrable Evolution Equations. Physica D 1989, 39, 77–94. [Google Scholar] [CrossRef]
- Weiss, J.; Tabor, M.; Carnevalle, G. The Painleve Property for Partial Differential Equations. J. Math. Phys. 1983, 24, 522–526. [Google Scholar] [CrossRef]
- Kudryashov, N.A. On Types of Nonlinear Nonintegrable Equations with Exact Solutions. Phys. Lett. A 1991, 155, 269–275. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Simplest Equation Method to Look for Exact Solutions of Nonlinear Differential Equations. Chaos Solitons Fractals 2005, 24, 1217–1231. [Google Scholar] [CrossRef]
- Kudryashov, N.A.; Loguinova, N.B. Extended Simplest Equation Method for Nonlinear Differential Equations. Appl. Math. Comput. 2008, 205, 361–365. [Google Scholar] [CrossRef]
- Kudryashov, N.A. Exact Solitary Waves of the Fisher Equation. Phys. Lett. A 2005, 342, 99–106. [Google Scholar] [CrossRef]
- Kudryashov, N.A. One Method for Finding Exact Solutions of Nonlinear Differential Equations. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 2248–2253. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I.; Vitanov, K.N. Simple Equations Method (SEsM): Algorithm, Connection with Hirota Method, Inverse Scattering Transform Method, and Several Other Methods. Entropy 2021, 23, 10. [Google Scholar] [CrossRef] [PubMed]
- Vitanov, N.K. Simple Equations Method (SEsM): Review and New Results. AIP Conf. Ser. 2022, 2459, 020003. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I. Simple Equations Method and Non-linear Differential Equations with Non-polynomial Non-linearity. Entropy 2021, 23, 1624. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I.; Vitanov, K.N. On the Use of Composite Functions in the Simple Equations Method to Obtain Exact Solutions of Nonlinear Differential Equations. Computation 2021, 9, 104. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Vitanov, K.N. Epidemic Waves and Exact Solutions of a Sequence of Nonlinear Differential Equations Connected to the SIR Model of Epidemics. Entropy 2023, 25, 438. [Google Scholar] [CrossRef]
- Martinov, N.; Vitanov, N. On Some Solutions of the Two-Dimensional Sine-Gordon Equation. J. Phys. A Math. Gen. 1992, 25, L419–L426. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Martinov, N.K. On the solitary waves in the sine-Gordon model of the two-dimensional Josephson junction. Z. Phys. Condens. Matter 1996, 100, 129–135. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Jordanov, I.P.; Dimitrova, Z.I. On Nonlinear Population Waves. Appl. Math. Comput. 2009, 215, 2950–2964. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I. Application of The Method of Simplest Equation for Obtaining Exact Traveling-Wave Solutions for Two Classes of Model PDEs from Ecology and Population Dynamics. Commun. Nonlinear Sci. Numer. Simul. 2010, 15, 2836–2845. [Google Scholar] [CrossRef]
- Vitanov, N.K. Modified Method of Simplest Equation: Powerful Tool for Obtaining Exact and Approximate Traveling-Wave Solutions of Nonlinear PDEs. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 1176–1185. [Google Scholar] [CrossRef]
- Vitanov, N.K. On Modified Method of Simplest Equation for Obtaining Exact and Approximate Solutions of Nonlinear PDEs: The Role of the Simplest Equation. Commun. Nonlinear Sci. Numer. Simul. 2011, 16, 4215–4231. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I.; Vitanov, K.N. Modified Method of Simplest Equation for Obtaining Exact Analytical Solutions of Nonlinear Partial Differential Equations: Further Development of the Methodology with Applications. Appl. Math. Comput. 2015, 269, 363–378. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I. Modified Method of Simplest Equation Applied to the Nonlinear Schrödinger Equation. J. Theor. Appl. Mech. Sofia 2018, 48, 59–68. [Google Scholar] [CrossRef]
- Vitanov, N.K. Simple Equations Method (SEsM) and Its Connection with the Inverse Scattering Transform Method. AIP Conf. Proc. 2021, 2321, 030035. [Google Scholar] [CrossRef]
- Vitanov, N.K.; Dimitrova, Z.I. Simple Equations Method (SEsM) and Its Particular Cases: Hirota Method. AIP Conf. Proc. 2021, 2321, 030036. [Google Scholar] [CrossRef]
- Brauer, F.; Castillo-Chavez, C.; Feng, Z. Mathematcal Models in Epidemiology; Springer: New York, NY, USA, 2019; ISBN 978-1-4939-9828-9. [Google Scholar]
- Diekmann, O.; Heesterbeek, H.; Britton, T. Mathematical Tools for Understanding Infectious Disease Dynamics; Princeton University Press: Princeton, NJ, USA, 2012; ISBN 978-0-6911-5539-5. [Google Scholar]
- Martcheva, M. An Introduction to Mathematical Epidemiology; Springer: New York, NY, USA, 2015; ISBN 978-14899-7612-3. [Google Scholar]
- Li, M.I. An Introduction to Mathematical Modeling of Infectious Diseases; Springer: Cham, Switzerland, 2018; ISBN 978-3-319-72122-4. [Google Scholar]
- Brauer, F. Mathematical Epidemiology: Past, Present and Future. Infect. Dis. Model. 2017, 2, 113–127. [Google Scholar] [CrossRef] [PubMed]
- Britton, T. Stochastic Epidemic Models: A Survey. Math. Biosci. 2010, 225, 24–35. [Google Scholar] [CrossRef]
- Hethcote, H.W. A Thousand and One Epidemic Models. In Frontiers in Mathematical Biology; Levin, S.A., Ed.; Springer: Berlin/Heidelberg, Germany, 1994; pp. 504–515. ISBN 978-3-642-50126-5. [Google Scholar]
- Capasso, V.; Serio, G. A Generalization of the Kermack- McKendrick Deterministic Epidemic Model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Teng, P.S. A Comparison of Simulation Approaches to Epidemic Modeling. Annu. Rev. Phytopathol. 1985, 23, 351–379. [Google Scholar] [CrossRef]
- Hethcote, H.W. The Mathematics of Infectious Diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Wang, W.; Tang, M.; Stanley, H.E.; Braunstein, L.A. Unification of Theoretical Approaches for Epidemic Spreading on Complex Networks. Rep. Prog. Phys. 2017, 80, 036603. [Google Scholar] [CrossRef] [PubMed]
- Godio, A.; Pace, F.; Vergnano, A. SEIR Modeling of the Italian Epidemic of SARS-CoV-2 Using Computational Swarm Intelligence. Int. J. Environ. Res. Public Health 2020, 17, 3535. [Google Scholar] [CrossRef]
- Frank, T.D. COVID-19 Epidemiology and Virus Dynamics; Springer: Cham, Switzerland, 2022; ISBN 978-3-030-97178-6. [Google Scholar]
- Vitanov, N.K.; Ausloos, M.R. Knowledge Epidemics and Population Dynamics Models for Describing Idea Diffusion. In Models of Science Dynamics; Scharnhorst, A., Boerner, K., Besselaar, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 69–125. ISBN 978-3-642-23068-4. [Google Scholar]
- Al-Shbeil, I.; Djenina, N.; Jaradat, A.; Al-Husban, A.; Ouannas, A.; Grassi, G. A New COVID-19 Pandemic Model including the Compartment of Vaccinated Individuals: Global Stability of the Disease-Free Fixed Point. Mathematics 2023, 11, 576. [Google Scholar] [CrossRef]
- Lee, S.J.; Lee, S.E.; Kim, J.-O.; Kim, G.B. Two-Way Contact Network Modeling for Identifying the Route of COVID-19 Community Transmission. Informatics 2021, 8, 22. [Google Scholar] [CrossRef]
- Harjule, P.; Poonia, R.C.; Agrawal, B.; Saudagar, A.K.J.; Altameem, A.; Alkhathami, M.; Khan, M.B.; Hasanat, M.H.A.; Malik, K.M. An Effective Strategy and Mathematical Model to Predict the Sustainable Evolution of the Impact of the Pandemic Lockdown. Healthcare 2022, 10, 759. [Google Scholar] [CrossRef]
- Etxeberria-Etxaniz, M.; Alonso-Quesada, S.; De la Sen, M. On an SEIR Epidemic Model with Vaccination of Newborns and Periodic Impulsive Vaccination with Eventual On-Line Adapted Vaccination Strategies to the Varying Levels of the Susceptible Subpopulation. Appl. Sci. 2020, 10, 8296. [Google Scholar] [CrossRef]
- Nkague Nkamba, L.; Manga, T.T. Modelling and Prediction of the Spread of COVID-19 in Cameroon and Assessing the Governmental Measures (March–September 2020). COVID 2021, 1, 622–644. [Google Scholar] [CrossRef]
- Batool, H.; Li, W.; Sun, Z. Extinction and Ergodic Stationary Distribution of COVID-19 Epidemic Model with Vaccination Effects. Symmetry 2023, 15, 285. [Google Scholar] [CrossRef]
- Khorev, V.; Kazantsev, V.; Hramov, A. Effect of Infection Hubs in District-Based Network Epidemic Spread Model. Appl. Sci. 2023, 13, 1194. [Google Scholar] [CrossRef]
- Jitsinchayakul, S.; Humphries, U.W.; Khan, A. The SQEIRP Mathematical Model for the COVID-19 Epidemic in Thailand. Axioms 2023, 12, 75. [Google Scholar] [CrossRef]
- Ni, G.; Wang, Y.; Gong, L.; Ban, J.; Li, Z. Parameters Sensitivity Analysis of COVID-19 Based on the SCEIR Prediction Model. COVID 2022, 2, 1787–1805. [Google Scholar] [CrossRef]
- Wang, W.; Xia, Z. Study of COVID-19 Epidemic Control Capability and Emergency Management Strategy Based on Optimized SEIR Model. Mathematics 2023, 11, 323. [Google Scholar] [CrossRef]
- Leonov, A.; Nagornov, O.; Tyuflin, S. Modeling of Mechanisms of Wave Formation for COVID-19 Epidemic. Mathematics 2023, 11, 167. [Google Scholar] [CrossRef]
- Margenov, S.; Popivanov, N.; Ugrinova, I.; Hristov, T. Mathematical Modeling and Short-Term Forecasting of the COVID-19 Epidemic in Bulgaria: SEIRS Model with Vaccination. Mathematics 2022, 10, 2570. [Google Scholar] [CrossRef]
- Chang, Y.-C.; Liu, C.-T. A Stochastic Multi-Strain SIR Model with Two-Dose Vaccination Rate. Mathematics 2022, 10, 1804. [Google Scholar] [CrossRef]
- Din, A.; Li, Y.; Khan, T.; Zaman, G. Mathematical Analysis of Spread and Control of the Novel Corona Virus (COVID-19) in China. Chaos Solitons Fractals 2020, 141, 110286. [Google Scholar] [CrossRef]
- Dimitrova, Z.I. Relation Between G’/G-expansion Method and the Modified Method of Simplest Equation. C. R. L’Academie Bulg. Des Sci. 2012, 65, 1513–1520. [Google Scholar]
- Dimitrova, Z.I. Several Examples of Application of the Simple Equations Method (SEsM) for Obtaining Exact Solutions of Nonlinear PDEs. AIP Conf. Proc. 2022, 2459, 030005. [Google Scholar] [CrossRef]
- Vitanov, N.K. Modified Method of Simplest Equation for Obtaining Exact Solutions of Nonlinear Partial Differential Equations: Past and Present. J. Theor. Appl. Mech. 2019, 49, 107–122. [Google Scholar] [CrossRef]
- Hirota, R. The Direct Method in Soliton Theory; Cambridge University Press: Cambridge, UK, 2004; ISBN 0-521-83660-3. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. A Contribution to the Mathematical Theory of Epidemics. Proc. R. Soc. Lond. Ser. A 1927, 115, 700–721. [Google Scholar] [CrossRef]
- Ross, R. Researches on Malaria: Being the Nobel Medical Prize Lecture for 1902; Forgotten Books: London, UK, 2018; ISBN 978-1332279968. [Google Scholar]
- Mandal, S.; Sarkar, R.R.; Sinha, S. Mathematical Models of Malaria—A Review. Malar. J. 2011, 10, 202. [Google Scholar] [CrossRef]
- Hethcote, H. The Basic Epidemiology Models: Models, Expressions for R0, Parameter Estimation, and Applications. In Mathematical Understanding of Infectious Disease Dynamics; Ma, S., Xia, Y., Eds.; World Scientific: Singapore, 2009; pp. 1–63. ISBN 978-981-283-482-9. [Google Scholar]
- Bauer, F.; van den Driessche, P.; Wu, J. Mathematical Epidemiology; Springer: Berlin/Heidelberg, Germany, 2008; ISBN 978-3-540-78910-9. [Google Scholar]
- Hethcote, H.W. Qualitative Analyses of Communicable Disease Models. Math. Biosci. 1976, 28, 335–356. [Google Scholar] [CrossRef]
- Hethcote, H.W.; Tudor, D.W. Integral Equation Models for Endemic Infectious Diseases. J. Math. Biol. 1980, 9, 37–47. [Google Scholar] [CrossRef]
- Aron, J.L.; Schwartz, I.B. Seasonality and Period-Doubling Bifurcations in an Epidemic Model. J. Theor. Biol. 1984, 110, 665–679. [Google Scholar] [CrossRef]
- Schwartz, I.B. Multiple Stable Recurrent Outbreaks and Predictability in Seasonally Forced Nonlinear Epidemic Models. J. Math. Biol. 1985, 21, 347–361. [Google Scholar] [CrossRef]
- Pare, P.E.; Beck, C.L.; Başar, T. Modeling, Estimation, and Analysis of Epidemics Over Networks: An Overview. Annu. Rev. Control 2020, 50, 345–360. [Google Scholar] [CrossRef]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans an Animals; Princeton University Press: Princeton, NJ, USA, 2008; ISBN 978-0-691-11617-4. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).