Abstract
Background: In present genomes, current relics of a circular RNA appear which could have played a central role as a primitive catalyst of the peptide genesis. Methods: Using a proximity measure to this circular RNA and the distance, a new unsupervised classifier called MaxwellTM has been constructed based on the Burrows–Wheeler transform algorithm. Results: By applying the classifier to numerous genomes from various realms (Bacteria, Archaea, Vegetables and Animals), we obtain phylogenetic trees that are coherent with biological trees based on pure evolutionary arguments. Discussion: We discuss the role of the combinatorial operators responsible for the evolution of the genome of many species. Conclusions: We opened up possibilities for understanding the mechanisms of a primitive factory of peptides represented by an RNA ring. We showed that this ring was able to transmit some of its sub-sequences in the sequences of genes involved in the mechanisms of the current ribosomal production of proteins.
1. Introduction
Among the molecules that have possibly played an important role in the origin of life on Earth, the first RNAs and peptides were formed by chance through a concatenation process among the nucleotides and amino acids pools, respectively, synthesized from the atoms (C, O, H, and N) of the primitive atmosphere due to sufficient electrical discharge [1,2]. They combined in same favorable sites (volcanic hot spring pools [3], clays like montmorillonite [4], alkaline hydrothermal vent/serpentinization [5], etc.) giving rise to large polymers, e.g., circular RNAs and proteins, whose interactions allowed their reproduction and isolation from the external environment. RNA core was made of rings or chains with catalytic properties helping amino acids to bind together. Peptides created via this peptide-bonding was later combined with lipids synthesized in the primitive atmosphere [6]. They could also assist with the synthesis of new RNA rings or chains that could serve further as ribozymes catalyzing the protein synthesis [7,8] as demonstrated in short segments of RNA [9,10]. By looking for the minimal circular RNA that first facilitated these interactions, we have previously identified an RNA structure [11,12], called AL (Archetypal Loop), capable of catalyzing peptide bonds between amino acids in its ring form (Figure 1A) and resisting denaturing environmental conditions in its hairpin form (Figure 1B) [13]. The AL sequence can be considered as the consensus sequence of tRNA loops of many species (only 4 species on Figure 1C and 242 others from GtRNAdB (see [14] and Supplementary Materials Table S1): ATGGTACTGCCATTCAAGATGA [15]. The RNA AL has interesting combinatorial properties: it comprises 22 nucleotides and offers 20 successive codons capable of binding transiently to the 20 amino acids of which they are the representatives in the genetic code via overlapping [15]. This AL structure is unique for being the barycenter (for the circular Hamming distance) of a set of only 25 other possible solutions with a minimal of 22 nt length and with these combinatorial properties. Moreover, if AL starts with AUG, it ends with UGA, which is the punctuation codons of the genetic code.

Figure 1.
(A) Ring form of the Archetypal Loop (AL) with indication of the tRNA loops; (B) hairpin form of AL with indication of the upper part containing the nine P-pentamers; and (C) examples of tRNA-Gly of different species (from [14]).
It has been proven that amino acids have an affinity with their cognate codons and anti-codons involving weak electromagnetic or van der Waals forces [16,17], which causes transient binding between amino acids and the AL ring containing the corresponding cognate triplets of nucleotides, and after being spatially close together, amino acids can bind to each other or to a neighboring peptide, with the mechanism being analog to that of the present protein synthesis in current cells. This mechanism was proposed by Katchalsky [18] and Eigen [19], which showed that RNA, in particular the ancestors of current transfer RNA, could have been involved in a primitive matrix capable of catalyzing the synthesis of both peptides and new RNAs, favoring the emergence of an RNA world made of RNA molecules with catalytic and replicative properties [20,21].
2. Materials and Methods
2.1. Calculation of the Archetypal Loop-Proximity
The methodology chosen starts from the calculation of a proximity called the AL proximity, which estimates the degree of possible heritability from the AL of an RNA sequence. The sequences are obtained from the RefSeq database of NCBI (National Center for Biotechnology Information) [22], which contains the genomes of many species. On 5 May 2023, the RefSeq Release 218 included the genome of 133,740 organisms, with 52,503,423 of mRNA transcripts of 260,776,371 proteins of which the gene contains 24,000 nucleotides and the mRNA transcript 1300 nucleotides on average in humans. The method used to compare an RNA sequence to the AL involves counting the number of common pentamers between those of the sequence and those located at the upper extremity of the hairpin form of the AL, which belongs to the following set, P, of 9 pentamers:
P = {AUUCA, UUCAA, UCAAG, CAAGA, AAGAU, AGAUG, GAUGA, AUGAA, UGAAU}.
The 9 elements of P are called P-pentamers. They are extracted from an AL sequence located near the head of the hairpin form of the AL. We use P for defining a criterion of proximity to the AL for any RNA sequence, that is, the number of standard deviations (SDs) between calculated and expected numbers of P-pentamers in the chosen sequence. For example, let us consider the nucleotide sequence of length n = 2697 observed for the mRNA of the nucleolin of Camelus dromedarius (Figure 2). Then, because the probability of observing a pentamer by chance is p = 9/1024, the average number of expected P-pentamers is np = 2720 × (9/1024) = 23.9, with a standard deviation σ = np(1 − p)~23.91/2~4.9. The number of calculated P-pentamers in the sequence is equal to 95; then, the difference between calculated and expected numbers is 95 − 23.9 = 71.1, corresponding to 71.1/4.9 = 14.5σ.

Figure 2.
mRNA sequence of nucleolin gene (NCL) of Camelus dromedarius breed African isolate Drom800 chromosome 5 (graphic extracted from NCBI Reference Sequence: XM_010985648,2 [22]). The P-pentamers are indicated in red bold (with possible overlaps).
Because the Bernoulli distribution of the P-pentamers checks the approximation conditions by the Gaussian distribution, n = 2720 ≥ 30, np~23.9 ≥ 5, and n(1 − p)~2696 ≥ 5, so the probability of observing such a difference is less than 1 − F(14.5) < Proba({X ≥ 14.5}), where F is the Gaussian distribution function. Then, using the Gaussian distribution function approximation proposed in [23], we get: Proba({X ≥ t})~0.5 − (1 − exp(−at2))1/2)/2, where a = 0.647 − 0.021t. Hence, t = 14.5, a = 0.3425 and Proba({X ≥ 14.5})~exp(−0.3425 × 210.25)/4~1.33 × 10−14. Because the value of the difference between the calculated and expected numbers of pentamers expressed as a number of standard deviations σ is directly linked to the probability of observing this difference, we retain this quantity as a measure of any RNA sequence’s proximity to the AL, called P-proximity.
If the ring AL has played a role in building the first peptides, it is reasonable to search for the remnants of its nucleotidic sequence inside RNAs playing the same role in building the current proteins, e.g., ribosomal RNAs and mRNA of ribosomal proteins or of proteins favoring the accretion of the ribosomal components.
The number of P-pentamers calculated in Figure 2 is 95 and the expected number is 23.9, with a difference equal to 14.5σ, where σ is equal to the standard deviation of the Bernoulli empirical distribution corresponding to the P-pentamers observed by chance. Then, the probability to observe these 95 P-pentamers equals to about 10−14. It is possible to search for relics such as the P-pentamers common to the AL and to rRNAs and mRNAs whose function is considered identical in the ribosomes of multiple species, like the mRNA of proteins nucleolin and NOL11 (see Supplementary Materials Tables S2 and S3). After calculating their P-proximity, we classify the corresponding mRNAs of various species using the classifier MaxwellTM, which is able to compare sequences of symbols [24], here the sequences of nucleotides, and conclude if the obtained clusters are coherent with the P-proximity values of their elements.
2.2. The Burrows–Wheeler Transform
The Burrows–Wheeler transform [25] is an algorithm used in lossless compression procedure which rearranges strings into runs of similar characters in a reversible way. Associated with a run-length algorithm, we obtain a function we use in “Normalized Compression Distance” (NCD) or Vitányi distance, in order to find similarities between them, like same repetition of motifs, same deletion or insertions, etc. The reason for the implementation of this “simplified” compression algorithm was to retrieve the symmetry of NCD. It is particularly convenient to compare genomic sequences independently of their length if they have coevolved under the action of the same operators. In evolution, there are 11 different genomic operators: Crossing-over, Mutation, Translocation, Insertion, Deletion, Transposition, Inversion, Repetition, Symmetrization, Palindromization, and Permutation. When these operators are used with the same frequency during evolution, Burrows–Wheeler transform serves to compress the sequences of the same origin which have similar evolutionary history.
First, Burrows–Wheeler transform involves organizing the circular permutation of a word following the lexicographic order, then taking the last letter of these permuted words and calculate the run-length encoding (RLE) of this new word formed by the rank of the permutation identical to the initial word followed by the sequence of the last letters of permuted words, by indicating before the number of repeated letters (Figure 3). This coding constitutes a lossless compression method and during decompression, the initial word can be reconstructed exactly from this information in a reversible (or adiabatic) way.
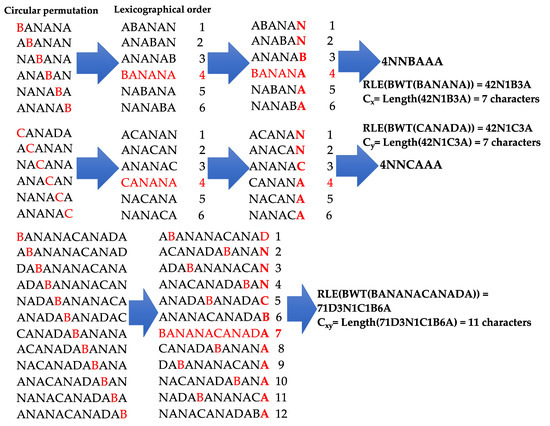
Figure 3.
Burrows–Wheeler transform (BWT) of two words BANANA and CANADA, with two mutations B/C and N/D. Lengths of run-lengths (RLE) of BWT transforms of BANANA, CANADA and concatenation BANANACANADA are, respectively, 7, 7 and 11 characters. The red words represent the initial words changed during the Burrows-Wheeler transform.
2.3. The Vitányi Distance
The Vitányi distance between two sequences x and y [26,27] involves calculating the length of the RLE version of their Burrows–Wheeler transform (BWT), that is, the values of the coefficients Cx = Length[RLE(BWT(x))] and Cy = Length[RLE(BWT(y))], respectively, and then the value of the coefficient for the concatenated word xy, Cxy = Length[RLE(BWT(xy))] and calculating the ratio (Figure 3): d(x,y) = [Cxy − min(Cx,Cy)]/max(Cx,Cy). Vitányi distance using Burrows–Wheeler transform and run-length between words BANANA and CANADA is equal to 0,57 (Figure 3). Vitányi distance is a real mathematical distance, with d(x,x) = 0, d(x,y) = d(y,x) (symmetry) and d(x,z) ≤ d(x,y) + d(y,z) (triangular inequality).
2.4. The MaxwellTM Classifier
The principle of the MaxwellTM classifier [26] is to constitute clusters of words belonging to the set {xi}i=1,n, from which the distance matrix Dij = d(xi,xj) has been calculated. Then, each triplet of words constitutes a triangle in the graph associated with D and the area of this triangle is calculated using the classical Héron formula, and the original algorithm of MaxwellTM has the following steps:
- -
- Calculating the mean and standard deviation on histograms of triangle areas for filtering “large and deformed triangles” considered as outliers of the empirical distribution according to the number of standard deviations retained;
- -
- Examining sub-graphs whose “useless” (respectively “best”) representative edges are identified as attached to the least (respectively the most) connected nodes and removing them (respectively keep them as cluster central node);
- -
- Processing sub-graphs with several local minima (i.e., nodes whose neighborhood does not contain another node that is closer to the sub-graph than the node itself) using Voronoï networking with the software Graphviz [28] for detecting internal boundaries;
- -
- Testing at the end for sub-graphs whose mean and standard deviation are varied until Graphviz no longer detects any boundaries;
- -
- Storing elements rejected by this statistics calculation in the form of “singleton clusters”;
- -
- Final recalling by clustering the population of singletons to detect new clusters.
3. Results
Table 1 shows that RNA classes whose content is homogeneous in AL-proximity, i.e., in evolutionary age (if the hypothesis on the primitivity of AL is true), are marked both by a large AL-proximity and by an upstream position in the MaxwellTM classification tree (Figure 4). They correspond to ancient species in purely biological phylogenetic trees, calculated without reference to an ancestral RNA, and resulting only from comparisons between the genomic sequences of the compared species (Figure 5). The MaxwellTM classification tree proposes a series of clusters organized from the root of the tree until its leaves and the content of each cluster is as presented in Table 1, which shows that one of the rules explaining the grouping in a class is the proximity to the AL of its members. It should be noted that at the root of the tree, where the hypothetical LUCA (the Last Universal Common Ancestor, defined first by C. Woese and G. Fox as the first living system [29,30]) is often placed, the ancient species of Salinarchaeum appears, which belongs to the very ancient classes of Archaea and Halobacteria from the Euryarchaeota branch (Figure 5).

Table 1.
MaxwellTM classification clusters. Background color (white or orange clear) differentiates the clusters.
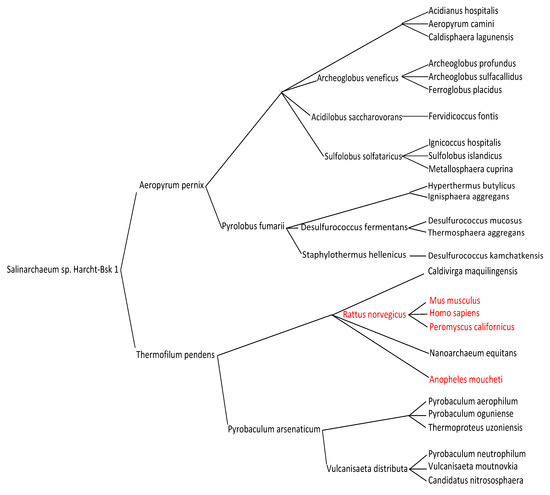
Figure 4.
Representation of a part of the MaxwellTM classification tree from the 5S ribosomal RNA (in black) and nucleolin mRNA (in red) of different species (see Supplementary Material).
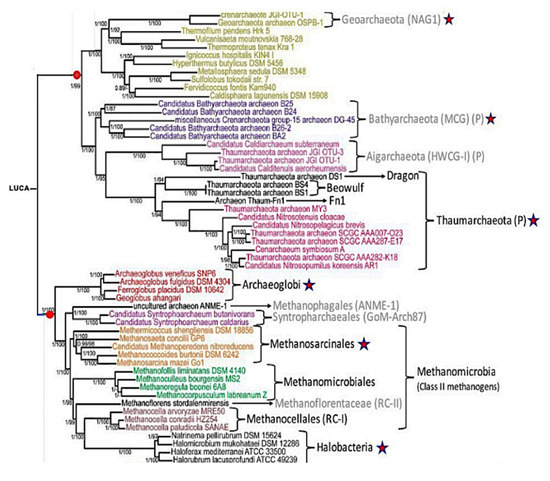
Figure 5.
From [30], phylogeny of Archaea. The red stars correspond to the clusters of the MaxwellTM classification. Red dots correspond to the two subtrees.
The first four clusters of the classification tree successively represent Archaea (class 1), Archaea with ancient Bacteria and Fungi (class 2), Bacteria with ancient Archaea (class 3) and Mammals (class 4). This classification respects the known hierarchies of successive clades, obtained by comparing genomes of the same nature (see the Supplementary Materials Table S4 for the whole clustering) and the MaxwellTM clustering with cladistic ranking can be described as a list, whose four first clusters are:
- (1)
- Cluster 1 Archaea
| Kingdom: | Archaea |
| Division: | Euryarchaeota |
| Class: | Halobacteria |
| Order: | Halobacteriales |
| Family: | Halobacteriaceae |
| Genus: | Halobacteriaceae halorabdus, Halovivax, Halomicrobium, and Halorubrum |
| Division: | Thaumarchaeota |
| Class: | Incertae sedis |
| Order: | Nitrosopumilales |
| Family: | Nitrosopumilaceae |
| Genus: | Nitrosopumilus nitrospumilus maritimus |
| Division: | Crenarchaeota |
| Class: | Thermoprotei |
| Order: | Sulfolobales |
| Family: | Sulfolobaceae sulfolobus solfataricus |
- (2)
- Cluster 2 Archaea and Bacteria
| Division: | Euryarchaeota |
| Class: | Methanomicrobia |
| Order: | Methanosarcinales |
| Family: | Methanosarcinaceae Methanolobus psychrophilus |
| Domain: | Bacteria |
| Phylum: | Bacteroidota |
| Class: | Chitinophagia |
| Order: | Chitinophagales |
| Family: | Chitinophagaceae Hydrobacter penzbergensis |
| Kingdom: | Fungi |
| Division: | Ascomycota |
| Class: | Saccharomycetes |
| Order: | Saccharomycetales |
| Family: | Saccharomycetaceae |
| Genus: | Ogataea Ogataea polymorpha |
| Domain: | Bacteria |
| Phylum: | Actinomycetota |
| Class: | Actinomycetia |
| Order: | Glycomycetales |
| Family: | Glycomycetaceae |
| Genus: | Stackebrandtia stackebrandtia nassauensis |
- (3)
- Cluster 3 Bacteria and Archaea
| Domain: | Bacteria |
| Phylum: | Bacteroidota |
| Class: | Chitinophagia |
| Order: | Chitinophagales |
| Family: | Chitinophagaceae hyperthermus butylicus |
| Phylum: | Euryarchaeota |
| Class: | Archaeoglobi |
| Order: | Archaeoglobales |
| Family: | Archaeoglobaceae ferroglobus placidus, Archaeoglobus sulfaticallidus, and Archaeoglobus profundus |
- (4)
- Cluster 4 Mammals
lynx, shrew, bat, elephant, squirrel, horse, and cat
4. Discussion
In the classification obtained using the classifier MaxwellTM, there exists no information about the species, except the succession of nucleotides of some of their RNAs or mRNAS (5S ribosomal RNAs, nucleolin (NCL) and nucleolar protein (NOL11) mRNAs).
In Figure 5, the Archaea phylogeny [31] shows an organization compatible with the MaxwellTM classification tree in Figure 4. In particular, all the classes marked with a red star correspond to classes of the MaxwellTM tree, even though all their contents have not been systematically explored in the present study. This consistency between the classes discovered using the MaxwellTM algorithm, only from the nucleotide sequence of some RNAs and the classes of an Archaea phylogeny, is an important argument validating the new MaxwellTM classification method.
5. Conclusions and Perspectives
The challenging problem of finding an ancestor to RNAs related to the ribosomal protein factory can be partially solved by looking at the nucleotide sequence of some ribosomal RNAs and mRNAs of proteins involved in the building of the ribosome itself. Some invariant parts of these nucleotide sequences are detected via MaxwellTM and future work will be dedicated to the classification of random sequences, using MaxwellTM, respecting some evolutionary rules based on precise operators among the eleven acting in genome evolution and used via the genetic algorithms: Crossing-over, Mutation, Translocation, Insertion, Deletion, Transposition, Inversion, Repetition, Symmetrization, Palindromization, and Permutation [32,33]. This will allow us to extensively understand the hidden mechanisms of the MaxwellTM algorithm in detecting common motifs in the nucleotide sequences of ribosomal and messenger RNAs. As the MaxwellTM classifier mainly detects repeats, insertions, mutations and palindromizations common to multiple genomes that we wish to compare, the clustering trees obtained via it will have biological significance. These trees will complement the classical phylogenetic trees from the primitive molecular structures of the current species in order to refine our current knowledge on evolution.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/computation11080158/s1. Table S1: List of tRNA-GlyGCC from 246 species extracted from GtRNAdB; Table S2: AL-pentamer content in nucleolin (NCL)) of species of Figure 2C. Red color represents P-pentamers, blue color corresponds to overlaps; Table S3: Examples of P-pentamer content in nucleophosmine (NPM1) of 8 species from Table S2. Red color represents P-pentamers, blue color corresponds to overlaps; Table S4: MaxwellTM classification clusters.
Author Contributions
Conceptualization, J.D. and J.G.; methodology, J.D., J.G., C.M. and D.B.; K.B. and I.T. have performed the calculations; all authors have equally participated in the other steps of article elaboration. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
All data are coming from public data bases and are given in Supplementary material.
Acknowledgments
The authors hereby acknowledge the support of the Orange Labs and the MIASH master (Mathematics and Informatics Applied to Human Sciences) of the University of Grenoble Alpes.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Miller, S.L. A Production of amino acids under possible primitive Earth conditions. Science 1953, 117, 528–529. [Google Scholar] [CrossRef]
- Bada, J.L.; Lazcano, A. Prebiotic soup—Revisiting the Miller experiment. Science 2003, 300, 745–746. [Google Scholar] [CrossRef] [PubMed]
- Damer, B.; Deamer, D. The Hot Spring Hypothesis for an Origin of Life. Astrobiology 2020, 20, 429–452. [Google Scholar] [CrossRef] [PubMed]
- Katchalsky, A. Prebiotic synthesis of biopolymers on inorganic templates. Naturwiss 1973, 60, 215–220. [Google Scholar] [CrossRef]
- Martin, W.; Russell, M.J. On the origin of biochemistry at an alkaline hydrothermal vent. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2007, 362, 1887–1925. [Google Scholar] [CrossRef] [PubMed]
- Deamer, D. The Role of Lipid Membranes in Life’s Origin. Life 2017, 7, 5. [Google Scholar] [CrossRef]
- Turk-MacLeod, R.M.; Puthenvedu, D.; Majerfeld, I.; Yarus, M. The Plausibility of RNA-Templated Peptides: Simultaneous RNA Affinity for Adjacent Peptide Side Chains. J. Mol. Evol. 2012, 74, 217–225. [Google Scholar] [CrossRef]
- Xiao, H.; Murakami, H.; Suga, H.; Ferré-D’Amaré, A.R. Structural basis of specific tRNA aminoacylation by a small in vitro selected ribozyme. Nature 2008, 454, 358–361. [Google Scholar] [CrossRef]
- Deng, J.; Wilson, T.J.; Wang, J.; Peng, X.; Li, M.; Lin, X.; Liao, W.; Lilley, D.M.J.; Huang, L. Structure and mechanism of a methyltransferase ribozyme. Nat. Chem. Biol. 2022, 18, 556–564. [Google Scholar] [CrossRef] [PubMed]
- Grum-Tokars, V.; Milovanovic, M.; Wedekind, J.E. Crystallization and X-ray diffraction analysis of an all-RNA U39C mutant of the minimal hairpin ribozyme. Acta Crystallogr. Sect. D Biol. Crystallogr. 2003, 59, 142–145. [Google Scholar] [CrossRef] [PubMed]
- Demongeot, J. Au Sujet de Quelques Modèles Stochastiques Appliqués à la Biologie. Modélisation et Simulation; Université Joseph-Fourier: Grenoble, France, 1975. [Google Scholar]
- Demongeot, J. Sur la possibilité de considérer le code génétique comme un code à enchaînement. Rev. Biomaths 1978, 62, 61–66. [Google Scholar]
- Demongeot, J.; Besson, J. Code génétique et codes à enchaînement. C. R. Seances L’Acad. Sci. Ser. III 1983, 296, 807–810. [Google Scholar]
- GtRNAdB. Available online: http://gtrnadb.ucsc.edu/ (accessed on 23 May 2023).
- Demongeot, J.; Moreira, A. A circular RNA at the origin of life. J. Theor. Biol. 2007, 249, 314–324. [Google Scholar] [CrossRef]
- Hobish, M.K.; Wickramasinghe, N.S.M.D.; Ponnamperuma, C. Direct interaction between amino-acids and nucleotides as a possible physico-chemical basis for the origin of the genetic code. Adv. Space Res. 1995, 15, 365–375. [Google Scholar] [CrossRef]
- Tamura, K.; Schimmel, P. Oligonucleotide-directed peptide synthesis in a ribosome- and ribozyme-free system. Proc. Natl. Acad. Sci. USA 2001, 98, 1393–1397. [Google Scholar] [CrossRef]
- Paecht-Horowitz, M.; Berger, J.; Katchalsky, A. Prebiotic synthesis of polypeptides by heterogeneous polycondensation of amino-acid adenylates. Nature 1970, 228, 636–639. [Google Scholar] [CrossRef]
- Eigen, M. Selforganization of matter and the evolution of biological macromolecules. Naturwissenschaften 1971, 58, 465–523. [Google Scholar] [CrossRef]
- Gilbert, W. Origin of life: The RNA world. Nature 1986, 319, 618. [Google Scholar] [CrossRef]
- Kauffman, S.A. Approaches to the origin of life on Earth. Life 2011, 1, 34–48. [Google Scholar] [CrossRef]
- NCBI. Available online: https://www.ncbi.nlm.nih.gov/refseq/ (accessed on 23 May 2023).
- Edous, M.; Eidous, O. A Simple Approximation for Normal Distribution Function. Math. Stat. 2018, 6, 47–49. [Google Scholar] [CrossRef]
- Gardes, J.; Maldivi, C.; Boisset, D.; Aubourg, T.; Vuillerme, N.; Demongeot, J. Maxwell®: An unsupervised learning approach for 5P medicine. Stud. Health Technol. Inform. 2019, 264, 1464–1465. [Google Scholar]
- Burrows, M.; Wheeler, D.J. A block-sorting lossless data compression algorithm. Digit. SRC Res. Rep. 1994, 124, 10009821328. [Google Scholar]
- Cilibrasi, R.; Vitanyi, P.M.B. Clustering by compression. IEEE Trans. Inf. Theory 2005, 51, 1523–1545. [Google Scholar] [CrossRef]
- Cohen, A.R.; Vitányi, P.M.B. Normalized Compression Distance of Multisets with Applications. IEEE Trans. PAMI 2015, 37, 1602–1614. [Google Scholar] [CrossRef] [PubMed]
- Graphviz. Available online: https://graphviz.org/ (accessed on 23 May 2023).
- Woese, C.; Fox, G. The concept of cellular evolution. J. Mol. Evol. 1977, 10, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Gogarten, J.P.; Deamer, D. Is LUCA a thermophilic progenote? Nat. Microbiol. 2016, 1, 16229. [Google Scholar] [CrossRef]
- Adam, P.S.; Borrel, G.; Brochier-Armanet, C.; Gribaldo, S. The growing tree of Archaea: New perspectives on their diversity, evolution and ecology. ISME J. 2017, 11, 2407–2425. [Google Scholar] [CrossRef]
- Schmitt, L.M. Theory of Genetic Algorithms. Theor. Comput. Sci. 2001, 259, 1–61. [Google Scholar] [CrossRef]
- Ighalo, J.O.; Marques, G. Current Trends and Advances in Computer-Aided Intelligent Environmental Data Engineering; Elsevier: Amsterdam, The Netherlands, 2022. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).