An Algebraic Approach to the Solutions of the Open Shop Scheduling Problem

Abstract

The open shop scheduling problem (OSSP) is one of the standard scheduling problems. It consists of scheduling jobs associated with a finite set of tasks developed by different machines. In this case, each machine processes at most one operation at a time, and the job processing order on the machines does not matter. The goal is to determine the completion times of the operations processed on the machines to minimize the largest job completion time, called C_max. This paper proves that each OSSP has associated a path algebra called Brauer configuration algebra whose representation theory (particularly its dimension and the dimension of its center) can be given using the corresponding C_max value. It has also been proved that the dimension of the centers of Brauer configuration algebras associated with OSSPs with minimal C_max are congruent modulo the number of machines.

1. Introduction

Nowadays, there is renewed interest in researching the OSSP due to its broad range of applications. It has been helpful in developing models for satellite communications, trade, healthcare management, transport, sports, etc. [1,2,3,4].

In an OSSP, a schedule assigns every operation ${\mathcal{O}}_{ij}$ to a time interval of length $p_{ij}$ in such a way that two different operations of a job are not simultaneously processed by two different machines [5]. Investigating the OSSP dates back to the 1970s. Gonzalez and Sahni [6] proved in 1976 that it is polynomially solvable to minimize the largest job completion time (called the makespan) of the well-known two-machine problem. Dell’Amico and Mortello [7] argued that the Gonzalez and Sahni algorithm is an implementation of some results obtained by Egerváry in 1931.

In the standard scheduling classification scheme proposed by Lawler, Lenstra, and Rinooy Kan [8] the optimization problem is denoted $\mathcal{O}|C_{max}$ (where the number of machines, m, is given as part of the input and $C_{max}$ denotes the corresponding makespan) [5]. The notation ${\mathcal{O}}_m|C_{max}$ is used if the number of machines, m, is a fixed constant number. Gonzalez and Sahni [6] proved that ${\mathcal{O}}_2|C_{max}$ is solvable in polynomial time and that for every $m\ge 3$, the problem ${\mathcal{O}}_m|C_{max}$ is NP-hard, taking into account that such a problem can be seen as a reduction of the partition problem.

Sevastianov and Woeginger [9] proved that ${\mathcal{O}}_m|C_{max}$ has a polynomial time approximation scheme (PTAS), whereas Fiala [10] proved that if an instance of ${\mathcal{O}}_m|C_{max}$ satisfies $L_{max}\ge (m^2+m-1)o_{max}$ then $C_{max}=L_{max}$, where $o_{max}$ ($L_{max}$) denotes the length of the longest operation (the maximum machine load).

Tautenhahn [11] used Latin rectangles to propose a polynomial algorithm for the open shop problem with UET (unit execution time) operations such that each operation is completed by its given deadline. He proposed an $O\left(n^{2}m\right)$ algorithm that outputs a schedule for $\mathcal{O}|\mathrm{UET}$, $C_j\le d_j|C_{max}$ and also for $\mathcal{O}|\mathrm{UET}$, $C_j\le d_j|\sum C_j$ and proved that there is a common optimal schedule for both problems. Where, $C_{ij}$ denotes the completion time of job j on machine i, $C_j=\underset{i\in M}{\max }\left\{C_{ij}\right\}$, and $d_j$ is the deadline of the jth job.

In 1993, Taillard [12] proposed instances for the OSSP characterized by a pair $(n,m)$ of n jobs and m machines. He investigated the OSSP for $n=m\in \{4,5,7,15,20\}$. In such a case the processing times $p_{ij}$ are randomly generated by a discrete uniform distribution over $[1,99]$. For each generated instance he obtained bounds of the form

$${\mathcal{L}}_{{\beta }_0}=\max \{\underset{i}{\max }\{p_{ij}\},\underset{j}{\max }\{p_{ij}\}\}$$

(1)

where $p_{ij}$ denotes the processing time of the ith job on the jth machine.

It is worth noting that Brucker, Sotskov and Werner [13] proved that for three machines $\mathcal{O}|C_{max}$ is NP-hard. In general, the complexity of the three-machine problem is still open if each job has exactly two operations.

In the literature, other linear-time algorithms differ from the ones proposed by Gonzalez and Sahni, for instance, the longest alternative processing time (LAPT) of Pinedo and Schrage [14] or de Werra’s algorithm [15] that Soper [16] generalized in 2015. Huang and Li have proposed alternative methods to investigate the OSSP [17], and Tellache and Boudhar [18], proposed a bee colony optimization algorithm and conflict graphs to solve it.

To date, max-plus algebra is one of the best-known algebraic tools for researching the job shop scheduling problems. Subiono [19] and Shofianaff used this algebra to study the behavior of flow shop production systems. Houssin [20] and Barman et al. [21] proposed a method based on max-plus algebra to solve different versions of the cyclic job shop problem, and Žužek et al. [22] used it to study job shop scheduling problems with a non-delay schedule.

The recent use of max-plus algebra to investigate several kinds of job shop scheduling problems can be seen in the works of Aminu et al., Bermanei, Bermanei et al., Chang et al., Sitahong et al., and Carnia et al. [23,24,25,26,27,28].

Brauer configuration algebras (BCAs) were introduced by Green and Schroll in 2017 [29,30]. BCAs are bound quiver algebras (multiserial and symmetric) induced by appropriated systems of multisets. Since their introduction, they have helped obtain applications in cryptography, graph energy theory, Yang-Baxter equation theory, wargames theory, quiver representation theory, etc. [31,32,33,34]. However, more work must be done on interactions between BCAs and job shop scheduling problems. This paper proves that open shop problems give rise to BCAs whose dimensions, and that of their corresponding centers [35], allow the establishment of optimal makespans of the associated open shop problems.

1.1. Motivations

There is currently great interest in researching the OSSP due to its new applications in various fields. Applications of this problem can be found in transport, healthcare, satellite communications, sports, and elsewhere [1,2,3,4]. However, few publications exist that connect investigations of the OSSP with investigations in algebra. ARguably one of the more remarkable works on these types of connections uses max-plus algebra or Tautenhahn’s approach [11], which employs Latin rectangles to solve the OSSP. It is worth noting that there are no works in the literature devoted to the interactions between the theory of representation of algebras and OSSP research. In particularly, more studies are needed on the relationships between Brauer configuration algebras and job shop scheduling problems in general.

This paper shows that associated with an OSSP (encoded by an appropriated processing matrix time) is a Brauer configuration algebra whose representation theory can be described using the corresponding $C_{max}$ value. It also proves that the dimensions of the centers of BCAs associated with two optimal equivalent processing time matrices (which give minimal $C_{max}$) are congruent modulo the number of machines.

1.2. Contributions

This work proposes something other than new algorithms to solve the OSSP. Instead, it proposes to use features of these kinds of problems to define new Brauer configuration algebras and their properties. It is worth noting that studies regarding this subject do not appear in the current literature.

The main results of this paper are Theorems 1–5. They are illustrated as targets of the red arrows in Figure 1, which shows how the different theories were related to each other to obtain our results.

Figure 1. The main results presented in this paper (targets of red arrows) allow the establishment of a connection between Brauer configuration algebras theory and OSSP research.

Theorem 1 proves that the BCA associated with an OSSP is indecomposable as an algebra. Theorem 2 gives formulas for the dimension of an algebra associated with an OSSP. Theorem 3 gives formulas for the center of an algebra associated with an OSSP. Theorem 4 provides a formula for the center of a BCA associated with an optimal configuration of an OSSP. Finally, Theorem 5 proves that the dimension of the centers of BCAs associated with optimal configurations are congruent modulo the number of machines.

The organization of this paper is as follows. Main definitions and notation are given in Section 2, with definitions and notation regarding the OSSP (Section 2.1) and Brauer configuration algebras (BCAs) (Section 2.3). The main results and some experimental data are presented in Section 3. Concluding remarks are given in Section 4. Histograms illustrating the behavior of $C_{max}$ values of the OSSPs induced by the experimental data and the dimension of the Brauer configuration algebras defined by such OSSPs are given in Appendix A.

2. Preliminaries

This section presents the basic notation and results regarding the OSSP and Brauer configuration algebras [4,5,29,30].

2.1. The Open Shop Scheduling Problem

An instance of the OSSP consists of m machines, $M_1,M_2,\dots ,M_m$ and n jobs, ${\mathcal{J}}_1,{\mathcal{J}}_2,\dots ,{\mathcal{J}}_n$. Each job ${\mathcal{J}}_j$ consists of m independent operations, ${\mathcal{O}}_{ij}$, with $i=1,2,\dots ,m$, the operation ${\mathcal{O}}_{ij}$ of job $J_j$ has to be processed on machine $M_i$, which takes $p_{ij}$ uninterrupted time units. For every job, the order in which its operations have to be processed does not matter. In fact, different jobs may receive different processing orders.

No job is simultaneously processed by two different machines. The optimal makespan is usually denoted by $C_{max}^{*}$. The overall processing time assigned to a machine $M_i$ is called the load of the machine, denoted $L_i={\displaystyle \sum _{j=1}^n}{p}_{ij}$ [4,5].

The maximum job processing time is denoted $P_{max}=\underset{j}{\max }{P}_j={\displaystyle {\displaystyle \sum _{i=1}^m}}{p}_{ij}$ and the maximum machine load is denoted $L_{max}=\underset{i}{\max }{L}_i$.

Since no job can be simultaneously processed by two machines, it holds that $C_{max}\ge P_{max}$ and $C_{max}\ge L_{max}$. Thus, $C_{max}^{*}\ge {\beta }^{*}=\max \{L_{max},P_{max}\}$. It is worth noting that there is always a schedule whose makespan equals the lower bound ${\beta }^{*}$.

For a schedule associated with an OSSP with m machines and n different jobs, the corresponding processing time matrix (PTM), $P=\left(p_{ij}\right)$, is defined. In such a case, the overall processing time of the work matrix is given by the sum $L={\displaystyle {\displaystyle \sum _{i=1}^m}}{L}_i$.

We let $r_j$ ($d_j$) denote the release time (due date) associated with a job J, where $d_j$ is the strict due date.

An objective of some OSSP problems is to minimize the $C_{max}$ value with certain constraints. For instance:

• Jobs must wait for the next machine to be available.
• Machines may be idle within the schedule period.

We recall that the idle time ${\mathfrak{i}}_M$ is a period of time in which a machine, M, is ready and available but is not doing anything productive. Let $\mathfrak{i}$ denote the idle time associated with all the machines, $M_1,M_2,\dots ,M_m$, of a schedule. The waiting time for job ${\mathcal{J}}_j$ is denoted ${\mathfrak{w}}_j$, whereas $\mathfrak{w}$ denotes the total waiting time associated with jobs ${\mathcal{J}}_1,{\mathcal{J}}_2,\dots ,{\mathcal{J}}_n$ of a schedule.

By way of example, the following is a PTM with three machines, $M_1,M_2$, and $M_3$, and two jobs, ${\mathcal{O}}_1$ and ${\mathcal{O}}_2$, for which $L=13$.

$$P=\left(\begin{array}{ccc}2& 3& 1\\ 1& 4& 2\end{array}\right)$$

(2)

For each PTM P, it is possible to define its cumulative matrix $C_P$ (CPTM) whose entries $c_{ij}$ give the time that the jth machine takes to process the ith job. $c_{ij}=-1$ ($c_{ij}=0$) is associated with waiting time (idle time).

The overall joint processing time (OJPT) $C_{max}$ is given by the following:

$$C_{max}=L+\sum _j({\mathfrak{i}}_j+{\mathfrak{w}}_j).$$

(3)

The cumulative matrix of the matrix (2) (whose entries have been organized according to the processing time, i.e., $P=\left(\begin{array}{ccc}1& 4& 2\\ 2& 3& 1\end{array}\right)$) is

$$C_P=\left(\begin{array}{ccccccccc}1& 2& 2& 2& 2& 3& 3& -1& -1\\ 0& 1& 1& 0& 0& 2& 2& 2& 3\end{array}\right)$$

(4)

If $P=\left(p_{ij}\right)$ is an $n\times m$-PTM then the matrix $\sigma =\left({\sigma }_{ij}\right)$ with ${\sigma }_{ij}={\sigma }_i\left(j\right)$, ${\sigma }_i$ is an element of the symmetry group $S_m$ and $1\le i\le n$. We let ${\mathfrak{i}}^{\sigma }$ (${\mathfrak{w}}^{\sigma }$) denote the idle time (waiting time) associated with configuration $\sigma$.

Calderon [36] proposed the minimum bound for a fixed configuration $\sigma$ encoding an OSSP as

$${\mathcal{L}}_{\iota }^{\sigma }={\mathfrak{i}}^{\sigma }+{\mathfrak{w}}^{\sigma }=nN-L$$

(5)

where

• $m_1=L_{max}$,
• $m_2=P_{max}$,
• $N={\beta }^{*}$,
• n is the number of jobs.

For example, the configuration $\sigma =\left(\begin{array}{ccc}1& 3& 2\\ 2& 1& 3\end{array}\right)$ optimizes $\mathfrak{T}$ for the PTM P given in (2) provided that

$$C_P=\left(\begin{array}{ccccccc}1& 3& 3& 2& 2& 2& 2\\ 2& 2& 2& 1& 1& 3& -1\end{array}\right)$$

(6)

In this case,

• ${\mathfrak{w}}^{\sigma }=1$, ${\mathfrak{i}}^{\sigma }=0$,
• $m_1=L_{max}=7$,
• $m_2=P_{max}=7$,
• $N={\beta }^{*}=7$,
• $L=13$,
• $n=2$,
• ${\mathcal{L}}_{\iota }=1$.

Calderon [36] observed that $95\%$ of the matrices that end the process without interruptions have a $C_{max}$ value bounded by ${\mathcal{L}}_{\iota }$. In such a case we say that the PMT satisfies the ${\mathcal{L}}_{\iota }$ condition. If the configuration $\sigma$ satisfies the ${\mathcal{L}}_{\iota }$ condition then we write $\sigma |={\mathcal{L}}_{\iota }$. Matrices obtained via column permutations of the cumulative matrix associated with a PTM are said to be configurations. We let $M_{C_P}$ denote the set of all configurations. Thus, an optimal configuration (giving an optimal $C_{max}$) arises from the configuration space with ${(m!)}^n$ elements.

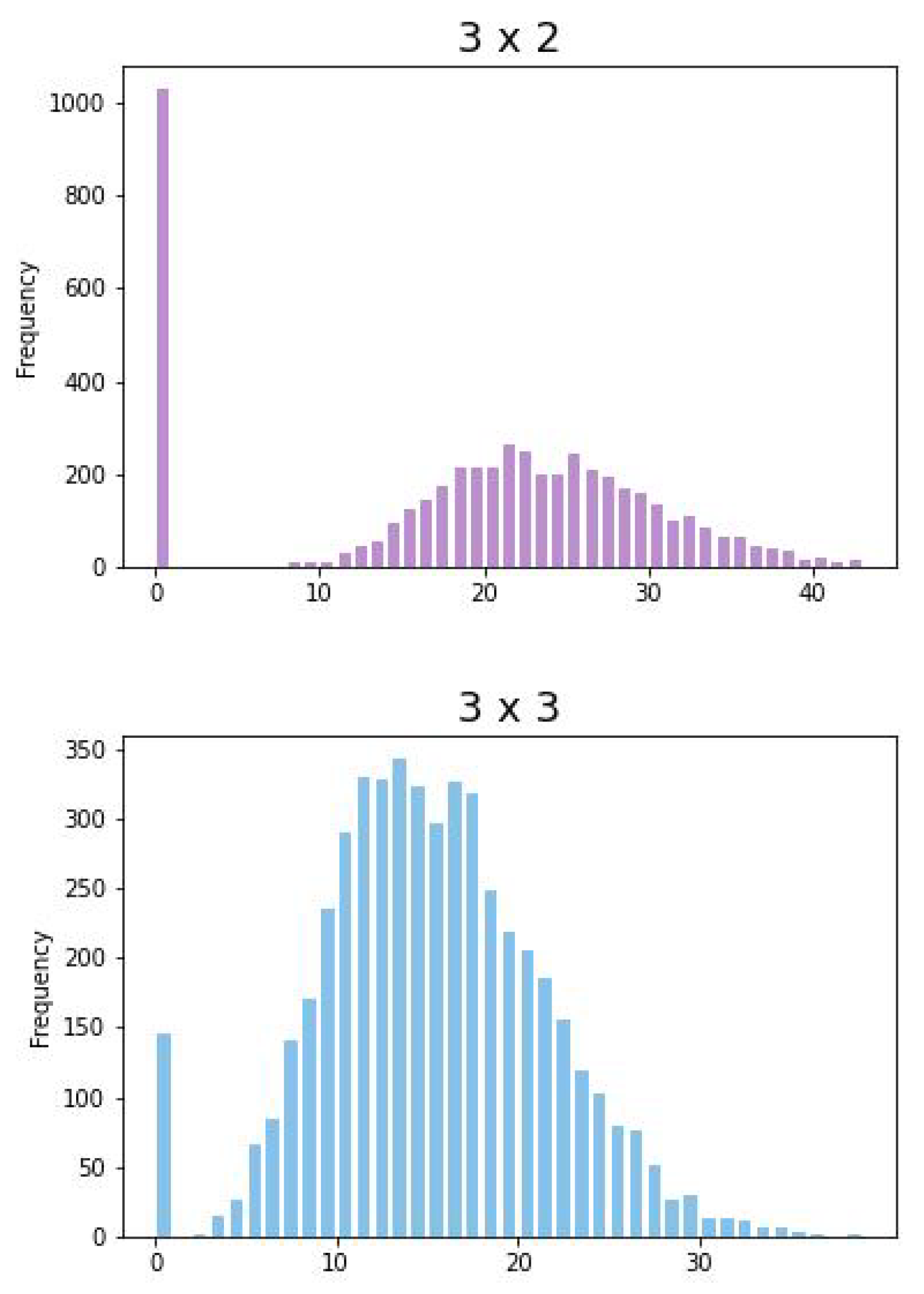
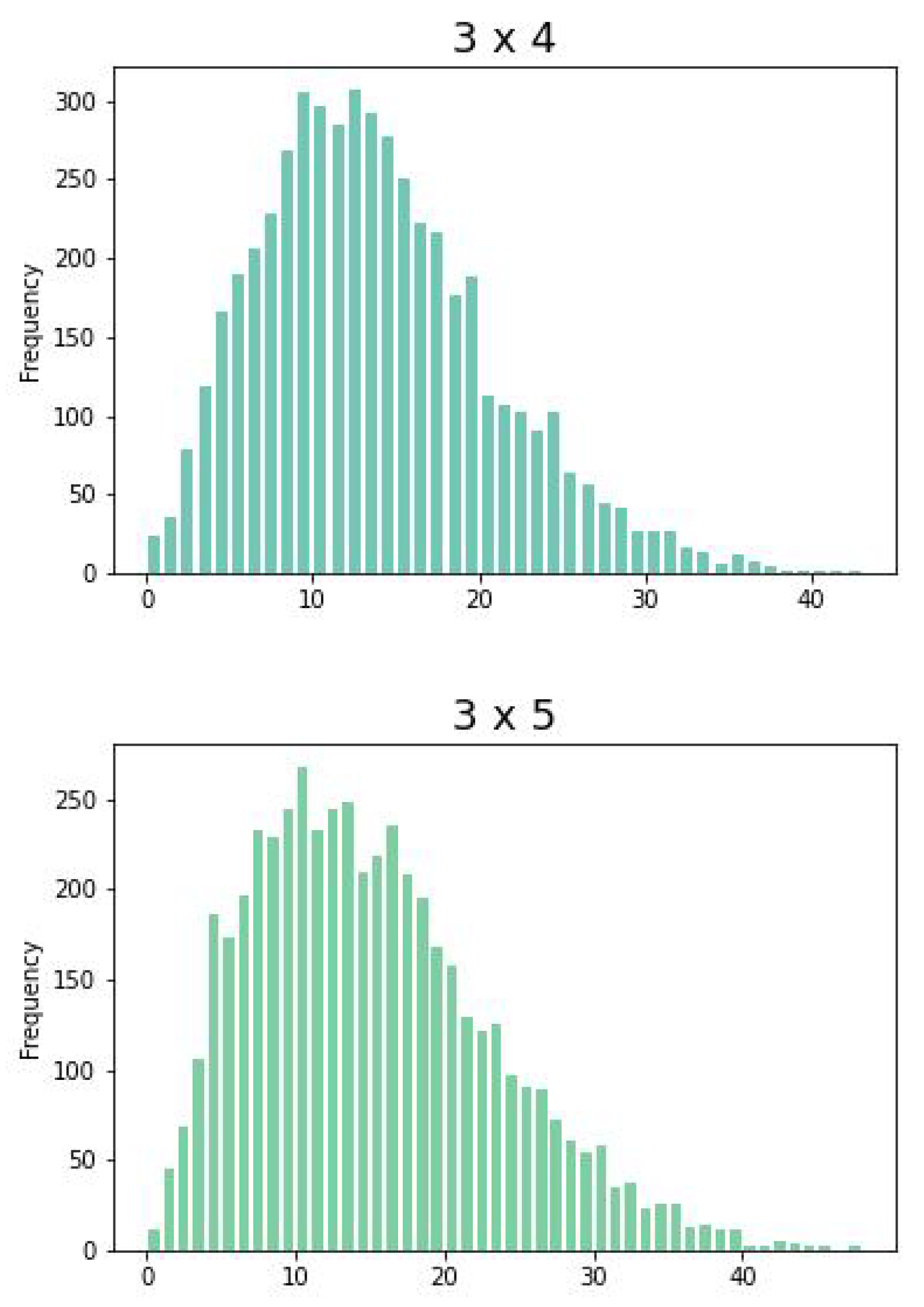
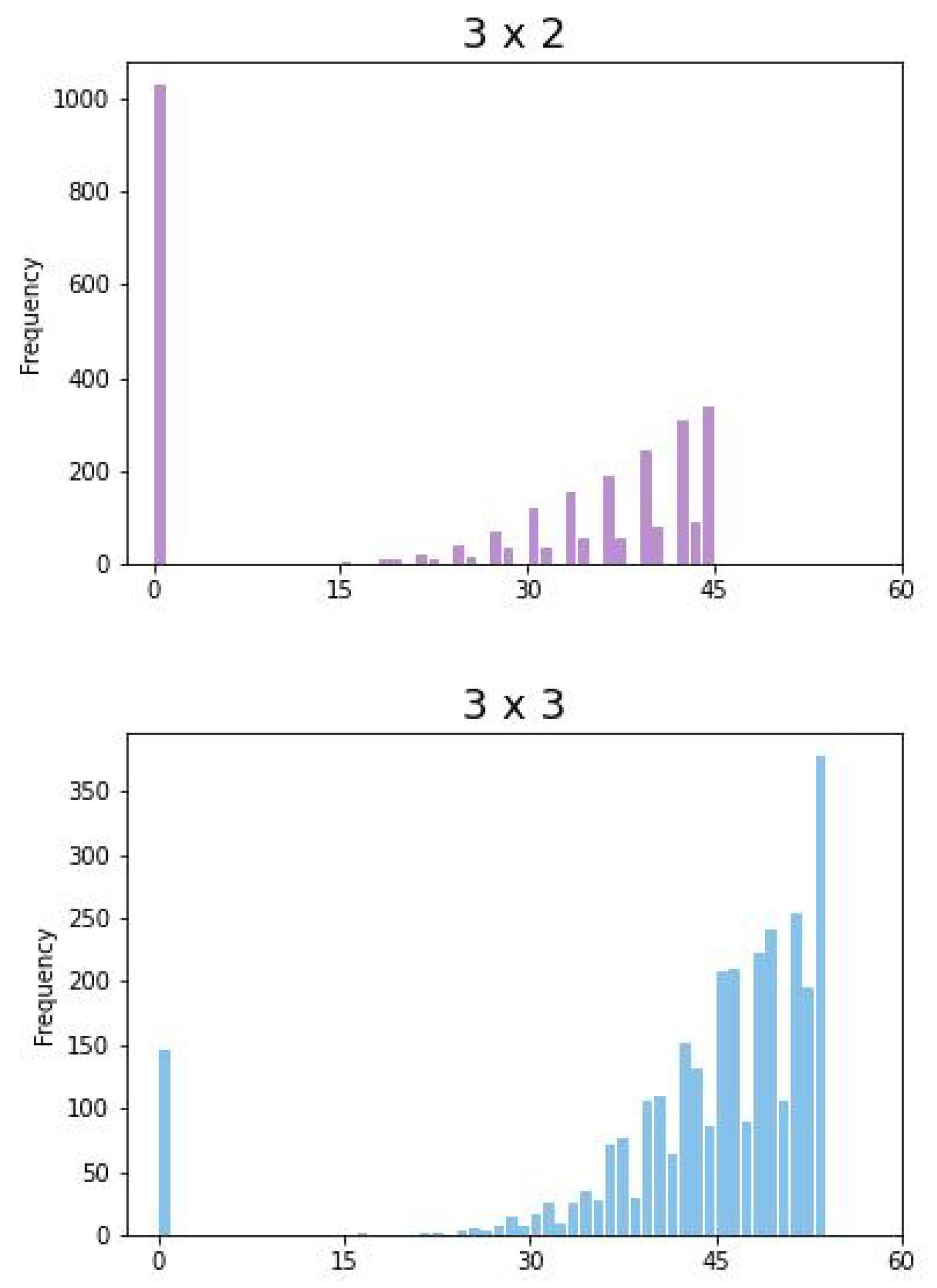
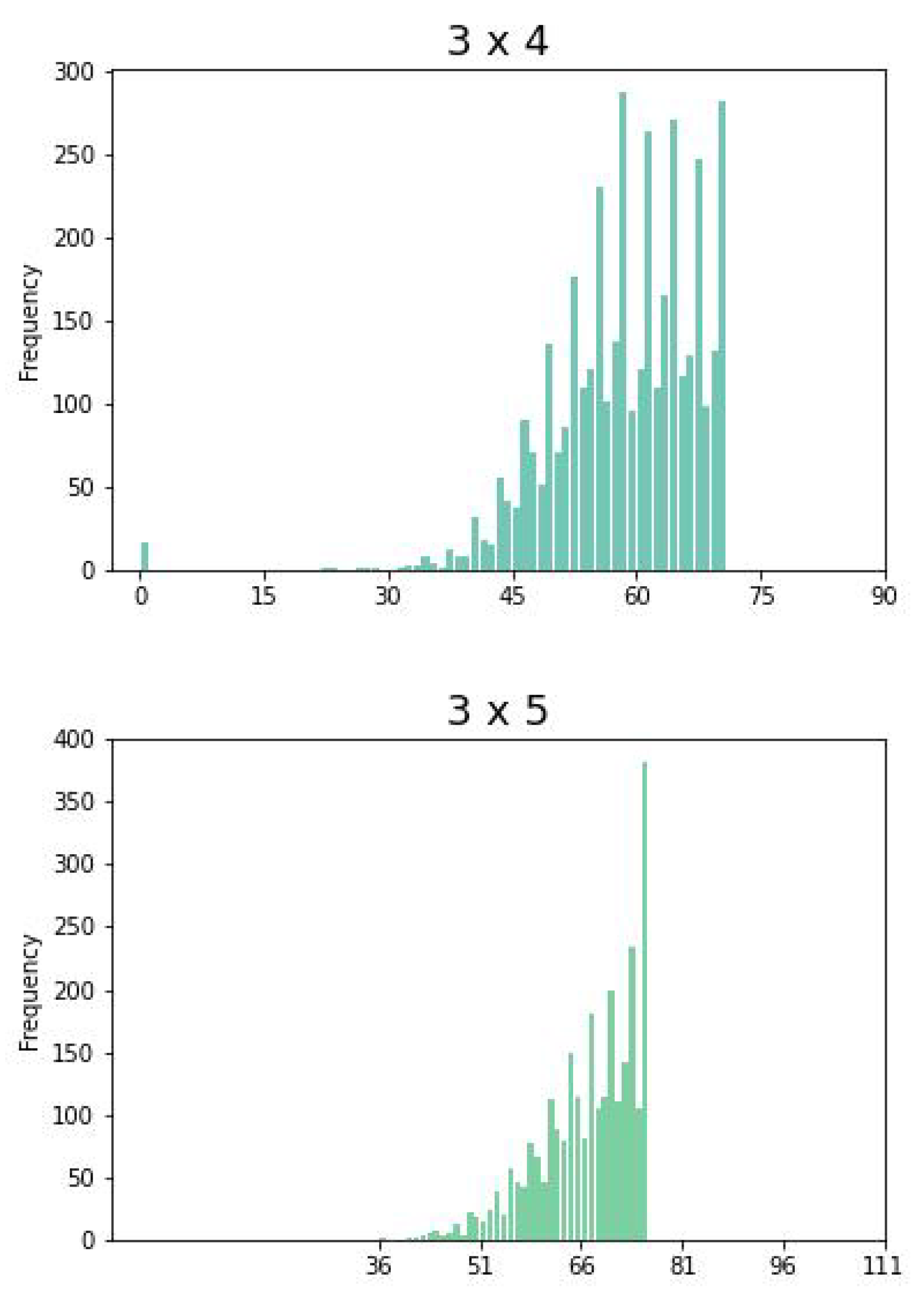
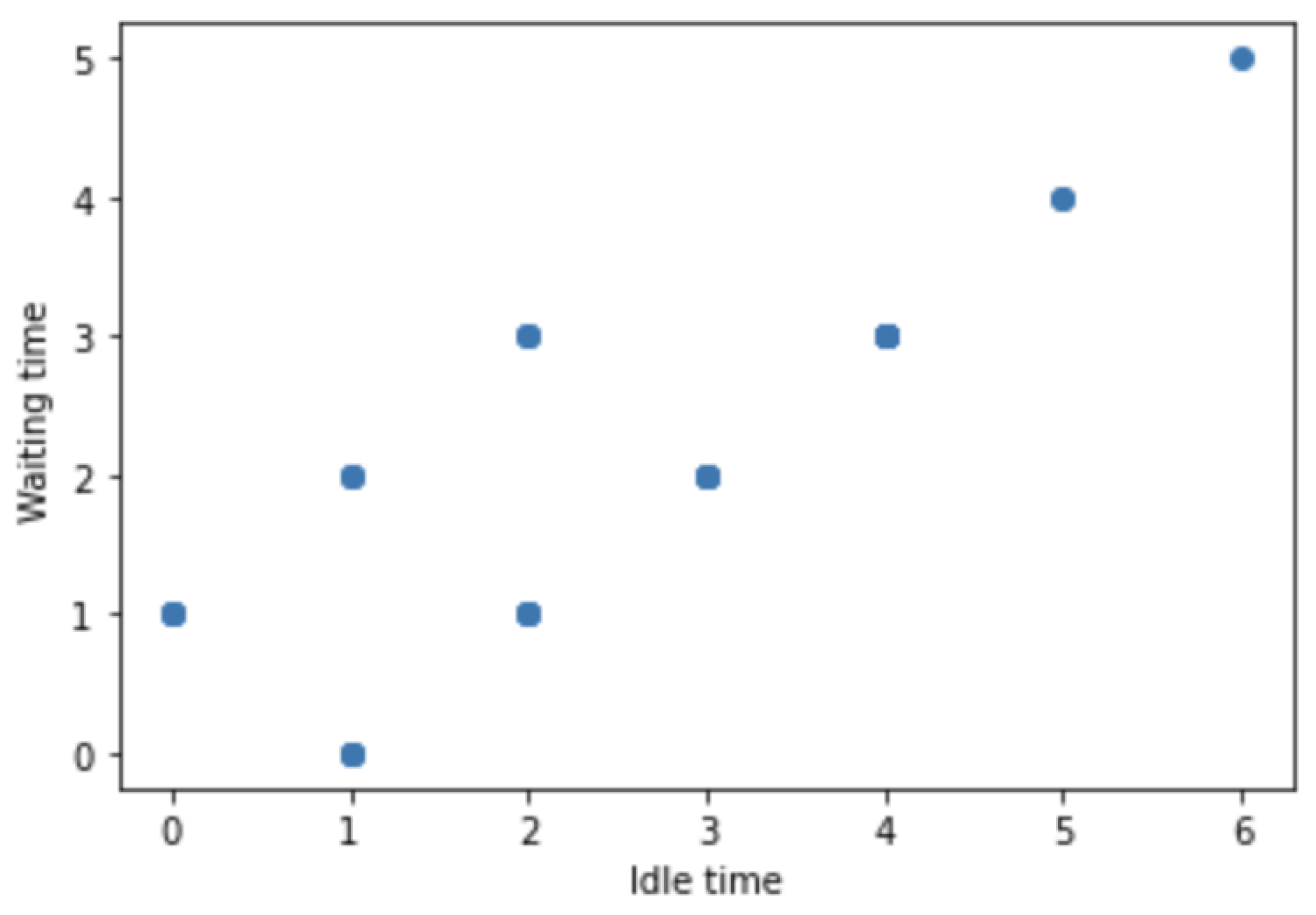
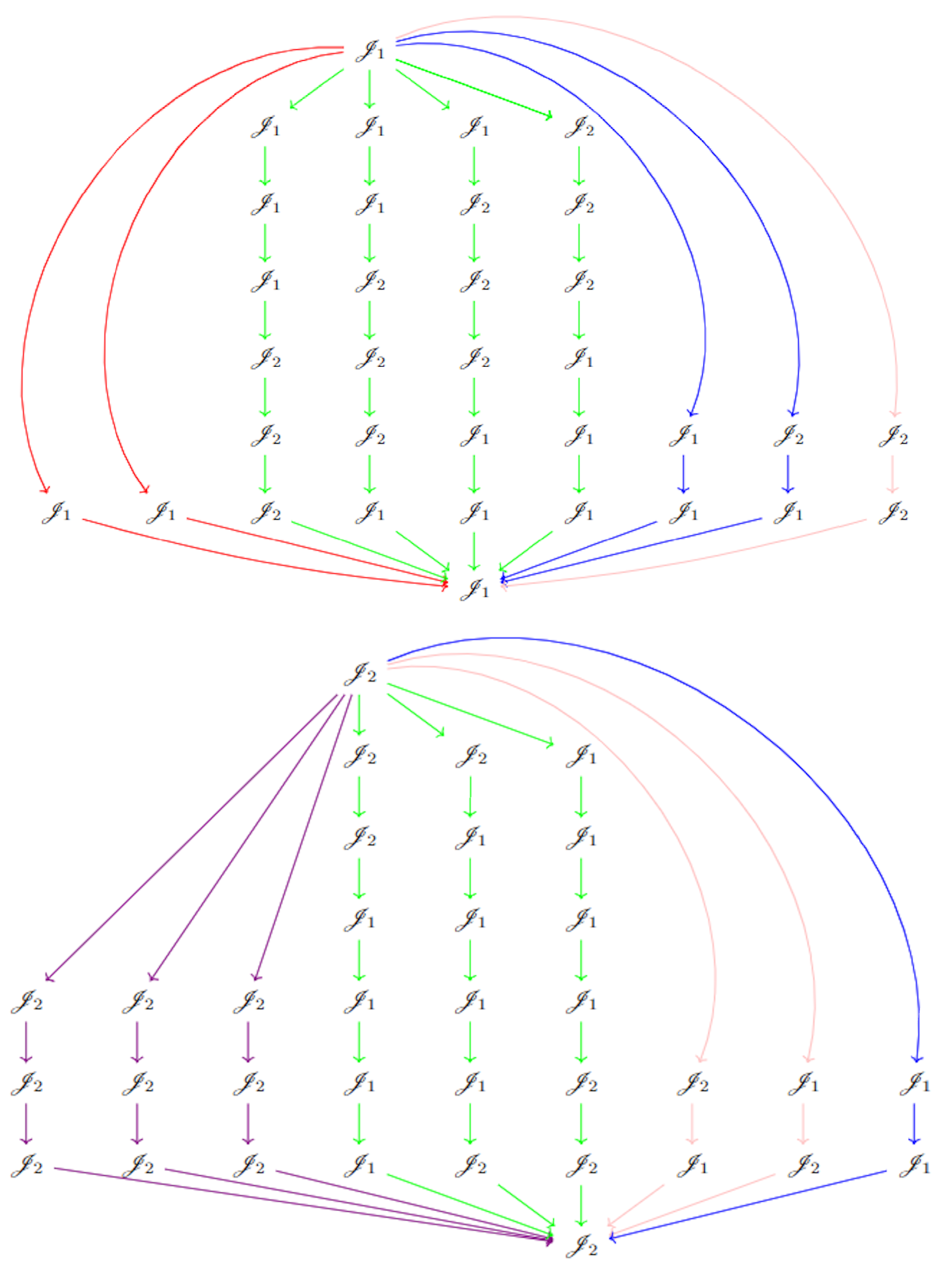
Figure 2 shows idle and waiting times of all different configurations given by the CPTM (6). Note that, the bound $L_{\iota }=1$ is given by the points $(1,0)$ and $(0,1)$. In general, $L_{\iota }$ is given by points on a optimal line ${\mathfrak{L}}^{*}$ of the form $y=-x+\underset{\sigma \in M_{C_P}}{\min }\{{\mathfrak{i}}^{\sigma }+{\mathfrak{w}}^{\sigma }\}$.

Figure 2. Optimal solutions of the OSSP defined by the cumulative matrix (6) are given by the corresponding idle and waiting times.

2.2. Path Algebras

This section presents some definitions and notation regarding path algebras.

A quiver, Q, is a quadruple of the form $Q=(Q_0,Q_1,s,t)$, where $Q_0$ is a set of vertices, $Q_1$ is a set of arrows, and $s,t:Q_1\to Q_0$ are maps that assign the starting vertex (ending vertex) $s\left(\alpha \right)$ ($t\left(\alpha \right)$) of an arrow $\alpha$. For instance, the arrow $\alpha$ denoted in the form $a\stackrel{\alpha }{⟶}b$ has a starting vertex $s\left(\alpha \right)=a$ and an ending vertex $t\left(\alpha \right)=b$.

A path of length $m\ge 1$ with source $a_0$ and target $a_m$ (or more briefly, from $a_0$ to $a_m$) is a sequence $\left(a_0\right|{\alpha }_1,{\alpha }_2,\dots ,{\alpha }_m\left|a_m\right)$ where ${\alpha }_j\in Q_1$ for all $1\le k\le m$, and $t\left({\alpha }_m\right)=a_m$. We let ${\alpha }_1{\alpha }_2\dots {\alpha }_m$ denote such a path. In particular, each point, $x\in Q_0$, has an associated stationary path, $e_x:x\Vert x$, of length 0.

If X is a set of paths in quiver Q then $Length\left(X\right)={\displaystyle {\displaystyle \sum _{x\in X}}}Length\left(x\right)$, where $Length\left(x\right)$ denotes the length of the path x (i.e., the number of arrows contained in x). We let $Length\left(P\right)$ ($Q_l$) denote the length of path P (the set of all paths P for which $Length\left(P\right)=l$).

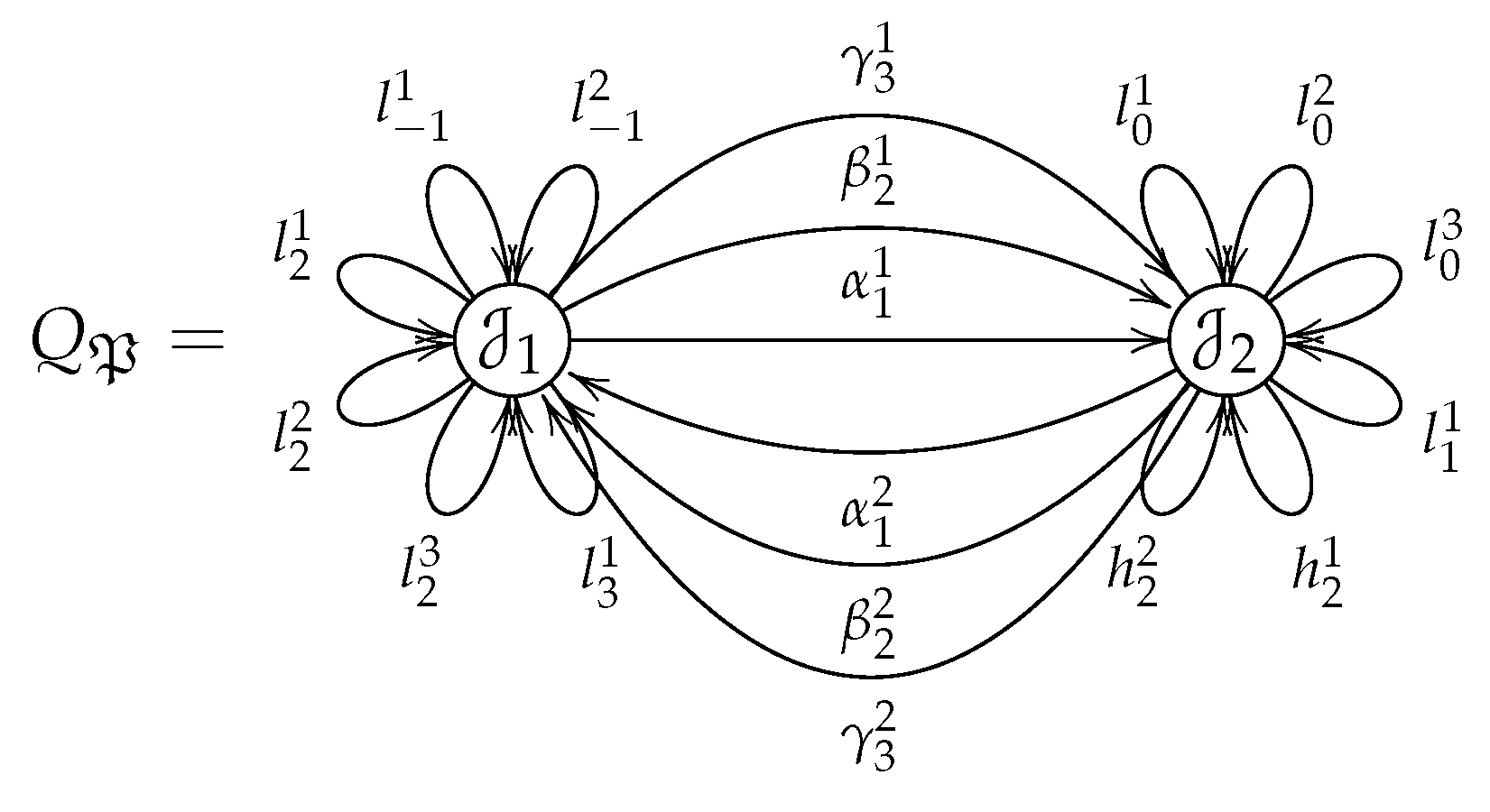
Figure 3 shows an example of a quiver, Q, with three vertices, $s_1,s_2$, and $s_3$, and three arrows, ${\gamma }_1,{\gamma }_2$, and ${\gamma }_3$.

$$\begin{array}{cc}\hfill Q_1& \hfill =\{{\gamma }_1,{\gamma }_2,{\gamma }_3\},\hfill \\ \hfill Q_2& \hfill =\{{\gamma }_1{\gamma }_2,{\gamma }_1{\gamma }_3\},\hfill \\ \hfill Q_i& \hfill =0,\mathrm{for}i\ge 3.\hfill \end{array}$$

(7)

Figure 3. Example of a quiver.

If $\mathbb{F}$ is an algebraically closed field then the path algebra $\mathbb{F}Q$ of Q is the $\mathbb{F}$-algebra whose underlying $\mathbb{F}$-vector space has as its basis the set of all paths of length $l\ge 0$ in Q, such that the product of two basis vectors is given by the usual concatenation of paths. Note that in general, path algebras are noncommutative. Let $Z\left(\mathcal{A}\right)$ denote the center of a path algebra ($x\in Z\left(\mathcal{A}\right)$ if and only if $xy=yx$, for all $y\in \mathcal{A}$). For instance, $\mathcal{B}=\{e_{s_1},e_{s_2},e_{s_3}\}\bigcup \underset{l=1}{\overset{2}{\cup }}{Q}_l$ (where $\{e_{s_1},e_{s_2},e_{s_3}\}$ is a complete set of primitive orthogonal idempotents) is a basis of the algebra $\mathbb{F}Q$, where Q is the quiver given in Figure 3, and $1=e_{s_1}+e_{s_2}+e_{s_3}\in Z\left(kQ\right)$.

Let Q be a finite and connected quiver. The two-sided ideal, $R_Q$, of the path algebra $\mathbb{F}Q$ generated (as an ideal) by the arrows of Q is called the arrow ideal of $\mathbb{F}Q$. A two-sided ideal, I, of $\mathbb{F}Q$ is said to be admissible if there exists $m\ge 2$ such that $R_Q^m\subseteq I\subseteq R_Q^2$.

If I is an admissible ideal of $\mathbb{F}Q$, the pair $(Q,I)$ is said to be a bound quiver. The quotient algebra $\mathbb{F}Q/I$ is said to be the algebra of the bound quiver $(Q,I)$ or, simply, a bound quiver algebra.

Let Q be a quiver. A relation in Q with coefficients in $\mathbb{F}$ is an $\mathbb{F}$-linear combination of paths of at least 2 in length, and having the same source and target. Thus, a relation $\mathfrak{p}$ is an element of $\mathbb{F}Q$ such that

$$\mathfrak{p}=\sum _{i=1}^m{\lambda }_i{\mathfrak{p}}_i$$

(8)

where the ${\lambda }_i$ are scalars (not all zero) and the ${\mathfrak{p}}_i$ are paths in Q of length at least 2 such that, if $i\ne j$, then the source (or the target, respectively) of ${\mathfrak{p}}_i$ coincides with that of ${\mathfrak{p}}_j$.

If $m=1$, the preceding relation is called a zero relation or a monomial relation. If it is of the form ${\mathfrak{p}}_1-{\mathfrak{p}}_2$ (where ${\mathfrak{p}}_1$ and ${\mathfrak{p}}_2$ are two paths), it is called a commutativity relation.

If ${\left({\mathfrak{p}}_j\right)}_{j\in J}$ is a set of relations for a quiver Q such that the ideal they generate $⟨{\mathfrak{p}}_j\mid j\in J⟩$ is admissible, we say that the quiver Q is bound by the relation ${\left({\mathfrak{p}}_j\right)}_{j\in J}$ or by the relations ${\mathfrak{p}}_j=0$ [29,30].

Henceforth, we let $\mathrm{rad}\mathsf{\Lambda }$ denote the radical of a path algebra $\mathsf{\Lambda }=\mathbb{F}Q$, which is the intersection of all maximal ideals. In fact, if I is an admissible ideal of $\mathsf{\Lambda }$, it holds that $\mathrm{rad}(\mathbb{F}Q/I)=R_Q/I$.

A module, M, over a bound quiver algebra is said to be decomposable, if there are nonzero modules $M_1$ and $M_2$ such that $M=M_1\oplus M_2$. Otherwise, M is said to be indecomposable.

Each vertex x in quiver Q has an associated indecomposable projective module, $P_x$, over a bound quiver algebra, ${\mathsf{\Lambda }}_Q=\mathbb{F}Q/I$, generated by all the paths in Q with x as its starting point. In particular, ${\mathsf{\Lambda }}_Q={\displaystyle \underset{x\in Q_0}{\oplus }}{P}_x$.

As an example, $I=⟨{\gamma }_1{\gamma }_3⟩$ is an admissible ideal of the algebra ${\mathsf{\Lambda }}_Q$ defined by the quiver shown in Figure 3. The algebra ${\mathsf{\Lambda }}_Q=\mathbb{F}Q/I$ is generated by the basis $\{e_{s_1}+I,e_{s_2}+I,e_{s_3}+I,{\gamma }_1+I,{\gamma }_2+I,{\gamma }_3+I,{\gamma }_1{\gamma }_2+I\}$. Thus, ${\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_Q=7$.

2.3. Multisets and Brauer Configuration Algebras

A multiset is an ordered pair $(M,f)$ where M is a set and f is a function from M to the nonnegative integers; for each $m\in M$, $f\left(m\right)$ is said to be the multiplicity of m [37].

If M is a finite set, say $\{m_1,m_2,\dots ,m_r\}$, then a multiset $(M,f)$ can be written as a word with the form described by identity (9).

$$(M,f)=\{m_1^{f\left(m_1\right)}{m}_2^{f\left(m_2\right)}\dots m_r^{f\left(m_r\right)}\}.$$

(9)

Multisets are helpful tools in the theory of partitions, where they are used to obtain formulas for restricted partitions via inversions.

If $(M_1,f_1)$ and $(M_2,f_2)$ are multisets then

$$\begin{array}{cc}\hfill (M_3,h)& =(M_1,f_1)\cup (M_2,f_2)=\{[x,h\left(x\right)]\mid x\in M_1\cup M_2=M_3,h\left(x\right)=\max \{f_1\left(x\right),f_2\left(x\right)\}\}\hfill \\ \hfill (M_3,i)& =(M_1,f_1)+(M_2,f_2)=\{[x,i\left(x\right)]\mid x\in M_1\cup M_2,i\left(x\right)=f_1\left(x\right)+f_2\left(x\right)\}\}\hfill \\ \hfill (M_3,s)& =(M_1,f_1)\cap (M_2,f_2)=\{[x,s\left(x\right)]\mid x\in M_1\cup M_2,s\left(x\right)=\min \{f_1\left(x\right),f_2\left(x\right)\}\}.\hfill \end{array}$$

(10)

The message $m\left(\mathfrak{V}\right)$ associated with a collection of multisets

$$\mathfrak{V}=\{({\mathfrak{V}}_1,g_1),({\mathfrak{V}}_2,g_2),\dots ,({\mathfrak{V}}_n,g_n)\}$$

(11)

is given by the usual word concatenation defined by the Formula (12)

$$m\left(\mathfrak{V}\right)=w\left(({\mathfrak{V}}_1,g_1)\right)w\left(({\mathfrak{V}}_2,g_2)\right)\dots w\left(({\mathfrak{V}}_n,g_n)\right)$$

(12)

where for h fixed, the word $w\left(({\mathfrak{V}}_h,g_h)\right)$ is given by the identity (13)

$$w\left(({\mathfrak{V}}_h,g_h)\right)={\mathfrak{v}}_{(h,1)}^{g_h\left({\mathfrak{v}}_{(h,1)}\right)}{\mathfrak{v}}_{(h,2)}^{g_h\left({\mathfrak{v}}_{(h,2)}\right)}\dots {\mathfrak{v}}_{(h,t_h)}^{g_h\left({\mathfrak{v}}_{(h,t_h)}\right)}$$

(13)

If an element ${\mathfrak{v}}_{(h,j)}\in {\displaystyle \bigcap _{z=1}^r}({\mathfrak{V}}_{h_z},g_{h_z})\subseteq {\displaystyle \sum _{z=1}^n}({\mathfrak{V}}_z,g_z)$ then its valency denoted $val\left({\mathfrak{v}}_{(h,j)}\right)$ is given by the Formula (14) [29,31].

$$\sum _{z=1}^r{g}_{h_z}\left({\mathfrak{v}}_{(h,j)}\right).$$

(14)

Green and Schroll [29] defined Brauer configurations which are oriented systems of multisets with the form

$$\mathfrak{V}=({\mathfrak{V}}_0=\bigcup _{h=1}^n{\mathfrak{V}}_h;\{({\mathfrak{V}}_1,g_1),({\mathfrak{V}}_2,g_2),\dots ,({\mathfrak{V}}_n,g_n)\};\nu ;\mathcal{O})$$

(15)

where $\nu$ is a multiplicity map $\nu :{\mathfrak{V}}_0={\displaystyle \bigcup _{h=1}^n}{\mathfrak{V}}_h\to \mathbb{N}\times \mathbb{N}$ such that $\nu \left(\mathfrak{v}\right)=\left(val\right(\mathfrak{v}),\nu (\mathfrak{v}\left)\right)$, with $\nu \left(\mathfrak{v}\right)\ge 1$, we let ${\nu }_{\mathfrak{v}}$ denote the product $\nu \left(\mathfrak{v}\right)val\left(\mathfrak{v}\right)$. Henceforth, if no confusion arises, we will omit the symbol $g_h$ to denote a multiset $({\mathfrak{V}}_h,g_h)$ associated with a Brauer configuration $\mathfrak{V}$.

Elements $\mathfrak{v}\in {\mathfrak{V}}_0$ (multisets ${\mathfrak{V}}_h\in \{{\mathfrak{V}}_1,\dots ,{\mathfrak{V}}_n\}$) were named vertices (polygons) by Green and Schroll [29]. If ${\mathfrak{v}}_{(h,j)}\in ({\mathfrak{V}}_h,g_h)$ is such that ${\nu }_{{\mathfrak{v}}_{(h,j)}}=1$ (${\nu }_{{\mathfrak{v}}_{(h,j)}}>1$) then the vertex ${\mathfrak{v}}_{(h,j)}$ is said to be truncated (non-truncated). A Brauer configuration is reduced if it has not truncated vertices.

In the theory of Brauer configuration algebras, the collection ${\left\{{\mathfrak{V}}_{h_z}\right\}}_{1\le z\le r}$ of all polygons containing a fixed vertex ${\mathfrak{v}}_{(h,j})$ is endowed with a linear order <. Thus, there is a minimum ${\mathfrak{V}}_{h_1}$ polygon and a maximum polygon ${\mathfrak{V}}_{h_r}$. In such a case, it holds that

$${\mathfrak{V}}_{h_z}^{\left(1\right)}<{\mathfrak{V}}_{h_z}^{\left(2\right)}<\dots <{\mathfrak{V}}_{h_z}^{\left(g_{h_z}\left({\mathfrak{v}}_{(h,j)}\right)\right)}={\mathfrak{V}}_{h_z}^{\left[g_{h_z}\left({\mathfrak{v}}_{(h,j)}\right)\right]}.$$

(16)

where ${\mathfrak{V}}_{h_z}^{\left(i\right)}$ denotes the ith copy of ${\mathfrak{V}}_{h_z}$.

Generally, we have that

$${\mathfrak{V}}_{h_1}^{[g_{h_1}({\mathfrak{v}}_{(h,j)})]}<{\mathfrak{V}}_{h_2}^{[g_{h_2}({\mathfrak{v}}_{(h,j)})]}<\dots <{\mathfrak{V}}_{h_r}^{[g_{h_r}({\mathfrak{v}}_{(h,j)})]}.$$

(17)

A chain (17) is a successor sequence associated with the vertex ${\mathfrak{v}}_{(h,j)}$.

An orientation $\mathcal{O}$ of a Brauer configuration is obtained by adding to each successor sequence a new relation ${\mathfrak{V}}_{h_r}<{\mathfrak{V}}_{h_1}$. Thus, it is obtained a circular ordering, which define equivalent orderings of the form

$${\mathfrak{V}}_{h_i}^{[g_h({\mathfrak{v}}_{(h,t_j)})]}<\dots <{\mathfrak{V}}_{h_r}^{[g_h({\mathfrak{v}}_{(h,t_j)})]}<{\mathfrak{V}}_{h_1}^{[g_h({\mathfrak{v}}_{(h,t_j)})]}<\dots <{\mathfrak{V}}_{h_{i-1}}^{[g_h({\mathfrak{v}}_{(h,t_j)})]}.$$

(18)

Remark 1.

Henceforth, we assume that relations between the same polygons in different circular orderings are the same [31].

If $\mathfrak{U}=({\mathfrak{U}}_0;\{{\mathfrak{U}}_1,{\mathfrak{U}}_2,\dots ,{\mathfrak{U}}_n\};{\nu }^{\mathfrak{U}};{\mathcal{O}}^{\mathfrak{U}})$, and $\mathfrak{V}=({\mathfrak{V}}_0;\{{\mathfrak{V}}_1,{\mathfrak{V}}_2,\dots ,{\mathfrak{V}}_m\};{\nu }^{\mathfrak{V}};{\mathcal{O}}^{\mathfrak{V}})$ are Brauer configurations then the Brauer configuration

$$\mathcal{P}=\mathfrak{U}+\mathfrak{V}=({\mathfrak{U}}_0+{\mathfrak{V}}_0,\{{\mathfrak{U}}_1,\dots ,{\mathfrak{U}}_n,{\mathfrak{V}}_1,{\mathfrak{V}}_2,\dots ,{\mathfrak{V}}_m\},{\nu }^{\mathfrak{U}+\mathfrak{V}},{\mathcal{O}}^{\mathfrak{U}+\mathfrak{V}})$$

(19)

such that

• ${\mathfrak{U}}_0\cap {\mathfrak{V}}_0=⌀$
• ${\nu }^{\mathfrak{U}+\mathfrak{V}}\left(x\right)=\left\{\begin{array}{cc}\hfill {\nu }^{\mathfrak{U}}\left(x\right),\hfill & \hfill \mathrm{if}x\in \mathfrak{U},\hfill \\ \hfill {\nu }^{\mathfrak{V}}\left(x\right),\hfill & \hfill \mathrm{if}x\in \mathfrak{V},\hfill \end{array}\right.$
• ${\mathcal{O}}^{\mathfrak{U}+\mathfrak{V}}={\mathcal{O}}^{\mathfrak{U}}+{\mathcal{O}}^{\mathfrak{V}}$,

is said to be disconnected, otherwise $\mathcal{P}$ is connected.

Brauer Configuration Algebras

Green and Schroll [29] named Brauer configuration algebras to those bound quiver algebras of type $\mathbb{F}{Q}_{\mathfrak{U}}/I_{\mathfrak{U}}$ defined by a Brauer configuration $\mathfrak{U}$ (see Remark 1). In such a case the polygons in $\mathfrak{U}$ give the set of vertices $Q_0$ of the quiver $Q_{\mathfrak{U}}$, whereas its arrows are defined by coverings in completed successor sequences [29,30,31].

$Q_{\mathfrak{U}}$ is bounded by relations of the following types:

• Identification of special cycles defined by vertices in the same polygon.
• Multiplication of each special cycle by its first arrow.
• If it exists, multiplication of arrows in different special cycles.

Henceforth, we will assume the notations Q, I, and $\mathsf{\Lambda }$ for quivers, admissible ideals and Brauer configuration algebras defined by a fixed Brauer configuration $\mathfrak{U}$.

Remark 2.

Green and Schroll [29] proved that Brauer configuration algebras are indecomposable as algebras if the corresponding Brauer configurations are connected. Furthermore, they are multiserial and symmetric. Particularly, they established that the underlying Brauer configuration’s nontruncated vertices give the indecomposable projective modules structure over a Brauer configuration algebra. For instance, the number of such vertices in a fixed polygon gives the number of summands in the radical and heart of the corresponding indecomposable projective module. They also introduced the formula (20) for the dimension of a Brauer configuration algebra ${\mathsf{\Lambda }}_{\mathfrak{V}}$ induced by a Brauer configuration $\mathfrak{V}$ with $|{\mathfrak{V}}_1|$ polygons.

$$\frac{1}{2}{\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_{\mathfrak{V}}-\left|{\mathfrak{V}}_1\right|=\sum _{i\in {\mathfrak{V}}_0}\frac{t_{{\nu }_i-1}}{\mu \left(i\right)},$$

(20)

where $t_j$ denotes the jth triangular number and ${\nu }_i=val\left(i\right)\mu \left(i\right)$ (see (15)).

The following is an interpretation of the formula introduced by Sierra [35] to obtain the dimension of the center of a Brauer configuration algebra ${\mathsf{\Lambda }}_{\mathfrak{V}}$.

$$\begin{array}{cc}\hfill {\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{\mathfrak{V}}\right)& \hfill =1+\sum _{i\in {\mathfrak{V}}_0}\mu \left(i\right)+|{\mathfrak{V}}_1|-|{\mathfrak{V}}_0|+\#\left(Loops{Q}_{\mathfrak{V}}\right)-\left|{\mathcal{C}}_{\mathfrak{V}}\right|,\hfill \end{array}$$

(21)

where ${\mathcal{C}}_{\mathfrak{V}}=\{i\in {\mathfrak{V}}_0\mid val\left(i\right)=1,\mathrm{and}{\nu }_i=t>1\}$.

3. Main Results

This section gives dimensions of BCAs associated with PTMs in terms of their overall joint processing time, waiting time, and idle time. In particular, the dimension of the centers of BCAs associated with PTMs satisfying the ${\mathcal{L}}_{\iota }$ condition is given.

If P is a PTM with m machines, $M=\{M_1,M_2,\dots ,M_m\}$, and n jobs, $\mathcal{J}=\{{\mathcal{J}}_1,{\mathcal{J}}_2,\dots ,{\mathcal{J}}_n\}$, and $C_P$ its corresponding cumulative matrix, then $C_P$ induces a Brauer configuration $\mathfrak{P}=({\mathfrak{P}}_0,{\mathfrak{P}}_1,{\nu }^{\mathfrak{p}},{\mathcal{O}}^{\mathfrak{p}})$, where

• ${\mathfrak{P}}_0$ is given by the set of entries of the cumulative matrix $C_P$, i.e., it consists of times $p_{ij}$ and the integers 0 and $-1$ associated with idle and waiting times,
• entries of each row $R_j\in C_P$ give rise to a polygon ${\mathcal{P}}_j\in {\mathfrak{J}}_1$, $1\le j\le n$,
• ${\nu }^{\mathfrak{p}}\left(\alpha \right)=\left\{\begin{array}{cc}(1,2),\hfill & \mathrm{if}val\left(\alpha \right)=1,\hfill \\ \left(val\right(\alpha ),1),\hfill & \mathrm{otherwise},\hfill \end{array}\right.$
• relations of the form $R_i<R_j$, if $i<j$, define the orientation ${\mathcal{O}}^{\mathfrak{p}}$.

As an example, the Brauer configuration $\mathfrak{P}=({\mathfrak{P}}_0,{\mathfrak{P}}_1,{\nu }^{\mathfrak{p}},{\mathcal{O}}^{\mathfrak{p}})$ associated with the CPTM (6) is defined as follows:

$$\begin{array}{cc}\hfill {\mathfrak{P}}_0& =\{-1,0,1,2,3\},\hfill \\ \hfill {\mathfrak{P}}_1& =\{{\mathfrak{J}}_1=\{1,2,2,2,2,3,3,-1,-1\},{\mathfrak{J}}_2=\{0,1,1,0,0,2,2,2,3\}\},\hfill \\ \hfill {\nu }^{\mathfrak{p}}(-1)& =(2,1),{\nu }^{\mathfrak{p}}\left(0\right)=(3,1),{\nu }^{\mathfrak{p}}\left(1\right)=(3,1),{\nu }^{\mathfrak{p}}\left(2\right)=(7,1),{\nu }^{\mathfrak{p}}\left(3\right)=(3,1)\hfill \end{array}$$

(22)

The following are successor sequences associated with vertices $-1,0,1,2,3$:

$$\begin{array}{cc}\hfill S_{-1}& ={\mathcal{J}}_1<{\mathcal{J}}_1<{\mathcal{J}}_1.\hfill \\ \hfill S_0& ={\mathcal{J}}_2<{\mathcal{J}}_2<{\mathcal{J}}_2<{\mathcal{J}}_2.\hfill \\ \hfill S_1& ={\mathcal{J}}_1<{\mathcal{J}}_2<{\mathcal{J}}_2<{\mathcal{J}}_1.\hfill \\ \hfill S_2& ={\mathcal{J}}_1<{\mathcal{J}}_1<{\mathcal{J}}_1<{\mathcal{J}}_1<{\mathcal{J}}_2<{\mathcal{J}}_2<{\mathcal{J}}_2<{\mathcal{J}}_1.\hfill \\ \hfill S_3& ={\mathcal{J}}_1<{\mathcal{J}}_1<{\mathcal{J}}_2<{\mathcal{J}}_1.\hfill \end{array}$$

(23)

Figure 4 shows the Brauer quiver associated with the Brauer configuration $\mathfrak{P}$.

Figure 4. Brauer quiver induced by the Brauer configuration (22).

The following are special cycles $C_{i,j}$ associated with vertices $i=-1,0,1,2,3$:

• $C_{-\mathrm{1,1}}=l_{-1}^1{l}_{-1}^2$, $C_{-\mathrm{1,2}}=l_{-1}^2{l}_{-1}^1$.
• $C_{\mathrm{0,1}}=l_0^1{l}_0^2{l}_0^3$, $C_{\mathrm{0,2}}=l_0^2{l}_0^3{l}_0^1$, $C_{\mathrm{0,3}}=l_0^3{l}_0^1{l}_0^2$.
• $C_{\mathrm{1,1}}={\alpha }_1^1{l}_1^1{\alpha }_1^2$, $C_{\mathrm{1,2}}=l_1^1{\alpha }_1^2{\alpha }_1^1$, $C_{\mathrm{1,3}}={\alpha }_1^2{\alpha }_1^1{l}_1^1$.
• $C_{\mathrm{2,1}}=l_2^1{l}_2^2{l}_2^3{\beta }_2^1{h}_2^1{h}_2^2{\beta }_2^2$, $C_{\mathrm{2,2}}=l_2^2{l}_2^3{\beta }_2^1{h}_2^1{h}_2^2{\beta }_2^2{l}_2^1$, $C_{\mathrm{2,3}}=l_2^3{\beta }_2^1{h}_2^1{h}_2^2{\beta }_2^2{l}_2^1{l}_2^2$,
  $C_{\mathrm{2,4}}={\beta }_2^1{h}_2^1{h}_2^2{\beta }_2^2{l}_2^1{l}_2^2{l}_2^3$, $C_{\mathrm{2,5}}=h_2^1{h}_2^2{\beta }_2^2{l}_2^1{l}_2^2{l}_2^3{\beta }_2^1$, $C_{\mathrm{2,6}}=h_2^2{\beta }_2^2{l}_2^1{l}_2^2{l}_2^3{\beta }_2^1{h}_2^1$,
  $C_{\mathrm{2,7}}={\beta }_2^2{l}_2^1{l}_2^2{l}_2^3{\beta }_2^1{h}_2^1{h}_2^2$.
• $C_{\mathrm{3,1}}=l_3^1{\gamma }_3^1{\gamma }_3^2$, $C_{\mathrm{3,2}}={\gamma }_3^1{\gamma }_3^2{l}_3^1$, $C_{\mathrm{3,3}}={\gamma }_3^2{l}_3^1{\gamma }_3^1$.

The admissible ideal $I_{\mathfrak{P}}=I$ is generated by the following set of relations:

• $C_{-1,j_1}\sim C_{2,j_2}\sim C_{3,j_3}$, $C_{0,j_4}\sim C_{1,j_5}\sim C_{2,j_2}$, for all possible values of $j_h$, $h=1,\dots ,5$.
• $C_{i,j}f$, where f is the first arrow of a cycle $C_{i,j}$, $i\in {\mathfrak{P}}_0$ for all possible values of j.
• Relations of type ${\sigma }_j^i{\delta }_l^k$, for all possible values of $i,j,k,$ and l with $\sigma \ne \delta$, $\sigma ,\delta \in \{\alpha ,\beta ,\gamma \}$.
• ${\alpha }_1^1{\alpha }_1^2$, ${\beta }_2^2{\beta }_2^1$, ${\beta }_2^2{\beta }_2^1$, ${\gamma }_3^2{\gamma }_3^1$.
• ${\alpha }_1^j{l}_i^{j^{\prime }}$, $i\ne 1$$l_n^m{\alpha }_1^j$, $n\ne 1$, for all possible values of $j,j^{\prime },$ and m.
• ${\beta }_2^j{l}_i^{j^{\prime }}$, $i\ne 2$$l_n^m{\beta }_2^j$, $n\ne 2$, for all possible values of $j,j^{\prime },$ and m.
• ${\gamma }_3^j{l}_i^{j^{\prime }}$, $i\ne 3$$l_n^m{\gamma }_3^j$, $n\ne 3$, for all possible values of $j,j^{\prime },$ and m.
• $l_j^i{l}_{j^{\prime }}^{i^{\prime }}$, $j\ne j^{\prime }$, ${\left(l_j^i\right)}^2$ for all possible values of $i,i^{\prime },j$, and $j^{\prime }$.
• $l_j^i{h}_n^m$, ${\left(h_n^m\right)}^2$, $h_n^m{\sigma }_j^i$, ${\sigma }_j^i{h}_n^m$, $\sigma \in \{\alpha ,\gamma \}$, for all possible values of $i,j,m,$ and n.
• ${\delta }_j^{i+1}{\delta }_j^i$, $j\ne -1$, $\delta \in \{l,h\}$.

Figure 5 shows indecomposable projective modules $P_{{\mathcal{J}}_1}$ and $P_{{\mathcal{J}}_2}$ over the BCA ${\mathsf{\Lambda }}_{\mathfrak{P}}=\mathbb{F}{Q}_{\mathfrak{P}}/I_{\mathfrak{P}}$.

Figure 5. Indecomposable projective modules $P_{{\mathcal{J}}_1}$ and $P_{{\mathcal{J}}_2}$ associated with polygons ${\mathcal{J}}_1$ and ${\mathcal{J}}_2$ (see Brauer configuration (22)). The colors denote uniserial modules given by vertices $-1$ (red), 0 (violet), 1 (pink), 2 (green), and 3 (blue).

Theorem 1.

Any BCA ${\mathsf{\Lambda }}_{\mathfrak{P}}$ associated with an OSSP given by a CPTM $C_P$ is connected and indecomposable as an algebra.

Proof. 

Since, by definition, the Brauer configuration $\mathfrak{P}$ induced by the matrix $C_P$ does not have truncated vertices, the result follows as a consequence of Remark 2, bearing in mind that all the jobs share the same set of machines. QED. □

The following results give formulas for the dimension of a BCA associated with an OSSP.

Theorem 2.

If ${\mathsf{\Lambda }}_{\mathfrak{P}}$ is the BCA associated with an OSSP given by a CPTM $C_P$ with m jobs and n machines then the dimension ${\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_{\mathfrak{P}}$ is given by the following identity:

$$\begin{array}{cc}\hfill {\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_{\mathfrak{P}}& =2m+\sum _{j=1}^k[{(\sum _{i=1}^m{p}_{ij})}^2-\sum _{j=1}^m{p}_{ij}]+\sum _{j=k+1}^n[2{(\sum _{i=1}^m{p}_{ij})}^2-\sum _{j=1}^m{p}_{ij}]+{\mathfrak{h}}_{iw}.\hfill \\ \hfill {\mathfrak{h}}_{iw}& ={\mathfrak{w}}^2\mu (-1)+{\mathfrak{i}}^2\mu (0)-C_{max}.\hfill \end{array}$$

(24)

where m is the number of jobs, $k=\left|\right\{\alpha \in {\mathfrak{P}}_0\mid {\nu }^{\mathfrak{p}}\left(\alpha \right)=(x,1),x>1\left\}\right|$, and $\mathfrak{i}$ ($\mathfrak{w}$) is the idle time (waiting time).

Proof. 

Suppose without loss of generality that vertices $val\left(\alpha \right)\ne 1$ for any vertex $\alpha$ associated with machines labeled by the set $\{1,2,\dots ,k\}$. Furthermore, vertices $\beta$ associated with machines labeled by the set $\{k+1,\dots ,n\}$ have valencies of $val\left(\beta \right)=1$, $val(-1)=\mathfrak{w}\ge 0$, and $val\left(0\right)=\mathfrak{i}$. Thus,

1.

$|{\mathfrak{P}}_1|=m$

2.

${\displaystyle 2\sum _{\alpha \in {\mathfrak{P}}_0}\frac{t_{{\nu }^{\mathfrak{p}}\left(\alpha \right)-1}}{{\mu }^{\mathfrak{p}}\left(\alpha \right)}=\sum _{j=1}^{n}val\left(j\right)({\mu }^{\mathfrak{p}}\left(j\right)val\left(j\right)-1)+{\mathfrak{h}}_{iw}}$.

Then

$$\begin{array}{cc}\hfill di{m}_{\mathbb{F}}{\mathsf{\Lambda }}_{\mathfrak{P}}& {\displaystyle =2m+2\sum _{j=1}^n\frac{t_{{\nu }^{\mathfrak{p}}\left(j\right)-1}}{\mu \left(j\right)}+{\mathfrak{h}}_{iw}}\hfill \\ \hfill & {\displaystyle =2m+\sum _{j=1}^n\left[\left(\sum _{i=1}^m{p}_{ij}\right)({\mu }^{\mathfrak{p}}\left(j\right)\left(\sum _{i=1}^m{p}_{ij}\right)-1)\right]+{\mathfrak{h}}_{iw}}\hfill \\ \hfill & {\displaystyle =2m+\sum _{j=1}^k\left[\sum _{i=1}^m{p}_{ij}(\sum _{i=1}^m{p}_{ij}-1)\right]+\sum _{j=k+1}^n\left[\sum _{i=1}^m{p}_{ij}(2\sum _{i=1}^m{p}_{ij}-1)\right]+{\mathfrak{h}}_{iw}}\hfill \\ \hfill & {\displaystyle =2m+\sum _{j=1}^k\left[{\left(\sum _{i=1}^m{p}_{ij}\right)}^2-\sum _{j=1}^m{p}_{ij}\right]+\sum _{j=k+1}^n\left[2{\left(\sum _{i=1}^m{p}_{ij}\right)}^2-\sum _{j=1}^m{p}_{ij}\right]+{\mathfrak{h}}_{iw}.}\hfill \end{array}$$

□

The following theorem gives formulas for the center of a BCA associated with an OSSP.

Theorem 3.

If ${\mathsf{\Lambda }}_{\mathfrak{P}}$ is the BCA associated with an OSSP defined by an $m\times n$-CPTM $C_P$, then

$$\begin{array}{cc}\hfill {\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{\mathfrak{P}}\right)-\mathfrak{l}& \hfill =1+C_{max}+m-(h+r),\hfill \end{array}$$

(25)

where $r={\displaystyle \sum _{i=1}^m}{r}_i$, with $r_i\in \{0,1,2\}$ for each row $R_i\in C_P$, $h\in P$, $0<h\le mn$, $\mathfrak{l}$ is the number of additional loops obtained by the construction of special cycles from the successor sequences, and m (n) is the number of jobs (machines).

Proof. 

For a CPTM $C_P=\left(c_{ij}\right)$ with $1\le i\le m$ and $1\le j\le n$ and the associated BCA ${\mathsf{\Lambda }}_{\mathfrak{P}}$. Suppose without loss of generality that there are $n+k$ vertices, with $k\in \{0,1,2\}$, according to the existence of idle and waiting times in $C_P$. Note that, for a fixed row $R_i\in C_P$, it holds that $r_i=0$ implies that $C_P$ has neither idle times nor waiting times. On the other hand, if $r_i=1$, then in $C_P$ there are entries giving either waiting time or idle time. Finally, if $r_i=2$ then $C_P$ has entries giving idle time and waiting time.

Note that, there are $n+k-z$ vertices $\alpha$ for which $val\left(\alpha \right)>1$ with $z=\left|\right\{\alpha \in {\mathfrak{P}}_0\mid {\nu }^{\mathfrak{p}}\left(\alpha \right)=(1,x),x>1\left\}\right|$. Then,

1.

$|{\mathfrak{P}}_1|=m$,

2.

$|{\mathfrak{P}}_0|=n+k$,

3.

$\#Loops=L-h\mathfrak{i}+\mathfrak{w}-r+\mathfrak{l}$.

The theorem follows as a consequence of the identity (21). □

As an example, we note that if P and $C_P$ are given by identities (2) and (4) then

$$\begin{array}{cc}\hfill {\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_{\mathfrak{P}}& \hfill =66,\hfill \\ \hfill {\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{\mathfrak{P}}\right)& \hfill =15.\hfill \end{array}$$

(26)

The following result gives the dimension of the center of a BCA associated with an OSSP with optimal configuration (giving minimal $C_{max}$ value) satisfying the $L_{\iota }$ condition.

Theorem 4.

Let $C_P$ be a CPTM satisfying the $L_{\iota }$ condition, σ a machine configuration for which $C_P$ has an optimal L value, and ${\mathsf{\Lambda }}_{\mathfrak{P}}$ the corresponding BCA. Then

$${\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{\mathfrak{P}}\right)-\mathfrak{l}=1+{\beta }^{*}m+m-(h+r)$$

(27)

where r, h, and $\mathfrak{l}$ are defined as in Theorem 3, and ${\beta }^{*}=\max \{L_{max},P_{max}\}$.

Proof. 

Since the PTM P satisfies the $L_{\iota }$ condition then $\mathfrak{i}+\mathfrak{w}=m{\beta }^{*}-L$. Thus, $L+\mathfrak{i}+\mathfrak{w}=m{\beta }^{*}$. The result follows as a consequence of Theorem 3. □

The following result is a consequence of Theorems 3 and 4.

Theorem 5.

Let $C_{P^{{\sigma }_1}}$ and $C_{P^{{\sigma }_2}}$ be $m\times n$ CPTMs given by optimal configurations ${\sigma }_1$ and ${\sigma }_2$, respectively. If ${\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_1}}$ and ${\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_2}}$ are the corresponding BCAs then

$${\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_1}}\right)+r_{{\sigma }_1}-{\mathfrak{l}}_{{\sigma }_1}\equiv {\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_2}}\right)+r_{{\sigma }_2}-{\mathfrak{l}}_{{\sigma }_2}modm$$

where $r_{{\sigma }_u}={\displaystyle \sum _{i=1}^m}{r}_{{\sigma }_{u,i}}$, ${\mathfrak{l}}_k$, with $u=1,2$.

Proof. 

Suppose that the machine-configurations ${\sigma }_1,{\sigma }_2\in M_P$ induce BCAs ${\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_1}}$ and ${\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_2}}$ respectively. Then

$${\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_k}}\right)=1+L+{\mathfrak{i}}^{{\sigma }_1}+{\mathfrak{w}}^{{\sigma }_k}-(r_{{\sigma }_1}+h),$$

$${\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_u}}\right)-\left({\mathfrak{l}}_{{\sigma }_u}\right)=1+L+{\mathfrak{i}}^{{\sigma }_u}+{\mathfrak{w}}^{{\sigma }_u}-(r_{{\sigma }_u}+h),\left(u\mathrm{fixed}\right)$$

where h is defined as in Theorem 3. Therefore,

${\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_1}}\right)+r_{{\sigma }_1}-({\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_2}}\right)+r_{{\sigma }_2})={\mathfrak{i}}^{{\sigma }_1}+{\mathfrak{w}}^{{\sigma }_1}-({\mathfrak{i}}^{{\sigma }_2}+{\mathfrak{w}}^{{\sigma }_2})+{\mathfrak{l}}_{{\sigma }_1}-{\mathfrak{l}}_{{\sigma }_2}$. Since, $\mathfrak{i}+\mathfrak{w}+L=mn$, it holds that

$$\begin{array}{cc}\hfill {\mathfrak{i}}^{{\sigma }_1}+{\mathfrak{w}}^{{\sigma }_1}-({\mathfrak{i}}^{{\sigma }_2}+{\mathfrak{i}}^{{\sigma }_2})& =length\left(C_{P^{{\sigma }_1}}\right)m-L-(length\left(C_{P^{{\sigma }_2}}\right)m-L)\hfill \\ \hfill & =m(length\left(C_{P^{{\sigma }_2}}\right)-length\left(C_{P^{{\sigma }_1}}\right))\hfill \end{array}$$

where, $length\left(X\right)$ denotes the number of columns of a matrix X and m is the number of jobs in the OSSP. Thus, ${\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_1}}\right)+r_{{\sigma }_1}-(di{m}_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_2}}\right)+r_{{\sigma }_2}=m(length\left(C_{P^{{\sigma }_1}}\right)-length\left(C_{P^{{\sigma }_2}}\right))+{\mathfrak{l}}_{{\sigma }_1}-{\mathfrak{l}}_{{\sigma }_2}$. Therefore

$${\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_1}}\right)+r_{{\sigma }_1}-{\mathfrak{l}}_{{\sigma }_1}\equiv {\dim }_{\mathbb{F}}Z\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_2}}\right)+r_{{\sigma }_2}-{\mathfrak{l}}_{{\sigma }_2}modm.$$

□

Table 1 gives idle time, waiting time, L value, $C_{max}$ value, and dimensions of the Brauer configuration algebra and the corresponding center associated with a fixed configuration ${\sigma }_i\in M_{C_P}$ equivalent to the configuration $\sigma$ defined by identities (2) and (4).

Table 1. Data associated with configurations equivalent to the configuration $\sigma$ defined by identities (2) and (4).

Configurations	Data
	${\mathfrak{i}}^{{\mathbf{\sigma }}_{\mathit{i}}}$	${\mathfrak{w}}^{{\mathbf{\sigma }}_{\mathit{i}}}$	${\mathit{L}}^{{\mathbf{\sigma }}_{\mathit{i}}}$	${\mathit{C}}_{\mathit{max}}^{{\mathbf{\sigma }}_{\mathit{i}}}$	${\mathbf{dim}}_{\mathbb{F}}{\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\mathbf{\sigma }}_{\mathit{i}}}}$	${\mathbf{dim}}_{\mathbb{F}}\mathbf{Z}\mathbf{\left(}{\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\mathbf{\sigma }}_{\mathit{i}}}}\mathbf{\right)}$
${\sigma }_1=\left(\begin{array}{ccc}1& 2& 3\\ 1& 2& 3\end{array}\right)$	3	2	13	18	66	15
${\sigma }_2=\left(\begin{array}{ccc}1& 2& 3\\ 1& 3& 2\end{array}\right)$	2	1	13	16	61	13
${\sigma }_3=\left(\begin{array}{ccc}1& 3& 2\\ 2& 1& 3\end{array}\right)$	0	1	13	14	59	11
${\sigma }_4=\left(\begin{array}{ccc}3& 1& 2\\ 3& 2& 1\end{array}\right)$	6	5	13	24	108	21
${\sigma }_5=\left(\begin{array}{ccc}2& 3& 1\\ 2& 1& 3\end{array}\right)$	4	3	13	20	76	17
${\sigma }_6=\left(\begin{array}{ccc}1& 3& 2\\ 2& 3& 1\end{array}\right)$	0	1	13	14	59	11

3.1. Some Experimental Data

This section includes statistical data from experiments conducted (on a computer ASUS VivoBook with processor AMD Ryzen 53500U with Radeon Vega Mobile Gfx 2.10 GH) to study the behavior of the ${\mathcal{L}}_{\iota }$ condition (see Table 2), Processing time to compute $C_{max}$ values (see Table 3), $C_{max}$ values (see Table 4 and Figure A1), the dimension of Brauer configuration algebras (see Table 5 and Table 6, and Figure A2 and Figure A3), and their centers associated with 5000 randomly chosen configurations defined by open shop scheduling problems of size $2\times 3$, $3\times 2$, $3\times 3$, $3\times 4$, $3\times 5$, $4\times 3$, $4\times 4$, and $5\times 3$. We include Appendix A with histograms describing the behavior of these values for configurations of size $3\times 2$, $3\times 3$, $3\times 4$, and $3\times 5$.

Table 2. This table shows the percentage of configurations, ${\sigma }_i$, that satisfy the ${\mathcal{L}}_i$-condition, which means that the corresponding $C_{max}$ value is bounded by ${\mathcal{L}}_{\iota }^{\sigma }$ (see identity (5)). Note that all the $2\times 3$ and $3\times 5$ configurations chosen in the sample satisfy the ${\mathcal{L}}_i$ condition.

Configurations (${\mathit{\sigma }}_{\mathit{i}}$)	$\mathit{\sigma }\mathbf{|}\mathbf{\ne }{\mathcal{L}}_{\mathit{\iota }}$	$\mathit{\sigma }\mathbf{|}\mathbf{=}{\mathcal{L}}_{\mathit{\iota }}$	Percentage
$2\times 3$	0	5000	100
$3\times 2$	1030	3970	$\mathrm{79,4}$
$3\times 3$	146	4854	$\mathrm{97,08}$
$3\times 4$	17	4983	$\mathrm{99,66}$
$3\times 5$	0	5000	100
$4\times 3$	565	4435	$\mathrm{88,70}$
$4\times 4$	16	4984	$\mathrm{99,68}$
$5\times 3$	190	4810	$\mathrm{96,20}$

Table 3. Processing time to obtain $C_{max}$ values for several configurations.

Configuration	Processing Time (s)
$2\times 3$	14
$3\times 2$	25
$3\times 3$	454
$3\times 4$	4031
$3\times 5$	$\mathrm{41,978}$
$4\times 3$	6027
$4\times 4$	$\mathrm{37,485}$
$5\times 3$	1014

Table 4. $C_{max}^{{\sigma }_i}$ values obtained from samples of 5000 randomly chosen configurations. Note that for configurations of size $2\times 3$ ($3\times 5$), 95 percent of the $C_{max}$ values vary between 48,936 and 5506 (143,708 and 150,492), respectively.

${\mathit{C}}_{\mathit{max}}^{{\mathit{\sigma }}_{\mathit{i}}}$
Configurations (${\mathit{\sigma }}_{\mathit{i}}$)	Average	Variance	Standard Deviation
$2\times 3$	$\mathrm{52,498}$	$0.0317$	$0.1781$
$3\times 2$	$\mathrm{188,100}$	$0.0569$	$0.2386$
$3\times 3$	$\mathrm{148,294}$	$0.0238$	$0.1544$
$3\times 4$	$\mathrm{133,148}$	$0.0262$	$0.1618$
$3\times 5$	$\mathrm{147,100}$	$0.0288$	$0.1696$
$4\times 3$	$\mathrm{346,068}$	$0.0349$	$0.1869$
$4\times 4$	$\mathrm{273,818}$	$0.0211$	$0.1452$
$5\times 3$	$\mathrm{721,320}$	$0.0237$	$0.1539$

Table 5. This table gives values of the ${\dim }_{\mathbb{F}}{\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\sigma }_i}}$ average from 5000 randomly chosen configurations. Note that, BCAs associated with optimal configurations of fixed-size tend to have the same dimension.

${\mathbf{dim}}_{\mathbb{F}}{\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\mathit{\sigma }}_{\mathit{i}}}}$
Configurations (${\mathit{\sigma }}_{\mathit{i}}$)	Average	Variance	Standard Deviation
$2\times 3$	$\mathrm{3,387,346}$	$0.0226$	$0.1505$
$3\times 2$	$\mathrm{6,112,742}$	$0.0539$	$0.2322$
$3\times 3$	$\mathrm{8,120,350}$	$0.0271$	$0.1646$
$3\times 4$	$\mathrm{10,416,072}$	$0.0170$	$0.1304$
$3\times 5$	$\mathrm{13,196,518}$	$0.0178$	$0.1332$
$4\times 3$	$\mathrm{18,726,494}$	$0.0309$	$0.1757$
$4\times 4$	$\mathrm{20,902,258}$	$0.0151$	$0.1230$
$5\times 3$	$\mathrm{49,975,976}$	$0.0247$	$0.1573$

Table 6. Dimensions of the centers in the BCAs shown in Table 5. As for the corresponding algebras, we note that these dimensions tend to be the same if optimal fixed-size configurations define them.

${\mathbf{dim}}_{\mathbb{F}}\mathit{Z}\left({\mathsf{\Lambda }}_{{\mathfrak{P}}^{{\mathit{\sigma }}_{\mathit{i}}}}\right)$
Configurations (${\mathit{\sigma }}_{\mathit{i}}$)	Average	Variance	Standard Deviation
$2\times 3$	$\mathrm{308,482}$	$0.0315$	$0.1773$
$3\times 2$	$\mathrm{373,980}$	$0.0826$	$0.2873$
$3\times 3$	$\mathrm{503,106}$	$0.0295$	$0.1718$
$3\times 4$	$\mathrm{621,820}$	$0.0137$	$0.1169$
$3\times 5$	$\mathrm{758,096}$	$0.0242$	$0.1556$
$4\times 3$	$\mathrm{763,204}$	$0.0539$	$0.2321$
$4\times 4$	$\mathrm{906,988}$	$0.0124$	$0.1112$
$5\times 3$	$\mathrm{1,280,868}$	$0.0263$	$0.1621$

3.1.1. Methodology

We applied Calderon’s algorithm [36] to obtain $C_{max}$ values, idle times, and waiting times to 40,000 randomly chosen configurations divided into sets of 5000 configurations of size $2\times 3$, $3\times 3$, $3\times 4$, $3\times 5$, $4\times 3$, $4\times 4$, and $5\times 3$ (we used the symbol ${\sigma }_i$ to denote configurations in tables); such configurations represent OSSPs and their entries are integer numbers from 0 to 9. Rows (columns) in the chosen configurations are determined by machines (jobs). Column permutations were applied to fixed configurations provided that in OSSPs the order of the jobs involved in processing a given task does not matter. We ran a Python routine on an ASUS computer to obtain $C_{max}$ values of the configurations and the dimension of the Brauer configuration algebras (and their centers) defined by them. We note that the complexity of Calderon’s algorithm when obtaining such values was $n^5{(n!)}^n$, which implies that the time needed to obtain $C_{max}$ values with this algorithm increases with the configuration size (see Table 3). The results verify Calderon’s hypothesis regarding the percentage of configurations satisfying the ${\mathcal{L}}_{\iota }$ condition (i.e., at least 95 percent of the configurations satisfied this condition). In the tables, we use the symbol $\sigma |={\mathcal{L}}_{\iota }$ to denote that a configuration ${\sigma }_i$ encoding an OSSP satisfies the ${\mathcal{L}}_{\iota }$ condition.

3.1.2. Discussion

It is possible to infer that at least 95 percent of the configurations satisfy the ${\mathcal{L}}_i$ condition. Therefore, the $C_{max}$ value is bounded by ${\mathcal{L}}_{\iota }^{\sigma }$ (see identity (2)) and as the dimension of Brauer configuration algebras associated with optimal solutions of the OSSP tends to have the same minimal value, such values can be obtained via corresponding makespan, idle time, and waiting time. The same conclusions can be derived from the corresponding centers whose dimensions are congruent modulo the number of machines involved in the optimization process.

4. Concluding Remarks and Future Work

The OSSP can be represented by processing time matrices which give rise to Brauer configuration algebras whose representation theory can be described via the corresponding makespan. These times ($C_{max}$, waiting time, and idle time) enable formulas to be obtained for the dimension of Brauer configuration algebras and their centers. In particularly, it is possible to prove that the dimension of the centers of Brauer configuration algebras associated with optimal configurations (processing time matrices giving minimal $C_{max}$) are congruent modulo the number of machines.

Future Work

There remain interesting tasks to develop in the future:

1.

to determine which configurations defined by open shop scheduling problems are characterized by the dimension of the center of the associated BCA;

2.

to improve the complexity of the algorithms applied to compute dimensions of the BCAs and $C_{max}$ values;

3.

to apply the theory of representation of Brauer configuration algebras in different kinds of job shop scheduling problems (e.g., to develop investigations regarding railroad and bus schedules).