1. Introduction
A mechanical phenomenon that results in oscillations and has an effect on the structural behavior and physical characteristics of the bodies subjected to it, is known as vibration. Vibrations are a prevalent issue for the human spine, which supports the rest of the body, links the various musculoskeletal systems, and facilitates communication between the brain and the rest of the body [
1,
2,
3,
4]. The functional human spinal column is required for spinal movement, trunk support stability, absorption and distribution of loads (gravity and muscle contraction), and maintenance of the nerve axis. These activities are age-dependent as the biomechanics and structure of the human spinal column change with age. Everyday activities like walking, running, driving, and traveling by train or plane can cause vibrational effects on the spine, which can lead to severe injuries [
5,
6].
Ericksen [
7] measured the lumbar spine vertebrae of 338 male and female skeletons aged between 20 to 90 years. They observed that the endplates spread more, but the middle section of the body widens enough to prevent the vertebrae from “flaring” with age. The lumbar body becomes wedge-shaped in males when the posterior body height lowers compared to the anterior, whereas females exhibit no change. Berne et al. [
8] studied the effects of aging on the spine and their natural evaluations at different ages. They found that the mechanical properties and anatomical structures of the spine changed at different phases of age. Due to these changes, the human spine no longer functions effectively during regular activities. The consequences of aging and its effects on the human spinal column were studied by Wilmink [
9]. Ageing was reported to cause biomechanical and geometric changes in the spinal column. They found that disc degeneration and protrusion are due to the aging effects of the spine that cause pain and instability in the spine. Del Grande et al. [
10] discussed the impact of disc herniation by imaging age-related disc changes and internal disc rupture in different segments of the spinal column. They found that imaging is most commonly used to diagnose disc herniation when there is radicular pain or radiculopathy. Galbusera et al. [
11] studied the aging and degenerative changes of the intervertebral disc, which helped to understand the biomechanics of the spine and its flexibility. They observed that when the intervertebral disc and surrounding tissues degrade, the biomechanical properties of the spinal column gradually deteriorate.
Smeathers [
5] used a skin-mounted accelerometer at multiple spinal column locations to assess a healthy person’s spinal column transmissibility while walking and running. Spine vibration transmission also produces back discomfort due to degenerative changes or external stress. Researchers observed that although a healthy spinal column had attenuated components at frequencies exceeding 20 Hz, those with ankylosing spondylitis behaved similar to a rigid strut. Wilder et al. [
12] used an impact system set up to experiment with the spines of 45 adults of varying ages, as they sat in a variety of postures and on various supports, and quantified the effects of vibration. They observed that the effect of the vibration transmission in the spinal system occurred at the first resonant frequency. Wilder and Pope [
13] studied the effects of vibration on the human spine and identified many contributing factors of low back pain, such as spine aging and disc degeneration. They observed that the human spine was profoundly affected by vibrational impact related to numerous aetiological, industrial, and environmental causes, leading to an increase in the intensity of lower back pain. Ramirez et al. [
14] investigated the transmission of vibrations throughout different vertebral sections of aged and young people with and without osteoporosis. The researchers found that these vibration transmissions while walking and other physical activities were associated with a higher incidence of thoracic spine fractures than lumbar spine fractures. Using the vibration platform and accelerometer, Brzuszkiewicz-Kuźmicka et al. [
15] performed experiments on 112 subjects in different age groups to estimate the effect of aging on the spine and characterize the spine’s shock absorption ability. The shock-absorbing properties of the spinal column are primarily attributable to the intervertebral discs. However, as a consequence of aging, all spinal components, including the discs, undergo degenerative changes. It can affect the spinal column’s mechanical properties and range of motion, and also reduce vibration absorption.
To study the vibration characteristics and dynamic behavior of a lumbar spine section under various cycle stress, Guo et al. [
16] created a nonlinear finite element model. They found that whole-body vibrations may cause greater injury to the back of the lumbar spine than to the front. Amiri et al. [
17] studied whole-body vibrations on the lumbar spine in various driving positions. The finite element model was used for different driver sitting positions and adjusted to understand vibration on the lumbar spine. They found that loads and stress affected spinal responses to whole-body vibration in sat postures with varying seatback inclinations. The vibrational effect of the human spine structure was studied by Guo et al. [
18] using modal analysis and finite element modeling. They found resonance frequencies and mode shapes of the human spine using a 3-D finite element model of spine T12-pelvis segments, and that the spine structure has multiple mode shapes and resonance frequencies in different directions, such as flexion-extension, lateral bending, and vertical orientation. Guo and Li [
19] developed a finite element model of the lumbar spine segment to investigate the biomechanical response and stress distribution under various frequency vibrations. When the entire human body is exposed to vibrations at work, it can accelerate spinal degeneration, leading to severe back pain and other spinal disorders. They found that the deformation and poroelastic properties of the intervertebral disc have a significant effect on a wide range of vibrational frequencies.
To the governing theory of non-linear elasticity, Barton et al. [
20,
21] proposed a high-order shock capture approach for simulating solid media that are deforming elastoplastically in a three-dimensional structure. In particular, a characteristic-based approach of the Riemann problem was presented, and achieved the high-order spatial accuracy. The techniques were developed on a basis of improved one dimensional equations that are easy to extend in many dimensions, and they have implications for other challenging issues which require material modification. Through extensive literature reviews, it was observed that, majorly, the lumbar segment was considered by the researchers to analyze the effect of vibrations on the spine. Additionally, all spine aging studies reported biomechanical property changes, degeneration of the intervertebral disc, and disc herniation [
22,
23,
24]. None of these studies reported vibration absorption or transmission capacity of different human spinal column segments, and the effect of age.
In the present work, a novel composite-based finite element model was developed to investigate the effects of vibration on different segments of the human spinal column at varying ages, including youth, middle age, and old age. Several geometrical simplifications were considered, such as modeling cylindrical vertebrae and discs and the lack of spinal curvature, to focus on the development of a finite element model which can be validated with previous works and used to characterize the effect of aging on a spinal column exposed to harmful vibrations. To achieve this aim, the natural frequencies of the spinal column were determined by solving the eigenvalue problem. The eigenvalue problem was used to estimate the dynamic behavior of spine segments under free and forced vibration effects. The results of this study will be essential for understanding how aging-induced vibrations affect the human spine and for predicting how both clinical physiotherapy and space travel will affect spinal health.
2. Materials and Methods
The human spine provides structural support, links the musculoskeletal systems, and allows the brain to communicate with other organs. It conveys sensation and movement via the back’s ligaments, bones, tissues, and the nerves of the back that surround them. [
25,
26]. As seen in
Figure 1, in the human spine structure there are several vertebrae and discs, and out of these, only the lumbar, thoracic, and cervical sections were considered. The extreme end of the human spine (i.e., the sacrum and coccyx) were not considered because there is no assembly of vertebrae and discs in these segments. Also, there is no relative motion or degrees of freedom. It behaves like a bone because it consists of vertebrae fused together without discs. Another reason is that their geometry is also not like a cylindrical beam, as we see in other segments of the human spine. The lumbar segment of the spine consists of five vertebrae and is the lowest portion of the spine. The thoracic portion, which is made up of a total of twelve vertebrae, is the middle section of the human spine. The cervical portion of the human spine, the uppermost component of the spine structure, consists of seven vertebrae combinations.
The human spine structure was modeled as a Timoshenko beam element, and the stiffness and mass matrices for the vertebrae and disc were obtained through the finite element method. The human spine was represented as a composite structure, with the vertebrae and discs each having their unique shape and characteristics, resulting in the many segmented configurations shown in
Figure 1. The global stiffness and mass matrices of the spine composite structure were derived by combining all the mass and stiffness matrices of the disc and vertebrae.
2.1. Finite Element Model of the Human Spine Structure
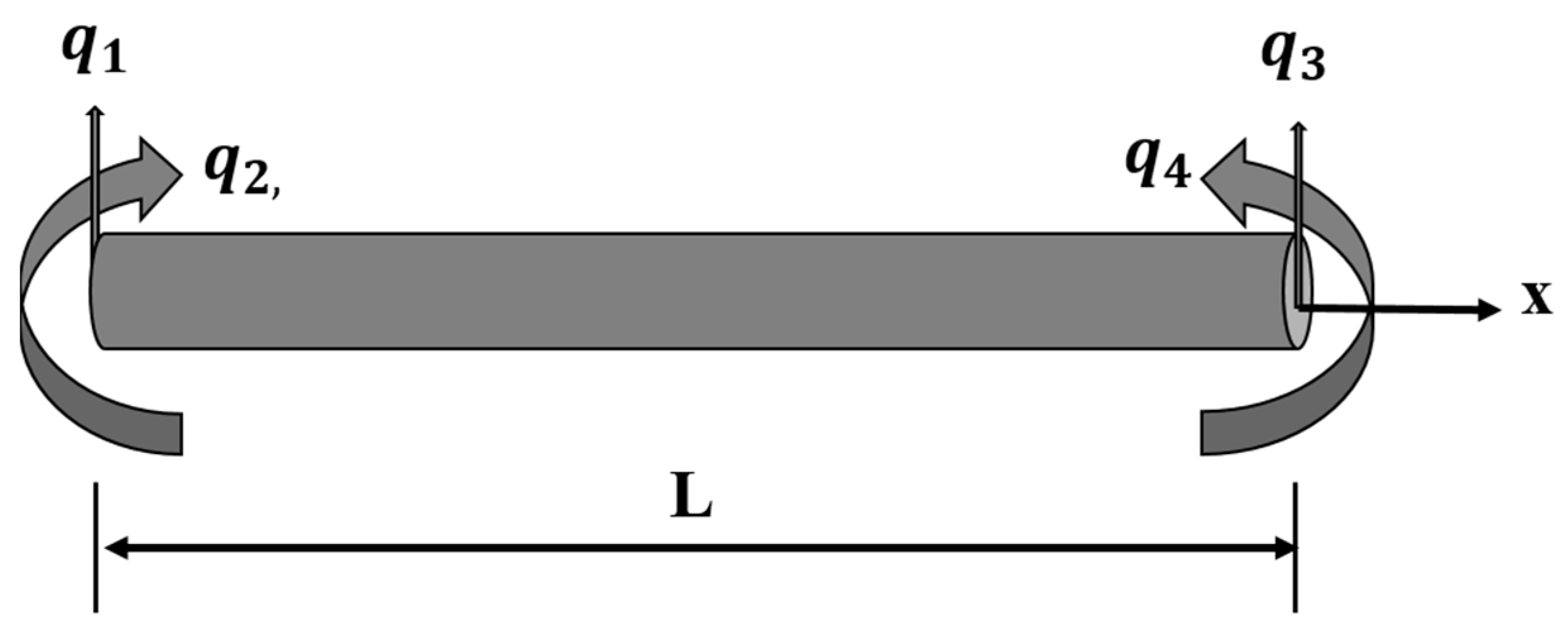
As illustrated in
Figure 2, a Timoshenko beam element of length L has two nodes, 1 and 2, with the transverse deflection,
and
, and the slope,
and
, respectively, as degrees of freedom. The displacement of the beam is taken into account due to bending and shear effects in accordance with the Timoshenko beam theory [
27].
Displacement functions for the bending and shear effects of the Timoshenko beam element were obtained using the static equilibrium equation, which included shear deformation and assumed displacement polynomials [
28].
These static equilibrium equations were developed using the Hamilton principle, and the boundary condition with no time variation was implemented, as stated in [
28].
The general solutions to the static equilibrium equation are as follows:
Equations (3) and (4) are dependent on these integration constants, and must be fulfilled for Equation (1) to be valid for the moment equilibrium. The following relationships were established using the static equilibrium equation and boundary condition.
By substituting the values of the integration constants from Equation (5) into Equation (4), we get
where
Here,
E stands for elastic modulus,
G for shear modulus or rigidity modulus,
A for shear correction area, and
k for shear correction factor. In order to solve problems using assumed polynomials, the following boundary conditions were used.
Applying the above boundary in Equations (3) and (6), we receive
The above equations were written in the matrix form
Solving the above Equation (14) to obtain the constant
in terms of the
where
substituting the values of
from above Equations (15)–(18) into Equations (3) and (6); these were written in the term of shape functions
where
shape functions correspond to the bending effect in the Timoshenko beam element
Now shape function due to the shear effect can be written as
where
shape functions correspond to the shear effect in the Timoshenko beam element.
2.1.1. Stiffness Matrix of the Timoshenko Beam Element
The stiffness matrix for a Timoshenko beam element due to bending and shear effects can be expressed as
where
are the stiffness matrix due to the bending effect and stiffness matrix due to the shear effect, respectively
where
represents the strain displacement matrix due to bending and
represents the shear strain displacement matrix. As a result of the bending and shear effects, it is the second derivative of the shape function.
The stiffness matrix of the Timoshenko beam element may be obtained by substituting the value of the strain displacement matrix resulting from the bending and shear effect from Equation (32) into the Equations (30) and (31), respectively.
2.1.2. Mass Matrix of the Timoshenko Beam Element
The mass matrix for a Timoshenko beam element due to bending and shear effects can be expressed as
where
where
is the density of the material,
is the cross-sectional area, and
the second moment of area of the cross-section.
To derive the mass matrix of the Timoshenko beam element under bending and shear effects, we substitute the values of the shape function under these conditions into Equations (35) and (36).
where
&
are the stiffness and mass matrix of a Timoshenko beam element.
2.2. Eigenvalue Problem for the Spine Structure
This section predicts the spatial model and modal model of the human spine structure. The spatial model includes the segmental composite spine’s mass and stiffness matrices. The modal-model parameters can be predicted by solving the eigenvalue problem, such as the structural natural frequencies and corresponding mode shapes [
29].
As a result of combining the elemental mass and stiffness matrices of the disc and vertebrae for various segments of the spine structure, we have obtained the equation of motion in the form of global mass and global stiffness, which is given as:
Assume that excitation force in the form
Assume that the solution of Equation (39)
Differentiating the above Equation (40), we receive
Substituting the value of
,
and
into the Equation (39), one can obtain
From Equation (45), we can rewrite in the from frequency response function
where
and
is the global mass matrix and global stiffness matrix,
and
are their eigenvalues and eigenvector, and
is the frequency response function (FRF). The eigenvalue problem can be solved by using the MATLAB ’eig’ command.
2.3. Spine Structure Properties of the Different Aging People
Table 1 represents the properties of the vertebrae and disc for the various parts of the spine structure for the various age groups, i.e., for the different ages [
30,
31,
32,
33,
34]. Each case’s stiffness and mass matrix for vertebrae and disc elements was calculated using these properties. The following properties were used to develop finite element models or mathematical models for the various segments of the composite spine structure. All of the spine’s segments were modeled using the finite element method, and their behavior was analyzed by using fixed–fixed boundary conditions, where ρ is the density of the material in Kg/m
3, E Modulus of elasticity in MPa, and υ is the Poisson ratio.
3. Result and Discussion
This section discusses the effects of aging on different segments of the human spine structure using a developed finite element model of the spine structure.
3.1. Variations in Vibration Frequency Caused by the Aging of Lumbar Spine Segments
In this section, the effects of aging on the natural frequencies of the lumbar spine segments are discussed. The lumbar region of the spine consists of five vertebrae (L
1–L
5), and these vertebrae are linked together by four intervertebral discs. As a result, the entire lumbar segment is composed of nine elements, each of which is linked to the other. The lumbar spine segment has greater flexibility due to the combination of vertebrae and discs. The lumbar spine was positioned between the thorax and sacrum, hence, clamped–clamped boundary conditions were considered. This structure was used to develop the finite element model or mathematical models for various age groups of the lumbar segments, which consist of different material and biomechanical properties, as shown in
Table 1. These mathematical models were used to obtain the natural frequencies of the lumbar segment with different ages, which are calculated by solving the eigenvalue problems.
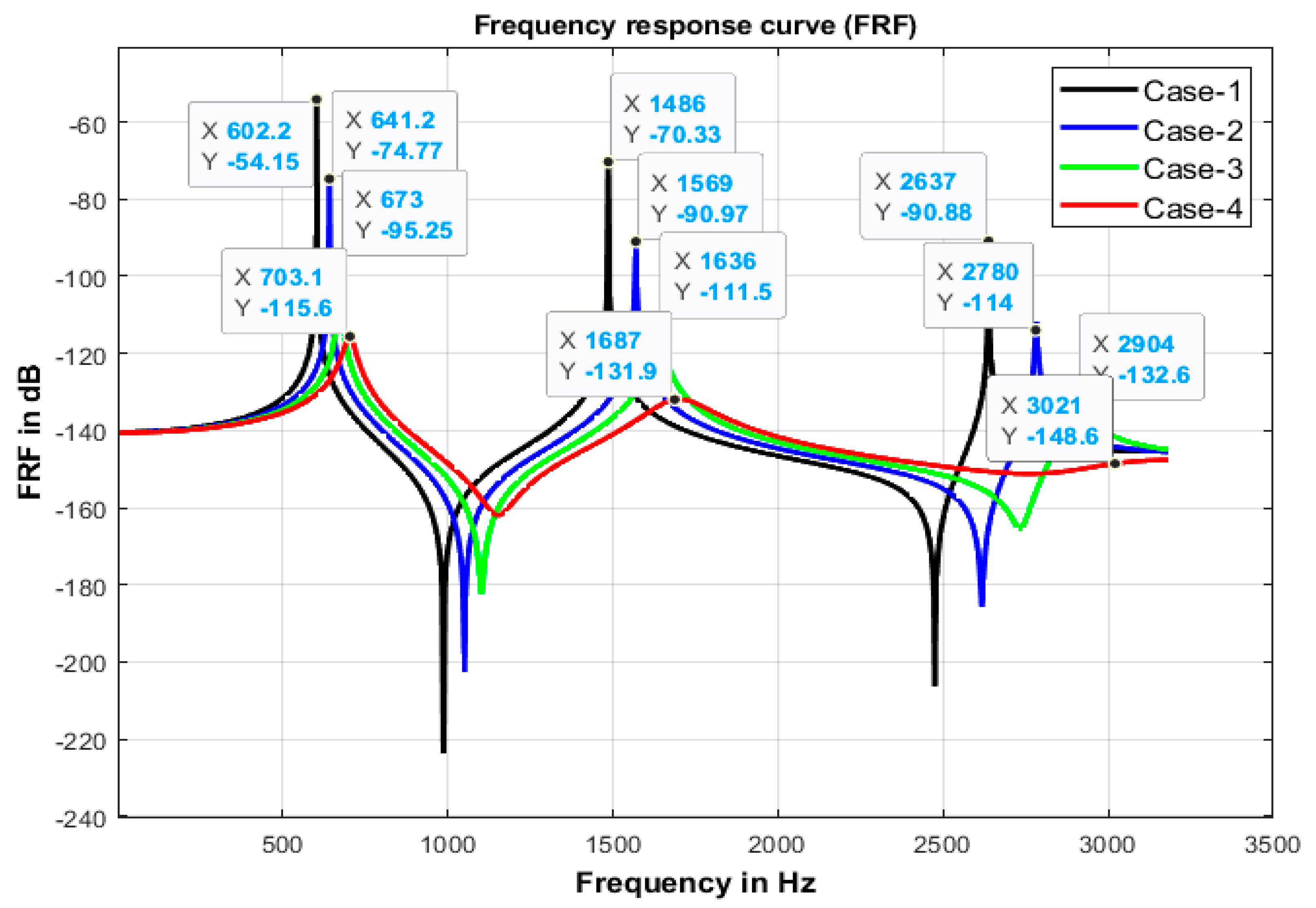
Figure 3 represents the overlay of the frequency response function (FRF) curve for the different age groups of the lumbar spine segments. The frequency response function curve shows the first three vibrations or natural frequencies of the different age groups as represented by various colors. It was observed from
Figure 3 that the minimum natural frequencies of different age groups are 602.2 Hz, 1486 Hz, and 2637 Hz, and the maximum natural frequencies are 703.1 Hz, 1687 Hz, and 3021 Hz. This indicates that the natural frequencies of the spinal column of different ages increase due to the aging of the spine.
The variation of natural frequencies in the lumber segment with age were validated with the literature [
35]. The values of all three natural frequencies were within 5–10%. In line with literature [
35], the investigation revealed that the effects of aging on the lumbar segments lead to changes in their natural or vibrational frequencies, which reduces the absorption capacity or vibration transmission because the spinal column behaves like a solid spine structure.
3.2. Variations in Vibration Frequency Caused by the Aging of Thoracic Spine Segments
There are twelve thoracic vertebrae (T1–T12) in the spine, connected by eleven discs. Therefore, the thoracic region is made up of 23 different parts. The thoracic spine structure is more flexible because of the mix of vertebrae and discs. Similarly, the finite element model or mathematical models were developed for the different age groups of the thoracic segments, which consist of different material properties, as shown in
Table 1. These mathematical models were employed to calculate the natural frequencies for the thoracic segment using eigenvalue problems.
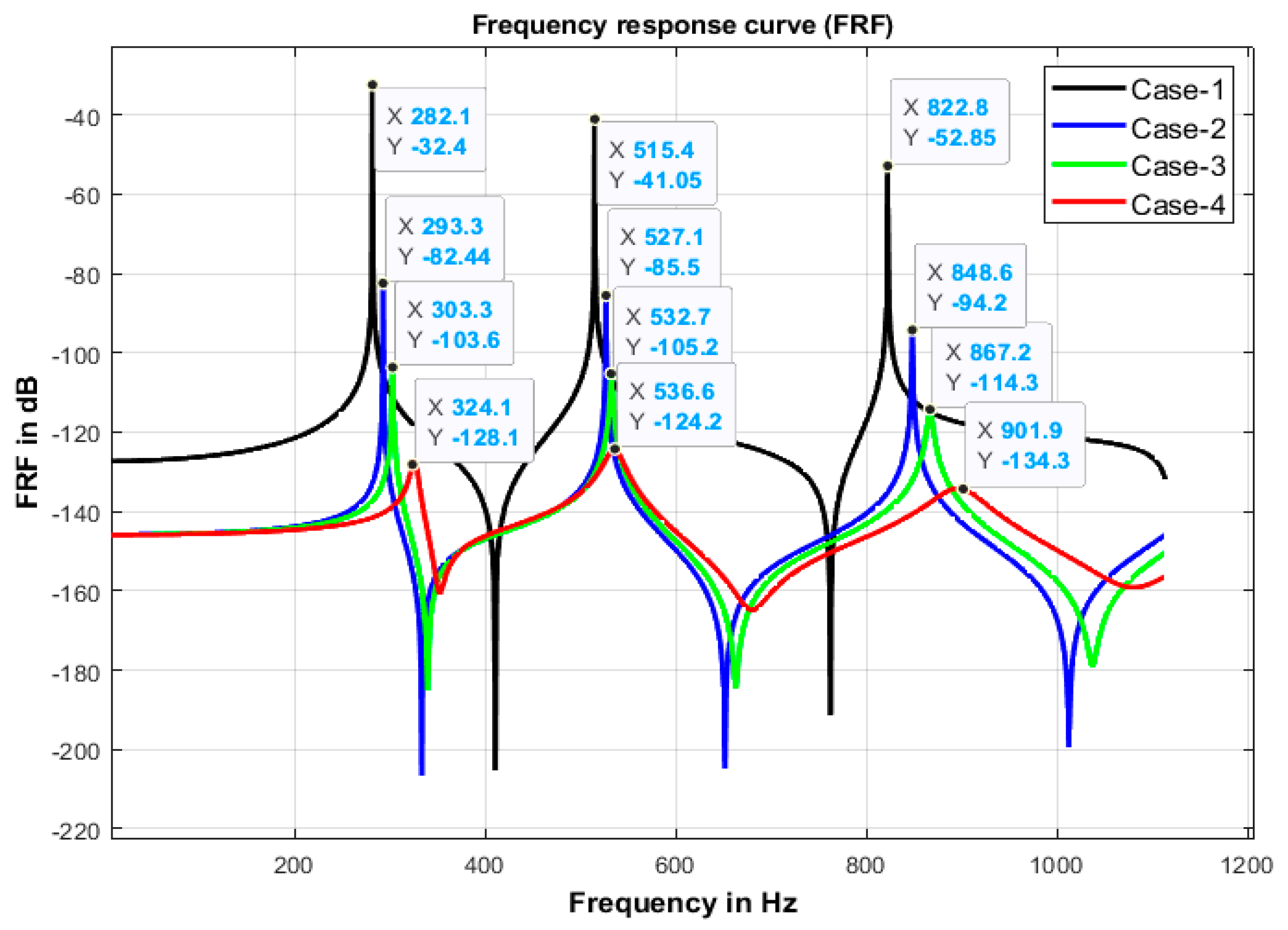
The overlay of the frequency response function (FRF) curve for several thoracic spine segment examples is shown in
Figure 4. The first three natural frequencies of the various age group of the thoracic segment of the spine structure are indicated by the peaks of the various frequency response function (FRF) curves.
Figure 4 illustrates that the lowest natural frequencies of various age groups are 282.1 Hz, 515 Hz, and 822.8 Hz. In comparison, the highest natural frequencies are 324.1 Hz, 536.6 Hz, and 901.9 Hz, indicating that the natural frequencies of the thoracic spinal column increase with age. The aging effect of the thoracic spinal column, reflected by variation in biomechanical characteristics and intervertebral disc degeneration or disc herniation, causes a rise in the first three vibrations or natural frequencies of the different ages of people, as observed by the curve of the frequency response function. These variations in natural frequencies compared to a normal spinal structure may result in sudden, severe injury to the thoracic region.
3.3. Variations in Vibration Frequency Caused by the Aging of Cervical Spine Segments
The uppermost part of the spine structure is called the cervical segment. There are seven vertebrae in the cervical spine, labeled C1 through C7, and held together by six intervertebral discs. Therefore, the cervical segment is made up of a total of 13 individual parts. Similarly, finite element models were developed for the numerous cervical segment cases of different ages, which are each composed of distinctive material characteristics, as listed in
Table 1. The effect of aging on the cervical region of the spine structure was observed by their first three natural frequencies, which are obtained by solving the eigenvalue problems.
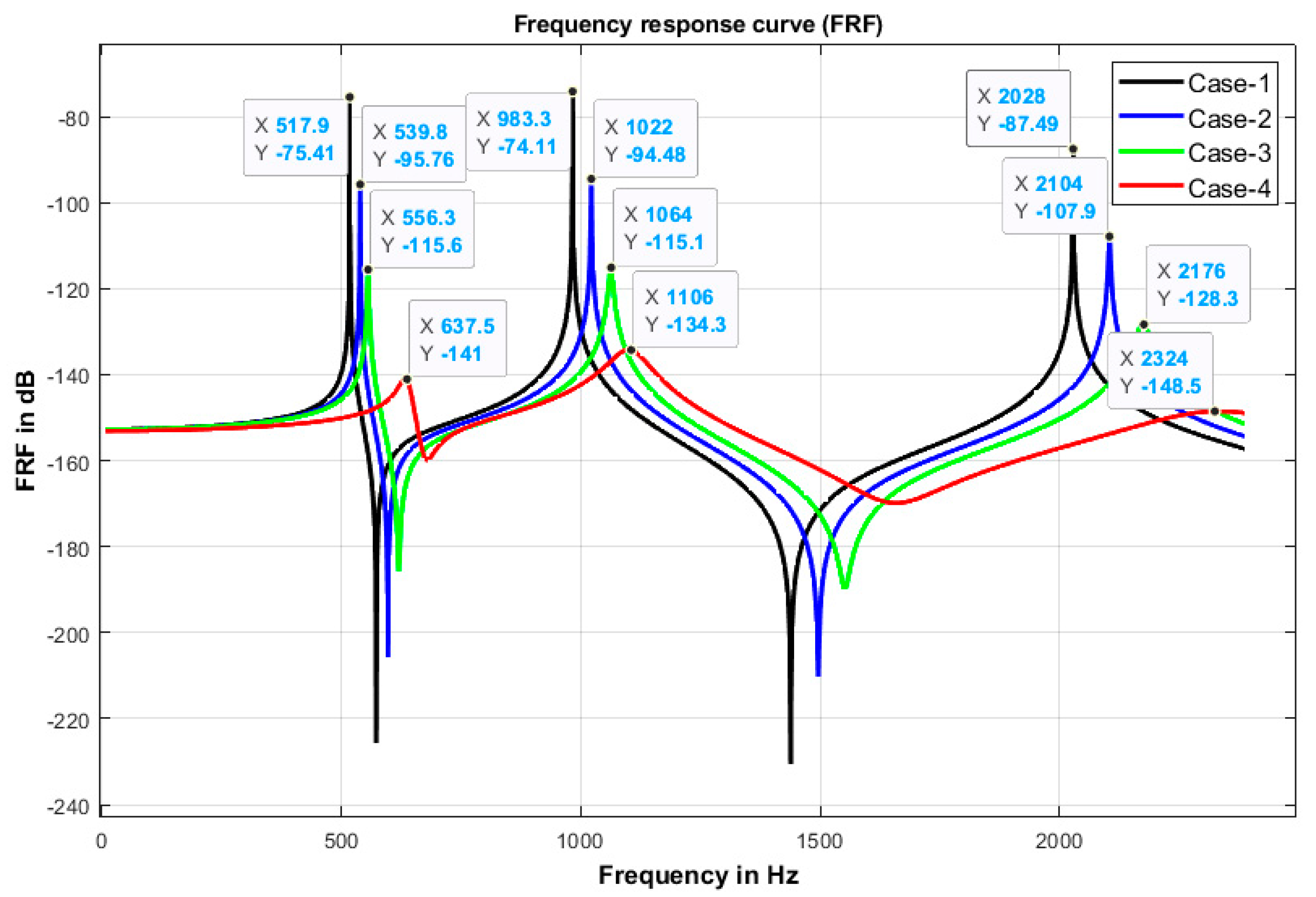
Figure 5 displays the overlay of the frequency response function (FRF) curve for several cervical spine segments for various age groups. The peaks of the various frequency response function (FRF) curves represent the first three natural frequencies of the different ages of the cervical segment of cervical spine structures. The natural frequencies of the cervical spinal column of various ages change as a result of the aging effect, as shown in
Figure 5, where the lowest natural frequencies of different age groups are 517.9 Hz, 983.3 Hz, and 2028 Hz, while the highest natural frequencies are 638.4 Hz, 1104 Hz, and 2323 Hz. These changes in the natural frequencies of the different age groups of cervical segments are helpful in studying the effects of aging, gender, and how tissue degeneration significantly affects the physical properties of the lumbar spinal segments, depending on the structure. Since vertebrae and discs are more susceptible to damage, their characteristics change with age. Due to the progressive loss of flexibility and tightening of the endplate and nucleus, the pulposus spine structure behaves like a solid. These changes in spine segments due to the aging effect may increase the possibility of failure of the cervical segments during various physical and daily life activities.
3.4. Sensitivity Analysis of Model Parameters
The first three fundamental natural frequencies of the lumbar, thoracic, and cervical segments were tested with normal properties, as well as with composite properties. The human spine is made up of homogeneous characteristics known as structures with normal properties, and composite properties refer to the human spine structure’s vertebrae and discs with different characteristics. The results for lumbar were obtained for normal properties (616 Hz, 1480 Hz, 2561 Hz), and composite properties (602 Hz, 1486 Hz, 2637 Hz), for thoracic, normal properties (169.6 Hz, 452.9 Hz, 854.2 Hz), and composite properties (282.1 Hz, 515.4 Hz, 822.6 Hz), and for cervical for normal properties (442.3 Hz, 1120 Hz, 2007 Hz) and composite properties (517.9 Hz, 983.3 Hz, 2028 Hz). In summary, with the change in the material properties, the results were within 5–10%. Therefore, we can conclude that these parameters were not highly sensitive to material choice.
4. Conclusions
In this study, a novel finite element model was developed to investigate the effects of aging on the various human spine segments. All the vertebrae and discs in the lumbar, thoracic, and cervical spine regions were modeled. The finite element models were developed for the distinct segments of the human spinal column for different age groups, which consist of different materials and biomechanical characteristics. The material properties of spinal segments are significantly influenced by aging, gender, and tissue degradation, which may affect the structure’s natural frequencies. As vertebrae and discs are more vulnerable to injuries and their characteristics change with age, the three first natural frequencies of the lumbar spine were evaluated for endplates and discs. The eigenvalue problem was solved using equations, and the natural frequencies for various spinal segments were determined for different finite element models. The first three natural frequencies of the lumbar portion were compared with the literature data to validate the developed finite element models. The comparisons also showed that the mathematical models of the spinal column segments were more accurate in replicating the realistic natural frequencies. Our results of the natural frequencies were compared and validated with the natural frequency of the lumbar segment reported for different age groups in literature, which were within 5–10%. The comparisons showed that the mathematical models of the spinal column segments were accurate in replicating the realistic natural frequencies. The validated finite element models were used to determine the natural frequencies of the thoracic and cervical segments for each age group (15–30 Yr., 30–50 Yr., 50–75 Yr., and above 75 Yr.) and characterize the effect of aging on these spinal column segments. This aging of the human spinal column was observed to lead to an increase in the natural frequencies of the spinal segments. As the age increased beyond 30 years, the natural frequency significantly increased for the thoracic segment, compared to lumber and cervical segments. With further aging, the increase in the natural frequencies was slow across spinal column segments. A range of such novel findings has not yet been reported in the literature. This may be useful for monitoring the many possible causes of back pain, including the aging influence on the spinal column, disc degeneration, and disc herniation. This understanding is anticipated to help spinal researchers, orthopaedic surgeons, and vehicle, train, aviation, and spaceship makers to design appropriate vibration-damping devices in the future. The novel computational model may also be used to further research on diseases (such as scoliosis) induced due to vibration effects on the spine in persons of all ages.
There are some limitations of this study that should be acknowledged. In this study, the human spinal column structure was simplified as a cylindrical beam, with all the vertebrae and intervertebral discs with cylindrical shapes, connected to each other. Additionally, no curvature in the spinal column structure was considered. This was done primarily to develop a finite element model which can be validated with literature-based results, and to focus on the study of the effect of aging spinal column on its vibrational properties. In future studies, more realistic human spinal column curvature and geometries of vertebrae and the intervertebral discs will be adopted to improve the accuracy of the results.