Abstract
This paper proposes a new approach to predicting the distribution of harmful substances in the atmosphere based on the combined use of the parameter estimation technique and machine learning algorithms. The essence of the proposed approach is based on the assumption that the concentration values predicted by machine learning algorithms at observation points can be used to refine the pollutant concentration field when solving a differential equation of the convection-diffusion-reaction type. This approach reduces to minimizing an objective functional on some admissible set by choosing the atmospheric turbulence coefficient. We consider two atmospheric turbulence models and restore its unknown parameters by using the limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm. Three ensemble machine learning algorithms are analyzed for the prediction of concentration values at observation points, and comparison of the predicted values with the measurement results is presented. The proposed approach has been tested on an example of two cities in the Republic of Kazakhstan. In addition, due to the lack of data on pollution sources and their intensities, an approach for identifying this information is presented.
1. Introduction
Outdoor air pollution has become a serious environmental problem that has a significant impact on public health, climate change and the health of ecosystems with the growth of industrialization and urbanization. It has been continuously monitored through a wide network of monitoring stations [1], which ranks the most polluted countries and regions based on average annual (particulate matter) concentration. The presented rating shows that air pollution exceeds WHO recommendations by more than ten times in many developing countries, and this figure exceeds three–five times in Kazakhstan. Therefore, the study of the problems caused by air pollution and predicting the spread of harmful substances in the atmosphere is still relevant throughout the world.
Modeling the distribution of harmful substances in the atmosphere is an important tool for studying and predicting their behavior and impact on the environment and human health. Strategies can be developed and measures be taken to minimize the impact of harmful substances on the environment with the help of models. Factors such as sources of emissions (for example, industrial enterprises, vehicles), meteorological conditions (wind velocity and its direction, turbulence, and atmospheric stability) and the chemical properties of the substances themselves are usually taken into account when modeling the distribution of harmful substances in the atmosphere.
Modeling of air pollution based on the solution of partial differential equations is a fairly reliable and well-established approach [2,3,4]. For example, Aydosov [5] developed a mathematical model for dispersion and transport of pollutants from an instantaneous point source in the atmosphere with partial absorption of surface impurities using a transport equation with a source term. To study the diffusion model of an accidental release of harmful substances under various conditions of atmospheric stability, the authors of [6] used the Reynolds-averaged Navier–Stokes model. The authors of [7] developed a mathematical model of mesoscale atmospheric processes, the transport and transformation of pollutants, and also numerically implemented the finite difference method assuming that the domain is rectangular. This technique was then improved in [8,9] in the case of a more complex geometry of the domain. In [3], a mathematical model was developed which is based on the equations of transfer and diffusion of aerosol emissions in the atmospheric boundary layer taking into account the terrain, weather and climatic factors. We also refer the reader to a comprehensive review [10] of relevant concepts, methods and models for the atmospheric transport of chemical, biological and radiologically hazardous pollutants. Also, the authors of [11] reviewed a number of methods for data analysis and modeling of air pollution and environmental impact, and identified the main parameters for choosing a method, namely the accuracy, interpretability, and spatiotemporal characteristics of the method. It should be noted that the accuracy of these models depends on the quality and reliability of input data such as emission data, meteorological conditions, topography and other parameters. It is also important to consider the uncertainty and variability of these parameters which can affect the accuracy of the model’s prediction. In practice, this is not always possible, since data are usually only available from stationary or mobile observation points which periodically measure the concentrations of pollutants at a few points.
Another approach for assessing and predicting the distribution of harmful substances in the atmosphere as well as managing air pollution is the use of machine learning algorithms. Machine learning analyzes a wealth of data such as meteorological conditions, geographic features, pollutant emissions and other factors to predict the spread of harmful substances and assess their impact on the environment and human health. Many studies have shown that this approach is effective due to its high robustness and accuracy, and it usually requires less labor.
The advantage of machine learning is that it helps to find patterns based on statistical data that are inherent in a particular area, depending on climatic and geographical features and terrain. For example, recent studies employed principal component analysis and an artificial neural network to predict concentrations in Urmia, Iran [12], the Harris Hawk multiobjective optimization algorithm to predict the hourly concentrations of and in Jinan, Nanjing, Chongqing [13], Lagrange and Bayesian methods to predict hourly concentrations of and in Xingtai [14], a hybrid remote sensing and machine learning approach to predict daily concentrations of in the Beijing-Tianjin-Hebei region [15], XGBoost, KNN, GNB, SVM and RF models to analyze and predict air quality in several cities in India [16], a spatiotemporal graph neural network to predict ozone concentration based on the GraphSAGE paradigm in Houston-TX [17], and a SVR-based model to predict and concentrations in Chile [18]. Feng et al. [19] used artificial neural networks and wavelet transform to predict concentrations from geographic models. Li et al. used integrated reinforcement learning to predict daily concentration of [20]. Moreover, hybrid artificial intelligence models are also used to predict environmental pollution, such as EEMD-LSSVM [21], PCA-CS-LSSVM [22], WPD-PSO-BNN-AdaBoost [23], PSO-ELM [24], GA-RF-BPNN [25], CEMD-PSOGSA-SVR-GRNN [26], WPD-CEEMD-LSSVR-CPSOM-GSA [27], VMD-SE-LSSVM [28], CEEMD-CS-GWO-SVM [29], WPD-Bi-LSTM-NSGA-II [30] and many others. A comprehensive overview of deep learning methods for predicting the concentration of air pollutants can be found in the papers [31,32]. The work [33] provides a comprehensive overview of the sources and impacts of pollutants on the environment and human health, on methods for predicting environmental pollution.
Some studies are aimed at a comparative analysis of machine learning algorithms in relation to the prediction of atmospheric pollution. For example, Kumar et al. [16] showed that the XGBoost model shows the best results among other models such as KNN, GNB, SVM, RF and provides the highest linearity between predicted and actual data. Li et al. [15] demonstrated that the proposed RSRF model provides better performance and relatively high prediction accuracy than the MLR, MARS and SVR models. Liang et al. [34] concluded that stacking ensemble and AdaBoost can outperform methods such as SVM, RF, and ANN. Bekkar et al. [35] compared the performance of deep learning algorithms such as LSTM, Bi-LSTM, GRU, Bi-GRU, CNN, and a CNN-LSTM hybrid model and showed through experimentation that the CNN-LSTM hybrid method produces more accurate predictions, and it has high precision and stability.
Note that the above approaches rely either on solving differential equations using measurement results as input data, or on machine learning models that allow for identifying a pattern in long-term measurement data and make a prediction of the pollutant distribution on their basis.
In this paper, we propose a new approach that combines both of these techniques. We assume that the process of pollutant propagation in the atmosphere is described by a differential equation of the convection-diffusion-reaction type. In addition, we assume that long-term measurement data of the concentration values at observation points are available, on the basis of which it is possible to make a forecast of future concentration values at these points by a machine learning algorithm. The essence of the proposed approach is based on the assumption that pollutant concentrations at observation points, predicted by a machine learning algorithm, can be used to refine the solution of a differential equation. This approach is reduced to minimizing a penalty function which is defined as the difference between the solution of the differential equation and the predicted values at observation points. We propose an effective numerical method to solve the resulting problem by a combined use of the parameter estimation technique and the finite element method.
The main hypothesis of the study is the assumption that the predicted concentration values at observation posts may serve as a good basis for refining the forecast results that are produced by solving differential equations.
The proposed methodology is tested on two cities of Kazakhstan, Ust-Kamenogorsk and Almaty. The choice of Ust-Kamenogorsk is justified by the fact that the most unfavorable situation was observed in this city according to the results of analysis of data obtained from stationary atmospheric air observation posts in 26 cities of Kazakhstan [36]. Many studies have been carried out regarding the atmospheric state of Ust-Kamenogorsk [7,37,38,39,40,41,42]. The fact that the city is located in a mountainous area is unfavorable, which prevents dispersion, and leads to the accumulation of harmful substances. Industrial processes in the East Kazakhstan region include a wide range of activities that lead to the emission of various harmful substances into the atmosphere [43]. The state of atmospheric air in the second city, Almaty, has been studied in many works [44,45,46,47,48,49]. It is believed that the main sources of air pollution in the city are vehicles, thermal power plants, industrial enterprises, as well as private houses with their own heating system.
The present paper is structured as follows. Section 2 describes the proposed approach to predicting the distribution of harmful substances in the atmosphere. Section 3 presents the results of some numerical results to confirm the theoretical analysis. Finally, in Section 4, we discuss the results obtained.
2. Materials and Methods
2.1. The Proposed Approach
Modeling the spread of harmful substances in the atmosphere is effectively carried out on the basis of the differential equation jointly taking into account convective, diffusion and reaction processes:
where is the pollutant concentration, is the domain in which the solution is sought, is the time interval for which the forecast is made, is the wind velocity vector, is the atmospheric turbulence coefficient, , is the number of point pollution sources, and are the coordinates and intensity of the s-th pollution source, respectively, and r is the reaction coefficient. Equation (1) is supplemented by the concentration distribution at the initial time
and homogeneous first-kind boundary conditions under the assumption that the boundary of the domain is far enough away:
Modeling real processes with Problem (1)–(3) is generally accompanied by many difficulties. First, a reliable determination of the atmospheric turbulence coefficient is a non-trivial problem. This is due to the fact that this parameter depends on local features of the area under study and is characterized by a rapid change from point to point [50]. This problem is especially complicated in urban areas where high-rise buildings are built up, which can lead to the formation of turbulent movements.
Secondly, it is rarely possible to reliably determine the location and release intensity of the pollution sources, i.e., the right-hand side of Equation (1). In practice, average statistical annual waste rates are often accepted as sources, or this information is recovered from the readings of stationary or mobile sensors installed at some observation points , . In some cases, the missing data is recovered using the specified sensor data.
There are many factors leading to uncertainty of the contaminants movement even in case the input parameters are identified exactly. However, if there are long-term measurements data of the pollutants concentration for a certain period, it is possible to identify a seasonal pattern of their dynamics. For example, increased distribution of a pollutant may be typical at certain times of the year or day. Recently, machine learning algorithms have been effectively used to identify such a pattern and extract additional auxiliary information that is unique to a given area [18,51]. In addition, based on the found pattern, these algorithms are able to make a fairly accurate prediction of the concentration , at observation points , for a certain period of time J in the future.
The main hypothesis of this study is the assertion that future concentration values predicted by machine learning algorithms can be used to refine the concentration field determined from Problem (1)–(3). Mathematically, this means that it is possible to impose a constraint on the desired solution by minimizing the functional
in some admissible domain. This condition means that the predicted concentration values at observation points , serve as reference values and can provide additional information about the concentration distribution while solving Problem (1)–(3).
Thus, the proposed approach to solve the problem, a flowchart of which is shown in Figure 1, consists of two stages.
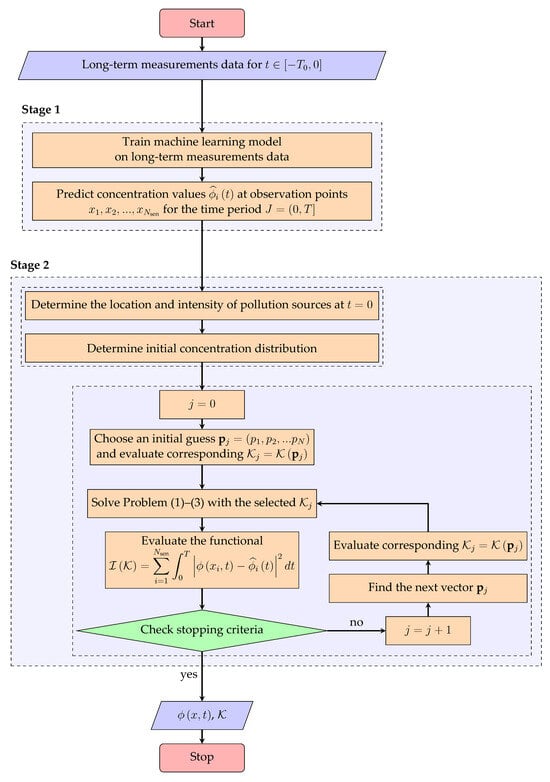
Figure 1.
Algorithm for solving the problem.
Stage 1. Train a machine learning model on long-term measurement data at observation points , to predict the concentration of a pollutant at these points for a certain period of time in future. A schematic representation of this stage is depicted in Figure 2.
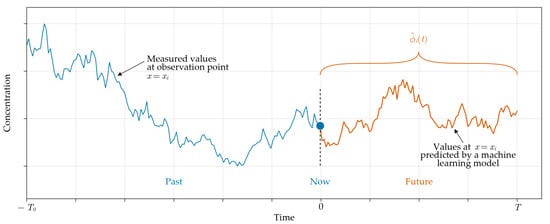
Figure 2.
Measured and predicted concentration values at observation point , .
Stage 2. Using the predicted values , minimize the functional (4). The essence of this stage is to find such a solution to the differential problem (1)–(3), in which the values at the observation points deviate least from the predicted values . We assume that this can be achieved by an appropriate choice of the atmospheric turbulence coefficient .
Suppose that can be unambiguously represented by a vector of several numerical parameters to be identified:
To determine them, an iterative process is constructed starting from an arbitrarily chosen initial estimate to generate a sequence of parameters (Figure 1). The iterative process consists in solving Problems (1)–(3) multiple times with the atmospheric turbulence coefficient and modifying with the use of an optimization algorithm. The iterative process is interrupted when the value of the functional (4) for the next found satisfies a certain stopping condition.
The process of adapting the solution of Problems (1)–(3) to the constraint (4) within the iterative process is schematically shown in Figure 3.
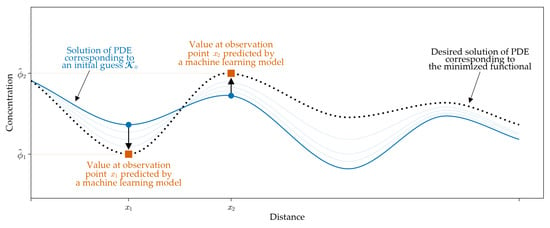
Figure 3.
A one-dimensional sketch of the process of determination of the solution satisfying the constraint (4).
The rest of Section 2 is devoted to a more detailed description of the above steps. Note that this problem is technically difficult in the general case. Let us introduce some assumptions to simplify the presentation of the method. First, we assume that wind flow velocity does not change over the entire time interval. In addition, we assume that the intensity of pollution sources is constant. These assumptions are valid when the forecast is made for a short period of time and can be eliminated by a slightly technical complication of the algorithm.
2.2. Prediction of Pollutant Concentrations at Observation Points Based on Machine Learning
According to the first stage of the proposed approach, machine learning algorithms are utilized to predict values of the pollutants concentration at observation points. Model training is preceded by several key steps, such as missing data imputation, the detection and removal of outliers, and feature selection based on statistical correlation. These steps are described in detail in many papers [16,18]. Then Sklearn’s GridSearchCV library was applied for cross-determining the optimal parameters of the model.
This study did not aim to determine the best machine learning model among all existing ones, so the results of this section are not exhaustive. However, based on a literature review, the choice fell on the so-called ensemble learning techniques, which have recently become popular and are recognized as effective. In this paper, we study the applicability of the following three ensemble machine learning models.
The first model, XGBoost [52], is an implementation of the stochastic gradient boosting algorithm. This is an ensemble decision tree algorithm in which new trees correct the errors of those trees that are already part of the model. Trees are added until no further improvements can be made to the model.
The second model, LightGBM [53], is a gradient boosting framework using tree-based learning algorithms. It is designed for distribution and efficiency and aims for a higher learning rate and higher efficiency, lower memory usage, better accuracy, support for parallel, distributed and graph learning, and large data processing capability. According to recent studies [54], LightGBM shows faster training results than XGBoost while showing similar accuracy.
The third model, Histogram-Based Gradient Boosting (HistGradientBoosting) [55], is a LightGBM-inspired implementation of gradient boosting trees. It also has built-in support for missing values, which avoids the need for an imputer.
The fit and stability of the models are measured by the determination coefficient (), mean absolute error (MAE) and root mean square error (RMSE). The value of the determination coefficient ranges from 0 to 1; approaching extreme values, 1 and 0, implies high and low efficiency, respectively. The RMSE evaluates the average difference between the observed and predicted values.
2.3. Identification of the Atmospheric Turbulence Coefficient
According to Stage 2 of the proposed approach, an optimization algorithm is used to modify the vector of parameters . Suppose that each of is bounded by finite numbers and . In this work, we study the applicability of several well-known algorithms to the parameter estimation problem. The study involved the Conjugate Gradient method, limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm (L-BFGS), Nelder-Mead method, Bound Optimization by Quadratic Approximation (BOBYQA), New Unconstrained Optimization with Quadratic Approximation (NEWUOA). The choice of these algorithms is based on their successful usage in previous studies on parameter estimation and related problems [56,57,58,59].
The limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm (L-BFGS) [60] is a quasi-Newton type algorithm that is based on calculating the inverse Hessian matrix to find the optimum in the admissible set. Unlike the classical BFGS algorithm from which it is derived, L-BFGS uses only a few vectors representing an approximation of the inverse Hessian matrix. Significant advantages of the method are the use of less memory, the speed of the algorithm and the ease of implementation. Therefore, this algorithm is widely used in multidimensional optimization problems.
NEWUOA is an optimization algorithm which is based on constructing a quadratic model using the values of the objective function [61]. The model is assumed to be valid in a neighborhood, the trust region, the radius of which is refined during the iterative process. After this, the model is minimized in the trust region with the use of a truncated conjugate gradient algorithm. BOBYQA is an generalization of the NEWUOA algorithm to the case of bounded problems [62].
The Nelder-Mead algorithm solves multidimensional unconstrained optimization problem which does not require any derivative information. This algorithm is known to be successfully applied to solve parameter estimation and related problems with uncertain values of the objective function.
Section 3.3 presents numerical tests to check the applicability of these algorithms to the problem of the identification of atmospheric turbulence coefficient.
2.4. Solving the Initial Boundary Value Problem
Let us briefly describe the finite element procedure for an approximate solution of the initial boundary value problem (1)–(3). To this end, we introduce the finite element space , where the standard notation for Sobolev spaces is used. Next, we introduce a partition in the time interval , where is a time discretization parameter. Denote by the finite element solution of the problem at the time stamp .
Let the solution , be known, where, in particular, is the -projection of the initial distribution of concentration . The finite element method for solving the problem is to find satisfying the identity
for all test functions , where is the dot product in , is the -approximation of the right-hand side of Equation (1) at time stamp defined as in [63].
We use quadratic finite elements on a quadrilateral mesh and applied the solution approach described in our previous paper [64]. Using Taylor expansion, it can be shown that the presented method converges with the first order with respect to the time step which is a sufficient accuracy for our purposes. However, higher order convergence can also be obtained using higher order approximation formulas.
2.5. Determination of the Initial Field of the Pollutant Concentration
It is assumed in most papers that there are no pollutants in the atmosphere before the air pollution incident, i.e., for all . This assumption significantly simplifies the solution of the problem. However, when this is not the case, determining the initial concentration field (2) is a complex problem that requires significant research. Moreover, in the presence of reliable data on the location and intensity of pollution sources, there are efficient methods that allow one to fairly accurately restore the concentration field in the entire domain.
In our case, we do not have the above information, so we relied on the following simple approach, which allowed us to approximately restore the missing data. First, we determine the pollution sources using the Gaussian plume model and a heuristic algorithm based on the measured concentration values at the observation points. Then, using the found values, we restore the concentration field in the entire domain.
To achieve this, we define the cost function as the sum of deviations between the actually measured values at the observation points , and their numerical approximations :
The use of the Gaussian plume model assumes that the numerical approximation is represented as the sum of the contributions from each of the sources:
There are many ways to evaluate the numerical approximation . According to one of them, the concentration value at the point scattered from the s-th source is defined as
where is the intensity of the s-th source, is the distance between point and pollution source , U is the wind speed, and is a unit vector along the -axis.
To minimize the objective function (6), we use the evolution centers algorithm [65] which relies on fundamental laws of physics and mechanics and utilizes the definition of the center of mass to identify new directions in order to move the worst elements in the population to the best parts of the admissible domain based on their objective function values. To apply the algorithm, we define a population with N solutions, where the tuple is represented by the source coordinate and intensity . According to the algorithm, a subset with K solutions is selected. Calculating the center of mass from U and randomly choosing a solution , we generate a direction for finding a new solution :
where
3. Results
In this section, we present some numerical results to verify the method proposed in Section 2.
3.1. Analysis of the Long-Term Measurement Data
The proposed methodology was tested on two datasets containing long-term measurement data in two cities of Kazakhstan. The first dataset, which will be referred to as Dataset A, is based on measurements from five sensors located in the industrial city of Ust-Kamenogorsk that analyze air quality and measure concentrations of several pollutants in the atmosphere. Several industries are located in the northern part of the city, but significant pollution is believed to come from motor vehicles and the areas with a cluster of residential buildings with their own heating systems. The location of automated observation points in the city was chosen so as to cover the most polluted part of the city and give an objective assessment of the air condition in different parts of the city due to the spread of harmful substances.
The dataset covers the results of observation from 2005 to 2021 and contains the results of measuring the concentration of seven chemical compounds in the atmosphere with some periodicity. The frequency of measurements in the specified period was not always the same—the interval between measurements was 4 h to a greater extent, less often measurements were taken every 3 h, and exceptional cases were limited to only three measurements a day. The data collected also includes the ambient air temperature, atmospheric pressure, wind direction and its velocity, relative humidity, and an atmospheric phenomenon code. The atmospheric phenomenon is represented by an integer from 0 to 9, the values and description of which are given in Table 1.

Table 1.
Definition of atmospheric phenomenon codes in Dataset A.
Table 2 lists the statistical characteristics of the pollutants in the dataset. The Count column indicates the number of values after the removal of deliberately incorrect values and outliers. The remaining columns characterize the mean, standard deviation, median, extreme values, and quartiles of the measured data.

Table 2.
Statistical characteristics of pollutants in Dataset A.
The second dataset, Dataset B, contains the results of measurements of five chemical compounds at 30 observation posts of an industrial city (Almaty) from 2020 to 2022 with a period of 20 min. The statistical characteristics of the dataset are given in Table 3.

Table 3.
Statistical characteristics of pollutants in Dataset B.
3.2. Comparison of Machine Learning Models
Let us focus on the selection of features for training the machine learning models. It follows from the analysis of the correlation matrices presented in Table 4 and Table 5 that the values, in general, do not correlate well with each other in both datasets. However, the influence of temperature, atmospheric pressure, and, in some cases, wind velocity and atmospheric phenomenon is clearly traced. Therefore, these four parameters were taken as features along with the chemical compound under study.

Table 4.
Correlation matrix for Dataset A.

Table 5.
Correlation matrix for Dataset B.
Note that the direct application of the three machine learning models did not give consoling results with the selected features set. The models could not find a pattern of concentration behavior over time, and verification on test data led to a large discrepancy between the predicted values and actual measurements. Therefore, the time lag approach is employed in order to better catch the pattern. In other words, target values from previous periods were utilized as features in addition to the selected ones. Namely, three features according to the time lags equal to 364, 728 and 1092 days were added.
The models were trained on the first dataset corresponding to the time period up to 2020, and verification was carried out on the data of 2021. For completeness of the study, training was carried out for each automated observation post separately.
The number of estimators varied between 500 and 1000 when training the XGBoost model. The LightGBM model was trained with the following set of parameters: maximum depth was chosen to be 50, the number of leaves was 512, maximum bin was 512, the number of iterations was 200, and the boosting type was GBDT. The HistGradientBoosting model was trained with the following parameters: maximum iterations was chosen to be 600, and the iterations interrupted when no changes took place in the last 10 iterations.
Table 6 shows the coefficient of determination obtained for the machine learning models and chemical compounds considered. It is clearly seen from the training results that all three models work quite well for chemical compounds in case the initial data is complete, and corresponding scores are close to each other. In particular, for the top three rows of Table 2, and , this indicator varied in the range of 0.91–0.95, which indicates a good trainability of the models considered.

Table 6.
The coefficient of determination ( Score) for Dataset A.
However, in the case of chemical compounds for which the data were insufficient, Table 6 clearly shows that the XGBoost model performed worse in training. In particular, for and , the XGBoost model showed the worst results where was between 0.4 and 0.7. On the contrary, the LightGBM and HistGradientBoosting models trained quite well and the scores on the specified data set ranged from 0.8 to 0.9. One can conclude that the LightGBM and HistGradientBoosting models are more resistant to data incompleteness, and therefore these models can be used to implement this stage of the proposed approach.
The mean absolute error (MAE) and root mean squared error (RMSE) indicators for the XGBoost, LightGBM and HistGradientBoosting models are shown in Table 7.

Table 7.
Mean squared error (MSE), mean absolute error (MAE) and root mean squared error (RMSE) for the XGBoost model.
Similarly, calculation results of the coefficient of determination for Dataset B are shown in Table 8. Due to relative completeness of information, score was mostly higher than 0.95. Occasionally, the dataset contained incomplete data for , , and on a few observation points. This was reflected in the coefficient of determination, and all three models showed fairly close values.

Table 8.
The coefficient of determination ( Score) for Dataset B.
Now let us verify the predicted values on the test data over a monthly time interval from 1 December 2021 to 1 January 2022 and depict the forecast values obtained by the XGBoost, LightGBM and HistGradientBoosting models, as well as the actually measured data for the same period. The results of such an analysis for the chemical variables , and at one of the automated posts are shown in Figure 4. It can be seen from the results that all three models make it possible to predict future concentration values quite well in cases where the data is complete.
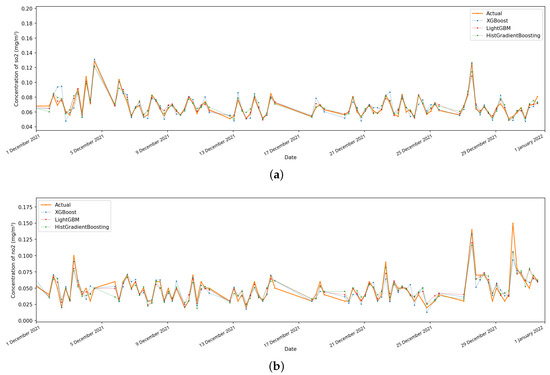
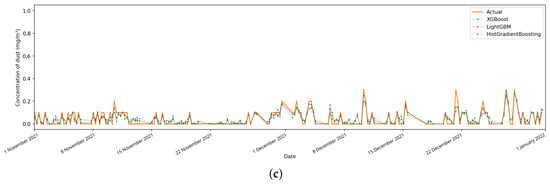
Figure 4.
Forecast and actual values of , and concentrations for last months of 2021 at Observation Point 5. (a) Concentration of ; (b) concentration of ; (c) concentration of .
3.3. Identification of the Atmospheric Turbulence Coefficient
There are many atmospheric turbulence diffusion coefficients commonly used in modeling of propagation of impurities in the atmosphere. In this study, we consider a few slightly modified models [66,67]:
where , , are some real parameters, M is a positive integer, is the distance function respresenting the downwind distance, is the diffusivity of the long-term diffusion limit, k is the wave number, is the wave number corresponding to the largest turbulent eddies, is a positive real number and B is a dimensionless constant which were chosen to be and in [66], is the crosswind dispersion, and U is the wind speed.
The aim of this computational experiment is to compare optimization algorithms in relation to the identification of atmospheric turbulence coefficient parameters based on the parameter estimation technique. To this end, consider Problem (1)–(4) in with , , and a known exact solution in the following four cases depending on the atmospheric turbulence coefficients (9)–(12).
Case 1. Consider the model (9) with and let be the pollution source. In this case, depends on two unknown parameters to be identified. In this numerical test, the right-hand side of Equation (1) is chosen as
Thus, the atmospheric turbulence coefficient to be identified is . The initial estimate for the parameters was chosen to be . Then a series of initial boundary value problems (1)–(3) with different coefficients , was solved according to Stage 2 of the proposed approach presented in Figure 1, where the subsequent values were determined by optimization algorithms listed in Section 2.3. The values of the exact solution at points , , and time stamps were utilized as the values of in the functional (4). Thus, the functional was evaluated with the use of 15 observation points in total.
Case 2. Consider the model (10) where we restrict ourselves to the case for simplicity of presentation. Then depends on six unknown parameters . The right-hand side of Equation (1) was chosen as follows:
Therefore, the atmospheric turbulence coefficient to be identified is
The problem was solved with an initial estimate . The rest of the computational experiment was carried out in the same way as in Case 1.
Case 3. Consider (11) with an unknown parameter . The rest of the parameters are chosen as follows: , , , . The initial estimate for the parameter was chosen as , then the computational experiment is continued as described in Case 1. The desired value of the parameter is 4/3.
Case 4. Consider (12) with unknown parameters , where we assume that the pollution sources are located at points and , and . The computational experiment started with the initial estimate for the parameters and continued as described in Case 1. The vector of the parameters to be identified is .
Numerical solution of the initial boundary value problem (1)–(3) was performed with the use of quadratic finite elements on a quadrilateral mesh consisting of 400 elements and 1681 nodes according to Section 2.4. The algorithm was implemented in the Julia programming language [68] with the use of the Ferrite package [69]. The time discretization parameter was chosen to be . The solution of one initial boundary value problem on a 10 core computer with the Intel Core i9 processor and 64 GB of RAM took less than 1 s.
Optimization algorithms were compared according to three criteria:
- (1)
- (2)
- The error of the identified parameters which was estimated using the formula , where is vector of exact parameter values.
- (3)
- Total execution time.
The result of the computational experiment is summarized in Table 9.

Table 9.
Comparison of optimization algorithms in the parameter estimation problem.
It can be seen that all the considered optimization algorithms make it possible to accurately identify the atmospheric turbulence coefficient when its parameters are positive multipliers (Cases 1 and 4). NEWUOA demonstrated an excellent result in terms of both iterations count and the execution time which allows it to be effectively used in this class of problems. The BOBYQA, L-BFGS, and Nelder-Mead algorithms required two–four times more iterations and time. In Case 3, when it was necessary to identify the degree of an expression, the Nelder-Mead algorithm failed to achieve convergence and NEWUOA is not applicable to identifying one parameter, while the BOBYQA, Conjugate Gradient and L-BFGS algorithms showed comparable results.
In Case 2, when the vector of unknown parameters contained both positive and negative coefficients, the BOBYQA and NEWUOA algorithms could not achieve convergence and the computational experiments were interrupted when the number of calls exceeded 20,000; the column “Error” indicates the best error indicator for the performed iterations in this case. In contrast, the Conjugate Gradient and L-BFGS algorithms were able to identify coefficients with almost the same accuracy. The obvious disadvantage of the conjugate gradient method in this test was the extremely slow convergence of the iterations.
In real atmospheric turbulence models, the parameters can take both positive and negative values. Therefore, this criterion was critical when choosing an algorithm. Overall, the L-BFGS algorithm turned out to be the most stable and successfully identified unknown parameters in a wide class of functions while achieving greater accuracy. Therefore, this algorithm was employed in subsequent numerical tests.
3.4. Forecasting the Spread of a Contaminant in the Atmosphere
We are now ready to apply the proposed approach to a more realistic problem. The goal of the first computational experiment is to predict the dynamics of the concentration field in the city of Ust-Kamenogorsk during one day, 31 December 2021.
As previously stated in Section 3.1, there are five observation points in Ust-Kamenogorsk. According to the first step of the algorithm presented in Figure 1, we first train a machine learning model to predict the values at the observation points. We utilized the LightGBM model based on the analysis of the score evaluated in Section 3.2.
Further, according to the second step of the algorithm, the location and intensity of pollution sources of , and are determined which are shown in Table 10. We considered two cases in which the maximum sources count in (7) was set to and , respectively. Overall, the coordinates found correspond to the real sources of air pollution in the city. For example, sulfur oxides are emitted to the atmosphere when coal, oil and natural gas are burned in thermal power plants, residential heating using wood and coal in the areas with a cluster of residential buildings, and metal smelting and sulfuric acid production. Indeed, most of the found points are close to the areas with a cluster of residential buildings, so in these areas there is territorial pollution from heating systems. In addition, the point with coordinates (49.977935, 82.643055) is located in close proximity to the Ust-Kamenogorsk metallurgical complex of Kazzinc LLP and Ulba Metallurgical Plant JSC. The point with coordinates (50.008971, 82.725308) is located near Ust-Kamenogorsk titanium-magnesium plant JSC and AES Sogrinskaya thermal power station LLP. In the area of the point with coordinates (50.008625, 82.576470) there is indeed a railway station, which is one of the sources of air pollutants. In addition, the source of formation of nitrogen oxides are the products of combustion of thermal power plants, vehicle exhausts, and waste from metallurgical industries.

Table 10.
Recovered sources of contaminants as of 31 December 2021 at 1 AM.
To check the correctness of the sources found, we calculate the concentration values at the observation points again based on these sources and compare the obtained values with the actual values at the same points as described in Section 2.5. Overall, one can conclude that the proposed method is able to quite accurately determine the sources of pollution based on the results of the comparison presented in Table 11. However the identification error varied between and under an assumption of six pollution sources, and the error increased considerably when the maximum pollution sources count was set to two.

Table 11.
Verification of the correctness of the found sources through comparison.
In addition, the initial concentration was approximated as described in Section 2.5.
Further, a finite element mesh was introduced in the domain , and in the neighborhood of observation points and identified sources, the mesh was refined for a more detailed study of the solution near these points. Then, scattered interpolation by Shepard’s method was used to interpolate wind vector field in each element using information about the direction and velocity of the wind at the observation points.
In order to verify the adequacy of the proposed approach, we conduct the algorithm presented in Figure 1 on the base of four observation points with internal numbers 5, 7, 8 and 12 to obtain the solution of Problem (1)–(3) satisfying the constraint (4). Then we compare the obtained solution with a real measurement value at the fifth observation point with an internal number 1 which will serve as a control point. Assessing the proximity of these values will allow us to evaluate the correctness of the resulting solution. The reason for choosing the location of the control point was to verify the concentration in the inner part of the city near industrial facilities.
The model (12) with was accepted as the atmospheric turbulence coefficient. Therefore, the coefficient depended on three unknown parameters— (), (m) and (m), which we represent by a vector . It was assumed that and the vector was taken as the initial estimate. This value was reported by the authors of [7] who studied propagation of contaminants in the atmosphere of Ust-Kamenogorsk based on photochemical reactions. Based on the conclusions of Section 3.3, subsequent vectors , in the iterative process of Stage 2 were found using the L-BFGS optimization algorithm.
In the time interval corresponding to 24 h, a uniform partition was introduced which contained 3200 time layers with a step of s. The integrals in (4) were evaluated by the trapezoidal rule; the value of the functional was calculated at four observation points every 6 h, which led to the minimization of a sum consisting of 16 terms. Moreover, in contrast to the problems considered earlier, we have replaced the boundary condition of the first kind with a homogeneous boundary condition of the second kind [70].
The value of the functional was approximately equal to 1.449949 for the chosen initial estimate vector. The value of the solution at the control point was equal to 0.067981 which differs from the actually measured value by 0.014019. The iterative process within Stage 2 was conducted until the objective function satisfied the condition
with . This condition was achieved at the 1287th iteration, and the following values of the parameters were identified: . The value of the objective function for these coefficients was approximately equal to 0.026079. The value of the solution at the fifth observation point was approximately equal to 0.081435 which differs from the actually measured value by 0.00281612 (Table 12). However, the obtained result can be considered acceptable despite the simplicity of the adopted model of the atmospheric turbulence coefficient.

Table 12.
Comparison of actual measured values, the values predicted by the machine learning algorithm and the values identified by the proposed algorithm in Ust-Kamenogorsk as of 31 December 2021 at 7 PM.
Verification of the proposed approach was conducted on Dataset B in a similar way. The goal was to predict concentration on 1 November 2022. First, we set the maximum sources count . The median identification error evaluated as in Table 11 was equal to .
Then we considered a subset of 10 observation points located in the center part of the city: Alm-002, Alm-005, Alm-007, Alm-008, Alm-010, PNZ-1, PNZ-2, PNZ-3, PNZ-5 and PNZ-6. The comparison of the solution was performed at Alm-002 and Alm-008, and the algorithm was conducted on the rest of the observation points. The sought coefficient depended on seven unknown parameters . Unfortunately, the literature review did not reveal studies aimed at determining the value of the turbulence coefficient for the city of Almaty. However, the surface roughness of the outskirts of the cities of Ust-Kamenogorsk and Almaty is identical, since both cities are surrounded on one side by the Altai and Alatau mountain ranges, respectively, and on the other side are plains. Therefore, it was expected that the nature of turbulent mixing of atmospheric air was approximately the same. In this regard, we took the vector with as defined above for the city of Ust-Kamenogorsk and as the initial estimate for Dataset B. The value of the functional was approximately equal to 1.199794 for the chosen initial estimate.
The stopping criterion (13) was satisfied at the 1784th iteration; the resulting parameters vector was , and the corresponding value of the objective function was equal to 0.068131. The values of the obtained solution at the two control points, Alm-002 and Alm-008, were equal to 0.008950 and 0.067400, respectively, which deviate from the actually measured values by 0.013 and 0.028, respectively. The result of the calculations made for Dataset B are presented in Table 13.

Table 13.
Comparison of actual measured values, the values predicted by the machine learning algorithm and the values identified by the proposed algorithm in Almaty as of 1 November 2022 at 8 PM.
4. Conclusions
Let us provide a few comments about the results obtained and outline future research directions.
(1) In general, the problem of determining the coefficient of atmospheric turbulence is quite complex, and the presence of a large number of different models of atmospheric turbulence indicates that there is still no unified method for its determination. Our work proposes one of the approaches that allows one to refine the parameters included in these models. In particular, in comparison with paper [7], a refined value of the atmospheric turbulence coefficient was obtained. In the computational experiment carried out, the error in determining the concentration at the control point was reduced from 0.014019 to 0.002816.
(2) Ensemble models can be effectively used when training machine learning models in the problems of predicting the distribution of harmful substances in the atmosphere. It can be concluded from the analysis made that all three considered models, XGBoost, LightGBM and Histogram-Based Gradient Boosting, can effectively make a prediction of the concentration at observation points. This observation is also consistent with the conclusions of the papers [71,72,73,74]. Additionally, it has been observed that the LightGBM and Histogram-Based Gradient Boosting models are more resistant to data incompleteness, therefore it is recommended to use these models in this case.
(3) A more realistic problem of the spread of a harmful substance in the atmosphere has been solved on the example of the city of Ust-Kamenogorsk, Kazakhstan using the proposed approach. Due to the methodological nature of the work, the results of the forecast can be considered quite acceptable. Note that the relatively large value of the target functional obtained in Section 3.4 may indicate that more significant factors were not taken into account when modeling the spread of a harmful substance. These may include orographic features of the area and high-rise buildings. In addition, the study uses data from a fairly small number of observation points. Another important factor is the use of a two-dimensional convection-diffusion-reaction model at a fixed height, as well as the use of the simplest Gaussian plume model in determining the initial distribution field.
(4) Since the approach is proposed for the first time, the technical methods used can be improved without significant difficulties. For example, a three-dimensional generalization of the governing equation with a more complex turbulence coefficient can be used, which can more accurately describe the motion of the harmful substance. Another possibility for improving the results is taking into account the terrain, high-rise buildings and other features of the area under study. These issues deserve a separate study, which will be the subject of a subsequent paper.
In general, despite many simplifying assumptions, the developed algorithm showed a plausible dispersion of the pollutant. Hence, we concluded that this algorithm can be taken as a basis when considering more complex models that take into account more factors.
Author Contributions
Conceptualization, N.T. and M.M.; methodology, M.M.; software, M.M. and Y.M.; validation, M.M., Y.Y. and N.A.; formal analysis, N.A.; investigation, M.M.; resources, Y.M.; data curation, Y.Y.; writing—original draft preparation, N.A.; writing—review and editing, M.M.; visualization, M.M.; supervision, N.T.; project administration, N.T.; funding acquisition, N.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research is funded by the Science Committee of the Ministry of Science and Higher Education of the Republic of Kazakhstan, grant number BR18574148 “Development of geoinformation systems and monitoring of environmental objects”.
Data Availability Statement
Data is unavailable due to privacy restrictions.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AdaBoost | Adaptive Boosting |
| BNN (or BPNN) | Backpropagation Neural Network |
| CEEMD | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| CEMD | Complementary Empirical Mode Decomposition |
| CNN | Convolutional Neural Network |
| CPSWOM | Chaotic Particle Swarm Optimization Method |
| CS | Cuckoo Search |
| EEMD | Ensemble Empirical Mode Decomposition |
| ELM | Extreme Learning Machine |
| GA | Genetic Algorithm |
| GNB | Gaussian Naive Bayes |
| GRNN | Generalized Regression Neural Network |
| GSA | Gravitation Search Algorithm |
| GWO | Grey Wolf Optimizer |
| HistGradientBoosting | Histogram-Based Gradient Boosting |
| KNN | k Nearest Neighbor |
| L-BFGS | Limited-Memory Broyden–Fletcher–Goldfarb–Shanno Algorithm |
| LightGBM | Light Gradient-Boosting Machine |
| LSSVM | Least Square Support Vector Machine |
| LSSVR | Least Squares Support Vector Regression |
| LSTM | Long Short-Term Memory |
| MAE | Mean Absolute Error |
| MDPI | Multidisciplinary Digital Publishing Institute |
| MSE | Mean Squared Error |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| PCA | Principal Component Analysis |
| PM | Particulate Matter |
| PSO | Particle Swarm Optimization |
| RAM | Random-Access Memory |
| RF | Random Forest |
| RMSE | Root Mean Squared Error |
| SE | Sample Entropy |
| SVR | Support Vector Regression |
| VMD | Variational Mode Decomposition |
| WHO | World Health Organization |
| WPD | Wavelet Packet Decomposition |
| XGBoost | eXtreme Gradient Boosting |
References
- World’s Most Polluted Countries & Regions (Historical Data 2018–2022). Available online: https://www.iqair.com/world-most-polluted-countries (accessed on 10 June 2023).
- Ravshanov, N.; Sharipov, D. Advanced mathematical model of transfer and diffusion process of harmful substances in the atmospheric boundary layer. J. Adv. Res. Comput. Sci. Eng. 2016, 3, 18–27. [Google Scholar]
- Sharipov, D. Computer modeling of spreading of harmful substances in the atmosphere taking into account the local terrain. Theor. Appl. Sci. 2018, 61, 386–392. [Google Scholar] [CrossRef]
- Shafiev, T.; Shadmanova, G.; Karimova, K.; Muradov, F. Nonlinear mathematical model and numerical algorithm for monitoring and predicting the concentration of harmful substances in the atmosphere. E3s Web Conf. 2021, 264, 01021. [Google Scholar] [CrossRef]
- Aydosov, A.; Urmashev, B.; Zaurbekova, G. Modeling the spread of harmful substances in the atmosphere at a variable velocity profile. Open Eng. 2016, 6, 264–269. [Google Scholar] [CrossRef]
- Zhou, H.; Song, W.; Xiao, K. Simulating flow and hazardous gas dispersion by using WRF–CFD coupled model under different atmospheric stability conditions. Atmosphere 2022, 13, 1072. [Google Scholar] [CrossRef]
- Danaev, N.T.; Temirbekov, A.N.; Malgazhdarov, E.A. Modeling of pollutants in the atmosphere based on photochemical reactions. Eurasian-Chem.-Technol. J. 2013, 16, 61. [Google Scholar] [CrossRef]
- Temirbekov, N.; Malgazhdarov, Y.; Tokanova, S.; Amenova, F.; Baigereyev, D.; Turarov, A. Information technology for numerical simulation of convective flows of a viscous incompressible fluid in curvilinear multiply connected domains. J. Theor. Appl. Inf. Technol. 2019, 97, 3166–3177. [Google Scholar]
- Temirbekov, A.; Baigereyev, D.; Temirbekov, N.; Urmashev, B.; Amantayeva, A. Parallel CUDA implementation of a numerical algorithm for solving the Navier-Stokes equations using the pressure uniqueness condition. AIP Conf. Proc. 2021, 2325, 020063. [Google Scholar]
- Zhang, X.; Wang, J. Atmospheric dispersion of chemical, biological, and radiological hazardous pollutants: Informing risk assessment for public safety. J. Saf. Sci. Resil. 2022, 3, 372–397. [Google Scholar] [CrossRef]
- Gardner-Frolick, R.; Boyd, D.; Giang, A. Selecting data analytic and modeling methods to support air pollution and environmental justice investigations: A critical review and guidance framework. Environ. Sci. Technol. 2022, 56, 2843–2860. [Google Scholar] [CrossRef]
- Nouri, A.; Lak, M.G.; Valizadeh, M. Prediction of PM2.5 concentrations using principal component analysis and artificial neural network techniques: A case study: Urmia, Iran. Environ. Eng. Sci. 2021, 38, 89–98. [Google Scholar] [CrossRef]
- Du, P.; Wang, J.; Hao, Y.; Niu, T.; Yang, W. A novel hybrid model based on multi-objective harris hawks optimization algorithm for daily PM2.5 and PM10 forecasting. Appl. Soft Comput. 2020, 96, 106620. [Google Scholar] [CrossRef]
- Guo, L.; Chen, B.; Zhang, H.; Zhang, Y. A new approach combining a simplified FLEXPART model and a bayesian-RAT method for forecasting PM10 and PM2.5. Environ. Sci. Pollut. Res. 2019, 27, 2165–2183. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Zhang, X. Predicting ground-level PM2.5 concentrations in the Beijing-Tianjin-Hebei region: A hybrid remote sensing and machine learning approach. Environ. Pollut. 2019, 249, 735–749. [Google Scholar] [CrossRef] [PubMed]
- Kumar, K.; Pande, B.P. Air pollution prediction with machine learning: A case study of indian cities. Int. J. Environ. Sci. Technol. 2023, 20, 5333–5348. [Google Scholar] [CrossRef] [PubMed]
- Oliveira Santos, V.; Costa Rocha, P.A.; Scott, J.; Van Griensven Thé, J.; Gharabaghi, B. Spatiotemporal Air Pollution Forecasting in Houston-TX: A Case Study for Ozone Using Deep Graph Neural Networks. Atmosphere 2023, 14, 308. [Google Scholar] [CrossRef]
- Carreño, G.; López-Cortés, X.A.; Marchant, C. Machine Learning Models to Predict Critical Episodes of Environmental Pollution for PM2.5 and PM10 in Talca, Chile. Mathematics 2022, 10, 373. [Google Scholar] [CrossRef]
- Feng, X.; Li, Q.; Zhu, Y.; Hou, J.; Jin, L.; Wang, J. Artificial neural networks forecasting of PM2.5 pollution using air mass trajectory based geographic model and wavelet transformation. Atmos. Environ. 2015, 107, 118–128. [Google Scholar] [CrossRef]
- Li, Y.; Liu, Z.; Liu, H. A novel ensemble reinforcement learning gated unit model for daily PM2.5 forecasting. Air Qual. Atmos. Health 2020, 14, 443–453. [Google Scholar] [CrossRef]
- Bai, Y.; Zeng, B.; Li, C.; Zhang, J. An ensemble long short-term memory neural network for hourly PM2.5 concentration forecasting. Chemosphere 2019, 222, 286–294. [Google Scholar] [CrossRef]
- Sun, W.; Sun, J. Daily PM2.5 concentration prediction based on principal component analysis and LSSVM optimized by cuckoo search algorithm. J. Environ. Manag. 2017, 188, 144–152. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Jin, K.; Duan, Z. Air PM2.5 concentration multi-step forecasting using a new hybrid modeling method: Comparing cases for four cities in China. Atmos. Pollut. Res. 2019, 10, 1588–1600. [Google Scholar] [CrossRef]
- Sun, W.; Huang, C. Predictions of carbon emission intensity based on factor analysis and an improved extreme learning machine from the perspective of carbon emission efficiency. J. Clean. Prod. 2022, 338, 130414. [Google Scholar] [CrossRef]
- Dotse, S.-Q.; Petra, M.I.; Dagar, L.; De Silva, L. Application of computational intelligence techniques to forecast daily PM10 exceedances in Brunei Darussalam. Atmos. Pollut. Res. 2018, 9, 358–368. [Google Scholar] [CrossRef]
- Zhu, S.; Lian, X.; Wei, L.; Che, J.; Shen, X.; Yang, L.; Qiu, X.; Liu, X.; Gao, W.; Ren, X.; et al. PM2.5 forecasting using SVR with PSOGSA algorithm based on CEEMD, GRNN and GCA considering meteorological factors. Atmos. Environ. 2018, 183, 20–32. [Google Scholar] [CrossRef]
- Gan, K.; Sun, S.; Wang, S.; Wei, Y. A secondary-decomposition-ensemble learning paradigm for forecasting PM2.5 concentration. Atmos. Pollut. Res. 2018, 9, 989–999. [Google Scholar] [CrossRef]
- Wu, Q.; Lin, H. Daily urban air quality index forecasting based on variational mode decomposition, sample entropy and LSTM neural network. Sustain. Cities Soc. 2019, 50, 101657. [Google Scholar] [CrossRef]
- Zhu, S.; Qiu, X.; Yin, Y.; Fang, M.; Liu, X.; Zhao, X.; Shi, Y. Two-step-hybrid model based on data preprocessing and intelligent optimization algorithms (CS and GWO) for NO2 and SO2 forecasting. Atmos. Pollut. Res. 2019, 10, 1326–1335. [Google Scholar] [CrossRef]
- Liu, H.; Duan, Z.; Chen, C. A hybrid multi-resolution multi-objective ensemble model and its application for forecasting of daily PM2.5 concentrations. Inf. Sci. 2020, 516, 266–292. [Google Scholar] [CrossRef]
- Zhang, B.; Rong, Y.; Yong, R.; Qin, D.; Li, M.; Zou, G.; Pan, J. Deep learning for air pollutant concentration prediction: A review. Atmos. Environ. 2022, 290, 119347. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Wang, J.; Zeng, H.; Zhou, F. Prediction of air pollutant concentration based on one-dimensional multi-scale CNN-LSTM considering spatial-temporal characteristics: A case study of Xi’an, China. Atmosphere 2021, 12, 1626. [Google Scholar] [CrossRef]
- Subramaniam, S.; Raju, N.; Ganesan, A.; Rajavel, N.; Chenniappan, M.; Prakash, C.; Pramanik, A.; Basak, A.K.; Dixit, S. Artificial intelligence technologies for forecasting air pollution and human health: A narrative review. Sustainability 2022, 14, 9951. [Google Scholar] [CrossRef]
- Liang, Y.-C.; Maimury, Y.; Chen, A.H.-L.; Juarez, J.R.-H. Machine learning-based prediction of air quality. Appl. Sci. 2020, 10, 9151. [Google Scholar] [CrossRef]
- Bekkar, A.; Hssina, B.; Douzi, S.; Douzi, K. Air-pollution prediction in smart city, deep learning approach. J. Big Data 2021, 8, 161. [Google Scholar] [CrossRef]
- Kenessary, D.; Kenessary, A.; Adilgireiuly, Z.; Akzholova, N.; Erzhanova, A.; Dosmukhametov, A.; Syzdykov, D.; Masoud, A.-R.; Saliev, T. Air pollution in Kazakhstan and its health risk assessment. Ann. Glob. Health 2019, 85, 133. [Google Scholar] [CrossRef]
- Tolepbayeva, A.K.; Urazbayeva, G.M. Pollution of atmospheric air in the basin of the river Ertis by emis-sions of sulfur dioxide (on an example of the city of Ust-Kamenogorsk). Eurasian J. Ecol. 2017, 3, 76–87. [Google Scholar] [CrossRef]
- Baklanov, A.E.; Baklanova, O.E.; Titov, D.N. Influence of emissions of harmful substances in atmosphere on population health. In Proceedings of the 2012 7th International Forum on Strategic Technology (IFOST), Tomsk, Russia, 18–21 September 2012. [Google Scholar]
- Shvets, O.; Györök, G. Possible implications for land-use planning mechanisms when considering the results of monitoring and modelling air pollution by industry and transport on the example of Kazakhstan cities. Acta Polytech. Hung. 2023, 20, 7–26. [Google Scholar] [CrossRef]
- Temirbekov, N.; Madiyarov, M.; Abdoldina, F.; Malgazhdarov, E. Numerical modeling of atmospheric processes in a limited area and their adaptation for modeling the microclimate of Ust-Kamenogorsk. Comput. Technol. 2006, 11, 41–45. [Google Scholar]
- Woszczyk, M.; Spychalski, W.; Boluspaeva, L. Trace metal (Cd, Cu, Pb, Zn) fractionation in urban-industrial soils of Ust-Kamenogorsk (Oskemen), Kazakhstan—Implications for the assessment of environmental quality. Environ. Monit. Assess. 2018, 190, 362. [Google Scholar] [CrossRef]
- Bazarkhanov, S.T.; Naukanova, G.K.; Pivovarov, E.I.; Baimakanova, F.S.; Zhakhmetov, R.T. Influence of environmental factors on the health of the population of the city of Ust-Kamenogorsk. Vestnik KazNMU 2014, 3, 171–175. (In Russian) [Google Scholar]
- Alimbaev, T.; Omarova, B.; Abzhapparova, B.; Ilyassova, K.; Yermagambetova, K.; Mazhitova, Z. Environment of East Kazakhstan: State and main directions of optimization. E3s Web Conf. 2020, 175, 14008. [Google Scholar] [CrossRef]
- Tursumbayeva, M.; Muratuly, A.; Baimatova, N.; Ferhat, K.; Kerimray, A. Cities of Central Asia: New hotspots of air pollution in the world. Atmos. Environ. 2023, 309, 119901. [Google Scholar] [CrossRef]
- Temirbekov, N.; Kasenov, S.; Berkinbayev, G.; Temirbekov, A.; Tamabay, D.; Temirbekova, M. Analysis of Data on Air Pollutants in the City by Machine-Intelligent Methods Considering Climatic and Geographical Features. Atmosphere 2023, 14, 892. [Google Scholar] [CrossRef]
- Vinnikov, D.; Rapisarda, V.; Babanov, S.; Vitale, E.; Strizhakov, L.; Romanova, Z.; Mukatova, I. High levels of indoor fine particulate matter during the cold season in Almaty prompt urgent public health action. PLoS ONE 2023, 18, e0285477. [Google Scholar] [CrossRef] [PubMed]
- Jailaybekov, Y.; Berkinbayev, G.; Yakovleva, N. Analysis and practice of reducing emissions of pollutants from road transport into the atmospheric air of the city of Almaty. Vibroengineering Procedia 2023, 48, 74–80. [Google Scholar] [CrossRef]
- Zakarin, E.; Baklanov, A.; Balakay, L.; Dedova, T.; Bostanbekov, K. Simulation of Air Pollution in Almaty City under Adverse Weather Conditions. Russ. Meteorol. Hydrol. 2021, 46, 121–128. [Google Scholar] [CrossRef]
- Issakhov, A.; Omarova, P. Modeling and analysis of the effects of barrier height on automobiles emission dispersion. J. Clean. Prod. 2021, 296, 126450. [Google Scholar] [CrossRef]
- Berdyshev, A.; Baigereyev, D.; Boranbek, K. Numerical Method for Fractional-Order Generalization of the Stochastic Stokes–Darcy Model. Mathematics 2023, 11, 3763. [Google Scholar] [CrossRef]
- Lei, T.M.T.; Siu, S.W.I.; Monjardino, J.; Mendes, L.; Ferreira, F. Using Machine Learning Methods to Forecast Air Quality: A Case Study in Macao. Atmosphere 2022, 13, 1412. [Google Scholar] [CrossRef]
- XGBoost. Available online: https://github.com/dmlc/xgboost (accessed on 10 June 2023).
- LightGBM. Available online: https://lightgbm.readthedocs.io/en/latest/ (accessed on 10 June 2023).
- Wang, S.; Wang, P.; Zhang, R.; Meng, X.; Kan, H.; Zhang, H. Estimating particulate matter concentrations and meteorological contributions in China during 2000–2020. Chemosphere 2023, 330, 138742. [Google Scholar] [CrossRef]
- Histogram-Based Gradient Boosting. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.HistGradientBoostingRegressor.html (accessed on 10 June 2023).
- Bacri, T.; Berentsen, G.D.; Bulla, J.; Stove, B. Computational issues in parameter estimation for hidden Markov models with Template Model Builder. arXiv 2023, arXiv:2302.10564. [Google Scholar] [CrossRef]
- Blekos, K.; Brand, D.; Ceschini, A.; Chou, C.-H.; Li, R.-H.; Pandya, K.; Summer, A. A Review on Quantum Approximate Optimization Algorithm and its Variants. arXiv 2023, arXiv:2306.09198. [Google Scholar]
- Goitom, S.K.; Papp, M.; Kovács, M.; Nagy, T.; Zsély, I.G.; Turányi, T.; Pál, L. Efficient numerical methods for the optimisation of large kinetic reaction mechanisms. Combust. Theory Model. 2022, 26, 1071–1097. [Google Scholar] [CrossRef]
- Najafabadi, M.M.; Khoshgoftaar, T.M.; Villanustre, F.; Holt, J. Large-scale distributed L-BFGS. J. Big Data 2017, 4, 22. [Google Scholar] [CrossRef]
- Liu, D.C.; Nocedal, J. On the limited memory BFGS method for large scale optimization. Math. Program. B 1989, 45, 503–528. [Google Scholar] [CrossRef]
- Powell, M.J.D. The NEWUOA Software for Unconstrained Optimization Without Derivatives. In Proceedings of the 40th the Workshop on Large Scale Nonlinear Optimization, Erice, Italy, 22 June–1 July 2004. [Google Scholar]
- Powell, M.J.D. The BOBYQA Algorithm for Bound Constrained Optimization without Derivatives; Technical Report NA2009/06; Department of Applied Mathematics and Theoretical Physics: Cambridge, UK, 2009. [Google Scholar]
- Bliyeva, D.; Baigereyev, D.; Imomnazarov, K. Computer Simulation of the Seismic Wave Propagation in Poroelastic Medium. Symmetry 2022, 14, 1516. [Google Scholar] [CrossRef]
- Baigereyev, D.; Omariyeva, D.; Temirbekov, N.; Yergaliyev, Y.; Boranbek, K. Numerical Method for a Filtration Model Involving a Nonlinear Partial Integro-Differential Equation. Mathematics 2022, 10, 1319. [Google Scholar] [CrossRef]
- Mejía-de-Dios, J.-A.; Mezura-Montes, E. A new evolutionary optimization method based on center of mass. In Decision Science in Action; Springer: Berlin/Heidelberg, Germany, 2018; pp. 65–74. [Google Scholar]
- Berkowicz, R. Spectral methods for atmospheric diffusion modeling. In Boundary Layer Structure; Kaplan, H., Dinar, N., Eds.; Springer: Dordrecht, The Netherlands, 1984. [Google Scholar]
- Ito, J.; Niino, H.; Nakanishi, M. Horizontal turbulent diffusion in a convective mixed layer. J. Fluid Mech. 2014, 758, 553–564. [Google Scholar] [CrossRef]
- Bezanson, J.; Edelman, A.; Karpinski, S.; Shah, V.B. Julia: A fresh approach to numerical computing. SIAM Review 2017, 59, 65–98. [Google Scholar] [CrossRef]
- Carlsson, K.; Ekre, F. Ferrite.jl [Computer Software]. Available online: https://github.com/Ferrite-FEM/Ferrite.jl (accessed on 10 June 2023).
- Zhumagulov, B.; Temirbekov, N.; Baigereyev, D. Efficient difference schemes for the three-phase non-isothermal flow problem. AIP Conf. Proc. 2017, 1880, 060001. [Google Scholar]
- Ayus, I.; Natarajan, N.; Gupta, D. Comparison of machine learning and deep learning techniques for the prediction of air pollution: A case study from China. Asian J. Atmos. Environ. 2023, 17, 4. [Google Scholar] [CrossRef]
- Dai, H.; Huang, G.; Wang, J.; Zeng, H. VAR-tree model based spatio-temporal characterization and prediction of O3 concentration in China. Ecotoxicol. Environ. Saf. 2023, 257, 114960. [Google Scholar] [CrossRef] [PubMed]
- Jung, C.-R.; Chen, W.-T.; Young, L.-H.; Hsiao, T.-C. A hybrid model for estimating the number concentration of ultrafine particles based on machine learning algorithms in central Taiwan. Environ. Int. 2023, 175, 107937. [Google Scholar] [CrossRef] [PubMed]
- Nhat-Duc, H.; Van-Duc, T. Comparison of histogram-based gradient boosting classification machine, random Forest, and deep convolutional neural network for pavement raveling severity classification. Autom. Constr. 2023, 148, 104767. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).