Mathematical Investigation of the Infection Dynamics of COVID-19 Using the Fractional Differential Quadrature Method
Abstract
:1. Introduction
2. Mathematical Model of COVID-19
3. Preliminaries and Method of Solution
3.1. Caputo’s Fractional Derivative
3.2. Polynomial Based Differential Quadrature Method
3.3. Discrete Singular Convolution Differential Quadrature Method
4. Numerical Results and Discussion
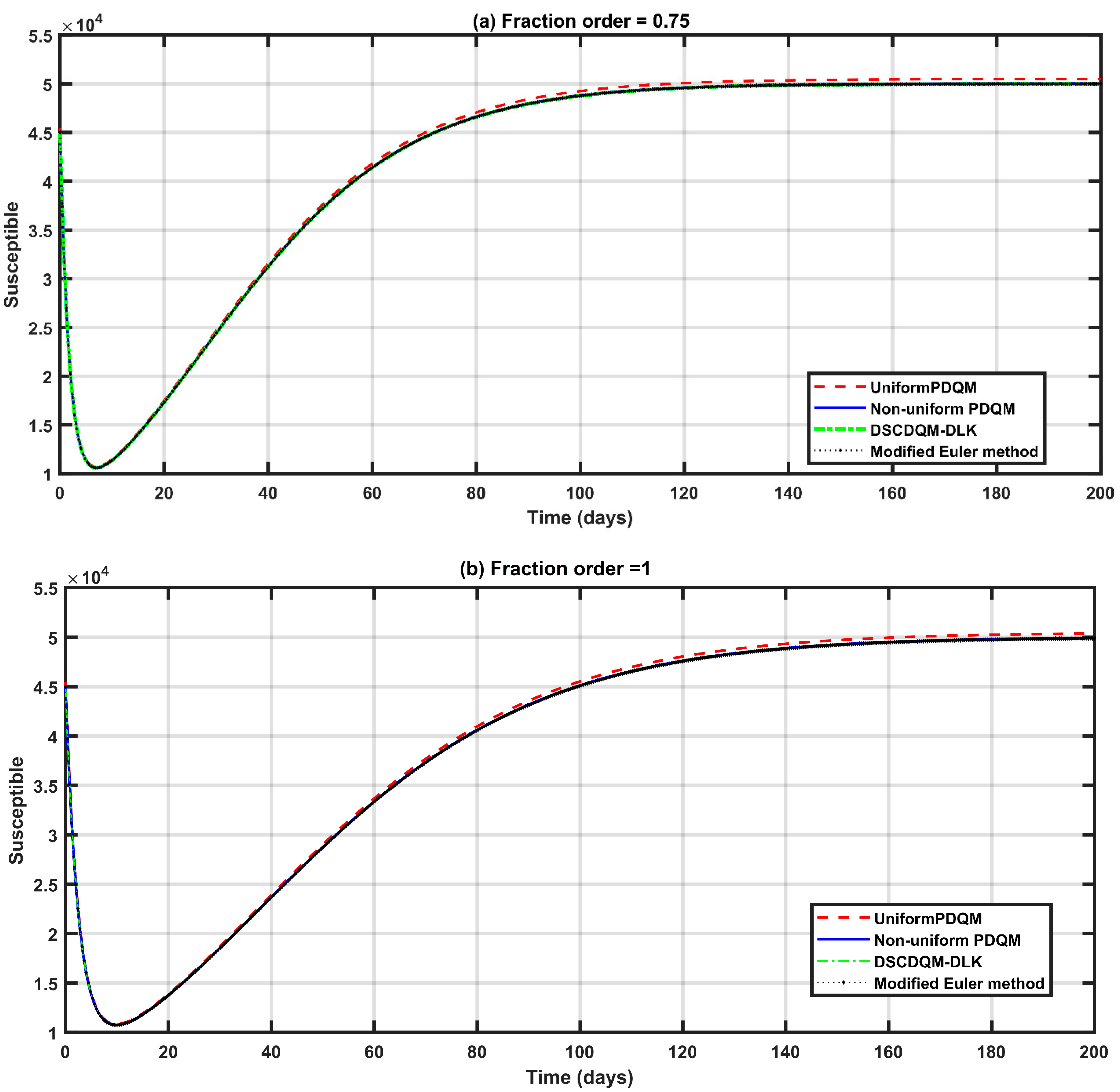
4.1. Validation of the DQM
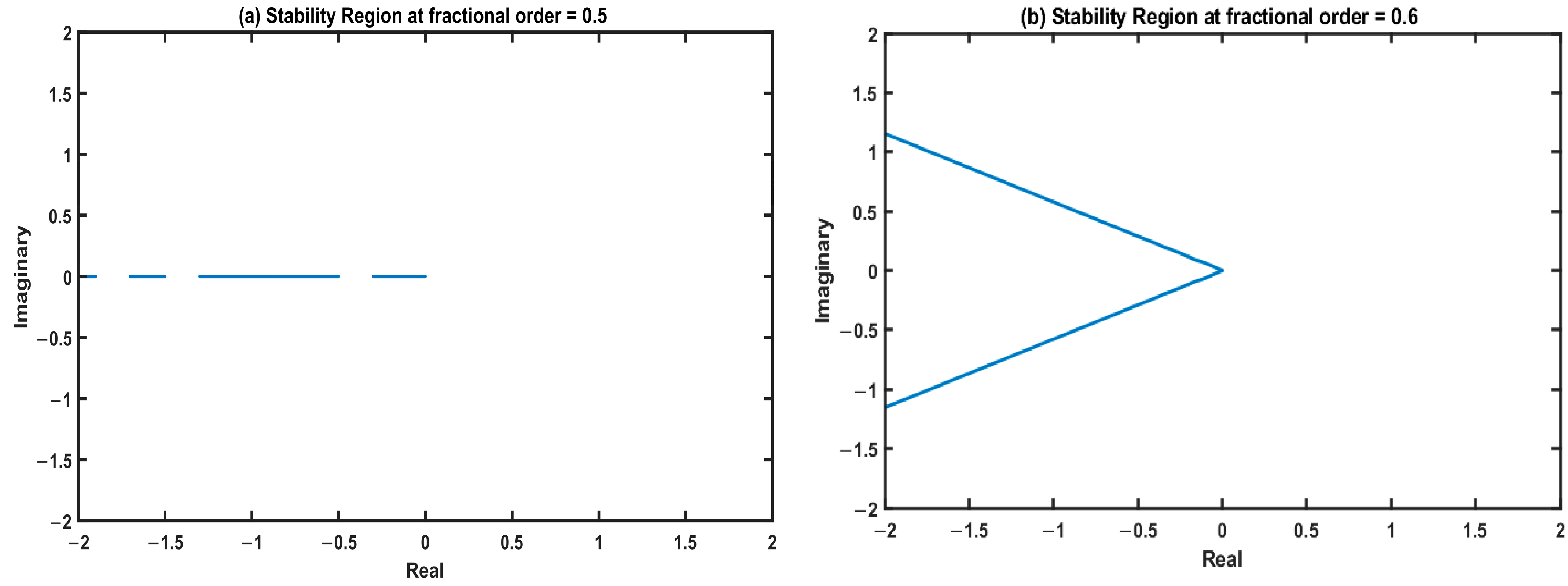
4.2. Stability Analysis
- are the unknown variables at the internal nodes of the grid;
- is a vector including the initial conditions;
- represents the right-hand side of Equations (22)–(27); and
- is the matrix of the weighting coefficient:
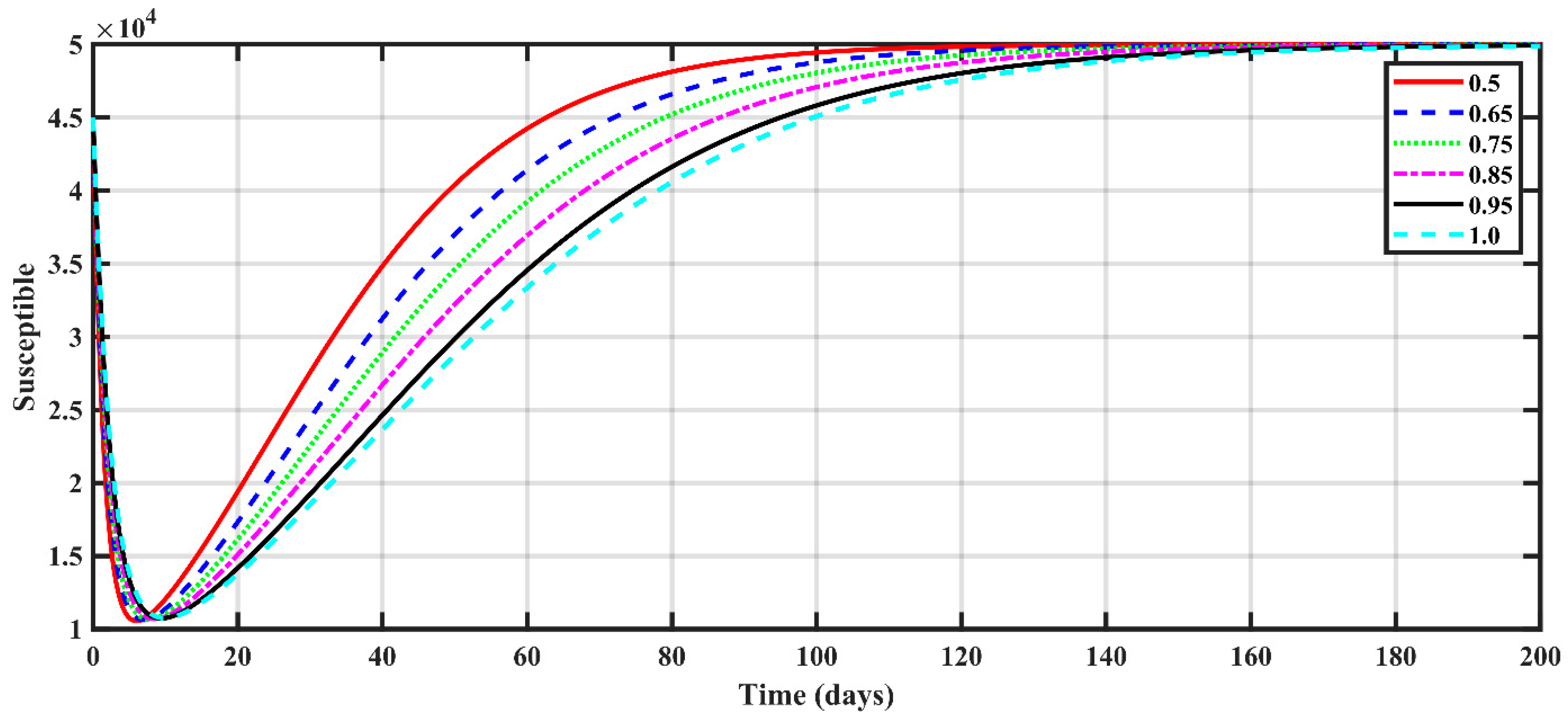
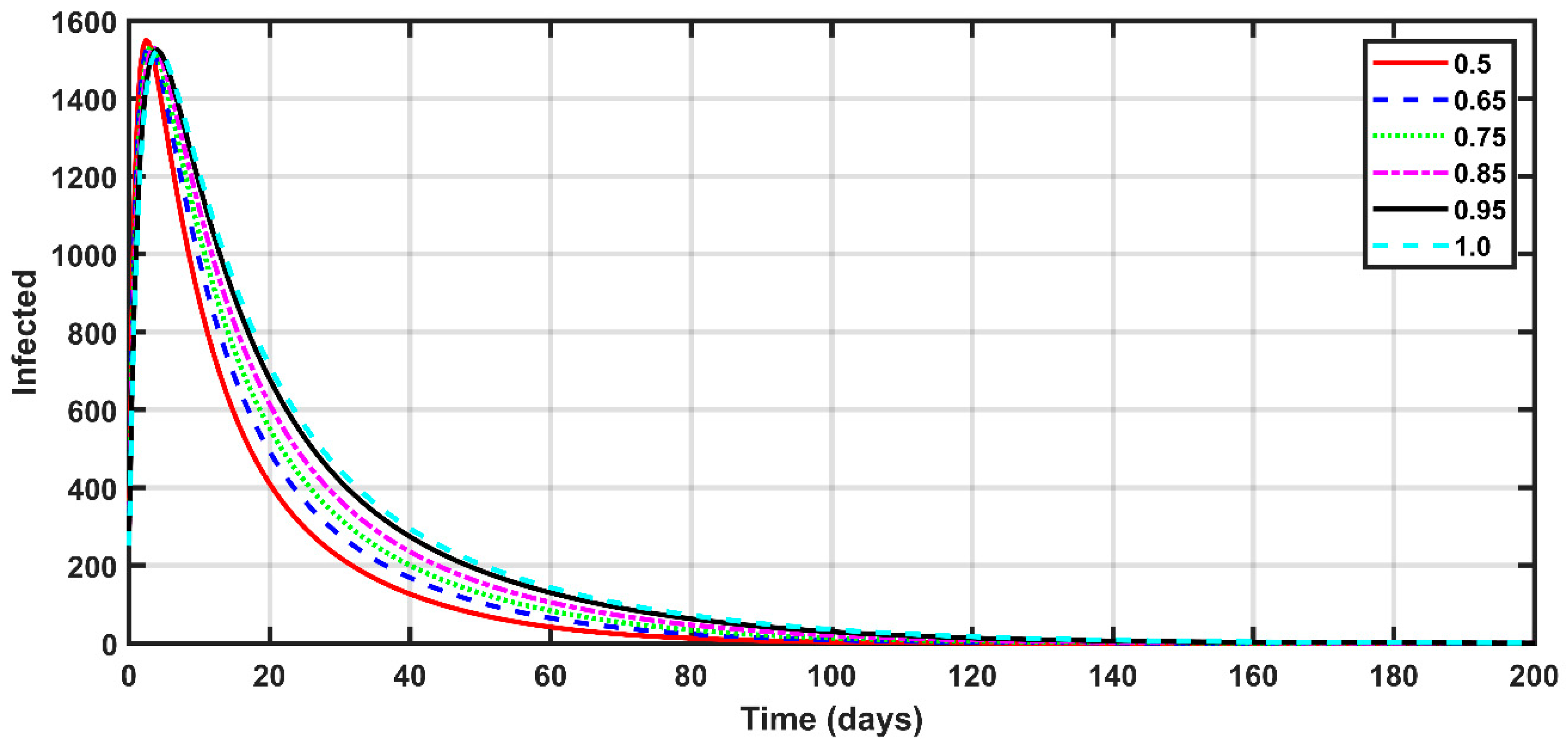
4.3. COVID-19 Dynamics
5. Conclusions
- The used techniques—uniform PDQM, non-uniform PDQM, and DSCDQM—showed higher accuracy than the modified Euler method [11], with better execution times.
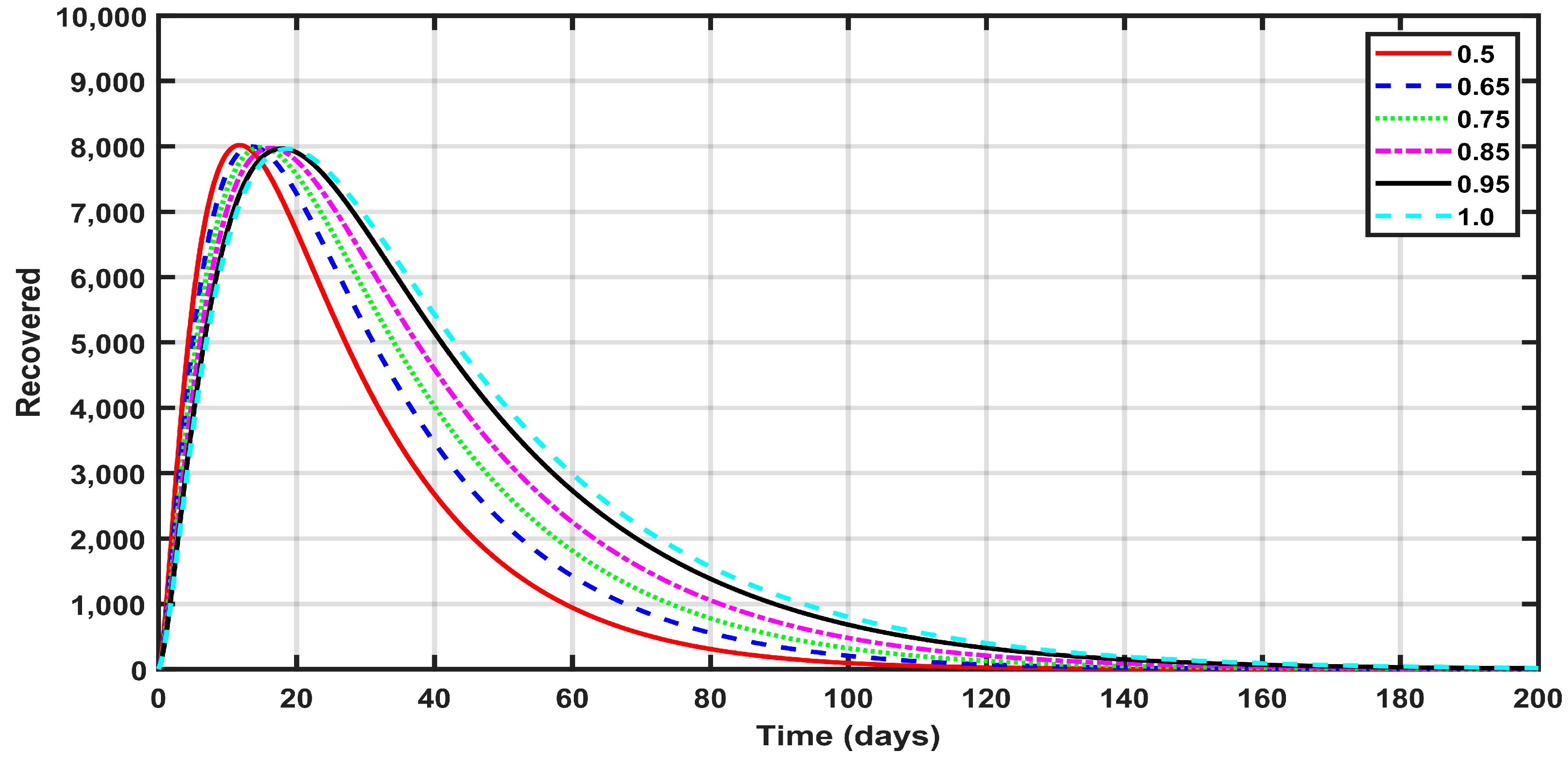
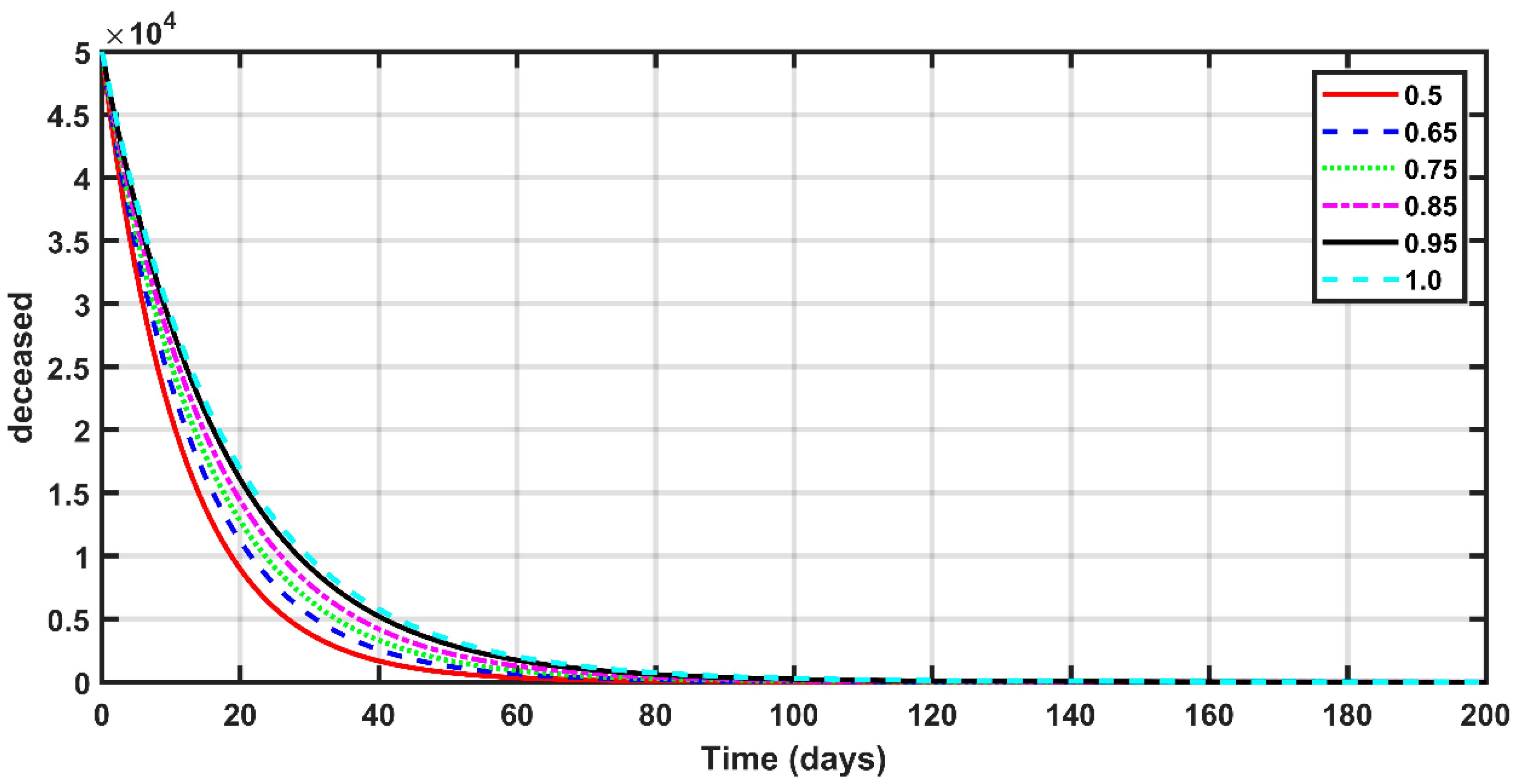
- The fractional order had a great impact on the results. As the fractional order approached one, the expected numbers of susceptible, exposed, deceased, asymptomatic, and recovered people became larger.
- The rise in the number of susceptible people was dramatic in the first month, then increased until it reached maximum values after a period, depending on the fractional order.
- The number of infected people increased significantly in the first week of the investigation, due to the high-spread rate of the disease. Consequently, the number of recovered people increased during the period with the higher number of infected people.
- The number of recovered people decreased due to the continuing medical care, which decreased the number of infected patients.
Author Contributions
Funding
Conflicts of Interest
References
- Rezaei, N. Coronavirus Disease—COVID-19; Springer: Cham, Switzerland, 2021. [Google Scholar]
- Murphy, P. COVID-19: Proportionality, Public Policy and Social Distancing; Palgrave Macmillan: Basingstoke, UK, 2020. [Google Scholar]
- Chen, T.M.; Rui, J.; Wang, Q.P.; Zhao, Z.Y.; Cui, J.A.; Yin, L. A mathematical model for simulating the phase-based transmissibility of a novel coronavirus. Infect. Dis. Poverty 2020, 9, 24. [Google Scholar] [PubMed]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Lakshmikantham, V.; Leela, S.; Vasundhara Devi, J. Theory of Fractional Dynamic Systems; CSP: Cambridge, UK, 2009. [Google Scholar]
- Mathai, A.M.; Haubold, H.J. An Introduction to Fractional Calculus; Nova Science Publishers: Hauppauge, NY, USA, 2017. [Google Scholar]
- Singh, J.; Hristov, J.Y.; Hammouch, Z. New Trends in Fractional Differential Equations with Real-World Applications in Physics; Frontiers Media SA: Lausanne, Switzerland, 2020. [Google Scholar]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Probing Families of Optical Soliton Solutions in Fractional Perturbed Radhakrishnan–Kundu–Lakshmanan Model with Improved Versions of Extended Direct Algebraic Method. Fractal Fract. 2023, 7, 512. [Google Scholar]
- Yasmin, H.; Aljahdaly, N.H.; Saeed, A.M.; Shah, R. Investigating Families of Soliton Solutions for the Complex Structured Coupled Fractional Biswas—Arshed Model in Birefringent Fibers Using a Novel Analytical Technique. Fractal Fract. 2023, 7, 491. [Google Scholar] [CrossRef]
- Naeem, M.; Yasmin, H.; Shah, R.; Shah, N.A.; Nonlaopon, K. Investigation of Fractional Nonlinear Regularized Long-Wave Models via Novel Techniques. Symmetry 2023, 15, 220. [Google Scholar] [CrossRef]
- Nazir, G.; Zeb, A.; Shah, K.; Saeed, T.; Khan, R.A.; Khan, S.I.U. Study of COVID-19 mathematical model of fractional order via modified Euler method. Alex. Eng. J. 2021, 60, 5287–5296. [Google Scholar] [CrossRef]
- Mpinganzima, L.; Ntaganda, J.M.; Banzi, W.; Muhirwa, J.P.; Nannyonga, B.K.; Niyobuhungiro, J.; Rutaganda, E. Analysis of COVID-19 mathematical model for predicting the impact of control measures in Rwanda. Inform. Med. Unlocked 2023, 37, 101195. [Google Scholar]
- Mpinganzima, L.; Ntaganda, J.M.; Banzi, W.; Muhirwa, J.P.; Nannyonga, B.K.; Niyobuhungiro, J.; Rutaganda, E.; Ngaruye, I.; Ndanguza, D.; Nzabanita, J.; et al. Compartmental mathematical modelling of dynamic transmission of COVID-19 in Rwanda. IJID Reg. 2023, 6, 99–107. [Google Scholar]
- Abioye, A.I.; Peter, O.J.; Ogunseye, H.A.; Oguntolu, F.A.; Ayoola, T.A.; Oladapo, A.O. A fractional-order mathematical model for malaria and COVID-19 co-infection dynamics. Heal. Anal. 2023, 4, 100210. [Google Scholar]
- Alaje, A.I.; Olayiwola, M.O. A fractional-order mathematical model for examining the spatiotemporal spread of COVID-19 in the presence of vaccine distribution. Heal. Anal. 2023, 4, 100230. [Google Scholar]
- Avusuglo, W.; Mosleh, R.; Ramaj, T.; Li, A.; Sharbayta, S.S.; Fall, A.A.; Ghimire, S.; Shi, F.; Lee, J.K.; Thommes, E.; et al. Workplace absenteeism due to COVID-19 and influenza across Canada: A mathematical model. J. Theor. Biol. 2023, 572, 111559. [Google Scholar]
- Singh, R.; Rehman, A.U.; Ahmed, T.; Ahmad, K.; Mahajan, S.; Pandit, A.K.; Abualigah, L.; Gandomi, A.H. Mathematical modelling and analysis of COVID-19 and tuberculosis transmission dynamics. Inform. Med. Unlocked 2023, 38, 101235. [Google Scholar] [CrossRef]
- Li, C.; Qian, D.; Chen, Y. On Riemann-Liouville and Caputo Derivatives. Discret. Dyn. Nat. Soc. 2011, 2011, 562494. [Google Scholar] [CrossRef]
- Caputo, M. Linear Models of Dissipation whose Q is almost Frequency Independent—II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar] [CrossRef]
- Zong, Z.; Zhang, Y. Advanced Differential Quadrature Methods; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Shu, C. Differential Quadrature and Its Application in Engineering; Springer: London, UK, 2000. [Google Scholar]
- Ragb, O.; Mohamed, M.; Matbuly, M. Vibration Analysis of Magneto-Electro-Thermo NanoBeam Resting on Nonlinear Elastic Foundation Using Sinc and Discrete Singular Convolution Differential Quadrature Method. Mod. Appl. Sci. 2019, 13, 49. [Google Scholar] [CrossRef]
- Wei, G.W. Discrete singular convolution for the solution of the Fokker–Planck equation. J. Chem. Phys. 1999, 110, 8930–8942. [Google Scholar] [CrossRef]
- Wan, D.C.; Zhou, Y.C.; Wei, G.W. Numerical solution of incompressible flows by discrete singular convolution. Int. J. Numer. Methods Fluids 2002, 38, 789–810. [Google Scholar] [CrossRef]
- Zhang, L.; Xiang, Y.; Wei, G. Local adaptive differential quadrature for free vibration analysis of cylindrical shells with various boundary conditions. Int. J. Mech. Sci. 2006, 48, 1126–1138. [Google Scholar] [CrossRef]
- Civalek, Ö.; Kiracioglu, O. Free vibration analysis of Timoshenko beams by DSC method. Int. J. Numer. Methods Biomed. Eng. 2010, 26, 1890–1898. [Google Scholar] [CrossRef]
- Civalek, Ö. Free vibration of carbon nanotubes reinforced (CNTR) and functionally graded shells and plates based on FSDT via discrete singular convolution method. Compos. Part B Eng. 2017, 111, 45–59. [Google Scholar]
- Ahmad, S.W.; Sarwar, M.; Shah, K.; Ahmadian, A.; Salahshour, S. Fractional order mathematical modeling of novel corona virus (COVID-19). Math. Methods Appl. Sci. 2021, 46, 7847–7860. [Google Scholar] [CrossRef]
- Anley, E.F.; Zheng, Z. Finite Difference Method for Two-Sided Two Dimensional Space Fractional Convection-Diffusion Problem with Source Term. Mathematics 2020, 8, 1878. [Google Scholar] [CrossRef]
- Dong, G.; Guo, Z.; Yao, W. Numerical methods for time-fractional convection-diffusion problems with high-order accuracy. Open Math. 2021, 19, 782–802. [Google Scholar]
- Khan, M.A.; Atangana, A. Modeling the dynamics of novel coronavirus (2019-nCov) with fractional derivative. Alex. Eng. J. 2020, 59, 2379–2389. [Google Scholar] [CrossRef]
- Yousif, R.; Jeribi, A.; Al-Azzawi, S. Fractional-Order SEIRD Model for Global COVID-19 Outbreak. Mathematics 2023, 11, 1036. [Google Scholar] [CrossRef]




| Parameters | Description of Parameters |
|---|---|
| Susceptible people | |
| Exposed people | |
| Infected people | |
| Asymptomatic people | |
| Recovered people | |
| Resivior | |
| Rate of death | |
| Total population and birth rate | |
| Incubation period | |
| Latent period | |
| Infectious period of symptomatic infection | |
| Infectious period of asymptomatic infection of people | |
| Transmission rate from to |
| N | Uniform PDQM | Non-Uniform PDQM | ||||||
|---|---|---|---|---|---|---|---|---|
| 100 | 0.00485996 | 0.12370351 | 0.81045132 | 3.66075705 | 0.00102353 | 0.06231845 | 0.61910253 | 3.65824812 |
| 150 | 0.00218186 | 0.08663727 | 0.70389814 | 3.65692309 | 2.507 × 10−4 | 3.436 × 10−2 | 0.49322681 | 3.65322267 |
| 200 | 4.984 × 10−4 | 0.04583646 | 0.55019547 | 3.65296345 | 6.885 × 10−5 | 0.02023349 | 0.40486598 | 3.64996646 |
| 250 | 1.297 × 10−4 | 0.02617926 | 0.44544264 | 3.65013186 | 3.737 × 10−5 | 0.01583587 | 0.37004211 | 3.64968175 |
| 300 | 3.737 × 10−5 | 0.01583587 | 0.37004211 | 3.64968174 | 2.069 × 10−5 | 0.01253342 | 0.33987774 | 3.64941908 |
| 350 | 2.069 × 10−5 | 0.01253338 | 0.33987770 | 3.64941911 | 2.069 × 10−5 | 0.01253332 | 0.33987764 | 3.64941908 |
| 400 | 2.069 × 10−5 | 0.01253332 | 0.33987764 | 3.64941908 | 2.069 × 10−5 | 0.01253332 | 0.33987764 | 3.64941908 |
| Nazir et al. [11] | 2.069 × 10−5 | 0.01253332 | 0.33987764 | 3.64941908 | 2.069 × 10−5 | 0.01253332 | 0.33987764 | 3.64941908 |
| Execution time | 1.75 (second)–uniform | 1.013 (second)–non-uniform N ≥ 300 | ||||||
| Time (Days) | Uniform PDQM | Non-Uniform PDQM | ||||||
|---|---|---|---|---|---|---|---|---|
| 50 | 0.0788283 | 3.63412536 | 22.296806 | 73.305437 | 0.0788282 | 3.63412535 | 22.296805 | 73.305437 |
| 100 | 2.069 × 10−5 | 0.01253332 | 0.33987764 | 3.64941908 | 2.069 × 10−5 | 0.01253332 | 0.33987764 | 3.64941908 |
| 150 | 3.652 × 10−5 | 0.00185976 | 0.0198937 | 0.1422236 | 3.652 × 10−5 | 0.00185975 | 0.0198932 | 0.1422236 |
| 200 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 |
| 250 | 1.886 × 10−7 | 4.121 × 10−6 | 3.164 × 10−5 | 1.973 × 10−4 | 1.886 × 10−7 | 4.121 × 10−6 | 3.164 × 10−5 | 1.973 × 10−4 |
| 300 | 2.053 × 10−8 | 2.597 × 10−7 | 1.470 × 10−6 | 7.287 × 10−6 | 2.053 × 10−8 | 2.597 × 10−7 | 1.470 × 10−6 | 7.287 × 10−6 |
| 350 | 2.692 × 10−9 | 1.881 × 10−8 | 7.369 × 10−8 | 2.680 × 10−7 | 2.692 × 10−9 | 1.881 × 10−8 | 7.369 × 10−8 | 2.680 × 10−7 |
| Execution time | 1.75 (second)–uniform | 1.0 (second)–non-uniform | ||||||
| N | Non-Uniform PDQM | DSCDQM-DLK | ||||||
|---|---|---|---|---|---|---|---|---|
| 100 | 1.977 × 10−5 | 0.813 × 10−4 | 1.717 × 10−3 | 0.0134789 | 2.405 × 10−6 | 8.321 × 10−5 | 7.874 × 10−4 | 0.0061135 |
| 150 | 0.155 × 10−5 | 0.344 × 10−4 | 0.265 × 10−3 | 0.0102579 | 2.354 × 10−6 | 7.925 × 10−5 | 7.659 × 10−4 | 0.0057321 |
| 200 | 2.632 × 10−6 | 8.001 × 10−5 | 7.913 × 10−4 | 0.0065217 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 |
| 250 | 2.401 × 10−6 | 7.877 × 10−5 | 7.725 × 10−4 | 0.0060214 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 |
| 300 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 |
| 350 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 |
| 400 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 |
| Nazir et al. [11] | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 | 2.213 × 10−6 | 7.790 × 10−5 | 7.474 × 10−4 | 0.0053206 |
| Execution time | 1.025 (second)–non-uniform | 0.5 (second)–non-uniform | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed, M.; Mabrouk, S.M.; Rashed, A.S. Mathematical Investigation of the Infection Dynamics of COVID-19 Using the Fractional Differential Quadrature Method. Computation 2023, 11, 198. https://doi.org/10.3390/computation11100198
Mohamed M, Mabrouk SM, Rashed AS. Mathematical Investigation of the Infection Dynamics of COVID-19 Using the Fractional Differential Quadrature Method. Computation. 2023; 11(10):198. https://doi.org/10.3390/computation11100198
Chicago/Turabian StyleMohamed, M., S. M. Mabrouk, and A. S. Rashed. 2023. "Mathematical Investigation of the Infection Dynamics of COVID-19 Using the Fractional Differential Quadrature Method" Computation 11, no. 10: 198. https://doi.org/10.3390/computation11100198
APA StyleMohamed, M., Mabrouk, S. M., & Rashed, A. S. (2023). Mathematical Investigation of the Infection Dynamics of COVID-19 Using the Fractional Differential Quadrature Method. Computation, 11(10), 198. https://doi.org/10.3390/computation11100198










