A General Procedure to Formulate 3D Elements for Finite Element Applications
Abstract
:1. Introduction
2. Materials and Methods
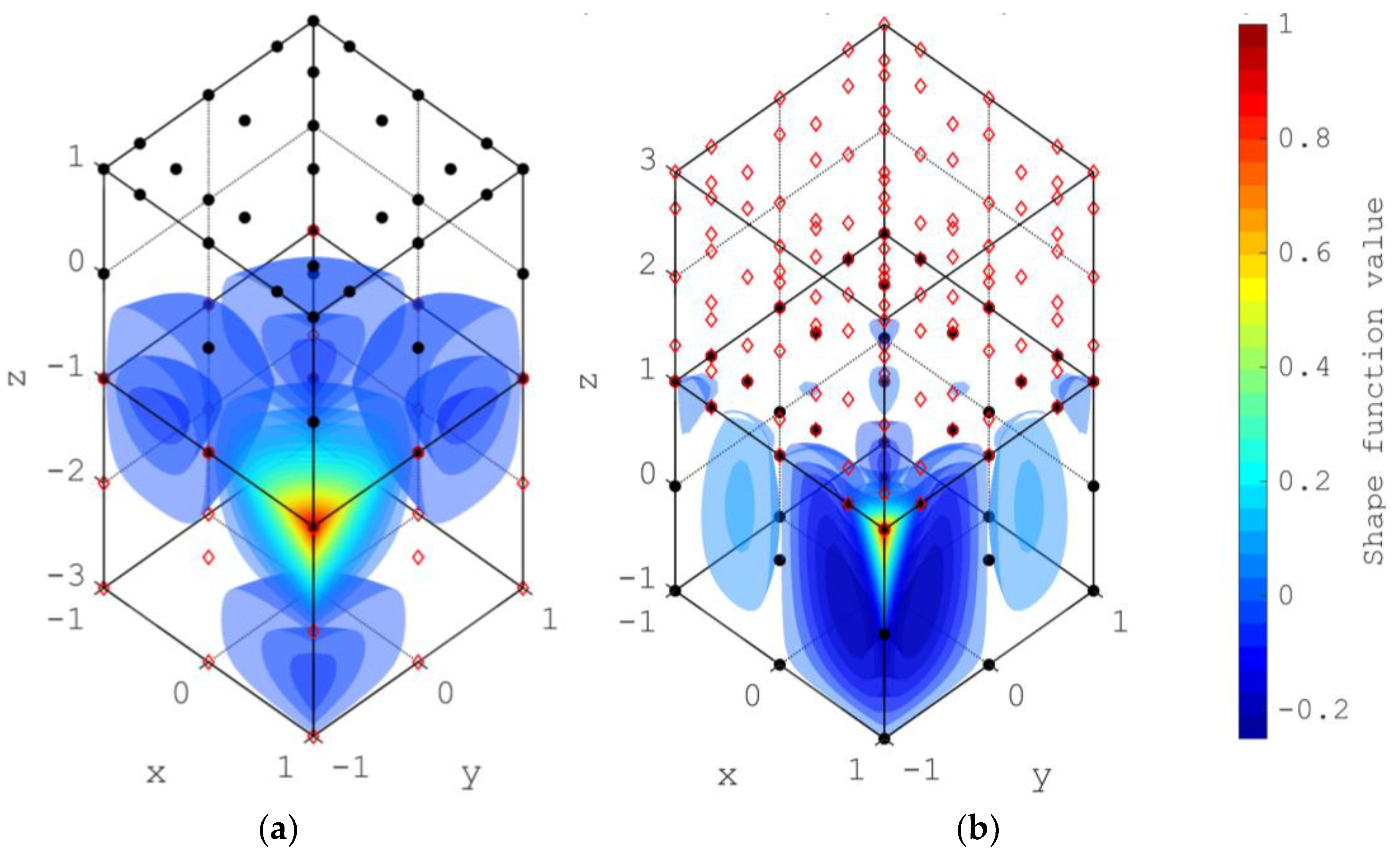
2.1. Computation of Shape Functions for a Given Nodal Distribution and Interpolation Function
2.2. Determination of Integration Quadrature for an Arbitrary Element
2.3. Formulation of Nodal Coordinates and Integration Quadrature for Hexahedron Elements
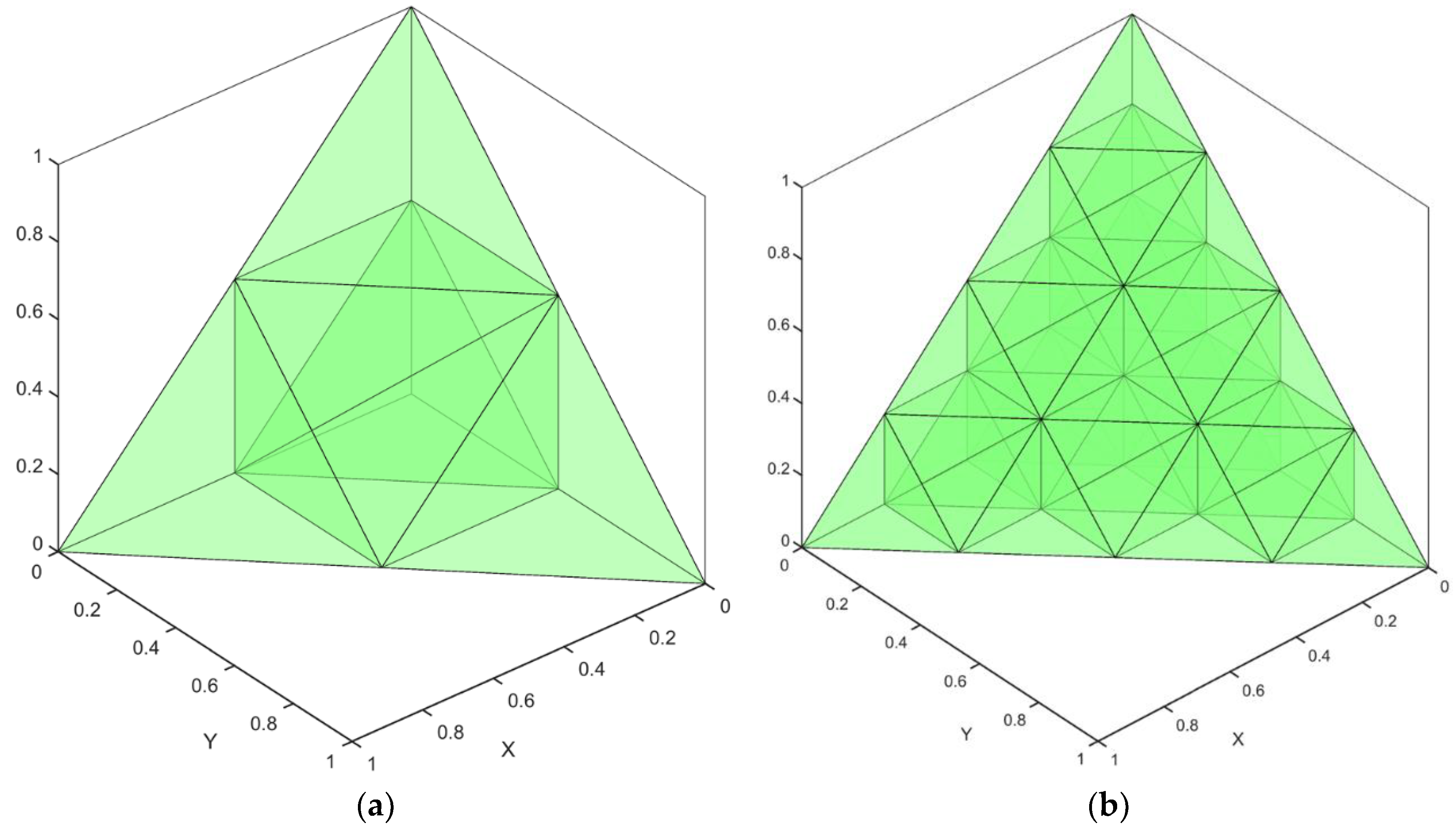
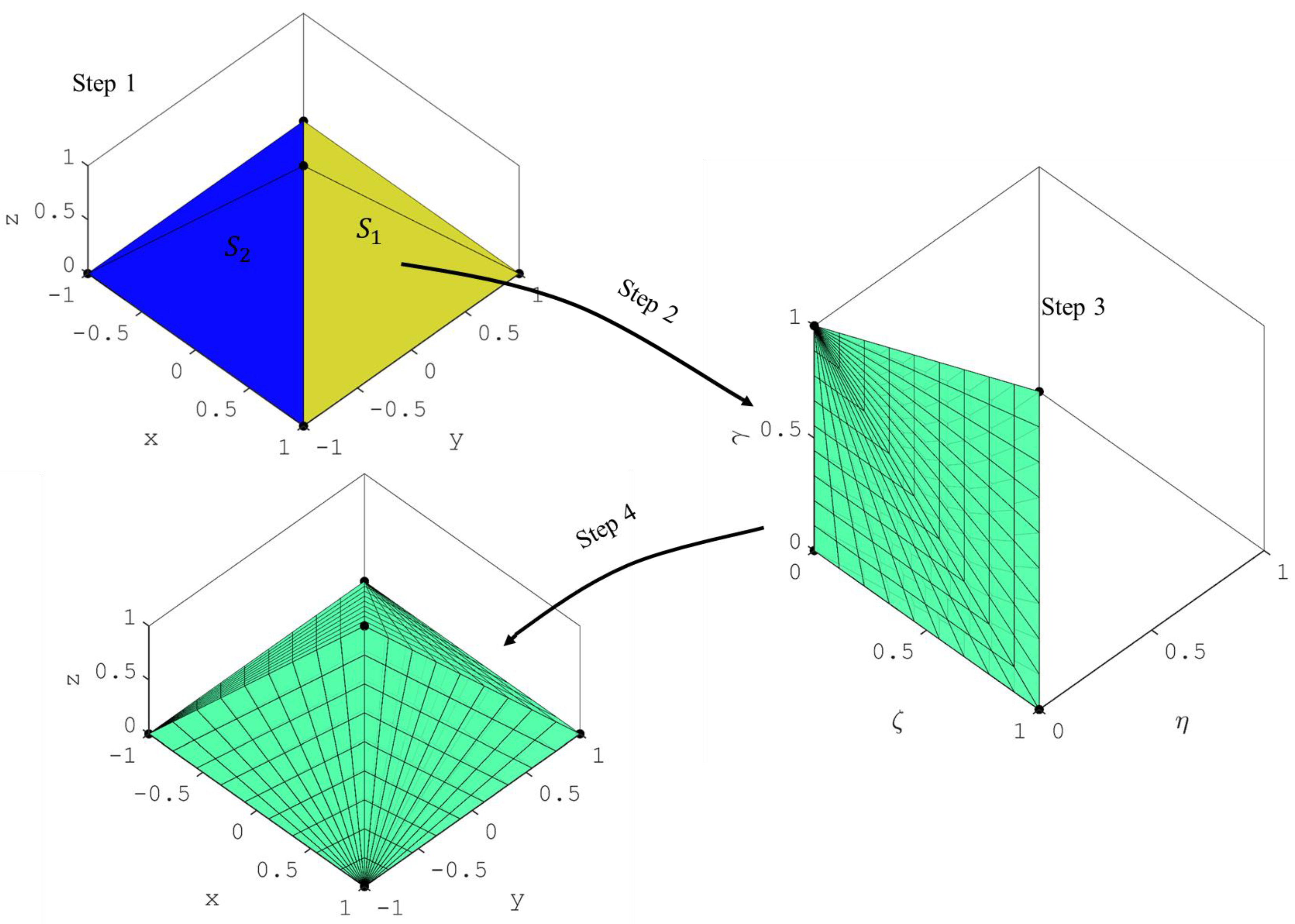
2.4. Formulation of Nodal Coordinates and Integration Quadrature for Tetrahedron Elements
- On the z = −1 surface with i = 1,2,…,m + 1, j = 1,2,…,m + 2, and l = m + 3 − i − j,
- On the x = −1 surface with j = 1,2,…,m, k = 2,3,…,m + 2 − j, and l = m + 3 − i − k,
- On the y = −1 surface with i = 2,3,…,m, k = 2,3,…,m + 2 − i, and l = m + 3 − i − k,
- On the slanted surface, x + y + z = 1 with i = 2,3,…,m, j = 2,3,….m + 1 − i, and l = m + 3 − i − j,
- Interior nodes with i = 2,3,…,m, j = 2,3,…,m + 1 − i, k = 2,3,…,m + 2 − i − j, and l = m + 4 − i − j − k,
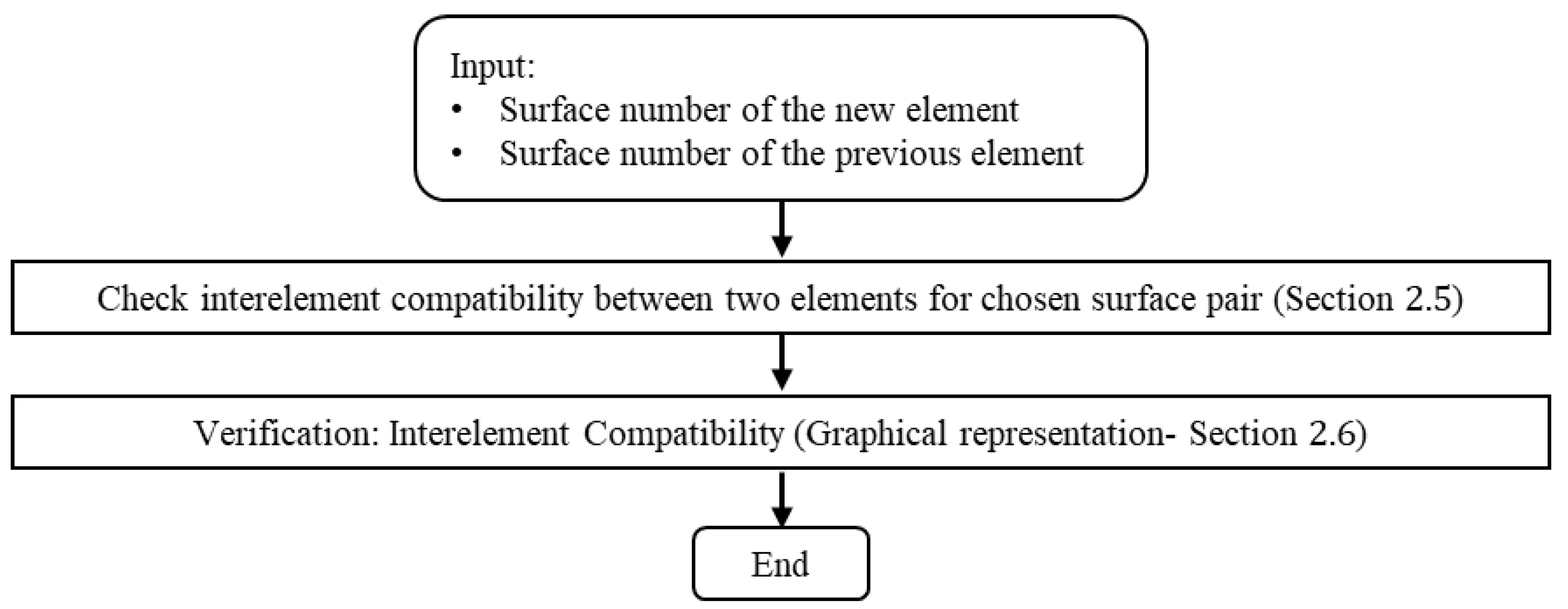
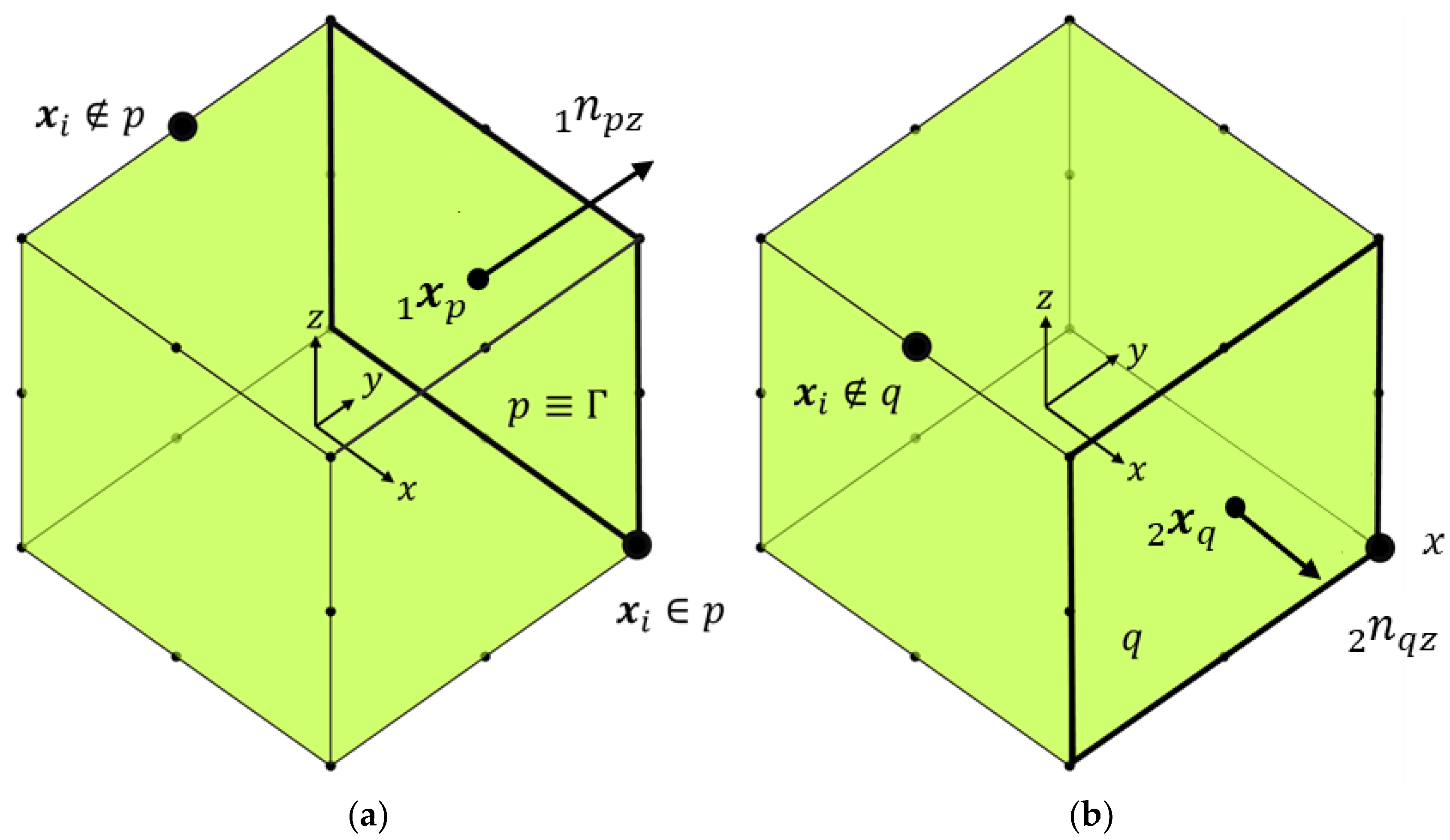
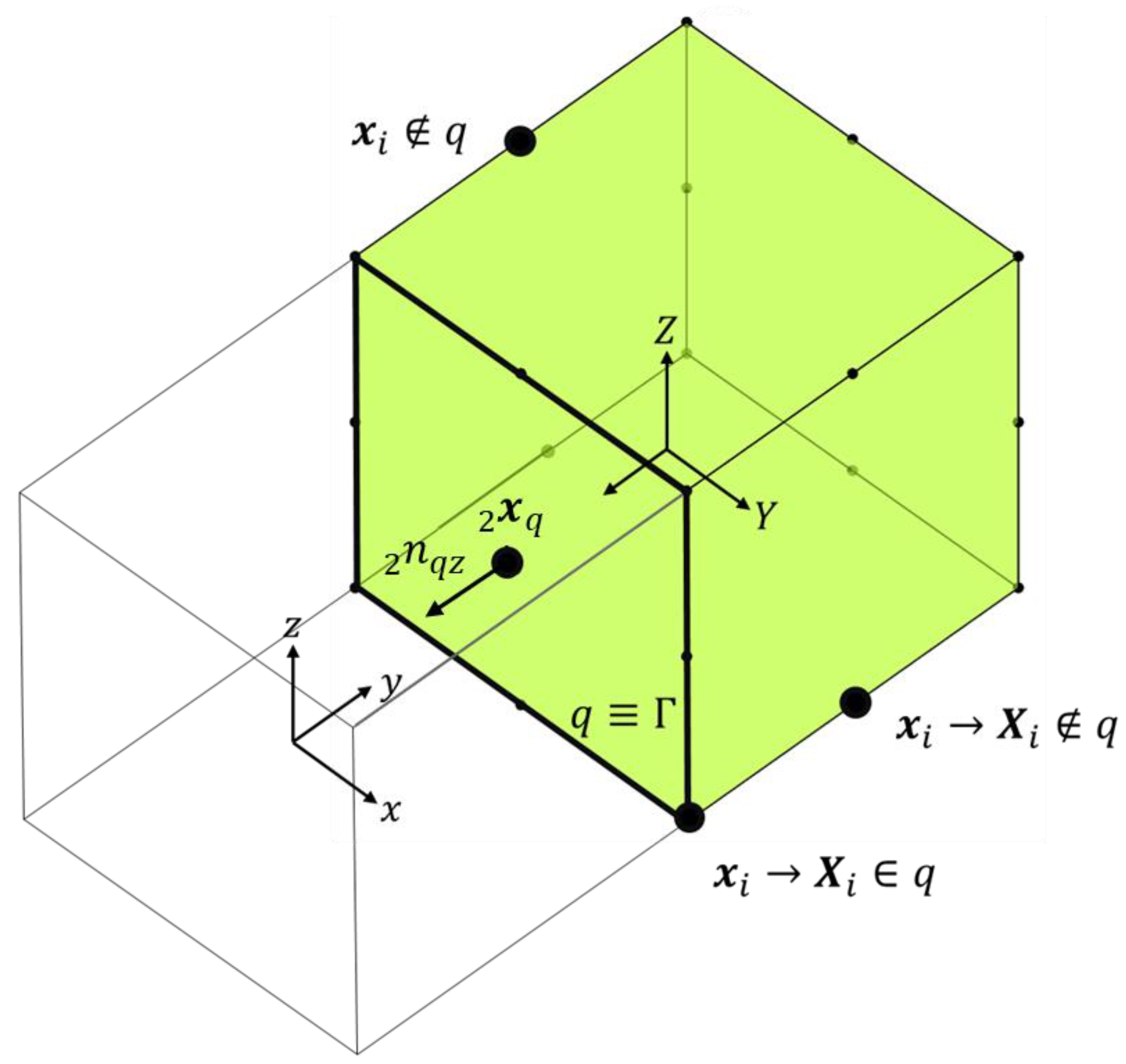
2.5. Interelement Compatibility Check between Two Elements for a Chosen Surface Pair
2.6. Generation of Graphical Representation of Element Properties
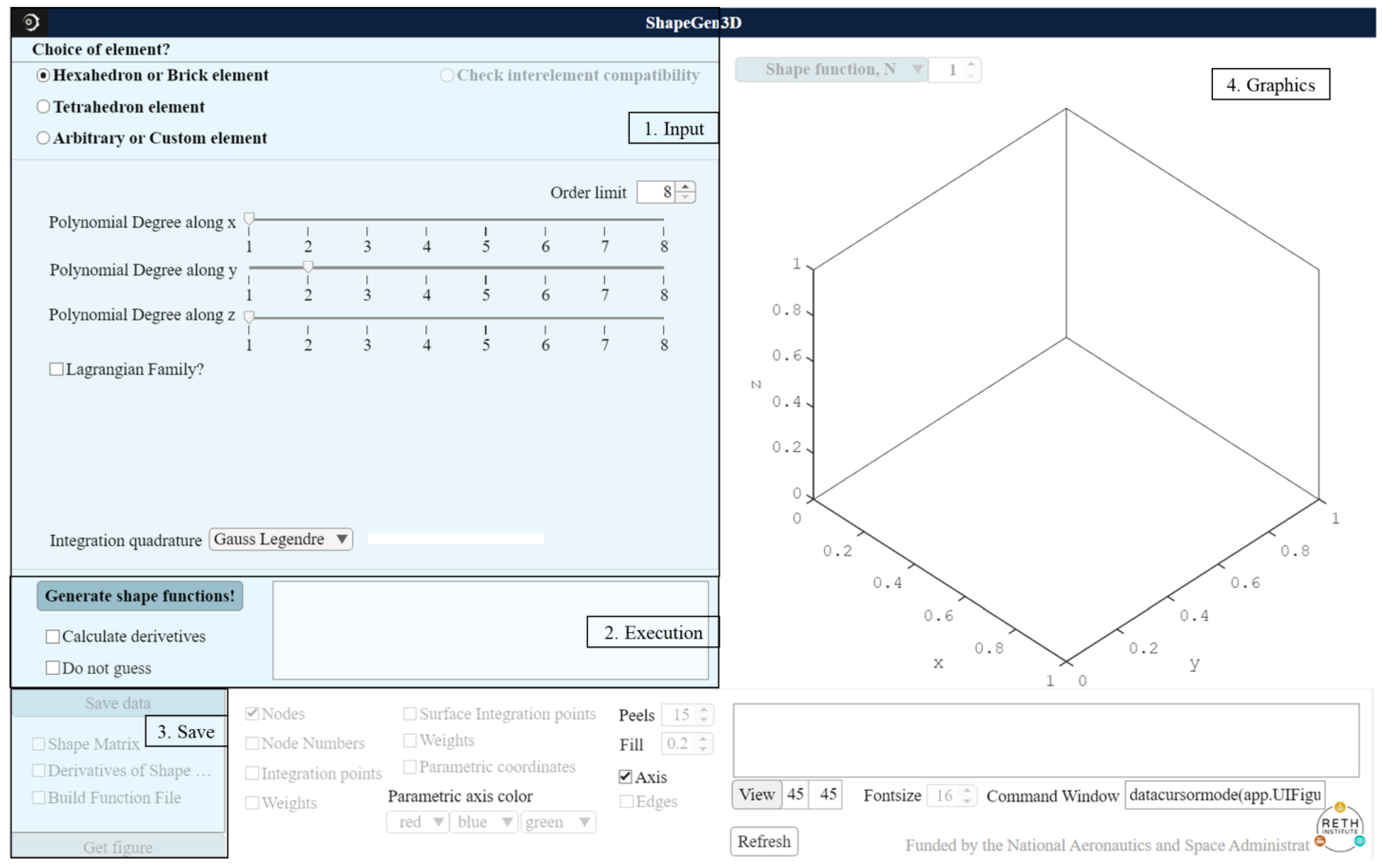
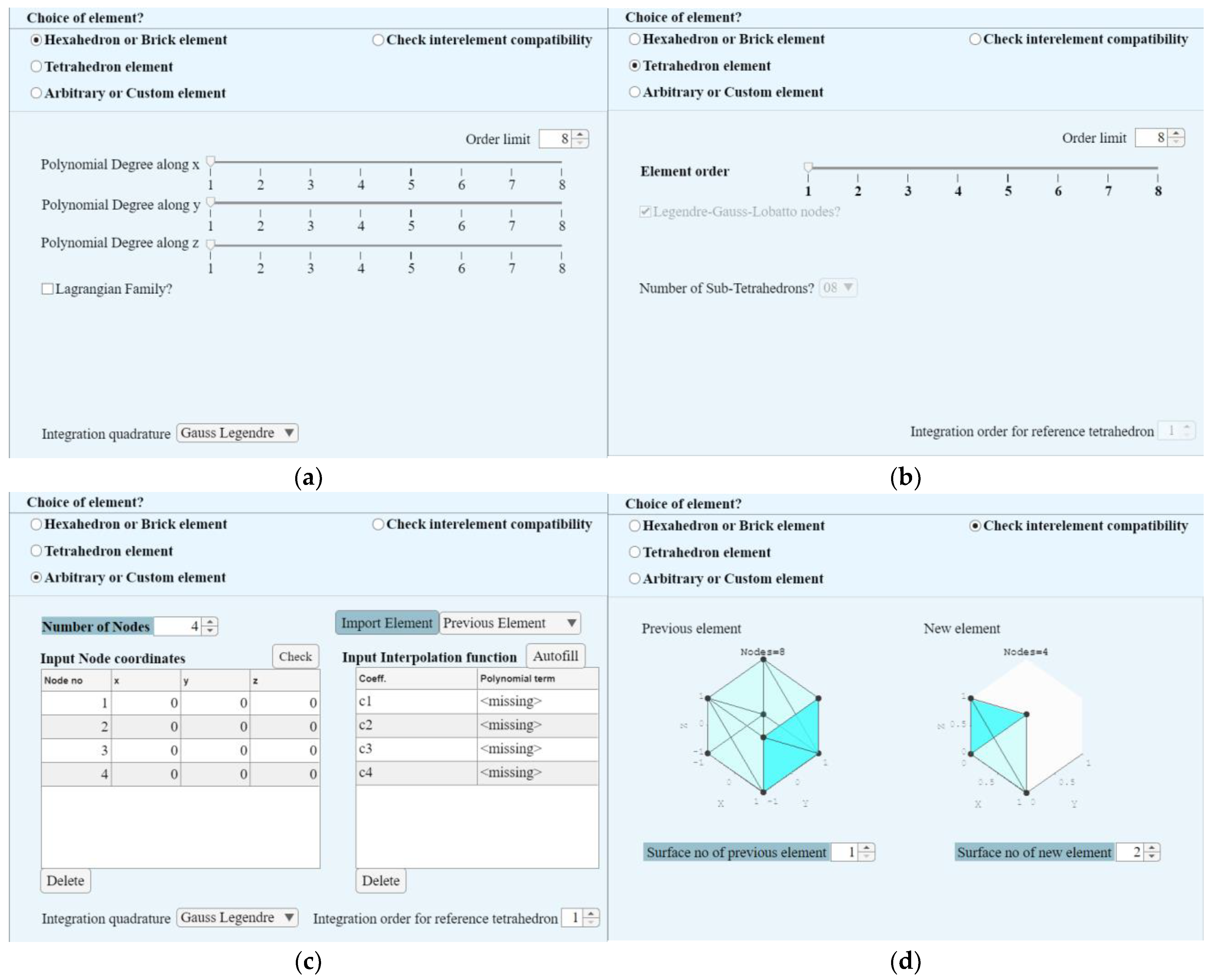
2.7. Implementation of GUI Interface
3. Numerical Examples
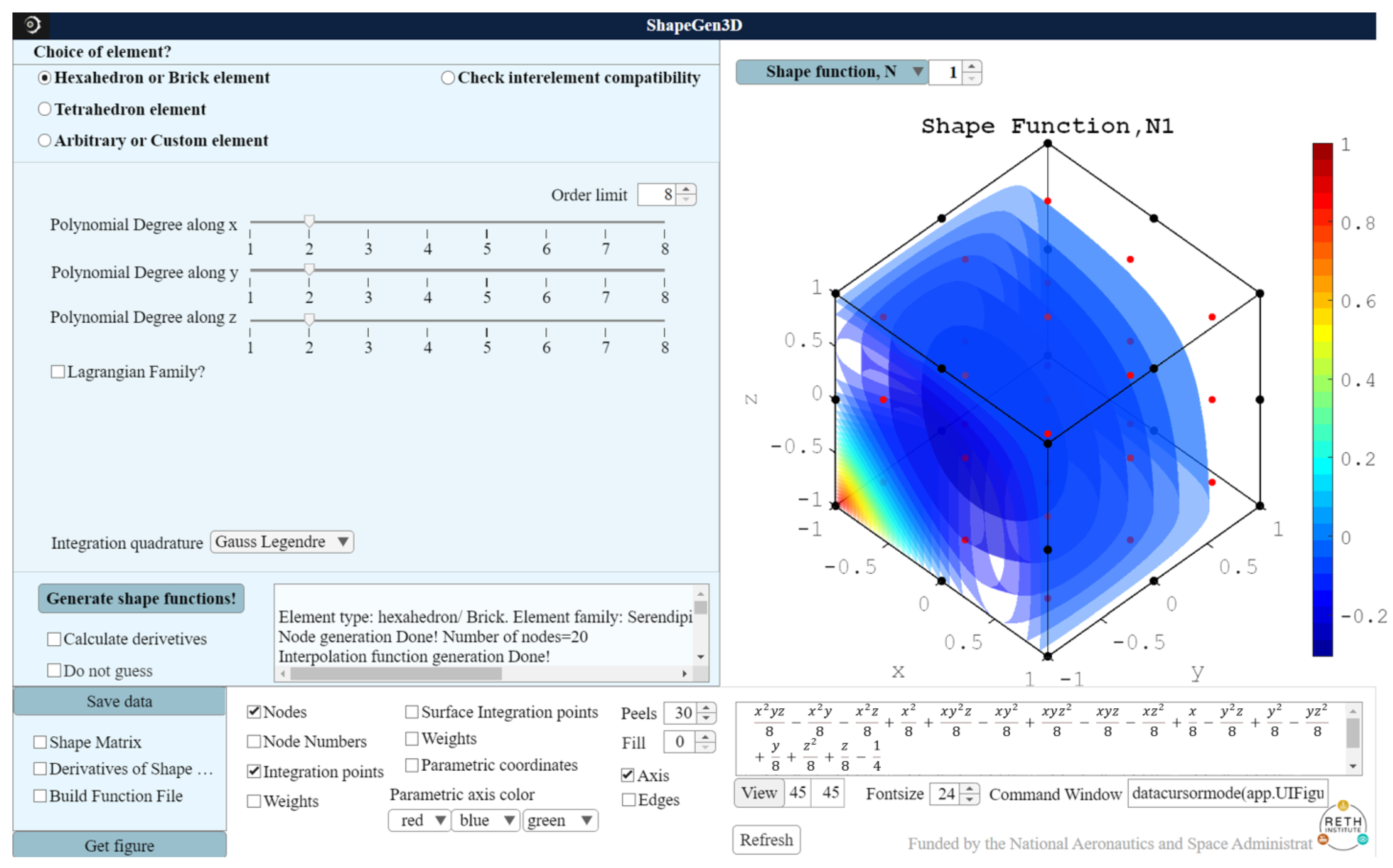
3.1. 20-Node Brick Element
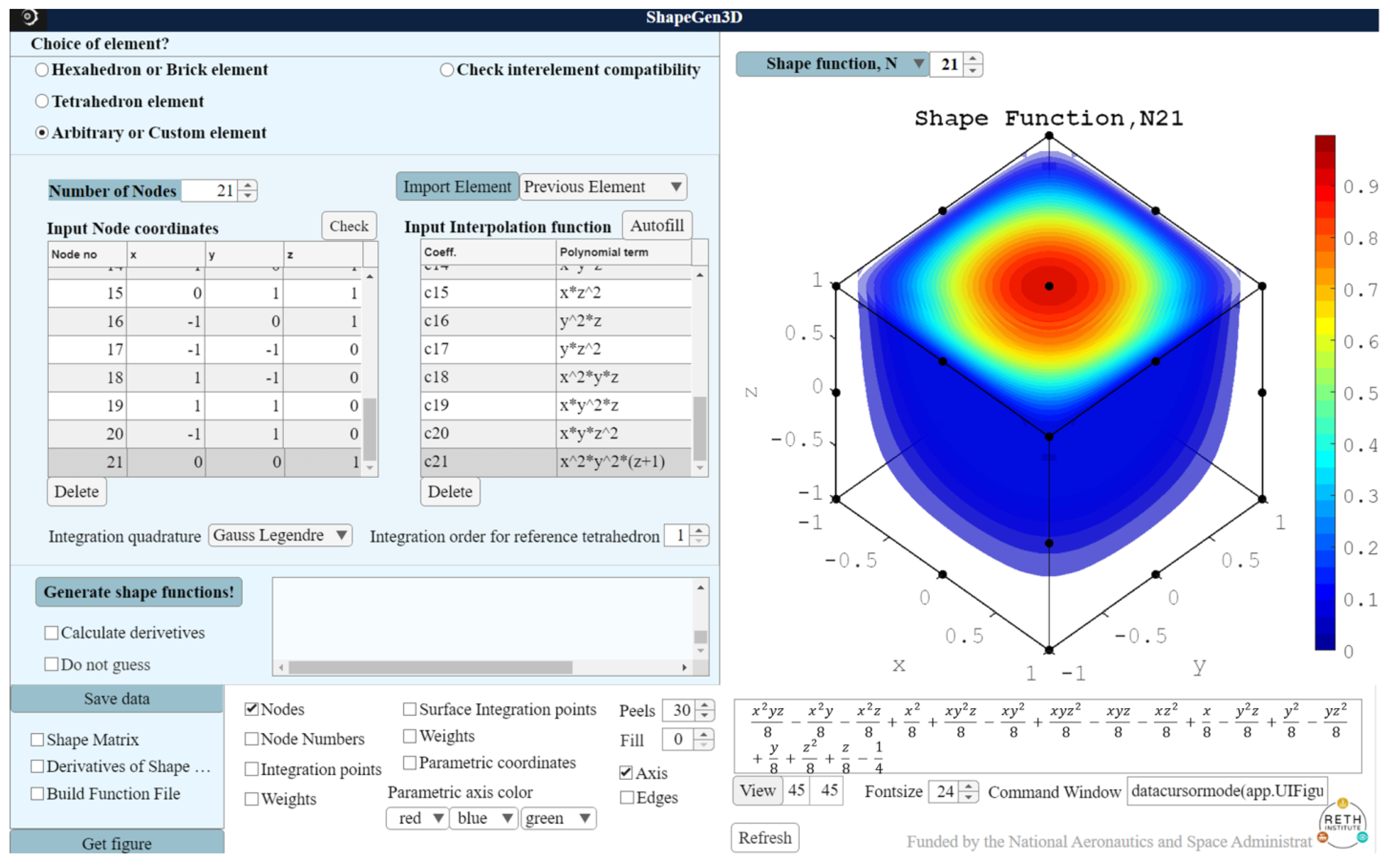
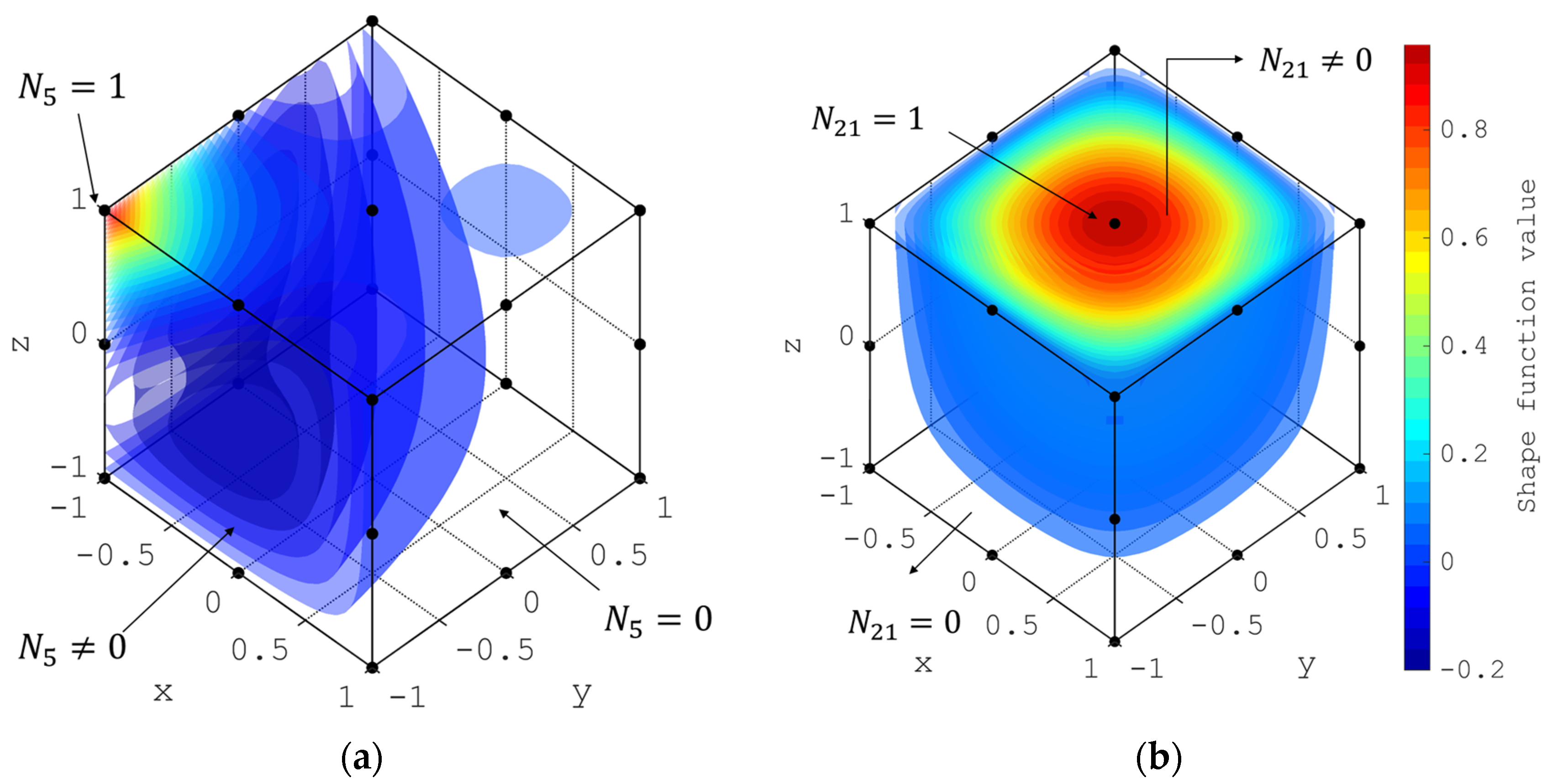
3.2. 21-Node Brick Element
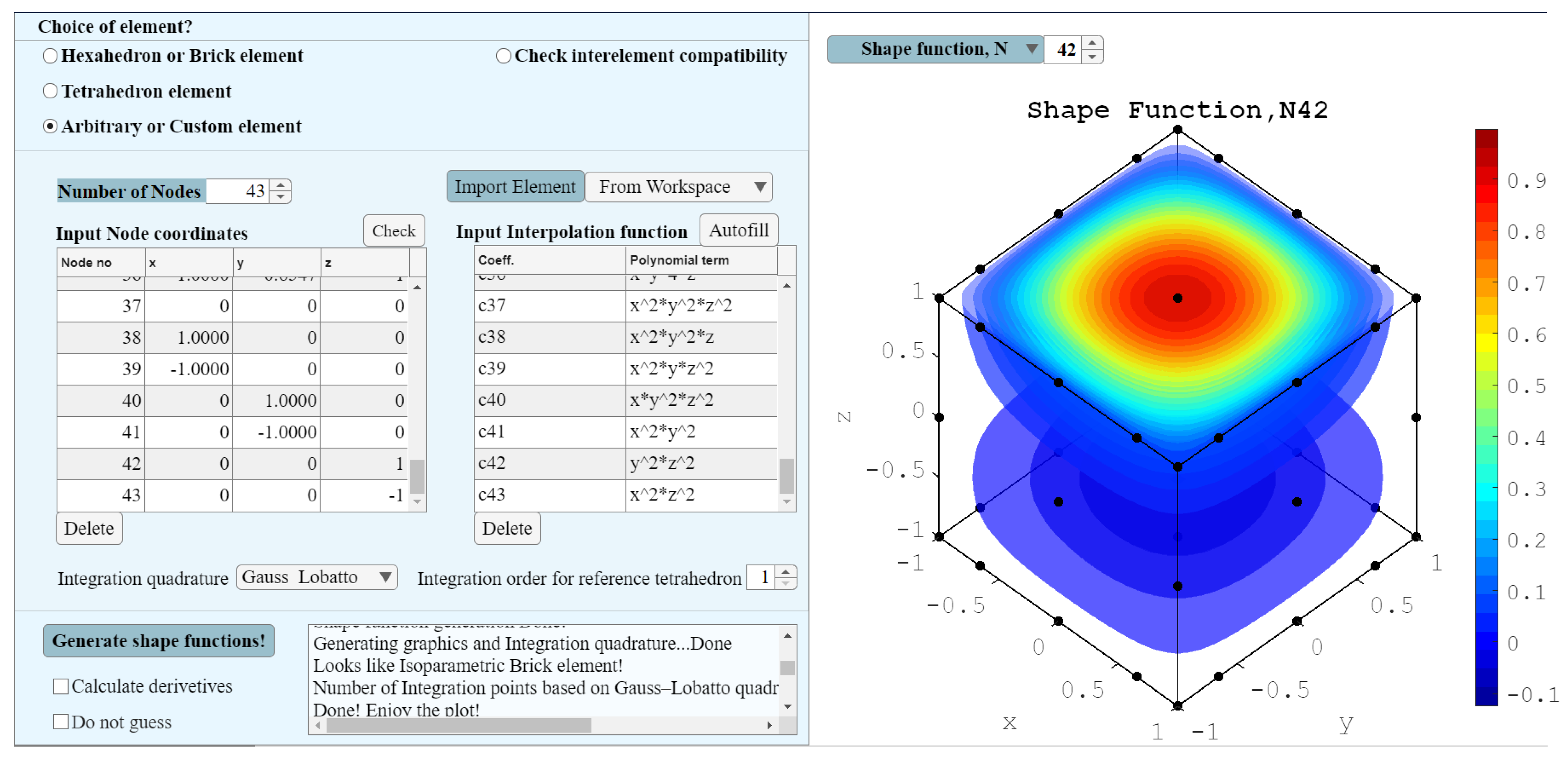
3.3. 43-Node Hexahedron Element
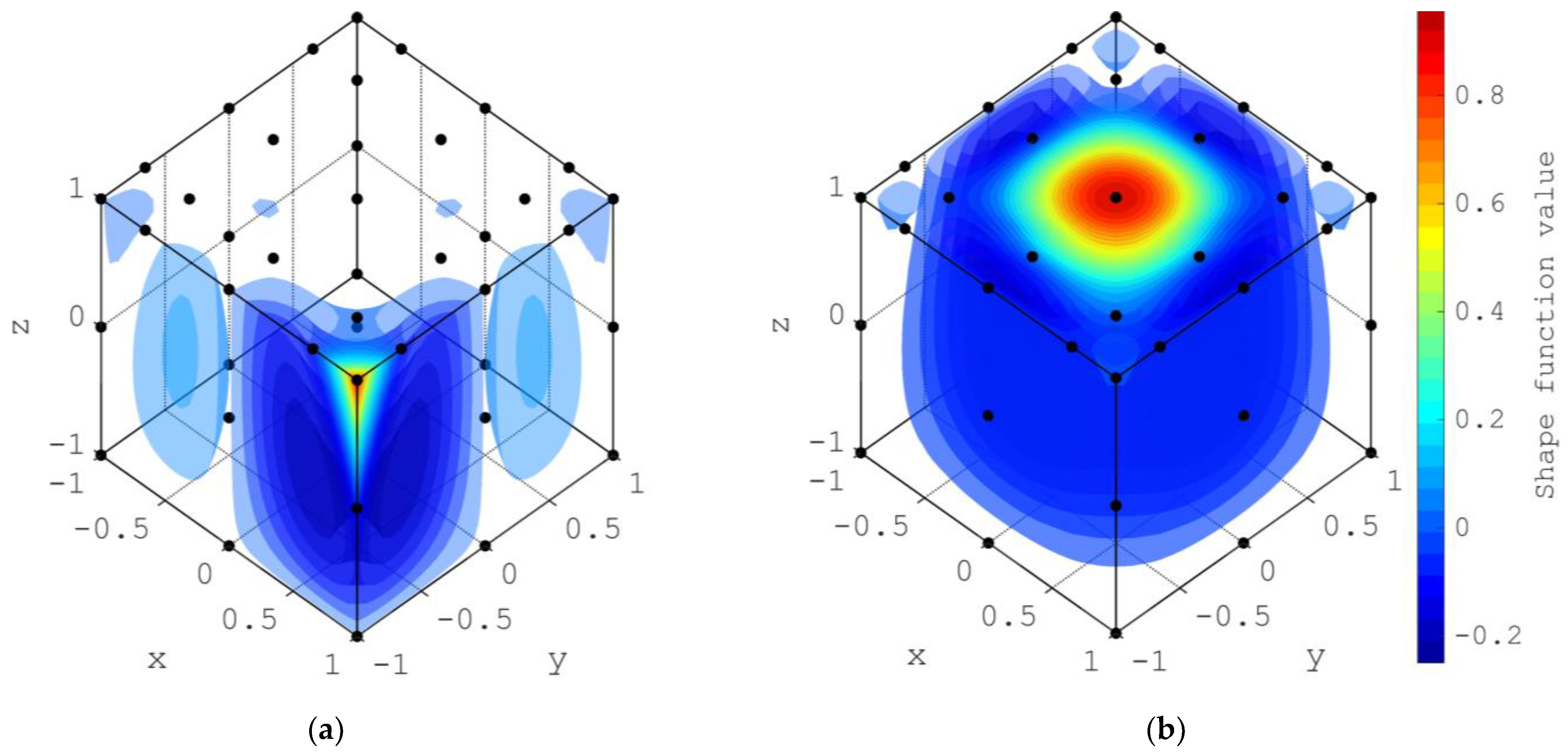
3.4. 43-Node Transition Element from Fourth to Second-Order Lagrangian Element
3.5. Spectral Elements
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Node Number | X | y | Z |
|---|---|---|---|
| 1 | −1 | −1 | −1 |
| 2 | 1 | −1 | −1 |
| 3 | 1 | 1 | −1 |
| 4 | −1 | 1 | −1 |
| 5 | −1 | −1 | 1 |
| 6 | 1 | −1 | 1 |
| 7 | 1 | 1 | 1 |
| 8 | −1 | 1 | 1 |
| 9 | 0 | −1 | −1 |
| 10 | 1 | 0 | −1 |
| 11 | 0 | 1 | −1 |
| 12 | −1 | 0 | −1 |
| 13 | 0 | −1 | 1 |
| 14 | 1 | 0 | 1 |
| 15 | 0 | 1 | 1 |
| 16 | −1 | 0 | 1 |
| 17 | −1 | −1 | 0 |
| 18 | 1 | −1 | 0 |
| 19 | 1 | 1 | 0 |
| 20 | −1 | 1 | 0 |
| Node | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 |
| Integration Point No | x | y | z | Weight |
|---|---|---|---|---|
| 1 | −0.7746 | −0.7746 | −0.7746 | 0.171468 |
| 2 | −0.7746 | −0.7746 | 0 | 0.274348 |
| 3 | −0.7746 | −0.7746 | 0.774597 | 0.171468 |
| 4 | −0.7746 | 0 | −0.7746 | 0.274348 |
| 5 | −0.7746 | 0 | 0 | 0.438957 |
| 6 | −0.7746 | 0 | 0.774597 | 0.274348 |
| 7 | −0.7746 | 0.774597 | −0.7746 | 0.171468 |
| 8 | −0.7746 | 0.774597 | 0 | 0.274348 |
| 9 | −0.7746 | 0.774597 | 0.774597 | 0.171468 |
| 10 | 0 | −0.7746 | −0.7746 | 0.274348 |
| 11 | 0 | −0.7746 | 0 | 0.438957 |
| 12 | 0 | −0.7746 | 0.774597 | 0.274348 |
| 13 | 0 | 0 | −0.7746 | 0.438957 |
| 14 | 0 | 0 | 0 | 0.702332 |
| 15 | 0 | 0 | 0.774597 | 0.438957 |
| 16 | 0 | 0.774597 | −0.7746 | 0.274348 |
| 17 | 0 | 0.774597 | 0 | 0.438957 |
| 18 | 0 | 0.774597 | 0.774597 | 0.274348 |
| 19 | 0.774597 | −0.7746 | −0.7746 | 0.171468 |
| 20 | 0.774597 | −0.7746 | 0 | 0.274348 |
| 21 | 0.774597 | −0.7746 | 0.774597 | 0.171468 |
| 22 | 0.774597 | 0 | −0.7746 | 0.274348 |
| 23 | 0.774597 | 0 | 0 | 0.438957 |
| 24 | 0.774597 | 0 | 0.774597 | 0.274348 |
| 25 | 0.774597 | 0.774597 | −0.7746 | 0.171468 |
| 26 | 0.774597 | 0.774597 | 0 | 0.274348 |
| 27 | 0.774597 | 0.774597 | 0.774597 | 0.171468 |
| Integration Point No | x | y | z | Weight | |||
|---|---|---|---|---|---|---|---|
| 1 | 1 | −0.7746 | −0.7746 | 0.30864 | 1 | 0 | 0 |
| 2 | 1 | −0.7746 | 0 | 0.49382 | 1 | 0 | 0 |
| 3 | 1 | −0.7746 | 0.77459 | 0.30864 | 1 | 0 | 0 |
| 4 | 1 | 0 | −0.7746 | 0.49382 | 1 | 0 | 0 |
| 5 | 1 | 0 | 0 | 0.79012 | 1 | 0 | 0 |
| 6 | 1 | 0 | 0.77459 | 0.49382 | 1 | 0 | 0 |
| 7 | 1 | 0.77459 | −0.7746 | 0.30864 | 1 | 0 | 0 |
| 8 | 1 | 0.77459 | 0 | 0.49382 | 1 | 0 | 0 |
| 9 | 1 | 0.77459 | 0.77459 | 0.30864 | 1 | 0 | 0 |
| 10 | −1 | −0.7746 | −0.7746 | 0.30864 | −1 | 0 | 0 |
| 11 | −1 | −0.7746 | 0 | 0.49382 | −1 | 0 | 0 |
| 12 | −1 | −0.7746 | 0.77459 | 0.30864 | −1 | 0 | 0 |
| 13 | −1 | 0 | −0.7746 | 0.49382 | −1 | 0 | 0 |
| 14 | −1 | 0 | 0 | 0.79012 | −1 | 0 | 0 |
| 15 | −1 | 0 | 0.77459 | 0.49382 | −1 | 0 | 0 |
| 16 | −1 | 0.77459 | −0.7746 | 0.30864 | −1 | 0 | 0 |
| 17 | −1 | 0.77459 | 0 | 0.49382 | −1 | 0 | 0 |
| 18 | −1 | 0.77459 | 0.77459 | 0.30864 | −1 | 0 | 0 |
| 19 | −0.7746 | 1 | −0.7746 | 0.30864 | 0 | 1 | 0 |
| 20 | −0.7746 | 1 | 0 | 0.49382 | 0 | 1 | 0 |
| 21 | −0.7746 | 1 | 0.77459 | 0.30864 | 0 | 1 | 0 |
| 22 | 0 | 1 | −0.7746 | 0.49382 | 0 | 1 | 0 |
| 23 | 0 | 1 | 0 | 0.79012 | 0 | 1 | 0 |
| 24 | 0 | 1 | 0.77459 | 0.49382 | 0 | 1 | 0 |
| 25 | 0.77459 | 1 | −0.7746 | 0.30864 | 0 | 1 | 0 |
| 26 | 0.77459 | 1 | 0 | 0.49382 | 0 | 1 | 0 |
| 27 | 0.77459 | 1 | 0.77459 | 0.30864 | 0 | 1 | 0 |
| 28 | −0.7746 | −1 | −0.7746 | 0.30864 | 0 | −1 | 0 |
| 29 | −0.7746 | −1 | 0 | 0.49382 | 0 | −1 | 0 |
| 30 | −0.7746 | −1 | 0.77459 | 0.30864 | 0 | −1 | 0 |
| 31 | 0 | −1 | −0.7746 | 0.49382 | 0 | −1 | 0 |
| 32 | 0 | −1 | 0 | 0.79012 | 0 | −1 | 0 |
| 33 | 0 | −1 | 0.77459 | 0.49382 | 0 | −1 | 0 |
| 34 | 0.77459 | −1 | −0.7746 | 0.30864 | 0 | −1 | 0 |
| 35 | 0.77459 | −1 | 0 | 0.49382 | 0 | −1 | 0 |
| 36 | 0.77459 | −1 | 0.77459 | 0.30864 | 0 | −1 | 0 |
| 37 | −0.7746 | −0.7746 | 1 | 0.30864 | 0 | 0 | 1 |
| 38 | −0.7746 | 0 | 1 | 0.49382 | 0 | 0 | 1 |
| 39 | −0.7746 | 0.77459 | 1 | 0.30864 | 0 | 0 | 1 |
| 40 | 0 | −0.7746 | 1 | 0.49382 | 0 | 0 | 1 |
| 41 | 0 | 0 | 1 | 0.79012 | 0 | 0 | 1 |
| 42 | 0 | 0.77459 | 1 | 0.49382 | 0 | 0 | 1 |
| 43 | 0.77459 | −0.7746 | 1 | 0.30864 | 0 | 0 | 1 |
| 44 | 0.77459 | 0 | 1 | 0.49382 | 0 | 0 | 1 |
| 45 | 0.77459 | 0.77459 | 1 | 0.30864 | 0 | 0 | 1 |
| 46 | −0.7746 | −0.7746 | −1 | 0.30864 | 0 | 0 | −1 |
| 47 | −0.7746 | 0 | −1 | 0.49382 | 0 | 0 | −1 |
| 48 | −0.7746 | 0.77459 | −1 | 0.30864 | 0 | 0 | −1 |
| 49 | 0 | −0.7746 | −1 | 0.49382 | 0 | 0 | −1 |
| 50 | 0 | 0 | −1 | 0.79012 | 0 | 0 | −1 |
| 51 | 0 | 0.77459 | −1 | 0.49382 | 0 | 0 | −1 |
| 52 | 0.77459 | −0.7746 | −1 | 0.30864 | 0 | 0 | −1 |
| 53 | 0.77459 | 0 | −1 | 0.49382 | 0 | 0 | −1 |
| 54 | 0.77459 | 0.77459 | −1 | 0.30864 | 0 | 0 | −1 |
| Node Number | |||
|---|---|---|---|
| 2 | 1 | 0 | 0 |
| 3 | 1 | 0 | 0 |
| 6 | 1 | 0 | 0 |
| 7 | 1 | 0 | 0 |
| 10 | 1 | 0 | 0 |
| 14 | 1 | 0 | 0 |
| 18 | 1 | 0 | 0 |
| 19 | 1 | 0 | 0 |
| 1 | −1 | 0 | 0 |
| 4 | −1 | 0 | 0 |
| 5 | −1 | 0 | 0 |
| 8 | −1 | 0 | 0 |
| 12 | −1 | 0 | 0 |
| 16 | −1 | 0 | 0 |
| 17 | −1 | 0 | 0 |
| 20 | −1 | 0 | 0 |
| 3 | 0 | 1 | 0 |
| 4 | 0 | 1 | 0 |
| 7 | 0 | 1 | 0 |
| 8 | 0 | 1 | 0 |
| 11 | 0 | 1 | 0 |
| 15 | 0 | 1 | 0 |
| 19 | 0 | 1 | 0 |
| 20 | 0 | 1 | 0 |
| 1 | 0 | −1 | 0 |
| 2 | 0 | −1 | 0 |
| 5 | 0 | −1 | 0 |
| 6 | 0 | −1 | 0 |
| 9 | 0 | −1 | 0 |
| 13 | 0 | −1 | 0 |
| 17 | 0 | −1 | 0 |
| 18 | 0 | −1 | 0 |
| 5 | 0 | 0 | 1 |
| 6 | 0 | 0 | 1 |
| 7 | 0 | 0 | 1 |
| 8 | 0 | 0 | 1 |
| 13 | 0 | 0 | 1 |
| 14 | 0 | 0 | 1 |
| 15 | 0 | 0 | 1 |
| 16 | 0 | 0 | 1 |
| 1 | 0 | 0 | −1 |
| 2 | 0 | 0 | −1 |
| 3 | 0 | 0 | −1 |
| 4 | 0 | 0 | −1 |
| 9 | 0 | 0 | −1 |
| 10 | 0 | 0 | −1 |
| 11 | 0 | 0 | −1 |
| 12 | 0 | 0 | −1 |
| Node Number | x | y | z |
|---|---|---|---|
| 1 | −1 | −1 | −1 |
| 2 | 1 | −1 | −1 |
| 3 | 1 | 1 | −1 |
| 4 | −1 | 1 | −1 |
| 5 | −1 | −1 | 1 |
| 6 | 1 | −1 | 1 |
| 7 | 1 | 1 | 1 |
| 8 | −1 | 1 | 1 |
| 9 | 0 | −1 | −1 |
| 10 | 1 | 0 | −1 |
| 11 | 0 | 1 | −1 |
| 12 | −1 | 0 | −1 |
| 13 | 0 | −1 | 1 |
| 14 | 1 | 0 | 1 |
| 15 | 0 | 1 | 1 |
| 16 | −1 | 0 | 1 |
| 17 | −1 | −1 | 0 |
| 18 | 1 | −1 | 0 |
| 19 | 1 | 1 | 0 |
| 20 | −1 | 1 | 0 |
| 21 | 0 | 0 | 1 |
| Node | |
|---|---|
| 1 | |
| 2 | |
| 3 | |
| 4 | |
| 5 | |
| 6 | |
| 7 | |
| 8 | |
| 9 | |
| 10 | |
| 11 | |
| 12 | |
| 13 | |
| 14 | |
| 15 | |
| 16 | |
| 17 | |
| 18 | |
| 19 | |
| 20 | |
| 21 |
| Node Number | |||
|---|---|---|---|
| 2 | 1 | 0 | 0 |
| 3 | 1 | 0 | 0 |
| 6 | 1 | 0 | 0 |
| 7 | 1 | 0 | 0 |
| 10 | 1 | 0 | 0 |
| 14 | 1 | 0 | 0 |
| 18 | 1 | 0 | 0 |
| 19 | 1 | 0 | 0 |
| 1 | −1 | 0 | 0 |
| 4 | −1 | 0 | 0 |
| 5 | −1 | 0 | 0 |
| 8 | −1 | 0 | 0 |
| 12 | −1 | 0 | 0 |
| 16 | −1 | 0 | 0 |
| 17 | −1 | 0 | 0 |
| 20 | −1 | 0 | 0 |
| 3 | 0 | 1 | 0 |
| 4 | 0 | 1 | 0 |
| 7 | 0 | 1 | 0 |
| 8 | 0 | 1 | 0 |
| 11 | 0 | 1 | 0 |
| 15 | 0 | 1 | 0 |
| 19 | 0 | 1 | 0 |
| 20 | 0 | 1 | 0 |
| 1 | 0 | −1 | 0 |
| 2 | 0 | −1 | 0 |
| 5 | 0 | −1 | 0 |
| 6 | 0 | −1 | 0 |
| 9 | 0 | −1 | 0 |
| 13 | 0 | −1 | 0 |
| 17 | 0 | −1 | 0 |
| 18 | 0 | −1 | 0 |
| 5 | 0 | 0 | 1 |
| 6 | 0 | 0 | 1 |
| 7 | 0 | 0 | 1 |
| 8 | 0 | 0 | 1 |
| 13 | 0 | 0 | 1 |
| 14 | 0 | 0 | 1 |
| 15 | 0 | 0 | 1 |
| 16 | 0 | 0 | 1 |
| 21 | 0 | 0 | 1 |
| 1 | 0 | 0 | −1 |
| 2 | 0 | 0 | −1 |
| 3 | 0 | 0 | −1 |
| 4 | 0 | 0 | −1 |
| 9 | 0 | 0 | −1 |
| 10 | 0 | 0 | −1 |
| 11 | 0 | 0 | −1 |
| 12 | 0 | 0 | −1 |
| Objective | Procedure | ||
|---|---|---|---|
| 20-node brick formulation | Segment 1 options | Hexahedron or Brick element | Click |
| Polynomial degree along | 2 | ||
| Polynomial degree along | 2 | ||
| Polynomial degree along | 2 | ||
| Lagrangian Family | Un-check | ||
| Integration quadrature | Gauss–Legendre | ||
| Segment 2 options | Do not guess | Unchecked | |
| Generate shape function! | Click | ||
| 21-node brick formulation | Segment 1 options | Arbitrary or Custom element | Click |
| Import Element | Previous Element | ||
| Number of nodes | 21 | ||
| Input Node coordinates in the 21st row | 0 0 1 | ||
| Input Interpolation function in the 21st row | |||
| Integration quadrature | Gauss–Legendre | ||
| Segment 2 options | Do not guess | Unchecked | |
| Generate shape function! | Click | ||
| 20 and 21-node brick compatibility test | Segment 1 options | Compare shape function | Click |
| Check interelement compatibility | Click | ||
| 36-node brick element | Segment 1 options | Hexahedron or Brick element | Click |
| Polynomial degree along | 4 | ||
| Polynomial degree along | 4 | ||
| Polynomial degree along | 2 | ||
| Lagrangian Family | Un-check | ||
| Integration quadrature | Gauss–Legendre | ||
| Segment 2 options | Do not guess | Unchecked | |
| Generate shape function! | Click | ||
| 43-node brick element for Germain–Lagrange plate bending | Segment 1 options | Arbitrary or Custom element | Click |
| Import Element | Previous Element | ||
| Number of nodes | 43 | ||
| Input Node coordinates | 0 0 1 | ||
| 0 0 −1 | |||
| 0 1 0 | |||
| 0 −1 0 | |||
| 1 0 0 | |||
| −1 0 0 | |||
| 0 0 0 | |||
| Input monomial basis functions | |||
| Integration quadrature | Gauss–Legendre | ||
| Segment 2 options | Do not guess | Unchecked | |
| Generate shape function! | Click | ||
| 75-node brick element | Segment 1 options | Hexahedron or Brick element | Click |
| Polynomial degree along | 4 | ||
| Polynomial degree along | 4 | ||
| Polynomial degree along | 2 | ||
| Lagrangian Family | Check | ||
| Integration quadrature | Gauss–Lobatto | ||
| Segment 2 options | Do not guess | Unchecked | |
| Generate shape function! | Click | ||
| 43-node transition element from fourth to second order Lagrangian element | Segment 1 options | Arbitrary or Custom element | Click |
| Import Element | Previous Element | ||
| Number of nodes | 43 | ||
| Remove Node coordinates | 0 0 1 | ||
| 0 0 −1 | |||
| 0 1 0 | |||
| 0 −1 0 | |||
| 1 0 0 | |||
| −1 0 0 | |||
| 0 0 0 | |||
| Remove monomial basis functions | Factors with | ||
| Modify monomial basis functions | |||
| Integration quadrature | Gauss–Lobatto | ||
| Segment 2 options | Do not guess | Unchecked | |
| Generate shape function! | Click | ||
| Spectral hexahedron formulation | Segment 1 options | Hexahedron or Brick element | Click |
| Polynomial degree along | 5 | ||
| Polynomial degree along | 5 | ||
| Polynomial degree along | 2 | ||
| Lagrangian Family | Check | ||
| Integration quadrature | Gauss–Lobatto | ||
| Segment 2 options | Do not guess | Unchecked | |
| Generate shape function! | Click | ||
| Spectral tetrahedron formulation | Segment 1 options | Tetrahedron element | Click |
| Element order | 5 | ||
| No of Sub-Tetrahedrons | 8 | ||
| Integration order for reference tetrahedron | 1 | ||
| Segment 2 options | Do not guess | Unchecked | |
| Generate shape function! | Click | ||
References
- Zienkiewicz, O.C.; Taylor, R.L.; Zhu, J.Z. The Finite Element Method: Its Basis and Fundamentals, 7th ed.; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar] [CrossRef]
- Bunting, C.F. Introduction to the finite element method. In Proceedings of the 2008 IEEE International Symposium on Electromagnetic Compatibility, Detroit, MI, USA, 18–22 August 2008; pp. 1–9. [Google Scholar] [CrossRef]
- Chari, M.; Salon, S. Numerical Methods in Electromagnetism; Elsevier: Amsterdam, The Netherlands, 2000. [Google Scholar] [CrossRef]
- Bathe, K.-J. Discontinuous Finite Element Procedures. In Computational Fluid and Solid Mechanics; Springer: London, UK, 2006; pp. 21–43. [Google Scholar] [CrossRef]
- Logg, A.; Lundholm, C.; Nordaas, M. Finite element simulation of physical systems in augmented reality. Adv. Eng. Softw. 2020, 149, 102902. [Google Scholar] [CrossRef]
- Liu, L.; Davies, K.B.; Křížek, M.; Guan, L. On Higher Order Pyramidal Finite Elements. Adv. Appl. Math. Mech. 2011, 3, 131–140. [Google Scholar] [CrossRef]
- Smith, M. ABAQUS/Standard User’s Manual, Version 6.9; Dassault Systèmes Simulia Corp.: Johnston, RI, USA, 2009. [Google Scholar]
- Staten, M.L.; Jones, N.L. Local refinement of three-dimensional finite element meshes. Eng. Comput. 1997, 13, 165–174. [Google Scholar] [CrossRef]
- Duczek, S.; Saputra, A.; Gravenkamp, H. High order transition elements: The xy-element concept—Part I: Statics. Comput. Methods Appl. Mech. Eng. 2020, 362, 112833. [Google Scholar] [CrossRef]
- Buczkowski, R. 21-node hexahedral isoparametric element for analysis of contact problems. Commun. Numer. Methods Eng. 1998, 14, 681–692. [Google Scholar] [CrossRef]
- Smith, I.M.; Kidger, D.J. Elastoplastic analysis using the 14-node brick element family. Int. J. Numer. Methods Eng. 1992, 35, 1263–1275. [Google Scholar] [CrossRef]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Zang, T.A. Spectral Approximation. In Spectral Methods in Fluid Dynamics; Springer: Berlin/Heidelberg, Germany, 1988; pp. 31–75. [Google Scholar] [CrossRef]
- Patera, A.T. A spectral element method for fluid dynamics: Laminar flow in a channel expansion. J. Comput. Phys. 1984, 54, 468–488. [Google Scholar] [CrossRef]
- Palacz, M.; Krawczuk, M.; Żak, A. Spectral Element Methods for Damage Detection and Condition Monitoring. In Smart Innovation, Systems and Technologies; Springer: Berlin/Heidelberg, Germany, 2020; Volume 166, pp. 549–558. [Google Scholar] [CrossRef]
- Soman, R.; Kudela, P.; Balasubramaniam, K.; Singh, S.K.; Malinowski, P. A Study of Sensor Placement Optimization Problem for Guided Wave-Based Damage Detection. Sensors 2019, 19, 1856. [Google Scholar] [CrossRef]
- Ostachowicz, W.; Kudela, P.; Krawczuk, M.; Zak, A. Guided Waves in Structures for SHM: The Time-Domain Spectral Element Method; John Wiley & Sons, Ltd.: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Komatitsch, D.; Tromp, J. Spectral-element simulations of global seismic wave propagation-I. Validation. Geophys. J. Int. 2002, 149, 390–412. [Google Scholar] [CrossRef]
- Arnold, D.N.; Awanou, G. The Serendipity Family of Finite Elements. Found. Comput. Math. 2011, 11, 337–344. [Google Scholar] [CrossRef]
- Silvester, P. Tetrahedral polynomial finite elements for the Helmholtz equation. Int. J. Numer. Methods Eng. 1972, 4, 405–413. [Google Scholar] [CrossRef]
- Duczek, S.; Duvigneau, F.; Gabbert, U. The finite cell method for tetrahedral meshes. Finite Elem. Anal. Des. 2016, 121, 18–32. [Google Scholar] [CrossRef]
- Kabir, H.; Matikolaei, S.A.H.H. Implementing an accurate generalized gaussian quadrature solution to find the elastic field in a homogeneous anisotropic media. J. Serbian Soc. Comput. Mech. 2017, 11, 11–19. [Google Scholar] [CrossRef]
- von Winckel, G. Legende-Gauss-Lobatto Nodes and Weights. MATLAB Central File Exchange. Available online: https://www.mathworks.com/matlabcentral/fileexchange/4775-legende-gauss-lobatto-nodes-and-weights (accessed on 20 September 2023).
- Sherwin, S.J.; Karniadakis, G.E. A new triangular and tetrahedral basis for high-order (hp) finite element methods. Int. J. Numer. Methods Eng. 1995, 38, 3775–3802. [Google Scholar] [CrossRef]
- Moore, J.L.; Morgan, N.R.; Horstemeyer, M.F. ELEMENTS: A high-order finite element library in C++. SoftwareX 2019, 10, 100257. [Google Scholar] [CrossRef]
- Cantwell, C.D.; Moxey, D.; Comerford, A.; Bolis, A.; Rocco, G.; Mengaldo, G. Nektar++: An open-source spectral/hp element framework. Comput. Phys. Commun. 2015, 192, 205–219. [Google Scholar] [CrossRef]
- Vishwanatha, J.S.; Swamy, R.H.M.S.; Mahesh, G.; Gouda, H.V. A toolkit for computational fluid dynamics using spectral element method in Scilab. Mater. Today Proc. 2023. [Google Scholar] [CrossRef]
- Bangerth, W.; Hartmann, R.; Kanschat, G. deal. II—a general-purpose object-oriented finite element library. ACM Trans. Math. Softw. 2007, 33, 24. [Google Scholar] [CrossRef]
- Bastian, P.; Blatt, M.; Dedner, A.; Engwer, C.; Klöfkorn, R.; Kornhuber, R.; Ohlberger, M.; Sander, O. A generic grid interface for parallel and adaptive scientific computing. Part II: Implementation and tests in DUNE. Computing 2008, 82, 121–138. [Google Scholar] [CrossRef]
- Kolev, T. Modular Finite Element Methods; No. MFEM; Lawrence Livermore National Lab. (LLNL): Livermore, CA, USA, 2020.
- Weng, W.-C. Web-based post-processing visualization system for finite element analysis. Adv. Eng. Softw. 2011, 42, 398–407. [Google Scholar] [CrossRef]
- Beneš, Š.; Kruis, J. Efficient methods to visualize finite element meshes. Adv. Eng. Softw. 2015, 79, 81–90. [Google Scholar] [CrossRef]
- Wachspress, E.L. A Rational Basis for Function Approximation. IMA J. Appl. Math. 1973, 11, 83–104. [Google Scholar] [CrossRef]
- Kien, D.N.; Zhuang, X. Radial basis function based finite element method: Formulation and applications. Eng. Anal. Bound. Elem. 2023, 152, 455–472. [Google Scholar] [CrossRef]
- Parvizian, J.; Düster, A.; Rank, E. Finite cell method. Comput. Mech. 2007, 41, 121–133. [Google Scholar] [CrossRef]
- Schillinger, D.; Kollmannsberger, S.; Mundani, R.-P.; Rank, E. The finite cell method for geometrically nonlinear problems of solid mechanics. In IOP Conference Series: Materials Science and Engineering; Elsevier: Amsterdam, The Netherlands, 2014; Volume 10, pp. 3768–3782. [Google Scholar] [CrossRef]
- Fortune, S. Voronoi diagrams and delaunay triangulations. In Handbook of Discrete and Computational Geometry, 3rd ed.; World Scientific: Singapore, 2017; pp. 705–721. [Google Scholar] [CrossRef]
- Maździarz, M. Unified isoparametric 3D lagrangeFinite elements. CMES—Comput. Model. Eng. Sci. 2010, 66, 1–24. [Google Scholar]
- Neto, M.A.; Amaro, A.; Roseiro, L.; Cirne, J.; Leal, R. Engineering Computation of Structures: The Finite Element Method; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar] [CrossRef]
- Bourbaki, N. Algebra I: Chapters 1–3; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1998; Volume 1. [Google Scholar]
- Luo, H.; Pozrikidis, C. A Lobatto interpolation grid in the tetrahedron. IMA J. Appl. Math. 2006, 71, 298–313. [Google Scholar] [CrossRef]
- Reddy, J.N. Theory and Analysis of Elastic Plates and Shells, 2nd ed.; Taylor and Francis Group: Abingdon, UK, 2006. [Google Scholar]
- Shahriar, A.; Reynolds, S.; Najarian, M.; Montoya, A. Development of a Computational Framework for the Design of Resilient Space Structures. Earth and Space 2021: Space Exploration, Utilization, Engineering, and Construction in Extreme Environments. In Proceedings of the 17th Biennial International Conference on Engineering, Science, Construction, and Operations in Challenging Environments, Online, 19–23 April 2021; pp. 1263–1271. [Google Scholar] [CrossRef]
- Kitching, R.; Mattingly, H.; Williams, D.; Marais, K. Resilient Space Habitat Design Using Safety Controls. Earth and Space 2021: Space Exploration, Utilization, Engineering, and Construction in Extreme Environments. In Proceedings of the 17th Biennial International Conference on Engineering, Science, Construction, and Operations in Challenging Environments, Online, 19–23 April 2021; pp. 992–1003. [Google Scholar] [CrossRef]




| Surface | Integration Point Weights | |||
|---|---|---|---|---|
| Surface | |||
|---|---|---|---|
| Seg 1: Input Options | Sub-Options | Description |
|---|---|---|
| Hexahedron or Brick element | Polynomial degree along | of Equation (17) |
| Polynomial degree along | of Equation (18) | |
| Polynomial degree along | of Equation (19) | |
| Lagrangian Family | Checking this option will formulate a Lagrangian element. Otherwise, a Serendipity element will be formulated | |
| Integration quadrature | This option offers two integration quadratures; (1) Gauss–Legendre (2) Gauss–Lobatto | |
| Tetrahedron element | Element order | in Equation (27) |
| Number of Sub-Tetrahedral | The number of sub-tetrahedrons used for integration quadrature following the finite cell method. It is active when an element order greater than 4 is used. | |
| Integration order for reference tetrahedron | The integration order for each sub-tetrahedron. It is active when an element order greater than 4 is used. | |
| Arbitrary or Custom element | Input node coordinates | A table where the user can input the nodal distribution of the desired element and cartesian coordinates (x, y, z) for each node. |
| Input interpolation function | A table where the user can input from Equation (3), where and is the number of nodes. | |
| Integration quadrature | If the software detects an arbitrary element from the isoparametric hexahedron family, it will determine the selected integration quadrature from one of the selected options: (1) Gauss–Legendre and (2) Gauss–Lobatto. | |
| Integration order for reference tetrahedron | If the element is not from an isoparametric hexahedron family, the integration quadrature is determined following the procedure presented in Section 2.2 with the integration order selected in this option | |
| Check interelement compatibility | Used to illustrate two consecutively generated elements |
| Workspace Filename | Description | Data Structure |
|---|---|---|
| Interpolation_Functions | Stores interpolation in symbolic format | : Function I of Equation 1 in symbolic format |
| Node_Coordinates | Stores node coordinates | where : coordinate of node . |
| Shape_Functions | Stores shape functions in symbolic format for the corresponding nodes | : Shape function in symbolic format. |
| Surface_Nodes_and_vectors | Stores nodes on surface and surface normal vector pointing outward of the domain for all surfaces | are node numbers and integers. is the normal vector pointing outward of the domain on the surface containing node . |
| Integration_Points_Coordinates_Weights | Stores integration points and weights inside the element | where coordinate of integration point . : weight of integration point . |
| Integration_Points_Coordinates_Weights_Vectors on_Surface | Stores integration points and weights on surfaces and surface normal vector pointing outward of the domain for all surfaces | where : coordinate of integration point . : weight of integration point. is the normal unit vector pointing outward of the domain on the surface at integration point . |
| Parametric_Coordinates | Stores parametric coordinates for each surface of the element | and are the parametric and y coordinates, respectively. represents the surface number. |
| Shape_Matrix | Stores the value of each shape function evaluated at each integration point | : shape function evaluated at integration point . |
| dx_Shape_Matrix | Stores the value of the first derivative of each shape function evaluated at each integration point | : shape function derivative evaluated at integration point . |
| Coefficient No. | 75 Node Element Factors | 43 Node Element Factors |
|---|---|---|
| Factors with, | Factors of | Factors of |
| Factors with | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shahriar, A.; Majlesi, A.; Montoya, A. A General Procedure to Formulate 3D Elements for Finite Element Applications. Computation 2023, 11, 197. https://doi.org/10.3390/computation11100197
Shahriar A, Majlesi A, Montoya A. A General Procedure to Formulate 3D Elements for Finite Element Applications. Computation. 2023; 11(10):197. https://doi.org/10.3390/computation11100197
Chicago/Turabian StyleShahriar, Adnan, Arsalan Majlesi, and Arturo Montoya. 2023. "A General Procedure to Formulate 3D Elements for Finite Element Applications" Computation 11, no. 10: 197. https://doi.org/10.3390/computation11100197
APA StyleShahriar, A., Majlesi, A., & Montoya, A. (2023). A General Procedure to Formulate 3D Elements for Finite Element Applications. Computation, 11(10), 197. https://doi.org/10.3390/computation11100197






