Comparison and Evaluation of Machine Learning-Based Classification of Hand Gestures Captured by Inertial Sensors
Abstract
1. Introduction
2. Materials and Methods
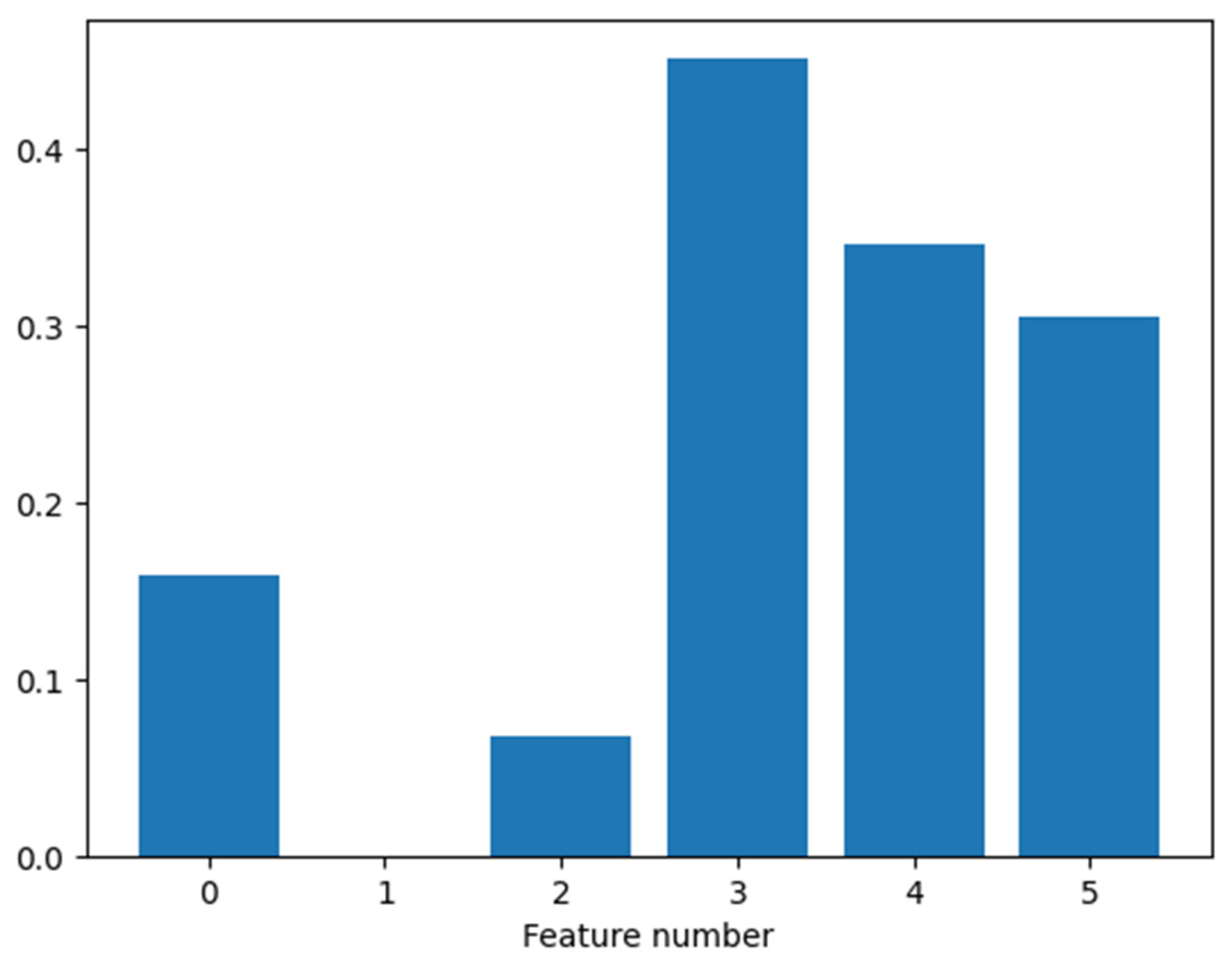
2.1. Features Definition and Selection
2.2. Classification Task
2.2.1. Decision Tree (DT)
2.2.2. Random Forests (RF)
2.2.3. Logistic Regression (LR)
2.2.4. Linear Discriminant Analysis (LDA)
2.2.5. Support Vector Machine (SVM) with Linear Kernel
2.2.6. Naïve Bayes Classifier (NB)
2.2.7. K-Nearest Neighbours (KNN)
2.2.8. Stochastic Gradient Descent (SGD)
2.2.9. Classifiers Evaluation Measures
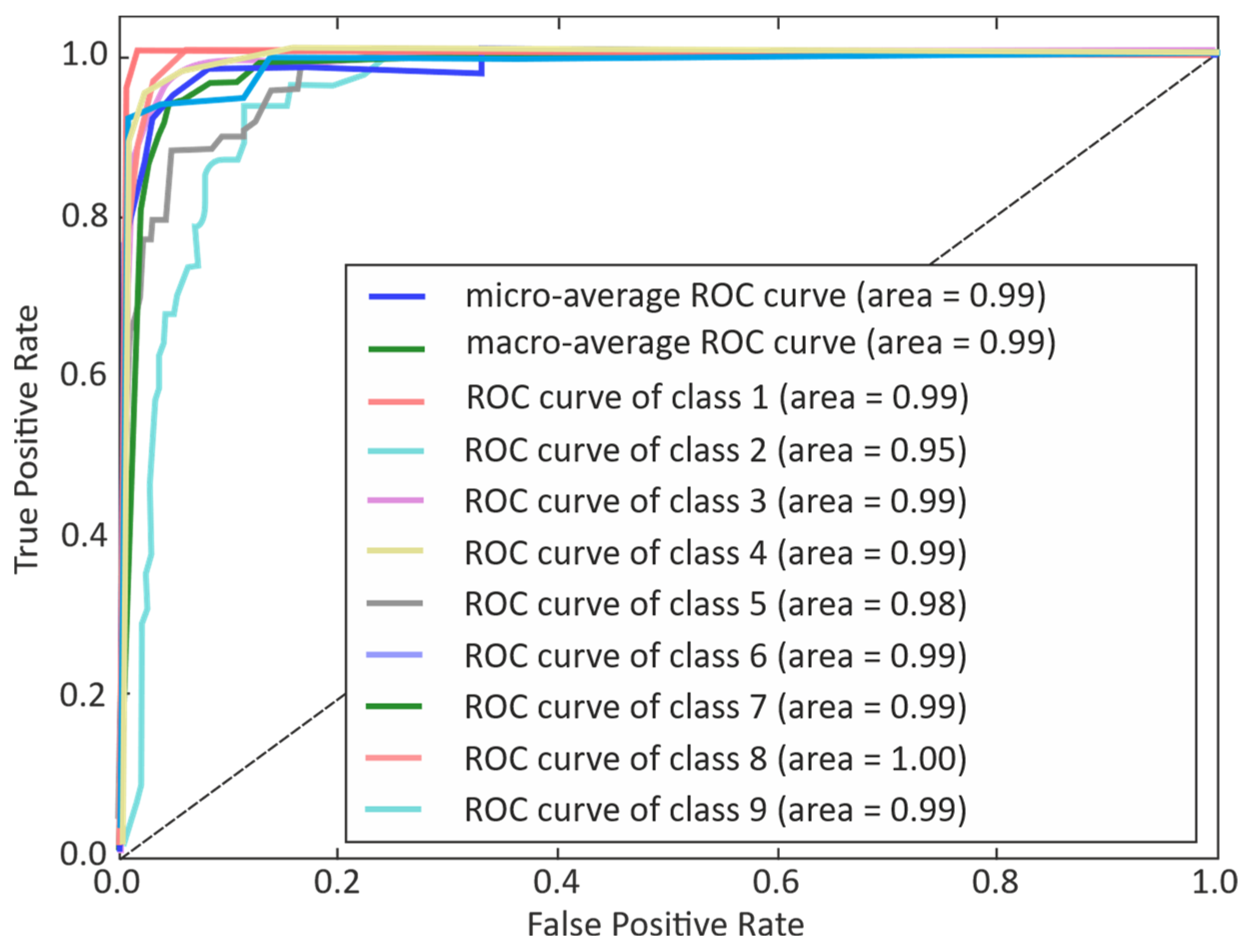
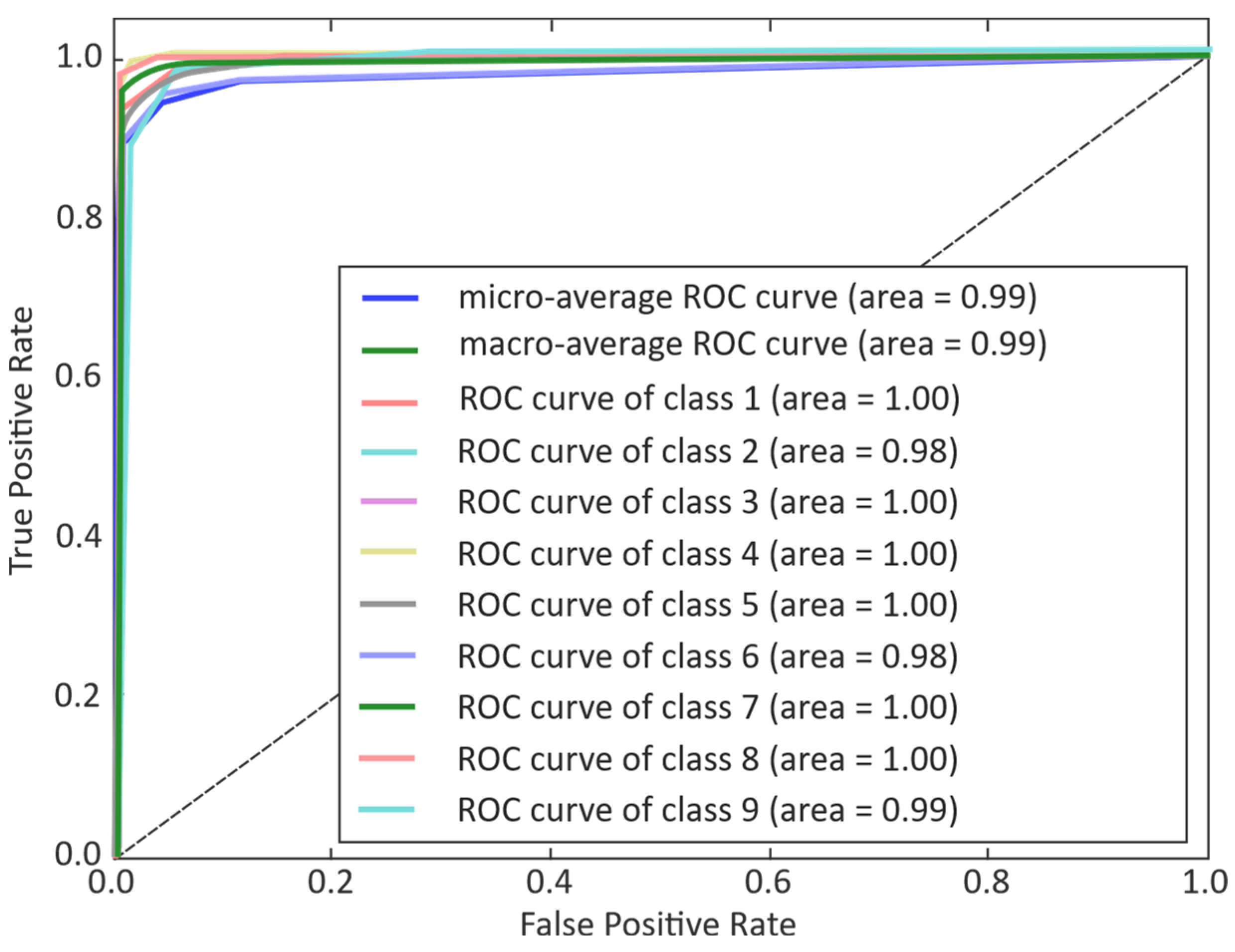
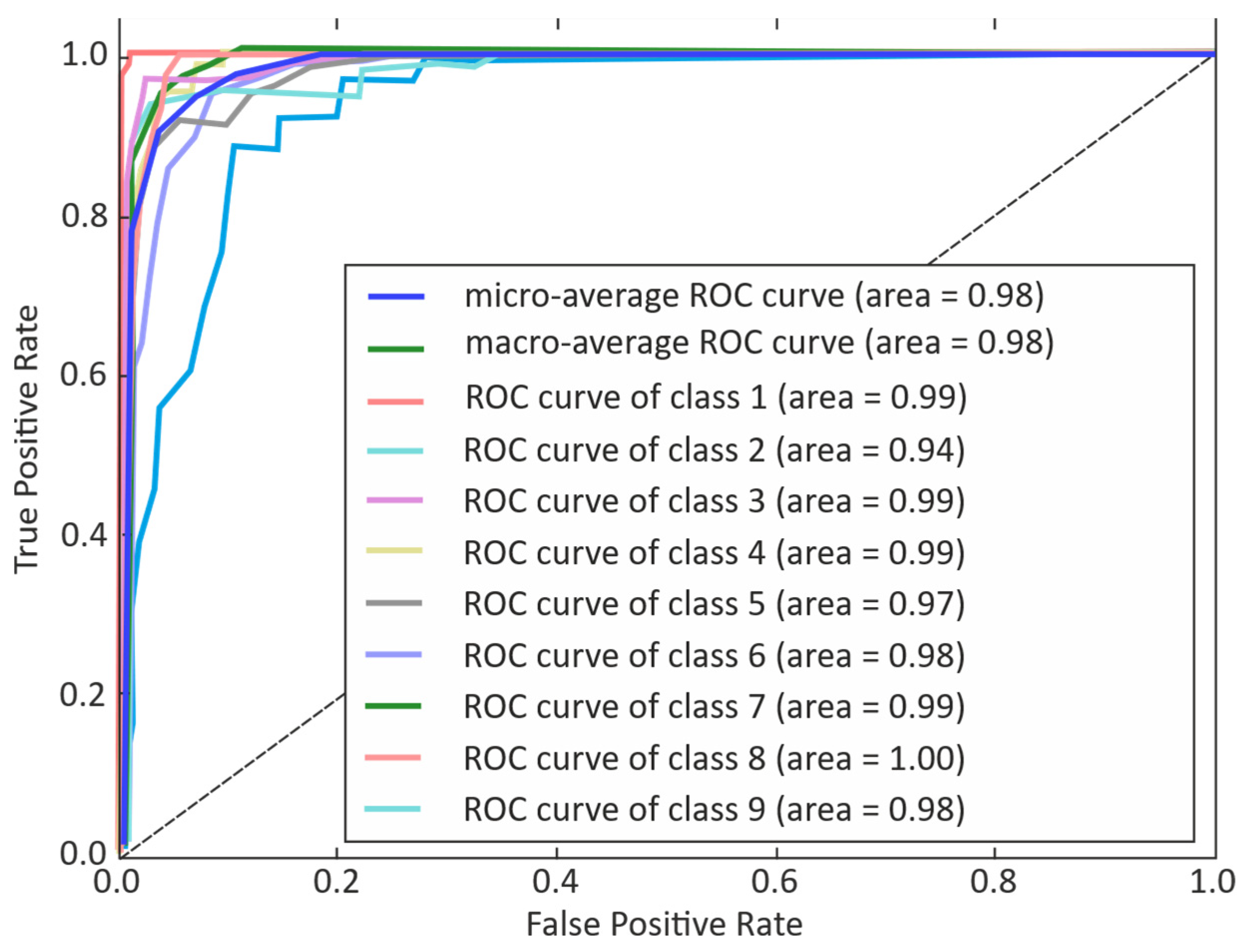
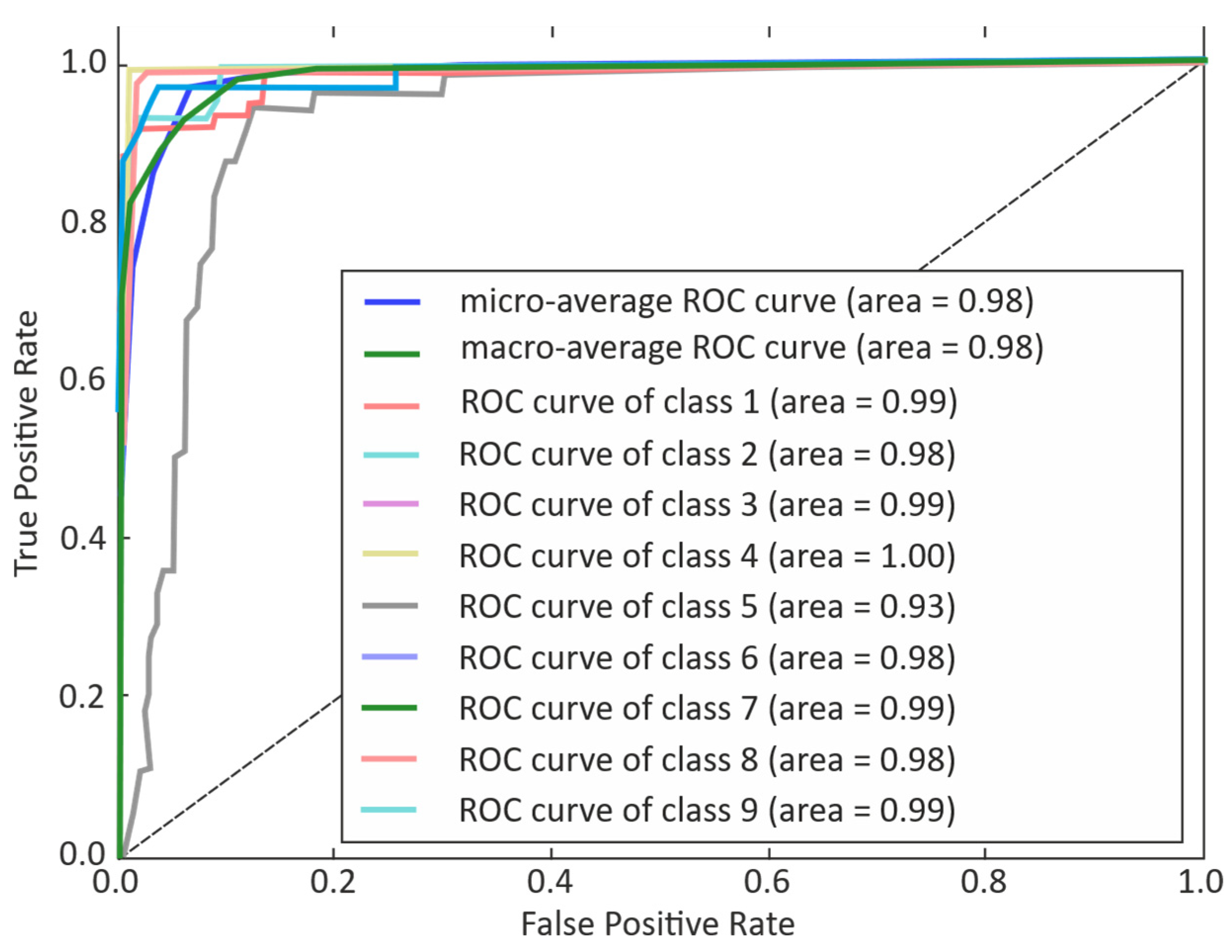
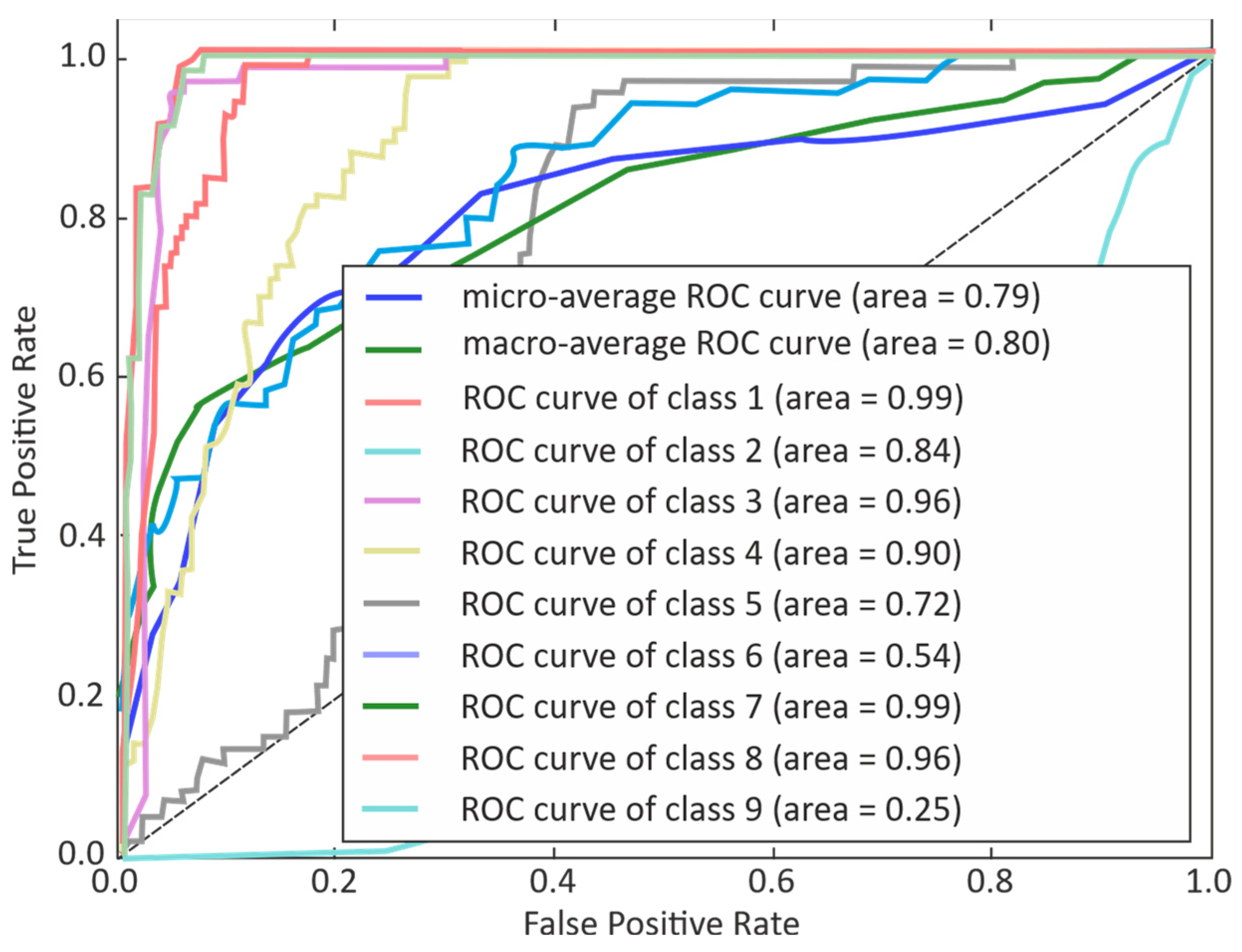
3. Results
4. Discussion
4.1. The Applicability of the Best-Performing Algorithms to 8-Bit AVR Microcontrollers
4.2. More Detailed Discussion Regarding the LR Algorithm
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vishwakarma, D.K.; Kapoor, R. An efficient interpretation of hand gestures to control smart interactive television. Int. J. Comput. Vis. Robot. 2017, 7, 454–471. [Google Scholar] [CrossRef]
- Stančić, I.; Musić, J.; Grujić, T. Gesture recognition system for real-time mobile robot control based on inertial sensors and motion strings. Eng. Appl. Artif. Intell. 2017, 66, 33–48. [Google Scholar]
- Oudah, M.; Al-Naji, A.; Chahl, J. Hand gesture recognition based on computer vision: A review of techniques. J. Imaging 2020, 6, 73. [Google Scholar] [CrossRef] [PubMed]
- Molina, J.; Pajuelo, J.A.; Martínez, J.M. Real-time motion-based hand gestures recognition from time-of-flight video. J. Signal Process. Syst. 2017, 86, 17–25. [Google Scholar] [CrossRef][Green Version]
- Chen, Y.-L.; Hwang, W.-J.; Tai, T.-M.; Cheng, P.-S. Sensor-based hand gesture detection and recognition by key intervals. Appl. Sci. 2022, 12, 7410. [Google Scholar] [CrossRef]
- Chu, Y.C.; Jhang, Y.J.; Tai, T.M.; Hwang, W.J. Recognition of hand gesture sequences by accelerometers and gyroscopes. Appl. Sci. 2020, 10, 6507. [Google Scholar] [CrossRef]
- Tai, T.M.; Jhang, Y.J.; Liao, Z.W.; Teng, K.C.; Hwang, W.J. Sensor-based continuous hand gesture recognition by long short-term memory. IEEE Sens. Lett. 2018, 2, 6000704. [Google Scholar] [CrossRef]
- Gupta, H.P.; Chudgar, H.S.; Mukherjee, S.; Dutta, T.; Sharma, K. Continuous hand gestures recognition technique for human–machine interaction using accelerometer and gyroscope sensors. IEEE Sens. J. 2016, 16, 6425–6432. [Google Scholar] [CrossRef]
- Lefebvre, G.; Berlemont, S.; Mamalet, F.; Garcia, C. Inertial gesture recognition with BLSTM-RNN. In Artificial Neural Networks; Springer Series in Bio-/Neuroinformatics; Springer: Berlin/Heidelberg, Germany, 2015; Volume 4, pp. 393–410. [Google Scholar]
- Jaramillo-Yánez, A.; Benalcázar, M.E.; Mena-Maldonado, E. Real-time hand gesture recognition using surface electromyography and machine learning: A systematic literature review. Sensors 2020, 20, 2467. [Google Scholar] [CrossRef]
- Kundid Vasić, M.; Galić, I.; Vasić, D. Human action identification and search in video files. In Proceedings of the 57th International Symposium on Electronics in Marine—ELMAR, Zadar, Croatia, 28–30 September 2015; IEEE: Piscataway, NJ, USA, 2015. [Google Scholar]
- Choondal, J.J.; Sharavanabhavan, C. Design and implementation of a natural user interface using hand gesture recognition method. Int. J. Innov. Technol. Explor. Eng. 2013, 10, 249–254. [Google Scholar]
- Xu, R.; Zhou, S.; Li, W.J. MEMS Accelerometer based nonspecific-user hand gesture recognition. IEEE Sens. J. 2012, 12, 1166–1173. [Google Scholar] [CrossRef]
- Ma, X.; Peng, J. Kinect sensor-based long-distance hand gesture recognition and fingertip detection with depth information. J. Sens. 2018, 2018, 5809769. [Google Scholar] [CrossRef]
- Kim, M.S.; Lee, C.H. Hand gesture recognition for Kinect v2 sensor in the near distance where depth data are not provided. Int. J. Softw. Eng. Its Appl. 2016, 10, 407–418. [Google Scholar] [CrossRef][Green Version]
- Karbasi, M.; Bhatti, Z.; Nooralishahi, P.; Shah, A.; Mazloomnezhad, S.M.R. Real-time hands detection in depth image by using distance with Kinect camera. Int. J. Internet Things 2015, 4, 1–6. [Google Scholar]
- Li, Y. Hand gesture recognition using Kinect. In Proceedings of the 2012 IEEE International Conference on Computer Science and Automation Engineering, Beijing, China, 22–24 June 2012. [Google Scholar]
- Filaretov, V.; Yukhimetsa, D.; Mursalimov, E. The universal onboard information-control system for mobile robots. In Proceedings of the 25th DAAAM International Symposium on Intelligent Manufacturing and Automation, Vienna, Austria, 26–29 November 2014; DAAAM: Vienna, Austria, 2014. [Google Scholar]
- Riek, L.; Rabinowitch, T.; Bremner, P.; Pipe, A.; Fraser, M. Cooperative Gestures: Effective signaling for humanoid robots. In Proceedings of the 5th ACM/IEEE International Conference on Human-Robot Interaction, Osaka, Japan, 2–5 March 2010. [Google Scholar]
- Ajani, T.S.; Imoize, A.L.; Atayero, A.A. An Overview of Machine Learning within Embedded and Mobile Devices–Optimizations and Applications. Sensors 2021, 21, 4412. [Google Scholar] [CrossRef]
- Mazlan, N.; Ramli, N.A.; Awalin, L.; Ismail, M.; Kassim, A.; Menon, A. A smart building energy management using internet of things (IoT) and machine learning. Test. Eng. Manag. 2020, 83, 8083–8090. [Google Scholar]
- Cornetta, G.; Touhafi, A. Design and evaluation of a new machine learning framework for IoT and embedded devices. Electronics 2021, 10, 600. [Google Scholar] [CrossRef]
- Al-Kofahi, M.M.; Al-Shorman, M.Y.; Al-Kofahi, O.M. Toward energy efficient microcontrollers and Internet-of-Things systems. Comput. Electr. Eng. 2019, 79, 106457. [Google Scholar] [CrossRef]
- Dudak, J.; Kebisek, M.; Gaspar, G.; Fabo, P. Implementation of machine learning algorithm in embedded devices. In Proceedings of the 19th International Conference on Mechatronics—Mechatronika (ME), Prague, Czech Republic, 2–4 December 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Sakr, F.; Bellotti, F.; Berta, R.; De Gloria, A. Machine learning on mainstream microcontrollers. Sensors 2020, 20, 2638. [Google Scholar] [CrossRef]
- Saha, S.S.; Sandha, S.S.; Srivastava, M. Machine Learning for Microcontroller-Class Hardware—A Review. IEEE Sens. J. 2022; accepted. [Google Scholar]
- Application Ideas for 8-Bit Low-Pin-Count Microcontrollers. Available online: https://www.digikey.com/en/articles/application-ideas-for-8-bit-low-pin-count-microcontrollers (accessed on 30 August 2022).
- Mannini, A.; Sabatini, A.M. Machine learning methods for classifying human physical activity from on-body accelerometers. Sensors 2010, 10, 1154–1175. [Google Scholar] [CrossRef] [PubMed]
- Sousa Lima, W.; Souto, E.; El-Khatib, K.; Jalali, R.; Gama, J. Human Activity Recognition Using Inertial Sensors in a Smartphone: An Overview. Sensors 2019, 19, 3213. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: Berlin, Germany, 2008. [Google Scholar]
- Wai, M.M.N. Classification based automatic information extraction. In Proceedings of the 10th WSEAS International Conference on Communications, Canary Islands, Spain, 24–26 March 2011. [Google Scholar]
- McCullagh, P.; Nelder, J. Generalized Linear Models; CRC Press: Boca Raton, FL, USA, 1989. [Google Scholar]
- Izenman, A.J. Linear discriminant analysis. In Modern Multivariate Statistical Techniques; Springer Texts in Statistics; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 3, 273–297. [Google Scholar] [CrossRef]
- Pardos, Z.; Heffernan, N. Modeling individualization in a Bayesian networks implementation of knowledge tracing. In Proceedings of the International Conference UMAP, Big Island, HI, USA, 20–24 June 2010. [Google Scholar]
- Burkov, A. The Hundred-Page Machine Learning Book; Burkov, A., Ed.; Andriy Burkov: Quebec City, QC, Canada, 2019. [Google Scholar]
- Chen, J.; Melo, G.D. Semantic information extraction for improved word embeddings. In Proceedings of the NAACL-HLT, Denver, CO, USA, 31 May–5 June 2015. [Google Scholar]
- Scikit-Learn: Machine Learning in Python. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html#sklearn.linear_model.LogisticRegression (accessed on 1 July 2022).
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- AIfES for Arduino. Available online: https://github.com/Fraunhofer-IMS/AIfES_for_Arduino (accessed on 20 July 2022).
- Coelho, C.N.; Kuusela, A.; Li, S.; Zhuang, H.; Ngadiuba, J.; Aarrestad, T.K.; Loncar, V.; Pierini, M.; Pol, A.A.; Summers, S. Automatic heterogeneous quantization of deep neural networks for low-latency inference on the edge for particle detectors. Nat. Mach. Intell. 2021, 3, 675–686. [Google Scholar] [CrossRef]


| Feature Name | Feature Description | Sensors Used 1 |
|---|---|---|
| Gesture duration | Gesture duration in ms | G1, G2 |
| Number of extremes | Number of extremes from differential gyroscope data (DGD) | G1, G2 |
| Gyroscope axis ratio | Mean ratio of axis of DGD, detects direction of motion | G1, G2 |
| Accelerometer ratio | Mean ratio A1 axis, detects hand orientation | A1 |
| Movement energy | Integrates absolute A1 and A2 magnitude over the duration of the whole gesture | A1, A2 |
| First rotation direction (flexion or extension) | Magnitude of the first large DGD peak, detects hand rotation direction | G1, G2 |
| Classifier | Optimised Parameter |
|---|---|
| Decision tree (DT) | Maximum number of splits |
| Random Forests (RF) | Maximum number of splits, Number of learners, Ensemble method |
| Logistic Regression (LR) | Solver, Penalty, Regularization strength, Convergence tolerance and maximum number of iteration steps, Elastic-Net mixing parameter |
| Linear Discriminant Analysis (LDA) | Discriminant type, solver |
| SVM | Kernel function, Optimiser |
| Naïve Bayes (Gaussian) (NB) | Iterations, Acquisition function, Optimiser |
| The K-Nearest Neighbours (KNN) | Optimiser, Number of grid divisions, Distance metric, Number of nearest neighbours |
| Stochastic Gradient Descent (SGD) | #none |
| Precision | Recall | F1-Score | |
|---|---|---|---|
| SVM | 0.9865 | 0.9861 | 0.9863 |
| Random Forests (RF) | 0.9863 | 0.9861 | 0.9862 |
| K-Nearest Neighbours (KNN) | 0.9835 | 0.9833 | 0.9834 |
| Logistic Regression (LR) | 0.9810 | 0.9810 | 0.9810 |
| Linear Discriminant Analysis (LDA) | 0.9653 | 0.9610 | 0.9631 |
| Decision tree (DT) | 0.9617 | 0.9621 | 0.9620 |
| Naïve Bayes (Gaussian) (NB) | 0.9432 | 0.9178 | 0.9303 |
| Stochastic Gradient Descent (SGD) | 0.2880 | 0.4120 | 0.2900 |
| Validation Accuracy | Test Accuracy | |
|---|---|---|
| Random Forests (RF) | 0.9861 | 0.9861 |
| Linear SVM | 0.9840 | 0.9861 |
| K-Nearest Neighbours (KNN) | 0.9780 | 0.9832 |
| Logistic Regression (LR) | 0.9805 | 0.9651 |
| Decision tree (DT) | 0.9540 | 0.9616 |
| Linear Discriminant Analysis (LDA) | 0.9240 | 0.9609 |
| Naïve Bayes (Gaussian) (NB) | 0.9070 | 0.9185 |
| ML Method | FLASH (kB) | RAM (kB) | Inference Time (ms) |
|---|---|---|---|
| SVM | 70.26 | 38.54 | N/A * |
| Random forest (RF) | 163.95 | 187.3 | N/A * |
| KNN (reduced dataset) | 26.19 | 0.58 | 1.5 |
| Logistic regression (LR) | 2.97 | 0.20 | 0.04 |
| Decision Tree (DT) | 1.63 | 0.24 | 0.716 |
| Parameter | Value |
|---|---|
| Solver | newton-cg, lbfgs, liblinear, sag, saga |
| Penalty | none, l1, l2, elasticnet |
| Inverse of regularization strength (C) | 10−7, 10−6, 10−5, 3 × 10−5, 10−4, 3 × 10−4, 10−3, 3 × 10−3, 10−2, 3 × 10−2, 10−1, 2 × 10−1, 25 × 10−2, 3 × 10−1, 35 × 10−3, 6 × 10−1, 8×10−1, 1, 2, 5 |
| Tolerance for stopping criteria | 10−6, 10−5, 5 × 10−2, 10−3, 5 × 10−1, 10−2, 10−1, 1, 2 |
| Maximum number of iterations for convergence | 50, 100, 500 |
| Elastic-Net mixing parameter (rati) 1 | 0.2, 0.4, 0.5, 0.6, 0.8 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stančić, I.; Musić, J.; Grujić, T.; Vasić, M.K.; Bonković, M. Comparison and Evaluation of Machine Learning-Based Classification of Hand Gestures Captured by Inertial Sensors. Computation 2022, 10, 159. https://doi.org/10.3390/computation10090159
Stančić I, Musić J, Grujić T, Vasić MK, Bonković M. Comparison and Evaluation of Machine Learning-Based Classification of Hand Gestures Captured by Inertial Sensors. Computation. 2022; 10(9):159. https://doi.org/10.3390/computation10090159
Chicago/Turabian StyleStančić, Ivo, Josip Musić, Tamara Grujić, Mirela Kundid Vasić, and Mirjana Bonković. 2022. "Comparison and Evaluation of Machine Learning-Based Classification of Hand Gestures Captured by Inertial Sensors" Computation 10, no. 9: 159. https://doi.org/10.3390/computation10090159
APA StyleStančić, I., Musić, J., Grujić, T., Vasić, M. K., & Bonković, M. (2022). Comparison and Evaluation of Machine Learning-Based Classification of Hand Gestures Captured by Inertial Sensors. Computation, 10(9), 159. https://doi.org/10.3390/computation10090159






