Snake Graphs Arising from Groves with an Application in Coding Theory
Abstract
:1. Introduction
1.1. Motivations
1.2. Contributions
2. Background and Related Work
2.1. Path Algebras
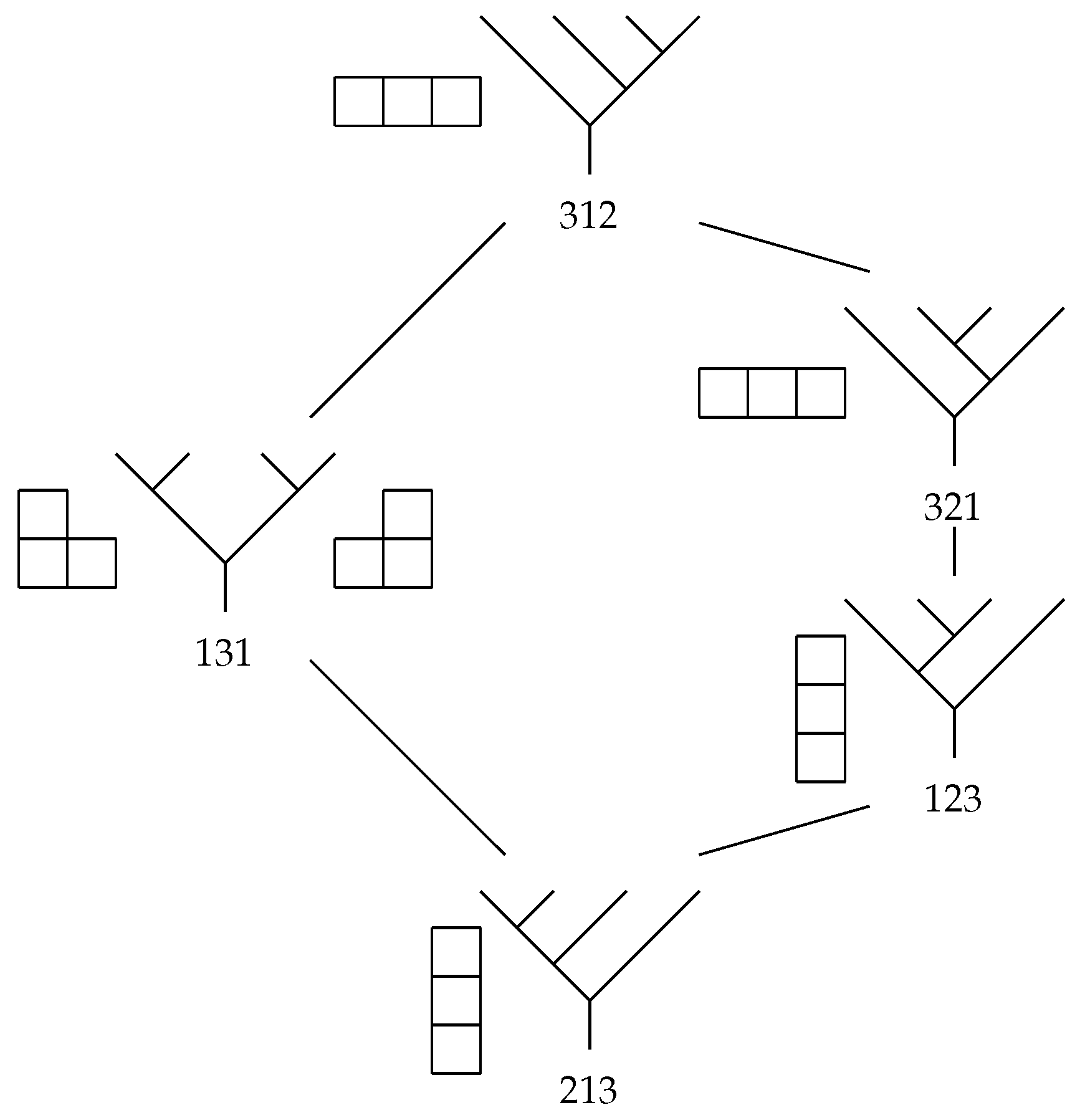
2.2. Snake Graphs
2.3. String Modules and Snake Graphs
- If , then the corresponding abstract snake graph is given by a single tile.
- If there is at least one letter, then is a concatenation of a collection of alternating maximal direct and inverse strings such that . Each might be of length 1.
- For each , we construct a zigzag snake graph with tiles, where is the number of direct or inverse arrows in . Let be the zigzag snake graph with tiles , such that is glued to the right (resp. on top) of if is direct (resp. inverse).
- We now glue to , for all i, by identifying the last tile of and the first tile of , such that , , is a straight piece.
- , which defines the zigzag snake graph containing the tiles, and 4.
- , which defines the straight snake graph containing the tiles 4 and 5.
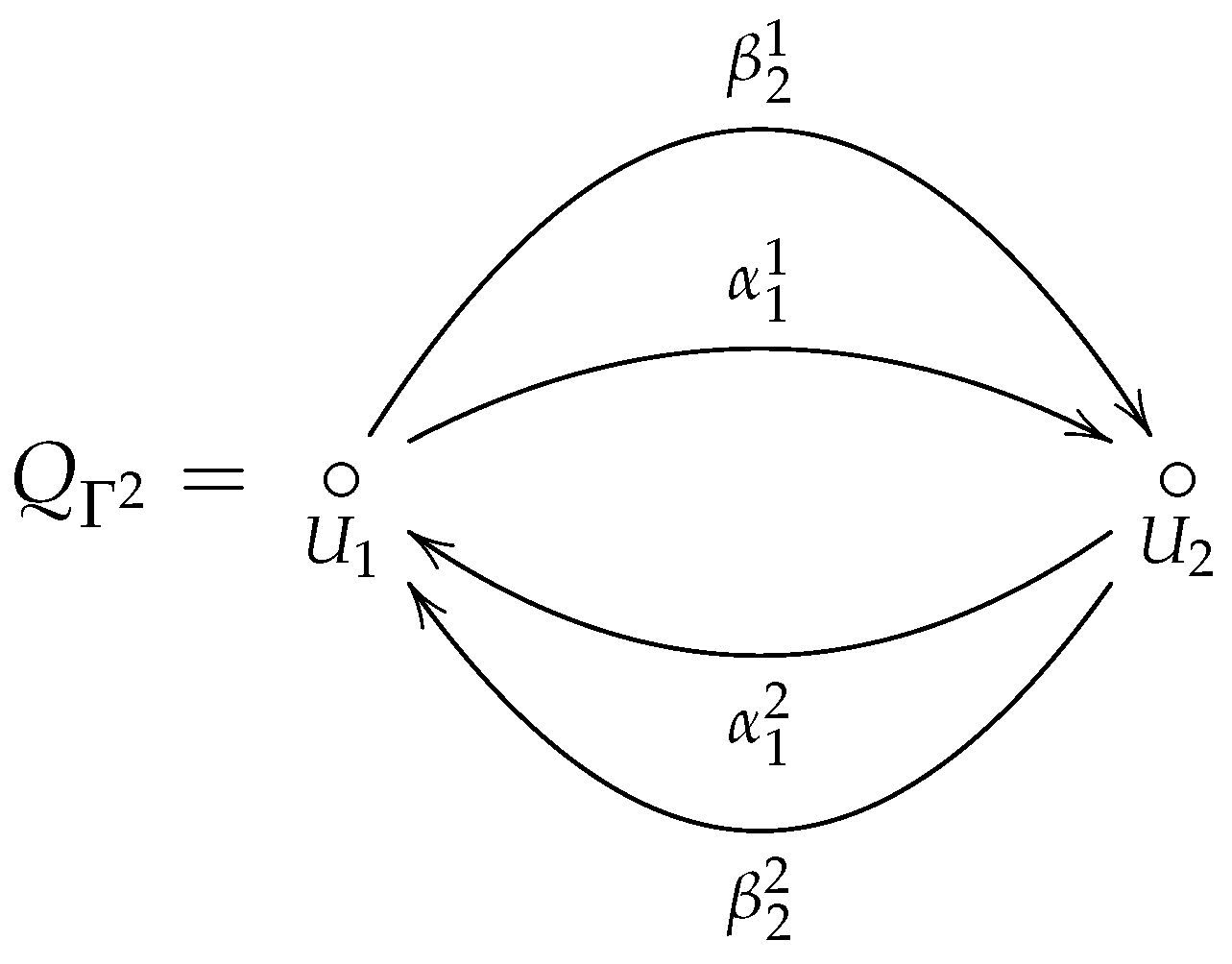
2.4. Brauer Configuration Algebras
- is a finite set of vertices.
- is a collection of polygons, which are labeled multisets consisting of vertices (vertices repetition allowed). Each polygon contains more than one vertex.
- is a map from the set of vertices to the set of positive integers ,
- is a choice for each vertex , of a cyclic ordering of the polygons in which occurs as a vertex including repetitions (see [9] for more details). For instance, if a vertex occurs in polygons , for suitable indices , then the cyclic order is obtained by linearly ordering the list, saywhere means that vertex occurs times in polygon , denoted . The cyclic order is completed by adding the relation . Note that if is the chosen ordering at vertex , then the same ordering can be represented by any cyclic permutation.The sequence (2) is said to be the successor sequence at vertex denoted , which is unique up to permutations.Henceforth, this paper assumes the notation used in [12] for successor sequences and special cycles. Namely, if a vertex belongs to some polygons ordered according to the already defined cyclic ordering associated with the vertex , then we will assume that, up to permutations, the cyclic ordering associated with the vertex is built, taking into account that polygons inherit the order given by the successor sequence .
- Identify special cycles associated with non-truncated vertices in the same polygon (i.e., if with , then ).
- If is a special cycle associated with a non-truncated vertex , then a product of the form , if a is the first arrow of .
- Quadratic monomial relations of the form in , where is not a subpath of any special cycle unless and a is a loop associated with a vertex of valency 1 and .
- 1.
- There is a bijection between and the set of indecomposable projective Λ-modules.
- 2.
- If P is a projective indecomposable Λ-module corresponding to a polygon V in Γ, then is a sum of r indecomposable uniserial modules, where r is the number of (non-truncated) vertices of V and where the intersection of any two of the uniserial modules is a simple Λ-module.
3. Main Results
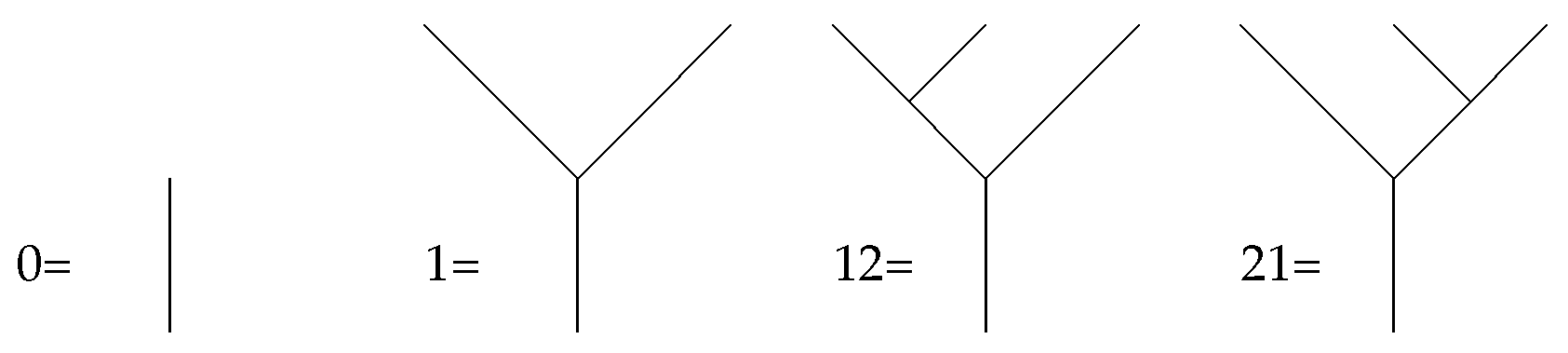
3.1. Admissible Words
- • is the usual concatenation of words. If no confusion arises, later on, we will write .
- If, for fixed , then . Moreover, .
- If , then . In such a case, we write , . In particular, , . Thus, any admissible word w can be written in the form .
- If , then . If , then . Moreover, .
- , where , and . In particular, if (), then ().
- , .
3.2. Brauer Configuration Algebras Associated with Snake Graphs
- 1.
- If is an indecomposable projective module over associated with the polygon . Then, the number of summands in is i, .
- 2.
- ,
- 3.
- ),
- 4.
- .
3.3. The Associated Code
4. Concluding Remarks and Future Work
Future Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| (jth Catalan number) | |
| (Dimension of a Brauer configuration algebra) | |
| (Dimension of the center of a Brauer configuration algebra) | |
| (Energy of a code ) | |
| (Field) | |
| (Set of vertices of a Brauer configuration ) | |
| (ith triangular number) | |
| (Number of occurrences of a vertex in a polygon V) | |
| (The word associated with a polygon V) | |
| (Ordered sequence of polygons) | |
| (Valency of a vertex ) |
Appendix A. Python Routines



References
- Propp, J. The combinatorics of frieze patterns and Markoff numbers. Integers 2020, 20, 1–38. [Google Scholar]
- Çanakçi, I.; Schiffler, R. Cluster algebras and continued fractions. Compos. Math. 2018, 54, 565–593. [Google Scholar] [CrossRef] [Green Version]
- Çanakçi, I.; Schiffler, R. Snake graphs and continued fractions. Eur. J. Combin. 2020, 86, 1–19. [Google Scholar] [CrossRef] [Green Version]
- Çanakçi, I.; Schiffler, R. Snake graphs calculus and cluster algebras from surfaces. J. Algebra 2013, 382, 240–281. [Google Scholar] [CrossRef]
- Çanakçi, I.; Schiffler, R. Snake graphs calculus and cluster algebras from surfaces II: Self-crossings snake graphs. Math. Z. 2015, 281, 55–102. [Google Scholar] [CrossRef] [Green Version]
- Çanakçi, I.; Schiffler, R. Snake graphs calculus and cluster algebras from surfaces III: Band graphs and snake rings. Int. Math. Res. Not. IMRN 2017, rnx157, 1–82. [Google Scholar] [CrossRef]
- Musiker, G.; Schiffler, R.; Williams, L. Posiivity for cluster algebras from surfaces. Adv. Math. 2011, 227, 2241–2308. [Google Scholar] [CrossRef] [Green Version]
- Çanakçi, I.; Schroll, S. Lattice bijections for string modules snake graphs and the weak Bruhat order. Adv. Appl. Math. 2021, 126, 102094. [Google Scholar] [CrossRef]
- Green, E.L.; Schroll, S. Brauer configuration algebras: A generalization of Brauer graph algebras. Bull. Sci. Math. 2017, 121, 539–572. [Google Scholar] [CrossRef] [Green Version]
- Schroll, S. Brauer Graph Algebras. In Homological Methods, Representation Theory, and Cluster Algebras, CRM Short Courses; Assem, I., Trepode, S., Eds.; Springer: Cham, Switzerland, 2018; pp. 177–223. [Google Scholar]
- Cañadas, A.M.; Gaviria, I.D.M.; Vega, J.D.C. Relationships between the Chicken McNugget Problem, Mutations of Brauer Configuration Algebras and the Advanced Encryption Standard. Mathematics 2021, 9, 1937. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Espinosa, P.F.F.; Muñetón, N.A. Brauer configuration algebras defined by snake graphs and Kronecker modules. Electron. Res. Arch. 2022, 30, 3087–3110. [Google Scholar] [CrossRef]
- Assem, I.; Skowronski, A.; Simson, D. Elements of the Representation Theory of Associative Algebras; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Andrews, G.E. The Theory of Partitions; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Sierra, A. The dimension of the center of a Brauer configuration algebra. J. Algebra 2018, 510, 289–318. [Google Scholar] [CrossRef]
- Loday, J.L. Arithmetree. J. Algebra 2002, 258, 275–309. [Google Scholar] [CrossRef] [Green Version]
- Boyvalenkov, P.; Dragnev, P.D.; Hardin, P.D.; Saff, E.B.; Stoyanova, M.M. Energy bounds for codes and designs in Hamming spaces. Des. Codes Cryptogr. 2017, 82, 411–433. [Google Scholar] [CrossRef] [Green Version]


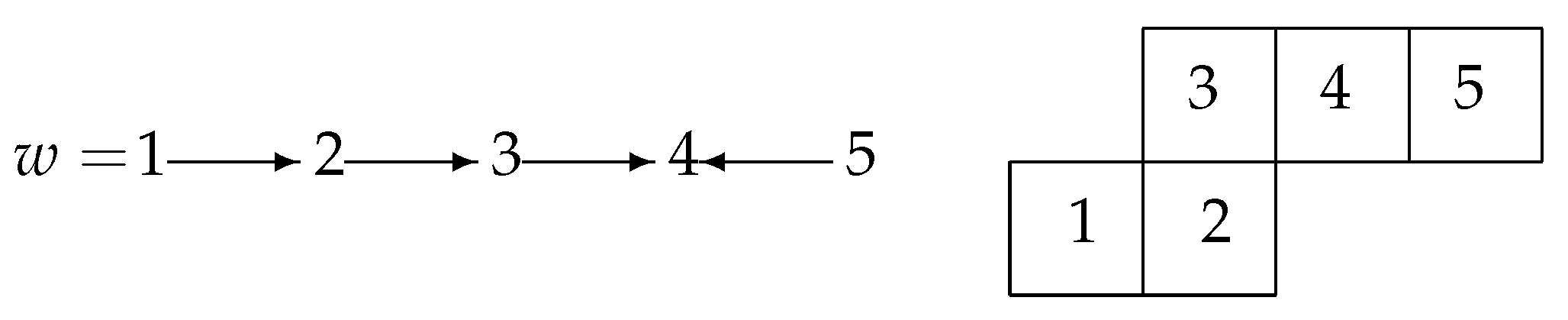
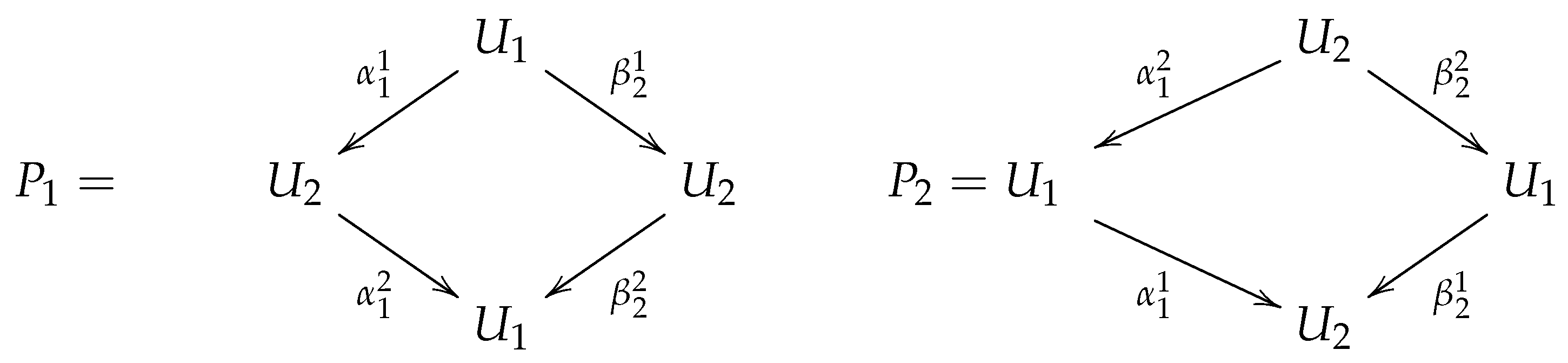

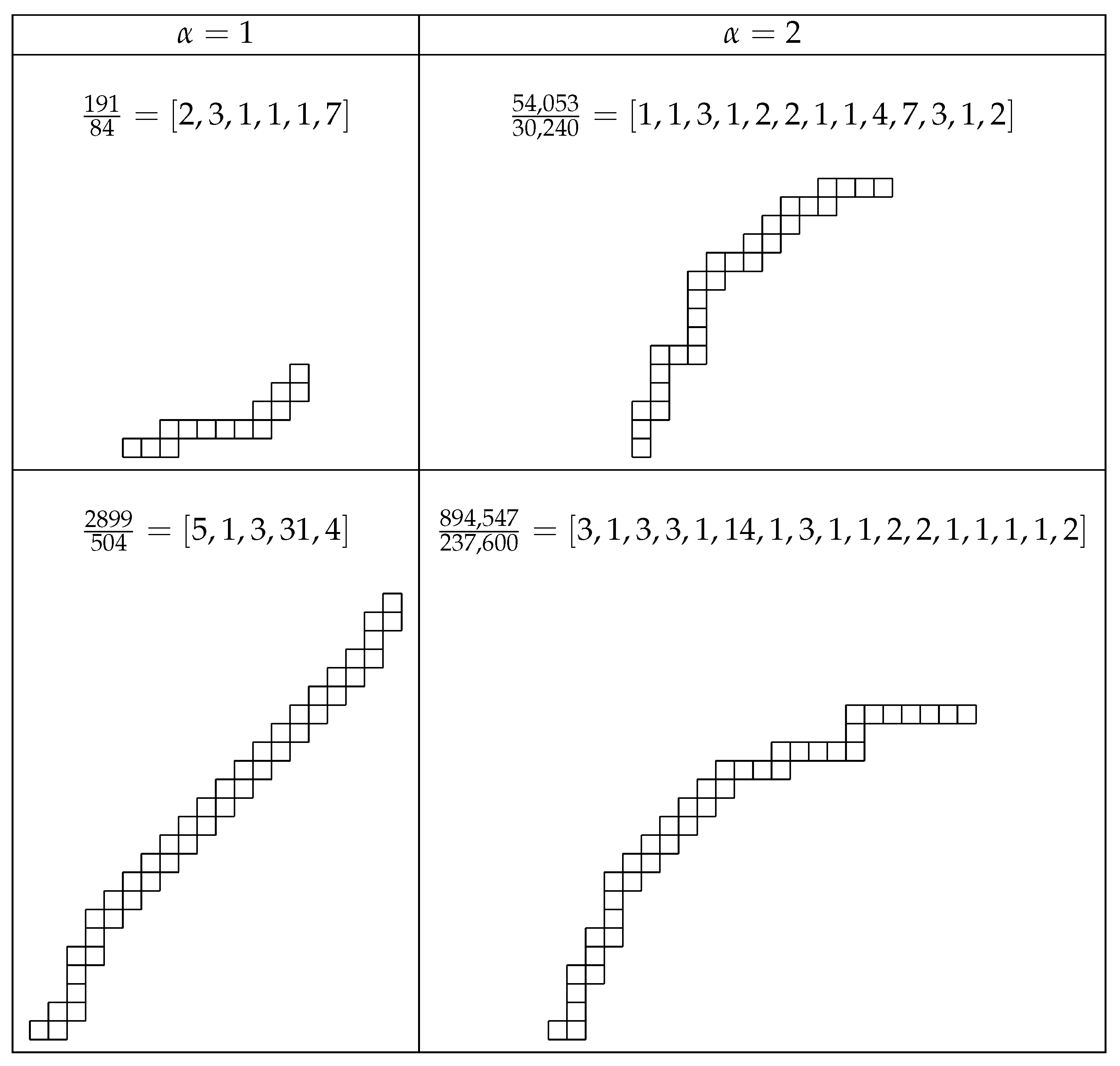
| 2 | 2 | 8 | ||
| 6 | 4 | 5 | 72 | |
| 20 | 12 | 10 | 812 | |
| 70 | 40 | 30 | 9822 | |
| 252 | 140 | 100 | 124,112 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | |
|---|---|---|---|---|---|---|---|---|
| 2 | 1 | |||||||
| 3 | 6 | 4 | ||||||
| 4 | 25 | 34 | 32 | |||||
| 5 | 100 | 172 | 329 | 260 | ||||
| 6 | 390 | 754 | 1990 | 3126 | 2386 | |||
| 7 | 1516 | 3130 | 9983 | 21,638 | 32,481 | 23,058 | ||
| 8 | 5869 | 12,660 | 45,872 | 119,312 | 251,334 | 351,506 | 235,182 | |
| 9 | 22,746 | 50,570 | 202,205 | 589,306 | 1,519,120 | 3,001,666 | 3,944,860 | 2,486,618 |
| 1/2 | 1/3 | 1/4 | 1/5 | 1/6 | 1/7 | 1/8 | 1/9 | ||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 1/2 | |||||||
| 3 | 3 | 4/3 | |||||||
| 4 | 25/2 | 34/3 | 8 | ||||||
| 5 | 50 | 172/3 | 329/4 | 52 | |||||
| 6 | 195 | 754/3 | 995/2 | 3126/5 | 1193/3 | ||||
| 7 | 758 | 3130/3 | 9983/4 | 21,638/5 | 10,827/2 | 3294 | |||
| 8 | 5869/2 | 4220 | 11,468 | 119,312/5 | 41,889 | 351,506/7 | 117,591/4 | ||
| 9 | 11,373 | 50,570/3 | 202,205/4 | 589,306/5 | 759,560/3 | 3,001,666/7 | 986,215/2 | 2,486,618/9 | |
| 2 | 2 | 1/4 | |||||||
| 3 | 3/2 | 4/9 | |||||||
| 4 | 25/4 | 34/9 | 2 | ||||||
| 5 | 25 | 172/9 | 329/16 | 52/5 | |||||
| 6 | 195/2 | 754/9 | 995/8 | 3126/25 | 1193/18 | ||||
| 7 | 379 | 3130/9 | 9983/16 | 21,638/25 | 3609/4 | 3294/7 | |||
| 8 | 5869/4 | 4220/3 | 2867 | 119,312/25 | 13,963/2 | 351,506/49 | 117,591/32 | ||
| 9 | 211,373/2 | 50,570/9 | 202,205/16 | 589,306/25 | 379,780/9 | 3,001,666/49 | 986,215/16 | 2,486,618/81 | |
| 3 | 2 | 1/8 | |||||||
| 3 | 3/4 | 4/27 | |||||||
| 4 | 25/8 | 34/27 | 1/2 | ||||||
| 5 | 25/2 | 172/27 | 329/64 | 52/25 | |||||
| 6 | 195/4 | 754/27 | 995/32 | 3126/125 | 1193/108 | ||||
| 7 | 379/2 | 3130/27 | 9983/64 | 21,638/125 | 1203/8 | 3294/49 | |||
| 8 | 5869/8 | 4220/9 | 2867/4 | 119,312/125 | 13,963/12 | 351,506/343 | 117,591/256 | ||
| 9 | 11,373/4 | 50,570/27 | 202,205/64 | 589,306/125 | 189,890/27 | 3,001,666/343 | 986,215/128 | 2,486,618/729 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno Cañadas, A.; Rios, G.B.; Serna, R.-J. Snake Graphs Arising from Groves with an Application in Coding Theory. Computation 2022, 10, 124. https://doi.org/10.3390/computation10070124
Moreno Cañadas A, Rios GB, Serna R-J. Snake Graphs Arising from Groves with an Application in Coding Theory. Computation. 2022; 10(7):124. https://doi.org/10.3390/computation10070124
Chicago/Turabian StyleMoreno Cañadas, Agustín, Gabriel Bravo Rios, and Robinson-Julian Serna. 2022. "Snake Graphs Arising from Groves with an Application in Coding Theory" Computation 10, no. 7: 124. https://doi.org/10.3390/computation10070124
APA StyleMoreno Cañadas, A., Rios, G. B., & Serna, R.-J. (2022). Snake Graphs Arising from Groves with an Application in Coding Theory. Computation, 10(7), 124. https://doi.org/10.3390/computation10070124







