Abstract
Cayley hash values are defined by paths of some oriented graphs (quivers) called Cayley graphs, whose vertices and arrows are given by elements of a group . On the other hand, Brauer messages are obtained by concatenating words associated with multisets constituting some configurations called Brauer configurations. These configurations define some oriented graphs named Brauer quivers which induce a particular class of bound quiver algebras named Brauer configuration algebras. Elements of multisets in Brauer configurations can be seen as letters of the Brauer messages. This paper proves that each point has an associated Brauer configuration algebra induced by a Brauer configuration . Additionally, the Brauer configuration algebras associated with points in a subset of the form have the same dimension. We give an analysis of Cayley hash values associated with Brauer messages defined by a semigroup generated by some appropriated matrices over a commutative ring . As an application, we use Brauer messages to construct explicit solutions for systems of linear and nonlinear differential equations of the form and for some suitable square matrices, M and . Python routines to compute Cayley hash values of Brauer messages are also included.
1. Introduction
Hash functions are compression functions that are easy to compute. They are helpful tools in several cryptographic tasks. Ensuring data integrity and password authentication systems are some of the primary roles of hash functions. Data integrity provided by hash functions prevents undesirable data modification [1].
To date, it is believed that well-posed hash functions such as SHA256 are unbreakable by several attacks, including those conducted by a quantum computer.
The Cayley graph associated with a subset of a multiplicative (semi)group is a k-regular graph, whose set of vertices V are in bijective correspondence with the set . In this case, if are vertices corresponding to the elements , then there is an arrow connecting and provided that there is an element , such that , where 1 is the identity element of the group . The idea behind the use of Cayley graphs in cryptography is to produce hash functions that are collision resistant. The input to these functions gives directions for walking around the graph, and the output is the ending vertex of the walk [2].
On the other hand, Brauer messages were introduced by Espinosa et al. [3] in their research regarding some bound quiver algebras called Brauer configuration algebras by Green and Schroll [4]. This paper provides Cayley hash values to some of these Brauer messages.
Brauer messages have applications in different science fields. For instance, they were used by Cañadas et al. in the graph energy theory to compute the trace norm of some matrices and in the war games theory to declare winners and losers in war games based on the behavior of a missile defense system (MDS) [5]. Furthermore, mutations of Brauer messages can be used to give an algebraic interpretation of the Advanced Encryption Standard (AES) key schedule [6].
1.1. Motivations
This paper uses an interaction between cryptography, algebraic geometry, combinatorics, and the theory of representation of associative algebras to obtain applications of the theory of Brauer configuration algebras in cryptography and differential equations.
Relationships between algebraic geometry and Brauer configuration algebras are motivated by a recent paper published by Green and Schroll [7], who proved that each point in an affine variety has an associated suitable associative algebra and that all these algebras have the same dimension. As an interpretation of this result, we prove that, associated with each point in , there is a suitable Brauer configuration algebra and that Brauer configuration algebras associated with points in a set of the form have the same dimension. The messages arising from these Brauer configurations (called Brauer messages) are used to provide solutions for linear and nonlinear systems of differential equations. We compute Cayley hash values of Brauer messages establishing for which integer numbers such hash values are collision-resistant.
Henceforth, we outline the main results presented in this paper and how previous works are used to obtain them.
1.2. Contributions
We prove that each point is associated with a suitable Brauer configuration algebra. Properties of these algebras are also established. In particular, it is proved that their dimensions can be computed by enumerating suitable lattice paths. Similar conditions have their corresponding centers.
As an application, we interpret message specializations of these Brauer configurations as appropriated matrices with applications in Catalan combinatorics and differential equations. It is also proved that some of these matrices are solutions to some linear and nonlinear systems of differential equations of the form and , where ) is a matrix whose entries are given by appropriated Brauer messages. It is worth noting that finding explicit solutions to nonlinear differential equations is in general a cumbersome problem.
Cayley hash functions based on matrix semigroups are applied to some Brauer messages to prove that these hash families are collision resistant.
Python routines to compute Cayley hash values of Brauer messages associated with points in the plane are also introduced.
Figure 1 shows how previous works, mutations, and Brauer configuration algebras (BCAs) can be related to obtain the main results (targets of red arrows) presented in this paper.
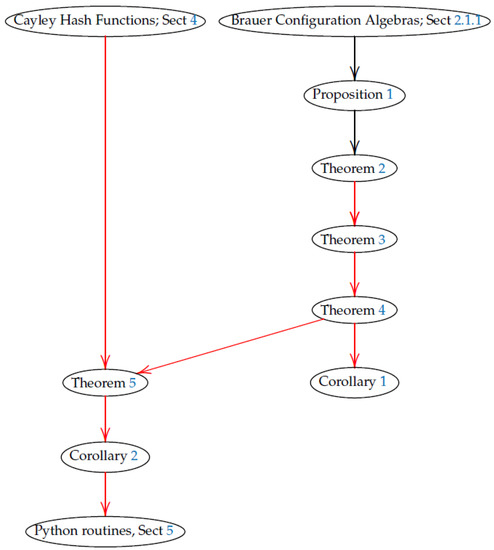
Figure 1.
This graph shows how the background relates to the main results presented in this paper.
In Section 2.1.1, we recall the main results regarding BCAs; Proposition 1 and Theorem 2 give formulas for the dimensions of these algebras and their centers.
Theorem 3 provides the properties of BCAs associated with points in the plane. Their dimensions and combinatorial data regarding indecomposable projective modules over these algebras are given.
Theorem 4 describes arithmetic properties of specialized matrices given by mutations of Brauer configurations associated with the plane.
Corollary 1 provides explicit solutions of linear and nonlinear systems of differential equations.
Section 4 is devoted to Cayley hash functions. Theorem 5 gives Cayley hash values for appropriated matrix semigroups. These results allow to give Cayley hash values of Brauer messages. Corollary 2 proves that Sosnovski hash functions are collision-resistant when they are applied to Brauer messages.
This paper is distributed as follows: Section 2 is devoted to recalling definitions and notation used throughout the document. In particular, we recall the notion of Brauer configuration algebra. In Section 3, we give our main results. We associate to each point an apropriated Brauer configuration algebra determining which of them have the same dimension. Mutations are defined for the variables associated with these algebras. Such mutations give rise to new classes of matrices with applications in combinatorics and differential equations. Section 4 is devoted to the values of Cayley hash functions associated with Brauer messages. Experimental data are given in Section 5. Concluding remarks and possible future works are described in Section 6. Appendix A gives Python routines to compute Brauer messsages, their Sosnovski hash values, and polygons of Brauer configurations associated with the plane.
2. Background and Related Work
In this section, we introduce some definitions and notation to be used throughout the paper. In particular, a brief overview regarding hash functions and Brauer configuration algebras is given [4].
Henceforth, the symbol ( denotes a field (the complex numbers field), and () denotes the smallest (greatest) integer greater (less) than or equal to a real number x. In path algebras , it is assumed that is an algebraic closed field.
2.1. Related Work on Cayley Hash Functions
This section gives a background on hash functions, in particular, Cayley hash functions.
Hash functions are easy-to-compute compression functions, as described before. Such functions are used in several contexts. For instance, they are helpful in password management systems. Servers that authenticate user passwords save a one-way hash associated with a unique password so that if an attacker steals the database, it may be unfeasible for the attacker to recover the original password as plaintext [1,8].
A hash family is a four-tuple , where
- is a set of possible messages, which could be finite or infinite.
- is a finite set of possible message digests or authentication tags.
- is the set of keys.
- For each , there is a hash function . If and denote the cardinals of and , and , then is said to be a compression function. If , and the hash function h is the identity, then h is said to be an unkeyed hash function [1,2].
A hash function is said to be secure if the following three problems are difficult to solve:
Preimage
Instance: A hash function and an element .
Find: such that .
Second Preimage
Instance: A hash function and an element .
Find: such that and .
Collision
Instance: A hash function and an element .
Find: such that and .
Hash functions are used to construct a short fingerprint or digest the message of some data. If an attacker alters the data, then the fingerprint will no longer be valid. One of the most used methods to construct iterated hash functions is the Merkle–Damgård scheme, which builds hash functions from a compression function. Rivest introduced, in 1990, the first scheme of this type named MD4. Soon afterwads, Rivest himself proposed an improved version of MD4 called MD5.
Collisions in the compression function of MD4 and MD5 were discovered in the 1990s.
The family of secured hash algorithms (SHAs) was proposed as a standard by NIST in 1993. SHA-0 was adopted as FIPS 180. Each of these hash algorithms was an improvement of the earlier versions to prevent previously found attacks.
It was shown in 1998 that SHA-0 allows collisions in approximately steps, whereas the first collision for SHA-1 was found in 2017. SHA-2 includes the four hash functions known as SHA-224, SHA-256, SHA-384, and SHA-512, according to the sizes of the corresponding fingerprints. It is worth pointing out that currently SHA-256, which outputs 256 bits fingerprints, is the most used hash function. It is the basis of many password authentication systems.
According to the National Academy of Sciences, Engineering, and Medicine [8] (NAE), although, nowadays it is believed to be essentially impossible to break a hash function such as SHA-256, password hashing is at higher risk due to the size of all 10-character passwords being only about passwords, and thus prone to an attack based on a quantum computer.
Possible attacks on the currently used hash functions have encouraged the use of provably secure hash functions, whose security is based on the difficulty of solving a known hard problem.
Cayley hash functions based on the Cayley graph of certain (semi)groups are examples of these types of schemes, whose security follows from the hardness of the expander graph problem associated with a (semi)group.
In 1991, Zémor [9] introduced hash function schemes based on matrix products in the special linear group , where p is a fixed prime number. Zémor himself and Tillich [10] broke such schemes. Furthermore, they introduced the group to increase the security of the original hash functions [11]. In this setting, is a field.
Due to the popularity of the hash functions introduced by Zémor and Tillich, several proposals in the same line were proposed by Petit and Lubotzki et al., who introduced Cayley hash functions based on Ramanujan graphs, in particular LPS hash functions [12,13,14,15].
The Tillich–Zémor hash function hashes each bit of a given message individually. In this case, the matrices have the form and , where , is the two-element field, is the ideal generated by an irreducible polynomial of degree n, and is a root of . For instance, the message is hashed to the matrix .
It is worth noting that the Tillich–Zémor hash function was successfully attacked by Grass et al. [16], who obtained collisions using the Euclidean algorithm for polynomials. Afterwards, Petit and Quisquater [17] introduced an extended form of Grass et al.’s algorithm to provide a second preimage algorithm. Grassl et al. also ran Grover’s algorithm on a quantum computer to study the strength of the cryptographic system AES [18].
Mullan and Tsaban [19] introduced a general attack for the Tillich–Zémor scheme. It runs with polynomial time to find collisions for an arbitrary q. It does not work for bit strings of length .
Other pairs of matrices such as in the Tillich–Zémor scheme have been proposed by Bromber et al. and Sosnovki, who introduced a semigroup platform corresponding to the hash functions and modulo a prime (the corresponding associated matrices have the form and ). In this case, the input string hash function can have an arbitrary length, and the output has the size .
In this paper, we applied Sosnovski hash functions to Brauer messages to investigate their collision-resistant property.
2.1.1. Background and Related Work on Brauer Configuration Algebras
Brauer configuration algebras (BCAs) were introduced by Green and Schroll [4] to generalize research on tame algebras. Soon afterwards, Cañadas et al. used these algebras and their associated messages to obtain applications in cryptography, cibersecurity, and the graph energy theory [3,5,6,20,21].
It is worth pointing out that Espinosa [3] introduced in his doctoral dissertation the notion of the message of a Brauer configuration as the element of a word algebra. He used Brauer messages to give formulas for the number of perfect matchings of a snake graph and the number of homological ideals associated with a Nakayama algebra. On the other hand, Cañadas et al. introduced mutations of Brauer configurations to give an algebraic description of the cryptosystem AES [6].
In this paper, we associate Brauer configuration algebras with points in the plane, establishing which points have associated Brauer configuration algebras with the same dimension.
2.1.2. Path Algebras
In this section, we give a brief discussion on quivers, path algebras, and their ideals based on the work of Assem et al. [22].
A quiver or directed graph is a quadruple consisting of two sets: (whose elements are called points or vertices) and (whose elements are called arrows) and two maps which associate to each arrow , its source , and its target , respectively. If is an algebraically closed field, then we let denote the path algebra associated with the quiver Q, whose underlying -vector space has as its basis the set of all paths of length in Q, such that the product of two basis vectors is given by the usual concatenation of paths.
The following Figure 2 shows a quiver Q with four vertices , , and and three arrows , , and . Note that, is the set of paths of length 1, whereas is the set of paths of length 2 in Q.
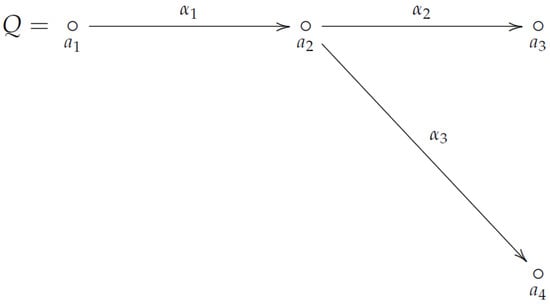
Figure 2.
A quiver Q with four vertices and three arrows , and , , , , and .
The basis of the algebra associated with the quiver Q shown in Figure 2 is , where is the set of primitive idempotents, with and if .
Let Q be a finite and connected quiver. The two-sided ideal of the path algebra generated (as an ideal) by the arrows of Q is called the arrow ideal of . A two-sided ideal I of is said to be admissible if there exists such that .
If I is an admissible ideal of , the pair is said to be a bound quiver. The quotient algebra is said to be the algebra of the bound quiver or, simply, a bound quiver algebra.
Let Q be a quiver. A relation in Q with coefficients in is an -linear combination of paths of length, with at least two having the same source and target.
If is a set of relations for a quiver Q such that the ideal they generate is admissible, we say that the quiver Q is bound by the relation or by the relations [22].
Henceforth, we let denote the radical of a path algebra , which is the intersection of all maximal ideals. Actually, if I is an admissible ideal of , it holds that .
If ≺ is an admissible well-ordering on the set of paths, i.e., ≺ is a well-ordering such that
- If , where and are both nonzero or .
- If , then .
Then, the tip of an element is the maximal path w with respect to ≺ such that w has a nonzero coefficient in x when it is written as a linear combination of the elements of a fixed basis of . is the set of tips of elements in X [7].
Let I be an ideal in a path algebra and let . If , then is a Gröbner basis for I with respect to ≺.
2.1.3. Brauer Configuration Algebras
In this section, we briefly discuss the main results regarding Brauer configuration algebras [4].
A Brauer configuration algebra (or simply if no confusion arises) is induced by a Brauer configuration , consisting of a pair of finite sets and , a function ( denote the set of positive integers), and an orientation .
- Elements of () are called vertices (polygons). Polygons are labeled multisets consisting of vertices.
- If , then (i.e., each polygon contains more than one vertex).
- is a choice for each vertex of a cyclic ordering of the polygons in which occurs as a vertex including repetitions (see [4] for more details). For instance, if a vertex occurs in polygons for suitable indices, then the cyclic order is obtained by linearly ordering the list, saywhere, means that vertex occurs times in polygon , denoted . The cyclic order is completed by adding the relation . Note that if is the chosen ordering at vertex , then the same ordering can be represented by any cyclic permutation.The sequence (1) is said to be the successor sequence at vertex , denoted , which is unique up to permutations. Note that Green and Schroll [4] mentioned that different orientation choices are typically associated to nonisomorphic Brauer configuration algebras.Henceforth, in this paper, if a vertex belongs to some polygons ordered according to the already defined cyclic ordering associated with the vertex , then we assume that up to permutations the cyclic ordering associated with the vertex is built, taking into account that polygons inherit the order given by the successor sequence .
- If denotes the underlying set defined by a polygon V (repetitions are not allowed in ), then .
If , then the valency of is given by the identity
If is such that , then is said to be truncated (it occurs once in just one polygon). Otherwise, is a nontruncated vertex. A Brauer configuration without truncated vertices is said to be reduced.
Algorithm 1 is a short version of an algorithm defined by Cañadas et al. in [5] to build a Brauer configuration algebra.
The following results describe the structure of Brauer configuration algebras [4,23].
| Algorithm 1: Construction of a Brauer configuration algebra |
|
Theorem 1
([4], Theorem B, Proposition 2.7, Theorem 3.10, Corollary 3.12). Let be a Brauer configuration algebra with Brauer configuration .
- There is a bijection between the set of indecomposable projective -modules and the polygons of . Moreover, if is an indecomposable -module induced by a polygon V with r nontruncated vertices, then , where for each i, is a uniserial -module. is uniserial for all .
- I is admissible, and is multiserial and symmetric.
- The number of summands in the of an indecomposable projective -module with equals the number of nontruncated vertices of the polygon V counting repetitions.
- If , , is a truncated vertex, , , with , then and are isomorphic.
Proposition 1 and Theorem 2 give formulas for the dimensions and of a Brauer configuration algebra and its center [4,23].
Proposition 1
([4], Proposition 3.13). Let be a Brauer configuration algebra associated with the Brauer configuration and let be a full set of equivalence class representatives of special cycles. Assume that for , is a special -cycle where is a nontruncated vertex in . Then,
,
where denotes the number of vertices of Q, denotes the number of arrows in the -cycle , and .
Theorem 2
(Theorem 4.9, [23]). Let be the Brauer configuration algebra associated with the connected and reduced Brauer configuration . Then,
where .
Proposition 2
([4], Proposition 3.6). Let be the Brauer configuration algebra associated with a connected Brauer configuration . The algebra has a length grading induced from the path algebra if and only if there is an such that for each nontruncated vertex .
2.2. The Message of a Brauer Configuration
The notion of the message of a Brauer configuration and labeled Brauer configurations were introduced by Espinosa et al. [3] to define suitable specializations of some Brauer configuration algebras. According to them, since polygons in a Brauer configuration are multisets, it is possible to assume that any polygon is given by a word of the form
where for each i, , .
The message is in fact an algebra of words element associated with a fixed Brauer configuration, such that for a given field the word algebra consists of formal sums of words with the form , is the empty word, and for any . The product in this case is given by the usual word concatenation. The formal product (or word product)
is said to be the message of the Brauer configuration .
If is a ring, then a specialization of a reduced Brauer configuration is a Brauer configuration
endowed with a suitable map , such that
The orientation is defined by the orientation , in such a way that if
is a successor sequence associated with a vertex (see (1)), then, for some , , it holds that
is contained in the successor sequence associated with .
(∝ is a suitable operation associated with the specialization ring) is the specialized message of the Brauer configuration provided that, in such a case, each word can be interpreted by a product of the specialization ring elements.
A Brauer configuration is said to be S-labeled (or simply labeled, if no confusion arises) by an integer sequence if each polygon is labeled by an integer number , . In such a case, we often write ,
For each vertex , a corresponding cyclic ordering of labeled polygons where occurs is defined. One advantage of labeling Brauer configurations is that the set S can be used to systematically define the orientation associated with each vertex or obtain the polygons recursively [3].
It is worth noticing that any finite set can be used to label Brauer configurations. In this paper, we use finite well-ordered sets of lattice paths to label Brauer configurations.
3. Main Results
In this section, we give properties of Brauer configuration algebras associated with points .
If , then defines a path connecting with . Internal vertices are such that;
An arrow connecting vertices () is labeled by a symbol x (y). The same is assumed if the arrow connects points and and ( and ). Since, it is easy to see that there are of such paths, we endowed this set with a linear order ⪯. We let denote such a set of paths, whose elements are ordered in the form:
A labeled (by the set ) Brauer configuration is associated with each point in such a way that:
Successor sequences and have the forms:
The following Figure 3 shows a Brauer quiver induced by a Brauer configuration , with .
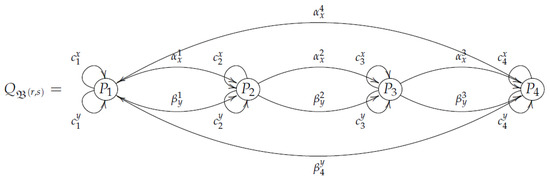
Figure 3.
Example of a Brauer quiver associated with a Brauer configuration . The symbol () denotes a set of loops () associated with the vertex x (y), , .
For all possible values of i, j, and k, the admissible ideal is generated by relations of the form:
- , , ,
- , , ,
- , .
- , , where () is a special cycle associated with vertex x (y), and a is the first arrow of a special cycle , .
The following result gives the structure of Brauer configuration algebras induced by Brauer configurations of type .
Theorem 3.
For , it holds that:
- The Brauer configuration algebra is reduced and connected.
- has length grading induced by the path algebra .
- The number of summands in the heart of the indecomposable projective module equals , and for any i, .
- .
- If , then .
- .
Proof.
- Since each polygon contains vertices x and y, it follows that the Brauer configuration is reduced. Furthermore, . Thus, is connected.
- Since , the result holds as a direct consequence of Proposition 2.
- Each polygon has r vertices denoted by x and s vertices denoted by y. Thus, has nontruncated vertices, counting repetitions.
- , , and .
- Since , it suffices to observe that
- We note that by definition , if .
□
Remark 1.
Similar results as those presented in Theorem 3 can be obtained in the other quadrants of by building sets connecting consecutive vertices in an appropriated fashion. For instance, in the fourth quadrant, arrows in paths connect vertices and with consecutive internal vertices of the form or of the form .
Mutation and Frozen Regions in the Plane
Let be a line segment containing points , with . Let be a differentiable increasingly monotone curve on the interval with , and , , and are real numbers such that , and , thus, . These inequalities define a region () bounded by the coordinate axes and (bounded by the coordinate axes and ). is said to be a frozen (mutation) region. Figure 4 shows regions and . We let denote the set .
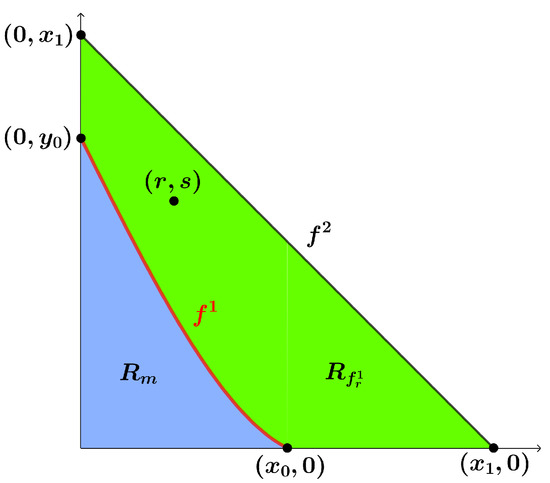
Figure 4.
Frozen () and mutation () regions.
Mutation and frozen regions allow defining a new labeling for sets of paths associated with Brauer configurations of type (8). Such a labeling is defined as follows:
- Arrows are labeled with symbols x (horizontal arrows), y (vertical arrows), and z (y mutations).
- An arrow is labeled with a new symbol z, i.e., , if the target . Where, () denotes the interior (boundary) of a set X endowed with the usual topology of .
- The labeling of an arrow is kept without changes if .
Figure 5 shows an example of this kind of labeling with , , and , .
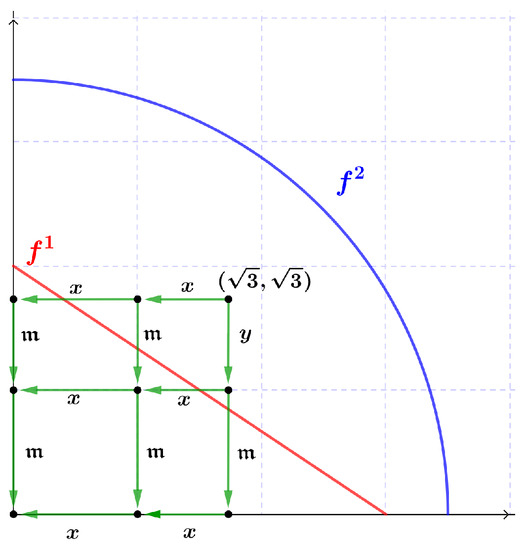
Figure 5.
Example of a labeling with mutations associated with a region .
The Brauer configuration is defined as follows:
- .
- .
- , , ,, , .
- .
- The successor sequences , , and at vertices x, y, and have the following forms:
- , , .
- .
- .
Figure 6 illustrates polygons, .
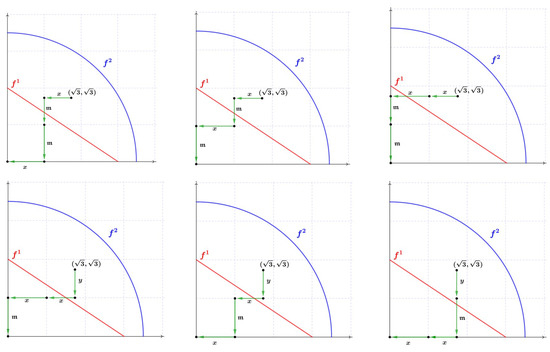
Figure 6.
Labeled polygons .
Figure 7 shows the Brauer quiver induced by the Brauer configuration .
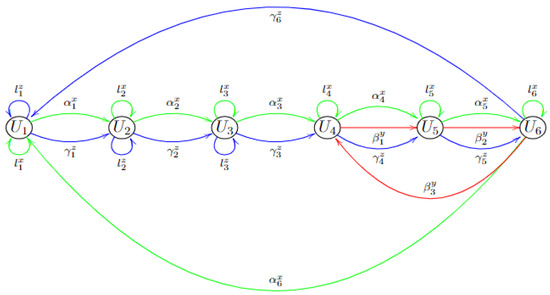
Figure 7.
Brauer quiver induced by the Brauer configuration .
The admissible ideal is generated by the following relations (together with those related to special cycles) for all possible values of i, j, and h:
- , , and .
- , if .
- , .
- , .
- , .
- , .
- , .
- , .
- , , and .
Remark 2.
Henceforth, we consider the specialization , with and for some fixed ϕ, associated with the Brauer configuration (8) and its mutation. A specialized word is given by a product over of the x, y, and specializations, whereas a message of the Brauer configuration is the sum over of the specialized words.
The following is an example of the specializations introduced in Remark 2:
The specialized message . If , then .
If , we can define new Brauer configuration algebras and corresponding messages associated with points and straight lines given by the formulas for , .
If , then , .
The labeled Brauer configuration is defined as follows:
- .
- .
- ,, , ,, , .
- .
- The successor sequences and at vertices x and have the following form:.
- .
Figure 8 shows the Brauer quiver induced by the Brauer configuration .
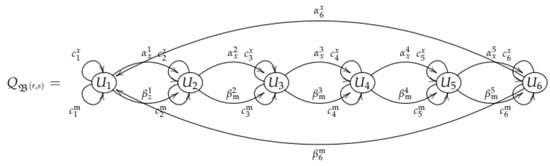
Figure 8.
Brauer quiver associated with the labeled Brauer configuration .
The specialized messages associated with Brauer configurations with are given in the following Table 1.

Table 1.
Specialized messages of type , .
Notation , , in Table 1 gives rise to a -matrix , for which and .
We call these matrices message-matrices associated with .
The next Theorem 4 gives some properties of message-matrices with , .
Theorem 4.
For fixed non-negative integers α, β, an integer ; the message-matrix associated with a linear map satisfies the following identities:
- .
- , if
- is the number of Dyck paths P in the plane from to with steps and that never pass below the x-axis.
- , where denotes the identity matrix.
- The determinant , where denotes the γth triangular number.
Proof.
- The first item follows from the identity
- (Induction) Suppose that entries of a -matrix B are obtained from entries of an matrix A via the property 1 and that entries of matrix A satisfy the property 2. According to the description, it suffices to prove that . Indeed,Suppose that matrix A satisfies property 2, i.e., . Thus,therefore,
- The identity is a direct consequence of property 1. Note that.
- If we proceed by induction, assuming that the assertion is true for any matrix , , then it holds that .
- It follows from the identity , where is the mth Catalan number.
- By construction, we note that if () is the th row (th column of )., then the inner product
□
The following Corollary 1 uses the properties given in Theorem 4 to obtain explicit solutions of some linear and nonlinear systems of differential equations.
Corollary 1.
If , , . And . Then
- is a solution of the linear system of differential equations
- is a solution of the nonlinear system of differential equations
Proof.
It suffices to note that
where () denote the usual hyperbolic sine (cosine) function. □
4. Cayley Hash Values of Brauer Messages Associated with the Plane
In this section, we compute and analyze Cayley hash values of Brauer messages
.
Cayley hash functions are examples of provably secure hash functions. The following Algorithm 2 allows building a hash function from an expander Cayley graph:
| Algorithm 2: Construction of a Cayley hash |
|
Remark 3.
Note that, under these circumstances, message specializations , as those defined in Remark 2 with and , are nothing but Cayley hash functions if . In such a case, we assume that is the group of nth roots of unity for fixed.
As an example of the setting posed in Remark 3. We assume , , and . Thus, up to permutation is the corresponding Cayley hash.
Figure 9 shows the Cayley graph defined in Remark 3. Labels of the arrows are given by the set , i.e., the arrow denotes the identity .
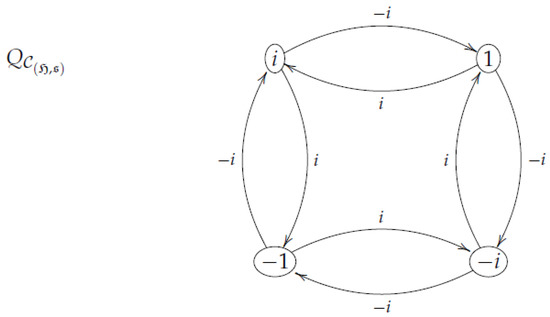
Figure 9.
Example of a Cayley graph associated with the 4th unity roots, with .
It is worth pointing out that Tillich and Zémor introduced hash functions associated with the special group with , where is an irreducible polynomial of degree n over . and are the generators of the Tillich–Zémor hash function. In such a case, if , then the corresponding Tillich–Zémor hash function assigns the matrix product , to the message .
The Tillich–Zémor ideas were generalized by Sosnovski [2], who introduced the semigroup generated by the linear functions and over the field with . Her algorithm (Algorithm 3) goes as follows:
| Algorithm 3: Sosnovski hash function. |
|
According to Sosnovski [2], a binary text is associated with a directed path P in the Cayley graph generated by and (the initial vertex of P is given by the identity). Her algorithm hashes a bit string with a time complexity of at most multiplications and additions in . In , each addition (multiplication) requires () bit operations. Thus, if for m fixed, then the number of bit operations to evaluate a hash value of an n bit string is .
The family of hash functions has the following properties:
- Variable size input and fixed output size.
- The Cayley graphs of the semigroup have relatively large girth.
- Efficient computation.
- Pseudorandom.
- Collision resistant.
In this paper, we compute the Sosnovski hash function to the Brauer messages . To perform this, we apply the assignment , ,
In other words, we obtain specialized Brauer messages
For , the Sosnovski–Brauer hash of a matrix is recursively obtained by applying the following procedure:
It is worth pointing out that the multiplication of two of these matrices takes . Thus, constructing requires bit operations, which can be reduced by using Theorem 5 and Sosnovki [2] arguments regarding the complexity of her hash function.
The following algorithm allows obtaining any block from the seeds and . Henceforth, all the products are assumed to be computed modulo a fixed prime number p.
Python gives the complexity and execution time of the algorithm proposed as and seconds, respectively, if consists of n, matrices, bearing in mind that choosing an orientation associated with a Brauer configuration at a point has complexity . Such an orientation gives the appropriate matrix multiplication sequence. For instance, for modulo , we have that , where .
The following Theorem 5 gives formulas for some Sosnovski hash functions associated with arbitrary products of the matrices , and (all the operations are assumed to be computed modulo a fixed prime number p).
Theorem 5.
If , ,
Then,
Proof.
It suffices noting that for :
□
Remark 4.
We recall that Cassaigne et al. [24] proved that if , , with . Then, the semigroup generated by A and B is free if . Additionally, there is a prime p for which , where is the p-adic value of the number z. Such a result proves that two words in the semigroup generated by matrices and are different if A and B do not commute.
The following result proves that the Sosnovski function is collision-resistant for any Brauer message , .
Corollary 2.
Let be the number of collisions associated with the Sosnovski hash values of Brauer messages for a fixed positive integer n. Then, .
Proof.
The result holds as a direct consequence of the results described in Remark 4. □
5. Experimental Data
This section gives some experimental results obtained by running Python routines in an Acer Predator Helios (intel core i7, 11th generation). We give execution times for Sosnovski and Tillich–Zémor hash values of Brauer messages associated with points in . Figure 10 shows the number of bits of the compressed Brauer messages.
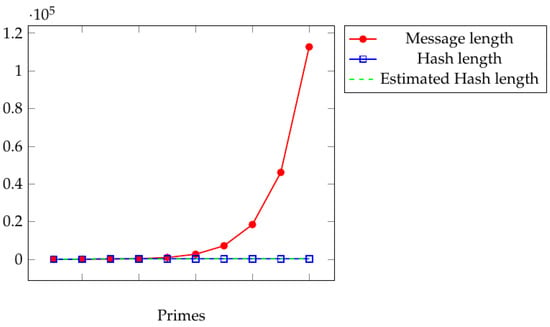
Figure 10.
The specialized Brauer message given by a product of . Sosnovski matrices are compressed by = 225.7621855345912 + 0.04323899371069182 bits.
Table 2 and Table 3 give matrices , (see Algorithms 4 and 5), which are hash values of Brauer messages in the sense of Tillich–Zémor (for ) and Sosnovski, respectively. These tables also show the number of collisions between these messages for the prime numbers considered by Sosnovski for her experimental data. Routine 4 in the appendix gives these values for arbitrary prime numbers and any matrix .
| Algorithm 4: Sosnovski –Brauer hash function. |
|

Table 2.
Matrices , give Tillich–Zémor hash values of Brauer messages .

Table 3.
Matrices , are used to compute hash values (see Algorithm 4).
| Algorithm 5: Building blocks . |
|
Table 4 and Table 5 give the execution time to compute Tillich–Zémor and Sosnovski hash values of the Brauer messages. Figure 10 shows how Brauer messages are compressed by Sosnovski hash values. Figure 11 shows a comparison between execution times to compute Sosnovski and Tillich–Zémor hash values of the Brauer messages , and for prime numbers to given in Table 4 and Table 5.

Table 4.
Execution time to compute Tillich–Zémor hash values of Brauer messages.

Table 5.
Execution time to compute Sosnovski hash values of Brauer messsages.
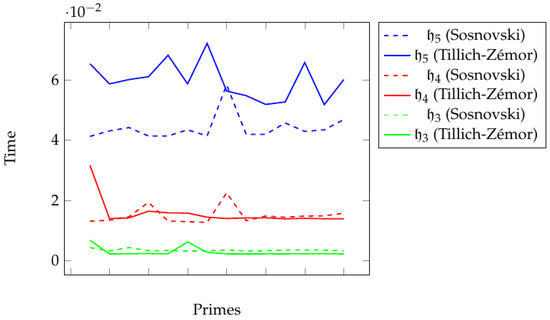
Figure 11.
Execution time of the Tillich–Zémor and Sosnovski hash values of the Brauer messages .
Discussion
Brauer messages associated with regions without mutations are nothing but bit strings, so the Sosnovski algorithm can be applied to obtain their corresponding hash values without increasing the algorithm’s execution time. On the other hand, the complexity of such an algorithm is exponential, and the execution time increases for Brauer messages associated with mutation regions.
Note that the hash values of Brauer messages associated with mutation regions obtained via Sosnovski matrices and their conjugates require fixing an orientation associated with a Brauer configuration at a point . To choose such an orientation has complexity .
6. Concluding Remarks and Future Work
Brauer configuration algebras can be associated to each point . Their dimensions can be computed by using appropriated binomial numbers. The same computations allow giving formulas for their centers. It is worth pointing out that suitable specializations allow obtaining matrices with applications in several scientific fields. For instance, such matrices give solutions to linear and no-linear differential equation systems. The specialized matrices give rise to elements in appropriated semigroups, which we call Brauer messages. The Sosnovski hash values of these messages are collision-resistant for large enough prime numbers. However, the execution time for giving such hashes is exponential when applied to Brauer messages with mutations.
Future Work
The following investigations are interesting tasks to be addressed in the future.
- To introduce new classes of matrices defined by specializations of variables associated with general bounded regions.
- To give explicit solutions for new classes of systems of differential equations by using specialized Brauer messages.
- To investigate hash values of Brauer messages associated with more general groups and semigroups. For instance, there is no up-to-date hash function based on generators of any of the Thompson groups. These approaches would decrease the complexity and execution time when computing hash values of Brauer messages arising from mutation regions.
Author Contributions
Investigation, M.A.O.A., A.M.C., C.C.F., O.M.M. and R.-J.S.; writing—review and editing, M.A.O.A., A.M.C., C.C.F., O.M.M. and R.-J.S. All authors have read and agreed to the published version of the manuscript.
Funding
Seminar Alexander Zavadskij on Representation of Algebras and their Applications, Universidad Nacional de Colombia. The fourth author was partially supported by MinCiencias-Colombia, Convocatoria 907 de 2021.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Set of vertices of a Brauer configuration | |
| Complex numbers field | |
| Dimension of a Brauer configuration algebra | |
| Dimension of the center of a Brauer configuration algebra | |
| The Sosnovski hash value associated with a matrix Brauer message | |
| The set of natural numbers | |
| Number of occurrences of a vertex in a polygon V | |
| The set of real numbers | |
| ith triangular number | |
| Ordered sequence of polygons | |
| Valency of a vertex | |
| The word associated with a polygon V | |
| The greatest integer less than or equal to x | |
| The smallest integer greater than or equal to x |
Appendix A. Python Routines
In this section, we give python routines to compute lattice paths (routine [2]), words associated with each point , i.e., (routine [3]). In other words, routine [3] computes the set of the Brauer configuration . Routine [4] computes matrices associated with the semigroup generated by matrices , , and over . Matrices , execution times, and collisions between hash values of specialized Brauer messages are computed modulo a prime number p via routine [7].



References
- Stinson, D.; Paterson, M. Cryptography: Theory and Practice, 4th ed.; Chapman and Hall/CRC Press: Boca Raton, FL, USA, 2019. [Google Scholar] [CrossRef]
- Sosnovski, B. Cayley Graphs of Semigroups and Applications to Hashing. Ph.D. Thesis, City University of New York, New York, NY, USA, 2016. [Google Scholar]
- Espinosa, P.F.F. Categorification of Integer Sequences and Its Applications. Ph.D. Thesis, Universidad Nacional de Colombia, Bogotá, Colombia, 2020. [Google Scholar]
- Green, E.L.; Schroll, S. Brauer configuration algebras: A generalization of Brauer graph algebras. Bull. Sci. Math. 2017, 141, 539–572. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Espinosa, P.F.F.; Rios, G.B. Wargaming with quadratic forms and Brauer configuration algebras. Mathematics 2022, 10, 729. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Gaviria, I.D.M.; Vega, J.D.C. Relationships between the Chicken McNugget Problem, Mutations of Brauer Configuration Algebras and the Advanced Encryption Standard. Mathematics 2021, 9, 1937. [Google Scholar] [CrossRef]
- Green, E.L.; Hille, L.; Schroll, S. Algebras and varieties. Algebr. Represent. Theor. 2021, 24, 367–388. [Google Scholar] [CrossRef]
- National Academies of Sciences, Engineering, and Medicine. Quantum Computing: Progress and Prospects; The National Academies Press: Washington, DC, USA, 2018. [Google Scholar] [CrossRef]
- Zémor, G. Hash functions and graphs with large girths. In Advances in Cryptology-EUROCRYPT’91; Springer: Berlin/Heidelberg, Germany, 1991; Volume 547, pp. 508–511. [Google Scholar] [CrossRef]
- Tillich, J.P.; Zémor, G. Group-theoretic hash functions. In Algebraic Coding: First French-Israeli Workshop, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 1994; Volume 781, pp. 90–110. [Google Scholar] [CrossRef]
- Tillich, J.P.; Zémor, G. Hashing with SL2. In Advances in Cryptology-CRYPTO’94; Springer: Berlin/Heidelberg, Germany, 1994; Volume 839, pp. 40–49. [Google Scholar] [CrossRef]
- Charles, D.X.; Lauter, K.E.; Goren, E.Z. Cryptographic hash Functions from expander graphs. J. Cryptol. 2007, 22, 93–113. [Google Scholar] [CrossRef]
- Petit, C. On Graph-Based Cryptographic Hash Functions. Ph.D. Thesis, Universit Catholique de Louvain, Ottignies-Louvain-la-Neuve, Belgium, 2009. [Google Scholar]
- Petit, C.; Lauter, K.; Quisquater, J.-J. Full cryptanalysis of LPS and Morgenstern hash functions. In Security and Cryptography for Networks, Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 5229. [Google Scholar] [CrossRef]
- Lubotzky, A.; Phillips, R.; Sarnak, P. Ramanujan graphs. Combinatorica 1988, 3, 261–277. [Google Scholar] [CrossRef]
- Grassl, M.; Ilić, I.; Magliveras, S.; Steiwandt, R. Cryptanalysis of the Tillich-Zémor hash function. J. Cryptol. 2011, 24, 148–156. [Google Scholar] [CrossRef]
- Petit, C.; Quisquater, J.-J. Preimages of the Tillich-Zémor hash function. In Selected Areas in Cryptography. SAC 2010. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6544. [Google Scholar] [CrossRef]
- Grassl, M.; Langenber, B.; Roetteler, M.; Steiwandt, R. Applying Grover’s algorithm to AES: Quantum resource estimates. In Post-Quantum Cryptography. PQCrypto 2016. Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2016; Volume 9606. [Google Scholar] [CrossRef]
- Mullan, C.; Tsaban, B. SL2 homomorphic hash functions: Worst case to average case reduction and short collision search. In Designs, Codes and Cryptography; Springer: Berlin/Heidelberg, Germany, 2016; Volume 81, pp. 83–107. [Google Scholar] [CrossRef][Green Version]
- Agudelo Muñeton, N.; Cañadas, A.M.; Gaviria, I.D.M.; Fernández, P.F.F. {0,1}-Brauer configuration algebras and their applications in the graph energy theory. Mathematics 2021, 9, 3042. [Google Scholar] [CrossRef]
- Cañadas, A.M.; Angarita, M.A.O. Brauer configuration algebras for multimedia based cryptography and security applications. Multimed Tools Appl. 2021, 80, 23485–23510. [Google Scholar] [CrossRef]
- Assem, I.; Skowronski, A.; Simson, D. Elements of the Representation Theory of Associative Algebras; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar] [CrossRef]
- Sierra, A. The dimension of the center of a Brauer configuration algebra. J. Algebra 2018, 510, 289–318. [Google Scholar] [CrossRef]
- Cassaigne, J.; Harju, T.; Karhumäki, J. On the undecidability of freeness of matrix semigroups. Intern. J. Algebra Comput. 1999, 9, 295–305. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).