Contactless Material Tensile Testing Using a High-Resolution Camera
Abstract
:1. Introduction
2. Non-Contact Methods for Tensile Test Evaluation
2.1. Video Extensometry
2.2. Laser Extensometry
3. Proposed System of Video Extensometry
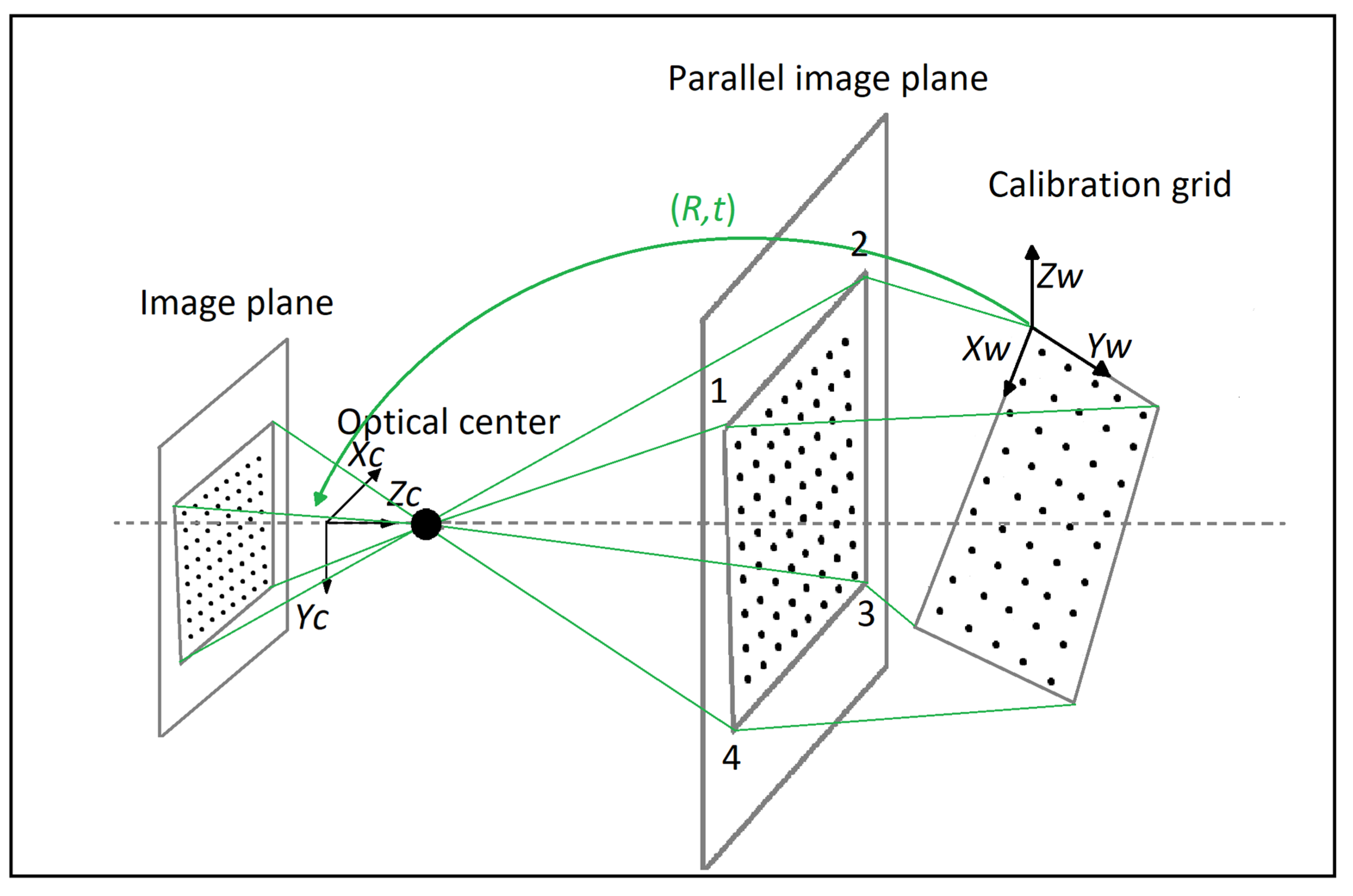
3.1. Camera Callibration
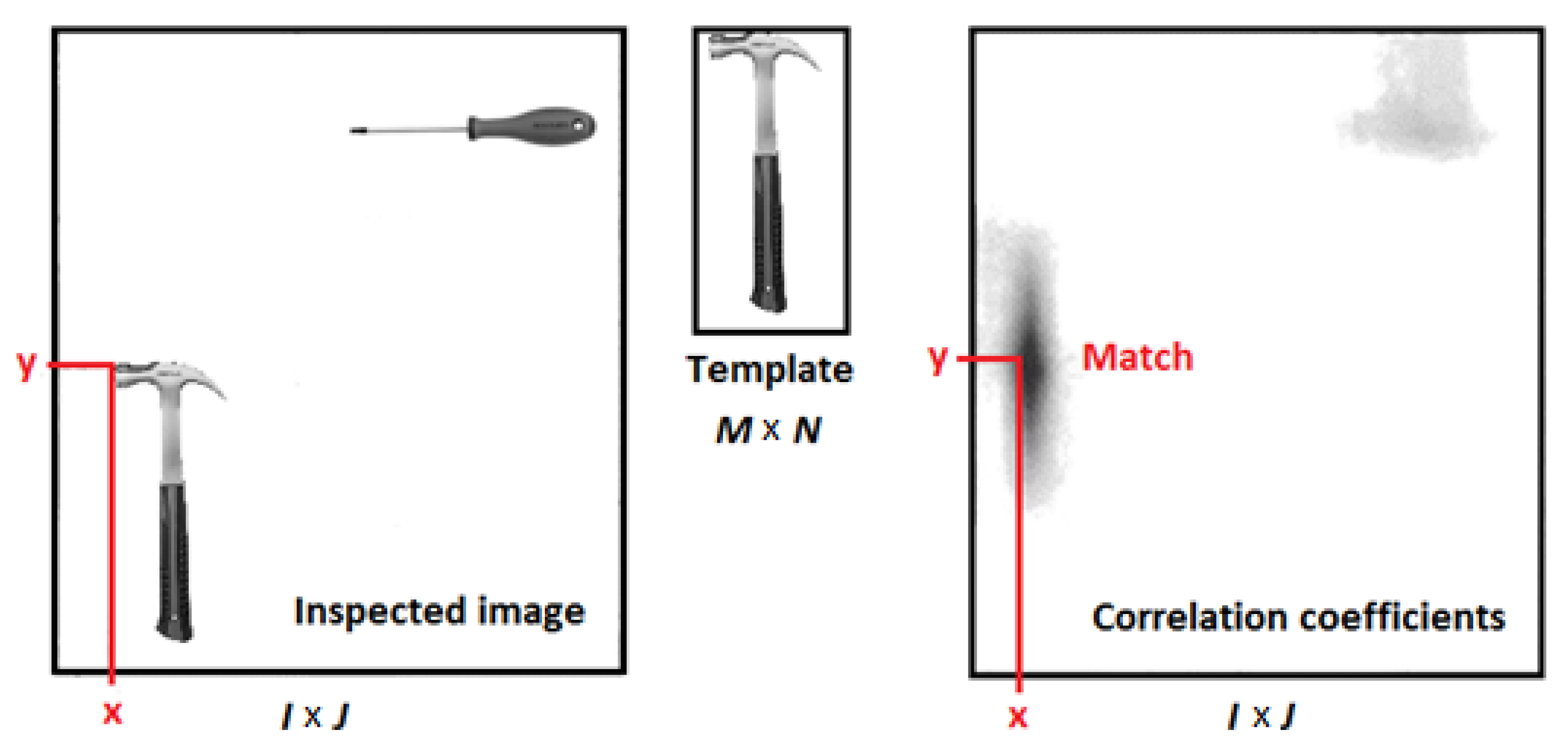
3.2. Pattern Matching
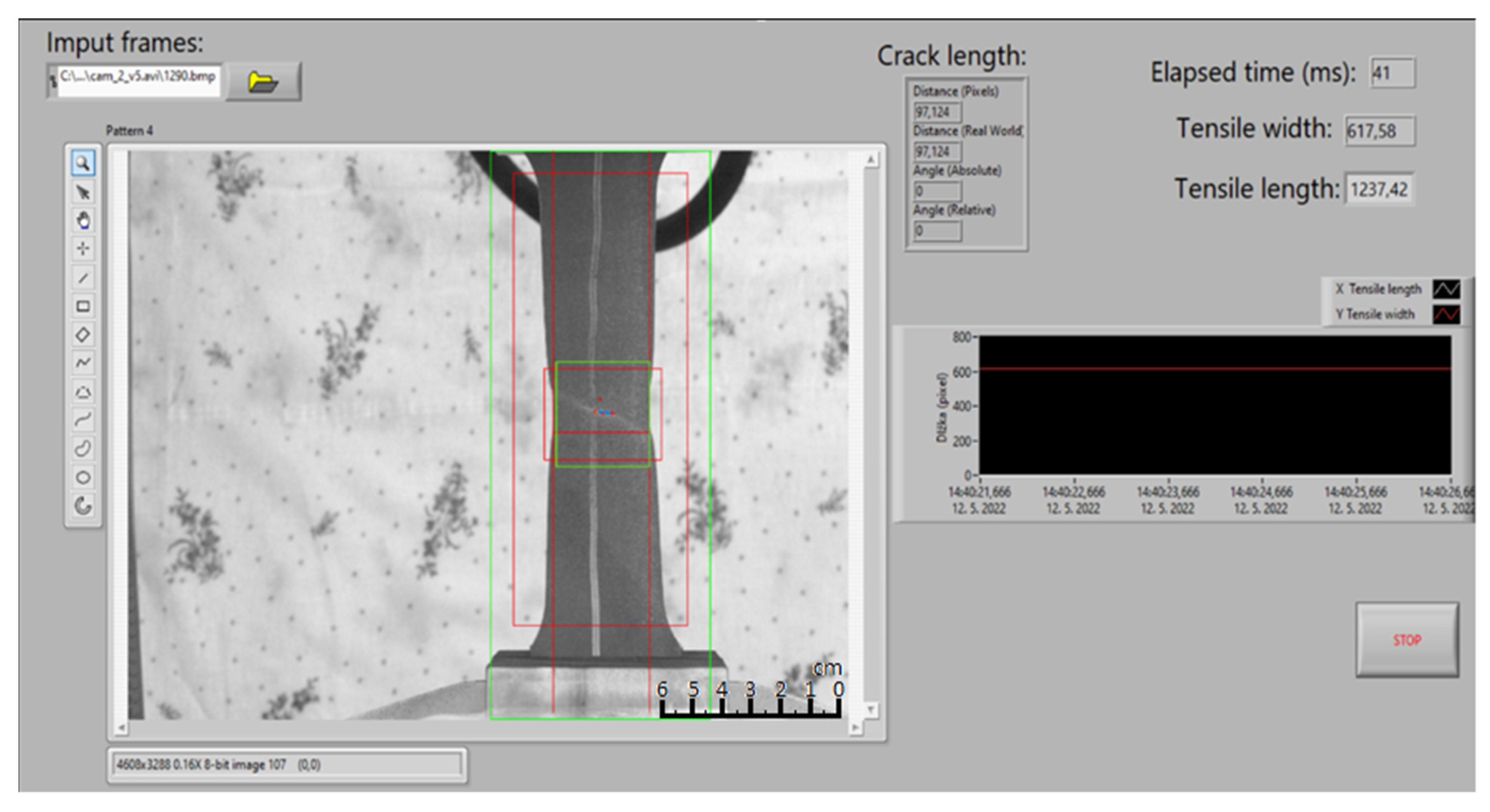
3.3. Labview Application
3.4. Hardware
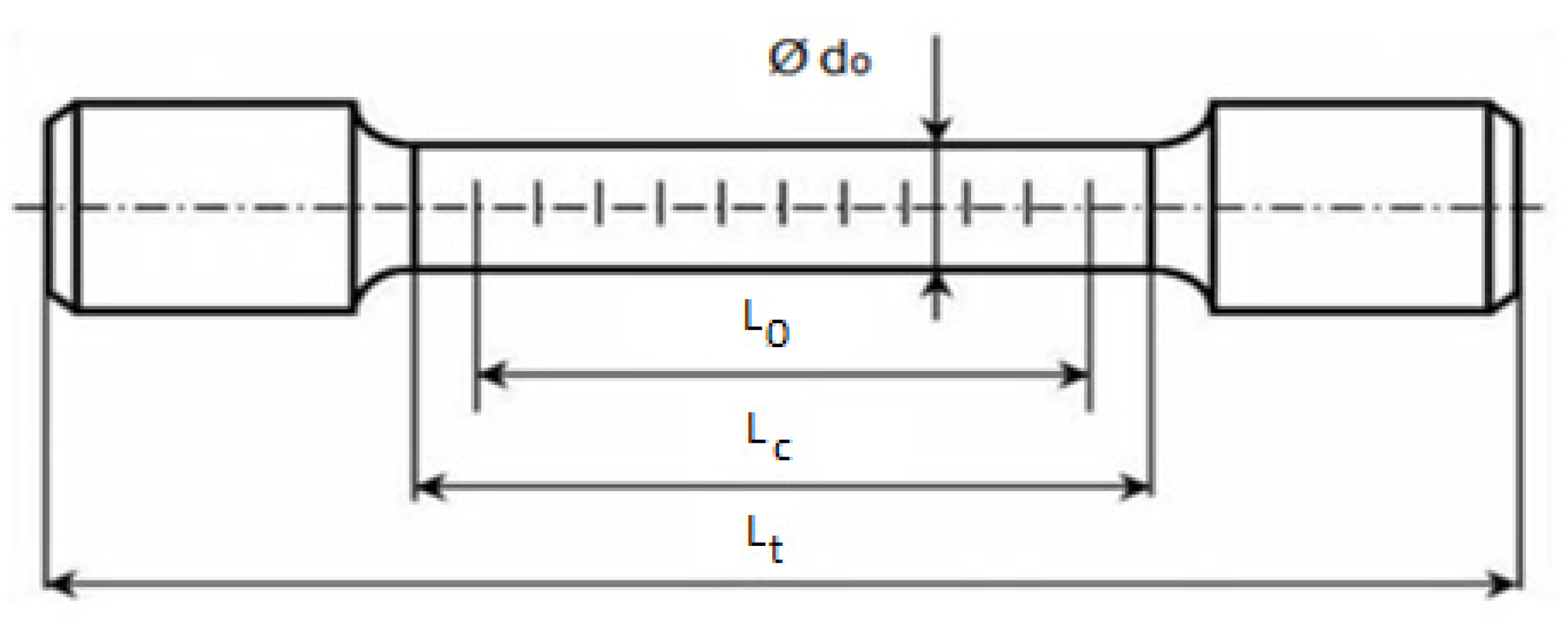
4. Experimental Measurement
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saba, N.; Jawaid, M.; Sultan, M.T.H. An Overview of Mechanical and Physical Testing of Composite Materials; Woodhead Publishing: Sawston, UK, 2019; ISBN 978-0-08-102292-4. [Google Scholar]
- Kašuba, M. Analysis of the Miniature Test Specimen Results with Variable Geometries. Available online: https://www.vutbr.cz/www_base/zav_prace_soubor_verejne.php?file_id=15103 (accessed on 30 May 2021).
- MatNet Slovakia. Static Tensile Test. Available online: http://www.matnet.sav.sk/index.php?ID=526 (accessed on 30 May 2022).
- Zheng, P.; Chen, R.; Liu, H.; Chen, J.; Zhang, Z.; Liu, X.; Shen, Y. On the standards and practices for miniaturized tensile test—A review. Fusion Eng. Des. 2020, 161, 112006. [Google Scholar] [CrossRef]
- Tran, K.Q.; Satomi, T.; Takahashi, H. Tensile behaviors of natural fiber and cement reinforced soil subjected to direct tensile test. J. Build. Eng. 2019, 24, 100748. [Google Scholar] [CrossRef]
- Ma, Q.; Rejab, M.R.M.; Qayyum, H.; Merzuki, M.N.M.; Darus, M.A.H. Experimental investigation of the tensile test using digital image correlation (DIC) method. Mater. Today Proc. 2020, 27, 757–763. [Google Scholar] [CrossRef]
- Vukelic, G.; Vizentin, G.; Ivosevic, S. Tensile strength behaviour of steel plates with corrosion-induced geometrical deteriorations. Ships Offshore Struct. 2021, 54, 154–162. [Google Scholar] [CrossRef]
- Tao, G.; Xia, Z. A non-contact real-time strain measurement and control system for multiaxial cyclic/fatigue tests of polymer materials by digital image correlation method. Polym. Test. 2005, 24, 844–855. [Google Scholar] [CrossRef]
- Pan, B.; Tian, L. Advanced video extensometer for non-contact, real-time, high-accuracy strain measurement. Opt. Express 2016, 24, 19082–19093. [Google Scholar] [CrossRef] [PubMed]
- Dong, B.; Tian, L.; Pan, B. Tensile testing of carbon fiber multifilament using an advanced video extensometer assisted by dual-reflector imaging. Measurement 2019, 138, 325–331. [Google Scholar] [CrossRef]
- Shao, X.; Eisa, M.M.; Chen, Z.; Dong, S.; He, X. Self-calibration single-lens 3D video extensometer for high-accuracy and real-time strain measurement. Opt. Express 2016, 24, 30124–30138. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Chen, W.; Pan, B. High-accuracy video extensometer based on a simple dual field-of-view telecentric imaging system. Measurement 2020, 166, 108209. [Google Scholar] [CrossRef]
- Dong, B.; Li, C.; Pan, B. Ultrasensitive video extensometer using single-camera dual field-of-view telecentric imaging system. Opt. Lett. 2019, 44, 4499–4502. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Bech, J.; Hansen, N. Low temperature annealing of cold-drawn pearlitic steel wire. Conf. Ser. Mater. Sci. Eng. 2015, 89, 012058. [Google Scholar] [CrossRef] [Green Version]
- Pan, B. Digital image correlation for surface deformation measurement: Historical developments, recent advances and future goals. Meas. Sci. Technol. 2018, 29, 082001. [Google Scholar] [CrossRef]
- Bulava, J.; Hargas, L.; Koniar, D.; Stefunova, S. Determination of material parameters using video extensometry during tensile testing. In Proceedings of the 2021 International Conference on Electrical Drives & Power Electronics (EDPE), Dubrovnik, Croatia, 22–24 September 2021. [Google Scholar]
- National Instruments Corp. Determining the Pose of an Object. 2022. Available online: https://zone.ni.com/reference/en-XX/help/372916M-01/nivisionconcepts/spatial_calibration_indepth/ (accessed on 30 May 2021).
- Sinkovics, N. Pattern matching in qualitative analysis. In The SAGE Handbook of Qualitative Business and Management Research Methods: Methods and Challenges; Cassell, C., Cunliffe, A.L., Grandy, G., Eds.; Sage Publications: Thousand Oaks, CA, USA, 2018; pp. 468–484. ISBN 9781526429278. [Google Scholar]
- Hak, T.; Dul, J. Pattern Matching. ERIM Report Series Reference. No. ERS-2009-034-ORG. 2009. Available online: https://ssrn.com/abstract=1433934 (accessed on 30 May 2022).
- Davis, J.R. Tensile Testing; ASM International: Materials Park, OH, USA, 2004; ISBN 9781615030958 1615030956. [Google Scholar]
- Edmund Optics Inc. Basler Ace acA4600-10uc Color USB 3.0 Camera. Available online: https://www.edmundoptics.com/p/basler-ace-aca4600-10uc-color-usb30-camera/32436/ (accessed on 30 May 2022).
- Tao, Q.B.; Benabou, L.; Tran, N.H.; Luu, D.B. A Digital Image Correlation setup for the analysis of lead-free solder alloys. In Proceedings of the International Conference on System Science and Engineering (ICSSE), Ho Chi Minh City, Vietnam, 21–23 July 2017; pp. 404–407. [Google Scholar] [CrossRef]
- Pelegrin, J.; Bailey, W.O.S.; Crump, D.A. Application of DIC to Extract Full Field Thermo-Mechanical Data from an HTS Coil. IEEE Trans. Appl. Supercond. 2018, 28, 1–5, Art no. 4604305. [Google Scholar] [CrossRef]
- Wang, L. Super-robust digital image correlation based on learning template. Opt. Lasers Eng. 2022, 158, 107164. [Google Scholar] [CrossRef]
- Park, J.; Yoon, S.; Kwon, T.-H.; Park, K. Assessment of speckle-pattern quality in digital image correlation based on gray intensity and speckle morphology. Opt. Lasers Eng. 2017, 91, 62–72. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, Q. A free and open-source software for generation and assessment of digital speckle pattern. Opt. Lasers Eng. 2022, 148, 106766. [Google Scholar] [CrossRef]
- Baldi, A. Robust Algorithms for Digital Image Correlation in the Presence of Displacement Discontinuities. Opt. Lasers Eng. 2020, 133, 106113. [Google Scholar] [CrossRef]
- Ghulam Mubashar, H. Digital Image Correlation for discontinuous displacement measurement using subset segmentation. Opt. Lasers Eng. 2019, 115, 208–216. [Google Scholar] [CrossRef]








| Method | Accuracy [cm] | Calculation Speed [ms] |
|---|---|---|
| DIC correlation | 0.05 | 1.3 |
| Optical flow | 0.33 | 1 |
| Thresholding + edge detection (Canny) | 0.33 | 32.7 |
| DIC + Optical flow | 0.05 | 0.6 |
| Pattern matching | 0.006 | 43.6 |
| Measurement | Video Frames | Tensile Sample Detection | Faulty Detection | without Detection |
|---|---|---|---|---|
| 1 | 1450 | 1428 | 7 | 15 |
| 2 | 1350 | 1220 | 53 | 77 |
| 3 | 1200 | 1158 | 27 | 15 |
| 4 | 1130 | 1094 | 16 | 20 |
| 5 | 1320 | 1286 | 5 | 29 |
| 6 | 1230 | 1207 | 7 | 16 |
| 7 | 480 | 463 | 9 | 8 |
| 8 | 240 | 239 | 0 | 1 |
| 9 | 1650 | 1602 | 14 | 34 |
| Summary [-] | 10,050 | 9697 | 138 | 215 |
| Summary [%] | 100 | 96.48756219 | 1.373134328 | 2.139303483 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulava, J.; Hargaš, L.; Koniar, D. Contactless Material Tensile Testing Using a High-Resolution Camera. Computation 2022, 10, 121. https://doi.org/10.3390/computation10070121
Bulava J, Hargaš L, Koniar D. Contactless Material Tensile Testing Using a High-Resolution Camera. Computation. 2022; 10(7):121. https://doi.org/10.3390/computation10070121
Chicago/Turabian StyleBulava, Jaroslav, Libor Hargaš, and Dušan Koniar. 2022. "Contactless Material Tensile Testing Using a High-Resolution Camera" Computation 10, no. 7: 121. https://doi.org/10.3390/computation10070121
APA StyleBulava, J., Hargaš, L., & Koniar, D. (2022). Contactless Material Tensile Testing Using a High-Resolution Camera. Computation, 10(7), 121. https://doi.org/10.3390/computation10070121







