Abstract
In this work, generalized polynomial chaos (gPC) expansion for land surface model parameter estimation is evaluated. We perform inverse modeling and compute the posterior distribution of the critical hydrological parameters that are subject to great uncertainty in the Community Land Model (CLM) for a given value of the output LH. The unknown parameters include those that have been identified as the most influential factors on the simulations of surface and subsurface runoff, latent and sensible heat fluxes, and soil moisture in CLM4.0. We set up the inversion problem in the Bayesian framework in two steps: (i) building a surrogate model expressing the input–output mapping, and (ii) performing inverse modeling and computing the posterior distributions of the input parameters using observation data for a given value of the output LH. The development of the surrogate model is carried out with a Bayesian procedure based on the variable selection methods that use gPC expansions. Our approach accounts for bases selection uncertainty and quantifies the importance of the gPC terms, and, hence, all of the input parameters, via the associated posterior probabilities.
1. Introduction
Land surface models (LSMs) are used by scientists to quantitatively simulate the exchange of water and energy fluxes at the Earth–atmosphere interface. LSMs have progressed from simplistic schemes defining simply the surface boundary conditions for general circulation models (GCMs) to complicated models incorporating modules representing biogeochemical, hydrological, and energy cycles at the surface–atmosphere interface over the last few decades (Pitman [1]). The model parameters are frequently related with definite physical meaning and have an influence on the primary model outputs, such as water and energy fluxes. They are built on mathematical formulations of the laws of physics. The assumption for Inter-comparison of Land Surface Parameterization Schemes is that the parameters are quantifiable and transferable between sites with similar physical properties or site conditions (PILPS) (Bastidas et al. [2], Henderson-Sellers et al. [3,4]). However, default assignment of parameter values are actually inappropriate according to (Bastidas et al. [2], Rosero et al. [5]). In the meantime, given the high dimensionality of the parameter space and the complexity of the land surface system, more research is needed to determine which parameters are more uncertain and the potential for using observations to constrain or calibrate the uncertain parameters in order to better capture uncertainty in the resulting land surface states (Hou et al. [6], Huang et al. [7]). The goal of this research is to quantify the uncertainty in a subset of parameters in a community LSM called the Community Land Model (CLM), which is the land component of the Community Earth System Model (CESM) (formerly known as the Community Climate System Model (CCSM) (Collins et al. [8], Gent et al. [9], Lawrence et al. [10]).
It is possible that model structural uncertainty in LSMs is attributable to simplified assumptions or representations of actual processes or events. Many of these assumptions hold true only in certain situations. Furthermore, LSMs are prone to ambiguity in terms of input parameter values, owing to the fact that many input characteristics, such as those related to land cover and land use, as well as soil qualities, are difficult to assess at the scales at which they are utilized. A common technique in land surface modeling is to define a set of universally applicable default parameter values. Over the last two decades, the land surface modeling community has worked hard to resolve uncertainty in model parameters, data, and model structure. The purpose of this study is to reduce model parameter uncertainty using generalized polynomial expansion and Bayesian inversion.
In a high-dimensional parameter space, the computational cost of stochastic inversion is significant. Surrogate models can be utilized to solve this problem instead of numerical simulators. Ensemble simulations, which are required to build surrogate models, can be efficiently executed in a task-parallel manner on supercomputing facilities. Surrogate creation, on the other hand, is a lengthy procedure. Surrogates are not utilized very often in climate model or LSM calibration. Using observations of latent heat fluxes, the authors used different surrogates (e.g., polynomials and/or universal kriging) to calibrate hydrological parameters of CLM 4.0 in (Ray et al. [11], Huang et al. [12]).
For the model–data mismatch, two competing models were utilized to construct a composite of measurement error and (a crude estimate of) CLM structural error. In (Gong et al. [13]), the authors employed adaptive surrogate-based optimization to estimate the parameters of the Common Land Model employing six observables at once; 12 independent parameters were (deterministically) calibrated.
Using Bayesian compressive sensing (BCS) and polynomial chaos expansions, (Sargsyan et al. [14]) sought to create surrogates for five variables of interest from CLM4 with prognostic carbon and nitrogen modules turned on (i.e., CLM4-CN) (PCEs). They discovered that the input–output relationship in CLM4-CN could be made up of qualitatively diverse regimes (i.e., living or dead vegetation regimes associated with various locations in the parameter space), necessitating the use of clustering and classification to generate piecewise PCEs.
The applicability of employing gPC for CLM4 hydrological model calibration is investigated in this study. Based on [15], we provide a completely Bayesian technique that combines fully Bayesian statistics, variable selection, and generalized polynomial chaos surrogate models to handle the uncertainty quantification and model inversion problem in CLM4. The procedure produces a cheap mathematical/statistical approximation of the model output (latent heat flux) as a function of a set of model parameters. Bayesian inversion of the model parameters’ given observations is performed by using the produced cheap gPC surrogate model instead of the expensive computer model output in the likelihood function, and then by performing Bayesian parametric inference facilitated by Markov chain Monte Carlo methods. The method allows for dimension reduction and the selection of the important model parameters that significantly influence the output parameter by computing inclusion posterior probabilities.
The layout of the paper is as follows: in Section 2, we describe the study site, input data, and the conducted numerical simulations, and present the parameters of interest that we calibrate; in Section 3, we present the inversion methodology using gPC in the Bayesian framework; in Section 4, we evaluate the inversion results; in Section 5, we draw our conclusions.
2. Dataset and Parameterization
The FLUXNET database (www.fluxdata.org, accessed on 20 March 2022) contains half-hourly observations of ecosystem CO2, heat fluxes, and meteorological data of more than 250 sites worldwide and for a total of 960 site-years. The study site in this study is US-ARM (ARM Southern Great Plains site, Lamont, Oklahoma) (Fischer et al. [16], Torn [17]). It has a vegetation type of croplands, covered with temporary crops followed by harvest and a bare soil period (e.g., single and multiple cropping systems), a humid subtropical climate, and clay-type soil texture.
Observational data used in parameter estimation are observed latent heat fluxes and runoff measurements, which are processed and gap-filled to obtain daily and monthly averaged data. We consider 10 critical hydrological parameters that are likely to have dominant impacts on the simulation of surface and subsurface runoff, latent and sensible fluxes, and soil moisture, as suggested in existing literature (Hou et al. [6], Niu et al. [18,19], Oleson et al. [20,21]). The selected parameters are fmax, Cs, fover, fdrai, qdrai,max (denoted as Qdm hereinafter), Sy, b, Ys, Ks, and s. Explanations of the 10 parameters and their prior information are shown in Table 1 in Hou et al. [6]. Prior distributions of the parameters are specified as independent truncated normal distributions with location, scale, and range parameters specified according to the values in Table 1 in Hou et al. [6]; in the cases that prior variance was not available, we considered uniform prior distributions. We recall that such values for the hyper-parameters are acceptable according to existing literature Oleson et al. [20,21]. It is important to highlight that, although truncated normals, these priors are essentially flat due to their large variances. Moreover, 256 samples were generated by using quasi Monte Carlo (QMC) sampling on the basis of the prior pdfs; QMC provides a good dispersion between sample points and can achieve a good uniformity in dimensionality at around 10 Caflisch [22], Wang and Sloan [23]. Numerical simulations corresponding to sampled parameter sets were conducted, which yield the data matrix of inputs (i.e., realizations of the 10 parameters) and outputs (i.e., latent heat fluxes), which enables the development of response surfaces or surrogates that can be used for sensitivity analysis, parameter ranking, and model calibration.
3. Bayesian Methodology
We describe a synergy of Bayesian methods aiming to quantify the importance of input CLM4 model parameters and calibrate these parameters against real measurements, as well as build a surrogate model describing the input–output relation in the CLM4 model, in the Bayesian framework.
3.1. Bayesian Inverse Problem Setup
Bayesian inverse methods allow for the uncertainty quantification of input parameters of a computer model from observations [24]. Bayesian inference is performed through the posterior distribution, which is derived according to the Bayes theorem. We need to specify two components: the likelihood function representing experimental information from the measurements, and the prior distribution representing the researcher’s prior information about the uncertain parameters.
We consider that the output value observed is associated to some unknown input via a forward model (e.g., CLM4) , and possibly contaminated by some additive observational noise (residuals); namely . A reasonable assumption is to model as a normally distributed variable with mean zero and variance . This is justified by central limit theorem arguments, and the fact that, in the noise term, there are several insignificant random measurement errors accumulated from observations and modeling errors due to model parameterization. Thus, the likelihood is:
To account for the uncertainty about the input parameters we assigned prior distribution , where are considered to be shifted beta distributions , with known and , . Here, , and can be specified because a reasonable range of the model parameter is often a priori known. In addition, and can be specified by using the method of moments or the maximum entropy method [25] because, often, reasonable values for the mean and variance of the model parameter are a priori known. A computationally convenient choice for the priors of the variance is the inverse gamma prior distribution with parameters , and , as it is a semi-conjugate prior to the likelihood. By considering the likelihood variance as random unknown parameters and treating the problem in the Bayesian framework, we let the data decide a proper value for through the posterior distribution. The prior hyper-parameters are considered to be fixed values and are pre-defined by the researcher.
The posterior distribution of given the observations is
by using the Bayes’ theorem, and marginal distribution quantifies the uncertainty about the model parameters .
The posterior distribution density (1) is usually intractable. If was known or was cheap to compute, inference on could be obtained using standard Markov chain Monte Carlo (MCMC) methodology [26]. In Algorithm 1, we present a simple MCMC sampler that updates and iteratively in two stages. The output sample of Algorithm 1 can be used to perform inference on and , e.g., expectation of any function of can be approximated as
for large T.
In the present application of the CLM4 model, is prohibitively expensive to compute iteratively because the forward model (CLM4) is too expensive to run. This prevents us from directly using this method, and, particularly, Algorithm 1. To overcome this issue, we built a cheap but accurate proxy (called surrogate model) for , and plugged it into (1). The construction of such a surrogate model in the Bayesian framework is discussed in Section 3.2.
| Algorithm 1 Updates of a single MCMC swap. |
|
3.2. Surrogate Model Specification
We describe a fully Bayesian procedure for building a surrogate model to be used as a cheap but accurate proxy of in (1) based on gPC expansions and MCMC methods. The highlight is that, apart from evaluating a surrogate model, the procedure is able to quantify the importance of each PC basis via inclusion posterior probabilities, which allows for the selection of the important input parameters: Fmax, Cs, Fover, Fdrai, Qdm, Sy, B, Psis, Ks, thetas.
3.2.1. Generalized Polynomial Chaos Expansion
We consider the output parameter as a function of the vector of random input variables that follow distribution .
The output parameter can be modeled as an expansion of PC bases and PC coefficients :
for [27]. We denote multi-indices of size that are defined on a set of non-negative integers . The family of polynomial bases contains multidimensional orthogonal polynomial bases with respect to the probability measure of . Each multidimensional PC basis results as a tensor product of univariate orthogonal polynomial bases of degree , namely:
where , for and .
Often, the PC bases are chosen so that they are orthogonal with respect to the distribution . A quite general family of polynomials is the Askey family [28], whose members are associated with standard distributions. In this work, we focus on the use of Jacobi polynomial bases [28], which can be defined recursively as:
where is a linear transformation , and , are the minimum and maximum of .
In practice, for computational reasons, we truncate (2) by considering a finite sub-set of PC bases based on the total truncated rule. Hence, the expansion form becomes:
which uses, for only a finite set of multi-indices, A, such that with cardinality . Other truncation rules can be adopted [14,29].
The PC coefficients are equal to , where , for [27]; however, they are intractable. Moreover, the number of unknown PC coefficients is of order and grows rapidly with the dimension and PC degree . This causes computational problems such as over-fitting [15,30], especially when the dimensionality of is high. If we consider a smaller PC degree or carelessly omit PC bases, it may lead to a significant increase in bias and hence produce inaccurate surrogate models. Hence, there is a particular interest in keeping only the inputs or bases that significantly affect the output in the gPC. The Bayesian procedure in Section 3.2.2 effectively addresses these matters.
3.2.2. Bayesian Training Procedure
We describe a stochastic and automatic Bayesian procedure that accurately evaluates the PC coefficients and the gPC surrogate model, while it allows for the selection of the the significant PC bases, and hence input model parameters. This procedure is able to trade off efficiently between the bias (caused by omitting bases) and the over-fitting, which are both required. Furthermore, it can select the significant PC bases and estimate the PC coefficients simultaneously, while providing credible intervals.
We assume that there is a training dataset available, where is the size of the dataset, denotes the random input value, and denotes the output value corresponding to the j-th input value . Then, we model
where is the error term, associated with the j-th observation. Equation (5) can be written in matrix form:
where , , , and is an dimensional matrix of basis functions.
The likelihood is:
where denotes the Gaussian probability density function with mean and variance . The likelihood function is considered as a proximity measure of the truncated gPC expansion to the observations. We specify a hierarchical prior model :
where , , , and are fixed prior hyper parameters, and predetermined by the researcher. In the Bayesian framework, inference on the uncertain model parameters can be performed based on the posterior distribution
Particular interest lies in the computation of the inclusion probabilities that refer to the marginal posterior probability that the a-th basis is important, and the that refers to the posterior density of the a-th PC coefficient.
To fit the Bayesian model, we resort to Markov chain Monte Carlo (MCMC) methods because the posterior distribution (9) is intractable and cannot be sampled directly. The conjugate prior model (8) allows for the design of a Gibbs sampler [31,32] whose updates involve sampling from the full conditional distributions of the parameter updated. In Algorithm 2, we represent a pseudo-code of one sweep of the Gibbs samples, along with the associated full conditional distributions. We highlight that the procedure is fully automatic because there is no need to tune the algorithmic parameters involved in Algorithm 2. The notation ( and ) refers to the vector c (and matrix X) excluding the a-th element (and column). Moreover, we denote .
| Algorithm 2 Updates of the Gibbs swap. |
|
In order to evaluate the surrogate model, as well as quantify the importance of the input model parameters, we consider two Bayesian procedures. One is the Bayesian model averaging [33] and the other is the median probability model.
Bayesian Model Averaging
Bayesian model averaging is most suitable when we are interested in the predictive ability of the surrogate model.
Let be a Gibbs sample from Algorithm 2. Estimates and associated standard errors of can be computed as and , where is the sample standard deviation and is the sample integrated autocorrelation time of for [26,33]. Estimates for , v, and can be computed by Monte Carlo integration using the ergodic average of quantities in Gibbs sample; for instance:
Median Probability Model Based Evaluation
A parsimonious (or sparse) surrogate model involving only significant basis functions and important input model parameters can be obtained by examining the estimated inclusion probabilities . A suitable probabilistic basis selection mechanism is the median probability model (MPM) [34].
Let be a Gibbs sample from Algorithm 2. The posterior distribution that the PC basis is significant can be estimated as . We call the marginal inclusion posterior probabilities. The inclusion parameters are estimated as , for . MPM consists of PC coefficients , and PC bases , whose marginal inclusion probabilities are such that (and hence ). Hereafter, we will refer to them as significant PC coefficients and PC bases.
After the selection of the significant PC bases, inference about the uncertain parameters can be made by re-running Algorithm 2 for fixed equal to in order to obtain a a larger Gibbs sample. The new Gibbs sample can be used to perform inference and estimation. For instance, estimates for , v, and can be computed by Monte Carlo integration and using the equations of the estimators in (10). Note that a number of the coefficients will be constantly zero for all . The reason is because, unlike in the BMA approach, here, we consider only a single subset of PC bases, and hence the inclusion parameter is a fixed parameter equal to , for .
The MPM approach allows the selection of the important input model parameters that significantly affect the output. If an input parameter is not represented by any significant PC basis in the gPC expansion, it would be reasonable to consider that input parameter does not significantly affect the output model and, hence, is omitted from the analysis.
4. Analysis of the US-ARM Data-Set
Here, we consider the US-ARM data set. The main interest lies in computing the posterior distributions of the 10 (random) input parameters of CLM4 , given an observed latent heat flux (LH) measurement as shown in Table 1.

Table 1.
Observed value for the US-ARM data-set.
We apply the above methodology, which involves two stages: (i) building a surrogate model to replace the accurate but expensive forward model CLM4 according to the methodology in Section 3.2, and (ii) conducting inversion of the 10 inputs according to the theory in Section 3.1.
Surrogate Model Building Step
For each month, we built a surrogate model that maps the input of CLM4 to the output LH u. For this type of dataset, Hou et al. [6] and Sun et al. [35] observed that the dependency between the output parameters LH corresponding to different months is weak and, hence, can be neglected. Therefore, here, we built surrogate models for each month independently. An advantage of assuming independence is that it leads to a simpler parameterization for the statistical model, which is easier to treat and interpret.
To build the gPC expansion, we followed the procedure in Section 3.2. For the design of the gPC expansion, we considered PC bases from the Jacobi polynomial family, and the total truncated rule with polynomial degree 4. The bases in the gPC expansion had the following arrangement: first, the main effects as Fmax, Cs, Fover, Fdrai, Qdm, Sy, B, Psis, Ks, , and, then, the interactions by increasing order, while interactions of the same order were arranged so that their interacting bases correspond to main effects in the aforesaid order. This rule identifies the order of the columns of the design matrix X, as well as that of the elements of the vector C in (6). The parameters of the Jacobi PC bases were set according to the prior information of the input of CLM4 in ([6], Table 1) by matching the moments of the corresponding shifted beta distribution, to which, they are orthogonal. We considered the prior model (8) with hyper-parameters , , , , , and . This choice of hyper-parameters leads to weakly informative priors. This is a reasonable choice because there is lack of prior information about the parameterization of the surrogate model. For training the gPC expansion, we used the training data set US-ARM. We ran Algorithm 2 for iterations, where the first were discarded as burn-in.
In Figure 1 and Figure 2, we present the marginal posterior probabilities computed by the ergodic average of the occurrences of the corresponding PC bases in the Gibbs sample. We observe that, during the period May-August, the marginal inclusion probabilities are higher than those of the rest months. This indicates that the input parameters of CLM4 may have a larger impact on the output LH during those months. From the hydrology point of view, this is expected because LH is higher on average and has a larger variability during these months, and the effects of hydrological parameters are expected to be more pronounced in the summer months.
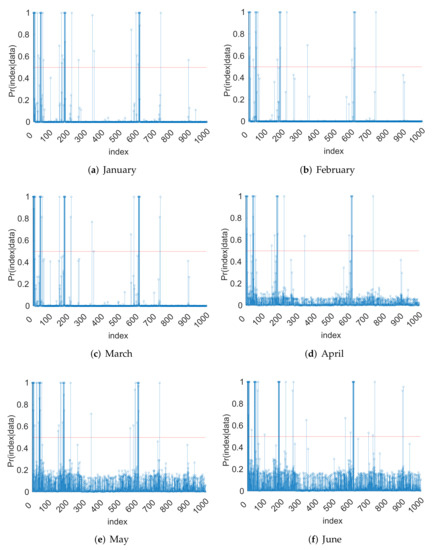
Figure 1.
Plots of the posterior marginal inclusion probabilities: January–June.
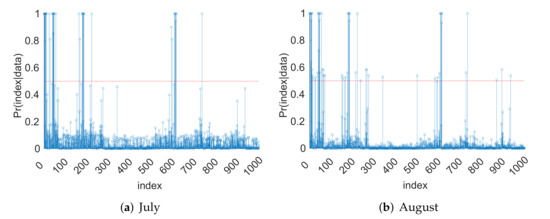
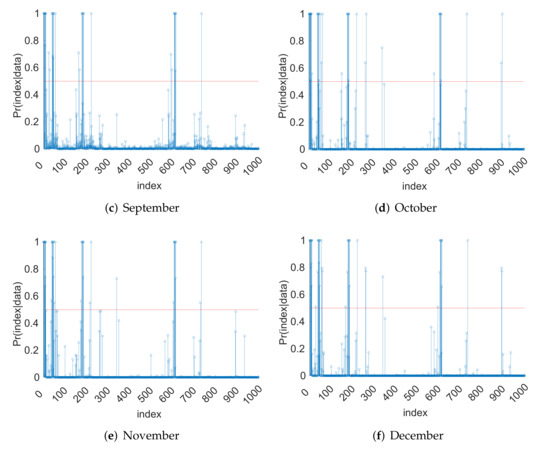
Figure 2.
Plots of significant posterior marginal inclusion probabilities: July–December.
We can infer that the input parameters Fmax, Cs, Fdrai, Qdm, and B are significant according to the MPM rule. This is because these input parameters are represented by significant PC basis functions; namely, the corresponding marginal inclusion probabilities in Figure 1 and Figure 2 are greater than . The order of the indices in Figure 1 and Figure 2 is the same as that mentioned above in the surrogate model building step section; namely, first, the main effects are followed by their interactions in the order of Fmax, Cs, Fover, Fdrai, Qdm, Sy, B, Psis, Ks, . The first 11 indexes correspond to the main effects, indices 12–66 correspond to the second-order interactions, indices 67–286 correspond to third-order interactions, and the rest of the indices correspond to fourth-order interactions. From the hydrology perspective, this is reasonable, because these parameters are major factors controlling the drainage and runoff generation, which, in turn, impact heat fluxes. The results are also consistent with the previous work in (Hou et al. [6]).
In Figure 3 and Figure 4, we use box-plots to represent the posterior density estimates of the PC coefficients generated by the Gibbs sampler. In these figures, we consider only the coefficients corresponding to bases characterized as significant according to the MPM rule; namely, those with . We observe that significant coefficients do not include zero in the range where the main posterior mass is concentrated. This shows that the method is consistent. Moreover, we observe that the significant PC coefficients that correspond to the period May-August have, in general, larger absolute values. This indicates that the variance of the output LH during those months is larger compared to that of the rest months, which is as expected. Finally, we can possibly infer that different input parameters may have a different effect of LH at different times, since we can observe different significant coefficients, or bases, in different months.
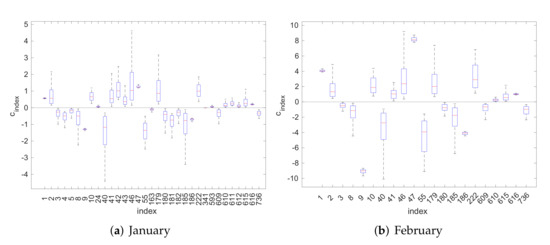
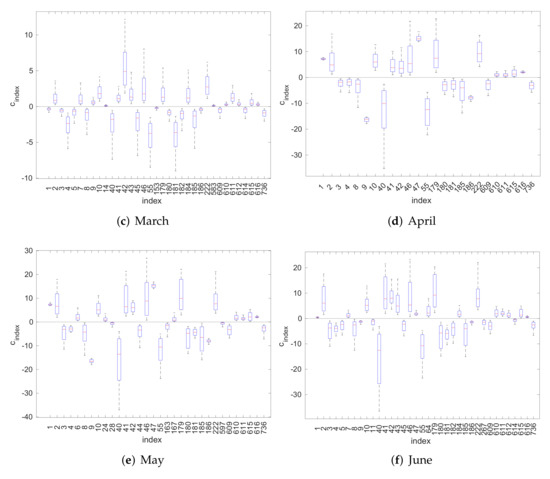
Figure 3.
Box-plots of the posterior PC coefficients: January–June.
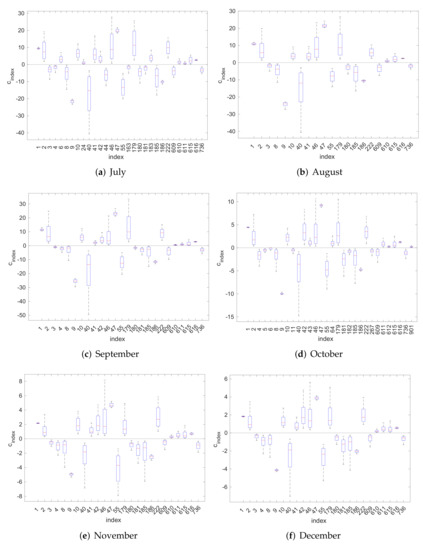
Figure 4.
Box-plots of significant posterior PC coefficients: July–December.
The gPC expansion of LH as a function of the input parameters can be evaluated according to the estimator in (10), which is the ergodic average of the Gibbs sample.
4.1. Inversion Step
We calibrate the 10 CLM parameters against the measurement of the parameter LH in Table 1, as in Section 3.1. We considered beta priors on the CLM parameters whose hyper-parameters are specified by using the method of moments and based on the prior information in Hou et al. [6].
Calibration was performed by running the MCMC sampler (Algorithm 1) and evaluating the posterior distributions according to the procedure in Section 3.1. Even though, in the previous step, we detected that the input model parameters Fmax, Cs, Fdrai, Qdm, and B are the significant ones, we also considered them for calibration to obtain information about them as well. In order to make the MCMC sampler tractable, we replaced the forward model CLM4 , in Algorithm 1, with the estimated gPC expansion that serves as a surrogate model. We ran the MCMC sampler (Algorithm 1) for iterations and discarded the first as burn-in.
In Figure 5 and Figure 6, we present the estimated posterior densities of the input parameters of CLM4, as generated by the MCMC sampler. The blue bars correspond to the histogram estimate, whereas the red line corresponds to the kernel density estimate. These posterior distributions allow us to find a reasonable range of input values that correspond to the given value of output . The associated box-plots of the marginal posteriors of the model parameters at each individual figure indicate the range of the main posterior density. We can see that we have successfully managed to shorten the ranges of the possible values for most of the input model parameters. For instance, we observe that the main density on the marginal posterior distribution of the density of Qdm is around the area in scale.
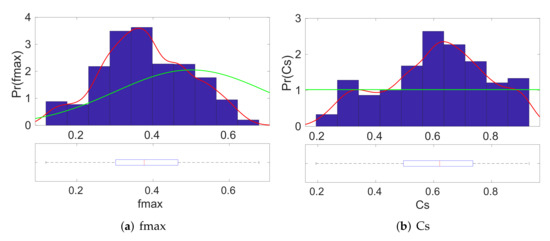
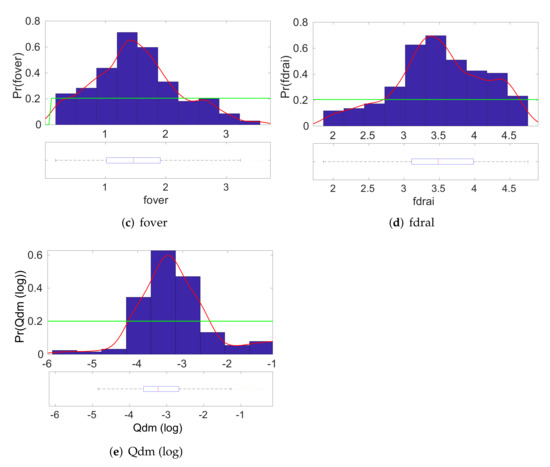
Figure 5.
A posteriori distributions of the input parameters of CLM4 for a given output . The red line indicates the posterior density, whereas the green line indicates the prior density of the parameter. (BMA evaluation).
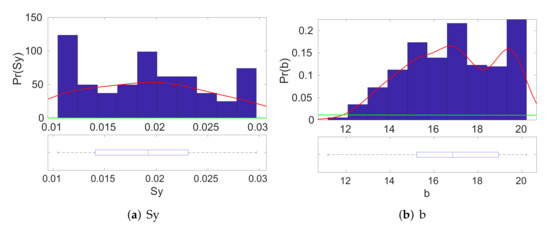
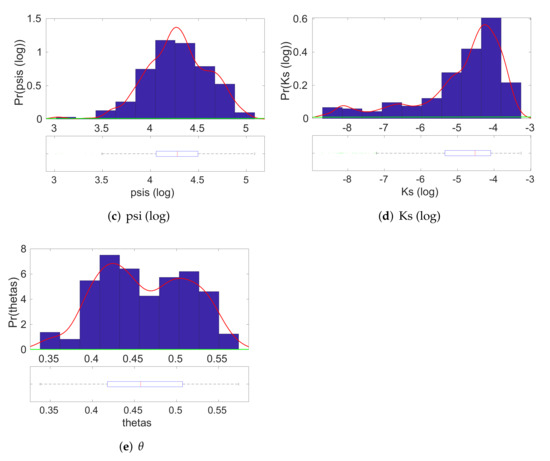
Figure 6.
A posteriori distributions of the input parameters of CLM4 for a given output . The red line indicates the posterior density, whereas the green line indicates the prior density of the parameter. (BMA evaluation).
4.2. Model Validation
We validated the effectiveness of the Bayesian inversion procedure. We evaluated the predictive distribution of the output parameter LH by using the derived gPC surrogate model and the MCMC sample of the input parameters generated by Algorithm 1. In Figure 7 and Figure 8, we present the resultant predictive distributions of the output LH for the 12 months. The blue bars are the histogram estimate, the red line is the kernel density estimate of the predictive distribution, and the green arrow represents the observed output value of LH. The plots show that, for each month, the observed output value for the LH lies below the modes of each of the marginal predictive distributions. This implies that the proposed methodology is valid and that the surrogate model derived from the method is able to produce accurate predictions.
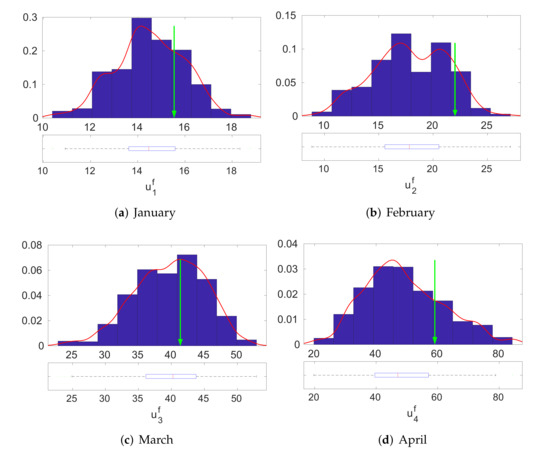
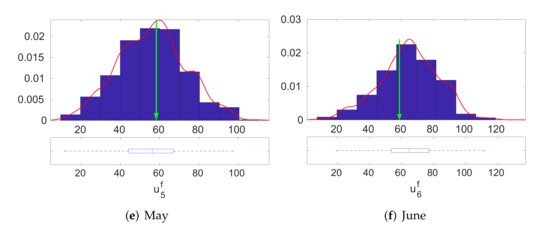
Figure 7.
Distributions of the output LH associated to input parameters of CLM4 drawn by the a posteriori distributions: January–June.
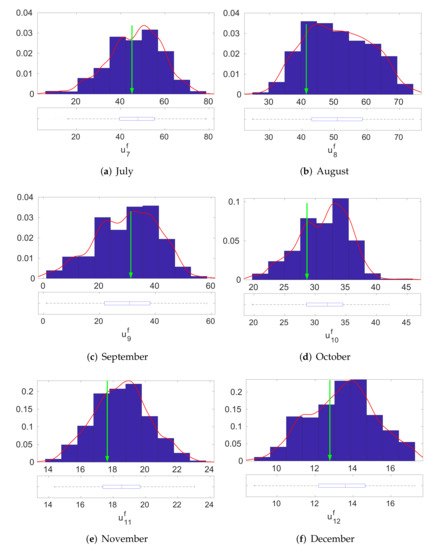
Figure 8.
Distributions of the output LH associated to input parameters of CLM4 drawn by the a posteriori distributions: July–December.
5. Conclusions
We focused on evaluating the uncertainties associated with the hydrologic parameters in CLM4 in the Bayesian framework. We presented a Bayesian methodology for the uncertainty quantification (UQ) framework that couples a generalized polynomial chaos model with the Bayesian variable selection methods. We presented a fully Bayesian methodology that involves two steps: building a surrogate step, which is the construction of a surrogate model to express the input–output mapping; and the inverse modeling step, which is the evaluation of the posterior distribution of the input parameters for a given value of the output LH.
For the construction of the surrogate model, we propose a Bayesian procedure, based on variable selection methods, that uses gPC expansions and accounts for bases selection uncertainty. The advantage of this approach is that it can quantify the significance of the gPC terms, and, hence, the importance of the input parameters, in a probabilistic manner. The input posterior distributions were evaluated according to Bayesian inverse modeling. Our numerical experiments suggested that the method presented is suitable for performing the inverse modeling of hydrologic parameters in CLM4, and able to effectively describe the uncertainty related to these parameters.
Our future work involves the comparison of the proposed method against other methods based on neural networks, and generalized linear models, on which, we are currently working.
Author Contributions
G.K. and G.L. derived the models and performed the computations. Z.H. and M.H. worked on the interpretation of the results from the analysis of the application. All authors have read and agreed to the published version of the manuscript.
Funding
The National Science Foundation (DMS-1555072, DMS-1736364, DMS-2053746, and DMS-2134209), and Brookhaven National Laboratory Subcontract 382247, and U.S. Department of Energy (DOE) Office of Science Advanced Scientific Computing Research program DE-SC0021142.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Supplementary data related to this article can be found at https://github.com/georgios-stats/Inverse-modeling-of-hydrologic-parameters-in-CLM4-via-generalized-polynomial-chaos-in-the-Bayesian-f, accessed on 20 March 2022.
Acknowledgments
Guang Lin would like to thank the support from the National Science Foundation (DMS-1555072, DMS-1736364, DMS-2053746, and DMS-2134209), and Brookhaven National Laboratory Subcontract 382247, and U.S. Department of Energy (DOE) Office of Science Advanced Scientific Computing Research program DE-SC0021142.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Pitman, A. The evolution of, and revolution in, land surface schemes designed for climate models. Int. J. Climatol. J. R. Meteorol. Soc. 2003, 23, 479–510. [Google Scholar] [CrossRef]
- Bastidas, L.; Gupta, H.V.; Sorooshian, S.; Shuttleworth, W.J.; Yang, Z.L. Sensitivity analysis of a land surface scheme using multicriteria methods. J. Geophys. Res. Atmos. 1999, 104, 19481–19490. [Google Scholar] [CrossRef] [Green Version]
- Henderson-Sellers, A.; Pitman, A.; Love, P.; Irannejad, P.; Chen, T. The project for intercomparison of land surface parameterization schemes (PILPS): Phases 2 and 3. Bull. Am. Meteorol. Soc. 1995, 76, 489–504. [Google Scholar] [CrossRef] [Green Version]
- Henderson-Sellers, A.; Chen, T.; Nakken, M. Predicting Global Change at the Land-Surface: The Project for Intercomparison of Land-Surface pArameterization Schemes (PILPS) (Phase 4); Technical Report; American Meteorological Society: Boston, MA, USA, 1996. [Google Scholar]
- Rosero, E.; Yang, Z.L.; Wagener, T.; Gulden, L.E.; Yatheendradas, S.; Niu, G.Y. Quantifying parameter sensitivity, interaction, and transferability in hydrologically enhanced versions of the Noah land surface model over transition zones during the warm season. J. Geophys. Res. Atmos. 2010, 115, D03106. [Google Scholar] [CrossRef] [Green Version]
- Hou, Z.; Huang, M.; Leung, L.R.; Lin, G.; Ricciuto, D.M. Sensitivity of surface flux simulations to hydrologic parameters based on an uncertainty quantification framework applied to the Community Land Model. J. Geophys. Res. Atmos. 2012, 117, D15. [Google Scholar] [CrossRef]
- Huang, M.; Hou, Z.; Leung, L.R.; Ke, Y.; Liu, Y.; Fang, Z.; Sun, Y. Uncertainty analysis of runoff simulations and parameter identifiability in the Community Land Model: Evidence from MOPEX basins. J. Hydrometeorol. 2013, 14, 1754–1772. [Google Scholar] [CrossRef]
- Collins, W.D.; Rasch, P.J.; Boville, B.A.; Hack, J.J.; McCaa, J.R.; Williamson, D.L.; Briegleb, B.P.; Bitz, C.M.; Lin, S.J.; Zhang, M. The formulation and atmospheric simulation of the Community Atmosphere Model version 3 (CAM3). J. Clim. 2006, 19, 2144–2161. [Google Scholar] [CrossRef] [Green Version]
- Gent, P.R.; Yeager, S.G.; Neale, R.B.; Levis, S.; Bailey, D.A. Improvements in a half degree atmosphere/land version of the CCSM. Clim. Dyn. 2010, 34, 819–833. [Google Scholar] [CrossRef]
- Lawrence, D.M.; Oleson, K.W.; Flanner, M.G.; Thornton, P.E.; Swenson, S.C.; Lawrence, P.J.; Zeng, X.; Yang, Z.L.; Levis, S.; Sakaguchi, K.; et al. Parameterization improvements and functional and structural advances in version 4 of the Community Land Model. J. Adv. Model. Earth Syst. 2011, 3. [Google Scholar] [CrossRef]
- Ray, J.; Hou, Z.; Huang, M.; Sargsyan, K.; Swiler, L. Bayesian calibration of the Community Land Model using surrogates. SIAM/ASA J. Uncertain. Quantif. 2015, 3, 199–233. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Ray, J.; Hou, Z.; Ren, H.; Liu, Y.; Swiler, L. On the applicability of surrogate-based Markov chain Monte Carlo-Bayesian inversion to the Community Land Model: Case studies at flux tower sites. J. Geophys. Res. Atmos. 2016, 121, 7548–7563. [Google Scholar] [CrossRef]
- Gong, W.; Duan, Q.; Li, J.; Wang, C.; Di, Z.; Dai, Y.; Ye, A.; Miao, C. Multi-objective parameter optimization of common land model using adaptive surrogate modeling. Hydrol. Earth Syst. Sci. 2015, 19, 2409–2425. [Google Scholar] [CrossRef] [Green Version]
- Sargsyan, K.; Safta, C.; Najm, H.N.; Debusschere, B.J.; Ricciuto, D.; Thornton, P. Dimensionality reduction for complex models via Bayesian compressive sensing. Int. J. Uncertain. Quantif. 2014, 4, 63–93. [Google Scholar] [CrossRef]
- Karagiannis, G.; Lin, G. Selection of polynomial chaos bases via Bayesian model uncertainty methods with applications to sparse approximation of PDEs with stochastic inputs. J. Comput. Phys. 2014, 259, 114–134. [Google Scholar] [CrossRef] [Green Version]
- Fischer, M.L.; Billesbach, D.P.; Berry, J.A.; Riley, W.J.; Torn, M.S. Spatiotemporal variations in growing season exchanges of CO2, H2O, and sensible heat in agricultural fields of the Southern Great Plains. Earth Interact. 2007, 11, 1–21. [Google Scholar] [CrossRef]
- Torn, M. AmeriFlux US-ARM ARM Southern Great Plains Site-Lamont; Technical Report, AmeriFlux; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2016. [Google Scholar]
- Niu, G.Y.; Yang, Z.L.; Dickinson, R.E.; Gulden, L.E. A simple TOPMODEL-based runoff parameterization (SIMTOP) for use in global climate models. J. Geophys. Res. Atmos. 2005, 110, D21. [Google Scholar] [CrossRef] [Green Version]
- Niu, G.Y.; Yang, Z.L.; Dickinson, R.E.; Gulden, L.E.; Su, H. Development of a simple groundwater model for use in climate models and evaluation with Gravity Recovery and Climate Experiment data. J. Geophys. Res. Atmos. 2007, 112, D7. [Google Scholar] [CrossRef]
- Oleson, K.; Niu, G.Y.; Yang, Z.L.; Lawrence, D.; Thornton, P.; Lawrence, P.; Stöckli, R.; Dickinson, R.; Bonan, G.; Levis, S.; et al. Improvements to the Community Land Model and their impact on the hydrological cycle. J. Geophys. Res. Biogeosci. 2008, 113, G1. [Google Scholar] [CrossRef]
- Oleson, K.W.; Lawrence, D.M.; Gordon, B.; Flanner, M.G.; Kluzek, E.; Peter, J.; Levis, S.; Swenson, S.C.; Thornton, E.; Feddema, J.; et al. Technical Description of Version 4.0 of the Community Land Model (CLM). 2010. Available online: https://www.researchgate.net/publication/277114326_Technical_Description_of_version_40_of_the_Community_Land_Model_CLM (accessed on 20 March 2022).
- Caflisch, R.E. Monte carlo and quasi-monte carlo methods. Acta Numer. 1998, 7, 1–49. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Sloan, I.H. Low discrepancy sequences in high dimensions: How well are their projections distributed? J. Comput. Appl. Math. 2008, 213, 366–386. [Google Scholar] [CrossRef] [Green Version]
- Marzouk, Y.; Xiu, D. A Stochastic Collocation Approach to Bayesian Inference in Inverse Problems. Commun. Comput. Phys. 2009, 6, 826–847. [Google Scholar] [CrossRef] [Green Version]
- Berger, J.O. Statistical Decision Theory and Bayesian Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Robert, C.P.; Casella, G. Monte Carlo Statistical Methods, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]
- Xiu, D. Numerical Methods for Stochastic Computations: A Spectral Method Approach; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Xiu, D.; Karniadakis, G.E. The Wiener–Askey Polynomial Chaos for Stochastic Differential Equations. SIAM J. Sci. Comput. 2002, 24, 619–644. [Google Scholar] [CrossRef]
- Blatman, G.; Sudret, B. Adaptive sparse polynomial chaos expansion based on least angle regression. J. Comput. Phys. 2011, 230, 2345–2367. [Google Scholar] [CrossRef]
- Doostan, A.; Owhadi, H. A non-adapted sparse approximation of PDEs with stochastic inputs. J. Comput. Phys. 2011, 230, 3015–3034. [Google Scholar] [CrossRef] [Green Version]
- Hans, C. Model uncertainty and variable selection in Bayesian LASSO regression. Stat. Comput. 2010, 20, 221–229. [Google Scholar] [CrossRef]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. 1984, 721–741. [Google Scholar] [CrossRef]
- Hoeting, J.A.; Madigan, D.; Raftery, A.E.; Volinsky, C.T. Bayesian model averaging: A tutorial. Stat. Sci. 1999, 14, 382–401. [Google Scholar]
- Barbieri, M.M.; Berger, J.O. Optimal Predictive Model Selection. Ann. Stat. 2004, 32, 870–897. [Google Scholar] [CrossRef]
- Sun, Y.; Hou, Z.; Huang, M.; Tian, F.; Ruby Leung, L. Inverse modeling of hydrologic parameters using surface flux and runoff observations in the Community Land Model. Hydrol. Earth Syst. Sci. 2013, 17, 4995–5011. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).