Abstract
In this study, we theoretically investigate the structural, electronic and magnetic properties of the Cu2OX2 (X = Cl, Br, I) compounds. Previous studies reported potential spin-driven ferroelectricity in Cu2OCl2, originating from a non-collinear magnetic phase existing below ∼70 K. However, the nature of this low-temperature magnetic phase is still under debate. Here, we focus on the calculation of J exchange couplings and enhance knowledge in the field by (i) characterizing the low-temperature magnetic order for Cu2OCl2 and (ii) evaluating the impact of the chemical pressure on the magnetic interactions, which leads us to consider the two new phases Cu2OBr2 and Cu2OI2. Our ab initio simulations notably demonstrate the coexistence of strong antiferromagnetic and ferromagnetic interactions, leading to spin frustration. The Néel temperatures were estimated on the basis of a quasi-1D AFM model using the J couplings. It nicely reproduces the value for Cu2OCl2 and allows us to predict an increase of under chemical pressure, with = 120 K for the dynamically stable phase Cu2OBr2. This investigation suggests that chemical pressure is an effective key factor to open the door of room-temperature multiferroicity.
1. Introduction
The design of multiferroics (MF) in which magnetic and ferroelectric orders are coupled is one of the hottest current topics in materials science [1]. These compounds appear as a fantastic playground to deeply investigate the origin and the interactions of the related ferroic properties and to design materials with improved or novel properties. Such multi-functional materials are also extremely appealing for the development of spintronic devices. For example, the control of a magnetic order by an electric field is targeted for several applications ranging from magnetic sensors to memory technologies. At the present time, very few MF compounds exhibit such properties at room temperature (RT), which dramatically limits potential industrial interests. In that context, we embarked on the quest for discovering high-temperature range MF materials, which ideally also show strong electric polarization.
Among the prospective strategies to tune MF stability domain(s) is the application of an hydrostatic (physical) pressure [2]. For instance, in 2013 [3], we predicted theoretically that under high pressure values of about 20 GPa, CuO would become MF at RT. This prediction has been confirmed through dielectric constants measurements up to 7 GPa in 2021 [4] and more recently by neutron diffraction up to 18.5 GPa [5]. An alternative route is to apply a chemical pressure through chemical substitutions, leading to create internal constraints. For instance, the two multiferroic compounds CuCl2 [6] and CuBr2 [7] are characterized by Néel temperatures of 23.9 K and 73.5 K, respectively. Such an increase of is the direct consequence of the chemical substitution of Cl by Br.
Herein, we propose to study the mixed anion system Cu2OX2 (with X = Cl, Br, I). It derives from the CuO compound in which half of the ions have been replaced by two ions. Magnetic measurements performed on Cu2OCl2 evidenced an antiferromagnetic order with a Néel temperature of ∼70 K [8,9], which was firstly attributed to an all-in-all-out arrangement of magnetic moments carried by Cu2+ centers forming a pyrochlore-like lattice [10]. Then, powder neutron diffraction analyses [11] revealed an incommensurate magnetic order, with a propagation vector = and concomitant with a ferroelectric phase. It has also been evidenced that the incommensurate magnetic structure induces a spin–phonon coupling similar to the ones observed in perovskite compounds [12]. In 2019, two contradictory neutron-scattering investigations were published. In the first investigation [13], the spin-driven nature of the multiferroicity of Cu2OCl2 was demonstrated, leading to the proposition of a cycloidal non-collinear magnetic order with competing magnetic exchange couplings and driven by an inverse Dzyaloshinskii–Moriya mechanism. In the second article [14], the authors claimed the simultaneous existence, at low temperature, of a collinear antiferromagnetic order and an antiferroelectric phase resulting from a Cl→O charge transfer.
In terms of J magnetic exchange values, only one experimental estimation from magnetic susceptibilty [8] has been proposed, one conference’s abstract gave contradicting values deduced from Density Functional Theory (DFT) calculations [15] without providing any details, and one last article [13] focused on the sign of J couplings by studying Wannier functions with DFT. The present study aims to clarify the understanding of the magnetic interactions in Cu2OCl2 by doing DFT calculations at ambient pressure but also under chemical pressure, by predicting the magnetic properties of Cu2OBr2 and Cu2OI2, for the very first time.
2. Materials and Methods
Geometry optimizations on the isostructural Cu2OX2 (X = Cl, Br, I) systems were performed within the Density Functional Theory (DFT) framework using the PAW method, as implemented in the VASP code [16,17,18]. Valence electrons were treated using the following electronic configurations for the different species: for Cu, for Cl, for Br, for I and for O. The PBE approach was considered for the exchange–correlation functional [19]. To improve the description of the electronic properties for Cu-3d orbitals, a Hubbard effective correction following Dudarev’s scheme [20] was used. We previously showed that = 6.5 eV enables us to recover the experimental volume variation under hydrostatic pressure for the CuO compound [3]. Here, an identical value was chosen. Long-distance van der Waals interactions were taken into account by introducing the DFT-D3 correction proposed by Grimme et al. [21]. Spin-polarized simulations were done with a 5 × 4 × 4 -centered k-mesh and a cutoff energy of 550 eV. The dynamical stability of all optimized structures was checked by computing the phonon modes with the finite-differences method for symmetrically non-equivalent displacements on a 2 × 1 × 1 supercell and a 2 × 4 × 4 -centered k-mesh.
For each compound, the exchange couplings were estimated based on the optimized structures with the Wien2K code, using DFT within the FP-LAPW approach [22]. The PBE0 on-site functional was chosen for the treatment of the exchange correlation part in the lines of our previous works [3,4]. The parameter was set to 7. Muffin-Tin radii were fixed to 1.94, 2.10, 2.20 and 1.71 for Cu, Cl, Br, I and O species, respectively. The first Brillouin zone was sampled with 52–58 irreducible k-points. The magnetic interactions were extracted from a least-squares fitting procedure applied between the DFT energy related to a given collinear magnetic state and the energy of an Ising Hamiltonian used to describe the magnetic structure:
where and are the spins carried by the and centers, respectively. The parameter represents the magnetic exchange interactions between and . Hereafter, indicates an antiferromagnetic (AFM) coupling, and indicates a ferromagnetic (FM) coupling.
3. Results and Discussion
3.1. Crystal Structure of Cu2OCl2
The melanothallite Cu2OCl2 crystallizes in the orthorhombic space group with a = 7.4477 Å, b = 9.5989 Å, c = 9.6888 Å, V = 692.65 , and Z = 8 [11]. The structure shown in Figure 1a is characterized by one symmetrically non-equivalent Cu2+ site located in a strongly distorted octahedral environment due to a Jahn–Teller effect. It can be viewed as a CuO2Cl2 square-planar environment (also called plaquette), in which the bond lengths are = 1.943 Å and = 2.283 Å. Two longer bonds are formed with chlorine ions in apical positions with = 3.123 Å. These CuO2Cl2 plaquettes are sharing edges to form ribbons which are inter-connected together by the oxygen ions in a three-dimensional network, which has many common features with the CuO atomic structure. For instance, both Cu2OCl2 and CuO [23,24,25] exhibit unusual thermal variations of lattice parameters due to the so-called hinge mechanism [26]. The ribbons are parallel to the and directions. As shown in Figure 1b, another vision of the structure is a pyrochlore-like lattice where the tridimensional network is based on O-centered OCu4 tetrahedra which are sharing corners. Here, the chlorine species are pointing toward the center of cavities.
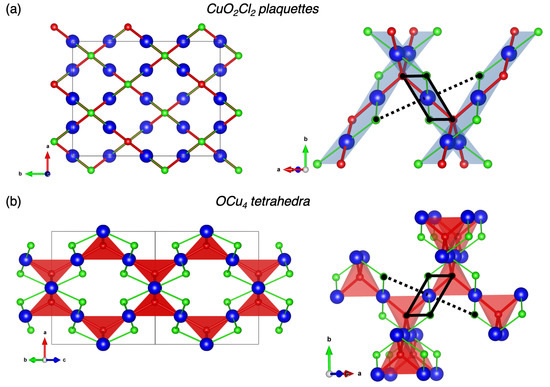
Figure 1.
Crystallographic structure of Cu2OCl2 described by (a) Cu-centered CuO2Cl2 square planar environments and (b) O-centered OCu4 tetrahedral environments. The blue, red and green spheres represent copper, oxygen and chlorine ions, respectively. Square planar and tetrahedral environments are evidenced in transparent blue and red, respectively. The CuO2Cl4 distorted octahedral environment is highlighted with black lines.
3.2. Geometry Optimization
Geometry relaxations have been performed at ambient pressure in order to validate our approach by comparing with the experimental data of Cu2OCl2 and to predict the atomic structure of Cu2OBr2 and Cu2OI2. The experimental Cu2OCl2 structure reported in Ref. [11] was used as an initial guess for all compounds. The main structural parameters of the optimized geometries are summarized in Table 1, including the experimental data of Cu2OCl2.

Table 1.
Optimized structural parameters of the Cu2OX2 compounds (X = Cl, Br, I) deduced from DFT+U calculations ( = 6.5 eV) and experimental data of Cu2OCl2 Ref. [11]. For Cu2OCl2, the deviation (in percentage) with respect to the experimental data is given in parentheses.
Regarding Cu2OCl2, an excellent agreement is found between the experimental and the theoretical structures. The optimized lattice parameters deviate from the experimental ones by less than 0.5%. Considering the first neighbor’s shell, the Cu-O, Cu-Cl and Cu-Cl bonds of the optimized geometry are 1.95, 2.30 and 3.13 Å, respectively (deviation smaller than 0.5%). Inside a ribbon, the Cu-O-Cu and Cu-Cl-Cu bond angles are computed at 102.8 and 85.25 (less than 0.2% deviation), respectively. Finally, the hinge angle that corresponds to the Cu-O-Cu angle between two ribbons is 63.1 (0.1% deviation).
Focusing now on the new Cu2OBr2 compound, one may notice that the lattice parameters are larger than the optimized ones of Cu2OCl2, as expected from the larger atomic size of bromine. It leads to a = 7.720 Å (3.4% larger compared to Cu2OCl2), b = 9.996 Å (3.6% larger), c = 9.766 Å (0.3% larger), and V = 753.69 (7.5% larger). This steric effect mainly affects a and b parameters, which are defining the directions of the ribbons. The optimized Cu-O, Cu-Br and Cu-Br bond lengths are 2.00, 2.41 and 3.21 Å, respectively. The angles within a ribbon, i.e., Cu-O-Cu and Cu-Br-Cu, are about 2 larger and 1.3 smaller than in Cu2OCl2, respectively. The hinge angle appears slightly smaller than in Cu2OCl2 at 62.42.
For the second new compound Cu2OI2, the lattice parameters are still increasing compared to the two former cases, following the chemical sense directed by the atomic radii (). In detail, we found a = 8.168 Å (9.4% larger compared to Cu2OCl2), b = 10.558 Å (9.5% larger), c = 10.123 Å (4.0% larger) and V = 872.93 (24.5% larger). Once more, the significant variation of volume results from more important changes reported for a and b lattice parameters. Regarding the distorted CuO2I4 environment, the optimized Cu-O, Cu-I and Cu-I bond lengths are respectively measured at 2.09, 2.54 and 3.39 Å. Focusing on the ribbons, the Cu-O-Cu angle equals 105.7 (2.3 larger than in Cu2OCl2), while the Cu-I-Cu angle is reduced to 82.0 (1.2% smaller).
No imaginary phonon frequencies were retrieved for both Cu2OCl2 and Cu2OBr2 systems. First, this result confirms that the present modeling reproduces properly both the atomic parameters and the dynamical stability of Cu2OCl2. Experimentally, the crystals are grown using the chemical vapor transport techniques with a stoichiometric mixture of CuO and CuCl2 compounds [11]. Second, Cu2OBr2 is predicted to be dynamically stable. For Cu2OI2, one imaginary phonon frequency was calculated at ∼20i , suggesting that such a phase does not exist. However, Cu2OI2 was kept in our investigation as a virtual compound allowing us to probe the chemical pressure effect.
3.3. Electronic Properties
Based on the optimized structures, the electronic properties were investigated using the Wien2K code. The projected density of states (pDOS) of the three Cu2OX2 systems are represented in Figure 2. The present PBE0 calculations lead to band gap values of 2.18 eV, 1.85 eV and 0.95 eV for X = Cl, Br and I, respectively, and rather similar pDOS. The valence band (VB) is based on the O-2p, Cl-3p (or Br-4p or I-5p) and Cu-3d states (from −7 to 0 eV with respect to ). While the top of the VB is mainly composed of O-2p states in Cu2OCl2, it is mainly based on Br-4p and I-5p states in Cu2OBr2 and Cu2OI2, respectively. Such a point is emphasized in Figure 3 by the electronic densities calculated in the energy range from −0.5 to 0 eV (with respect to ). The magnetically active orbital, i.e., the one carrying the magnetic moment, is the Cu-3, as expected from the electronic configuration and the square planar environment. The calculated magnetic moment of copper is 0.6–0.7 in Cu2OX2, which is in good agreement with the available experimental data for Cu2OCl2. Indeed, the ordered magnetic moment was found to be 0.64(5) and 0.66(2) from powder and single-crystal neutron refinements, respectively [13].
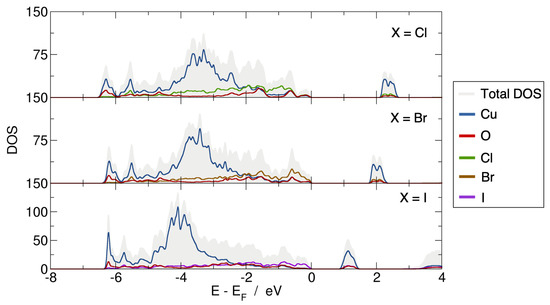
Figure 2.
Total and projected densities of states for the Cu2OX2 compounds (X = Cl, Br, I) deduced from PBE0 on-site calculations on the ground-state AFM collinear order. Energies for pDOS are given with respect to .
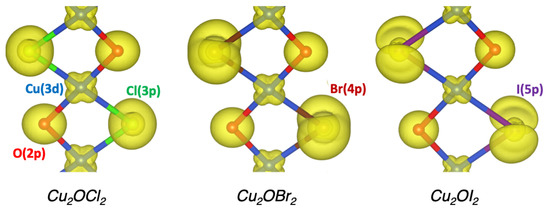
Figure 3.
Electronic density corresponding to the top of the valence band (from −0.5 to 0 eV with respect to ) for the Cu2OX2 compounds (X = Cl, Br, I) deduced from PBE0 on-site calculations on the ground state AFM collinear order. Isovalue is set to 0.1 electron/. Blue, red, green, brown and violet spheres indicate Cu, O, Cl, Br and I atoms, respectively.
3.4. Magnetic Exchange Interactions
Magnetic susceptibiltity measurements on Cu2OCl2 provided a Néel temperature of ∼70 K followed by a broad maximum at ∼140 K [8,9]. Many investigations were carried out to determine the nature of the magnetic order at lower temperatures, leading to several propositions such as an all-in-all-out model [10], an incommensurate spin spiral phase [11], an incommensurate spin cycloidal phase [13] and a collinear antiferromagnetic (AFM) phase [14]. However, only one of these experimental investigations proposed magnetic exchange coupling (J) values extracted from magnetic susceptibility fits [8], which are in disagreement with the reported J values estimated from DFT calculations [15]. However, these latter values were found in a conference abstract and no related publication is available, to our knowledge.
Based on the optimized geometries, we have thus calculated the J exchange values using PBE0 on-site functional as we did for CuO [3,4]. Examining the atomic structure leads to defining four magnetic interactions depicted in Figure 4 for both ribbons- and pyrochlore-like lattices. The related bond lengths and Cu-O-Cu angles are specified in Table 2 for Cu2OCl2, Cu2OBr2 and Cu2OI2. More specifically, considering the ribbons-like structure, we targeted two intra-ribbon ( and ) and two inter-ribbon ( and ) couplings. It should be noticed that among these four interactions, only is based on a super-superexchange (SSE) path, i.e., the magnetic moments are mediated through an orbital overlap implying two ligand atoms (namely Cu-L-L-Cu, with L = O, Cl, Br or I), the others being based on a superexchange (SE) path implying only one ligand atom (namely Cu-L-Cu, with L = O, Cl, Br or I).
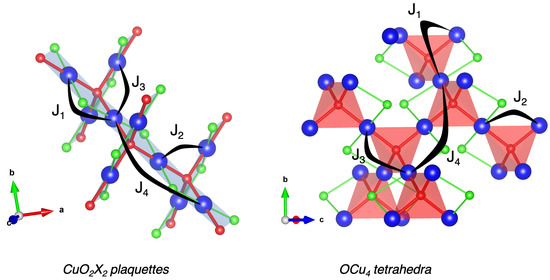
Figure 4.
Representation of J exchange couplings between copper sites in both CuO2X2- and OCu4-based frameworks. Cu, O and X atoms are depicted by blue, red and green spheres, respectively. CuO2X2 plaquettes and OCu4 tetrahedra are shown in transparent blue and red, respectively.

Table 2.
Geometrical parameters related to the four magnetic couplings for the Cu2OX2 compounds (X = Cl, Br, I) deduced from DFT+U relaxation ( = 6.5 eV). The experimental data of Cu2OCl2 taken from Ref. [11] are given in parentheses.
The J couplings were estimated using the mapping analysis procedure. The strategy consists of (1) determining the DFT energies of a set of magnetic states, (2) defining the related energy expressions in terms of J parameters using an Ising Hamiltonian, and (3) refining the J parameters on top of the DFT results using a least squares method. One may underline that the accuracy of such an approach strongly depends on the size and the quality of the set of magnetic states [27]. In our case, eight collinear magnetic structures were selected to obtain four J values. The results are summarized in Table 3.

Table 3.
Magnetic exchange interactions (in meV) calculated at the PBE0 on-site level for the Cu2OX2 compounds (X = Cl, Br, I). The available experimental and theoretical data are given for comparison. indicates an AFM coupling, and indicates an FM coupling.
Before discussing our results, let us on comment the experimental values extracted by Okabe et al. [8] considering the ribbons-like picture. They considered two effective J parameters which were found to be both AFM and very close to each other, i.e., = 9.7 meV and = 9.3 meV, thus leading to strong magnetic frustrations. These mean field values can be compared to our J parameters considering that and . It leads to DFT effective intra- and inter-ribbon couplings, which are respectively FM and AFM, i.e., = −5.3 meV and = 16.8 meV, in disagreement with Okabe et al. [8]. In contrast, in Ref. [15], three DFT J values have been proposed, i.e., two intra-ribbon ( = −15.5 meV and = 8.6 meV) and one inter-ribbon ( = 19.0 meV), which are in good agreement with our values, i.e., = −14.0 meV and = 8.7 meV for the intra-ribbon interactions and = −2.2 meV and = 19.1 meV for the inter-ribbon ones.
In other words, the present calculations evidenced that the ribbons are mainly FM ordered due to the first-neighbor (SE) interaction , and the spins are frustrated due to the AFM second-neighbor (SSE) interaction , which is 1.6 times smaller than in amplitude. Between the ribbons, the interaction is AFM due to ( appears negligible). In the pyrochlore-like lattice, each OCu4 tetrahedron is globally AFM with two up and two down magnetic centers, which further emphasizes the spin frustration character of the magnetic structure. The resulting most stable collinear magnetic order is depicted in Figure 5.
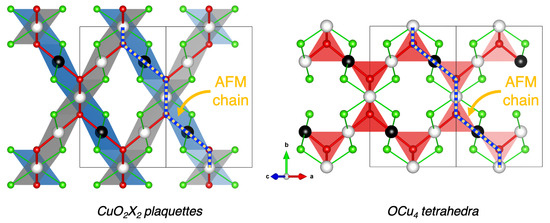
Figure 5.
Schematic representation of the ground-state AFM collinear magnetic structure within the (left) ribbons- and (right) pyrochlore-like lattices. Black and white spheres indicate up and down spins carried by Cu sites, respectively. Red and green spheres represent oxygen and halogen species, respectively. The OCu4 tetrahedral coordinations are represented in transparent red. The CuO2X2 plaquettes are shown in transparent blue and gray for an up or down spin carried by the central Cu, respectively. One AFM spin chain, formed by the coupling and considered within the quasi-1D AFM model, is evidenced by a yellow–blue dotted line.
A similar picture is obtained for Cu2OBr2 and Cu2OI2 compounds. Regarding the intra-ribbon interactions, one may notice that the FM coupling decreases to −13.1 meV and −8.1 meV, respectively, while the AFM coupling is enhanced to 9.2 meV and 15.1 meV, respectively. For the inter-ribbon interactions, the FM coupling becomes AFM at 1.9 meV for Cu2OBr2 and strongly increases up to 24.2 meV for Cu2OI2. stays the strongest (AFM) coupling and is increased to 25.2 meV and 41.0 meV, respectively. The larger values for cannot be explained only based on geometrical arguments. Indeed, the related Cu-O bond length and Cu-O-Cu angle, respectively, increases and decreases, when Cl is substituted by Br or I. It is the signature that the halogen element indirectly participates in this interaction by setting the size and the shape of the magnetic orbital due to the nephelauxetic effect, which increases in the series Cl– < Br– < I–, leading to an expansion of the copper 3d orbitals and thus larger interactions. Figure 6 shows that the spin densities of the three compounds are quite similar, with spin-up densities (in yellow) along the FM coupling for both copper and halogen elements involved in this interaction. For oxygen atoms, which are also involved in the AFM couplings ( and ), two lobes are found with one up- and one down-spin densities in yellow and cyan, respectively. These observations have a direct consequence on the magnetic moments carried by the ligands, which are 0.11, 0.10, 0.08 and 0.00 for Cl, Br, I and O, respectively. Indeed, the magnetic moment of the oxygen is null due to its participation in AFM couplings.
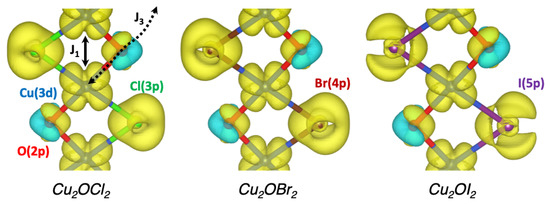
Figure 6.
Spin density for the AFM ground state of Cu2OCl2, Cu2OBr2 and Cu2OI2. The isovalue is set to 0.017 electron/, up and down regions of the spin density are evidenced in transparent yellow and cyan, respectively. Blue, red, green, brown and violet spheres indicate Cu, O, Cl, Br and I atoms, respectively. The FM and AFM couplings are indicated.
To go further, we focused more deeply on the magnetically active orbital, i.e., Cu-3, and its interaction with the surrounding ligands. The spin-polarized pDOS of Cu-3, O-2p and Cl-3p states of one plaquette are given in Figure 7a for Cu2OCl2. It appears that the occupied Cu-3 states are mainly positioned within the energy range from −7 to −5 eV (highlighted by the gray dotted line rectangle). The electronic charge density () and spin density related to this energy window are shown in Figure 7b,c, respectively. First of all, from the analysis of both pDOS and , it appears that the Cu-3 orbital interaction is larger with O-2p than Cl-3p states. It confirms that the magnetic moment of the magnetically active orbital is mainly mediated by oxygen atoms and thus justifies that the largest coupling is along a Cu-O-Cu superexchange path. In addition, the up- and down-pDOS of O-2p states are perfectly symmetric, leading to a net magnetic moment of zero. Similarly, the spin-density around oxygen is constituted of two equivalent lobes with opposite spins (as previously discussed). Looking in more detail, Figure 7c evidenced the pivotal role of oxygen that connects two ribbons (with opposite spins), which are nearly perpendicular. To summarize the results of the present analysis, the magnetically active orbital results from an overlap of Cu-3 with O-2p and to a less extent with Cl-3p states in Cu2OCl2. One may notice that in this energy range, the pDOS of the magnetically active orbital is constituted by two peaks: (1) the lower in energy originating from the Cu-O interaction, while (2) the higher in energy is associated to the Cu-Cl interaction. A similar picture can be retrieved for Cu2OBr2 and Cu2OI2, except that the first peak (Cu-O interaction) increases and the second peak (Cu-X interaction) decreases (see Figure 2). This observation explains the enhancement of from Cu2OCl2 to Cu2OBr2 and to Cu2OI2.
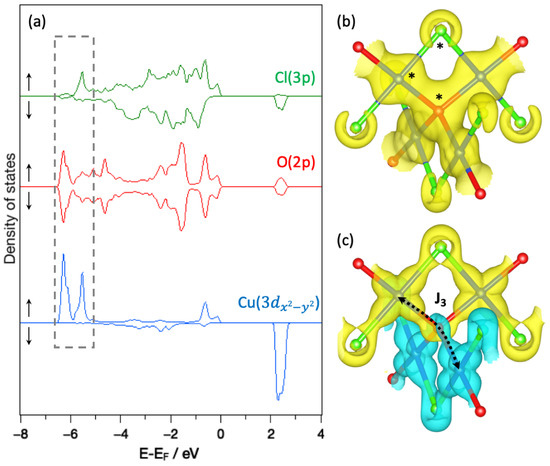
Figure 7.
(a) Spin-polarized projected density of states (pDOS) of one plaquette in Cu2OCl2. The energy window of Cu-3 occupied states is evidenced by a gray dotted rectangle on the pDOS. The (b) electronic charge density and (c) the spin density calculated in this energy range are also displayed. The atoms considered for the pDOS are shown by black stars on the electronic charge density. Up and down spin channels of the pDOS are evidenced by ↑ and ↓, respectively. Isovalues are set to 0.1 and 0.017 electron/ for electronic charge density and the spin density, respectively. Up and down regions of the spin density are highlighted in transparent yellow and cyan, respectively. Blue, red and green spheres indicate Cu, O and Cl atoms, respectively.
Interestingly, these three systems can be compared to their parent compound CuO, for which the atomic and magnetic structures are described using different descriptors. While the atomic structure can be viewed as based on ribbons of edge-sharing CuO4 plaquettes, the magnetic order is mainly governed by AFM spin chains of corner-sharing CuO4 plaquettes. Here also, it appears that the strongest magnetic coupling, i.e., , is at the origin of AFM spin chains of corner-sharing CuO2X2 plaquettes, highlighted by a yellow–blue dotted line in Figure 5. The presence of such AFM spin chains can be more clearly seen and understood in the OCu4-based vision, where these AFM spin chains propagate along tetrahedra.
As we did previously for CuO [3,4], we can thus estimate based on the random phase approximation model of a quasi-1D AFM Heisenberg cubic lattice [28]:
where = 2.6 and c = 0.233 are numerical parameters, is an effective inter-chain coupling and J is the intra-chain coupling. In the present case, half of the spin chains are 90 rotated, leading to half as many inter-chain couplings. The resulting ground-state expression is , instead of in the CuO model where all chains are oriented in the same direction. Such an expression has to be compared to the collinear ground-state (Figure 5) energy defined as:
Thus, one may define:
Using the aforementioned J values and the original c and parameters, we obtain = 65, 111 and 294 K for Cu2OCl2, Cu2OBr2 and Cu2OI2, respectively (see Figure 8). Experimentally, 70 K for Cu2OCl2. Such a good agreement validates the present magnetic model, which consists of considering AFM spin chains based on interacting through an effective coupling defined as . It should be noticed that if we use the refined value for CuO c = 0.284 [3], we obtain = 77, 131 and 344 K for Cu2OCl2, Cu2OBr2 and Cu2OI2, respectively (see Figure 8). The agreement for Cu2OCl2 is still very good with the experiment, and whatever the c value is, we predict a significant increase of when Cl is replaced by either Br or I in the compound. A similar trend has been reported experimentally for CuCl2 and CuBr2 [6,7], for which = 23.9 and 77 K, respectively.
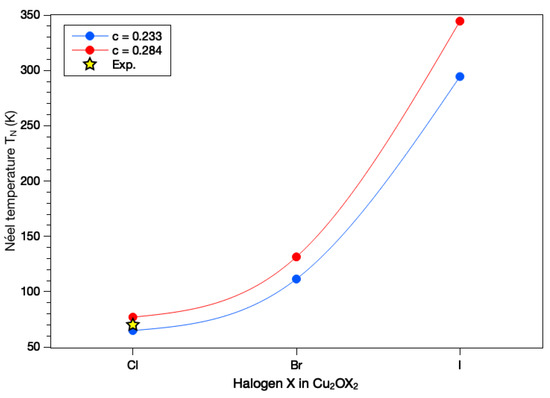
Figure 8.
Estimation of the Néel temperature depending on the nature of halogen species and considering two sets of parameters for the magnetic model presented in Equation (2): (1, in blue) = 2.6 and c = 0.233, and (2, in red) = 2.6 and c = 0.284. The experimental value for Cu2OCl2 is represented by a yellow star.
4. Conclusions
In summary, we have investigated the magnetic properties of Cu2OX2 (X = Cl, Br, I) systems based on first-principles calculations. The atomic structure of Cu2OX2 can be viewed either as based on ribbons of CuO2X2 edge-sharing plaquettes or as a pyrochlore-like lattice constituted of OCu4 corner-sharing tetrahedra. The present study shows that the magnetic order is governed by AFM spin chains of CuO2X2 corner-sharing plaquettes, which defines an AFM intra-chain coupling . These spin chains interact with each other through three inter-chain couplings, which leads to an effective interaction . Using these two parameters J and in an analytical expression for a quasi-1D AFM Heisenberg system, one may recover the Néel temperature of the known multiferroic compound Cu2OCl2 at = 70 K. We also predict that Cu2OBr2 could be a stable phase and is expected to have a larger value, which is evaluated to be about 120 K. Using chemical pressure to enhance is thus an effective and appealing technique to design new mixed anion compounds in order to reach RT operating MF. Ongoing investigations in our group consist of combining chemical and physical pressures to reach this goal.
Author Contributions
Investigation, W.L.-D.-H.; supervision, X.R.; formal analysis, writing—original draft preparation, review and editing, W.L.-D.-H., X.R. All authors have read and agreed to the published version of the manuscript.
Funding
Research funded by Agence Nationale de la Recherche (ANR-19-CE08-0013).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available in insert article.
Acknowledgments
The theoretical work was granted access to the HPC resources of TGCC/CINES /IDRIS under Allocation No. 2019-A0050907682 made by GENCI. The authors also acknowledge the CCIPL (Centre de Calcul Intensif des Pays de la Loire) for computational resources. Crystal structures were represented using the VESTA software [29].
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fiebig, M.; Lottermoser, T.; Meier, D.; Trassin, M. The evolution of multiferroics. Nat. Rev. Mater. 2016, 1, 16046. [Google Scholar] [CrossRef]
- Gilioli, E.; Ehm, L. High pressure and multiferroics materials: A happy marriage. Int. Union Crystallogr. J. 2014, 1, 590–603. [Google Scholar] [CrossRef] [PubMed]
- Rocquefelte, X.; Schwarz, K.; Blaha, P.; Kumar, S.; van den Brink, J. Room-temperature spin-spiral multiferroicity in high-pressure cupric oxide. Nat. Commun. 2013, 4, 2511. [Google Scholar] [CrossRef] [PubMed]
- Lafargue-Dit-Hauret, W.; Braithwaite, D.; Huxley, A.D.; Kimura, T.; Saúl, A.; Rocquefelte, X. Potential room-temperature multiferroicity in cupric oxide under high pressure. Phys. Rev. B 2021, 103, 214432. [Google Scholar] [CrossRef]
- Manuel, P. Private communication. 2022. [Google Scholar]
- Banks, M.G.; Kremer, R.K.; Hoch, C.; Simon, A.; Ouladdiaf, B.; Broto, J.M.; Rakoto, H.; Lee, C.; Whangbo, M.H. Magnetic ordering in the frustrated Heisenberg chain system cupric chloride CuCl2. Phys. Rev. B 2009, 80, 024404. [Google Scholar] [CrossRef]
- Zhao, L.; Hung, T.L.; Li, C.C.; Chen, Y.Y.; Wu, M.K.; Kremer, R.K.; Banks, M.G.; Simon, A.; Whangbo, M.H.; Lee, C.; et al. CuBr2—A New Multiferroic Material with High Critical Temperature. Adv. Mater. 2012, 24, 2469–2473. [Google Scholar] [CrossRef]
- Okabe, H.; Suzuki, K.; Kawashima, K.; Muranaka, T.; Akimitsu, J. New Pyrochlore-like Compound Cu2OCl2 with S = 1/2. J. Phys. Soc. Jpn. 2006, 75, 123705. [Google Scholar] [CrossRef]
- Kawashima, K.; Okabe, H.; Suzuki, K.; Kuroiwa, S.; Akimitsu, J.; Sato, K.H.; Koda, A.; Kadono, R. Antiferromagnetic ordering in Cu2OCl2 studied by the muon spin rotation/relaxation technique. J. Phys. Condens. Matter 2007, 19, 145275. [Google Scholar] [CrossRef]
- Nishiyama, M.; Oyamada, A.; Itou, T.; Maegawa, S.; Okabe, H.; Akimitsu, J. NMR study of pyrochlore lattice antiferromagnet, melanothallite Cu2OCl2. J. Phys. Conf. Ser. 2011, 320, 012030. [Google Scholar] [CrossRef]
- Zhao, L.; Fernández-Díaz, M.T.; Tjeng, L.H.; Komarek, A.C. Oxyhalides: A new class of high-Tc multiferroic materials. Sci. Adv. 2016, 2, e1600353. [Google Scholar] [CrossRef]
- Araújo, B.S.; Arévalo-López, A.M.; Attfield, J.P.; Paschoal, C.W.A.; Ayala, A.P. Spin-phonon coupling in melanothallite Cu2OCl2. Appl. Phys. Lett. 2018, 113, 222901. [Google Scholar] [CrossRef]
- Guo, H.; Zhao, L.; Schmidt, W.; Fernández-Díaz, M.T.; Becker, C.; Melendez-Sans, A.; Peng, W.; Zbiri, M.; Hansmann, P.; Komarek, A.C. Multiferroic properties of melanothallite Cu2OCl2. Phys. Rev. Mater. 2019, 3, 124405. [Google Scholar] [CrossRef]
- Wu, H.C.; Yuan, J.K.; Chandrasekhar, K.D.; Lee, C.H.; Li, W.H.; Wang, C.W.; Chen, J.M.; Lin, J.Y.; Berger, H.; Yen, T.W.; et al. Observation of charge–transfer–driven antiferroelectricity in 3d-pyrochlore multiferroic Cu2OCl2. Mater. Today Phys. 2019, 8, 34–42. [Google Scholar] [CrossRef]
- Tsirlin, A.A.; Janson, O.; Rosner, H. Electronic Structure and Magnetic Properties of Melanothallite (Cu2OCl2), a Gateway to Understanding Copper Oxychlorides; Russian Mineralogical Society: Kirovsk, Russia, 2010; Volume 1, p. 61. [Google Scholar]
- Kresse, G.; Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 1996, 6, 15–50. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef]
- Dudarev, S.L.; Botton, G.A.; Savrasov, S.Y.; Humphreys, C.J.; Sutton, A.P. Electron-energy-loss spectra and the structural stability of nickel oxide: An LSDA+U study. Phys. Rev. B 1998, 57, 1505–1509. [Google Scholar] [CrossRef]
- Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef]
- Blaha, P.; Schwarz, K.; Madsen, G.K.H.; Kvasnicka, D.; Luitz, J.; Laskowsk, R.; Tran, F.; Marks, L.; Marks, L. WIEN2k: An Augmented Plane Wave Plus Local Orbitals Program for Calculating Crystal Properties; Vienna University of Technology Institute of Materials Chemistry Getreidemarkt 9/165-TC A-1060: Vienna, Austria, 2019; ISBN 3-9501031-1-2. [Google Scholar]
- Krivovichev, S.V.; Filatov, S.K.; Burns, P.C. The cuprite-like framework of OCu4 tetrahedra in the crystal structure of synthetic melanothallite, Cu2OCl2, and its negative thermal expansion. Can. Mineral. 2002, 40, 1185–1190. [Google Scholar] [CrossRef][Green Version]
- Filatov, S.K.; Bubnova, R.S. The nature of special points on unit cell parameters temperature dependences for crystal substances. In Tenth European Powder Diffraction Conference: Geneva, Switzerland, 1–4 September 2006; Für Kristallographie, D.G., Ed.; Number 26; Oldenbourg Wissenschaftsverlag: Munchen, Germany, 2007; pp. 447–452. [Google Scholar]
- Zheng, X.G.; Kubozono, H.; Yamada, H.; Kato, K.; Ishiwata, Y.; Xu, C.N. Giant negative thermal expansion in magnetic nanocrystals. Nat. Nanotechnol. 2008, 3, 724–726. [Google Scholar] [CrossRef] [PubMed]
- Sleight, A.W. Compounds That Contract on Heating. Inorg. Chem. 1998, 37, 2854–2860. [Google Scholar] [CrossRef]
- Rocquefelte, X.; Schwarz, K.; Blaha, P. Comment on High-Tc Ferroelectricity Emerging from Magnetic Degeneracy in Cupric Oxide. Phys. Rev. Lett. 2011, 107, 239701. [Google Scholar] [CrossRef] [PubMed]
- Yasuda, C.; Todo, S.; Hukushima, K.; Alet, F.; Keller, M.; Troyer, M.; Takayama, H. Néel Temperature of Quasi-Low-Dimensional Heisenberg Antiferromagnets. Phys. Rev. Lett. 2005, 94, 217201. [Google Scholar] [CrossRef]
- Momma, K.; Izumi, F. VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).