Abstract
Tera Hertz radiation is currently the most researched and useful area in almost all fields of science and industry. The additional challenge is expressed in the form of radiation, pulses of femto-seconds in length are supposed to pass through a transmission line (TL) most efficiently, at a wide range of frequencies. These are complex beams, which make up the electromagnetic (EM) field, represented in the frequency domain in terms of cavity eigenmodes. A simulation allows to describe of the phase-amplitude and spectral characteristics of multimode radiation free-electron laser (FEL) operating in various operational parameters. The analysis is performed through the transmission of optical rays accurately, with each ray being characterized by amplitude, position, and angle in 3D space. A light field representation of a complex EM field is obtained via Wigner Distribution Function, which allows to describe of the dynamics of field evolution in future propagation by a ray tracing (RT) method. The final diagnostics will determine the design of the TL to be assembled in an innovative accelerator under construction at the Schlesinger Family Center for Compact Accelerators, Radiation Sources, and Applications.
1. Introduction
The world of science and technology is showing great interest in terahertz (THz) radiation recently. The THz (0.3–3.75 THz) research and applications have become widely popular and accessible [1,2]. There is a growing interest in developing high-intensity radiation sources at the Schlesinger Family Center for Compact Accelerators, Radiation Sources & Applications (THz Free Electron Laser THz-FEL), Ariel University [3]. The heart of the Center is a hybrid S-band (2856 MHz) photo injector, was designed by the Particle Beam Physics Laboratory (PBPL) group at UCLA [4,5,6]. A small-scale prototype of such a hybrid structure was previously designed and tested [7]. A photo-injector rf-LINAC gun produces short electron pulses which drive the FEL. The rf-LINAC has a hybrid structure with both standing and traveling wave sections. Such a structure produces ultrawide, femtosecond electron beams with a controlled energy chirp. The THz-radiation emission is being carried out from a (12 × 6 mm) flat aperture. The general layout of the THz FEL is shown in Figure 1. The THz radiation has a frequency spread of 10% around the resonance frequency. A spectrum tunable in the range of 1–3.5 THz. A short-pulse THz-FEL with a power of 150 kW using a 90 cm Undulator, will be driven by this photoinjector beam. Radiation emitted coherently from all the electrons within the pulse, causes an effect of enhanced emission [8,9,10,11]. A super-radiation at 1–3 THz [3,12] is achieved as a result. (if the emitting electron bunch is less than 0.1 mm pulse length, the emitting electron bunch must be shorter than the wavelength for the coherent emission in the super-radiant regime).
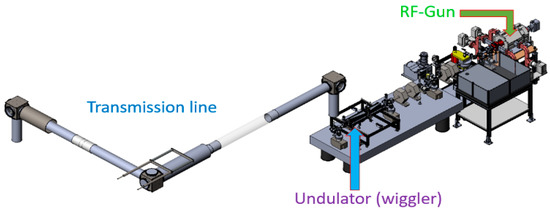
Figure 1.
THz FEL setup at the Schlesinger Center.
The THz range lies between the millimeter wave (MW) range and the infrared. Therefore, it naturally behaves as a MW on one side and a light wave on the other. It means, the THz radiation (propagation) has light waves properties on the one hand and the properties of a MW on the other. Therefore, a transmission calculation of a THz signal (from a source) is a very complex task.
This work characterizes THz radiation in general. In particular in the transmission of ultra-short pulses in a wide spectrum frequency. When the EM field is complex. The final diagnosis will help determine the design of the quasi-optical transmission line (TL) through which the radiation is supposed to pass. The TL will conduct a beam of radiation from the FEL to the user room, where the experiments will be performed. The user’s room is located about 10 m from the source.
The ultimate goal is a need to transfer an EM field with the maximum efficiency of energy along with the TL. Therefore, paramount importance comes down to the accurate calculation of the TL. To this end, research is conducted for the analysis and characterization of radiation.
The FEL is under construction and the TL is not built yet at all. An approximation model of the EM complex beams was obtained from WB3D (wide band 3D) numerical code [13]. The EM field energy is distributed in three waveguide modes [13]. This EM field constitutes the THz radiation source for this work, emitting from a waveguide output, inside a wiggler (a detailed explanation regarding this approach appears in previous work, FEL simulation, see [14] and references therein). Note, that the model is based on a coupled-mode approach expressed in the frequency domain; when an electron beam passes through a planar undulator (into the waveguide). The total EM field is obtained as the results (see [13,14] and references therein). It is worth noting that this model changes from time to time depending on the dimensions of the waveguide, the type of the waveguide and a general structure of the undulator. In this unique study it is about the rectangular waveguide, 12 × 6 mm. It will also note that the waveguide will also be assembled, the vacuum will be introduced and only then will the experimental researchers be able to obtain preliminary results and a comparison with the model mentioned above.
The purpose of this work is THz radiation researching from the source mentioned above through simulations, using a Wigner distribution function (WDF) [15]. The WDF provides an extended characterization of the desired signal and also enables the discovery of hidden features. The WDF allows describing the EM field in terms of geometrical optical (GO) rays. The GO rays can be calculated by simple GO rules. In this research, the additional contribution of the WDF is the representation of the EM field as a set of rays. This work is a general tool for calculating the propagation of the THz complex beams. A general approach based on the WDF is propagated via a ray-tracing (RT) method with help of Zemax software [16]. The emphasis here is on spatial-frequency representation of the EM field.
The scientific question of the paper is how to describe in adequate way a ultra-short THz pulse as a set of GO rays for future application in convectional propagation solvers.
Another emphasis of this work is reflected in the fact that here the contribution of each mode is researched separately. This is done in order to test the response of the TL to each mode and in addition to your estimate of how the future parameters of the TL should be changed depending on changes in the parameters of waveguide within the undulator. In the previous work [14], an analysis of the general field was obtained, when instead of the waveguide an imaginary flat aperture measuring 7.5 × 5 mm appeared. In this work the contribution to each mode is calculated analytically, for maximum accuracy.
1.1. Review of Simulation Methods
There are many methods for calculating electromagnetic radiation transmission. Some are classic, and some are new, whether it is by analytical or numerical calculation. This work uses a combination of techniques, with the field being converted to a light field by the WDF. The WDF allows integration with the RT technique, which is implemented in the Zemax software, which was developed precisely for this purpose. The rest of the techniques were rejected due to inconsistency and are well explained in the article [14] which saves an explanation here. At the same time, a study was conducted to characterize the TL when the Hermit-Gaussian mode was used for the transmission of radiation [17]. According to the results, it was decided that it would be most optimal to continue research using the RT method. As mentioned earlier, this work uses Zemax which performs precise RT, for which it exists. It also emphasizes the need for precision radiation analysis for the optical path. It should only be noted that RT has been widely used not only in games and optical field transfer. It is also a very popular method of transmitting and characterizing the scale even in radio waves [18]. If this has been proven and is very good for the millimeter wave—surely suitable for THz as well. Because the wavelength of the terahertz is shorter and closer to infrared. In this field, as in light waves, the RT is the most accepted method for calculating radiation transfer.
1.2. Purpose
A simulation has been developed for a purpose, of future TL’s design which enables the imaging of an EM field propagation along the trajectory. The scatter and size of the beams will ultimately determine the sights, focuses, and distances.
The emitted radiation will be transmitted from the source to the user room by the TL. The radiation is in a vacuum via four confocal off-axis parabolic mirrors in a 30 cm pipe, as shown in Figure 2. According to classical method, the early calculation of the TL is proposed.
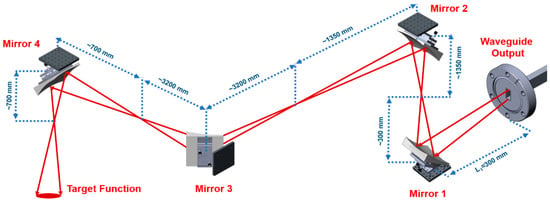
Figure 2.
THz transmission line.
2. Wigner Methodology
2.1. WDF-Wigner Methodology
The WDF was introduced by E. Wigner [18] as the simplest quantum analogue of the classical phase space distribution function allowing to find the probabilities and mathematical expectations of quantum operators in as classical a way as possible. Actually, is a phase-space representation that was used in optics over 30 years ago [19].
Nowadays, the WDF found widespread use for the theoretical analysis of optical [20] (including quasi-optical) systems, acoustics [21], signal processing [22], radio waves used in wireless technology [23], and in numerous applications in general. Furthermore, it is used to represent the characteristics of radar emitters [24]. As can be seen from the articles, the vast majority of the deals with the WDF in one dimension, relate to time-frequency analysis [25]. In this research, 3D spatial frequencies are of greater importance with a general approach to electromagnetic fields (EM), especially an inexact description of free electromagnetic wave fields in terms of rays [26]. The technique is applying on THz radiation systems (see [27,28] and references therein), but can be applicable to all types of radiation.
The imaging of partially coherent optical beams in particular and the general analysis of EM fields in is a new way. The EM field evaluation during the propagation, represent by the pure space or the pure spatial-frequency representation of a stochastic process via its mutual intensity (MI) [29]. The concept is exploring in a phase space of most important beam parameters (such as intensity, phase coherence, beam-width, etc.).
The MI describes the beam parameters evaluation by * which is a function of four variables: the vectors r1 and r2. The asterisk * means a complex conjugate and the brackets for spatial (or time) averaging. We prefer to call the general process of the MI as a Modified Correlation Function (MCF) between the beam oscillations at two points r1 and r2. An intensity distribution I(r) can be measured, corresponds to the .
The WDF of an EM Field can be defined by the MCF, or equivalently in terms of its directional spectrum [29]:
2.2. Light Field or Ray Concept
As can be easily seen space-frequency description is equal to a light field [30] theory (LF) where each ray passing through the point r with a frequency p (i.e., direction q). Let’s define some “Ray Concept” where each ray defined by the position and direction and has an amplitude W(r, p), which is complex in our case.
According to LF [30], LF and Computational Imaging [31] and the ray concept [32] that the EM field propagation in the space from a source point may be represented by a set of GO rays. The rays were obtained via WDF. A 2D case is described below of the EM field, which is propagate perpendicular to the z-axis inside the waveguide. Note that, on the output of the waveguide, the beams propagate in 3D. Let define a simple monochromatic field distribution on the aperture, the wave guide output. Therefore, the WDF is defined by:
When:
The are the WDF of EM field, x, y are the coordinates on the aperture surface, and are Fourier conjugated variables to the space coordinates. By adding a time-dependence of the beam transfers, the WDF dimension rises from 4D to 6D.
The light field, the rays from each point x y on the aperture are obtained as the result. The wave number where define a 3D direction of each ray, therefore, the third-dimension propagation is:
The WDF can also be described using the spatial frequency:
where and are the projection of the fund on the X-axis and the Y-axis respectively.
The magnitude and polarization (I) of each ray are defined by the WDF:
Due to the orthogonality in any uniform media of the ray polarization to the ray wavenumber ():
Thus, the LF is obtained and described as the set of GO rays. Where each ray defined by initial coordinate (x, y) on the aperture with the given field distribution (E) defined by the amplitude I) and the direction: . From here, any signal is propagating in the space by the GO (ray) [32] rules.
2.3. A System’s Simulations Preparation: Planning and Building
In order to build the radiation transfer simulation, Matlab files must be prepared in the format of the Zemax simulator. At the same time, a model of the TL was built, which had previously been simplified and optimized, such as building a model of the thin lenses in place of the mirrors, aligning the model, simplifying the common transition matrix of the confocal mirrors, etc. The preparation and planning of the TL are beyond the scope of this work.
The method proposed here for simulating the beam propagation in the THz frequency range, is a compromise between the linear optics, and an analytical calculation of the Maxwell equations. The linear optic solution is relatively simple but is unable to accurately describe the propagation of the beam in space in this frequency range. In contrast, an analytical calculation of Maxwell’s equations whose solution is often difficult and complicated to solve.
This method is based on WDF and the transition from a continuous distribution to a discrete set of rays. They can be treated as classical optics. This method is presented here for the THz domain. First the E-field WDF thinks analytically. An array of rays is then constructed with each beam having a position, angle and intensity according to the WDF. The rays can then be transferred through the optical system and the WDF received again on the other side. Finally, the E-field can be retrieved from the WDF if necessary. Note, the WDF is not a dual function and therefore the inverse transform is not really trivial.
There are many methods for approximating the reverse transformation when in some cases there is a singular point in the center. For the purpose of this study, and even for the future design of the TL no reverse transformation is required. On the contrary, it is easier to characterize the EM field by the GO rays (or the LF). It is also easier to shoot (propagate) the rays, especially when working with the Zemax simulator.
The algorithm can calculate any TEmn or TMmn type. The article will focus on only three of them: TE01x, TE21x, TE23x. These are most dominant modes in the FEL system (around TE01-33%, TE21-22%, TE23-30% of the total energy participant [33]) as can also be seen in Figure 3.
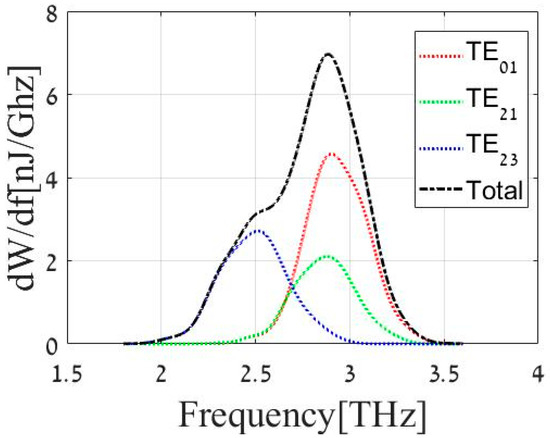
Figure 3.
Output amplitude radiation spectrum of Israeli free-electron THz source.
2.4. Analytical WDF Calculation
Let’s focus on the distribution of the electric field perpendicular to the direction of the beam in the waveguide. Therefore, a spatial component of the electric field function (E-field) of the beam in the mode of TE mode [34]:
The modes are defined in the range X [0, a] Y [0, b], where:
λ—the wavelength of the beam; c—Speed of light in a vacuum;
μ0—Permeability of free space; a, b—waveguide sizes; m, n—Mode numbers.
The variables x and y are symmetrical around zero, i.e., X [−a/2, a/2] Y [−b/2, b/2], so the wave function E (x, y) can be moved by (a/2, b/2) so that the WDF will still be calculated in the desired range of X [0, a] Y [0, b]. Then, the axes can be set as we wish. Hence the scope of WDF integration will be limited as follows:
On the X-axis:
On the Y-axis:
Considering the limits from Equations (13) and (14) and the analytical solution, with the emphasis given to the Ex field only:
The expression can be rewritten as two independent integrals, hence:
When:
Respectively:
2.5. Transfer to Discreet Rays
According to the analytical calculation a continuous WDF distribution was obtained and now it is necessary to make a transition to discreet (solitary) rays. The idea to a discrete system transition is that each combination of actually represents a GO ray having an position and an angle By placing in WDF it gets a certain “Wigner” value that does not change from the beginning to the end of the optical trajectory (the TL). Physically this equates to the transition between the presentation of radiation by the distribution of a continuous EM field to the presentation of the radiation by discrete photons.
The calculated WDF is finite both in the spatial and in the k domain (the ray’s angle).
The WDF, like the EM field, is limited to the size of the waveguide (a, b) in terms of the spatial domain (hence it is bounded, according to the boundary conditions). In terms of the range of angles, a magnitude order of the diffraction limit of the beam as 𝜆/a = 8.3 𝑚𝑟𝑎𝑑 ~ 0.47° [35] can be estimated. This means a beam at an angle of 10 times larger (about 4.7°) will have a WDF value that tends to 0. Hence, there is no need to consider an angle with the larger (relative to Z axis). In this work a range of up to (15°) was taken. The angle’s range was calculated by Equation (21).
2.6. Loading and Inserting the Files into the Simulator
In practice, a MATLAB code was built according to the analytical calculation which makes up a matrix of rays. The following details will enter: the number of Mode (m, n), the wavelength (λ = 0.1 mm), the dimensions of the waveguide on the X-axis (a = 12 mm) and the Y-axis (b = 6 mm), the number of different points and angles () where the rest of l, m, n are the COS angle with the X, Y and Z axes respectively.
In the other words, a matrix of rays in size of 40 × 80 points will be composed in XY, with 2500 rays coming out of each point at 50 different angles in X and 50 in Y.
2.7. The Beams Transmission through the Optical System
The results from the previous section will be entered into an optical system simulating the TL was designed in Zemax (as mentioned above). The TL is used to transfer the beams from the accelerator to the experimental laboratory in the THz beams. It should only be noted that the TL consists of 4 parabolic off-axis mirrors. And the system itself is built according to the principle of “Gaussian beam telescope” [35]. Therefore, in a paraxial approximation there is no dependence on the wavelength.
The TL is built this way for a range of frequencies pass through it, and not just a single frequency. In addition, it allows to focus the beam at different wavelengths at the same point (around the same point, for accuracy).
Separately, every mode was entered into Zemax and as a result the position XY, l, m and the optical path passed by each beam were obtained. Another algorithm written in MATLAB retrieves the information that interests us from the Zemax, “.ZRD” files and saved it as MATLAB files for further work.
3. Results
As is well known, the famous expression, that most of the trees do not see the forest. Therefore, all the figures, which are representing the rays have passed through the smoothing function. That is, an average is made of all 3 pixels on the X and Y axes. In order to see the general picture, rather than points indicating solitary rays, which are less convenient for general vision of the propagation limits, for the purpose of determining future TL parameters.
3.1. The EM Field Representation by Eigenmodes
Each individual mode is shown in Figure 4, when their sum constitutes the total field.
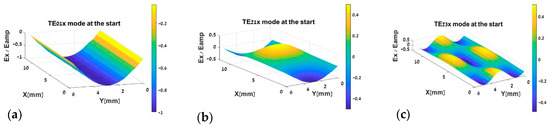
Figure 4.
The Ex field at the waveguide output: (a) TE01 mode; (b) TE21, and (c) TE23 modes. Note: In this case for a convenience, the EM field is in the −180° time phase at the output of the waveguide at zero moment. Therefore, is each mode respectively. For convenience, each mode is displayed in a normalized form. When Eamp is calculated by following form: Eamp = ExMAX − ExMIN.
3.2. The Modes Propagation in Term of Rays
3.2.1. The TE01 Mode Propagation
The TE01 mode is reminiscent in shape of a rectangular slot, hence it is expected that the shape of the interference will be similar the rectangular slot [36]:
where Dx, Dy is a slot size. According to the Equation (22), one can see a “sinc behavior” of the . The greater the length of the slot parameter (Dx, Dy) cause to the greater decay in this particular axis.
When the ray’s amplitude tends to “−1”, one can see that the background has a “higher potential” (zero), as shown in Figure 5a. This is due to the fact that the TE01 mode at the time of sampling was in phase of −180°. As indicated on the Figure 4a. That is another known indication the WDF is keeping the original EM field properties and follows it. For example the attribute of the form about this field and how WDF keeping and tracking it is explained work [10].
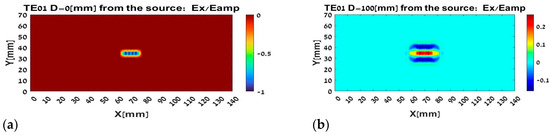
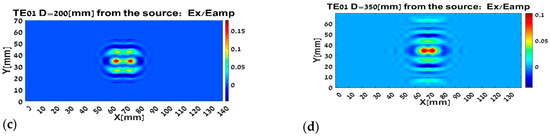
Figure 5.
The TE01 mode propagation in term of the rays: (a) at the out of the waveguide; (b) after passing 100 mm, (c) after passing 200 mm, and (d) after passing 350 mm.
In Figure 5c one can see that the size of the field is spread over the cast more than 2 times. than in Figure 5b. We will only note that at lower frequencies the signal shape slides past the window of the initial aperture at this distance.
In Figure 5b it can be seen that the size of the field is spread over the cast more than 2 times. Remaining on the initial aperture, in Figure 5a. These distances were omitted for convenience, easy to remember and measure. There is no reference here to doubling wavelengths or the like and there is no need for this because the FEL is designed to work in the 1–3.5 THz range.
In Figure 5d one can see that the size of the field slides past the window of the initial aperture, which we just used as a relative measure in this work. These distances were omitted for convenience, easy to remember and measure. There is no reference here to doubling wavelengths or the like and there is no need for this because the FEL is designed to work in the 1–3.5 THz range. It is appropriate that the intensity is smaller as the distance is greater and the field is spread over more area in the illustrations.
3.2.2. The TE21 Mode Propagation
Propagation in free space of the TE21 mode in Figure 6 resembles in its form the interference of three sources, and the propagation is almost identical in both directions.
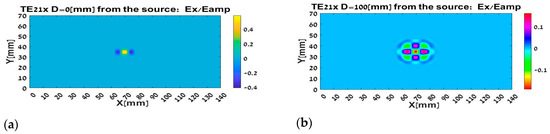
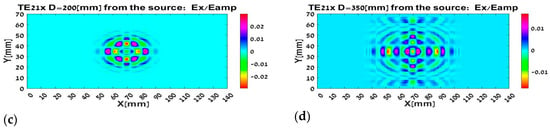
Figure 6.
The TE21 mode propagation in term of the rays: (a) at the out of the waveguide; (b) after passing 100 mm, and (c) after passing 200 mm, and (d) after passing 350 mm.
3.2.3. The TE23 Mode Propagation
It can be seen that the mode TE23 spreads at a higher rate, relative to mode TE21 and mode TE01.
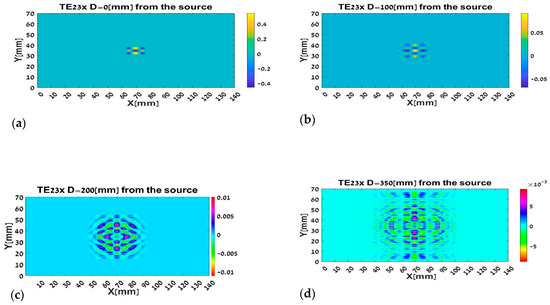
Figure 7.
The TE23 mode propagation in term of the rays: (a) at the out of the waveguide; (b) after passing 100 mm, and (c) after passing 200 mm, and (d) after passing 350 mm.
4. Discussion
In this work, imaging was performed using computer software (Zemax, Matlab) of three TE modes that carry most of the energy of the beam. With its help the field distribution was investigated the electric and power (intensity) distribution of each mode.
It can be easily seen that after every 100 mm each meter doubles in circumference. Quite a large scatter in the optical sense. When after 350 mm the rays are already completely out of the initial aperture. An important conclusion is that the radiation should be focused before 350 mm from the exit of the waveguide. Therefore, must have a focusing mirror. This will therefore be the first point that will affect the whole need. From here, confocal distances and points will be calculated.
Without going into the actual design of the TL, which is outside the scope of this work it can be noted that the original analytical design, on paper and with the help of the equations was successful. After all, the critical point necessary for the initial focusing can be clearly seen.
The study will continue for the purpose of determining the boundaries of the TL. On the one hand, the smaller the diameter of the mirrors, the cheaper the cost of the mirrors. The production is simpler, these are mirrors for THz. On the other hand, the distances are not typical for focusing so it will significantly increase the cost of mirrors. At the same time the diameter of the pipes is also very important. These are the pipes that are supposed to withstand the pressure. Therefore, in this study each mode was diagnosed individually, for the purpose of determining the scattering limits. When the general field was examined by the method of the rays, cross-terms and the other phenomena known from the WDF would be obtained. Therefore, each significant mode is examined individually.
5. Conclusions
In conclusion it can be said that with the help of the method tried here it is certainly possible to get a good simulation of distribution field and intensity in various TE modes passing through a quasi-optical system.
The choice of beam propagation was successful, due to the fact that one can clearly see the directions, the intensity of the propagation, its shape and boundaries. As is well known, the WDF maintains the original pattern of the field and is therefore a good indication for the selection and planning of the optical path in general and the TL in particular.
In the future, it will be possible to develop the algorithms into one software that receives the desired mode and the wave length, automatically feeds the data from Matlab to Zemax [37] transmits the rays through an optical path any and returns to Matlab for processing results.
After a recalculation and more accurate design of the TL, it will be possible to continue working with the whole EM field in general, or with each mode again, in particular, if will be necessary.
As stated in the discussion, the first mirror should be positioned up to 350 mm. In order to avoid too much dispersion, if you want to maintain the dimensions of the original signal. The first mirror has the most important role, and its quality depends on the entire system. In fact, after focusing at a confocal point to choose mirrors with identical characteristics, in order to complete the transfer of the radiation, but as mentioned, the actual design of the TL is outside the scope of this work.
This work is part of the design of the innovative compact particle accelerator. A general system is under construction and the TL is in the planning stages. As already understood, the distances are not characteristic of the size of the desired mirrors. The initial design was based on classical THz quasi-optics calculations. This work sheds light on the importance of the subject, when it provides an answer to the main working frequency, resonant frequency. In the future, when the construction of the accelerator is completed and it is clear what the lowest frequency and the highest frequency are, it will be possible to redefine all the parameters of the TL.
At this stage, an optimal waveguide inside the undulator has not yet been selected. Therefore, studies are being carried out with different types such as 15 × 10, 7.5 × 5 as mentioned in article [14] or 12 × 6 which currently seems optimal, as planned in this work. Where these are rectangular waveguides. There is also research interest with round waveguides. That is why simulations are carried out for the purpose of selecting the best system parameters, before construction.
As stated in the introduction, the ultimate goal of the research is to transfer the radiation in the most efficient way. We came to the most important conclusion: the first mirror is of utmost importance. Therefore, here the main emphasis will be placed on the combination of artificial intelligence to obtain an accurate function of the first mirror which will concentrate the radiation for transmission in the entire TL. This is actually an idea for future research.
Author Contributions
Conceptualization, M.G. and A.F.; Methodology, E.D. and A.F.; Software, M.G., B.P. and J.G.; Validation, M.G., B.P. and A.F.; Formal analysis, B.P. and J.G.; Investigation, M.G. and E.D.; Resources, M.G. and A.F.; Data curation, M.G. and J.G.; Writing—original draft preparation, M.G. and B.P.; Writing—review and editing, E.D., J.G. and A.F.; Visualization, M.G.; Supervision, E.D. and A.F.; Project administration, M.G., B.P. and A.F.; Funding acquisition, A.F.; J.G. and M.G. contributed eqully to this paper. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Technology State of Israel, grant no. 3-16652 and no. 3-16461. The APC was funded by Schlesinger Family Center for Compact Accelerators, Radiation Sources and Applications.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to belonging to the research and development of part of a compact particle accelerator at the Schlesinger Family Center for Compact Accelerators, Radiation Sources and Applications (FEL).
Acknowledgments
This research was supported by the Ministry of Science and Technology State of Israel. Science Research project “Development of an Artificial Intelligence System for the Design of a Terahertz Optical Mode Converter”, grant no. 3-16652. In the field: applied science and engineering for students in the direct/combined third degree program named after Ze’ev Jabotinsky. In addition, the authors would like to thank to a manager of the Schlesinger Family Center for Compact Accelerators, Radiation Sources and Applications (FEL), Yehiel Vashdi for their valuable help in the research.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chamberlain, M.; Jones, B.; Wilke, I.; Williams, G.; Parks, B.; Heinz, T.; Siegel, P. Opportunities in THz Science. Science 2004, 80, 123. [Google Scholar]
- Tripathi, S.R.; Miyata, E.; Ishai, P.B.; Kawase, K. Morphology of human sweat ducts observed by optical coherence tomography and their frequency of resonance in the terahertz frequency region. Sci. Rep. 2015, 5, 9071. [Google Scholar] [CrossRef]
- Friedman, A.; Balal, N.; Bratman, V.; Dyunin, E.; Lurie, Y.; Magory, E.; Gover, A.; Aviv, T. Configuration and Status of the Israeli Thz Free Electron Laser. In Proceedings of the 36th International Free Electron Laser Conference, Basel, Switzerland, 25–29 August 2014; pp. 553–555. [Google Scholar]
- Fukasawa, A.; Badakov, H.; Shea, B.D.O.; Rosenzweig, J.; Alesini, D.; Ficcadenti, L.; Spataro, B.; Lnf, I.; Palumbo, L.; Lnf, I.; et al. A Hybrid Standing Wave-Traveling Wave Photoinjector. In Proceedings of the FEL08, Gyeongju, Korea, 24–29 August 2008; pp. 334–337. [Google Scholar]
- Spataro, B.; Valloni, A.; Alesini, D.; Biancacci, N.; Faillace, L.; Ficcadenti, L.; Fukusawa, A.; Yakub, A. Nuclear Instruments and Methods in Physics Research A RF properties of a X-band hybrid photoinjector. Nucl. Inst. Methods Phys. Res. A 2011, 657, 99–106. [Google Scholar] [CrossRef]
- Rosenzweig, J.B.; Valloni, A.; Alesini, D.; Andonian, G.; Bernard, N.; Faillace, L.; Ficcadenti, L.; Spataro, B.; Yakub, A. Nuclear Instruments and Methods in Physics Research A Design and applications of an X-band hybrid photoinjector. Nucl. Inst. Methods Phys. Res. A 2011, 657, 107–113. [Google Scholar] [CrossRef]
- Angeles, L.; Alesini, D.; Ficcadenti, L.; Spataro, B.; Lnf, I.; Palumbo, L.; Lnf, I.; Sapienza, L. Beam Dynamics and RF Cavity Design of a Standing/Traveling-Wave Hybrid Photoinjector for High Brightness Beam Generation. In Proceedings of the Particle Accelerator Conference 2009, Vancouver, BC, Canada, 4–8 May 2009; pp. 4434–4436. [Google Scholar]
- Gover, A. Superradiant and stimulated-superradiant emission in prebunched electron-beam radiators. I. Formulation. Phys. Rev. Spec. Top.-Accel. Beams 2005, 8, 030701. [Google Scholar] [CrossRef]
- Emma, C.; Sudar, N.; Musumeci, P.; Urbanowicz, A.; Pellegrini, C. High efficiency tapered free-electron lasers with a prebunched electron beam. Phys. Rev. Accel. Beams 2018, 20, 110701. [Google Scholar] [CrossRef]
- Giannessi, L.; Bellaveglia, M.; Chiadroni, E.; Cianchi, A.; Couprie, M.E.; Del Franco, M.; Di Pirro, G.; Ferrario, M.; Gatti, G.; Labat, M.; et al. Superradiant Cascade in a Seeded Free-Electron Laser. Phys. Rev. Lett. 2013, 110, 044801. [Google Scholar] [CrossRef]
- Marinelli, A.; Ratner, D.; Lutman, A.A.; Turner, J.; Welch, J.; Decker, F.; Loos, H.; Behrens, C.; Gilevich, S.; Miahnahri, A.A.; et al. High-intensity double-pulse X-ray free-electron laser. Nat. Commun. 2015, 6, 6369. [Google Scholar] [CrossRef]
- Nause, A. Beam-line optimization based on implementation provides high-quality e-beam via a dogleg section Beam-line optimization based on realistic electron-optics 3D field-maps implementation provides high-quality e-beam via a dogleg section. Phys. Plasmas 2022, 29, 063104. [Google Scholar] [CrossRef]
- Lurie, Y.; Friedman, A.; Pinhasi, Y. Single pass, THz spectral range free-electron laser driven by a photocathode hybrid rf linear accelerator. Phys. Rev. Spec. Top. Accel. Beams 2015, 18, 070701. [Google Scholar] [CrossRef]
- Gerasimov, M.; Dyunin, E.; Gerasimov, J.; Ciplis, J.; Friedman, A. Application of wigner distribution function for THz propagation analysis. Sensors 2022, 22, 240. [Google Scholar] [CrossRef]
- Alonso, M.A. Wigner functions in optics: Describing beams as ray bundles and pulses as particle ensembles. Adv. Opt. Photonics 2016, 365, 272–365. [Google Scholar] [CrossRef]
- Radiant Zemax, L.L.C. Zemax® Optical Design Program User’s Manual; SPIE Press: Bellingham, WA, USA, 2015. [Google Scholar]
- Horowits, O.; Gerasimov, M.; Lurie, Y.; Friedman, A. Study of the transmission line for Israeli THz free-electron radiation source. Phys. Plasmas 2022, 29. [Google Scholar] [CrossRef]
- Wigner, E. On the quantum correction for thermodynamic equilibrium. Phys. Rev. 1932, 40, 749–759. [Google Scholar] [CrossRef]
- Bastiaans, M.J. The Wigner distribution function applied to optical signals and systems. Opt. Commun. 1978, 25, 26–30. [Google Scholar] [CrossRef]
- Shabtay, G.; Mendlovic, D.; Zalevsky, Z. Proposal for optical implementation of the Wigner distribution function. Appl. Opt. 1998, 37, 2142–2144. [Google Scholar] [CrossRef]
- Tanner, G.; Madenoor Ramapriya, D.; Gradoni, G.; Creagh, S.C.; Moers, E.; Lopéz Arteaga, I. A Wigner function approach to near-field acoustic holography-Theory and experiments. In Proceedings of the INTER-NOISE and NOISE-CON Congress and Conference Proceedings, San Diego, CA, USA, 26–28 August 2019. [Google Scholar]
- Dragoman, D. Applications of the Wigner Distribution Function. EURASIP J. Adv. Signal Process. 2005, 10, 1520–1534. [Google Scholar]
- Orovi, I.; Stankovi, S.; Dragani, A. Time-frequency based analysis of wireless signals. In Proceedings of the 2012 Mediterranean Conference on Embedded Computing (MECO), Bar, Montenegro, 19–21 June 2012. [Google Scholar]
- Feature, T.D. Robust Radar Emitter Recognition Based on theThree-Dimensional Distribution Feature and Transfer Learning. Sensors 2016, 16, 289. [Google Scholar] [CrossRef]
- Sun, K.; Jin, T.; Yang, D. An improved time-frequency analysis method in interference detection for GNSS receivers. Sensors 2015, 15, 9404–9426. [Google Scholar] [CrossRef]
- Alonso, M. Exact description of free electromagnetic wave fields in terms of rays. Opt. Express 2003, 11, 3128. [Google Scholar] [CrossRef]
- Jepsen, P.U.; Cooke, D.G.; Koch, M. Terahertz spectroscopy and imaging–Modern techniques and applications. Laser Photonics Rev. 2011, 166, 124–166. [Google Scholar] [CrossRef]
- Adibi, A. Springer Series in Optical Sciences; Springer: New York, NY, USA, 2009; ISBN 9783642295638. [Google Scholar]
- Methods, C. Mathematical Optics: Classical, Quantum, and Computational Methods; CRC Press: Boca Raton, FL, USA, 2012; ISBN 9781439869611. [Google Scholar]
- Gershun, A. The Light Field. J. Math. Phys. 1939, 18, 51–151. [Google Scholar] [CrossRef]
- Levoy, M. Light Fields and Computational Imaging. IEEE Comput. 2006, 39, 46–55. [Google Scholar] [CrossRef]
- Torre, A. Linear Ray and Wave Optics in Phase Space. In Bridging Ray and Wave Optics via the Wigner Phase-Space Picture; Elsevier: Amsterdam, The Netherlands, 2005. [Google Scholar] [CrossRef]
- Kapilevich, B.; Lurie, Y.; Perutski, B.; Litvak, B.; Etinger, A.; Friedman, A. Radiation Fields of THz Free Electron Laser: 3D EM Simulation and Experimental Study. In Proceedings of the 2014 IEEE 28th Convention of Electrical & Electronics Engineers in Israel (IEEEI), Eilat, Israel, 3–5 December 2014; pp. 28–31. [Google Scholar]
- Pozar, D.M. Microwave Engineering; Pozar, D.M., Ed.; John Wiley&Sons: New York, NY, USA, 2012. [Google Scholar]
- Paul, F. Goldsmith Quasioptical Systems: Gaussian Beam Quasioptical Propogation and Applications; IEEE Press: New York, NY, USA, 1998. [Google Scholar]
- Saleh, B.E.A.; Teich, M.C. Fundamentals of Photonics; Wiley-Blackwell: Hoboken, NJ, USA, 2019; ISBN 9781119506874. [Google Scholar]
- Griffith, D. How to Talk to Zemax from MATLAB. Available online: http://www.ZEMAX.com (accessed on 3 January 2006).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).