Quantization-Based Image Watermarking by Using a Normalization Scheme in the Wavelet Domain
Abstract
1. Introduction
2. Related Work
2.1. Image Normalization
2.2. The Wavelet Transform
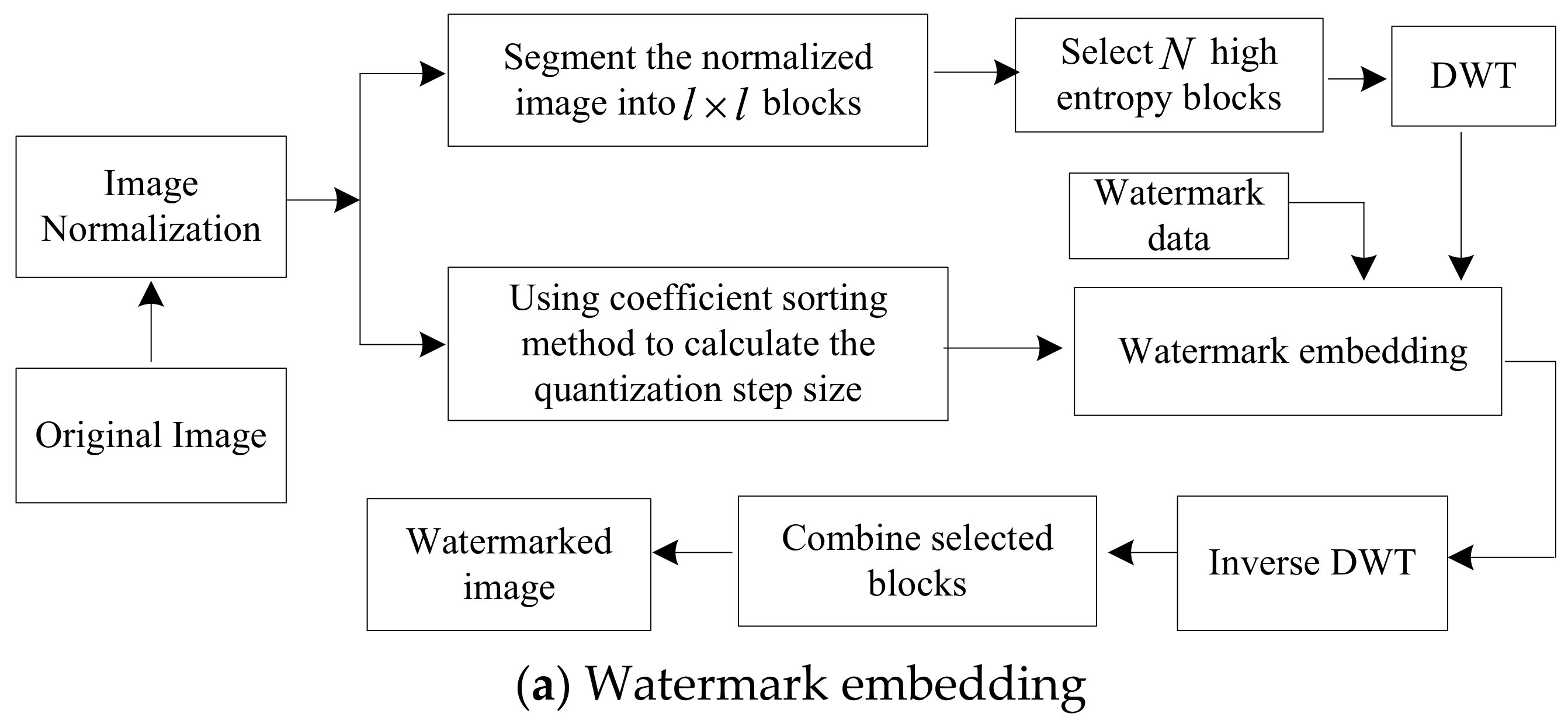
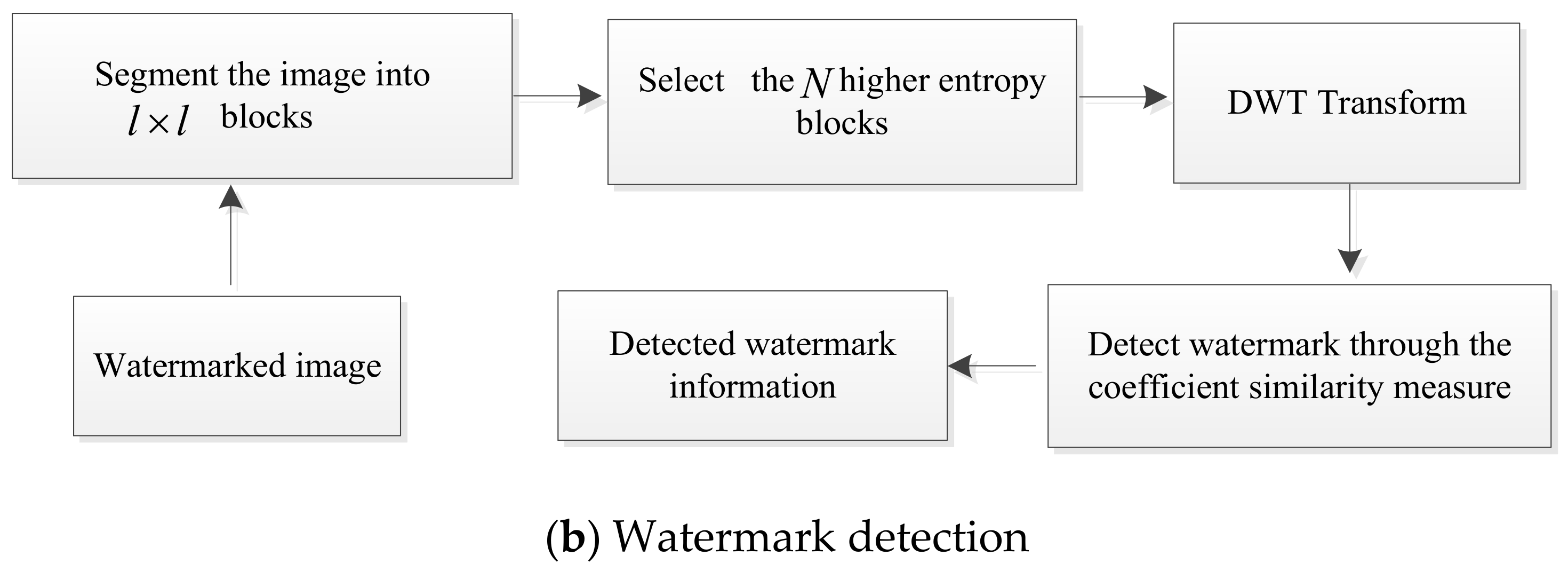
3. Proposed Watermarking Method
3.1. Watermark Embedding
3.2. Watermark Detection
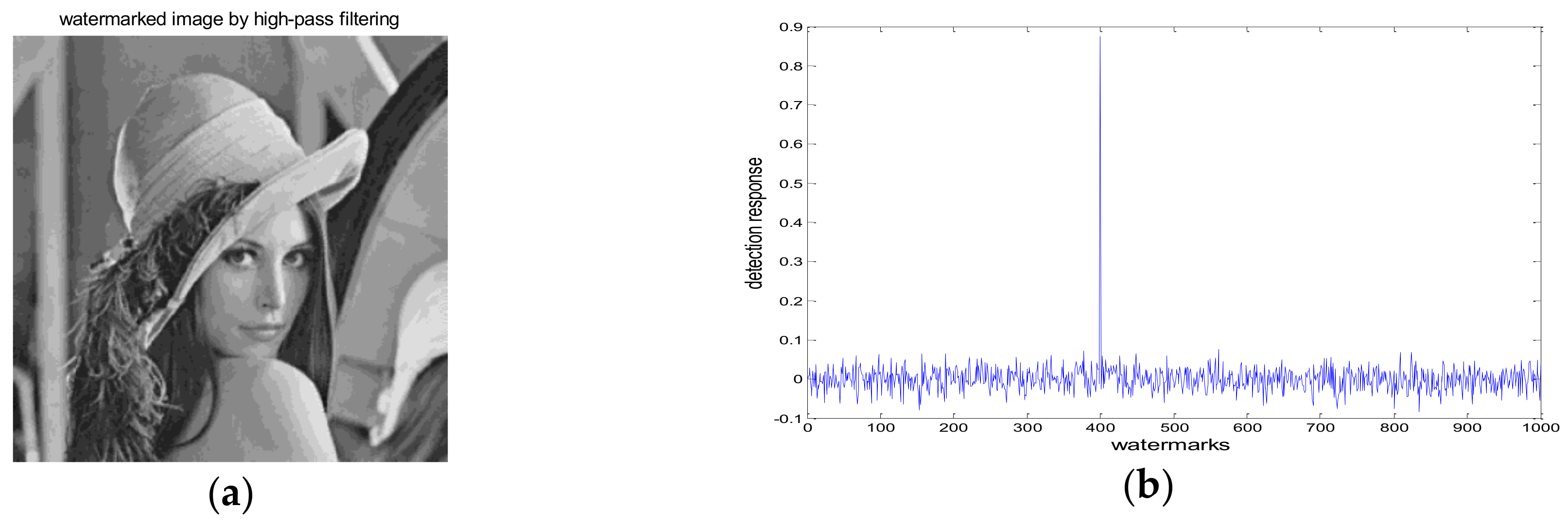
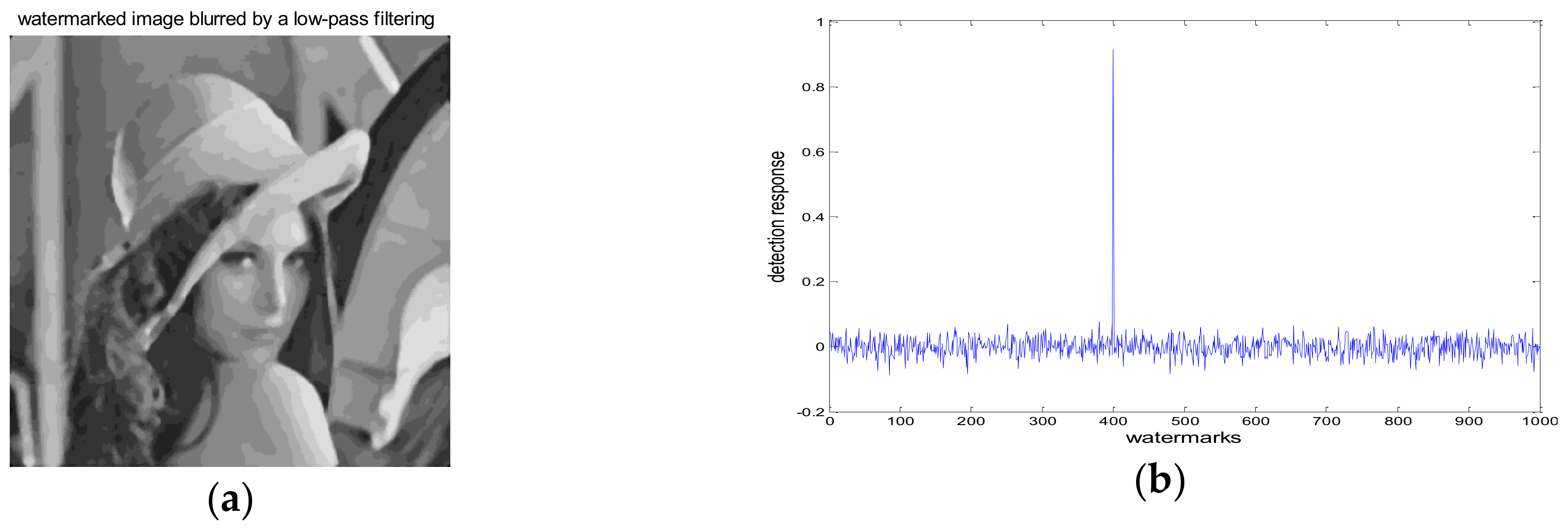
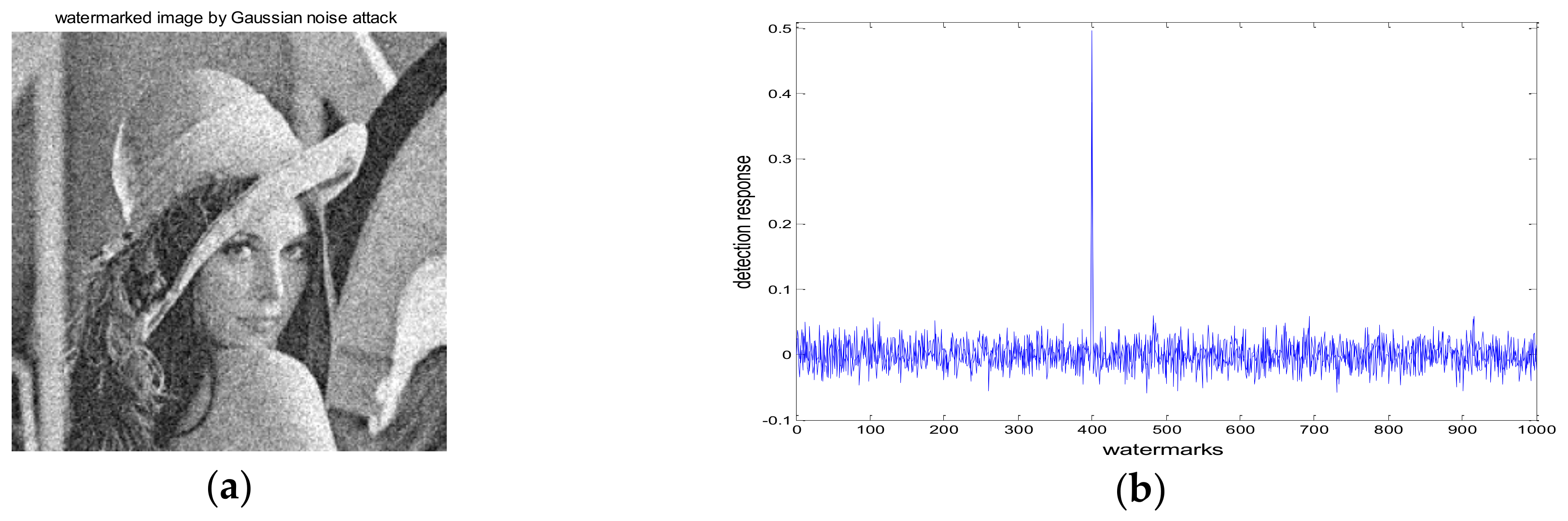
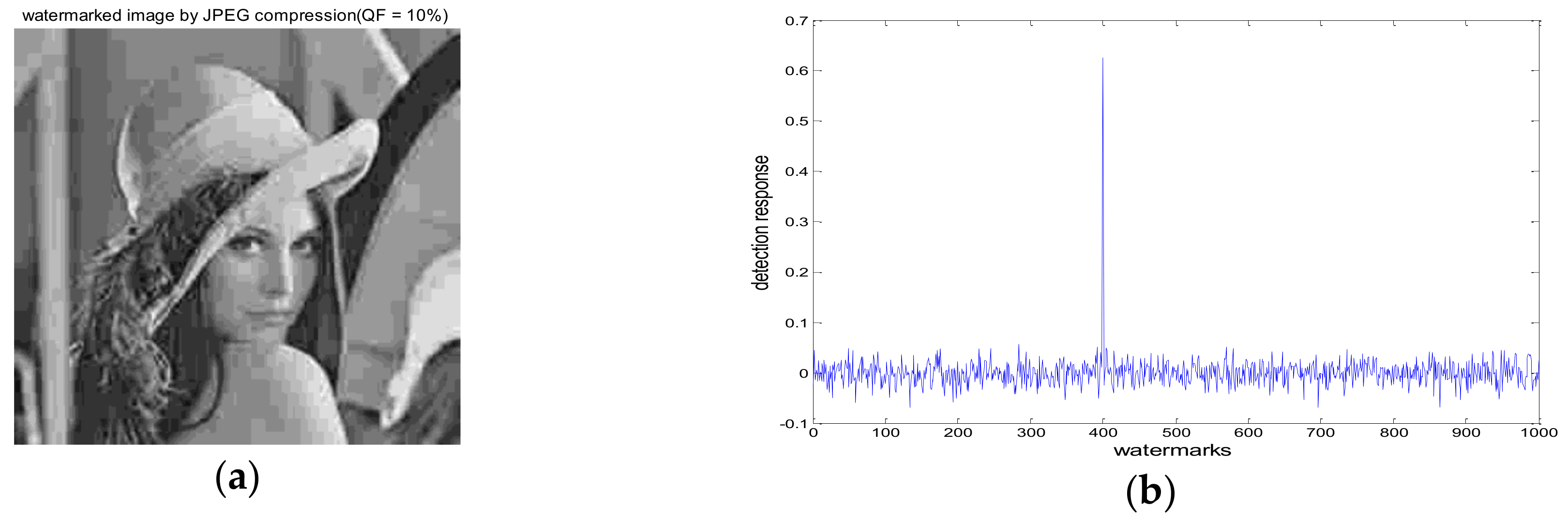
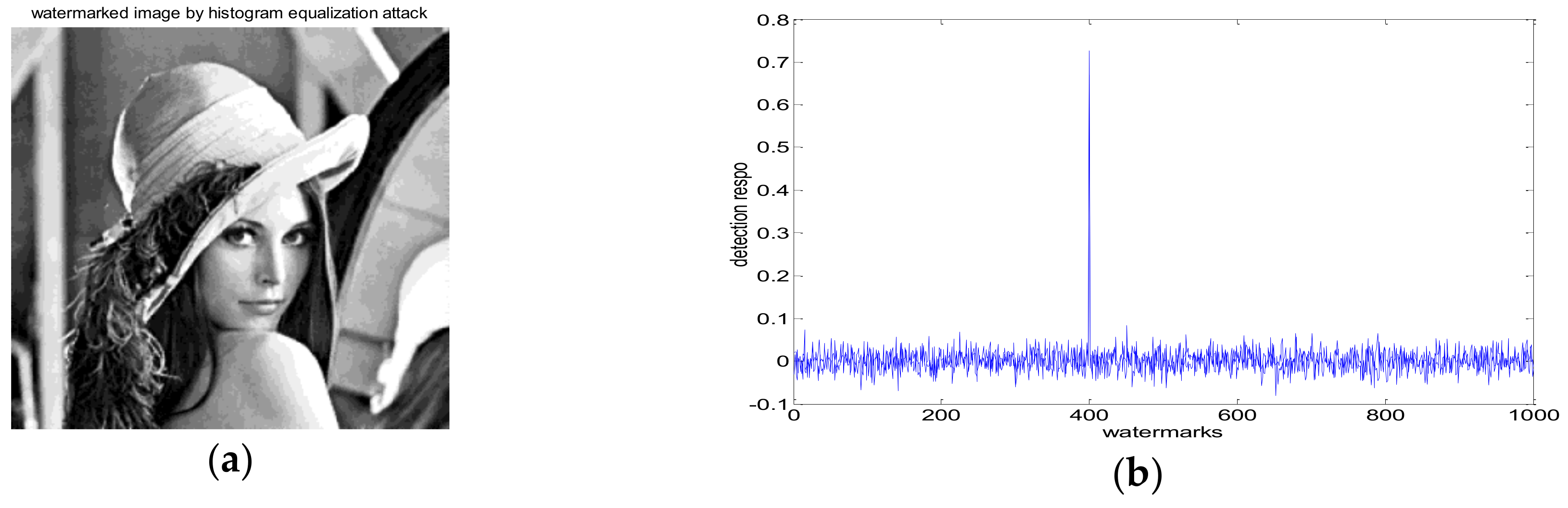
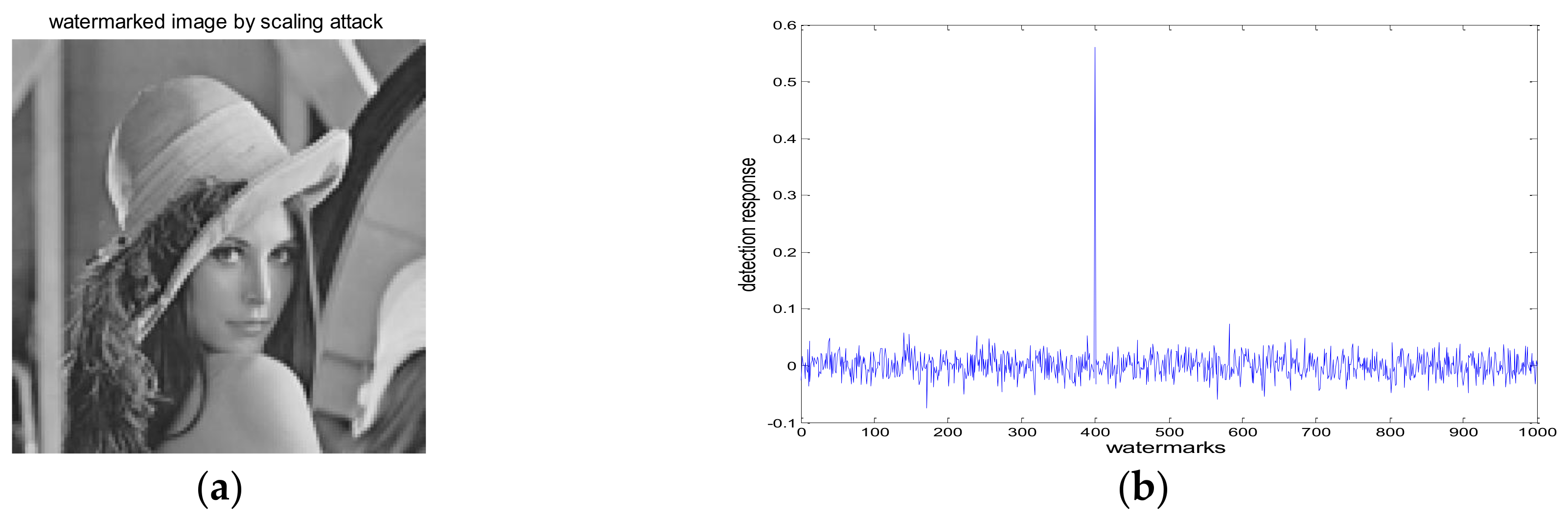
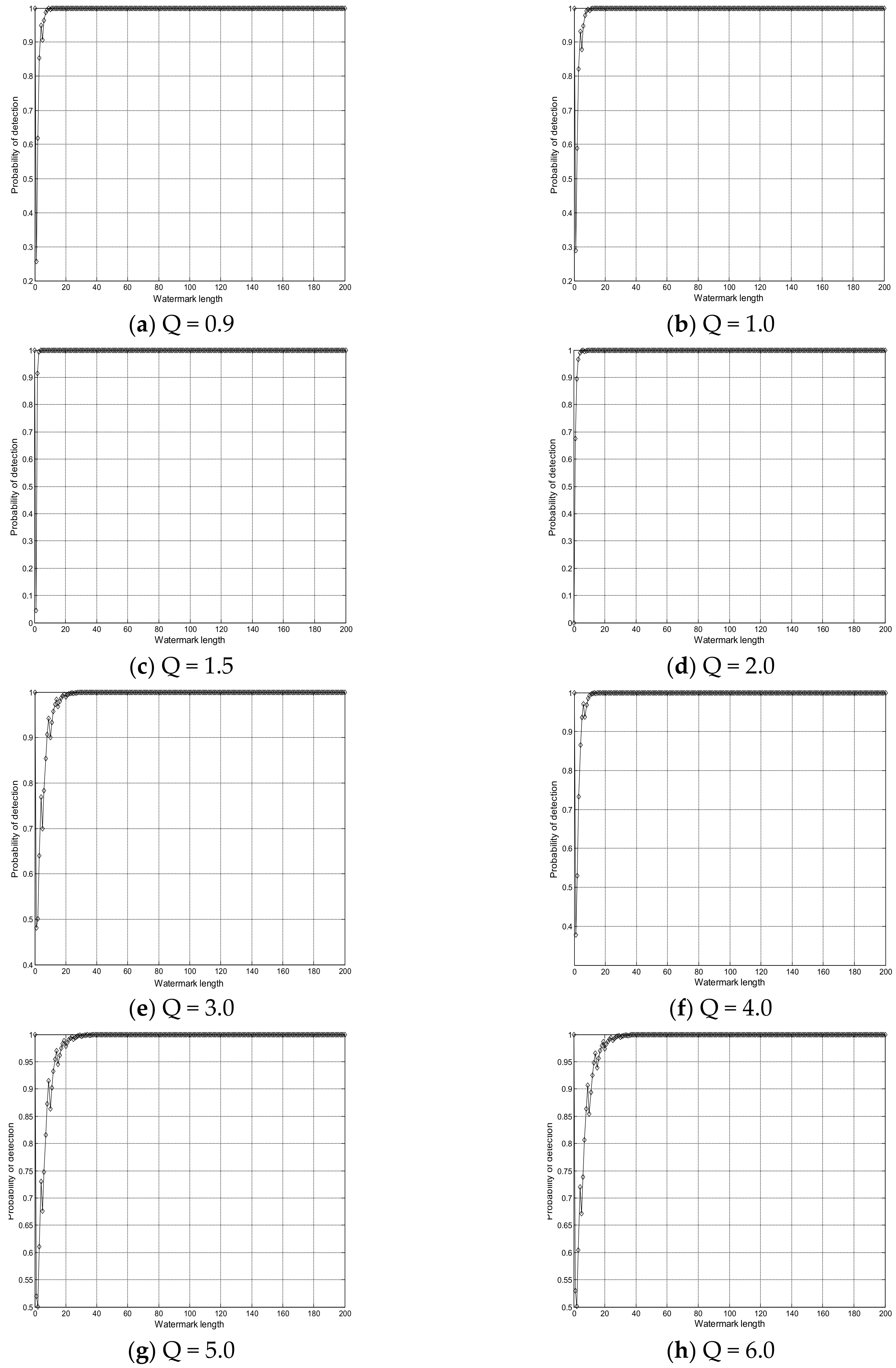
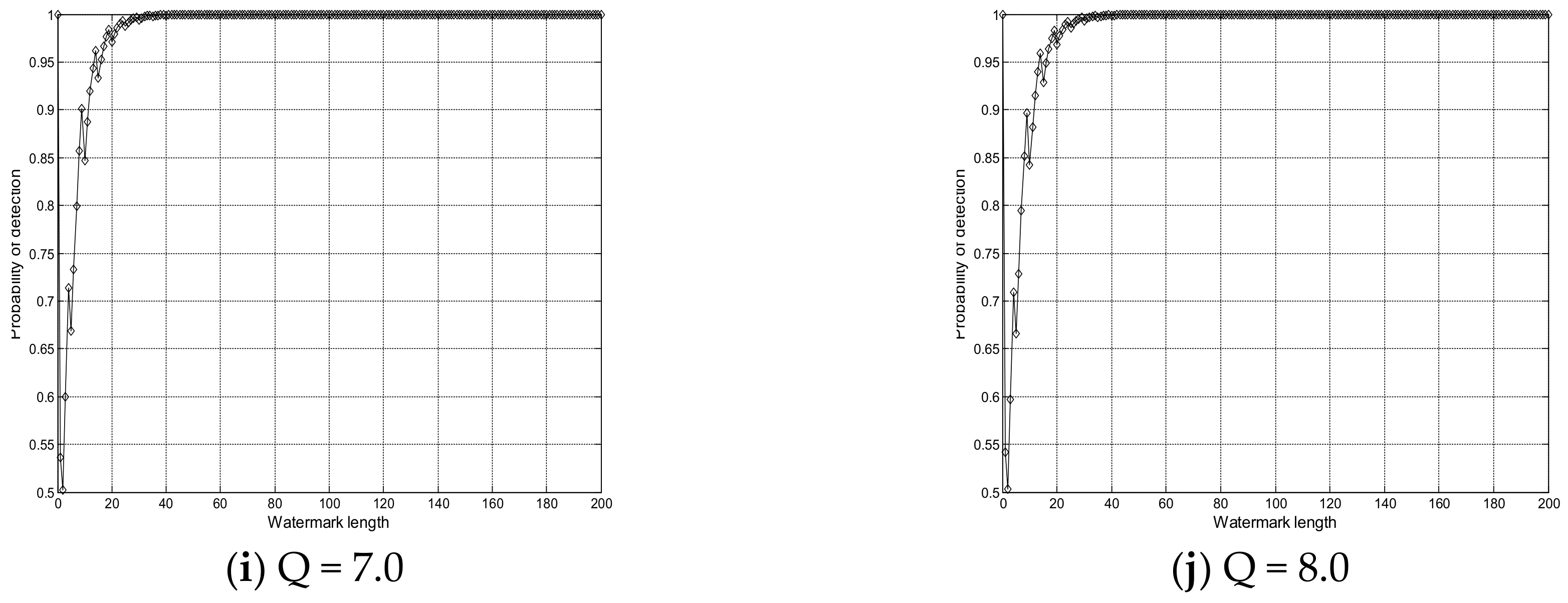
4. Experimental Results and Analysis
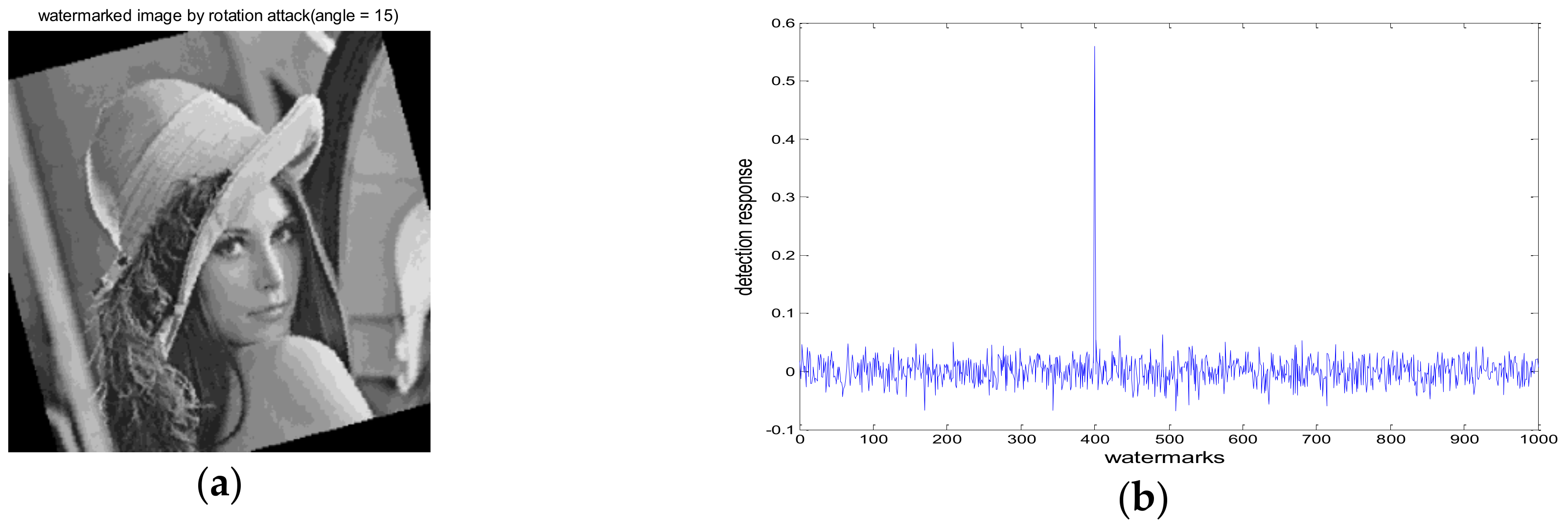
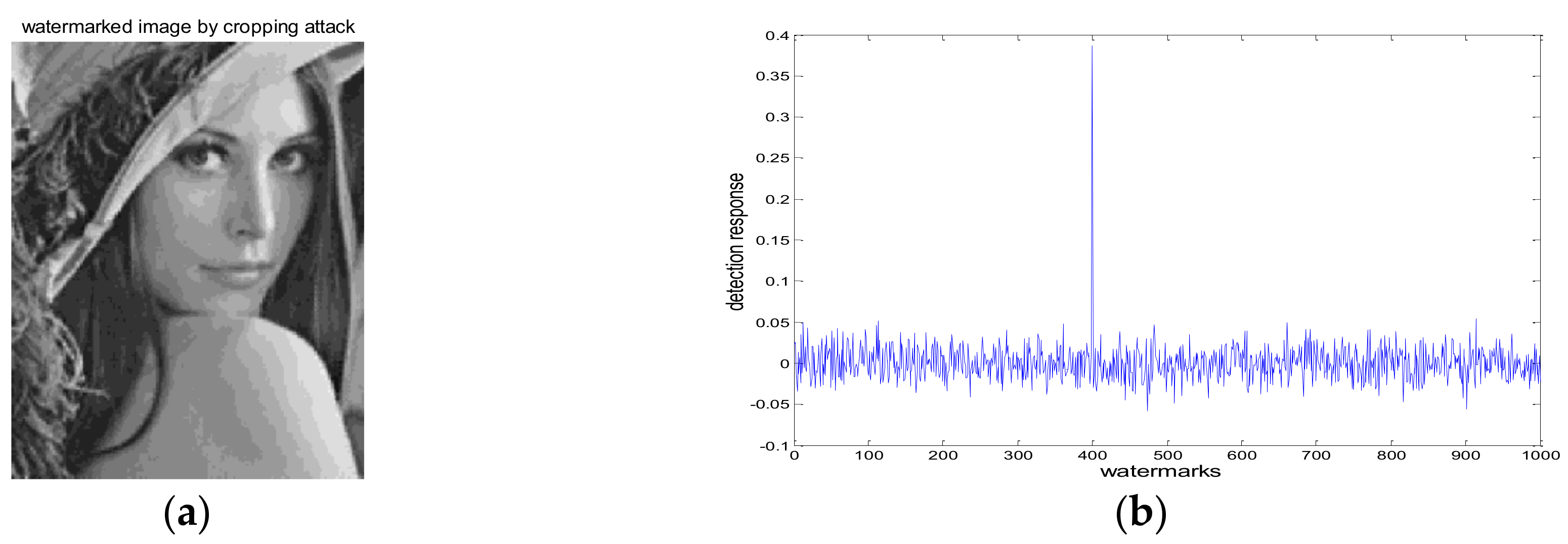
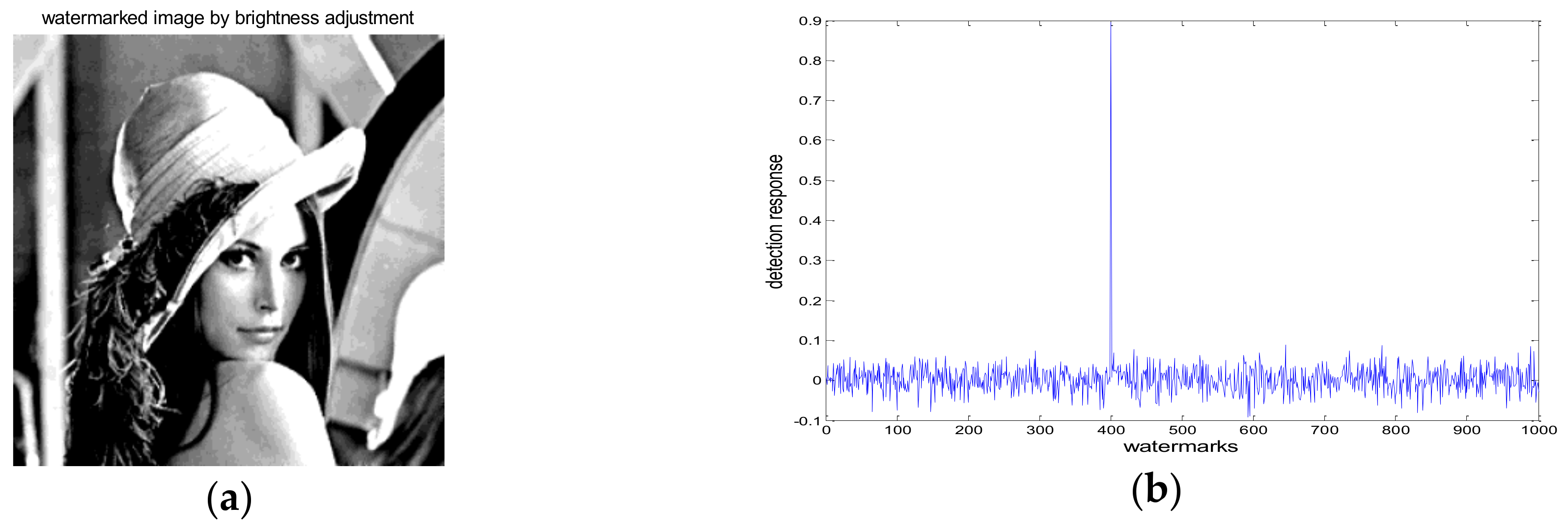
4.1. Robustness Test
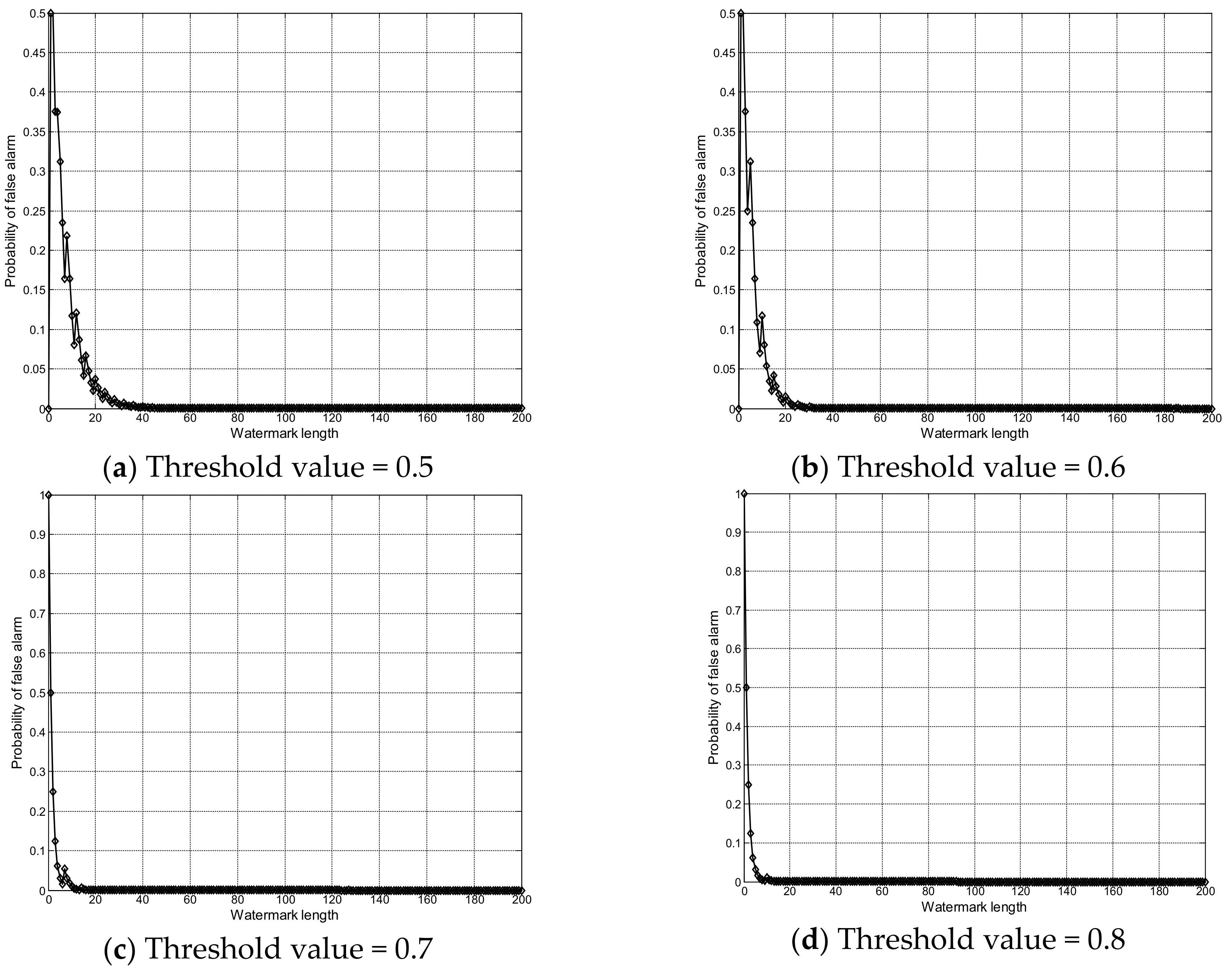
4.2. Performance Analysis
4.3. Comparison with Other Watermarking Method
5. Conclusions
- (1)
- The high entropy image region was selected as the watermark embedding space, which improves the imperceptibility of the watermarking.
- (2)
- The proposed watermarking is blind, that is the watermark detection does not require the original image.
- (3)
- The image normalization strategy is used to designing the watermarking algorithm, which enhances the robustness of watermarking when against some geometric distortions.
Author Contributions
Funding
Conflicts of Interest
References
- Asikuzzaman, M.; Pickering, M.R. An overview of digital video watermarking. IEEE Trans. Circuits Syst. Video Technol. 2017, 99, 1. [Google Scholar] [CrossRef]
- Qin, C.; Ji, P.; Wang, J.W.; Chang, C.C. Fragile image watermarking scheme based on VQ index sharing and self-embedding. Multimed. Tools Appl. 2017, 76, 2267–2287. [Google Scholar] [CrossRef]
- Zhou, J.T.; Sun, W.W.; Dong, L.; Liu, X.M.; Au, O.C.; Tang, Y.Y. Secure reversible image data hiding over encrypted domain via key modulation. IEEE Trans. Circuits Syst. Video Tech. 2016, 26, 441–451. [Google Scholar] [CrossRef]
- Wang, C.X.; Zhang, T.; Wan, W.B.; Han, X.Y.; Xu, M.L. A novel STDM watermarking using visual saliency-based JND model. Information 2017, 8, 103. [Google Scholar] [CrossRef]
- Castiglione, A.; Pizzolante, R.; Palmieri, F.; Masucci, B.; Carpentieri, B.; Santis, A.D.; Castiglione, A. On-board format-independent security of functional magnetic resonance images. ACM Trans. Embedded Comput. Syst. 2017, 16, 56–71. [Google Scholar] [CrossRef]
- Castiglione, A.; Santis, A.D.; Pizzolante, R.; Castiglione, A.; Loia, V.; Palmieri, F. On the protection of fMRI images in multi-domain environments. In Proceedings of the 2015 IEEE 29th International Conference on Advanced Information Networking and Applications, Gwangiu, Korea, 25–27 March 2015; pp. 24–27. [Google Scholar]
- Cox, I.J.; Kilian, J.; Leighton, T. Secure spread spectrum watermarking for multimedia. IEEE Trans. Image Process. 1997, 6, 1673–1687. [Google Scholar] [CrossRef] [PubMed]
- Barni, M.; Bartolini, F.; Cappellini, V.; Piva, A.A. DCT-domain system for robust image watermarking. Signal Process. 1998, 66, 357–372. [Google Scholar] [CrossRef]
- Kundur, D.; Hatzinakos, D. Digital watermarking using multiresolution wavelet decomposition. In Proceedings of the International Conference on Acoustic, Speech and Signal Processing, Seattle, WA, USA, 12–15 May 1998; pp. 2969–2972. [Google Scholar]
- Chen, L.H.; Lin, J.J. Mean quantization based image watermarking. Image Vision Comput. 2003, 21, 717–727. [Google Scholar] [CrossRef]
- Watson, A.B.; Yang, G.Y.; Solomon, J.A.; Villasenor, J. Visibility of wavelet quantization noise. IEEE Trans. Image Process. 1997, 6, 1164–1175. [Google Scholar] [CrossRef] [PubMed]
- Chen, B.; Wornell, G.W. Quantization index modulation: A class of provably good methods for digital watermarking and information embedding. IEEE Trans. Inf. Theory 2001, 47, 1423–1443. [Google Scholar] [CrossRef]
- Perez-Gonzalez, F.; Mosquera, C.; Barni, M.; Abrardo, A. Rational Dither Modulation: A high-rate data-hiding method invariant to gain attacks. IEEE Trans. Signal Process. 2005, 53, 3960–3975. [Google Scholar] [CrossRef]
- Li, Q.; Cox, I.J. Using perceptual models to improve fidelity and provide resistance to valumetric scaling for quantization index modulation watermarking. IEEE Trans. Inf. Forensics Secur. 2007, 2, 127–139. [Google Scholar] [CrossRef]
- Kalantari, N.K.; Ahadi, S.M. Logarithmic quantization index modulation for perceptually better data hiding. IEEE Trans. Image Process. 2010, 19, 1504–1518. [Google Scholar] [CrossRef] [PubMed]
- Zareian, M.; Tohidypour, H.R. A novel gain invariant quantization-based watermarking approach. IEEE Trans. Inf. Forensics Secur. 2014, 9, 1804–1813. [Google Scholar] [CrossRef]
- Munib, S.; Khan, A. Robust image watermarking technique using triangular regions and Zernike moments for quantization based embedding. Multimed. Tools Appl. 2017, 76, 8695–8710. [Google Scholar] [CrossRef]
- Chauhan, D.S.; Singh, A.K.; Kumar, B.; Saini, J.P. Quantization based multiple medical information watermarking for secure e-health. Multimed. Tools Appl. 2017, 8, 1–13. [Google Scholar] [CrossRef]
- Dong, P.; Brankov, J.G.; Galatsanos, N.P.; Yang, Y.Y.; Davoine, F. Digital Watermarking robust to geometric distortions. IEEE Trans. Image Process. 2005, 14, 2140–2150. [Google Scholar] [CrossRef] [PubMed]
- Akhaee, M.A.; Sahraeian, S.M.E.; Sankur, B.; Marvasti, F. Robust scaling-based image watermarking using maximum-likelihood decoder with optimum strength factor. IEEE Trans. Multimed. 2009, 11, 822–833. [Google Scholar] [CrossRef]
- Kwitt, R.; Meerwald, P.; Uhl, A. Efficient detection of additive watermarking in the DWT-domain. In Proceedings of the 17th European Signal Processing Conference, Glasgow, UK, 24–28 August 2009; pp. 2072–2076. [Google Scholar]
- Fan, M.Q.; Wang, H.X. Chaos-based discrete fractional Sine transform domain audio watermarking scheme. Comput. Electr. Eng. 2009, 35, 506–516. [Google Scholar] [CrossRef]
- Lyu, W.L.; Chang, C.C.; Nguyen, T.S.; Lin, C.C. Image watermarking scheme based on scale-invariant feature transform. KSII Trans. Internet Inf. Syst. 2014, 8, 3591–3606. [Google Scholar]
- Zhou, G.X.; Zhang, Y.; Mandic, D.P. Group component analysis for multiblock data: Common and individual feature extraction. IEEE Trans. Neural Netw. Learn Syst. 2016, 27, 2426–2439. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Nam, C.S.; Zhou, G.; Jin, J.; Wang, X.; Cichocki, A. Temporally constrained sparse group spatial patterns for motor imagery BCI. IEEE Trans. Cybernet. 2018, 9, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.X.; Zhang, Y.; Cichocki, A.; Matsuno, F. A novel EOG/EEG hybrid human–machine interface adopting eye movements and ERPs: Application to robot control. IEEE Trans. Biomed. Eng. 2015, 62, 876–889. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.Q.; Zhang, Y.; Waytowich, N.R.; Krusienski, D.J.; Zhou, G.X.; Jin, J.; Wang, X.Y.A. Discriminative feature extraction via multivariate linear regression for SSVEP-based BCI. IEEE Trans. Neural Syst. Rehabil. Eng. 2016, 24, 532–541. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Wang, Y.; Zhou, G.X.; Jin, J.; Wang, B.; Wang, X.Y.; Cichocki, A. Multi-kernel extreme learning machine for EEG classification in brain-computer interfaces. Expert Syst. Appl. 2018, 96, 302–310. [Google Scholar] [CrossRef]



| Parameter Name | Configuration |
|---|---|
| Experimental platform | Window 7, MATLAB R2016a |
| Test images | Fingerprint, Lena, Barbara, Crowd, Mandrill, Boat, Mit and Bridge |
| Image size | 512 × 512 |
| Wavelet filters of DWT | biorthogonal CDF 9/7 |
| Watermark length (bits) | 4096 |
| Decomposition level | Three-level |
| Robustness evaluation | Normalized Correlation coefficient |
| Image | Fingerprint | Lena | Barbara | Crowd | Mandrill | Boat | Mit | Bridge |
|---|---|---|---|---|---|---|---|---|
| Time | 10.2095 | 10.4930 | 10.6398 | 9.9376 | 9.8795 | 10.4172 | 10.6883 | 10.5062 |
| Images | Lena | Fingerprint | ||||||
|---|---|---|---|---|---|---|---|---|
| Attacks | [10] | [14] | [23] | Proposed | [10] | [14] | [23] | Proposed |
| Gaussian filtering (3 × 3) | 0.6859 | 0.7024 | 0.7359 | 0.8435 | 0.7231 | 0.7458 | 0.7190 | 0.8729 |
| Median filtering (3 × 3) | 0.6530 | 0.6947 | 0.6728 | 0.7846 | 0.6714 | 0.7256 | 0.6980 | 0.8105 |
| Additive noise ( = 20) | 0.5317 | 0.6848 | 0.6169 | 0.7582 | 0.5734 | 0.7023 | 0.6347 | 0.7664 |
| Histogram equalization | 0.7215 | 0.7649 | 0.7553 | 0.8065 | 0.7403 | 0.7891 | 0.7622 | 0.8458 |
| JPEG (10) | 0.3502 | 0.2617 | 0.2984 | 0.5936 | 0.3278 | 0.2921 | 0.3040 | 0.5983 |
| JPEG (30) | 0.5129 | 0.4562 | 0.4890 | 0.7024 | 0.5343 | 0.4816 | 0.4953 | 0.7191 |
| JPEG 2000 (20) | 0.6749 | 0.3481 | 0.6872 | 0.7658 | 0.6939 | 0.4124 | 0.7009 | 0.7815 |
| JPEG 2000 (50) | 0.7923 | 0.6738 | 0.8155 | 0.8742 | 0.8011 | 0.6934 | 0.8225 | 0.8901 |
| JPEG 2000 (90) | 0.9258 | 0.9016 | 0.9345 | 0.9503 | 0.9312 | 0.9089 | 0.9396 | 0.9647 |
| Brightness adjustment | 0.8033 | 0.6836 | 0.7529 | 0.8734 | 0.8122 | 0.7240 | 0.7659 | 0.8936 |
| Images | Lena | Fingerprint | ||||||
|---|---|---|---|---|---|---|---|---|
| Attacks | [10] | [14] | [23] | Proposed | [10] | [14] | [23] | Proposed |
| Scaling (1/2) | 0.6434 | 0.8627 | 0.8539 | 0.8910 | 0.6513 | 0.8476 | 0.8208 | 0.9025 |
| Scaling (1/4) | 0.5626 | 0.7643 | 0.8027 | 0.8258 | 0.5842 | 0.7719 | 0.7894 | 0.8032 |
| Scaling (1/8) | 0.3015 | 0.5354 | 0.5768 | 0.6524 | 0.3116 | 0.5208 | 0.5833 | 0.6917 |
| Rotation (5°) | 0.7904 | 0.8525 | 0.9182 | 0.9316 | 0.8226 | 0.8734 | 0.9246 | 0.9479 |
| Rotation (10°) | 0.6520 | 0.7938 | 0.8748 | 0.9122 | 0.6419 | 0.7856 | 0.8845 | 0.9065 |
| Rotation (20°) | 0.5939 | 0.6826 | 0.7530 | 0.8124 | 0.6005 | 0.6920 | 0.7652 | 0.8008 |
| Center Cropping (25%) | 0.6413 | 0.6957 | 0.7628 | 0.7835 | 0.6531 | 0.7124 | 0.7785 | 0.7931 |
| JPEG (50) + Scal. (0.9) | 0.6322 | 0.4958 | 0.6559 | 0.7023 | 0.6414 | 0.5170 | 0.6771 | 0.7246 |
| JPEG (30) + Scal. (0.7) | 0.5421 | 0.3982 | 0.5816 | 0.6219 | 0.5526 | 0.3990 | 0.5902 | 0.6334 |
| JPEG 2000 (50) + Scal. (0.8) | 0.6020 | 0.3659 | 0.6428 | 0.6546 | 0.6175 | 0.4032 | 0.6533 | 0.6750 |
| JPEG 2000 (30) + Scal. (0.5) | 0.4521 | 0.3056 | 0.5355 | 0.5769 | 0.4609 | 0.3248 | 0.5580 | 0.5906 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Tu, Q.; Xu, X. Quantization-Based Image Watermarking by Using a Normalization Scheme in the Wavelet Domain. Information 2018, 9, 194. https://doi.org/10.3390/info9080194
Liu J, Tu Q, Xu X. Quantization-Based Image Watermarking by Using a Normalization Scheme in the Wavelet Domain. Information. 2018; 9(8):194. https://doi.org/10.3390/info9080194
Chicago/Turabian StyleLiu, Jinhua, Qiu Tu, and Xinye Xu. 2018. "Quantization-Based Image Watermarking by Using a Normalization Scheme in the Wavelet Domain" Information 9, no. 8: 194. https://doi.org/10.3390/info9080194
APA StyleLiu, J., Tu, Q., & Xu, X. (2018). Quantization-Based Image Watermarking by Using a Normalization Scheme in the Wavelet Domain. Information, 9(8), 194. https://doi.org/10.3390/info9080194





